江苏省徐州市2019年中考数学总复习第三单元函数及其图像第16课时二次函数的应用课件
2019年徐州中考数学专题复习-题型六 二次函数综合题课件

不在坐标轴上的顶点作坐标轴
的垂线
【温馨提示】求四边形的面积时,先判断四边形是否为规则四边形.①规
则四边形直接用面积公式求解;②不规则的四边形用分割法求解.
2. 面积倍数关系:先求出其中一个图形面积,再用含未知数的式子表示
所求图形(另一个图形)的面积,根据两图形间的面积关系,列方程求解;
或用含相同的未知数分别表示两个图形的面积,再用题中等量关系列方程
∵点P与点C不重合,
∴xP≠0.
∴满足条件的点P有3个,坐标分别为(1+ 7 ,3)或(1- 7 ,3)或(2,
-3);
(3)连接BM,CM,求△BCM的面积;
【思维教练】要求△BCM的面积,可将△BCM的面积转化为求两个同底三
角形的面积和.过点M作MN⊥x轴交BC于点N,求得N点坐标,即可求得
面积,而N点坐标通过直线BC解析式可得;
2. 求线段和的最小值或周长最小值时不妨先联想到用“对称性质”,把要求
的某些线段集中在一起,根据“两点之间线段最短”来解决.有以下两种模
型:
(1)一线两点型(如图①)
已知一直线及直线同侧两点,在直线上找一点使其到已知两点的距离的和
最小,通常作其中一点关于直线的对称点,对称点与另一点的连线与直线
的交点即为所求点.
1 2 5 1 ∴MH=- 2 m + 2 m-2- 2 m+2 1 =- 2 m2+2m =- 1 (m-2)2+2, 2
1 2
m2+
5 2
1 m-2),点H坐标为(m,2
m-2),
∴当m=2时,MH有最大值,最大值为2;
(3)设点G是y轴上一点,点D是抛物线的顶点,是否存在点G,使得GD+
GB的值最小;若存在,求出点G的坐标;若不存在,请说明理由;
中考数学总复习 第三单元 函数及其图象 课时16 二次函

(1)求y与x之间的函数关系式,并写出自变量x的取值范围.
(2)若矩形空地的面积为160 m2,求x的值.
(3)若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地
面积如下表),问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理
课前考点过关 考点自查
考点 用二次函数的性质解决实际问题 二次函数的应用关键在于建立二次函数的数学模型,利用二次函数解决实际问题,常见的是根据二次函 数的最值确定最大利润、最优方案等问题.
【疑难典析】在实际问题中,自变量的取值往往受到制约,不要忽视自变量的取值范围,要在其允许的范 围内取值.
课堂互动探究
第三单元 函数及其图像
课时 16 二次函数的实际应用
课前考 1. [2018·衡阳] 一名在校大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为10元/件,已 知销售价不低于成本价,且物价部门规定这种产品的销售价不高于16元/件,市场调查发现,该产品每天的 销售量y(件)与销售价x(元/件)之间的函数关系如图16-1. (1)求y与x之间的函数关系式,并写出自变量x的取值范围. (2)求每天的销售利润W(元)与销售价x(元/件)之间的函数关系式,并求出每件 销售价为多少元时,每天的销售利润最大,最大利润是多少?
A. 10 m B. 15 m
C. 20 m D. 22. 5 m
【答案】B
������ = 54, 【解析】由题意得 400������ + 20������ + ������ = 57.9,
1600������ + 40������ + ������ = 46.2,
2019年中考数学总复习课件:二次函数的图象与性质(共39张PPT)教育精品.ppt

★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
★知识点3 ★考点3
★知识点4 ★考点4
★知识点5
★知识要点导航 ★热点分类解析
★知识点1 ★考点1
★知识点2 ★考点2
(江苏专版)2019年中考数学一轮复习第三章函数及其图象3.4.1二次函数的图象与性质(讲解部分)素材(pdf)
需要根据二次函数的性质确定最值的大小.
若给出函数的自变量的取值范围, 或函数的对称轴不定, 则
例 2㊀ ( 2017 四川乐山, 9, 3 分 ) 已知二次函数 y = x 2 - 2mx ( m 为常数) , 当 - 1ɤ x ɤ2 时, 函数值 y 的最小值为 - 2, 则 m 的 值是 3 A. 2 3 B. 2 C. 或 2 2 2 2 2 解析㊀ y = x -2mx = ( x - m) - m , 3 D.- 或 2 2 (㊀ ㊀ )
b 4ac - b 2 b , ,对称轴是直线 x = - . 2a 4a 2a
)
b 2a
-b ( aʂ0) , ) + 4ac 4a
2 2
A.(1,-5)
( m,- m2 -4) ,ʑ Mᶄ的坐标为 ( - m, m2 + 4) ,ȵ 点 Mᶄ 在抛物线上, ʑ m2 +2m2 -4 = m2 + 4,ʑ m2 = 4. ȵ m > 0,ʑ m = 2,ʑ M ( 2, -8) , 故 选 C. ㊀ ㊀ 变式训练㊀ ( 2018 陕西,10,3 分) 对于抛物线 y = ax 2 +( 2a - 1) x + a -3,当 x = 1 时,y >0,则这条抛物线的顶点一定在 ( ㊀ ㊀ ) A. 第一象限 C. 第三象限 答案㊀ C B. 第二象限 D. 第四象限 答案㊀ C
a <0
(
对称轴方 b ㊀ 2a
b >0,对称轴在 y 轴������ ������㊀ 左侧㊀; ������ a b <0,对称轴在 y 轴������ ������㊀ 右侧㊀ ������ a
程为 x = ������ ������㊀- ������
)
图象
c
决定 抛 物 线 与 y 轴 交点的位置
江苏省徐州市2019年中考数学总复习第三单元函数及其图像第15课时二次函数与一元二次方程及不等式课件

Δ>0
Δ=0
Δ<0
一切实数 无解
无解
课前双基巩固
对点演练
题组一 必会题
1. [2018· 滨州] 如图 15-1,若二次函数 y=ax2+bx+c(a≠0) 图像的对称轴为直线 x=1,与 y 轴交于点 C,与 x 轴交 于点 A,点 B(-1,0).则①二次函数的最大值为 a+b+c;
[答案] B [解析] 由图像可知,当 x=1 时,函数取到最大值, 最大值为:a+b+c,故①正确;因为抛物线经过点 B(-1,0),所以当 x=-1 时,y=a-b+c=0,故②错误;因 为该函数图像与 x 轴有两个交点 A,B,所以 b2-4ac>0,故③错误;因为点 A 与点 B 关于直线 x=1 对称,所以 A(3,0),根据图像可知,当 y>0 时,-1<x<3,故④正确.故选 B.
部分对应值如下表: x … -1 0 y … 10 5 则当 y<5 时,x 的取值范围是 1 2 2 1 . 3 … 2 …
而减小,故抛物线的开口向上,当 x=0 时,y=5,由抛物线的对称性知,当 x=4 时,y=5,则当 y<5 时,0<x<4.
高频考向探究
[方法模型] 根据抛物线的对称性,在表格中找出顶点坐标,再由函数的增减性确定开口方向,然后就能由 y 的范 围确定 x 的范围,或由 x 的范围来确定 y 的范围了.
对称轴为③ y 对称轴在 y 轴左侧 对称轴在 y 轴右侧 经过④ 原点 与 y 轴正半轴相交 与 y 轴负半轴相交
课前双基巩固
(续表)
b2-4ac=0 b2-4ac b2-4ac>0 b2-4ac<0 与 x 轴有唯一交点(顶点) 与 x 轴有两个不同交点 与 x 轴没有交点 当 x=1 时,y=a+b+c 特殊关系 当 x=-1 时,y=a-b+c 若 a+b+c>0,则当 x=1 时,y>0 若 a-b+c>0,则当 x=-1 时,y>0
2019届中考数学复习 第三章 函数 3.4 二次函数课件PPT

陕西考点 解读
考点3 二次函数图像的平移规律
【特别提示】
陕西考点解读
1.抛物线在平移的过程中,a的值不发生变化,变化的只是顶点的位置,且与平移方 2.涉及抛物线的平移时,先将一般式转化为顶点式,即y=a(x-h)2+k的形式。 3.抛物线的平移主要看顶点的平移,抛物线y=ax2的顶点是(0,0),抛物线y=ax2+k的顶 抛物线y=a(x-h)2的顶点是(h,0),抛物线y=a(x-h)2+k的顶点是(h,k)。我们只需在坐标 几个顶点,即可看出平移的方向。 4.抛物线的平移口诀:自变量加减左右移,函数值加减上下移。
陕西考点 解读
陕西考点 解读
【提分必练】
陕西考点解读
1.已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),
有下列结论:①抛物线过原点;② 4a+b+c=0;③a-b+c<0;④抛物线的顶点坐标为
y随x的增大而增大。其中结论正确的是( )
A.①②③
C
解得
∴二4a a次k函k3数,0,的解析式 ak 为 4y。1=,-(x+1)2+4=-x2-2x+3。故选D。
பைடு நூலகம் 陕西考点解 读
5.已知二次函数y有最大值4,且图像与x轴的两交点间的距离是8,对称轴为直
此二次函数的解析式为y=_____________。
- 1 x2 3 x 7 4 24
【解析】∵该函数图像与x轴的两交点间的距离是8,对称轴为直线x=-3,∴
陕西考点解读
【提分必练】
4.若二次函数的部分图像如图,对称轴是直线x=-1,则这个二次函数的解析式为( )
第16课时 二次函数的实际应用 课件 2025年中考数学一轮总复习
上抛出一小球,小球的高度h(m)与
小球的运动时间t(s)之间的关系式是
h=30t-5t2(0≤t≤6).有下列结论:①小球从抛出到落地需要6s;②小球运动中的高度可以是30m;③小球运动2s时的高度小于运动5 s时的
高度.
其中,正确结论的个数是( C )
(2)y=-2x2-16x+3(-1≤x≤2).
[答案] 解:(2)y=-2x2-16x+3=
-2(x+4)2+35.当-1≤x≤2时,y随x的增大而减小,∴当x=-1时,y取最大值17;当x=2时,y取最小值-37.
考点二 利用二次函数模型解决几何面
积问题
例2 (1)如图,在等腰直角三角形
ABC中,∠A=90°,BC=8,点D,
(2)若小球离地面的最大高度为20m,
求小球被发射时的速度;
解:(2)根据题意,得当t= 时,h=20,∴-5× +v0× =20,∴v0=20m/s(负值舍去).
(3)按(2)中的速度发射小球,小球
离地面的高度有两次与实验楼的高度相
同.小明说:“这两次间隔的时间为3s.”已
知实验楼高15 m,请判断他的说法是否
4. (2024·河南)从地面竖直向上发射的
物体离地面的高度h(m)满足关系式h
=-5t2+v0t,其中t(s)是物体运动的
时间,v0(m/s)是物体被发射时的速
度.社团活动时,科学小组在实验楼前从
地面竖直向上发射小球.
(1)小球被发射后 s时离地面的
高度最大(用含v0的式子表示);
∴FO=40m或FO=60m,∵FO<OD,∴FO的长为40m.
1. 用长12m的铝合金条制成矩形窗框
2019年中考数学第三章函数及其图象3.4.1二次函数的图象与性质(讲解部分)素材
b a
>0,对称轴在
y
轴������������ 左侧 ;
) 程为
x
=
������������ -
b 2a
b a
<0,对称轴在
y
轴������������ 右侧
c = 0,抛物线过������������ 原点 ;
决定抛 轴;
交点的位置
c<0,抛物线与 y 轴交于负半轴
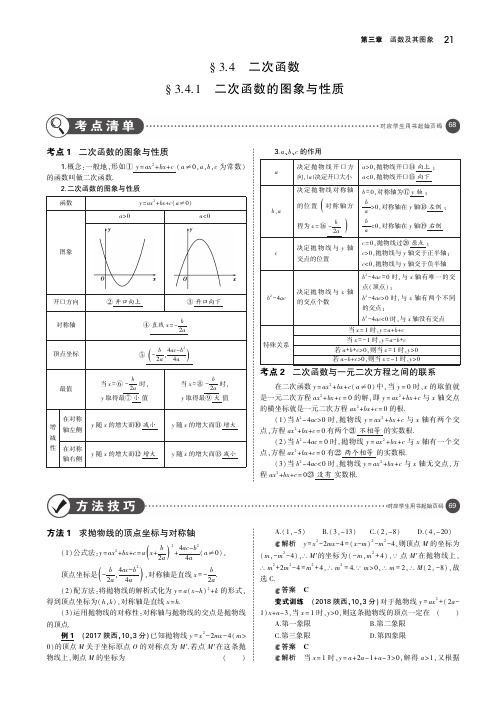
考点 2 二次函数与一元二次方程之间的联系
在二次函数 y = ax2 +bx+c( a≠0) 中,当 y = 0 时,x 的取值就 是一元二次方程 ax2 +bx+c = 0 的解,即 y = ax2 +bx+c 与 x 轴交点 的横坐标就是一元二次方程 ax2 +bx+c = 0 的根.
式:y = a( x-h) 2 +k( a≠0) ,其中顶点坐标为( h,k) ,对称轴为直
线 x = h;
(3)若已知抛物线与 x 轴的交点的坐标,则可设解析式为 y
= a(x-x1) ( x -x2 ) ( a≠0),其中与 x 轴的交点坐标为( x1,0), ( x2 ,0) .
例 3 (2017 广西百色,17,3 分) 经过 A( 4,0) ,B( - 2,0) ,
68
考点 1 二次函数的图象与性质
1.概念:一般地,形如① y = ax2 +bx+c ( a≠0,a,b,c 为常数) 的函数叫做二次函数.
2.二次函数的图象与性质
函数
y = ax2 +bx+c( a≠0)
a>0
a<0
图象
开口方向 对称轴
顶点坐标
② 开口向上
③ 开口向下
④ 直线
x
(2) 在这 30 天内,哪一天的利润是 6 300 元?
【K12教育学习资料】[学习]江苏省徐州市2019年中考数学总复习 第三单元 函数及其图像 课时训练
课时训练(十四)二次函数的图像与性质(限时:30分钟)|夯实基础|1.抛物线y=(x-1)2+2的顶点坐标是()A.(-1,2)B.(―1,―2)C.(1,-2)D.(1,2)2.[2018·无锡滨湖区一模]将抛物线y=x2-4x-3向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为()A.y=(x+1)2-2B.y=(x-5)2-2C.y=(x-5)2-12D.y=(x+1)2-123.[2018·岳阳]在同一直角坐标系中,二次函数y=x2与反比例函数y=(x>0)的图像如图K14-1所示,若两个函数图像上有三个不同的点A(x1,m),B(x2,m),C(x3,m),其中m为常数,令ω=x1+x2+x3,则ω的值为()图K14-1A.1B.mC.m2D.4.[2018·泸州]已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y 的最大值为9,则a的值为()A.1或-2B.-或C.D.15.[2018·菏泽]已知二次函数y=ax2+bx+c的图像如图K14-2所示,则一次函数y=bx+a与反比例函数y=在同一平面直角坐标系中的图像大致是()图K14-2 图K14-36.[2018·白银]如图K14-4是二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图像的一部分,与x轴的交点A在点(2,0)和(3,0)之间,对称轴是直线x=1,关于下列说法:①ab<0,②2a+b=0,③3a+c>0,④a+b≥m(am+b)(m为常数),⑤当-1<x<3时,y>0,其中正确的是()图K14-4A.①②④B.①②⑤C.②③④D.③④⑤7.[2018·广州]已知二次函数y=x2,当x>0时,y随x的增大而(填“增大”或“减小”).8.[2018·淮阴中学开明分校期中]写出一个二次函数,使得它在x=-1时取得最大值2,它的表达式可以为.9.根据图K14-5中的抛物线可以判断:当x 时,y随x的增大而减小;当x= 时,y有最小值.图K14-510.[2018·淄博]已知抛物线y=x2+2x-3与x轴交于A,B两点(点A在点B的左侧),将这条抛物线向右平移m(m>0)个单位,平移后的抛物线与x轴交于C,D两点(点C在点D的左侧).若B,C是线段AD的三等分点,则m的值为. 11.求二次函数y=-2x2-4x+1图像的顶点坐标,并在下列坐标系内画出函数的大致图像.说出此函数的三条性质.图K14-612.如图K14-7,抛物线y=ax2+bx+与直线AB交于点A(-1,0),B4,,点D是抛物线上A,B两点间部分的一个动点(不与点A,B重合),直线CD与y轴平行,交直线AB于点C,连接AD,BD.(1)求抛物线的解析式;(2)设点D的横坐标为m,△ADB的面积为S,求S关于m的函数关系式,并求出当S取最大值时的点C的坐标.图K14-7|拓展提升|13.[2018·陕西]对于抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,则这条抛物线的顶点一定在()A.第一象限B.第二象限C.第三象限D.第四象限14.[2018·安徽]如图K14-8,直线l1,l2都与直线l垂直,垂足分别为M,N,MN=1,正方形ABCD的边长为,对角线AC在直线l上,且点C位于点M处,将正方形ABCD沿l向右平移,直到点A与点N重合为止,记点C平移的距离为x,正方形ABCD的边位于l1,l2之间部分的长度和为y,则y关于x的函数图像大致为 ()图K14-8 图K14-915.如图K14-10,在平面直角坐标系xOy中,A(-3,0),B(0,1),形状相同的抛物线C n(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C2的顶点坐标为;抛物线C8的顶点坐标为.图K14-1016.我们把a,b中较大的数记作max{a,b},若直线y=kx+1与函数y=max{x2+(k-1)x-k,-x2-(k-1)x+k}(k>0)的图像只有两个公共点,则k的取值范围是.17.一次函数y=x的图像如图K14-11所示,它与二次函数y=ax2-4ax+c的图像交于A,B两点(其中点A在点B的左侧),与这个二次函数图像的对称轴交于点C.(1)求点C的坐标.(2)设二次函数图像的顶点为D.①若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的关系式.②若CD=AC,且△ACD的面积等于10,求此二次函数的关系式.图K14-11参考答案1.D2.A3.D[解析] 根据题意可得A,B,C三点中有两个在二次函数图像上,一个在反比例函数图像上,不妨设A,B两点在二次函数图像上,点C在反比例函数图像上,∵二次函数y=x2图像的对称轴是y轴,∴x1+x2=0.∵点C在反比例函数y=(x>0)图像上,∴x3=,∴ω=x1+x2+x3=.故选D.4.D[解析] 原函数可化为y=a(x+1)2+3a2-a+3,对称轴为直线x=-1,当x≥2时,y随x的增大而增大,所以a>0,抛物线开口向上,因为-2≤x≤1时,y的最大值为9,结合对称轴及增减性可得,当x=1时,y=9,代入可得,a1=1,a2=-2,又因为a>0,所以a=1.5.B[解析] ∵抛物线开口向上,∴a>0;∵抛物线对称轴在y轴右侧,∴b<0;∵抛物线与y轴交于正半轴,∴c>0;再由二次函数的图像看出,当x=1时,y=a+b+c<0;∵b<0,a>0,∴一次函数y=bx+a的图像经过第一,二,四象限;∵a+b+c<0,∴反比例函数y=的图像位于第二,第四象限,两个函数图像都满足的是选项B.故选B.6.A[解析] ∵抛物线的开口向下,∴a<0.∵抛物线的对称轴为直线x=1,即x=-=1,∴b=-2a>0,∴ab<0,2a+b=0.∴①②正确.∵当x=-1时,y=a-b+c=3a+c,由对称轴为直线x=1和抛物线过x轴上的A点,A点在(2,0)与(3,0)之间,得抛物线与x轴的另一个交点则在(-1,0)到(0,0)之间,所以当x=-1时,y=3a+c<0.所以③错误.∵当x=1时,y=a+b+c,此点为抛物线的顶点,即抛物线的最高点.当x=m时,y=am2+bm+c=m(am+b)+c,∴此时有:a+b+c≥m(am+b)+c,即a+b≥m(am+b),所以④正确.∵抛物线过x轴上的A点,A点在(2,0)与(3,0)之间,则抛物线与x轴的另一个交点则在(-1,0)到(0,0)之间,由图知,当2<x<3时,有一部分图像位于x轴下方,说明此时y<0,同理,当-1<x<0时,也有一部分图像位于x轴下方,说明此时y<0.所以⑤错误.故选A.7.增大8.y=-(x+1)2+2(答案不唯一)9.<11[解析] 根据图像可知对称轴为直线x=(-1+3)÷2=1,所以当x<1时,y随x的增大而减小;当x=1时,y有最小值.10.2或8[解析] 易求得点A(-3,0),B(1,0),若平移后C在A,B之间且B,C是线段AD的三等分点,则AC=CB,此时C(-1,0),m=2;若平移后C在B点右侧且B,C是线段AD的三等分点,则AB=BC,此时C(5,0),m=8.11.解:∵y=-2x2-4x+1=-2(x+1)2+3,∴抛物线开口向下,对称轴为直线x=-1,顶点坐标为(-1,3),在y=-2x2-4x+1中,令y=0可求得x=-1±,令x=0可得y=1,∴抛物线与x轴的交点坐标为-1+,0和-1-,0,与y轴的交点坐标为(0,1),其图像如图所示,其性质有:①开口向下,②有最大值3,③对称轴为直线x=-1.(答案不唯一)12.解:(1)由题意得解得:∴抛物线的解析式为y=-x2+2x+.(2)设直线AB为:y=kx+n,则有解得∴y=x+.则D m,-m2+2m+,C m,m+,CD=-m2+2m+-m+=-m2+m+2,∴S=(m+1)·CD+(4-m)·CD=×5×CD=×5×-m2+m+2=-m2+m+5.∵-<0,∴当m=时,S有最大值,当m=时,m+=×+=,∴点C,.13.C[解析] ∵抛物线y=ax2+(2a-1)x+a-3,当x=1时,y>0,∴a+2a-1+a-3>0.解得:a>1.∵-=-,==,∴抛物线顶点坐标为:-,,∵a>1,∴-<0,<0,∴该抛物线的顶点一定在第三象限.故选择C.14.A[解析] 这是一道动态问题,需要分段思考,求解关键是先确定函数解析式,再选择图像.其中,在图形运动过程中,确定三种运动状态下的图形形态是重中之重.其中关键是确定图形变化瞬间的静态图形位置,从而得到分界点,然后再思考动态时的情况,确定各种情况下的取值范围,最后求出各部分对应的函数解析式,运用函数的图像、性质分析作答.有时,直接根据各运动状态(如前后图形的对称状态带来函数图像的对称,前后图形面积的增减变化带来函数图像的递增或递减等)就能求解.∵正方形ABCD的边长为,∴AC=2.(1)如图①,当C位于l1,l2之间,0≤x<1时,设CD,BC与l1分别相交于点P,Q,则PC=x,∴y=2x;①(2)如图②,当D位于l1,l2之间,1≤x<2时,②设AD与l1相交于点P,CD与l2相交于点Q,连接BD,作PR⊥BD于R,QS⊥BD于S.设PR=a,则SQ=1-a,DP+DQ=a+(1-a)=,所以y=2;(3)如图③,当A位于l1,l2之间,2≤x≤3时,设AD,AB分别与l2相交于点P,Q,∵AN=3-x,∴AP=(3-x)=3-x, ∴y=6-2x.③综上所述,y关于x的函数图像大致如选项A所示.故选A.15.(3,2)55,[解析] 设直线AB的解析式为y=kx+b,则解得∴直线AB的解析式为y=x+1.∵抛物线C2的顶点的横坐标为3,且顶点在直线AB上,∴抛物线C2的顶点坐标为(3,2).∵对称轴与x轴的交点的横坐标依次为2,3,5,8,13,∴每个数都是前两个数的和,∴抛物线C8的顶点的横坐标为55,∴抛物线C8的顶点坐标为55,.16.0<k<或k>1[解析] ①当k>1时,如图①(图中实线),设直线y=kx+1与x轴的交点C的坐标为-,0,∵<k,∴->-k,∴C在B的右侧,此时,直线y=kx+1与函数y=max{x2+(k-1)x-k,-x2-(k-1)x+k}(k>0)的图像只有两个公共点;②当k=1时,如图②(图中实线),此时,直线y=x+1与函数y=max{x2+(k-1)x-k,-x2-(k-1)x+k}(k>0)的图像有三个公共点,不符合题意;③当0<k<1时,如图③(图中实线),∵0<k<1,∴>k,∴-<-k,当y=kx+1与y=-x2-(k-1)x+k无公共点时,符合要求,∴无解,∴kx+1=-x2-(k-1)x+k无实数根,∴Δ=(2k-1)2-4(1-k)<0,∴(2k+)(2k-)<0,∵2k+>0,∴2k-<0,∴k<,∴0<k<,综上所述:0<k<或k>1.故答案为:0<k<或k>1.17.解:(1)y=ax2-4ax+c=a(x-2)2+c-4a,∴二次函数图像的对称轴为直线x=2.当x=2时,y=×2=,∴C点坐标为2,.(2)①若点D和点C关于x轴对称,则点D坐标为2,-,CD=3.∵△ACD的面积等于3,∴点A到CD的距离为2,∴点A的横坐标为0(点A在点B左侧).∵点A在直线y=x上,∴点A的坐标为(0,0).将点A,点D坐标代入二次函数解析式可求得∴二次函数解析式为y=x2-x.②若CD=AC,如图,设CD=AC=x(x>0).过A点作AH⊥CD于H,则AH=AC=x,S△ACD=×CD×AH=x·x=10.∵x>0,∴x=5.D点坐标为2,或2,-,A点坐标为-2,-.将A-2,-,D2,-代入二次函数y=ax2-4ax+c中可求得∴二次函数解析式为y=x2-x-3,或将A-2,-,D2,代入二次函数y=ax2-4ax+c中,求得∴二次函数解析式为y=-x2+2x+.综上可得,二次函数关系式为:y=x2-x-3或y=-x2+2x+.。
初三数学复习《二次函数》(专题复习)PPT课件
面积问题
面积问题
在二次函数中,可以通过求函数与坐标轴的交点来计算图形的面积。例如,当函数与x轴交于两点时 ,可以计算这两点之间的面积;当函数与y轴交于一点时,可以计算这一点与原点之间的面积。这些 方法在解决实际问题时非常有用,例如在计算利润、产量等方面。
求解方法ቤተ መጻሕፍቲ ባይዱ
求出二次函数与x轴和y轴的交点坐标,然后根据这些坐标计算图形的面积。对于更复杂的问题,可能 需要使用积分或其他数学方法来求解。
05
综合练习与提高
基础练习题
巩固基础 覆盖全面 由浅入深
基础练习题主要针对二次函数的基本概念、性质和公 式进行设计,旨在帮助学生巩固基础知识,提高解题的 准确性和速度。
基础练习题应涵盖二次函数的各个方面,包括开口方 向、顶点坐标、对称轴、与坐标轴的交点等,确保学生 对二次函数有全面的了解。
题目难度应从易到难,逐步引导学生深入理解二次函 数,从简单的计算到复杂的综合题,逐步提高学生的解 题能力。
初三数学复习《二次函数》(专题复习)ppt课 件
目录 Contents
• 二次函数的基本概念 • 二次函数的解析式 • 二次函数的图像与性质 • 二次函数的实际应用 • 综合练习与提高
01
二次函数的基本概念
二次函数的定义
总结词
理解二次函数的定义是掌握其性 质和图像的基础。
详细描述
二次函数是形式为$f(x) = ax^2 + bx + c$的函数,其中$a, b, c$是 常数,且$a neq 0$。这个定义表 明二次函数具有两个变量$x$和 $y$,并且$x$的最高次数为2。
03
二次函数的图像与性质
开口方向
总结词:根据二次项系数a的正负判断开口方向 a>0时,开口向上
