2015年 浙江省衢州市中考数学试卷及答案(word版)
浙江省衢州地区2015届九年级数学下学期阶段检测试题(一) 新人教版
某某省某某地区2015届九年级数学下学期阶段检测试题（一）卷Ⅰ说明：本卷共有1大题，10小题，共30分．一、选择题（本题有10小题，每小题3分，共30分） 1．在实数1322-，-2，，中，最小的是（） A ．3-B ．2-C ．12D ．2 2．下列计算正确的是（）A ．428a a a ⋅=B ．23+a a a =C ．()2362a ba b =D ．2(3)26x y x y --=--3．南海是我国的固有领土，2014年在我国南海某海域探明可燃冰储量约有194亿立方米．194亿用科学记数法表示为（） A ． 1.94×109B ． 0.194×1010C ． 19.4×109D ． 1.94×10104．如图，四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体中有三个的某一种视图都是同一种几何图形，则另一个几何体是（）5．在一个不透明的布袋中装有3个白球和5个红球，它们除了颜色不同外，其余均相同．从中随机摸出一个球，摸到红球的概率是（） A ．15B ．13C ．38D ．586．把不等式组的解集表示在数轴上，下列选项正确的是（）A ．B ．C ．D ．7．如图，在Rt △ACB 中，∠ACB=90°，∠A=25°，D 是AB 上一点．将Rt △ABC 沿CD 折叠，使B 点落在AC 边上的B ′处，则∠ADB ′等于（） A ．25° B ．30° C ．35° D ．40°8．如图，Rt △ABC 中，∠A=90°，AD ⊥BC 于点D ， 若BD ：CD=3：2，则tanB=（）A ．32B ．63C ．62D ．23B'CDA9．如图，已知A 、B 是反比例函数上的两点，BC ∥x 轴，交y 轴于C ，动点P 从坐标原点O 出发，沿O→A→B→C 匀速运动，终点为C ，过运动路线上任意一点P 作PM ⊥x 轴于M ，PN ⊥y 轴于N ，设四边形OMPN 的面积为S ，P 点运动的时间为t ，则S 关于t 的函数图象大致是（） A ．B ．C ．D ．10．已知直线(1)122n y x n n -+=+++（n 为正整数）与坐标轴围成的三角形的面积为S n ，则S 1+S 2+S 3+…+S 2012的值为（） A ．5032015B ．10062015C ．10062014D ．5032014卷Ⅱ说明：本卷共有2大题，14小题，共90分． 二、填空题（本题有6小题，每小题4分，共24分） 11．分解因式：24a a -=．12．扇形的半径为4，圆心角θ为90︒，用这个扇形围成一个圆锥的侧面，所得圆锥的底面半径为． 13．为了解某毕业班学生的睡眠时间情况，小红随机调查了该班15名同学，结果如下表：则这15名同学每天睡眠时间的众数是小时，中位数是小时．14．如图，△ABC 内接于⊙O ，∠BAC=120°，AB=AC ，BD 为⊙O 的直径，AD=6，则DC=．15．如图，以扇形OAB 的顶点O 为原点，半径OB 所在的直线为x 轴，建立平面直角坐标系，点B 的坐标为（2，0），若抛物线y=x 2+k 与扇形OAB 的边界总有两个公共点，则实数k 的取值X 围是． 16．如图，ABCD 中，AB ＞AD ，AE ，BE ，CM ，DM 分别为∠DAB ，∠ABC ，∠BCD ，∠CDA的平分线，AE 与DM 相交于点F ，BE 与CM 相交于点N ，连接EM ．若ABCD 的周长为42cm ，FM=6cm ，EF=8cm ，则EM=cm ，AB=cm ．三、解答题（本题有8小题，第17～19题每题6分，第20，21题每题8分，第22，23题每题10分，第24题12分，共66分.各小题都必须写出解答过程）每天睡眠时间（单位：小时） 78 9 人数24531第16题图第15题第14题图第9题图17．-20112(31)4sin 602⎛⎫----+ ⎪⎝⎭18．先化简，再求值：231839x x ---，其中103x =-． 19．如图，AB 是⊙O 的直径，弦CD ⊥AB 与点E ，点P 在⊙O 上， ∠1=∠C ，（1）求证：CB ∥PD ； （2）若BC=3，sin ∠P=35，求⊙O 的直径．20．如图，在直角坐标系中，矩形OABC 的顶点O 与坐标原点重合，A 、C 分别在坐标轴上，点B 的坐标为（6，3），直线142y x =-+交AB ，BC 分别于点M ，N ，反比例函数y=kx的图象经过点M ，N ．（1）求反比例函数的解析式；（2）若点P 在y 轴上，且△OPM 的面积与四边形BMON 的面积相等，求点P 的坐标．21．2015年体育中考在即，学校体育组对九（1）班50名学生进行了长跑项目的测试，根据测试成绩制作了下面两个统计图。
2015年浙江衢州中考数学真题及解析word完整版
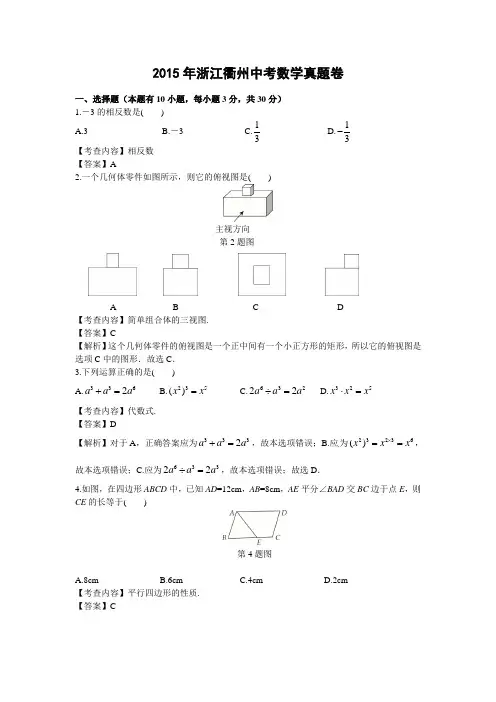
2015年浙江衢州中考数学真题卷一、选择题（本题有10小题，每小题3分，共30分）1.－3的相反数是( )A.3B.－3C.13D.13- 【考查内容】相反数【答案】A2.一个几何体零件如图所示，则它的俯视图是( )主视方向第2题图A B C D【考查内容】简单组合体的三视图.【答案】C【解析】这个几何体零件的俯视图是一个正中间有一个小正方形的矩形，所以它的俯视图是选项C 中的图形．故选C ．3.下列运算正确的是( )A.3362a a a +=B.235()x x =C.63222a a a ÷=D.325x x x ⋅= 【考查内容】代数式.【答案】D【解析】对于A ，正确答案应为3332a a a +=，故本选项错误；B.应为23236()x x x ⨯==，故本选项错误；C.应为63322a a a ÷=，故本选项错误；故选D ．4.如图，在四边形ABCD 中，已知AD =12cm ，AB =8cm ，AE 平分∠BAD 交BC 边于点E ，则CE 的长等于( )第4题图A.8cmB.6cmC.4cmD.2cm【考查内容】平行四边形的性质.【答案】C【解析】因为四边形ABCD是平行四边形，所以BC=AD=12cm，AD∥BC，∠DAE=∠BEA，因为AE平分∠BAD，所以∠BAE=∠DAE，所以∠BEA=∠BAE，故BE=AB=8cm，得CE=BC －BE=4cm；故答案为C．5.某班七个兴趣小组人数分别为4，4，5，x，6，6，7．已知这组数据的平均数是5，则这组数据的中位数是( )A.7B. 6C.5D.4【考查内容】中位数【答案】C【解析】因为某班七个兴趣小组人数分别为4，4，5，x，6，6，7．已知这组数据的平均数是5，所以x=5×7－4－4－5－6－6－7=3，所以这一组数从小到大排列为：3，4，4，5，6，6，7，所以这组数据的中位数是5．故选C．6.下列四个函数图象中，当x＞0时，y随x的增大而减小的是( )A BC D【考查内容】二次函数的图象；一次函数的图象；反比例函数的图象.【答案】B【解析】当x＞0时，y随x的增大而减小的是B，故选B.7.数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a．小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是( )第7题图A.勾股定理B.直径所对的圆心角是直角C.勾股定理的逆定理2015年浙江衢州中考数学真题卷第3页，共12页D. 90°的圆周角所对的弦是直径 【考查内容】作图，勾股定理的逆定理，圆周角定理【答案】B【解析】由作图痕迹可以看出O 为AB 的中点，以O 为圆心，AB 为半径作圆，然后以B 为圆心BC =a 为半径花弧与圆O 交于一点C ，故∠ACB 是直径所对的圆周角，所以这种作法中判断∠ACB 是直角的依据是：直径所对的圆心角是直角．故选：B ．8.如图，已知某广场菱形花坛ABCD 的周长是24米，∠BAD =60°，则花坛对角线AC 的长等于()第8题图A. B.6米C. D.3米【考查内容】菱形的性质.【答案】A【解析】四边形ABCD 为菱形，所以AC ⊥BD ，OA =OC ，OB =OD ，AB =BC =CD =AD =24÷4=6（米），又∠BAD =60°，从而△ABD 为等边三角形，所以BD =AB =6米，OD =OB =3米， 在Rt △AOB 中，据勾股定理得：OA=AC =2OA=A ．9.如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60 cm 长的绑绳EF ，5tan 2α=，则“人字梯”的顶端离地面的高度AD 是( )第9题图A. 144 cmB. 180 cmC. 240 cmD. 360 cm【考查内容】解直角三角形的应用.【答案】B【解析】如图根据题意可知：△AFO ∽△ABD ，OF =12EF =30cm ，,OF AF DC AC∴= 30 2.56DC ∴=∴CD =72cm ，tan α=52AD DC =,AD =572180cm 2⨯=.故选B ． 10.如图，已知△ABC ，AB=BC ，以AB 为直径的圆交AC 于点D ，过点D 的⊙O 的切线交BC 于点E ．若CD =5，CE =4，则⊙O 的半径是( )第10题图A. 3B. 4C.256 D. 258【考查内容】切线的性质.【答案】D第10题图【解析】如图，连接OD 、BD ，DE ⊥BC ，CD =5，CE =4，∴DE =3，AB 是⊙O 的直径，∴∠ADB =90°，BCD S =△22BD CD BC DE ⋅÷=⋅÷，∴5BD =3BC ∴35BD BC = 222BD CD BC +=，∴2223()55BC BC +=，解得BC =254，AB =BC ，∴AB =254，∴⊙O 的半径是；2525248÷=.故选D ． 二、填空题（本题有6小题，每小题4分，共24分）11.(4分）从小明、小聪、小惠和小颖四人中随机选取1人参加学校组织的敬老活动，则小明被选中的概率是 ．【考查内容】概率公式 【答案】14【解析】因为小明、小聪、小惠和小颖四人中随机选取1人参加学校组织的敬老活动， 所以小明被选中的概率是14，故答案为14． 12.(4分）如图，小聪与小慧玩跷跷板，跷跷板支架高EF 为0.6米，E 是AB 的中点，那么小聪能将小慧翘起的最大高度BC 等于 米．2015年浙江衢州中考数学真题卷第5页，共12页第12题图【考查内容】三角形中位线定理【答案】1.2【解析】因为EF ⊥AC ，BC ⊥AC ，所以EF ∥BC ，因为E 是AB 的中点，所以F 为AC 的中点，所以BC =2EF ，因为EF =0.6米，所以BC =1.2米，故答案为：1.2．13.(4分）写出一个解集为x ＞1的一元一次不等式____．【考查内容】不等式的解集【答案】x －1＞0【解析】移项，得x －1＞0（答案不唯一）．14.(4分）一条排水管的截面如图所示，已知排水管的半径OA =1m ，水面宽AB =1.2m ，某天下雨后，水管水面上升了0.2m ，则此时排水管水面宽CD 等于 m ．第14题图【考查内容】垂径定理的应用；勾股定理【答案】1.6【解析】因为AB =1.2m ，OE ⊥AB ，OA =1m ，所以AE =0.8m ，因为水管水面上升了0.2m ， 所以AF =0.8﹣0.2=0.6m ，所以CF0.8==m ，所以CD =1.6m ．15.(4分）已知，正六边形ABCDEF 在直角坐标系内的位置如图所示，A (2,0)-，点B 在原点，把正六边形ABCDEF 沿x 轴正半轴作无滑动的连续翻转，每次翻转60°，经过2015次翻转之后，点B 的坐标是_____________．第15题图【考查内容】坐标与图形变化，旋转【答案】（4031．【解析】因为正六边形ABCDEF 沿x 轴正半轴作无滑动的连续翻转，每次翻转60°，所以每6次翻转为一个循环组循环，因为2015÷6=335余5，所以经过2015次翻转为第336循环组的第5次翻转.点B 在开始时点C 的位置，因为A (2,0-)，所以AB =2，所以翻转前进的距离=2×2015=4030，如图，过点B 作BG ⊥x 于G ，则∠BAG =60°，所以，AG=2×12=1，BG OG =4030+1=4031，所以，点B 的坐标为（4031．故答案为(4031．16.(4分）如图，已知直线334y x =-+分别交x 轴、y 轴于点A 、B ，P 是抛物线21252y x x =-++的一个动点，其横坐标为a ，过点P 且平行于y 轴的直线交直线334y x =-+于点Q ，则当PQ =BQ 时，a 的值是 ．第16题图【考查内容】二次函数综合题【答案】－1，4，4＋4－【解析】设点P 的坐标为21(,25)2a a a -++则点Q 为3(,3)4a a -+，点B 为（0，3），当点P 在点Q 上方时，BQ 54a =，PQ =21325(3)24a a a -++--+ 2111224a a =-++，因为PQ =BQ ，所以251112424a a a =-++整理得2340a a --=解得1,4a a =-=，当点P 在点Q 下方BQ 54a =PQ =2313(25)42a a a -+--++ 2111224a a =--，因为PQ =BQ ，所以251112424a a a =--，整理得：2840a a --=解得：4a =+4a =-a 的值为：－1，4，4＋4－答案为－1，4，4＋4－2015年浙江衢州中考数学真题卷第7页，共12页三、解答题（本题有8小题，第17-19小题每小题6分，第20-21小题每小题6分，第22-23小题每小题6分，第24小题12分，共66分。
资料：年浙江衢州中考数学试卷及答案(word版)
浙江省2014年初中毕业生学业考试（衢州卷）数 学 试 题 卷满分为120分，考试时间为120分钟参考公式：二次函数)0(2≠++=a c bx ax y 图象的顶点坐标是（a b 2-，ab ac 442-）；一组数据1x ，2x ，3x ，…，n x 的方差：])()()()[(122322212x x x x x x x x nS n -++-+-+-=（其中x 是这组数据的平均数）。
一、选择题（本题有10小题，每小题3分，共30分） 1. 在数32，1，-3，0中，最大的数．．．．是 A.32B. 1C. -3D. 0 2. 下列四个几何体中，主视图为圆的是3. 下列式子运算正确的是A. 628a a a =÷ B. 532a a a =+C. 1)1(22+=+a a D. 12322=-a a4. 如图，直线a ∥b ，AC ⊥AB ，AC 交直线b 于点C ，∠1=60°，则∠2的度数是A. 50°B. 45°C. 35°D. 30°5. 如图，河坝横断面迎水坡AB 的坡比是3:1（坡比是坡面的铅直高度BC 与水平宽度AC 之比），坝高BC=3m ，则坡面AB 的长度是A. 9mB. 6mC. 36mD. 33m6. 某地区5月3日至5月9日这7天的日气温最高值统计图如图所示。
从统计图看，该地区这7天日气温最高值的众数与中位数分别是A. 23，25B. 24，23C. 23，23D. 23，247. 如图，小红在作线段AB 的垂直平分线时，是这样操作的：分别以点A ，B 为圆心，大于线段AB 长度一半的长为半径画弧，相交于点C ，D ，则直线CD 即为所求。
连结AC ，BC ，AD ，BD ，根据她的作图方法可知，四边形ADBC 一定是．．． A. 矩形 B. 菱形 C. 正方形 D. 等腰梯形8. 在同一平面直角坐标系内，将函数3422-+=x x y 的图象向右平移2个单位，再向下平移1个单位得到图象的顶点坐标是A.（-3，-6）B. （1，-4）C. （1，-6）D. （-3，-4） 9. 如图，半径为5的⊙A 中，弦BC ，ED 所对的圆心角分别是∠BAC ，∠EAD 。
中考数学——2015浙江中考汇编
2015年浙江省中考试卷汇编浙江省杭州市2015年中考数学试卷 (2)浙江省湖州市2015年中考数学试卷 ................................................................................................ 错误!未定义书签。
浙江省湖州市2015年中考数学试卷 ................................................................................................ 错误!未定义书签。
浙江省金华市2015年中考数学试卷 ................................................................................................ 错误!未定义书签。
浙江省金华市2015年中考数学试卷 ................................................................................................ 错误!未定义书签。
浙江省宁波市2015年中考数学试卷 ................................................................................................ 错误!未定义书签。
浙江省衢州市2015年中考数学试卷 ................................................................................................ 错误!未定义书签。
浙江省绍兴市2015年中考数学试卷 ................................................................................................ 错误!未定义书签。
2015年浙江省衢州市中考一模数学试卷(解析版)
2015年浙江省衢州市中考数学一模试卷一、选择题（本题有10小题，每小题3分，共30分）1．（3分）在实数﹣，﹣2，，中，最小的是（）A．﹣B．﹣2C．D．2．（3分）下列计算正确的是（）A．a4•a2＝a8B．a+a2＝a3C．（a3b）2＝a6b2D．﹣2（x﹣3y）＝﹣2x﹣6y3．（3分）南海是我国的固有领土，2014年在我国南海某海域探明可燃冰储量约有194亿立方米．194亿用科学记数法表示为（）A．1.94×109B．0.194×1010C．19.4×109D．1.94×1010 4．（3分）如图，四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体中有三个的某一种视图都是同一种几何图形，则另一个几何体是（）A．长方体B．圆柱体C．球体D．三棱柱5．（3分）在一个不透明的布袋中装有3个白球和5个红球，它们除了颜色不同外，其余均相同．从中随机摸出一个球，摸到红球的概率是（）A．B．C．D．6．（3分）把不等式组的解集表示在数轴上，下列选项正确的是（）A．B．C．D．7．（3分）如图，在Rt△ACB中，∠ACB＝90°，∠A＝25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（）A．25°B．30°C．35°D．40°8．（3分）如图，Rt△ABC中，∠A＝90°，AD⊥BC于点D，若BD：CD＝3：2，则tan B＝（）A．B．C．D．9．（3分）如图，已知A、B是反比例函数上的两点，BC∥x 轴，交y轴于C，动点P从坐标原点O出发，沿O→A→B→C匀速运动，终点为C，过运动路线上任意一点P作PM⊥x轴于M，PN⊥y轴于N，设四边形OMPN的面积为S，P点运动的时间为t，则S关于t的函数图象大致是（）A．B．C．D．10．（3分）已知直线y＝x+（n为正整数）与坐标轴围成的三角形的面积为S n，则S1+S2+S3+…+S2012的值为（）A ． B． C ． D ．二、填空题（本题有6小题，每小题4分，共24分）11．（4分）分解因式：a 2﹣4a ＝ ．12．（4分）扇形的半径为4，圆心角θ为90°，用这个扇形围成一个圆锥的侧面，所得圆锥的底面半径为 ．13．（4分）为了解某毕业班学生的睡眠时间情况，小红随机调查了该班15名同学，结果如表，则这15名同学每天睡眠时间的众数是 小时，中位数是 小时．14．（4分）如图，△ABC 内接于⊙O ，∠BAC ＝120°，AB ＝AC ，BD 为⊙O 的直径，AD ＝6，则DC ＝ ．15．（4分）如图，以扇形OAB 的顶点O 为原点，半径OB 所在的直线为x 轴，建立平面直角坐标系，点B 的坐标为（2，0），若抛物线y ＝x 2+k 与扇形OAB 的边界总有两个公共点，则实数k 的取值范围是 ．16．（4分）如图，▱ABCD 中，AB ＞AD ，AE ，BE ，CM ，DM 分别为∠DAB ，∠ABC ，∠BCD ，∠CDA 的平分线，AE 与DM 相交于点F ，BE 与CM 相交于点N ，连接EM ．若▱ABCD 的周长为42cm ，FM ＝6cm ，EF ＝8cm ，则EM ＝cm，AB＝cm．三、解答题（本题有8小题，第17～19题每题6分，第20，21题每题8分，第22，23题每题10分，第24题12分，共66分.各小题都必须写出解答过程）17．（6分）（﹣）﹣2﹣﹣（﹣1）0+4sin60°．18．（6分）先化简，再求值：，其中．19．（6分）如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1＝∠C，（1）求证：CB∥PD；（2）若BC＝3，sin∠P＝，求⊙O的直径．20．（8分）如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（6，3），直线y＝﹣x+4交AB，BC分别于点M，N，反比例函数y＝的图象经过点M，N．（1）求反比例函数的解析式；（2）若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P 的坐标．21．（8分）2015年体育中考在即，学校体育组对九（1）班50名学生进行了长跑项目的测试，根据测试成绩制作了如图两个统计图．根据统计图解答下列问题：（1）本次测试的学生中，得4分的学生有多少人？（2）本次测试的平均分是多少？（3）通过一段时间的训练，体育组对该班学生的长跑项目进行第二次测试，测得成绩的最低分为3分，且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中，得4分、5分的学生分别有多少人？22．（10分）3月15日是国际消费者权益日．某品牌专卖店准备出售甲、乙两种服装．其中甲、乙两种服装的进价和售价如表：已知：专卖店用3000元购进甲种服装的数量与用2400元购进乙种服装的数量相同．（1）求m的值；（2）要使购进的甲、乙两种服装共200件的总利润（利润＝售价﹣进价）不少于21700元，且甲种服装的件数不超过总件数的一半，问该专卖店有几种进货方案？（3）在（2）的条件下，专卖店准备对甲种服装进行优惠促销活动，决定对甲种服装每件优惠a（50＜a＜70）元出售，乙种服装价格不变．那么该专卖店要获得最大利润应如何进货？23．（10分）请利用两个直角三角形完成以下两个探究问题：探究一：如图①，在等腰直角△ABC中，点D是斜边BC上的中点，点E为AB 边上的一点，连接DE，过D点作DE的垂线交AC于点F，连接AD，EF．求证：△AED≌△CDF；探究二：如图②，将△DEF的顶点D放在Rt△ABC斜边BC的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连接MN．已知∠B＝45°，BC＝3，在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由．24．（12分）已知：如图，直线y＝x+与x轴、y轴分别交于A、B两点，动点D从A点出发向O点运动（运动到O点停止），过D作DE∥AB交y轴于点E；对称轴过点A且顶点为M的抛物线y＝a（x﹣k）2+h（a＜0）始终经过点E，过E作EG∥OA交抛物线于点G，交AB于点F，连结DE、DF、AE、BG．设D的运动速度是1个单位长度/秒，运动时间为t秒．（1）用含t代数式分别表示EF、BE、AF的长；（2）在整个运动过程中是否存在点D，使AE∥BG？若存在，求出t的值，并判断此时四边形ADEF的形状且说明理由；若不存在，请说明理由；（3）当△ADF是直角三角形，且抛物线的顶点M恰好在BG上时，求抛物线的解析式．2015年浙江省衢州市中考数学一模试卷参考答案与试题解析一、选择题（本题有10小题，每小题3分，共30分）1．（3分）在实数﹣，﹣2，，中，最小的是（）A．﹣B．﹣2C．D．【解答】解：正数有：；负数：，﹣2，∵，∴，∴最小的数是﹣2，故选：B．2．（3分）下列计算正确的是（）A．a4•a2＝a8B．a+a2＝a3C．（a3b）2＝a6b2D．﹣2（x﹣3y）＝﹣2x﹣6y【解答】解：A、a4•a2＝a6，故此选项错误；B、a+a2，无法计算，故此选项错误；C、（a3b）2＝a6b2，正确；D、﹣2（x﹣3y）＝﹣2x+6y，故此选项错误；故选：C．3．（3分）南海是我国的固有领土，2014年在我国南海某海域探明可燃冰储量约有194亿立方米．194亿用科学记数法表示为（）A．1.94×109B．0.194×1010C．19.4×109D．1.94×1010【解答】解：将194亿用科学记数法表示为1.94×1010．故选：D．4．（3分）如图，四个几何体分别为长方体、圆柱体、球体和三棱柱，这四个几何体中有三个的某一种视图都是同一种几何图形，则另一个几何体是（）A．长方体B．圆柱体C．球体D．三棱柱【解答】解：长方体、圆柱体、三棱体为柱体，它们的主视图都是矩形；球的三种视图都是圆形．故选：C．5．（3分）在一个不透明的布袋中装有3个白球和5个红球，它们除了颜色不同外，其余均相同．从中随机摸出一个球，摸到红球的概率是（）A．B．C．D．【解答】解：根据题意可得：一个不透明的袋中装有除颜色外其余均相同的3个白球和5个红球，共5个，从中随机摸出一个，则摸到红球的概率是＝．故选：D．6．（3分）把不等式组的解集表示在数轴上，下列选项正确的是（）A．B．C．D．【解答】解：由第一个不等式得：x＞﹣1；由x+2≤3得：x≤1．∴不等式组的解集为﹣1＜x≤1．故选：B．7．（3分）如图，在Rt△ACB中，∠ACB＝90°，∠A＝25°，D是AB上一点．将Rt△ABC沿CD折叠，使B点落在AC边上的B′处，则∠ADB′等于（）A．25°B．30°C．35°D．40°【解答】解：∵在Rt△ACB中，∠ACB＝90°，∠A＝25°，∴∠B＝90°﹣25°＝65°，∵△CDB′由△CDB反折而成，∴∠CB′D＝∠B＝65°，∵∠CB′D是△AB′D的外角，∴∠ADB′＝∠CB′D﹣∠A＝65°﹣25°＝40°．故选：D．8．（3分）如图，Rt△ABC中，∠A＝90°，AD⊥BC于点D，若BD：CD＝3：2，则tan B＝（）A．B．C．D．【解答】解：在Rt△ABC中，∵AD⊥BC于点D，∴∠ADB＝∠CDA，∵∠B+∠BAD＝90°，∠BAD+∠DAC＝90°，∴∠B＝∠DAC，∴△ABD∽△CAD，∴＝，∵BD：CD＝3：2，设BD＝3x，CD＝2x，∴AD＝＝x，则tan B＝＝＝．故选：D．9．（3分）如图，已知A、B是反比例函数上的两点，BC∥x 轴，交y轴于C，动点P从坐标原点O出发，沿O→A→B→C匀速运动，终点为C，过运动路线上任意一点P作PM⊥x轴于M，PN⊥y轴于N，设四边形OMPN的面积为S，P点运动的时间为t，则S关于t的函数图象大致是（）A．B．C．D．【解答】解：①点P在AB上运动时，此时四边形OMPN的面积S＝K，保持不变，故排除B、D；②点P在BC上运动时，设路线O→A→B→C的总路程为l，点P的速度为a，则S＝OC×CP＝OC×（l﹣at），因为l，OC，a均是常数，所以S与t成一次函数关系．故排除C．故选：A．10．（3分）已知直线y＝x+（n为正整数）与坐标轴围成的三角形的面积为S n，则S1+S2+S3+…+S2012的值为（）A ．B．C ．D ．【解答】解：令x＝0，则y ＝，令y＝0，则x+＝0，解得x ＝，所以，S n ＝••＝（﹣），所以，S1+S2+S3+…+S2012＝（﹣+﹣+﹣+…+﹣）＝（﹣）＝．故选：D．二、填空题（本题有6小题，每小题4分，共24分）11．（4分）分解因式：a2﹣4a＝a（a﹣4）．【解答】解：a2﹣4a＝a（a﹣4）．故答案为：a（a﹣4）．12．（4分）扇形的半径为4，圆心角θ为90°，用这个扇形围成一个圆锥的侧面，所得圆锥的底面半径为1．【解答】解：∵扇形的弧长＝＝2π，∴圆锥的底面半径为2π÷2π＝1．故答案为：1．13．（4分）为了解某毕业班学生的睡眠时间情况，小红随机调查了该班15名同学，结果如表，则这15名同学每天睡眠时间的众数是8小时，中位数是8小时．【解答】解：睡眠时间出现的次数最多的是8小时，因而众数是8小时；15个数据大小处于中间位置的是第8位，是8小时，因而中位数是8小时．故答案是：8；8．14．（4分）如图，△ABC内接于⊙O，∠BAC＝120°，AB＝AC，BD为⊙O的直径，AD＝6，则DC＝2．【解答】解：∵BD为⊙O的直径，∴∠BAD＝∠BCD＝90°，∵∠BAC＝120°，∴∠CAD＝120°﹣90°＝30°，∴∠CBD＝∠CAD＝30°，又∵∠BAC＝120°，∴∠BDC＝180°﹣∠BAC＝180°﹣120°＝60°，∵AB＝AC，∴∠ADB＝∠ADC，∴∠ADB＝∠BDC＝×60°＝30°，∵AD＝6，∴在Rt△ABD中，BD＝AD÷sin60°＝6÷＝4，在Rt△BCD中，DC＝BD＝×4＝2．故答案为：2．15．（4分）如图，以扇形OAB的顶点O为原点，半径OB所在的直线为x轴，建立平面直角坐标系，点B的坐标为（2，0），若抛物线y＝x2+k与扇形OAB 的边界总有两个公共点，则实数k的取值范围是﹣2＜k＜．【解答】解：由图可知，∠AOB＝45°，∴直线OA的解析式为y＝x，联立消掉y得，x2﹣2x+2k＝0，△＝b2﹣4ac＝（﹣2）2﹣4×1×2k＝0，即k＝时，抛物线与OA有一个交点，此交点的横坐标为1，∵点B的坐标为（2，0），∴OA＝2，∴点A的坐标为（，），∴交点在线段AO上；当抛物线经过点B（2，0）时，×4+k＝0，解得k＝﹣2，∴要使抛物线y＝x2+k与扇形OAB的边界总有两个公共点，实数k的取值范围是﹣2＜k＜．故答案为：﹣2＜k＜．16．（4分）如图，▱ABCD中，AB＞AD，AE，BE，CM，DM分别为∠DAB，∠ABC，∠BCD，∠CDA的平分线，AE与DM相交于点F，BE与CM相交于点N，连接EM．若▱ABCD的周长为42cm，FM＝6cm，EF＝8cm，则EM＝10cm，AB＝15.5cm．【解答】解：∵AE为∠DAB的平分线，∴∠DAE＝∠EAB＝∠DAB，同理：∠ABE＝∠CBE＝∠ABC，∠BCM＝∠DCM＝∠BCD，∠CDM＝∠ADM＝∠ADC．∵四边形ABCD是平行四边形，∴∠DAB＝∠BCD，∠ABC＝∠ADC，AD＝BC．∴∠DAF＝∠BCN，∠ADF＝∠CBN．在△ADF和△CBN中，∴△ADF≌△CBN（ASA）．∴DF＝BN．∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAB+∠ABC＝180°．∴∠EAB+∠EBA＝90°．∴∠AEB＝90°．同理可得：∠AFD＝∠DMC＝90°．∴∠EFM＝90°．∵FM＝6，EF＝8，∴ME＝＝10（cm）．∵∠EFM＝∠FMN＝∠FEN＝90°．∴四边形EFMN是矩形．∴EN＝FM＝6．∵∠DAF＝∠EAB，∠AFD＝∠AEB，∴△AFD∽△AEB．∴＝．∴＝．∴8DF＝6AF．设DF＝6k，则AF＝8k．∵∠AFD＝90°，∴AD＝10k．∵∠AEB＝90°，AE＝8（k+1），BE＝6（k+1），∴AB＝10（k+1）．∵2（AB+AD）＝42，∴AB+AD＝21．∴10（k+1）+10k＝21．∴k＝0.55．∴AB＝15.5（cm）．故答案为：10；15.5．三、解答题（本题有8小题，第17～19题每题6分，第20，21题每题8分，第22，23题每题10分，第24题12分，共66分.各小题都必须写出解答过程）17．（6分）（﹣）﹣2﹣﹣（﹣1）0+4sin60°．【解答】解：原式＝4﹣2﹣1+4×＝4﹣2﹣1+2＝3．18．（6分）先化简，再求值：，其中．【解答】解：原式＝﹣＝＝＝，当x＝﹣3时，原式＝＝＝．19．（6分）如图，AB是⊙O的直径，弦CD⊥AB与点E，点P在⊙O上，∠1＝∠C，（1）求证：CB∥PD；（2）若BC＝3，sin∠P＝，求⊙O的直径．【解答】（1）证明：∵∠C＝∠P又∵∠1＝∠C∴∠1＝∠P∴CB∥PD；（2）解：连接AC∵AB为⊙O的直径，∴∠ACB＝90°又∵CD⊥AB，∴＝，∴∠P＝∠CAB，又∵sin∠P＝，∴sin∠CAB＝，即＝，又知，BC＝3，∴AB＝5，∴直径为5．20．（8分）如图，在直角坐标系中，矩形OABC的顶点O与坐标原点重合，A、C分别在坐标轴上，点B的坐标为（6，3），直线y＝﹣x+4交AB，BC分别于点M，N，反比例函数y＝的图象经过点M，N．（1）求反比例函数的解析式；（2）若点P在y轴上，且△OPM的面积与四边形BMON的面积相等，求点P 的坐标．【解答】解：（1）∵B（6，3），四边形OABC是矩形，∴OA＝BC＝3，将y＝3代入y＝﹣x+4得：x＝2，∴M（2，3），把M的坐标代入y＝得：k＝6，∴反比例函数的解析式是y＝；（2）∵S四边形BMON ＝S矩形OABC﹣S△AOM﹣S△CON＝6×3﹣6＝12，由题意得：OP×AM＝12，∵AM＝2，∴OP＝12，∴点P的坐标是（0，12）或（0，﹣12）．21．（8分）2015年体育中考在即，学校体育组对九（1）班50名学生进行了长跑项目的测试，根据测试成绩制作了如图两个统计图．根据统计图解答下列问题：（1）本次测试的学生中，得4分的学生有多少人？（2）本次测试的平均分是多少？（3）通过一段时间的训练，体育组对该班学生的长跑项目进行第二次测试，测得成绩的最低分为3分，且得4分和5分的人数共有45人，平均分比第一次提高了0.8分，问第二次测试中，得4分、5分的学生分别有多少人？【解答】解：（1）得4分的学生有50×50%＝25（人）；（2）本次测试的平均分是：＝3.7（分）；（3）设第二次测试中得4分的学生有x人，得5分的学生有y人，由题意，得，解得：．答：第二次测试中得4分的学生有15人，得5分的学生有30．22．（10分）3月15日是国际消费者权益日．某品牌专卖店准备出售甲、乙两种服装．其中甲、乙两种服装的进价和售价如表：已知：专卖店用3000元购进甲种服装的数量与用2400元购进乙种服装的数量相同．（1）求m的值；（2）要使购进的甲、乙两种服装共200件的总利润（利润＝售价﹣进价）不少于21700元，且甲种服装的件数不超过总件数的一半，问该专卖店有几种进货方案？（3）在（2）的条件下，专卖店准备对甲种服装进行优惠促销活动，决定对甲种服装每件优惠a（50＜a＜70）元出售，乙种服装价格不变．那么该专卖店要获得最大利润应如何进货？【解答】解：（1）依题意得，，整理得，3000（m﹣20）＝2400m，解得m＝100经检验，m＝100是原分式方程的解，所以，m＝100；（2）设购进甲种服装x件，则乙种服装（200﹣x）件，根据题意得，（240﹣100）x+（160﹣80）（200﹣x）≥21700解不等式得，x≥95，∵x≤100，所以95≤x≤100∵x是正整数，100﹣95+1＝6，∴共有6种方案；（3）设总利润为W，则W＝（140﹣a）x+80（200﹣x）＝（60﹣a）x+16000（95≤x≤100），①当50＜a＜60时，60﹣a＞0，W随x的增大而增大，所以，当x＝100时，W有最大值，即此时应购进甲种服装100件，购进乙种服装100件；②当a＝60时，60﹣a＝0，W＝16000，（2）中所有方案获利都一样；③当60＜a＜70时，60﹣a＜0，W随x的增大而减小，所以，当x＝95时，W有最大值，即此时应购进甲种服装95件，购进乙种服装105件．23．（10分）请利用两个直角三角形完成以下两个探究问题：探究一：如图①，在等腰直角△ABC中，点D是斜边BC上的中点，点E为AB 边上的一点，连接DE，过D点作DE的垂线交AC于点F，连接AD，EF．求证：△AED≌△CDF；探究二：如图②，将△DEF的顶点D放在Rt△ABC斜边BC的中点处，并以点D为旋转中心旋转△DEF，使△DEF的两直角边与△ABC的两直角边分别交于M、N两点，连接MN．已知∠B＝45°，BC＝3，在旋转△DEF的过程中，△AMN的周长是否存在有最小值？若存在，求出它的最小值；若不存在，请说明理由．【解答】探究一：证明：∵在等腰直角△ABC中，∴∠C＝45°，∠BAC＝90°，又∵点D为AB上的中点，∴∠DAE＝∠C＝45°，AD＝DC，AD⊥BC，∴∠ADF+∠FDC＝90°，∵∠EDF＝90°，∴∠ADF+∠ADE＝90°，∴∠FDC＝∠ADE，在△AED与△CDF中，，∴△AED≌△CDF；探究二：△AMN的周长存在有最小值．如答图3所示，连接AD，∵△ABC为等腰直角三角形，点D为斜边BC的中点，∴AD＝CD，∠C＝∠MAD＝45°，∵∠EDF＝90°，∠ADC＝90°，∴∠MDA＝∠NDC，∵在△AMD与△CND中，，∴△AMD≌△CND（ASA），∴AM＝CN，DM＝DN．∴AM+AN＝AC．则△AMN的周长等于MN+AC．所以当MN取最小值时，△AMN的周长存在最小值．由DM＝DN，∠EDF＝90°可知△DMN是等腰直角三角形，所以MN＝DN．当DN⊥AC时，DN取得最小值，则MN取得最小值．在等腰直角△ABC中，AC＝BC．在等腰直角△ADC中，当DN⊥AC时，DN＝AC＝BC．此时MN＝DN ＝BC．所以△AMN的周长最小值为：BC+BC＝．24．（12分）已知：如图，直线y＝x+与x轴、y轴分别交于A、B两点，动点D从A点出发向O点运动（运动到O点停止），过D作DE∥AB交y轴于点E；对称轴过点A且顶点为M的抛物线y＝a（x﹣k）2+h（a＜0）始终经过点E，过E作EG∥OA交抛物线于点G，交AB于点F，连结DE、DF、AE、BG．设D的运动速度是1个单位长度/秒，运动时间为t秒．（1）用含t代数式分别表示EF、BE、AF的长；（2）在整个运动过程中是否存在点D，使AE∥BG？若存在，求出t的值，并判断此时四边形ADEF的形状且说明理由；若不存在，请说明理由；（3）当△ADF是直角三角形，且抛物线的顶点M恰好在BG上时，求抛物线的解析式．【解答】解：（1）在直线解析式y＝x+中，令x＝0，得y＝；令y＝0，得x＝﹣1．∴A（﹣1，0），B（0，），OA＝1，OB＝．∴tan∠OAB＝．∴∠OAB＝60°．∴AB＝2OA＝2．∵EG∥OA，DE∥AB，∴四边形ADEF为平行四边形．∴EF＝AD＝t，BF＝2EF＝2t．∴BE＝t，∴AF＝AB﹣BF＝2﹣2t；（2）存在，∵GE＝2OA＝2，∴GF＝2﹣t，若AE∥BG，则△FGB∽△FEA，∵∠GFB＝∠EF A，∴，，解得t＝．∴t＝时，AE∥BG．此时四边形ADEF是菱形，EF＝AF＝，∴四边形ADEF是菱形；（3）当△ADF是直角三角形时，①若∠ADF＝90°，此时AF＝2DA，即2﹣2t＝2t，解得t＝．∴BE＝EF＝t＝，OE＝OB﹣BE＝．∴E（0，），G（﹣2，）．设直线BG的解析式为y＝kx+b，将B（0，），G（﹣2，）代入得：，解得．∴直线BG的解析式为y＝．令x＝﹣1，得y＝，∴M（﹣1，）．设抛物线解析式为y＝a（x+1）2+，∵点E（0，）在抛物线上，∴，解得a＝﹣．抛物线解析式为y＝﹣（x+1）2+，即y＝﹣x2﹣+；②若∠AFD＝90°，此时AD＝2AF，即：t＝2（2﹣2t），解得：t＝．∴BE＝t＝，OE＝OB﹣BE＝．∴E（0，），G（﹣2，）．设直线BG的解析式为y＝k1x+b1，将B（0，），G（﹣2，）代入得：，解得，．∴直线BG的解析式为y＝x+．令x＝﹣1，得y＝，∴M（﹣1，）．设抛物线解析式为y＝a（x+1）2+，∵点E（0，）在抛物线上，∴，解得a＝﹣．∴抛物线解析式为y＝﹣（x+1）2+，即y＝﹣x2﹣x+．。
衢州中考数学试题与答案
数学试卷（一）一、单项选择题1、数2-的相反数为( ) A 、2 B 、21 C 、2- D 、21- 2、某市“十二五”规划纲要指出，力争到2015年，全市农民人均年纯收入超13000元，数13000用科学记数法可以表示为( )A 、31013⨯ B 、4103.1⨯ C 、41013.0⨯ D 、210130⨯3、在九年级体育中考中，某校某班参加仰卧起坐测试的一组女生(每组8人)测试成绩如下(单位：次/分)：44，45，42，48，46，43，47，45.则这组数据的极差为( ) A 、2 B 、4 C 、6 D 、84、如下图，下列几何体的俯视图是右面所示图形的是( )5、某市新农村建设推动了农村住宅旧貌变新颜， 如图为一农村民居侧面截图，屋坡AF 、AG 分别架 在墙体的点B 、点C 处，且AB=AC ，侧面四边形 BDEC 为矩形，则∠FBD=( ) A 、35° B 、40° C 、55° D 、70°6、如图，OP 平分∠MON ，PA ⊥ON 于点A ，点Q 是射线OM 上的 一个动点，若PA=2，则PQ 的最小值为( ) A 、1 B 、2 C 、3 D 、47、5月19日为中国旅游日，某市推出“读万卷书，行万里 路，游某市景”的主题系列旅游惠民活动，市民王先生准备 在优惠日当天上午从孔氏南宗家庙、烂柯山、龙游石窟中随 机选择一个地点；下午从江郎山、三衢石林、开化根博园中 随机选择一个地点游玩，则王先生恰好上午选中孔氏南宗家庙， 下午选中江郎山这两个地的概率是( ) A 、91 B 、31 C 、32 D 、92 8、小亮同学骑车上学，路上要经过平路、下坡、上坡和平路(如图)，若小亮上坡、平路、下坡的速度分别为1v ，2v ，3v ，1v <2v <3v ，则小亮同学骑车上学时，离家的路程s 与所用时间t 的函数关系图象可能是( ) BC DEGOAPO QMN小亮家学校s(第4题) (第5题)(第6题)(第9题)二、填空题9、方程0x 2x 2=-的解为___________________；10、如图，直尺一边AB 与量角器的零刻度线CD 平行，若量角 器的一条刻度线OF 的读数为70°，OF 与AB 交于点E ， 那么∠AEF=___________11、在一资助夏令营活动中，小明同学从营地A 出发，要到A 地 的北偏东60°方向的C 处，他先沿正东方向走了200m 到达B 地， 再沿北偏东30°方向走，恰能到达目的地C(如图)，那么，由此 可知，B 、C 两地相距___________m 。
浙江省衢州市实验学校2015届九年级中考一模数学试卷
1 的图象上，另“7”字形有两个顶点落在 x 轴上，一 x
个顶点落在 y 轴上． （1）图 1 中的每一个小正方形的面积是 ； （2）按照图 1→图 2→图 3→图 4→…这样的规律拼接下去，第 n 个图形中每一个小正方 形的面积是 ． （用含 n 的代数式表示）
三、解答题（有 8 题，共 66 分） 17． （6 分）计算： 12 4sin 60 ( 2015 5) 0 ( ) 1
版权所有：中华资源库
21.（8 分）如图，△ABC 是等腰三角形，AB＝BC，点 D 为 BC 的中点． （1）用圆规和没有刻度的直尺作图，并保留作图痕迹： C ①过点 B 作 AC 的平行线 BP； ②过点 D 作 BP 的垂线，分别交 AC，BP， BQ 于点 E，F，G． D （2）在（1）所作的图中，连接 BE，CF． 求证：四边形 BFCE 是平行四边形．
版权所有：中华资源库
版权所有：中华资源库
衢州市实验学校 下
2014 学年 学 期
九年级数学综合测试卷（一）
参考答案
一、 选择题（本题共 10 小题，每小题 3 分，共 30 分） 题号 答案 1 A 2 B 3 C 4 B 5 C 6 C 7 D 8 D 9 B 10 C
2
b 4ac b 2 , ） ； 2a 4a
一组数据 x1，x2，x3， ，xn 的方差：
1 S 2 = [( x1 x) 2 ( x2 x) 2 ( x3 x) 2 ( xn x) 2 ] （其中 x 是这组数据的平均数）. n
卷 Ⅰ
说明：本卷共有 1 大题，10 小题，共 30 分.请用 2B 铅笔在“答题纸”上将你认为正确 的选项对应的小方框涂黑、涂满，不选、多选、错选均不给分. 一、选择题（有 10 小题，每题 3 分，共 30 分） 1． 3 的相反数等于（ A． 3 B． 3 ） C．
2015年中考数学试题及答案(Word版)
2015年初中毕业暨升学考试试卷数学本试卷由选择题、填空题和解答题三大题组成，共28小题，满分130分，考试时间120分钟．注意事项：1．答题前，考生务必将自己的姓名、考点名称、考场号、座位号用0.5毫米黑色墨水签字笔填写在答题卡相应位置上，并认真核对条形码上的准考号、姓名是否与本人的相符；2．答选择题必须用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其他答案；答非选择题必须用0.5毫米黑色墨水签字笔写在答题卡指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题；3．考生答题必须答在答题卡上，保持卡面清洁，不要折叠，不要弄破，答在试卷和草稿纸上一律无效．一、选择题：本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的．请将选择题的答案用2B铅笔涂在答题卡相应位置上．．．．．．．．．1．2的相反数是A．2 B．12C．-2 D．-122．有一组数据：3，5，5，6，7，这组数据的众数为A．3 B．5 C．6 D．73．月球的半径约为1 738 000m，1 738 000这个数用科学记数法可表示为A．1.738×106B．1.738×107C．0.1738×107D．17.38×1054．若()2m=-，则有A．0＜m＜1 B．-1＜m＜0 C．-2＜m＜-1 D．-3＜m＜-2 5．小明统计了他家今年5月份打电话的次数及通话时间，并列出了频数分布表：则通话时间不超过15min的频率为A．0.1 B．0.4 C．0.5 D．0.96．若点A（a，b）在反比例函数2yx=的图像上，则代数式ab-4的值为A．0 B．-2 C．2 D．-67．如图，在△ABC 中，AB =AC ，D 为BC 中点，∠BAD =35°，则∠C 的度数为 A ．35° B ．45°C ．55°D ．60°8．若二次函数y =x 2+bx 的图像的对称轴是经过点（2，0）且平行于y 轴的直线，则关于x的方程x 2+bx =5的解为 A ．120,4x x ==B ．121,5x x ==C ．121,5x x ==-D ．121,5x x =-=9．如图，AB 为⊙O 的切线，切点为B ，连接AO ，AO 与⊙O 交于点C ，BD 为⊙O 的直径，连接CD ．若∠A =30°，⊙O 的半径为2，则图中阴影部分的面积为 A．43πB．43π-C．πD．23π10．如图，在一笔直的海岸线l 上有A 、B 两个观测站，AB =2km ，从A 测得船C 在北偏东45°的方向，从B 测得船C 在北偏东22.5°的方向，则船C 离海岸线l 的距离（即CD 的长）为 A ．4kmB．(2kmC．D．(4-km二、填空题：本大题共8小题，每小题3分，共24分．把答案直接填在答题卡相应位置上．．．．．．．．． 11．计算：2a a ⋅= ▲ ．12．如图，直线a ∥b ，∠1=125°，则∠2的度数为 ▲ °．DCB A（第7题）（第9题）（第10题）l13．某学校在“你最喜爱的球类运动”调查中，随机调查了若干名学生（每名学生分别选了一项球类运动），并根据调查结果绘制了如图所示的扇形统计图．已知其中最喜欢羽毛球的人数比最喜欢乒乓球的人数少6人，则该校被调查的学生总人数为 ▲ 名． 14．因式分解：224a b -= ▲ ．15．如图，转盘中8个扇形的面积都相等．任意转动转盘1次，当转盘停止转动时，指针指向大于6的数的概率为 ▲ ．16．若23a b -=，则924a b -+的值为 ▲ ．17．如图，在△ABC 中，CD 是高，CE 是中线，CE =CB ，点A 、D 关于点F 对称，过点F作FG ∥CD ，交AC 边于点G ，连接GE ．若AC =18，BC =12，则△CEG 的周长为 ▲ ．18．如图，四边形ABCD 为矩形，过点D 作对角线BD 的垂线，交BC 的延长线于点E ，取BE 的中点F ，连接DF ，DF =4．设AB =x ，AD =y ，则()224x y +-的值为 ▲ ． 三、解答题：本大题共10小题，共76分．把解答过程写在答题卡相应位置上．．．．．．．．，解答时应写出必要的计算过程、推演步骤或文字说明．作图时用2B 铅笔或黑色墨水签字笔．（第17题）GF E D CBA F EDC B A （第18题）ba（第13题）20%10%30%40%其他乒乓球篮球羽毛球（第15题）19．（本题满分5分）(052--． 20．（本题满分5分）解不等式组：()12,31 5.x x x +≥⎧⎪⎨-+⎪⎩＞21．（本题满分6分）先化简，再求值：2121122x x x x ++⎛⎫-÷⎪++⎝⎭，其中1x ．22．（本题满分6分）甲、乙两位同学同时为校文化艺术节制作彩旗．已知甲每小时比乙多做5面彩旗，甲做60面彩旗与乙做50面彩旗所用时间相等，问甲、乙每小时各做多少面彩旗？23．（本题满分8分）一个不透明的口袋中装有2个红球（记为红球1、红球2）、1个白球、1个黑球，这些球除颜色外都相同，将球摇匀．（1）从中任意摸出1个球，恰好摸到红球的概率是 ▲ ；（2）先从中任意摸出1个球，再从余下的3个球中任意摸出1个球，请用列举法（画树状图或列表）求两次都摸到红球的概率．24．（本题满分8分）如图，在△ABC中，AB=AC．分别以B、C为圆心，BC长为半径在BC下方画弧，设两弧交于点D，与AB、AC的延长线分别交于点E、F，连接AD、BD、CD．（1）求证：AD平分∠BAC；（2）若BC=6，∠BAC＝50︒，求 DE、 DF的长度之和（结果保留π）．25．（本题满分8分）如图，已知函数kyx=（x＞0）的图像经过点A、B，点B的坐标为（2，2）．过点A作AC⊥x轴，垂足为C，过点B作BD⊥y轴，垂足为D，AC与BD交于点F．一次函数y=ax+b的图像经过点A、D，与x轴的负半轴交于点E．（1）若AC=32OD，求a、b的值；（2）若BC∥AE，求BC的长．（第24题）F EDCBA26．（本题满分10分）如图，已知AD 是△ABC 的角平分线，⊙O 经过A 、B 、D 三点，过点B 作BE ∥AD ，交⊙O 于点E ，连接ED ． （1）求证：ED ∥AC ；（2）若BD =2CD ，设△EBD 的面积为1S ，△ADC 的面积为2S ，且2121640S S -+=，求△ABC 的面积．27．（本题满分10分）如图，已知二次函数()21y x m x m =+--（其中0＜m ＜1）的图像与x 轴交于A 、B 两点（点A 在点B 的左侧），与y 轴交于点C ，对称轴为直线l ．设P 为对称轴l 上的点，连接P A 、PC ，P A =PC ． （1）∠ABC 的度数为 ▲ °；（2）求P 点坐标（用含m 的代数式表示）；（3）在坐标轴上是否存在点Q （与原点O 不重合），使得以Q 、B 、C 为顶点的三角形与△P AC 相似，且线段PQ 的长度最小？如果存在，求出所有满足条件的点Q 的坐标；如果不存在，请说明理由．（第26题）28．（本题满分10分）如图，在矩形ABCD 中，AD =a cm ，AB =b cm （a ＞b ＞4），半径为2cm的⊙O 在矩形内且与AB 、AD 均相切．现有动点P 从A 点出发，在矩形边上沿着A →B →C →D 的方向匀速移动，当点P 到达D 点时停止移动；⊙O 在矩形内部沿AD 向右匀速平移，移动到与CD 相切时立即沿原路按原速返回，当⊙O 回到出发时的位置（即再次与AB 相切）时停止移动．已知点P 与⊙O 同时开始移动，同时停止移动（即同时到达各自的终止位置）．（1）如图①，点P 从A →B →C →D ，全程共移动了 ▲ cm （用含a 、b 的代数式表示）； （2）如图①，已知点P 从A 点出发，移动2s 到达B 点，继续移动3s ，到达BC 的中点．若点P 与⊙O 的移动速度相等，求在这5s 时间内圆心O 移动的距离；（3）如图②，已知a =20，b =10．是否存在如下情形：当⊙O 到达⊙O 1的位置时（此时圆心O 1在矩形对角线BD 上），DP 与⊙O 1恰好相切？请说明理由．（第28题）（图②）（图①）2015年苏州市初中毕业暨升学考试数学试题答案一、选择题1．C 2．B 3．A 4．C 5．D6．B 7．C 8．D 9．A 10．B二、填空题11．3a12．55 13．60 14．()()22a b a b+-15．1416．3 17．27 18．16三、解答题19.解：原式＝3+5-1 ＝7．20.解：由12x+≥，解得1x≥，由()315x x-+＞，解得4x＞，∴不等式组的解集是4x＞．21.解：原式＝()21122xxx x++÷++＝()2121211x xx xx++⨯=+++．当1x===．22.解：设乙每小时做x面彩旗，则甲每小时做（x+5）面彩旗．根据题意，得60505x x=+．解这个方程，得x=25．经检验，x=25是所列方程的解．∴x+5=30．答：甲每小时做30面彩旗，乙每小时做25面彩旗．23.解：（1）1．（2）用表格列出所有可能的结果：由表格可知，共有12种可能出现的结果，并且它们都是等可能的，其中“两次都摸到红球”有2种可能．∴P（两次都摸到红球）=212=16．24.证明：（1）由作图可知BD =CD ．在△ABD 和△ACD 中，,,,AB AC BD CD AD AD =⎧⎪=⎨⎪=⎩∴△ABD ≌△ACD （SSS ）．∴∠BAD ＝∠CAD ，即AD 平分∠BAC ．解：（2）∵AB =AC ，∠BAC =50°，∴∠ABC ＝∠ACB=65°．∵BD = CD = BC ，∴△BDC 为等边三角形． ∴∠DBC ＝∠DCB=60°． ∴∠DBE ＝∠DCF=55°． ∵BC =6，∴BD = CD =6．∴ DE的长度= DF 的长度=556111806ππ⨯⨯=． ∴ DE、 DF 的长度之和为111111663πππ+=． 25．解：（1）∵点B （2，2）在ky x=的图像上，∴k =4，4y x=． ∵BD ⊥y 轴，∴D 点的坐标为（0，2），OD =2． ∵AC ⊥x 轴，AC =32OD ，∴AC =3，即A 点的纵坐标为3． ∵点A 在4y x=的图像上，∴A 点的坐标为（43，3）．∵一次函数y =ax +b 的图像经过点A 、D ， ∴43,3 2.a b b ⎧+=⎪⎨⎪=⎩ 解得3,42.a b ⎧=⎪⎨⎪=⎩ （2）设A 点的坐标为（m ，4m），则C 点的坐标为（m ，0）． ∵BD ∥CE ，且BC ∥DE ，∴四边形BCED 为平行四边形． ∴CE = BD =2．∵BD ∥CE ，∴∠ADF =∠AEC ．∴在Rt △AFD 中，tan ∠ADF =42AF mDF m -=， 在Rt △ACE 中，tan ∠AEC =42AC mEC =， ∴4422m m m -=，解得m =1．∴C 点的坐标为（1，0），BC26．证明：（1）∵AD 是△ABC 的角平分线， ∴∠BAD =∠DAC ．∵∠E=∠BAD ，∴∠E =∠DAC ． ∵BE ∥AD ，∴∠E =∠EDA ． ∴∠EDA =∠DA C ． ∴ED ∥AC ．解：（2）∵BE ∥AD ，∴∠EBD =∠ADC ．∵∠E =∠DAC ，∴△EBD ∽△ADC ，且相似比2BDk DC==． ··················· ∴2124S k S ==，即124S S =． ∵2121640S S -+=，∴222161640S S -+=，即()22420S -=．∴212S =． ∵233ABC S BC BD CD CD S CD CD CD +==== ，∴32ABC S = ． 27．解：（1）45．理由如下：令x =0，则y =-m ，C 点坐标为（0，-m ）．令y =0，则()210x m x m +--=，解得11x =-，2x m =．∵0＜m ＜1，点A 在点B 的左侧，∴B 点坐标为（m ，0）．∴OB =OC =m ．∵∠BOC ＝90°，∴△BOC 是等腰直角三角形，∠OBC ＝45°． （2）解法一：如图①，作PD ⊥y 轴，垂足为D ，设l 与x 轴交于点E ，由题意得，抛物线的对称轴为12mx -+=． 设点P 坐标为（12m-+，n ）． ∵P A = PC ， ∴P A 2= PC 2，即AE 2+ PE 2=CD 2+ PD 2．∴()222211122m m n n m -+-⎛⎫⎛⎫++=++ ⎪ ⎪⎝⎭⎝⎭．解得12m n -=．∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭． 解法二：连接PB ．由题意得，抛物线的对称轴为12m x -+=． ∵P 在对称轴l 上，∴P A =PB ． ∵P A =PC ，∴PB =PC ．∵△BOC 是等腰直角三角形，且OB =OC ，∴P 在BC 的垂直平分线y x =-上．∴P 点即为对称轴12mx -+=与直线y x =-的交点． ∴P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭．图①图②（3）解法一：存在点Q 满足题意．∵P 点的坐标为11,22m m -+-⎛⎫⎪⎝⎭， ∴P A 2+ PC 2=AE 2+ PE 2+CD 2+ PD 2=222221111112222m m m m m m -+---⎛⎫⎛⎫⎛⎫⎛⎫+++++=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭． ∵AC 2=21m +，∴P A 2+ PC 2=AC 2．∴∠APC ＝90°． ∴△P AC 是等腰直角三角形．∵以Q 、B 、C 为顶点的三角形与△P AC 相似， ∴△QBC 是等腰直角三角形．∴由题意知满足条件的点Q 的坐标为（-m ，0）或（0，m ）． ①如图①，当Q 点的坐标为（-m ，0）时，若PQ 与x 轴垂直，则12m m -+=-，解得13m =，PQ =13． 若PQ 与x 轴不垂直， 则22222221151521222222510m m PQ PE EQ m m m m --+⎛⎫⎛⎫⎛⎫=+=++=-+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ ．＜13， ∴当25m =，即Q 点的坐标为（25-，0）时， PQ 的长度最小．②如图②，当Q 点的坐标为（0，m ）时，若PQ 与y 轴垂直，则12m m -=，解得13m =，PQ =13． 若PQ 与y 轴不垂直， 则22222221151521222222510m m PQ PD DQ m m m m --⎛⎫⎛⎫⎛⎫=+=+-=-+=-+ ⎪ ⎪⎪⎝⎭⎝⎭⎝⎭． ∵0＜m ＜1，∴当25m =时，2PQ 取得最小值110，PQ．＜13， ∴当25m =，即Q 点的坐标为（0，25）时， PQ 的长度最小．综上：当Q 点坐标为（25-，0）或（0，25）时，PQ 的长度最小．解法二： 如图①，由（2）知P 为△ABC 的外接圆的圆心． ∵∠APC 与∠ABC 对应同一条弧AC ，且∠ABC ＝45°， ∴∠APC ＝2∠ABC ＝90°．下面解题步骤同解法一．28．解：（1）a +2b ．（2）∵在整个运动过程中，点P 移动的距离为()2a b +cm ，圆心O 移动的距离为()24a -cm ， 由题意，得()224a b a +=-． ①∵点P 移动2s 到达B 点，即点P 用2s 移动了b cm ，点P 继续移动3s ，到达BC 的中点，即点P 用3s 移动了12a cm ．∴1223a b =． ② 由①②解得24,8.a b =⎧⎨=⎩∵点P 移动的速度与⊙O 移动的速度相等，∴⊙O 移动的速度为42b=（cm/s ）． ∴这5s 时间内圆心O 移动的距离为5×4=20（cm ）． （3）存在这种情形．解法一：设点P 移动的速度为v 1cm/s ，⊙O 移动的速度为v 2cm/s ，由题意，得()()1222021052422044v a b v a ++⨯===--．FE如图，设直线OO 1与AB 交于点E ，与CD 交于点F ，⊙O 1与AD 相切于点G ． 若PD 与⊙O 1相切，切点为H ，则O 1G =O 1H ． 易得△DO 1G ≌△DO 1H ，∴∠ADB =∠BDP ． ∵BC ∥AD ，∴∠ADB =∠CBD ． ∴∠BDP =∠CBD ．∴BP =DP ．设BP =x cm ，则DP =x cm ，PC =（20-x ）cm ，在Rt △PCD 中，由勾股定理，可得222PC CD PD +=，即()2222010x x -+=，解得252x =．∴此时点P 移动的距离为25451022+=（cm ）． ∵EF ∥AD ，∴△BEO 1∽△BAD ． ∴1EO BE AD BA =，即182010EO =． ∴EO 1=16cm ．∴OO 1=14cm ．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ， ∴此时点P 与⊙O 移动的速度比为454521428=．∵455284≠， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ）， ∴此时点P 与⊙O 移动的速度比为45455218364==． ∴此时PD 与⊙O 1恰好相切． 解法二：∵点P 移动的距离为452cm （见解法一）， OO 1=14cm （见解法一），1254v v =，∴⊙O 应该移动的距离为4541825⨯=（cm ）． ①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的距离为14cm ≠18 cm ， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的距离为2×(20-4)-14=18（cm ），∴此时PD 与⊙O 1恰好相切．解法三：点P 移动的距离为452cm ，（见解法一） OO 1=14cm ，（见解法一） 由1254v v =可设点P 的移动速度为5k cm/s ，⊙O 的移动速度为4k cm/s ， ∴点P 移动的时间为459252k k=（s ）．①当⊙O 首次到达⊙O 1的位置时，⊙O 移动的时间为1479422k k k=≠， ∴此时PD 与⊙O 1不可能相切．②当⊙O 在返回途中到达⊙O 1的位置时，⊙O 移动的时间为2(204)14942k k⨯--=， ∴此时PD 与⊙O 1恰好相切．。
2015-2016年浙江省衢州市初三上学期期末数学试卷及答案
2015-2016学年浙江省衢州市初三上学期期末数学试卷一、选择题（共10小题，每小题3分，满分30分）1．（3分）sin30°的值是（）A．B．C．D．12．（3分）已知=，则的值是（）A．B．C．2D．3．（3分）一个几何体的三视图如图所示，那么这个几何体是（）A．B．C．D．4．（3分）一个不透明的布袋中装有1个黄球，2个红球和3个白球，这些球除颜色不同外其他完全相同，则从布袋中随机摸出一个球是白球的概率为（）A．B．C．D．5．（3分）二次函数y=2x2的图象向上平移1个单位，则平移后图象的函数表达式是（）A．y=2（x﹣1）2B．y=2x2﹣1C．y=2（x+1）2D．y=2x2+1 6．（3分）如图，若∠ABC=30°，则∠AOC的度数为（）A．30°B．45°C．60°D．70°7．（3分）如图，PA、PB分别切⊙O于点A、B，且PA=8，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长为（）A．8B．16C．24D．328．（3分）如图，在半径为2cm，圆心角为90°的扇形OAB内，以OB为直径作半圆交弦AB于点C，则图中阴影部分的面积是（）A．π﹣1B．π﹣2C．D．9．（3分）综合实践课上，小敏将一张两直角边长分别为6cm、8cm的直角三角：S 形纸片，按如图所示那样折叠，使点A与点B重合，折痕为DE，则S△BCE等于（）△BDEA．2：5B．14：25C．16：25D．4：21 10．（3分）如图，二次函数y=﹣x2+2x+m+1的图象交x轴于点A（a，0）和B（b，0），交y轴于点C，图象的顶点为D．下列四个命题：①当x＞0时，y＞0；②若a=﹣1，则b=4；③点C关于图象对称轴的对称点为E，点M为x轴上的一个动点，当m=2时，△MCE周长的最小值为2；④图象上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2，其中真命题的个数有（）A．1个B．2个C．3个D．4个二、填空题（共6小题，每小题4分，满分24分）11．（4分）在“海上生明月”这幅图中，把月亮与地平线分别抽象成圆和直线，则该图所呈现的直线与圆之间的位置关系是．12．（4分）某种品牌牛奶包装盒的表面展开图如图所示（单位：mm），那么这种牛奶包装盒的容积是mm3（包装材料厚度不计）．13．（4分）在创建全国文明城市活动中，衢州市园林部分为了扩大市区的绿化面积，进行了大量的树木移栽，如表记录的是在相同条件下移栽某种幼树的棵树和成活棵树：移栽棵树1005001000500010000成活棵树8945891044989000请根据表中数据估计，现园林部门移栽5000棵这种幼树，大约能成活棵．14．（4分）如图，正方形网格中每个小正方形的边长均为1，点A、B、O都在格点上，则∠OAB的余弦值是．15．（4分）已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如表：x…﹣10123…y…105212…则当y＜5时，x的取值范围是．16．（4分）如图，在平面直角坐标系中，含30°锐角的三角板的直角顶点C落在第二象限，其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm，OB=6cm．点C′是第二象限内不与点C重合的一个点，且以A、B、C′为顶点的三角形与△ABC相似（相似比不为1），则点C′的坐标为．三、解答题（共8小题，满分66分）17．（6分）计算：﹣3tan60°+（﹣2）0．18．（6分）红花中学现要从甲、乙两位男生和丙、丁两位女生中，选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛．（1）请用树状图或列表法列举出各种可能选派的结果；（2）求恰好选派一男一女两位同学参赛的概率．19．（6分）美丽的衢江宛如一条玉带穿城而过，沿江两岸的江滨大道和风景带是我市最美的景观之一．教学课外实践活动中，小峰在衢江西岸学仕路AC上的A，B两点处，利用测角仪分别对东岸的观景亭D进行了测量，如图，测得∠DAC=45°，∠DBC=60°．若AB=100米，求观景台D到学仕路AC的距离约为多少米（精确到1米）（≈1.41，≈1.73）20．（8分）如图，在⊙O中，半径OC⊥AB于点D，连结BC．（1）若D是OC的中点，求∠C的度数；（2）若AB=8，CD=2，求⊙O的半径．21．（8分）某商场要经营一种新上市的文具，进价为20元/件，试营销阶段发现；当销售单价25元/件时，每天的销售量是250件，销售单价每上涨1元，每天的销售量就减少10件．（1）写出商场销售这种文具，每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；（2）求销售单价为多少元时，该文具每天的销售利润最大？最大利润是多少？22．（10分）如图，以线段AB为直径作⊙O，CD与⊙O相切于点E，交AB的延长线于点C，连结BE，过点O作OD∥BE交切线CE于点D，连结AD．（1）求证：AD是⊙O的切线；（2）若AD=6，AC=8，求BC的长．23．（10分）如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a＞0）的顶点为M，直线l与x轴平行，且与抛物线交于点A、B，若△AMB为等腰直角三角形，我们就把抛物线上A、B两点之间的部分与线段AB围成的图象称为该抛物线对应的“准蝶形”，线段AB的长称为碟宽，顶点M称为碟顶．（1）填空：抛物线y=x2的碟宽为，碟顶坐标为；（2）求抛物线y=a（x﹣2）2+3（a＞0）的碟宽（用含a的代数式表示）；（3）若抛物线y=ax2﹣4ax﹣（a＞0）的碟宽为6，求该抛物线的碟顶坐标．24．（12分）如图，菱形ABCD中，AB=4，∠ABC=60°，对称中心为P，点F为BC边上一个动点，点E在AB边上，且满足条件∠EPF=60°，图中两块阴影部分图形关于直线AC成轴对称，设它们的面积和为S1．（1）△APE和△CFP是否相似？若相似，请说明理由；（2）设四边形CMPF的面积为S2，CF=x，y=，①求y关于x的函数表达式及自变量x的取值范围；②当图中两块阴影部分图形关于点P成中心对称时，求y的值．2015-2016学年浙江省衢州市初三上学期期末数学试卷参考答案与试题解析一、选择题（共10小题，每小题3分，满分30分）1．（3分）sin30°的值是（）A．B．C．D．1【解答】解：sin30°=．故选：A．2．（3分）已知=，则的值是（）A．B．C．2D．【解答】解：由和比性质，得==，故选：D．3．（3分）一个几何体的三视图如图所示，那么这个几何体是（）A．B．C．D．【解答】解：由于俯视图为圆形可得为球、圆柱、圆锥．主视图和左视图为三角形可得此几何体为圆锥．故选：B．4．（3分）一个不透明的布袋中装有1个黄球，2个红球和3个白球，这些球除颜色不同外其他完全相同，则从布袋中随机摸出一个球是白球的概率为（）A．B．C．D．【解答】解：∵一个不透明的布袋中装有1个黄球，2个红球和3个白球，∴共有1+2+3=6个，∴从布袋中随机摸出一个球是白球的概率为=；故选：C．5．（3分）二次函数y=2x2的图象向上平移1个单位，则平移后图象的函数表达式是（）A．y=2（x﹣1）2B．y=2x2﹣1C．y=2（x+1）2D．y=2x2+1【解答】解：原抛物线的顶点为（0，0），向上平移1个单位，那么新抛物线的顶点为（0，1）；可设新抛物线的解析式为y=（x﹣h）2+k，代入得：y=2x2+1．故选：D．6．（3分）如图，若∠ABC=30°，则∠AOC的度数为（）A．30°B．45°C．60°D．70°【解答】解：∵∠AOC=2∠ABC，∴∠AOC=2×30°=60°，故选：C．7．（3分）如图，PA、PB分别切⊙O于点A、B，且PA=8，CD切⊙O于点E，交PA、PB于C、D两点，则△PCD的周长为（）A．8B．16C．24D．32【解答】解：∵PA、PB分别切⊙O于点A、B，∴PA=PB=8，∵CD切⊙O于点E，∴CA=CE，DB=DE，∴△PCD的周长=PC+CD+PD=PC+CE+DE+PD=PC+AC+BD+PD=PA+PB=16．故选：B．8．（3分）如图，在半径为2cm，圆心角为90°的扇形OAB内，以OB为直径作半圆交弦AB于点C，则图中阴影部分的面积是（）A．π﹣1B．π﹣2C．D．【解答】解：：在Rt△ACB中，AB==2，∵BC是半圆的直径，∴∠CDB=90°，在等腰Rt△ACB中，CD垂直平分AB，CD=BD=，∴D为半圆的中点，∴S阴影部分=S扇形ACB﹣S△ADC=π×22﹣×（）2=π﹣1．故选：A．9．（3分）综合实践课上，小敏将一张两直角边长分别为6cm、8cm的直角三角形纸片，按如图所示那样折叠，使点A与点B重合，折痕为DE，则S△BCE：S △BDE等于（）A．2：5B．14：25C．16：25D．4：21【解答】解：在Rt△BAC中，BC=6，AC=8，∴AB==10，∵把△ABC沿DE使A与B重合，∴AD=BD，EA=EB，∴BD=AB=5，设AE=x，则BE=x，EC=8﹣x，在Rt△BEC中，∵BE2=EC2+BC2，即x2=（8﹣x）2+62，∴x=，∴EC=8﹣x=8﹣=，∴S△BCE=BC•CE=×6×=，在Rt△BED中，∵BE2=ED2+BD2，∴ED==，∴S△BDE=BD•DE=×5×=，∴S△BCE ：S△BDE=：=14：25．故选：B．10．（3分）如图，二次函数y=﹣x2+2x+m+1的图象交x轴于点A（a，0）和B（b，0），交y轴于点C，图象的顶点为D．下列四个命题：①当x＞0时，y＞0；②若a=﹣1，则b=4；③点C关于图象对称轴的对称点为E，点M为x轴上的一个动点，当m=2时，△MCE周长的最小值为2；④图象上有两点P（x1，y1）和Q（x2，y2），若x1＜1＜x2，且x1+x2＞2，则y1＞y2，其中真命题的个数有（）A．1个B．2个C．3个D．4个【解答】解：①当a＜x＜b时，y＞0．故①错误．②==1，∴当a=﹣1时，b=3，故②错误．③当m=2时，C（0，3），E（2，3）．E′与E关于x轴对称，∴E′（2，﹣3），∴CE′=2，∴△MCE的周长的最小值为2+2，故③错误．④设x1关于对称轴的对称点x1′，∴x1′=2﹣x1，∵x1+x2＞2，∴x2＞﹣x1+2，∴x2＞x1′，∵x1＜1＜x2，∴x1＜1＜x1′＜x2，∵函数图象在x＞1时，y随x增大而减小，∴y2＜y1，∴④正确．故选：A．二、填空题（共6小题，每小题4分，满分24分）11．（4分）在“海上生明月”这幅图中，把月亮与地平线分别抽象成圆和直线，则该图所呈现的直线与圆之间的位置关系是相离．【解答】解：∵月亮与地平线没有公共点，∴该图所呈现的直线与圆之间的位置关系是相离．故答案为相离．12．（4分）某种品牌牛奶包装盒的表面展开图如图所示（单位：mm），那么这种牛奶包装盒的容积是 2.24×105mm3（包装材料厚度不计）．【解答】解：根据图形可知：长方体的容积是：40×70×80=2.24×105；故答案为：2.24×105．13．（4分）在创建全国文明城市活动中，衢州市园林部分为了扩大市区的绿化面积，进行了大量的树木移栽，如表记录的是在相同条件下移栽某种幼树的棵树和成活棵树：移栽棵树1005001000500010000成活棵树8945891044989000请根据表中数据估计，现园林部门移栽5000棵这种幼树，大约能成活4500棵．【解答】解：设能成活x棵，根据题意得：，解得：x=4500，故答案为：4500．14．（4分）如图，正方形网格中每个小正方形的边长均为1，点A、B、O都在格点上，则∠OAB的余弦值是．【解答】解：在Rt△OAC中，AC=4，OA==2，则cos∠OAB====，故答案为：15．（4分）已知二次函数y=ax2+bx+c中，函数y与自变量x的部分对应值如表：x…﹣10123…y…105212…则当y＜5时，x的取值范围是0＜x＜4．【解答】解：由表可知，二次函数的对称轴为直线x=2，所以，x=4时，y=5，所以，y＜5时，x的取值范围为0＜x＜4．故答案为：0＜x＜4．16．（4分）如图，在平面直角坐标系中，含30°锐角的三角板的直角顶点C落在第二象限，其斜边两端点A、B分别落在x轴、y轴上，且AB=12cm，OB=6cm．点C′是第二象限内不与点C重合的一个点，且以A、B、C′为顶点的三角形与△ABC相似（相似比不为1），则点C′的坐标为（﹣6，24）、（﹣2，12）、（﹣12，18）和（﹣8，6）．【解答】解：依照题意画出图形，如图所示．∵AB=12cm，OB=6cm，∴sin∠BAO==，∴∠BAO=30°，∠ABO=60°，OA=6．①当AB为较短的直角边且∠ABC1′为直角时，BC1′=AB•tan∠BAC1′=12，在Rt△BC1′D中，∠BDC1′=90°，∠C1′BD=30°，BC1′=12，∴C1′D=6，BD=18，∴OD=24，点C1′的坐标为（﹣6，24）；②当AB为较长的直角边且∠ABC2′为直角时，BC2′=AB•tan∠BAC=4，在Rt△BC2′E中，∠BEC2′=90°，∠C2′BE=30°，BC2′=4，∴C2′E=2，BE=6，∴OE=12，点C2′的坐标为（﹣2，12）；③当AB为较短的直角边且∠BAC3′为直角时，AC3′=AB÷tan∠BC3′A=12，在Rt△AC3′F中，∠AFC3′=90°，∠C3′AF=60°，AC3′=12，∴C3′F=18，AF=6，∴OF=12，点C3′的坐标为（﹣12，18）；④当AB为较长的直角边且∠BAC4′为直角时，AC4′=AB÷tan∠BC4′A=4，在Rt△AC4′M中，∠AMC4′=90°，∠C4′AM=60°，AC4′=4，∴C4′M=6，AM=2，∴OM=8，点C4′的坐标为（﹣8，6）．综上可知：点C′的坐标可以为（﹣6，24）、（﹣2，12）、（﹣12，18）和（﹣8，6）．故答案为：（﹣6，24）、（﹣2，12）、（﹣12，18）和（﹣8，6）．三、解答题（共8小题，满分66分）17．（6分）计算：﹣3tan60°+（﹣2）0．【解答】解：原式=2﹣3+1=1﹣．18．（6分）红花中学现要从甲、乙两位男生和丙、丁两位女生中，选派两位同学分别作为①号选手和②号选手代表学校参加全县汉字听写大赛．（1）请用树状图或列表法列举出各种可能选派的结果；（2）求恰好选派一男一女两位同学参赛的概率．【解答】解：（1）画树状图得：则共有12种等可能的结果；（2）∵恰好选派一男一女两位同学参赛的有8种情况，∴恰好选派一男一女两位同学参赛的概率为：=．19．（6分）美丽的衢江宛如一条玉带穿城而过，沿江两岸的江滨大道和风景带是我市最美的景观之一．教学课外实践活动中，小峰在衢江西岸学仕路AC上的A，B两点处，利用测角仪分别对东岸的观景亭D进行了测量，如图，测得∠DAC=45°，∠DBC=60°．若AB=100米，求观景台D到学仕路AC的距离约为多少米（精确到1米）（≈1.41，≈1.73）【解答】解：设CD为xm，∵∠CAD=45°，∠CDB=60°，∴AC=x，BC==x，∴AB=x﹣x=100，则x=100，解得：x=150+50≈150+86.5≈237，答：观景台D到学仕路AC的距离约为237米．20．（8分）如图，在⊙O中，半径OC⊥AB于点D，连结BC．（1）若D是OC的中点，求∠C的度数；（2）若AB=8，CD=2，求⊙O的半径．【解答】解：（1）连接OB，∵OC⊥AB，D是OC的中点，∴OD=OB，∴∠COB=60°，∴△OBC是等边三角形，∴∠C=60°；（2）设⊙O的半径为r，由勾股定理得，r2=（r﹣2）2+16，解得，r=5，则⊙O的半径为5．21．（8分）某商场要经营一种新上市的文具，进价为20元/件，试营销阶段发现；当销售单价25元/件时，每天的销售量是250件，销售单价每上涨1元，每天的销售量就减少10件．（1）写出商场销售这种文具，每天所得的销售利润w（元）与销售单价x（元）之间的函数关系式；（2）求销售单价为多少元时，该文具每天的销售利润最大？最大利润是多少？【解答】解：（1）由题意可得：w=（x﹣20）[250﹣10（x﹣25）]=﹣10（x﹣20）（x﹣50）=﹣10x2+700x﹣10000；（2）∵w=﹣10x2+700x﹣10000=﹣10（x﹣35）2+2250，∴当x=35时，w取到最大值2250，即销售单价为35元时，每天销售利润最大，最大利润为2250元．22．（10分）如图，以线段AB为直径作⊙O，CD与⊙O相切于点E，交AB的延长线于点C，连结BE，过点O作OD∥BE交切线CE于点D，连结AD．（1）求证：AD是⊙O的切线；（2）若AD=6，AC=8，求BC的长．【解答】（1）证明：连接EO，∵OD∥BE，∴∠3=∠2，∠1=∠4，∵EO=BO，∴∠1=∠2，∴∠3=∠4，在△ADO和△EDO中，∴△ADO≌△EDO（SAS），∴∠DEO=∠DAO=90°，∴AD是⊙O的切线；（2）∵AD=6，AC=8，∴DC=10，∴EC=4，设BC=x，∴（x+）2=16+（）2，解得：x=2，∴BC=2．23．（10分）如图，在平面直角坐标系中，抛物线y=ax2+bx+c（a＞0）的顶点为M，直线l与x轴平行，且与抛物线交于点A、B，若△AMB为等腰直角三角形，我们就把抛物线上A、B两点之间的部分与线段AB围成的图象称为该抛物线对应的“准蝶形”，线段AB的长称为碟宽，顶点M称为碟顶．（1）填空：抛物线y=x2的碟宽为2，碟顶坐标为（0，0）；（2）求抛物线y=a（x﹣2）2+3（a＞0）的碟宽（用含a的代数式表示）；（3）若抛物线y=ax2﹣4ax﹣（a＞0）的碟宽为6，求该抛物线的碟顶坐标．【解答】解：（1）∵a＞0，∴y=ax2的图象大致如下：其必过原点O，记AB为其碟宽，AB与y轴的交点为C，连接OA，OB．∵△OAB为等腰直角三角形，AB∥x轴，∴OC⊥AB，∴∠AOC=∠BOC=∠AOB=×90°=45°，∴△ACO与△BCO亦为等腰直角三角形，∴AC=OC=BC，∴x A=y A，x B=y B，代入y=ax2，∴A（﹣，），B（，），C（0，），∴AB=，OC=，即y=ax2的碟宽为．∵抛物线y=x2对应的a=1，得碟宽为2；碟顶（0，0），故答案为：2，（0，0）（2）由（1）知抛物线y=ax2（a＞0），碟宽为；抛物线y=a（x﹣2）2+4（a＞0）可看成y=ax2向右平移2个单位长度，再向上平移3个单位长度后得到的图形，∵平移不改变形状、大小、方向，∴抛物线y=a（x﹣2）2+3（a＞0）与抛物线y=ax2的碟宽一样，∵抛物线y=ax2（a＞0），碟宽为，∴抛物线y=a（x﹣2）2+3（a＞0），碟宽为．（3）∵y=ax2﹣4ax﹣=a（x﹣2）2﹣（4a+），∴同（1），其碟宽为，∵y=ax2﹣4ax﹣的碟宽为6，∴=6，解得a=．把a=代入y=ax2﹣4ax﹣=x2﹣x﹣，∴顶点坐标为（2，﹣3），即：碟顶为（2，﹣3）．24．（12分）如图，菱形ABCD中，AB=4，∠ABC=60°，对称中心为P，点F为BC边上一个动点，点E在AB边上，且满足条件∠EPF=60°，图中两块阴影部分图形关于直线AC成轴对称，设它们的面积和为S1．（1）△APE和△CFP是否相似？若相似，请说明理由；（2）设四边形CMPF的面积为S2，CF=x，y=，①求y关于x的函数表达式及自变量x的取值范围；②当图中两块阴影部分图形关于点P成中心对称时，求y的值．【解答】解：（1）如图1中，相似．理由如下：∵四边形ABCD是菱形，∠ABC=60°，∴AB=BC=AD=CD，∠ABC=∠ADC=60°，∴△ABC，△ADC都是等边三角形，∴∠4=∠5=60°，∵∠EPF=60°，∴∠1+∠2=120，∠2+∠3=120°，∴∠1=∠3，∴△PAE∽△FCP．（2）②如图2中，作PG⊥AB于G，PH⊥BC于H，连接PB．∵BA=BC，AP=PC，∴∠PBA=∠PBC，∵PG⊥AB，PH⊥BC，∴PG=PH，∵△PAE∽△FCP，∴=，∴=，∴AE=，∴BE=4﹣，∴y==﹣﹣1（1≤x≤4）．③如图3中，∵图中两块阴影部分图形关于点P成中心对称，∴∠APE=∠APN=∠CPF=∠CPM，∵∠EPF=∠MPN=60°，∴∠APE=∠CPF=60°，∴∠1=∠2=30°，∠C=∠CPF=60°，∴△PCF是等边三角形，∴CF=CP=x=2，∴y=﹣﹣1=2．。
衢州中考试卷
衢州中考试卷篇一：2015年衢州市中考科学试卷(扫描版有答案)2015年衢州市中考科学试卷及参考答案篇二：2015浙江中考衢州科学试卷和参考答案2015浙江中考衢州科学试卷本卷可能用到的相对原子质量：H－1 C－12 O－16 Na－23 Cl －35.5 Ca－40 Cu－64 Ba－137一．选择题（本题有15小题，1－10题每小题3分，11－15题每小題2分，共40分。
请选出各题中一个符合题意的选项，不选、多选、错选均不给分）1．下列各图能正确反映电荷之间、磁极之间相互作用规律的是（）第1题图2．2014年我市重新发现白蚁家族中的“大熊猫”——浙江亮白蚁，它体表有外骨骼，身体分头、胸、腹三部分。
在生物分类上它属于（）A．昆虫类 B．两栖类 C．爬行类 D．鸟类3．系统由器官组成，下列器官属于循环系统的是（）第3题图4．地球是人类生存的家园。
下列有关的叙述错误的是（）A．全球有六大板块组成 B．火山和地震都是地壳变动的表现C．地球由外向内分为地壳、地幔、地核三屋 D．地球上的水是循环不息的，不必担心水资短缺5．近年来禽流感等传染病流行，向人类发出了新的挑战。
下列有关传染病的说法错误的是（）A．病毒是传染源 B．传染病有传染性、流行性和免疫性C．积极研制疫苗，进行预防接种是预防传染病的有效措施D．传染病的流行具备传染源、传播途径和易感人群三个环节6．科学家发现一种新元素。
该元素原子核外电子数为117，中子数为174，相对原子质量为291，元素名称Ununseptium，符号Uus。
请模仿甲，将该元素对应信息编写到图乙中相应位置，“①”处应填（）A．291 B．174 C．117D．577．如图是桃树的果实，下列说法正确的是（）A．桃树是裸子植物 B．①是种子，②是果皮C．桃花的子房发育成种子 D．桃子是桃树的生殖系统8．如图所示，一束光线斜射到平面镜上，其中反射角是（）A．∠1B．∠2 C．∠3 D．∠49．我国科学家在甲烷高效转化研究中获得重大突破，如图为该转化的微观示意图。
浙江省衢州市中考数学试题及答案(word版)
浙江省2009年初中毕业生学业考试(衢州卷)数 学 试 卷1.本卷共三大题，24小题．全卷满分为150分，考试时间为120分钟．2.答题前,请用蓝、黑墨水的钢笔或圆珠笔将县(市、区)、学校、姓名、准考证号分别填在密封线内相应的位置上，不要遗漏．3.本卷不另设答题卡和答题卷，请在本卷相应的位置上直接答题． 答题必须用蓝、黑墨水的钢笔或圆珠笔（画图请用铅笔），答题时允许使用计算器． 温馨提示：用心思考，细心答题，相信你一定会有出色的表现！一、选择题（本大题有10小题，每小题4分，共40分．请选出各题中一个符合题意的正确选项填在相应的答案栏内，不选、1. 计算：-2+3 = A ．5B ．-5C ．1D ．-12. 外切两圆的圆心距是7，其中一圆的半径是4，则另一圆的半径是A ．11B ．7C ．4D ．33. 从红桃A 、黑桃A 、梅花A 、方块A 四张牌中，随机抽取一张，则抽到方块A 的概率为A ．14 B ．13C ．12 D ．1 4. 二次函数2(1)2y x =--的图象上最低点的坐标是A ．(-1，-2)B ．(1，-2)C ．(-1，2)D ．(1，2)得 分 评卷人(第3题)5.为测量如图所示上山坡道的倾斜度，小明测得图中所示的数据(单位：米)，则该坡道倾斜角α的正切值是A．14B．4CD6.据统计，2008年在国际金融危机的强烈冲击下，我国国内生产总值约30 067 000 000 000元，仍比上年增长9.0％．30 067 000 000 000元用科学记数法表示为A．30 067×109元B．300.67×1011元C．3.006 7×1013元D．0.300 67×1014元7.P1(x1，y1)，P2(x2，y2)是正比例函数y= -x图象上的两点，则下列判断正确的是A．y1>y2B．y1<y2C．当x1<x2时，y1>y2D．当x1<x2时，y1<y28.某班体育委员调查了本班46名同学一周的平均每天体育活动时间，并制作了如图所示的频数分布直方图，从直方图中可以看出，该班同学这一周平均每天体育活动时间的中位数和众数依次是A．40分，40 分B．50分，40分C．50分，50 分D．40分，50分9.在△ABC中，AB=12，AC=10，BC=9，AD是BC边上的高.将△ABC按如图所示的方式折叠，使点A与点D重合，折痕为EF，则△DEF的周长为A．9.5 B．10.5C．11 D．15.510. 如图，△ABC中，A，B两个顶点在x轴的上方，点C的坐标是(-1，0)．以点C为位似中心，在x轴的下方作△ABC的位似图形，并把△ABC的边长放大到原来的2倍，记所得的像是△A′B′C．设点B的对应点B′的横坐标是a，则点B的横坐标是A．12a-B．1(1)2a-+C．1(1)2a--D．1(3)2a-+(分)某班46名同学一周平均每天体育活动时间频数分布直方图(第8题)(第9题)CBDAE FCBA二、填空题（本大题有6小题，每小题5分，共30分．将答案填在题中横线上） 11.计算：01)= ． 12. 化简：2111x x x x -+=++ ． 13. 如图，AB ∥CD ，∠BAC 的平分线和∠ACD 的平分线交于点E ，则∠AEC 的度数是 ． 14. 据《衢州日报》2009年5月2日报道：“家电下乡”农民得实惠．村民小郑购买一台双门冰箱，在扣除13%的政府财政补贴后，再减去商场赠送的“家电下乡”消费券100元，实际只花了1 726.13元钱，那么他购买这台冰箱节省了 元钱． 15. 陈老师要为他家的长方形餐厅(如图)选择一张餐桌，并且想按如下要求摆放：餐桌一侧靠墙，靠墙对面的桌边留出宽度不小于80cm 的通道，另两边各留出宽度不小于60cm的通道．那么在下面四张餐桌中，其大小规格符合要求的餐桌编号是 (把符合要求的编号都写上)．16. 如图，DB 为半圆的直径，A 为BD 延长线上一点，AC 切半圆于点E ，BC ⊥AC 于点C ，交半圆于点F ．已知BD =2，设AD =x ，CF =y ，则y 关于x 的函数解析式是 ．三、解答题（本大题有8小题，共80分，请务必写出解答过程） 17.（本题8分）给出三个整式a 2，b 2和2ab ． (1) 当a =3，b =4时，求a 2+b 2+2ab 的值； (2) 在上面的三个整式中任意选择两个整式进行加法或减法运算，使所得的多项式能够因式分解．请写出你所选的式子及因式分解的过程．B 得 分 评卷人得 分 评卷人(第13题)E D C BA(第15题)桌面是边长为80cm 的正方形桌面是长、宽分别为100cm 和64cm 的长方形桌面是半径 为45cm 的圆 桌面的中间是边长为60cm 的正方形， 两头均为半圆18.（本题8分）解不等式组 231,1(1).2x x x -<⎧⎪⎨-⎪⎩≥19.（本题8分）水产公司有一种海产品共2 104千克，为寻求合适的销售价格，进行了8天试销，试销情况如下：第1天 第2天 第3天 第4天 第5天 第6天 第7天 第8天 售价x (元/千克) 400 250 240 200 150 125 120 销售量y (千克)304048608096100观察表中数据，发现可以用反比例函数刻画这种海产品的每天销售量y (千克)与销售价格x (元/千克)之间的关系．现假定在这批海产品的销售中，每天的销售量y (千克)与销售价格x (元/千克)之间都满足这一关系．(1) 写出这个反比例函数的解析式，并补全表格；(2) 在试销8天后，公司决定将这种海产品的销售价格定为150元/千克，并且每天都按这个价格销售，那么余下的这些海产品预计再用多少天可以全部售出？得 分 评卷人得 分 评卷人20.（本题8分）如图，四边形ABCD 是矩形，△PBC 和△QCD 都是等边三角形，且点P 在矩形上方，点Q 在矩形内． 求证：（1）∠PBA =∠PCQ =30°；（2）P A =PQ ．21.（本题10分）一个几何体的三视图如图所示，它的俯视图为菱形．请写出该几何体的形状，并根据图中所给的数据求出它的侧面积．得 分 评卷人主视图俯视图左视图ACBD PQ得 分 评卷人22.（本题12分）2009年5月17日至21日，甲型H1N1流感在日本迅速蔓延，每天的新增病例和累计确诊病例人数如图所示．(1) 在5月17日至5月21日这5天中，日本新增甲型H1N1流感病例最多的是哪一天？该天增加了多少人？(2) 在5月17日至5月21日这5天中，日本平均每天新增加甲型H1N1流感确诊病例多少人？如果接下来的5天中，继续按这个平均数增加，那么到5月26日，日本甲型H1N1流感累计确诊病例将会达到多少人？(3) 甲型H1N1流感病毒的传染性极强，某地因1人患了甲型H1N1流感没有及时隔离治疗，经过两天．．传染后共有9人患了甲型H1N1流感，每天．．传染中平均一个人传染了几个人？如果按照这个传染速度，再经过5天的传染后，这个地区一共将会有多少人患甲型H1N1流感？得 分 评卷人161718 192021 日本2009年5月16日至5月21日 甲型H1N1流感疫情数据统计图人数(人)23.（本题12分）如图，AD是⊙O的直径．(1)如图①，垂直于AD的两条弦B1C1，B2C2把圆周4等分，则∠B1的度数是，∠B2的度数是；(2)如图②，垂直于AD的三条弦B1C1，B2C2，B3C3把圆周6等分，分别求∠B1，∠B2，∠B3的度数；(3)如图③，垂直于AD的n条弦B1C1，B2C2，B3 C3，…，B n C n把圆周2n等分，请你用含n的代数式表示∠B n的度数(只需直接写出答案)．得分评卷人图①B C2图②nB-2图③24. （本题14分）如图，已知点A (-4，8)和点B (2，n )在抛物线2y ax =上．(1) 求a 的值及点B 关于x 轴对称点P 的坐标，并在x 轴上找一点Q ，使得AQ +QB 最短，求出点Q 的坐标；(2) 平移抛物线2y ax =，记平移后点A 的对应点为A ′，点B 的对应点为B ′，点C (-2，0)和点D (-4，0)是x 轴上的两个定点． ① 当抛物线向左平移到某个位置时，A ′C +CB ′ 最短，求此时抛物线的函数解析式； ② 当抛物线向左或向右平移时，是否存在某个位置，使四边形A ′B ′CD 的周长最短？若存在，求出此时抛物线的函数解析式；若不存在，请说明理由．浙江省2009年初中毕业生学业考试（衢州卷）数学试题参考答案及评分标准得 分 评卷人ACBDPQ二、填空题（每小题5分，共30分）11. 1 12. 1 13. 90° 14. 372.87 15. ①②③④ 16. 1x y x=+ 三、解答题（共80分） 17.（本题8分）解：(1) 当a =3，b =4时， a 2+b 2+2ab =2()a b +=49．……4分(2) 答案不唯一，式子写对给2分，因式分解正确给2分．例如， 若选a 2，b 2，则a 2-b 2=(a +b )(a -b )．……4分 若选a 2，2ab ，则a 2±2ab =a (a ±2b )． ……4分 18.（本题8分）解：不等式231x -<的解是 x <2，……3分 不等式1(1)2x x -≥的解是 x ≥-1，……3分 ∴ 不等式组的解是 -1≤x <2 ．……2分19.（本题8分）解：(1) 函数解析式为12000y x=． ……2分填表如下：第1天 第2天第3天 第4天 第5天 第6天 第7天 第8天 售价x (元/千克) 400 300250 240200 150 125 120 销售量y (千克)30404850608096100……2分(2) 2 104-(30+40+48+50+60+80+96+100)=1 600， 即8天试销后，余下的海产品还有1 600千克． (1)分当x =150时，12000150y ==80． ……2分 1 600÷80=20，所以余下的这些海产品预计再用20天可以全部售出． (1)分20.（本题8分）证明：(1) ∵ 四边形ABCD 是矩形，∴ ∠ABC =∠BCD =90°．……1分∵ △PBC 和△QCD 是等边三角形， ∴ ∠PBC =∠PCB =∠QCD =60°， ……1分 ∴ ∠PBA =∠ABC －∠PBC =30°， ……1分∠PCD = ∠BCD －∠PCB =30°．∴ ∠PCQ =∠QCD －∠PCD =30°． ∴ ∠PBA =∠PCQ =30°． ……1分 (2) ∵ AB =DC =QC ，∠PBA =∠PCQ ，PB =PC ，……1分 ∴ △P AB ≌△PQC ， ……2分 ∴ P A =PQ ． ……1分 21.（本题10分）解：该几何体的形状是直四棱柱(答直棱柱，四棱柱，棱柱也给4分)．……4分 由三视图知，棱柱底面菱形的对角线长分别为4cm ，3cm ．……2分 ∴ 菱形的边长为52cm ， ……2分 棱柱的侧面积=52×8×4=80(cm 2)．……2分22.（本题12分）解：(1) 18日新增甲型H1N1流感病例最多，增加了75人；……4分 (2) 平均每天新增加267452.65-=人，……2分 继续按这个平均数增加，到5月26日可达52.6×5+267=530人；……2分(3) 设每天传染中平均一个人传染了x 个人，则 1(1)9x x x +++=，2(1)9x +=，解得2=x (x = -4舍去)． ……2分再经过5天的传染后，这个地区患甲型H1N1流感的人数为 (1+2)7=2 187（或1+2+6+18+54+162+486+1 458=2 187）， 即一共将会有2 187人患甲型H1N1流感． ……2分 23.（本题12分） 解：(1) 22.5°，67.5°……4分(2) ∵ 圆周被6等分，∴ 11B C =12C C =23C C =360°÷6＝60°． ……1分∵ 直径AD ⊥B 1C 1，∴ 1AC =1211B C =30°，∴ ∠B 1m=121AC =15°．……1分 ∠B 2m=122AC =12×(30°＋60°)=45°， ……1分 ∠B 3m=123AC =12×(30°＋60°＋60°)=75°． (1)分(3) 11360360[(1)]2222n B n n n ︒︒∠=⨯+-⨯(9045)n n-︒=． (或3604590908n B n n ︒︒∠=︒-=︒-) (4)分24.（本题14分）解：(1) 将点A (-4，8)的坐标代入2y ax =，解得12a =． ……1分将点B (2，n )的坐标代入212y x =，求得点B 的坐标为(2，2)， ……1分则点B 关于x 轴对称点P 的坐标为(2，-2)． ……1分 直线AP 的解析式是5433y x =-+．……1分 令y =0，得45x =．即所求点Q 的坐标是(45，0)．……1分 (2)① 解法1：CQ =︱-2-45︱=145，……1分故将抛物线212y x =向左平移145个单位时，A ′C +CB ′最短， ……2分此时抛物线的函数解析式为2114()25y x =+．……1分解法2：设将抛物线212y x =向左平移m 个单位，则平移后A ′，B ′的坐标分别为A ′(-4-m ，8)和B ′(2-m ，2)，点A ′关于x 轴对称点的坐标为A ′′(-4-m ，-8)．直线A ′′B ′的解析式为554333y x m =+-．……1分要使A ′C +CB ′最短，点C 应在直线A ′′B ′上，……1分 将点C (-2，0)代入直线A ′′B ′的解析式，解得145m =．……1分故将抛物线212y x =向左平移145个单位时A ′C +CB ′最短，此时抛物线的函数解析式为2114()25y x =+．……1分② 左右平移抛物线212y x =，因为线段A ′B ′和CD 的长是定值，所以要使四边形A ′B ′CD 的周长最短，只要使A ′D +CB ′最短； ……1分第一种情况：如果将抛物线向右平移，显然有A ′D +CB ′>AD +CB ，因此不存在某个位置，使四边形A ′B ′CD 的周长最短．……1分 第二种情况：设抛物线向左平移了b 个单位，则点A ′和点B ′的坐标分别为A ′(-4-b ，8)和B ′(2-b ，2)．因为CD =2，因此将点B ′向左平移2个单位得B ′′(-b ，2)，要使A ′D +CB ′最短，只要使A ′D +DB ′′最短． ……1分 点A ′关于x 轴对称点的坐标为A ′′(-4-b ，-8)，(第24题(1))直线A ′′B ′′的解析式为55222y x b =++．……1分 要使A ′D +DB ′′最短，点D 应在直线A ′′B ′′上，将点D (-4，0)代入直线A ′′B ′′的解析式，解得165b =． 故将抛物线向左平移时，存在某个位置，使四边形A ′B ′CD 的周长最短，此时抛物线的函数解析式为2116()25y x =+．……1分。
浙江省中考数学试题附答案
浙江省2015年中考数学试题（附答案）浙江省2015年中考数学试题（附答案）满分150分，考试时间120分钟一、选择题（本题有10小题，每小题4分，共40分）1.计算的结果是A.-3B.-2C.2D.32.据中国电子商务研究中心监测数据显示，2015年第一季度中国轻纺城市场群的商品成交额达27800000000元，将27800000000用科学计数法表示为A.2.78×1010B.2.78×1011C.27.8×1010D.0.278×10113.有6个相同的立方体搭成的几何体如图所示，则它的主视图是4.下面是一位同学做的四道题：①；②；③；④，其中做对的一道题的序号是A.①B.②C.③D.④5.在一个不透明的袋子中装有除颜色外其它均相同的3个红球和2个白球，从中任意摸出一个球，则摸出白球的概率是A.B.C.D.6.化简的结果是A.B.C.D.7.如图，小敏做了一个角平分仪ABCD，其中AB=AD，BC=DC，将仪器上的点A与∠PRQ的顶点R重合，调整AB 和AD，使它们分别落在角的两边上，过点A，C画一条射线AE，AE就是∠PRQ的平分线。
此角平分仪的画图原理是：根据仪器结构，可得△ABC≌△ADC，这样就有∠QAE=∠PAE。
则说明这两个三角形全等的依据是A.S8.如图，四边形ABCD是⊙O的内接四边形，⊙O的半径为2，∠B=135°，则的长A.B.C.D.9.如果一种变换是将抛物线向右平移2个单位或向上平移1个单位，我们把这种变换称为抛物线的简单变换。
已知抛物线经过两次简单变换后的一条抛物线是，则原抛物线的解析式不可能的是A.B.C.D.10.挑游戏棒是一种好玩的游戏，游戏规则：当一根棒条没有被其它棒条压着时，就可以把它往上拿走。
如图中，按照这一规则，第1次应拿走⑨号棒，第2次应拿走⑤号棒，…，则第6次应拿走A.②号棒B.⑦号棒C.⑧号棒D.⑩号棒二、填空题（本题有6小题，每小题5分，共30分）11.因式分解：=▲12.如图，已知点A（0，1），B（0，-1），以点A为圆心，AB为半径作圆，交轴的正半轴于点C，则∠BAC等于▲度13.由于木质衣架没有柔性，在挂置衣服的时候不太方便操作。
2015年中考数学试题(含答案)
2015年河南初中学业水平暨高级中等学校招生考试试题数 学注意事项：1. 本试卷共6页，三个大题，满分120分，考试时间100分钟。
2. 本试卷上不要答题，请按答题卡上注意事项的要求直接把答案填写在答题卡上。
答在试卷上的答案无效。
一、选择题（每小题3分，共24分）下列各小题均有四个答案，其中只有一个是正确的。
1. 下列各数中最大的数是（ ）A. 5B.3C. πD. －8 2. 如图所示的几何体的俯视图是（ ）3. 据统计，2014年我国高新技术产品出口总额达40 570亿元，将数据40 570亿用科学记数法表示为（ ） A.4.0570×109 B. 0.40570×1010 C. 40.570×1011 D. 4.0570×10124. 如图，直线a ，b 被直线c ，d 所截，若∠1=∠2，∠3=125°，则∠4的度数为（ ） A. 55° B. 60° C.70° D. 75°5. 不等式组⎩⎨⎧>-≥+13,05x x 的解集在数轴上表示为（ ）6. 小王参加某企业招聘测试，他的笔试，面试、技能操作得分分别为85分，80分，90分，若依次按照2:3:5的比例确定成绩，则小王的成绩是（ ）A. 255分B. 84分C. 84.5分D.86分7. 如图，在□ABCD 中，用直尺和圆规作∠BAD 的平分线AG 交BC 于点E ，若BF =6，AB =5，则AE 的长为（ ）C DB A 正面 第2题dc ba第4题-52 0 -520 -52 0 -520 CDBAA. 4B. 6C. 8D. 108. 如图所示，在平面直角坐标系中，半径均为1个单位长度的半圆O 1，O 2，O 3，… 组成一条平滑的曲线，点P 从原点O 出发，沿这条曲线向右运动，速度为每秒2π个单位长度，则第2015秒时，点P 的坐标是（ ）A.（2014,0）B.（2015，－1）C. （2015,1）D. （2016,0）二、填空题（每小题3分，共21分） 9.计算：(－3)0+3－1=.10. 如图，△ABC 中，点D 、E 分别在边AB ，BC 上，DE //AC ，若DB =4，DA =2，BE =3，则EC = . 11. 如图，直线y =kx 与双曲线)0(2>=x xy 交于点 A （1，a ）,则k = .12. 已知点A （4，y 1），B （2，y 2），C （－2，y 3）都在二次函数y =(x －2)2－1的图象上，则y 1，y 2，y 3的大小关系是 . 13. 现有四张分别标有数字1，2，3，4的卡片，它们除数字外完全相同，把卡片背面朝上洗匀，从中随机抽取一张后放回，再 背面朝上洗匀，从中随机抽取一张，则两次抽出的卡片所标数 字不同的概率是 .14. 如图，在扇形AOB 中，∠AOB =90°，点C 为OA 的中点，CE ⊥OA 交AB 于点E ，以点O 为圆心，OC 的长为半径 作CD 交OB 于点D ，若OA =2，则阴影部分的面积为 .15. 如图，正方形ABCD 的边长是16，点E 在边AB 上，AE =3，点F 是边BC 上不与点B 、C 重合的一个动点，把△EBF 沿EF 折叠，点B 落在B ′处，若△CDB ′恰为等腰三角形，则DB ′的长为 .E FCDBGA第7图第8题E CDBA第14题EFCDBA 第15题B ′三、解答题（本大题共8个小题，满分75分）16.（8分）先化简，再求值：)11(22222ab b a b ab a -÷-+-，其中15+=a ，15-=b .17.（9分）如图，AB 是半圆O 的直径，点P 是半圆上不与点A 、B 重合的一个动点，延长BP 到点C ，使PC =PB ，D 是AC 的中点，连接PD ，PO . （1）求证：△CDP ≌△POB ； （2）填空：① 若AB =4，则四边形AOPD 的最大面积为 ； ② 连接OD ，当∠PBA 的度数为 时，四边形BPDO18.（9分）为了了解市民“获取新闻的最主要途径”，某市记者开展了一次抽样调查，根据调查结果绘制了如下尚不完整的统计图。
2013-2019年浙江省衢州市中考数学试题汇编(含参考答案与解析)
【中考数学试题汇编】2013—2019年浙江省衢州市中考数学试题汇编（含参考答案与解析）1、2013年浙江省衢州市中考数学试题及参考答案与解析 (2)2、2014年浙江省衢州市中考数学试题及参考答案与解析 (25)3、2015年浙江省衢州市中考数学试题及参考答案与解析 (49)4、2016年浙江省衢州市中考数学试题及参考答案与解析 (72)5、2017年浙江省衢州市中考数学试题及参考答案与解析 (94)6、2018年浙江省衢州市中考数学试题及参考答案与解析 (115)7、2019年浙江省衢州市中考数学试题及参考答案与解析 (137)2013年浙江省衢州市中考数学试题及参考答案与解析一、选择题（本大题共有10小题，每小题3分，共30分.请选出各题中一个符合题意的选项，不选、多选、错选均不给分.）1．比1小2的数是（）A．3 B．1 C．﹣1 D．﹣22．下列计算正确的是（）A．3a+2b=5ab B．a﹣a4=a4C．a6÷a2=a3D．（﹣a3b）2=a6b23．衢州新闻网2月16日讯，2013年春节“黄金周”全市接待游客总数为833100人次．将数833100用科学记数法表示应为（）A．0.833×106B．83.31×105C．8.331×105D．8.331×1044．下面简单几何体的左视图是（）A．B．C．D．5．若函数2myx+=的图象在其所在的每一象限内，函数值y随自变量x的增大而增大，则m的取值范围是（）A．m＜﹣2 B．m＜0 C．m＞﹣2 D．m＞06．将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上．另一个顶点在纸带的另一边沿上，测得三角板的一边与纸带的一边所在的直线成30°角，如图，则三角板的最大边的长为（）A．3cm B．6cm C．D．7．一次数学测试，某小组五名同学的成绩如下表所示（有两个数据被遮盖）．那么被遮盖的两个数据依次是（）A．80，2 B．80C．78，2 D．788．如图，小敏同学想测量一棵大树的高度．她站在B处仰望树顶，测得仰角为30°，再往大树的方向前进4m，测得仰角为60°，已知小敏同学身高（AB）为1.6m，则这棵树的高度为（）（结果精确到0.1m≈1.73）．A ．3.5mB ．3.6mC ．4.3mD ．5.1m9．抛物线y=x 2+bx+c 的图象先向右平移2个单位，再向下平移3个单位，所得图象的函数解析式为y=（x ﹣1）2﹣4，则b 、c 的值为（ ）A ．b=2，c=﹣6B ．b=2，c=0C ．b=﹣6，c=8D ．b=﹣6，c=210．如图，正方形ABCD 的边长为4，P 为正方形边上一动点，沿A→D→C→B→A 的路径匀速移动，设P 点经过的路径长为x ，△APD 的面积是y ，则下列图象能大致反映y 与x 的函数关系的是（ ）A ．B ．C ．D ．二、填空题（本大题共有6小题，每小题4分，共24分．）11．不等式组2031x x x -⎧⎨+⎩≥＞的解集是 ．12．化简：224442x x xx x ++-=-- ． 13．小芳同学有两根长度为4cm 、10cm 的木棒，她想钉一个三角形相框，桌上有五根木棒供她选择（如图所示），从中任选一根，能钉成三角形相框的概率是 ．14．如图，将一块三角板和半圆形量角器按图中方式叠放，三角板一边与量角器的零刻度线所在直线重合，重叠部分的量角器弧()AB 对应的圆心角（∠AOB ）为120°，OC 的长为2cm ，则三角板和量角器重叠部分的面积为 ．15．某果园有100棵橘子树，平均每一棵树结600个橘子．根据经验估计，每多种一颗树，平均每棵树就会少结5个橘子．设果园增种x 棵橘子树，果园橘子总个数为y 个，则果园里增种 棵橘子树，橘子总个数最多．16．如图，在菱形ABCD 中，边长为10，∠A=60°．顺次连结菱形ABCD 各边中点，可得四边形A 1B 1C 1D 1；顺次连结四边形A 1B 1C 1D 1各边中点，可得四边形A 2B 2C 2D 2；顺次连结四边形A 2B 2C 2D 2各边中点，可得四边形A 3B 3C 3D 3；按此规律继续下去…．则四边形A 2B 2C 2D 2的周长是 ；四边形A 2013B 2013C 2013D 2013的周长是 ．三、简答题（本大题共有8小题，共66分．务必写出解答过程．）17．（6﹣23÷|﹣2|×（﹣7+5）18．（6分）如图所示，在长和宽分别是a 、b 的矩形纸片的四个角都剪去一个边长为x 的正方形． （1）用a ，b ，x 表示纸片剩余部分的面积；（2）当a=6，b=4，且剪去部分的面积等于剩余部分的面积时，求正方形的边长．19．（6分）如图，函数y 1=﹣x+4的图象与函数22k y x=（x ＞0）的图象交于A （a ，1）、B （1，b ）两点．（1）求函数y 2的表达式；（2）观察图象，比较当x ＞0时，y 1与y 2的大小．20．（8分）如图，已知AB是⊙O的直径，BC⊥AB，连结OC，弦AD∥OC，直线CD交BA的延长线于点E．（1）求证：直线CD是⊙O的切线；（2）若DE=2BC，求AD：OC的值．21．（8分）据《2012年衢州市国民经济和社会发展统计公报》（2013年2月5日发布），衢州市固定资产投资的相关数据统计图如下：根据以上信息，解答下列问题：（1）求2012年的固定资产投资增长速度（年增长速度即年增长率）；（2）求2005﹣2012年固定资产投资增长速度这组数据的中位数；（3）求2006年的固定资产投资金额，并补全条形图；（4）如果按照2012年的增长速度，请预测2013年衢州市的固定资产投资金额可达到多少亿元（精确到1亿元）？22．（10分）【提出问题】（1）如图1，在等边△ABC中，点M是BC上的任意一点（不含端点B、C），连结AM，以AM 为边作等边△AMN，连结CN．求证：∠ABC=∠ACN．【类比探究】（2）如图2，在等边△ABC中，点M是BC延长线上的任意一点（不含端点C），其它条件不变，（1）中结论∠ABC=∠ACN还成立吗？请说明理由．【拓展延伸】（3）如图3，在等腰△ABC中，BA=BC，点M是BC上的任意一点（不含端点B、C），连结AM，以AM为边作等腰△AMN，使顶角∠AMN=∠ABC．连结CN．试探究∠ABC与∠ACN的数量关系，并说明理由．23．（10分）“五•一”假期，某火车客运站旅客流量不断增大，旅客往往需要长时间排队等候检票．经调查发现，在车站开始检票时，有640人排队检票．检票开始后，仍有旅客继续前来排队检票进站．设旅客按固定的速度增加，检票口检票的速度也是固定的．检票时，每分钟候车室新增排队检票进站16人，每分钟每个检票口检票14人．已知检票的前a分钟只开放了两个检票口．某一天候车室排队等候检票的人数y（人）与检票时间x（分钟）的关系如图所示．（1）求a的值．（2）求检票到第20分钟时，候车室排队等候检票的旅客人数．（3）若要在开始检票后15分钟内让所有排队的旅客都能检票进站，以便后来到站的旅客随到随检，问检票一开始至少需要同时开放几个检票口？24．（12分）在平面直角坐标系x、y中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒．（1）当点P移动到点D时，求出此时t的值；（2）当t为何值时，△PQB为直角三角形；（3）已知过O、P、Q三点的抛物线解析式为y=1t（x﹣t）2+t（t＞0）．问是否存在某一时刻t，将△PQB绕某点旋转180°后，三个对应顶点恰好都落在上述抛物线上？若存在，求出t的值；若不存在，请说明理由．参考答案与解析一、选择题（本大题共有10小题，每小题3分，共30分.请选出各题中一个符合题意的选项，不选、多选、错选均不给分.）1．比1小2的数是（）A．3 B．1 C．﹣1 D．﹣2【知识考点】有理数的减法．【思路分析】根据有理数的减法运算法则进行计算即可得解．【解答过程】解：1﹣2=﹣1．故选C．【总结归纳】本题考查了有理数的减法，是基础题．2．下列计算正确的是（）A．3a+2b=5ab B．a﹣a4=a4C．a6÷a2=a3D．（﹣a3b）2=a6b2【知识考点】同底数幂的除法；合并同类项；幂的乘方与积的乘方．【思路分析】根据同底数幂相除，底数不变指数相减；幂的乘方，底数不变指数相乘；合并同类项，只把系数相加减，字母与字母的次数不变，对各选项分析判断后利用排除法求解．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数学中考教学资料2019年编
2015年浙江省衢州市中考数学试卷
一、选择题（本题有10小题，每小题3分，共30分）
1．﹣3的相反数是（）
A．3 B．﹣3 C．D．﹣
2．一个几何体零件如图所示，则它的俯视图是（）
3．下列运算正确的是（）
A．a3+a3=2a6B．（x2）3=x5C．2a6÷a3=2a2D．x3•x2=x5
4．如图，在▱ABCD中，已知AD=12cm，AB=8cm，AE平分∠BAD交BC边于点E，则CE的长等于（）
A．8cm B．6cm C．4cm D．2cm
5．某班七个兴趣小组人数分别为4，4，5，x，6，6，7．已知这组数据的平均数是5，则这组数据的中位数是（）
A．7 B．6C．5D．4
6．下列四个函数图象中，当x＞0时，y随x的增大而减小的是（）
7．数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a．小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（）
A．勾股定理
B．直径所对的圆心角是直角
C．勾股定理的逆定理
D．90°的圆周角所对的弦是直径
8．如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60°，则花坛对角线AC的长等于（）
A．6米B．6米C．3米D．3米
9．如图，已知“人字梯”的5个踩档把梯子等分成6份，从上往下的第二个踩档与第三个踩档的正中间处有一条60cm长的绑绳EF，tanα=，则“人字梯”的顶端离地面的高度AD是（）
A．144cm B．180cm C．240cm D．360cm
10．如图，已知△ABC，AB=BC，以AB为直径的圆交AC于点D，过点D的⊙O的切线交BC于点E．若CD=5，CE=4，则⊙O的半径是（）
A．3 B．4C．D．
二、填空题（本题有6小题，每小题4分，共24分）
11．（4分）（2015•衢州）从小明、小聪、小惠和小颖四人中随机选取1人参加学校组织的敬老活动，则小明被选中的概率是．
12．（4分）（2015•衢州）如图，小聪与小慧玩跷跷板，跷跷板支架高EF为0.6米，E是AB的中点，那么小聪能将小慧翘起的最大高度BC等于米．
13．（4分）（2015•衢州）写出一个解集为x＞1的一元一次不等式：．
14．（4分）（2015•衢州）一条排水管的截面如图所示，已知排水管的半径OA=1m，水面宽AB=1.2m，某天下雨后，水管水面上升了0.2m，则此时排水管水面宽CD等于m．
15．（4分）（2015•衢州）已知，正六边形ABCDEF在直角坐标系内的位置如图所示，A（﹣2，0），点B 在原点，把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转，每次翻转60°，经过2015次翻转之后，点B的坐标是．
16．（4分）（2015•衢州）如图，已知直线y=﹣x+3分别交x轴、y轴于点A、B，P是抛物线y=﹣x2+2x+5的一个动点，其横坐标为a，过点P且平行于y轴的直线交直线y=﹣x+3于点Q，则当PQ=BQ时，a的值是．
三、解答题（本题有8小题，第17-19小题每小题6分，第20-21小题每小题6分，第22-23小题每小题6分，第24小题12分，共66分。
请务必写出解答过程）
17．（6分）（2015•衢州）计算：﹣|﹣2|+﹣4sin60°．
18．（6分）（2015•衢州）先化简，再求值：（x2﹣9）÷，其中x=﹣1．
19．（6分）（2015•衢州）如图，已知点A（a，3）是一次函数y1=x+b图象与反比例函数y2=图象的一个
交点．
（1）求一次函数的解析式；
（2）在y轴的右侧，当y1＞y2时，直接写出x的取值范围．
20．（8分）（2015•衢州）某校在开展读书交流活动中全体师生积极捐书．为了解所捐书籍的种类，对部分书籍进行了抽样调查，李老师根据调查数据绘制了如图所示不完整统计图．请根据统计图回答下面问题：
（1）本次抽样调查的书籍有多少本？请补全条形统计图；
（2）求出图1中表示文学类书籍的扇形圆心角度数；
（3）本次活动师生共捐书1200本，请估计有多少本科普类书籍？
21．（8分）（2015•衢州）如图1，将矩形ABCD沿DE折叠，使顶点A落在DC上的点A′处，然后将矩形展平，沿EF折叠，使顶点A落在折痕DE上的点G处．再将矩形ABCD沿CE折叠，此时顶点B恰好
落在DE上的点H处．如图2．
（1）求证：EG=CH；
（2）已知AF=，求AD和AB的长．
22．（10分）（2015•衢州）小明在课外学习时遇到这样一个问题：
定义：如果二次函数y=a1x2+b1x+c1（a1≠0，a1，b1，c1是常数）与y=a2x2+b2x+c2（a2≠0，a2，b2，c2是常数）满足a1+a2=0，b1=b2，c1+c2=0，则称这两个函数互为“旋转函数”．
求函数y=﹣x2+3x﹣2的“旋转函数”．
小明是这样思考的：由函数y=﹣x2+3x﹣2可知，a1=﹣1，b1=3，c1=﹣2，根据a1+a2=0，b1=b2，c1+c2=0，求出a2，b2，c2，就能确定这个函数的“旋转函数”．
请参考小明的方法解决下面问题：
（1）写出函数y=﹣x2+3x﹣2的“旋转函数”；
（2）若函数y=﹣x2+mx﹣2与y=x2﹣2nx+n互为“旋转函数”，求（m+n）2015的值；
（3）已知函数y=﹣（x+1）（x﹣4）的图象与x轴交于点A、B两点，与y轴交于点C，点A、B、C关于原点的对称点分布是A1，B1，C1，试证明经过点A1，B1，C1的二次函数与函数y=﹣（x+1）（x﹣4）互为“旋转函数．”
23．（10分）（2015•衢州）高铁的开通，给衢州市民出行带来了极大的方便，“五一”期间，乐乐和颖颖相约到杭州市的某游乐园游玩，乐乐乘私家车从衢州出发1小时后，颖颖乘坐高铁从衢州出发，先到杭州火车站，然后再转车出租车取游乐园（换车时间忽略不计），两人恰好同时到达游乐园，他们离开衢州的距离y（千米）与乘车时间t（小时）的关系如图所示．
请结合图象解决下面问题：
（1）高铁的平均速度是每小时多少千米？
（2）当颖颖达到杭州火车东站时，乐乐距离游乐园还有多少千米？
（3）若乐乐要提前18分钟到达游乐园，问私家车的速度必须达到多少千米/小时？
24．（12分）（2015•衢州）如图，在△ABC中，AB=5，AC=9，S△ABC=，动点P从A点出发，沿射线
AB方向以每秒5个单位的速度运动，动点Q从C点出发，以相同的速度在线段AC上由C向A运动，当Q点运动到A点时，P、Q两点同时停止运动，以PQ为边作正方形PQEF（P、Q、E、F按逆时针排序），以CQ为边在AC上方作正方形QCGH．
（1）求tanA的值；
（2）设点P运动时间为t，正方形PQEF的面积为S，请探究S是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由；
（3）当t为何值时，正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上，请直接写出t的值．。