北京大学acm1001题详细解答
acm初赛试题及答案

acm初赛试题及答案# acm初赛试题及答案1. 问题描述给定一个整数n,求出n以内所有正整数的和。
2. 输入格式输入包含一个整数n(1≤n≤10000)。
3. 输出格式输出一个整数,表示n以内所有正整数的和。
4. 样例输入```100```5. 样例输出```5050```6. 问题分析本题要求计算从1到n的所有正整数的和。
这是一个简单的数学问题,可以通过公式求解。
7. 解题思路使用求和公式:\( \sum_{i=1}^{n} i = \frac{n(n+1)}{2} \)。
8. 算法实现编写一个函数,输入n,输出计算结果。
9. 代码示例```pythondef sum_of_numbers(n):return n * (n + 1) // 2n = int(input())print(sum_of_numbers(n))```10. 注意事项输入的n可能会非常大,需要考虑整数溢出的问题。
11. 测试用例- 输入:1输出:1- 输入:10输出:55- 输入:10000输出:5000500012. 评分标准- 正确性:算法正确,输出结果符合预期。
- 效率:算法执行效率高,能在规定时间内完成计算。
- 代码风格:代码可读性好,注释清晰。
13. 常见错误- 未考虑整数溢出。
- 未正确使用求和公式。
- 代码中存在语法错误。
14. 扩展思考- 如果要求计算从m到n的所有正整数的和,应该如何修改算法? - 如何优化算法以处理更大的输入值?15. 参考答案- 对于扩展思考的第一个问题,可以将求和公式修改为:\( \sum_{i=m}^{n} i = \frac{n(n+1)}{2} - \frac{(m-1)m}{2} \)。
- 对于扩展思考的第二个问题,可以考虑使用更高效的数据结构或者算法来减少计算量。
以上是ACM初赛试题及答案的完整内容。
大学ACM考试题目及作业答案整理

ACM作业与答案整理1、平面分割方法:设有n条封闭曲线画在平面上,而任何两条封闭曲线恰好相交于两点,且任何三条封闭曲线不相交于同一点,问这些封闭曲线把平面分割成的区域个数。
#include <iostream.h>int f(int n){if(n==1) return 2;else return f(n-1)+2*(n-1);}void main(){int n;while(1){cin>>n;cout<<f(n)<<endl;}}2、LELE的RPG难题:有排成一行的n个方格,用红(Red)、粉(Pink)、绿(Green)三色涂每个格子,每格涂一色,要求任何相邻的方格不能同色,且首尾两格也不同色.编程全部的满足要求的涂法.#include<iostream.h>int f(int n){if(n==1) return 3;else if(n==2) return 6;else return f(n-1)+f(n-2)*2;}void main(){int n;while(1){cin>>n;cout<<f(n)<<endl;}}3、北大ACM(1942)Paths on a GridTime Limit: 1000MS Memory Limit: 30000K DescriptionImagine you are attending your math lesson at school. Once again, you are bored because your teacher tells things that you already mastered years ago (this time he's explaining that (a+b)2=a2+2ab+b2). So you decide to waste your time with drawing modern art instead.Fortunately you have a piece of squared paper and you choose a rectangle of size n*m on the paper. Let's call this rectangle together with the lines it contains a grid. Starting at the lower left corner of the grid, you move your pencil to the upper right corner, taking care that it stays on the lines and moves only to the right or up. The result is shown on the left:Really a masterpiece, isn't it? Repeating the procedure one more time, you arrive with the picture shown on the right. Now you wonder: how many different works of art can you produce?InputThe input contains several testcases. Each is specified by two unsigned 32-bit integers n and m, denoting the size of the rectangle. As you can observe, the number of lines of the corresponding grid is one more in each dimension. Input is terminated by n=m=0.OutputFor each test case output on a line the number of different art works that can be generated using the procedure described above. That is, how many paths are there on a grid where each step of the path consists of moving one unit to the right orone unit up? You may safely assume that this number fits into a 32-bit unsigned integer.Sample Input5 41 10 0Sample Output1262#include<iostream>using namespace std;longlong f(long long m, long long n){if(n==0) return 1;else return f(m-1,n-1)*m/n;}int main(){longlongm,n;while(scanf("%I64d %I64d",&n,&m) &&n+m){printf("%I64d\n",f(m+n,min(m,n)));}return 0;}1、(并查集)若某个家族人员过于庞大,要判断两个是否是亲戚,确实还很不容易,现在给出某个亲戚关系图,求任意给出的两个人是否具有亲戚关系。
ACM试题及参考答案
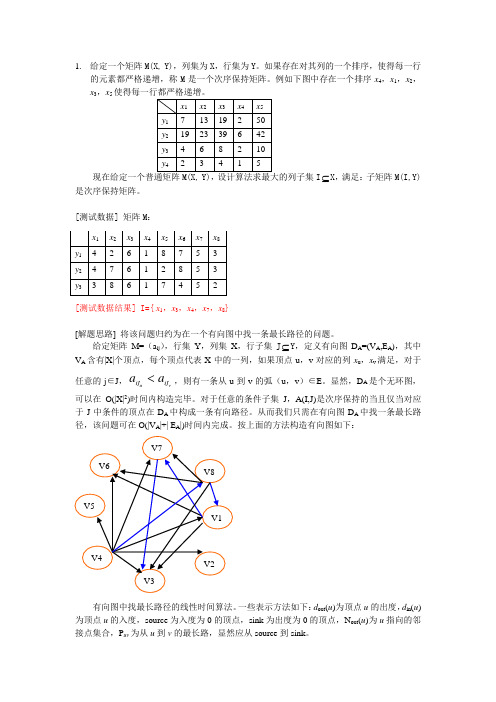
1. 给定一个矩阵M(X, Y),列集为X ,行集为Y 。
如果存在对其列的一个排序,使得每一行的元素都严格递增,称M 是一个次序保持矩阵。
例如下图中存在一个排序x 4,x 1,x 2,x 3,x 5I ⊆X ,满足:子矩阵M(I,Y)是次序保持矩阵。
[测试数据] 矩阵M :[测试数据结果] I={ x 1,x 3,x 4,x 7,x 8}[解题思路] 将该问题归约为在一个有向图中找一条最长路径的问题。
给定矩阵M=(a ij ),行集Y ,列集X ,行子集J ⊆Y ,定义有向图D A =(V A ,E A ),其中V A 含有|X|个顶点,每个顶点代表X 中的一列,如果顶点u ,v 对应的列x u ,x v 满足,对于任意的j ∈J ,u v ij ij a a <,则有一条从u 到v 的弧(u ,v )∈E 。
显然,D A 是个无环图,可以在O(|X|2)时间内构造完毕。
对于任意的条件子集J ,A(I,J)是次序保持的当且仅当对应于J 中条件的顶点在D A 中构成一条有向路径。
从而我们只需在有向图D A 中找一条最长路径,该问题可在O(|V A |+| E A |)时间内完成。
按上面的方法构造有向图如下:有向图中找最长路径的线性时间算法。
一些表示方法如下:d out (u )为顶点u 的出度,d in (u )为顶点u 的入度,source 为入度为0的顶点,sink 为出度为0的顶点,N out (u )为u 指向的邻接点集合,P uv 为从u 到v 的最长路,显然应从source 到sink 。
在每一步为每个顶点关联一个永久的或临时的标签。
v被赋了一个临时标签(v’,i v)表明在当前步,算法找出的最长的从source到v的有向路长度为i v,且经由v’而来。
v被赋了一个永久标签[v’,i v]表明从source到v的最长有向路长度为i v,且经由v’而来,通过回溯每个顶点的永久标签就可以找出最长有向路。
c acm试题及答案

c acm试题及答案ACM(Association for Computing Machinery)是计算机科学领域的国际性学术组织,旨在推动计算机科学的发展与研究。
ACM竞赛是ACM组织举办的一项计算机算法编程竞赛,每年都有数以千计的计算机专业学生参加。
这篇文章将介绍一道ACM试题,并提供解答。
题目描述:给定一个整数数组nums,其中所有元素都是非负整数,现在要求你计算nums中连续子数组的最大和,并输出该最大和。
输入:第一行输入一个整数n,表示数组长度(1 <= n <= 10^5)。
第二行输入n个整数,表示数组nums的元素(元素范围为0 <= nums[i] <= 100)。
输出:输出一个整数,表示nums中连续子数组的最大和。
示例:输入:51 2 3 4 5输出:15解释:最大和子数组为[1, 2, 3, 4, 5],和为15。
解答:首先,我们可以使用一个变量maxSum来记录当前得到的最大和,初始化为0。
同时,我们还使用一个变量sum来记录当前连续子数组的和,初始化为0。
接下来,我们对数组nums进行遍历。
对于每一个元素nums[i],我们将其加到sum中,并判断sum是否大于0。
如果sum大于0,说明当前连续子数组的和对后面的结果是有正向贡献的,我们可以继续累加后面的元素。
如果sum小于等于0,说明当前连续子数组的和对后面的结果没有正向贡献,我们可以将sum重新置为0,重新开始计算连续子数组的和。
在遍历过程中,我们不断更新maxSum的值,保证其为当前得到的最大和。
最终,遍历结束后的maxSum即为所求的最大和。
下面是具体的实现代码:```cpp#include <iostream>#include <vector>#include <algorithm>using namespace std;int maxSubArray(vector<int>& nums) { int maxSum = 0;int sum = 0;for(int i = 0; i < nums.size(); i++) { sum += nums[i];if(sum > maxSum) {maxSum = sum;}if(sum <= 0) {sum = 0;}}return maxSum;}int main() {int n;cin >> n;vector<int> nums(n);for(int i = 0; i < n; i++) {cin >> nums[i];}int result = maxSubArray(nums);cout << result << endl;return 0;}```以上就是解答c acm试题并提供相应代码的文章。
acm竞赛试题及答案

acm竞赛试题及答案ACM竞赛试题及答案1. 问题描述:给定一个整数数组,找出数组中没有出现的最小的正整数。
2. 输入格式:第一行包含一个整数n,表示数组的长度。
第二行包含n个整数,表示数组的元素。
3. 输出格式:输出一个整数,表示数组中没有出现的最小的正整数。
4. 样例输入:53 4 1 2 55. 样例输出:66. 问题分析:首先,我们需要理解题目要求我们找出数组中缺失的最小正整数。
这意味着我们需要检查数组中的每个元素,并确定最小的正整数是否在数组中。
7. 算法描述:- 遍历数组,使用一个哈希集合记录出现的数字。
- 从1开始,检查每个正整数是否在哈希集合中,直到找到不在集合中的最小正整数。
8. 代码实现:```pythondef find_missing_positive(nums):seen = set()for num in nums:if num <= 0:continuewhile num in seen or num > len(nums):num += 1seen.add(num)return min(set(range(1, len(nums) + 1)) - seen)```9. 测试用例:- 输入:[3, 4, -1, 1]- 输出:210. 答案解析:在给定的测试用例中,数组[3, 4, -1, 1]中没有出现的最小正整数是2。
这是因为-1不是正整数,所以可以忽略。
数组中已经出现了1和3,所以下一个最小的正整数就是2。
11. 注意事项:- 确保数组中的元素是整数。
- 考虑数组中可能包含0或负数的情况。
- 算法的时间复杂度应尽可能低。
12. 扩展思考:- 如果数组非常大,如何优化算法?- 如果数组中的元素可以是浮点数,算法应该如何修改?13. 参考答案:- 针对大数组,可以考虑使用更高效的数据结构,如平衡二叉搜索树。
- 如果元素是浮点数,需要先将其转换为整数,然后再进行处理。
acm大赛试题及答案

acm大赛试题及答案ACM大赛试题及答案1. 题目一:字符串反转问题描述:编写一个程序,输入一个字符串,输出其反转后的字符串。
输入格式:输入包含一个字符串,字符串长度不超过100。
输出格式:输出反转后的字符串。
示例:输入:hello输出:olleh答案:```pythondef reverse_string(s):return s[::-1]input_string = input().strip()print(reverse_string(input_string))```2. 题目二:计算阶乘问题描述:编写一个程序,输入一个非负整数n,输出n的阶乘。
输入格式:输入包含一个非负整数n,n不超过20。
输出格式:输出n的阶乘。
示例:输入:5输出:120答案:```pythondef factorial(n):if n == 0:return 1else:return n * factorial(n - 1)n = int(input())print(factorial(n))```3. 题目三:寻找最大数问题描述:给定一个包含n个整数的数组,找出数组中的最大数。
输入格式:输入包含一个整数n,表示数组的大小,随后是n个整数。
输出格式:输出数组中的最大数。
示例:输入:5 1 2 3 4 5输出:5答案:```pythonn = int(input())numbers = list(map(int, input().split()))max_number = max(numbers)print(max_number)```4. 题目四:判断闰年问题描述:编写一个程序,输入一个年份,判断该年份是否为闰年。
输入格式:输入包含一个整数,表示年份。
输出格式:如果输入的年份是闰年,则输出"Yes",否则输出"No"。
示例:输入:2000输出:Yes答案:```pythonyear = int(input())if (year % 4 == 0 and year % 100 != 0) or (year % 400 == 0):print("Yes")else:print("No")```5. 题目五:斐波那契数列问题描述:编写一个程序,输入一个非负整数n,输出斐波那契数列的第n项。
ACM入门题(北大oj)

1000#include<stdio.h>int main(){int a,b,c;while(scanf("%d%d",&a,&b)!=EOF){c=a+b;printf("%d\n",c);}}1067#include<stdio.h>#include<math.h>#include<stdlib.h>int main(){int a,b;while(scanf("%d%d",&a,&b)!=EOF){if(a>b){int t=a;a=b;b=t;}int k=b-a;int a0=(int)(k*(1+sqrt(5.0))/2);if(a0==a) printf("0\n");else printf("1\n");}}1080#include<stdio.h>#include<stdlib.h>int a[5][5]={5,-1,-2,-1,-3,-1,5,-3,-2,-4,-2,-3,5,-2,-2,-1,-2,-2,5,-1,-3,-4,-2,-1,0};int main(){int ca;scanf("%d",&ca);while(ca--){int n,m,i,j,max[105][105],b[105],d[105];char s[105],c[105];scanf("%d%s",&n,s);scanf("%d%s",&m,c);for(i=1;i<=n;i++){if(s[i-1]=='A') b[i]=0;if(s[i-1]=='C') b[i]=1;if(s[i-1]=='G') b[i]=2;if(s[i-1]=='T') b[i]=3;}for(i=1;i<=m;i++){if(c[i-1]=='A') d[i]=0;if(c[i-1]=='C') d[i]=1;if(c[i-1]=='G') d[i]=2;if(c[i-1]=='T') d[i]=3;}max[0][0]=0;for(i=1;i<=n;i++)max[i][0]=max[i-1][0]+a[b[i]][4];for(i=1;i<=m;i++)max[0][i]=max[0][i-1]+a[4][d[i]];for(i=1;i<=n;i++)for(j=1;j<=m;j++){max[i][j]=max[i-1][j-1]+a[b[i]][d[j]];if(max[i-1][j]+a[b[i]][4]>max[i][j])max[i][j]=max[i-1][j]+a[b[i]][4];if(max[i][j-1]+a[4][d[j]]>max[i][j])max[i][j]=max[i][j-1]+a[4][d[j]];}printf("%d\n",max[n][m]);}}1013#include<stdio.h>#include<algorithm>#include<math.h>#include<stdlib.h>#define PI 3.141592653using namespace std;struct point{double x;double y;}p[30005],res[30005];int cmp(point p1,point p2){return p1.y<p2.y||(p1.y==p2.y&&p1.x<p2.x);}bool ral(point p1,point p2,point p3){if((p2.x-p1.x)*(p3.y-p1.y)<=(p2.y-p1.y)*(p3.x-p1.x)) return true;return false;}double dis(point p1,point p2){return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));}int main(){int n,m;while(scanf("%d%d",&n,&m)!=EOF){int i,j;for(i=0;i<n;i++)scanf("%lf%lf",&p[i].x,&p[i].y);sort(p,p+n,cmp);res[0]=p[0];res[1]=p[1];int top=1;for(i=2;i<n;i++){while(top&&ral(res[top-1],res[top],p[i]))top--;res[++top]=p[i];}int len=top;res[++top]=p[n-2];for(i=n-3;i>=0;i--){while(top!=len&&ral(res[top-1],res[top],p[i]))top--;res[++top]=p[i];}double t=0;for(i=0;i<top;i++)t=t+dis(res[i],res[i+1]);printf("%.lf\n",t+2*PI*m);}}1149#include<iostream>#include<cstring>using namespace std;#define inf 0x5fffffffint a[105][105],f[1005],ct[1005],pre[205],n,m,q[105]; int bfs(){int flow=inf,qh=0,qe=1,i;memset(pre,-1,sizeof(pre));q[1]=0;pre[0]=-1;while(qh<qe){int t=q[++qh];for(i=1;i<=n+1;i++)if(pre[i]==-1&&a[t][i]>0){pre[i]=t;if(a[t][i]<flow) flow=a[t][i];if(i==n+1) return flow;q[++qe]=i;}}return -1;}void maxflow(){int res=0,ans,t;while((ans=bfs())!=-1){res=res+ans;t=n+1;while(t)a[pre[t]][t]-=ans;a[t][pre[t]]+=ans;t=pre[t];}}printf("%d\n",res);}int main(){while(scanf("%d%d",&m,&n)!=EOF){memset(f,-1,sizeof(f));memset(a,0,sizeof(a));int i,j,k,t;for(i=1;i<=m;i++)scanf("%d",&ct[i]);for(i=1;i<=n;i++){scanf("%d",&k);for(j=1;j<=k;j++){scanf("%d",&t);if(f[t]!=-1) a[f[t]][i]=inf;else a[0][i]=a[0][i]+ct[t];f[t]=i;}scanf("%d",&k);a[i][n+1]=k;}maxflow();}}1157#include<stdio.h>#include<stdlib.h>int a[105][105],b[105][105];int main(){int max(int x,int y);int n,m;while(scanf("%d%d",&n,&m)!=EOF){for(i=1;i<=n;i++)for(j=1;j<=m;j++)scanf("%d",&a[i][j]);b[1][1]=a[1][1];for(i=2;i<=m-n+1;i++){if(a[1][i]<b[1][i-1]) b[1][i]=b[1][i-1];else b[1][i]=a[1][i];}for(i=2;i<=n;i++)for(j=i;j<=i+m-n;j++){a[i][j]=a[i][j]+b[i-1][j-1];if(i==j) b[i][j]=a[i][j];else{if(a[i][j]>b[i][j-1]) b[i][j]=a[i][j];else b[i][j]=b[i][j-1];}}printf("%d\n",b[n][m]);}}1200#include<stdio.h>#include<string.h>bool flag[20000000];int a[300];char s[20000000];int main(){int n,m;while(scanf("%d%d",&n,&m)!=EOF){memset(flag,0,sizeof(flag));scanf("%s",s);int i,j=0,len=strlen(s);memset(a,0,sizeof(a));for(i=0;i<len;i++)a[s[i]]=1;for(i=0;i<256;i++)if(a[i]==1) a[i]=j++;int mod=1,res=0;for(i=0;i<n-1;i++)mod=mod*m;for(i=0;i<n;i++)res=res*m+a[s[i]];flag[res]=1;for(i=n;i<len;i++){res=res%mod*m+a[s[i]];flag[res]=1;}int count=0;mod=mod*m;for(i=0;i<=mod;i++)if(flag[i]==1) count++;printf("%d\n",count);}}1207#include<stdio.h>#include<stdlib.h>int main(){int b,c,i,j,max=0,k,t,r;while(scanf("%d%d",&b,&c)!=EOF){if(b>c){t=b;r=c;}else{t=c;r=b;}max=0;for(i=r;i<=t;i++){j=1;k=i;while(k!=1){j++;if(k%2==0) k=k/2;else k=3*k+1;}if(j>max) max=j;}printf("%d %d %d\n",b,c,max);}//system("pause");}1273#include<iostream>#include<cstring>#include<queue>using namespace std;#define inf INT_MAXint n,m,a[205][205],pre[205],lev[205],num[205]; void bfs(){queue<int>Q;memset(lev,-1,sizeof(lev));memset(num,0,sizeof(num));Q.push(n);lev[n]=0;num[0]=1;while(!Q.empty()){int t=Q.front(),i;Q.pop();for(i=1;i<=n;i++)if(lev[i]==-1&&a[i][t]>0){lev[i]=lev[t]+1;num[lev[i]]++;Q.push(i);}}}int maxflow(){int flow=0,i,ans,cur=1;bfs();while(lev[cur]<n){if(cur==n){ans=inf;while(cur!=1){if(a[pre[cur]][cur]<ans) ans=a[pre[cur]][cur];cur=pre[cur];}cur=n;while(cur!=1){a[pre[cur]][cur]-=ans;a[cur][pre[cur]]+=ans;cur=pre[cur];}flow=flow+ans;}for(i=1;i<=n;i++)if(a[cur][i]>0&&lev[cur]==lev[i]+1){pre[i]=cur;cur=i;break;}if(i>n){lev[cur]=n+1;num[lev[cur]]--;if(num[lev[cur]]==0) break;for(i=1;i<=n;i++)if(a[cur][i]>0&&lev[i]+1<lev[cur]) lev[cur]=lev[i]+1;num[lev[cur]]++;if(cur!=1) cur=pre[cur];}}return flow;}int main(){while(scanf("%d%d",&m,&n)!=EOF){int i,j;memset(a,0,sizeof(a));for(i=0;i<m;i++){int b,c,d;scanf("%d%d%d",&b,&c,&d);a[b][c]+=d;}printf("%d\n",maxflow());}}1285#include<stdio.h>#include<string.h>int num[55];unsigned __int64 f[55][55];int main(){int n,m,ct=0;while(scanf("%d%d",&n,&m)!=EOF){if(n==0&&m==0) break;int i,j,a,k;memset(num,0,sizeof(num));for(i=0;i<n;i++){scanf("%d",&a);num[a]++;}memset(f,0,sizeof(f));f[0][0]=1;for(i=0;i<50;i++)for(j=0;j<=50;j++)for(k=0;k<=num[i+1];k++)f[i+1][j+k]=f[i+1][j+k]+f[i][j];printf("Case %d:\n",++ct);for(i=0;i<m;i++){scanf("%d",&a);printf("%I64d\n",f[50][a]);}}}1364#include <iostream>#include <queue>#include <cstring>using namespace std;int v[105],pre[105],w[105],h[105],flag[105],ct[105],d[105],n,m,num; void add(int a,int b,int c){v[num]=b;pre[num]=h[a];w[num]=c;h[a]=num++;}bool spfa(){int i;queue<int> Q;for(i=0;i<=n;i++){Q.push(i);flag[i]=1;d[i]=0;}while(!Q.empty()){int t=Q.front();Q.pop();flag[t]=0;for(i=h[t];i>=0;i=pre[i]){int p=v[i];if(d[t]+w[i]<d[p]){d[p]=d[t]+w[i];ct[p]++;if(flag[p]==0){Q.push(p);flag[p]=1;}}if(ct[p]>n) return false;}}return true;}int main(){while(cin>>n){if(n==0) break;cin>>m;int a,b,c;char s[3];num=0;memset(flag,0,sizeof(flag));memset(ct,0,sizeof(ct));memset(h,-1,sizeof(h));for(int i=1;i<=m;i++){cin>>a>>b>>s>>c;if(strcmp(s,"gt")==0) add(a-1,a+b,-1-c);else add(a+b,a-1,c-1);}if(spfa()) cout<<"lamentable kingdom"<<endl;else cout<<"successful conspiracy"<<endl;}return 0;}1384#include<stdio.h>#include<stdlib.h>int b[10005],a[600][2];int main(){int ca;scanf("%d",&ca);while(ca--){int M1,M2,M,n,i,j,value;scanf("%d%d",&M1,&M2);M=M2-M1;scanf("%d",&n);for(i=0;i<n;i++)scanf("%d%d",&a[i][0],&a[i][1]);for(i=0;i<=M;i++)b[i]=-1;b[0]=0;for(i=0;i<n;i++)for(j=0;j+a[i][1]<=M;j++)if(b[j]!=-1){value=b[j]+a[i][0];if(value<b[j+a[i][1]]||b[j+a[i][1]]==-1)b[a[i][1]+j]=value;}if(b[M]==-1) printf("This is impossible.\n");elseprintf("The minimum amount of money in the piggy-bank is %d.\n",b[M]);}}1473#include<stdio.h>#include<math.h>#include<stdlib.h>#include<string.h>int main(){char S[300],c[300][100];int count1=0;while(scanf("%s",S)!=EOF){if(strcmp(S,"END")==0) break;int len=strlen(S),i,count=0,j=0,d;for(i=0;i<len;i++){if(S[i]!=','&&S[i]!='.'){c[count][j]=S[i];j++;}else{c[count][j]='\0';j=0;count++;}}int nw=0,ne=0,sw=0,se=0,n=0,s=0,e=0,w=0;for(i=0;i<count;i++){char cc[10];sscanf(c[i],"%[0-9]",cc);sscanf(cc,"%d",&d);if(strlen(c[i])==strlen(cc)+1){if(c[i][strlen(cc)]=='N') n+=d;if(c[i][strlen(cc)]=='S') s+=d;if(c[i][strlen(cc)]=='E') e+=d;if(c[i][strlen(cc)]=='W') w+=d;}if(strlen(c[i])==strlen(cc)+2){if(c[i][strlen(cc)]=='N'&&c[i][strlen(cc)+1]=='W')nw+=d;if(c[i][strlen(cc)]=='N'&&c[i][strlen(cc)+1]=='E') ne+=d;if(c[i][strlen(cc)]=='S'&&c[i][strlen(cc)+1]=='W') sw+=d;if(c[i][strlen(cc)]=='S'&&c[i][strlen(cc)+1]=='E') se+=d;}}double x=e-w+((ne+se-nw-sw)*sqrt(2))/2;double y=n-s+((nw+ne-sw-se)*sqrt(2))/2;double ss=sqrt(x*x+y*y);count1++;printf("Map #%d\n",count1);printf("The treasure is located at (%.3lf,%.3lf).\n",x,y);printf("The distance to the treasure is %.3lf.\n",ss);printf("\n");}}1505#include<stdio.h>#include<string.h>#include<stdlib.h>int a[510],s[510],t[505][505],num[505],flag[505];int ma(int x,int y){if(x<y) return y;return x;}int main(){int ca;scanf("%d",&ca);while(ca--){int n,m,i,j,k,res;scanf("%d%d",&n,&m);for(i=1;i<=n;i++)scanf("%d",&a[i]);s[0]=0;for(i=1;i<=n;i++)s[i]=s[i-1]+a[i];for(i=1;i<n;i++)t[1][i]=s[i];memset(flag,0,sizeof(flag));for(i=2;i<m;i++)for(j=i;j<n;j++){res=1000000000;for(k=i-1;k<=j-1;k++)if(res>ma(t[i-1][k],s[j]-s[k])) res=ma(t[i-1][k],s[j]-s[k]);t[i][j]=res;}res=s[n];for(i=m-1;i<n;i++)if(ma(t[m-1][i],s[n]-s[i])<res) res=ma(t[m-1][i],s[n]-s[i]);num[0]=n;for(i=1;i<m;i++){int ti=0;for(j=num[i-1];j>m-i;j--){ti=ti+a[j];if(ti>res) break;}num[i]=j;flag[j]=1;}for(i=1;i<n;i++){if(flag[i]==0) printf("%d ",a[i]);else printf("%d / ",a[i]);}printf("%d\n",a[i]);}}1511#include<iostream>#include<cstring>#include<cstdio>#include<queue>#define inf 2000000000using namespace std;int ct,pre[1000005],len[1000005],v[1000005],h[1000005],n,m,vis[1000005],l[1000005]; int a[1000005],b[1000005],c[1000005];queue<int> Q;void add(int a,int b,int c){pre[ct]=h[a];len[ct]=c;v[ct]=b;h[a]=ct++;}void spfa(){int i;memset(vis,0,sizeof(vis));Q.push(1);vis[1]=1;for(i=1;i<=n;i++)l[i]=inf;l[1]=0;while(!Q.empty()){int t=Q.front();for(i=h[t];i!=-1;i=pre[i])if(l[t]+len[i]<l[v[i]]){l[v[i]]=l[t]+len[i];if(vis[v[i]]==0){vis[v[i]]=1;Q.push(v[i]);}}Q.pop();vis[t]=0;}}int main(){int ca;scanf("%d",&ca);while(ca--){scanf("%d%d",&n,&m);int i,j;__int64 res=0;ct=0;memset(h,-1,sizeof(h));for(i=0;i<m;i++){scanf("%d%d%d",&a[i],&b[i],&c[i]);add(a[i],b[i],c[i]);}spfa();for(i=2;i<=n;i++)res=res+l[i];ct=0;memset(h,-1,sizeof(h));for(i=0;i<m;i++)add(b[i],a[i],c[i]);spfa();for(i=2;i<=n;i++)res=res+l[i];printf("%I64d\n",res);}}1609#include<stdio.h>#include<stdlib.h>int a[105][105];int main(){int n;while(scanf("%d",&n)!=EOF){if(n==0){printf("*\n");break;}int i,j;for(i=0;i<101;i++)for(j=0;j<101;j++)a[i][j]=0;for(i=0;i<n;i++){int m,k;scanf("%d%d",&m,&k);a[m][k]=a[m][k]+1;}for(i=1;i<101;i++)for(j=1;j<101;j++)if(i*j!=1){if(a[i][j-1]>=a[i-1][j])a[i][j]=a[i][j]+a[i][j-1];elsea[i][j]=a[i][j]+a[i-1][j];}printf("%d\n",a[100][100]);}}1611#include<iostream>using namespace std;int f[30005],cont[30005];int findf(int a){if(f[a]!=a) f[a]=findf(f[a]);return f[a];}void com(int a,int b){int x=findf(a);int y=findf(b);if(x==y) return;if(cont[x]<=cont[y]){f[x]=y;cont[y]=cont[x]+cont[y];}else{f[y]=x;cont[x]=cont[x]+cont[y];}}int main(){int m,n;while(scanf("%d%d",&n,&m)!=EOF&&n){int num,st,i,j,ed;for(i=0;i<n;i++){f[i]=i;cont[i]=1;}for(i=0;i<m;i++){scanf("%d%d",&num,&st);for(j=1;j<num;j++){scanf("%d",&ed);com(st,ed);}}printf("%d\n",cont[findf(0)]);}}1651#include<stdio.h>#include<stdlib.h>long a[105],i,s[105][105],j,t,k;int main(){int n;while(scanf("%d",&n)!=EOF){for(i=0;i<n;i++)scanf("%ld",&a[i]);for(i=0;i<n-1;i++)s[i][i+1]=0;for(j=2;j<n;j++)for(i=0;i+j<n;i++){t=100000000;for(k=i+1;k<i+j;k++)if(s[i][k]+s[k][i+j]+a[i]*a[k]*a[i+j]<t)t=s[i][k]+s[k][i+j]+a[i]*a[k]*a[i+j];s[i][i+j]=t;}printf("%ld\n",s[0][n-1]);}}1753#include<iostream>using namespace std;int t[]={19,39,78,140,305,626,1252,2248,4880,10016,20032,35968,12544,29184,58368,51200}; #define SIZE 65535int BFS(int state){int visited[SIZE],d[SIZE],u,v,i;int Qu[SIZE],rear,front;memset(visited,0,sizeof(visited));visited[state]=1;d[state]=0;rear=front=0;Qu[++rear]=state;while(rear!=front){u=Qu[++front];for(i=0;i<16;++i) {v=u^t[i];if(v==0 || v==65535) return d[u]+1;if(visited[v]==0){visited[v]=1;d[v]=d[u]+1;Qu[++rear]=v;}visited[u]=-1;}return -1;}int main(){char ch[5][5];int i,j,start;start=0;for(i=0;i<4;++i)scanf("%s",ch[i]);for(i=0;i<4;++i)for(j=0;j<4;++j)if(ch[i][j]=='b') start^=(1<<((3-i)*4+(3-j)));if(start==0||start==65535) printf("0\n");else{int result=BFS(start);if(result==-1) printf("Impossible\n");else printf("%d\n",result);}}1797#include<stdio.h>#include<string.h>int a[1005][1005],vis[1005],len[1005];int mm(int a,int b){return a<b?a:b;}int main(){int ca,ct=0;scanf("%d",&ca);while(ca--){int n,m;scanf("%d%d",&n,&m);int i,j;memset(a,0,sizeof(a));for(i=1;i<=m;i++)int r,t,l;scanf("%d%d%d",&r,&t,&l);a[r][t]=l;a[t][r]=l;}memset(vis,0,sizeof(vis));for(i=2;i<=n;i++)len[i]=a[1][i];vis[1]=1;for(i=1;i<n;i++){int mmax=0,k;for(j=2;j<=n;j++)if(vis[j]==0&&len[j]>mmax){mmax=len[j];k=j;}vis[k]=1;if(k==n) break;for(j=2;j<=n;j++)if(vis[j]==0){int length=mm(len[k],a[k][j]);if(length>len[j]) len[j]=length;}}printf("Scenario #%d:\n%d\n\n",++ct,len[n]);}}1845#include<iostream>#include<cstring>using namespace std;#define mod 9901__int64 pri[7505],a[100],num[100];void prime(){memset(pri,0,sizeof(pri));int i,j;for(i=2;i<=90;i++)for(j=2;i*j<=7500;j++)j=0;for(i=2;i<=7500;i++)if(pri[i]==0) pri[j++]=i;}__int64 yu(__int64 a,__int64 b){__int64 res=1,c=mod;while(b){if(b%2==0){a=(a%c)*(a%c)%c;b=b/2;}else{res=res*a%c;b--;}}return res;}__int64 f(__int64 a,__int64 b){if(b==0) return 1;if(b==1) return (1+a)%mod;if(b%2==0) return (yu(a,b/2)+(1+yu(a,b/2+1))*f(a,b/2-1))%mod;return ((1+yu(a,b/2+1))*f(a,b/2))%mod;}int main(){prime();int n,m;while(scanf("%d%d",&n,&m)!=EOF){int i,j=0;if(n==0){printf("1\n");continue;}for(i=0;pri[i]*pri[i]<=n;i++)if(n%pri[i]==0){int t=0;while(n%pri[i]==0){t++;n=n/pri[i];}a[j]=pri[i];num[j++]=t;}if(n!=1){a[j]=n;num[j++]=1;}__int64 res=1;for(i=0;i<j;i++)res=res*f(a[i],num[i]*m)%mod;printf("%I64d\n",res);}}1941#include<stdio.h>#include<string.h>int h[22],s[22];char c[1025][2050],ss[1025][2050];void solve(int m){int i,j;if(m==1){h[m]=4;s[m]=2;c[1][1]=' ';c[1][4]=' ';c[1][2]='/';c[1][3]='\\';c[2][1]='/';c[2][2]='_';c[2][3]='_';c[2][4]='\\';memcpy(ss,c,sizeof(c));}if(m!=1){memset(c,' ',sizeof(c));solve(m-1);h[m]=h[m-1]*2;s[m]=s[m-1]*2;for(i=s[m-1]+1;i<=s[m];i++)for(j=1;j<=h[m-1];j++)c[i][j]=c[i][j+h[m-1]]=ss[i-s[m-1]][j];for(i=1;i<=s[m-1];i++)for(j=h[m-1]/2*3;j>h[m-1]/2;j--){c[i][j]=ss[i][j-h[m-1]/2];c[i][j-h[m-1]/2]=' ';}memcpy(ss,c,sizeof(c));}}int main(){int n,i,j,k;h[0]=2;solve(10);while(scanf("%d",&n)!=EOF&&n){for(i=1;i<=s[n];i++){for(j=h[9]-h[n]/2+1;j<=h[9]+i;j++)printf("%c",c[i][j]);printf("\n");}printf("\n");}}1947#include<iostream>#include<algorithm>using namespace std;#define big 10000000int num[155],flag[155],son[155][155],step[155][155],n,m,root; void dsf(int v)int i,j,k;if(v!=root) step[v][1]=num[v]+1;else step[v][1]=num[v];for(i=0;i<num[v];i++){dsf(son[v][i]);for(j=m-1;j>=1;j--)if(step[v][j]<big){for(k=1;k+j<=m;k++)step[v][k+j]=min(step[v][k+j],step[v][j]+step[son[v][i]][k]-2);}}}int main(){while(scanf("%d%d",&n,&m)!=EOF){memset(num,0,sizeof(num));memset(flag,0,sizeof(flag));int i,a,b,j;for(i=1;i<n;i++){scanf("%d%d",&a,&b);flag[b]=1;son[a][num[a]++]=b;}for(i=1;i<=150;i++)for(j=1;j<=150;j++)step[i][j]=big;for(i=1;i<=n;i++)if(flag[i]==0){root=i;dsf(i);break;}int res=big;for(i=1;i<=n;i++)if(step[i][m]<res) res=step[i][m];printf("%d\n",res);}}1964#include<stdio.h>#include<string.h>char s[1005][1005][2];int a[1005][1005],pre[1005],next[1005];int main(){int ca;scanf("%d",&ca);while(ca--){int n,m,i,j,k,res=0;scanf("%d%d",&n,&m);for(i=0;i<n;i++)for(j=0;j<m;j++)scanf("%s",s[i][j]);for(i=0;i<m;i++)if(strcmp(s[0][i],"F")==0) a[0][i]=1;else a[0][i]=0;for(i=1;i<n;i++)for(j=0;j<m;j++)if(strcmp(s[i][j],"F")==0) a[i][j]=a[i-1][j]+1;else a[i][j]=0;for(i=0;i<n;i++){memset(pre,-1,sizeof(pre));for(j=1;j<m;j++)for(k=j-1;k!=-1;k=pre[k])if(a[i][k]<a[i][j]){pre[j]=k;break;}for(j=0;j<m;j++)next[j]=m;for(j=m-2;j>=0;j--)for(k=j+1;k!=m;k=next[k])if(a[i][k]<a[i][j]){next[j]=k;break;}for(j=0;j<m;j++)if((next[j]-pre[j]-1)*a[i][j]>res) res=(next[j]-pre[j]-1)*a[i][j];}printf("%d\n",res*3);}}。
北京大学poj1001解题报告

00748067 张姣
Poj 1001
Description Problems involving the computation of exact values of very large magnitude and precision are common. For example, the computation of the national debt is a taxing experience for many computer systems.
二分法求乘幂
a2n+1=a2n*a a2n=(an)2 其中,a是单精度数
二分法求乘幂之优化平方算法
怎样优化
(a+b)2=a2+2ab+b2 例:123452=1232*10000+452+2*123*45*100 把一个n位数分为一个t位数和一个n-t位数,再求平方
高精度的加法
ncarry=0; for (i=0;i<=len;i++) {
k=a[i]+b[i]+ncarry; a[i+1]+=k/N; ncarry=k%N; } 当最后ncarry>0时,len会变化!!
高精度的减法
先比较大小,大的为a,用一个变量记录符号。 ncarry=0; for (i=0;i<=len;i++) {
题目描述:
涉及到大数据的要求精确计算的问题是很 常见的。比如要求计算国家借款对于许多 电脑系统是一个非常繁重的任务。
本题中要求计算一个在零到一百以内的实 数的n次方(0<n<=25)。
在计算机上进行高精度计算,首先要处 理好以下几个基本问题:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
输入和存储
运算因子超出了整型、实型能表示的范围,肯定不能直接用一个 数的形式来表示。能表示多个数的数据类型有两种:数组和字符 串。
(1)数组:每个数组元素存储1位(在优化时,这里是一个重 点!),有多少位就需要多少个数组元素; 优点:每一位都是数的形式,可以直接加减;运算时非常方便 缺点:数组不能直接输入;输入时每两位数之间必须有分隔符, 不符合数值的输入习惯;
是乘法的时候,就要用int64,否则会出现越 界的情况。
还有就是:输出时对非最高位的补零处理。
另一个问题:
正序?? 逆序??
存储顺序
还有就是一定不要忘了初始化!!
计算结果位数的确定
两数之和的位数最大为较大的数的位数加1。 乘积的位数最大为两个因子的位数之和。 阶乘:lgn!=lgn+lg(n-1)+lg(n-2)...................+lg3+lg2+lg1 =lnn/ln10+ln(n-1)/ln10+ln(n-2)/ln10+................+ln3/ln10+
二分法求乘幂
a2n+1=a2n*a a2n=(an)2 其中,a是单精度数
二分法求乘幂之优化平方算法
怎样优化
(a+b)2=a2+2ab+b2 例:123452=1232*10000+452+2*123*45*100 把一个n位数分为一个t位数和一个n-t位数,再求平方
高精度的加法
ncarry=0; for (i=0;i<=len;i++) {
k=a[i]+b[i]+ncarry; a[i+1]+=k/N; ncarry=k%N; } 当最后ncarry>0时,len会变化!!
高精度的减法
先比较大小,大的为a,用一个变量记录符号。 ncarry=0; for (i=0;i<=len;i++) {
一般来说,我们会构造函数。 还是要注意初始化。 以及 总的位数。
高精度的除法
A÷B 精确值有两种情况: ①、A能被B整除,没有余数。 ②、A不能被B整除,对余数进行处理。首 先,我们知道,在做除法运算时,有一个 不变的量和三个变化的量,不变的量是除 数,三个变化的量分别是:被除数、商和 余数。
可以用减法代替除法运算:不断比较A[1..n] 与B[1..n]的大小,如果A[1..n]>=B[1..n] 则商C[1..n]+1→C[1..n],然后就是一个减 法过程:A[1..n]-B[1..n]→A[1..n]。
无论以何种顺序相乘,乘法次数一定为n(n-1)/2次。 (n为积的位数)
证明:
设F(n)表示乘法次数,则F(1)=0,满足题设 设k<n时,F(k)=k(k-1)/2,现在计算F(n) 设最后一次乘法计算为“k位数*(n-k)位数”,则 F(n)=F(k)+F(n-k)+k (n-k)=n(n-1)/2(与k的选择无关)
This problem requires that you write a program to compute the exact value of Rn where R is a real number ( 0.0 < R < 99.999 ) and n is an integer such that 0 < n <= 25. Input The input will consist of a set of pairs of values for R and n. The R value will occupy columns 1 through 6, and the n value will be in columns 8 and 9. Output The output will consist of one line for each line of input giving the exact value of R^n. Leading zeros should be suppressed in the output. Insignificant trailing zeros must not be printed. Don't print the decimal point if the result is an integer.
否则采用ax+kbx更快
可以先计算两种算法的乘法次数,再解不等式, 就可以得到结论
也可以换一个角度来分析。其实,两种算法主 要差别在最后一步求积上。由于两种方法,积 的位数都是一样的,所以两个因数的差越大, 乘法次数就越小
10!=28*34*52*7
n!分解质因数的复杂度远小于nlogn,可以忽略 不计
与普通算法相比,分解质因数后,虽然因子个 数m变多了,但结果的位数n没有变,只要使用 了缓存,乘法次数还是约为n(n-1)/2次
因此,分解质因数不会变慢(这也可以通过实 践来说明)
分解质因数之后,出现了大量求乘幂的运算, 我们可以优化求乘幂的算法。这样,分解质因 数的好处就体现出来了
if (a[i]-b[i]-ncarry>=0) a[i]=a[i]-b[i]-ncarry,ncarry=0;
else a[i]=a[i]+N-b[i]-ncarry,ncarry=1;
}
高精度的乘法
For (i=0;i<=lena;i++) for (j=0;j<=lenb;j++) c[i+j]+=a[i]*b[j];
For (i=0;i<=lena+lenb;i++) { c[i+j+1]+=c[i+j]/N; c[i+j]=c[i+j]/N; }
这道题:
1.处理小数点问题,以及反序。 2.进行n次乘法。 3.进行输出,并加上小数点。
while(scanf("%s%d",d,&n)!=EOF) {
int a[150]={0},b[150]={0},c[150]={0}. int temp,flag,i,j,k,digit,s; int lend,lena,lenb,lenc,len; lend=strlen(d)-1; for(i=0;d[i];i++)
高精度பைடு நூலகம்
00748067 张姣
Poj 1001
Description Problems involving the computation of exact values of very large magnitude and precision are common. For example, the computation of the national debt is a taxing experience for many computer systems.
方法一:顺序连乘
5*6=30,1*1=1次乘法 30*7=210,2*1=2次乘法 210*8=1680,3*1=3次乘法
方法二:非顺序连乘
5*6=30,1*1=1次乘法 7*8=56,1*1= 1次乘法 30*56=1680,2*2=4次乘法
若“n位数*m位数=n+m位数”,则n个单精度数。
题目描述:
涉及到大数据的要求精确计算的问题是很 常见的。比如要求计算国家借款对于许多 电脑系统是一个非常繁重的任务。
本题中要求计算一个在零到一百以内的实 数的n次方(0<n<=25)。
在计算机上进行高精度计算,首先要处 理好以下几个基本问题:
1、数据的接收与存储; 2、计算结果位数的确定; 3、进位处理和借位处理; 4、商和余数的求法;
ln2/ln10+ln1/ln10 =trunc(1/ln10* (lnn+ln(n-1)+ln(n-2)+...........+ln3+ln2+ln1) 乘方:lg(a ^b)=trunc(lg(a^b))+1
=trunc(b*lg a )+1 =trunc(b*ln a / ln10)+1
for(i=1;i<=n-1;i++) { for(j=0;j<=lenb;j++) for(k=0;k<=lena;k++) { c[j+k]+=a[k]*b[j]; c[k+j+1]+=c[j+k]/10; c[j+k]%=10; } k--; j--; if(c[k+j+1]!=0) lenc=j+k+1; else lenc=j+k; for(j=0;j<=lenc;j++) b[j]=c[j]; lenb=lenc; memset(c,0,sizeof(c));
}
digit=n*digit; len=lenb+1-digit; flag=0; for(i=lenb-len;i>=0;i--)
if(b[i]!=0){flag=1;break;} if(flag==0) {
for(i=lenb;i>=lenb-len+1;i--)printf("%d",b[i]); printf("\n"); continue; } if(len==1&&b[lenb]==0) printf("."); else { for(i=lenb;i>=lenb-len+1;i--)printf("%d",b[i]); printf("."); } for(i=0;i<=lenb-len;i++) if(b[i]!=0) {temp=i;break;} for(i=lenb-len;i>=temp;i--) printf("%d",b[i]); printf("\n");
