信号与系统 奥本海姆 中文答案 chapter 7
信号与系统课后习题与解答第七章

15- 分别绘出以下各序列的图形)()21()()1(n u n x n = )(2)()2(n u n x n =)()21()()3(n u n x n -= )()2()()4(n u n x n -=)1(2)()5(1-=-n u n x n )()21()()6(1n u n x n -=解)()1(n x 序列的图形如图5-1(a)所示。
)()2(n x 序列的图形如图5-1(b)所示。
)()3(n x 序列的图形如图5-1(c)所示。
)()4(n x 序列的图形如图5-1(d)所示。
)()5(n x 序列的图形如图5-1(e)所示。
(b)图5-1(a)(f)(e)(d)25- 分别绘出以下各序列的图形)()()1(n nu n x = )()()2(n nu n x --= )(2)()3(n u n x n -= )()21()()4(n u n x n --=)()21()()5(n u n x n --= )1()21()()6(1+=+n u n x n解) 序列的图形如图5-2(b)所示。
x()2(n 序列的图形如图5-2(c)所示。
x))3(n(x 序列的图形如图5-2(d)所示。
)4(n())5(n 序列的图形如图5-2(e)所示。
x()x 序列的图形如图5-2(f)所示。
())6(n(b)图5-2(c)(f)(e)(d)8-(a)35- 分别绘出以下各序列的图形)5sin()()1(πn n x =)510cos()()2(ππ-=n n x)5sin()65()()3(πn n x n =解)()1(n x 序列的图形如图5-3(a)所示。
)()2(n x 序列的图形如图5-3(b)所示。
)()3(n x 序列的图形如图5-3(c)所示。
图5-3(a)45- 判断以下各序列是否是周期性的,如果是周期性的,试确定其周期。
)873sin()()1(ππ-=n A n x)8()()2(π-=ne n x j解)1(因为3147322==πππw 是有理数,所以)(n x 是周期性的,且周期为14。
信号与系统第七章课后答案
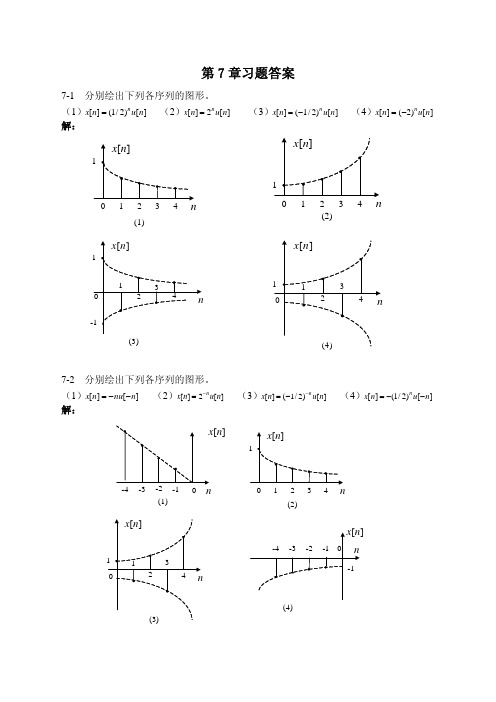
7-1 分别绘出下列各序列的图形。 (2)x[n] 2n u[n] (3)x[n] (1/ 2)n u[n] (4)x[n] (2) n u[ n] (1)x[n] (1/ 2)n u[n] 解:
x[ n ]
1
x[n]
1
0 1 2 (1) 3 4
n
0
1
2 3 (2)
x[n]
1
x[n]
-4
-3
-2 (1)
-1
0
n
0
1
2 (2)
3
4
n
x[n]
-4 1 0 1 2 3 4 -3 -2 -1 0
x[n] n
-1
n
(4)
(3)
7-3
分别绘出下列各序列的图形。 (2) x[n] cos
n 10 5
n (1) x[n] sin 5
1 z2 X (z) ( 1 1 2 z 1 )( 1 2 z 1 ) ( z 1 2 )( z 2 ) X (z) z 1 4 z ( z 1 2 )( z 2 ) 3( z 1 2 ) 3( z 2 )
X (z)
z 4z 3( z 1 2 ) 3 ( z 2 )
N
)
由于 x[n] 、 h[n] 均为因果序列,因此 y[n] 亦为因果序列,根据移位性质可求得
y [ n ] Z 1 [Y ( z )]
1 1 (1 a n 1 ) u [ n ] (1 a n 1 N ) u [ n N ] 1 a 1 a
7-24 计算下列序列的傅里叶变换。
(2)
信号与系统第二版课后答案_西安交大_奥本海姆(汉语)

第一章1.3 解:(a). 2401lim(),04Tt T TE x t dt e dt P ∞-∞∞→∞-====⎰⎰(b) dt t x TP T TT ⎰-∞→∞=2)(21lim121lim ==⎰-∞→dt T TTT∞===⎰⎰∞∞--∞→∞dt t x dt t x E TTT 22)()(lim(c).222lim()cos (),111cos(2)1lim()lim2222TT TTTT T TTE x t dt t dt t P x t dt dt TT∞∞→∞--∞∞→∞→∞--===∞+===⎰⎰⎰⎰(d) 034121lim )21(121lim ][121lim 022=⋅+=+=+=∞→=∞→-=∞→∞∑∑N N n x N P N Nn n N N N n N 34)21()(lim202===∑∑-∞=∞→∞nNNn N n x E (e). 2()1,x n E ∞==∞211lim []lim 112121N NN N n N n NP x n N N ∞→∞→∞=-=-===++∑∑ (f) ∑-=∞→∞=+=NNn N n x N P 21)(121lim 2∑-=∞→∞∞===NNn N n x E 2)(lim1.9. a). 00210,105T ππω===; b) 非周期的; c) 00007,,22mN N ωωππ=== d). 010;N = e). 非周期的; 1.12 解:∑∞=--3)1(k k n δ对于4n ≥时,为1即4≥n 时,x(n)为0,其余n 值时,x(n)为1易有:)3()(+-=n u n x , 01,3;M n =-=- 1.15 解:(a)]3[21]2[][][222-+-==n x n x n y n y , 又2111()()2()4(1)x n y n x n x n ==+-, 1111()2[2]4[3][3]2[4]y n x n x n x n x n ∴=-+-+-+-,1()()x n x n = ()2[2]5[3]2[4]y n x n x n x n =-+-+- 其中][n x 为系统输入。
奥本海姆《信号与系统》(第2版)课后习题-第7章至第9章(下册)(圣才出品)

第二部分课后习题第7章采样基本题7.1已知实值信号x(t),当采样频率时,x(t)能用它的样本值唯一确定。
问在什么ω值下保证为零?解:对于因其为实函数,故是偶函数。
由题意及采样定理知的最大角频率即当时,7.2连续时间信号x(t)从一个截止频率为的理想低通滤波器的输出得到,如果对x(t)完成冲激串采样,那么下列采样周期中的哪一些可能保证x(t)在利用一个合适的低通滤波器后能从它的样本中得到恢复?解:因为x(t)是某个截止频率的理想低通滤波器的输出信号,所以x(t)的最大频率就为=1000π,由采样定理知,若对其进行冲激采样且欲由其采样m点恢复出x(t),需采样频率即采样时间问隔从而有(a)和(c)两种采样时间间隔均能保证x(t)由其采样点恢复,而(b)不能。
7.3在采样定理中,采样频率必须要超过的那个频率称为奈奎斯特率。
试确定下列各信号的奈奎斯特率:解:(a)x(t)的频谱函数为由此可见故奈奎斯特频率为(b)x(t)的频谱函数为由此可见故奈奎斯特频率为(c)x(t)的频谱函数为由此可见,当故奈奎斯特频率为7.4设x(t)是一个奈奎斯特率为ω0的信号,试确定下列各信号的奈奎斯特率:解:(a)因为的傅里叶变换为可见x(t)的最大频率也是的最大频率,故的奈奎斯特频率为0 。
(b)因为的傅里叶变换为可见x (t)的最大频率也是的最大频率.故的奈奎斯特频率仍为。
(c)因为的傅里叶变换蔓可见的最大频率是x(t)的2倍。
从而知x 2(t)的奈奎斯特频率为2(d)因为的傅里叶变换为,x(t)的最大频率为,故的最大频率为,从而可推知其奈奎斯特频率为7.5设x(t)是一个奈奎斯特率为ω0的信号,同时设其中。
当某一滤波器以Y(t)为输入,x(t)为输出时,试给出该滤波器频率响应的模和相位特性上的限制。
解:p(t)是一冲激串,间隔对x(t)用p(t-1)进行冲激采样。
先分别求出P(t)和P(t-1)的频谱函数:注意0ω是x(t)的奈奎斯特频率,这意味着x(t)的最大频率为02ω,当以p(t-1)对x(t)进行采样时,频谱无混叠发生。
信号与系统第七章课后习题答案

k 1
z
1
k
1 z 1 z
0 z
F( z )
k 1
f (k )z k
k
[(k 1) (k 2)]z k z2 z 1 z
k 1
z k z 1 z 1
例 7.1- 2 已知无限长因果序列f(k)=akε(k)。求f(k)
d d k f ( k ) ( z ) ( z ) F ( z ) z dz dz
d d d z k f ( k ) ( z ) z F ( z ) dz dz dz
|a|<|z|<|b|
Im[z]
Im[z] |a |
Im[z]
|a | o Re[z] o Re[z] o
|a|
Re[z] |b |
(a)
(b)
(c)
图 7.1-1 例7.1-2、例7.1-3、例7.1-4图
7.1.3 常用序列的双边Z变换
(1) f (k ) (k )。
F ( z)
k
例 7.2-3 已知
1 k 1 f (k ) 3 (k 1), 2
k
求f(k)的双边Z变换及其收敛域。 解 令f1(k)=3k+1ε(k+1),则有
1 f ( k ) f1 ( k ) 2
z z2 由于 F1 ( z ) Z [ f1 (k )] z z3 z3
k
(k ) z k 1
(2) f1 (k ) (k m), f 2 (k ) (k m), m为正整数.
奥本海姆 信号与系统 习题参考答案
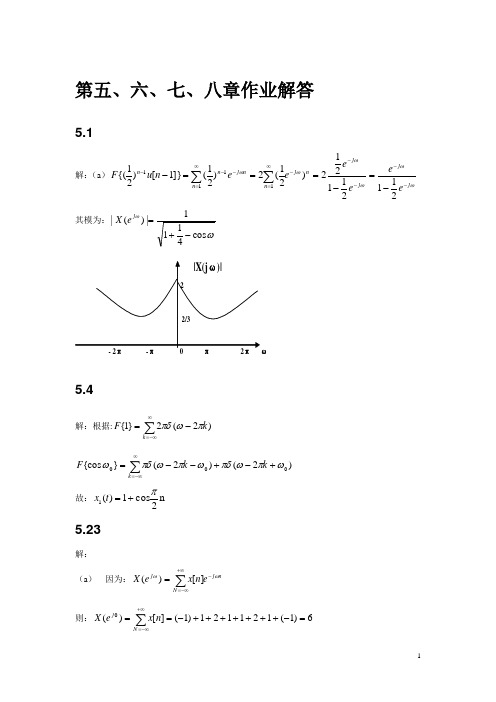
第五、六、七、八章作业解答5.1解:(a )ωωωωωωj j j j n j n n j n n n e e e ee e n u F -----∞=--∞=--=-===-∑∑211211212)21(2)21(]}1[)21{(1111 其模为:ωωcos 4111|)(|-+=j e X5.4解:根据:∑∞-∞=-=k k F )2(2}1{πωπδ)2()2(}{c o s 000ωπωπδωπωπδω+-+--=∑∞-∞=k k F k故:n 2cos1)(1π+=t x5.23解:(a ) 因为:nj N j en x eX ωω-+∞-∞=∑=][)(则:6)1(121121)1(][)(0=-+++++++-==∑+∞-∞=N j n x e X(b )设]2[][1+=n x n x则]2[][1-=n x n x ωωω21)()(j j j e e X e X -=x1[n]是实偶对称信号,则⎪⎩⎪⎨⎧<>=∠0)(0)(0)(111ωωωπj j j e X e X e X故:⎪⎩⎪⎨⎧<->-=∠+-=∠0)(20)(2)(2)(111ωωωωωπωωj j j j e X e X e X e X(c )因为: ⎰=πωωωπ2)(21][d e e X n x n j j则:ππωππω4]0[2)(==⎰-x d e X j(d) 因为:nj N j en x eX ωω-+∞-∞=∑=][)(2)1()1(12)1(112)1(1)1()1()1(][][)(=-+-⨯++-⨯+++-⨯+-⨯-=-==∑∑+∞-∞=+∞-∞=nN nj N j n x en x e X ππ(e) 2][][][)}(Re{n x n x n x eX e Fj -+=−→←π(图略)(f) I 根据帕斯瓦尔关系式:⎰∑+∞-∞==πωωπ222|)(|21|][|d e X n x j n 则:πππωωππ28)11411411(2|][|2|)(|22=+++++++==∑⎰+∞-∞=-n j n x d e XII 根据:ωωd e dX n nx j FT)(][j −→←-则:πππωωωππ316)4925649119(2|][-j |2|)(|22=++++++==−→←∑⎰∞-∞=-n j FTn nx d d e dX6.5解:而:ttt h c πωsin )(1= 的傅里叶变换为:0 ωc ω -ωc则)()()(1t g t h t h = 而:)2()2()(11c c j H j H j H ωωωωω-++= 故:t e e t g c t j tj c c ωωω2cos 2)(22=+=-6.23(a) ttt h c πωsin )(=(b) ⎩⎨⎧<=othere j H c Tj 0||)(ωωωω则:)()(sin )(T t T t t h c ++=πω(c )⎪⎪⎪⎩⎪⎪⎪⎨⎧<<-<<=-othere e j H c j c j 000)(22ωωωωωππ故:ωπωπωωπωωπd e e d e e t h t j jtj jcc⎰⎰+=--02022121)(c c t j jt j je t e e t e ωωπωωπππ0202|j 2|j 2+=--c c t j jt j je te e t e ωωπωωπππ0202|j 2|j 2+=-- ]1[2]1[222-+-=--t j jt j jc c e t j e e t j e ωπωπππ]}[]{[21122t j t j j j c c e e e e jt ωωπππ---+-=]}[]{[211)2/()2/(22πωπωπππt j t j j j c c e e e e jt -+--+-=]1[cos 1-=t t c ωπ7.3解:(a))(t x 的最高频率为4000π,故奈奎斯特率为8000π; (b ) 同上;(c ) 时域相乘,频域相卷,故)(t x 的最高频率为8000π,则奈奎斯特率为16000π;7.22解: y(t)为:)()()(ωωωj H j X j Y =πωω1000||0)(>=j Y对y(t)进行采样,则要求采样频率fs>2000π,故采样周期因为ms T 120002=<ππ7.27解: (a )x (t)e ∑∞-∞=-=n nT t t p )()(δx p (t)因为:ω0如下图图所示,为ω1与ω2的中点位置:X(j ω) ωω1 -ω2 -ω11ω2 ω0(a ))()(01ωωω+=j X j X)()()(12ωωωj H j X j X =21X2(j ω) ω(ω2-ω1)/21-(ω2-ω1)/2(b )最大的采样周期为:122ωωπ-(c)该系统为:先通过如下图所示的低通滤波器,得到X2(j ω),然后将其乘以 e j ω0t ,则信号频移ω0,然后通过一个反折系统,其系统框图图下图所示:H (j ω) ω(ω2-ω1)/2T-(ω2-ω1)/2e j ω0t说明:因为)(X ωj a 为实数,则有:)(X )(X *ωωj j a a =而)()()}(Re{2)(x *t x t x t x t aa a +==)()()(*ωωωj X j X j X a a -+=又因为)(X )(X *ωωj j a a =故:)(X )(X *ωωj j aa -=-则:)()()(ωωωj X j X j X a a -+=得到结论8.3解:定性的理解由于载波信号与同步信号的相位相差为90o ,故输出信号为0; (也可以通过调制、解调的时域表达式计算出结果也为0)。
《信号与系统》奥本海姆第七章
采样频率: 1 f s 2 f M 或 s 2M T
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
信号重建:
x(t)
连续信号
∞
xp(t)
FT
x1 (t ) X1 ( j) 0,| | 1 ;
FT
x2 (t ) X 2 ( j) 0,| | 2 ;
[1 2 ]
计算 x(t ) x1 (t ) x2 (t ) 的采样频率.
20
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
1 1 n 0时, X p j X j , 包 T 含原信号的全部信息, 幅度差T倍。
Xp( j)
A/ T
2
X p j 以s为周期的连续谱 , 有 新的频率成分 ,即 X j 的周期 性延拓。
s
0
s
A
X ( j)
s s M
M M
离散信号与系统的主要优点:
(1) 信号稳定性好 (2) 信号可靠性高 (3) 信号处理简便 (4) 系统灵活性强
4
Generated by Foxit PDF Creator © Foxit Software For evaluation only.
7.0 引言
采样定理是从连续信号到离散信号的桥梁, 也是对信号进行数字处理的第一个环节。
fs (t )
f (t )
A/ D
量化编码
f (n)
数字 滤波器
g(n)
信号与系统 奥本海姆 第二版 习题详解
对方程两边同时做反变换得:
y[n] −
1 处有一个二阶极点,因为系统是因果的,所以 H ( z ) 的收敛域是 z > , (b)H ( z) 在 z = 1 3 3 包括单位圆,所以系统是稳定的。
解: (a) x[n] = δ [n + 5] ← → X ( z ) = z , ROC : 全部z 因为收敛域包括单位圆,所以傅立叶变换存在。
( )
χ (s ) = uL{e −2t u (t )} =
H (s ) =
H (s )如图所示。
Y (s ) 1 = 2 . X (s ) s − s − 2
1 1 1 3 3 ( ) , ⇒ H s = − s2 − s − 2 s − 2 s +1 (i )如果系统是稳定的,H (s )的ROC为 − 1〈ℜe {s}〈2.
∞ ∞
n =−∞
∑
∞
x[n]z − n =
− n−2
1 −n ∞ 1 n z = ∑− z ∑ −3 3 n =−∞ n =2
−2 n −n
z n + 2 = 9 z 2 /(1 + 3z ) = 3z /(1 + (1/ 3) z −1 ), z < 1 3 1 = ∑ n =2 3
1 1 (b) H (s) = 1 − 3 s − 2 s +1
(1)系统是稳定的,说明 H (s) 的收敛域应该包括虚轴在内,即: − 1 < Re{s} < 2 , 所以 h(t ) = 1 (− e u (−t ) − e u (t )) 3 (2)系统是因果的,则 H (s) 的收敛域应为 Re{s} > 2 ,所以 h(t ) = 1 (e u (t ) − e u (t )) 3 ( 3 ) 系 统 既 不 因 果 又 不 稳 定 , 则 H (s) 的 收 敛 域 应 为 Re{s} < −1 , 所 以
本海默信号与系统第二版课后习题解信号与系统部分习题答案51页文档
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
本海默信号与系统第二版课后习题解 信号与系统部分习题答案
6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若ห้องสมุดไป่ตู้
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
信号与系统课后习题答案第7章
第7章 离散信号与系统的Z域分析 63
第7章 离散信号与系统的Z域分析 64
第7章 离散信号与系统的Z域分析 65
第7章 离散信号与系统的Z域分析
(3) 对差分方程 取单边Z变换,得
66
第7章 离散信号与系统的Z域分析 67
第7章 离散信号与系统的Z域分析 68
第7章 离散信号与系统的Z域分析 69
第7章 离散信号与系统的Z域分析 7
第7章 离散信号与系统的Z域分析 8
第7章 离散信号与系统的Z域分析 9
第7章 离散信号与系统的Z域分析 10
第7章 离散信号与系统的Z域分析 11
第7章 离散信号与系统的Z域分析 12
第7章 离散信号与系统的Z域分析 13
第7章 离散信号与系统的Z域分析
第7章 离散信号与系统的Z域分析
第7章离散信号与系统
➢
➢ 的Z域分析
1
第7章 离散信号与系统的Z域分析
7.1 用定义求下列信号的双边Z变换及收敛域。
2
第7章 离散信号与系统的Z域分析 3
第7章 离散信号与系统的Z域分析 4
第7章 离散信号与系统的Z域分析 5
第7章 离散信号与系统的Z域分析 6
7.25 已知一阶、二阶因果离散系统的系统函数分别如下, 求离散系统的差分方程。
111
第7章 离散信号与系统的Z域分析 112
第7章 离散信号与系统的Z域分析 113
第7章 离散信号与系统的Z域分析 114
第7章 离散信号与系统的Z域分析
7.26 已知离散系统如题图7.5所示。 (1) 画出系统的信号流图; (2) 用梅森公式求系统函数H(z); (3) 写出系统的差分方程。
第7章 离散信号与系统的Z域分析
