人教版九年级数学下册《位似》课件
合集下载
《位似》九年级初三数学下册PPT课件(第27.3课时)

车尾离开桥共需要3分钟。这列火车长多少米?
900×3-2400 =300(m)
答:这列火车长300米。
人教版小学数学五年级上册
第八单元 总复习
感 谢 你 的 聆 听
M E N T A L
H E A L T H
C O U N S E L I N G
讲解人: 时间:2020.6.1
P P T
指针停在红色区域的可能
性最大,停在黄色区域的
可能性最小。
指针停在蓝色区域的可
能性最大,停在红色区
域的可能性最小。
二、复习可能性
12. (P117“练习二十五”第12题)
两个都是正面,两个都是反面,
一个正面一个反面。
三、复习植树问题
常见类型:
①两端都栽的植树问题;
棵数=间隔数+1;
②两端都不栽的植树问题;
3、了解平移、轴对称、旋转、位似的联系和区别,并能在复杂图
形中找出这些变换。
02
重点
03
难点
通过图形的坐标的变化来表示图形的位似变换。
把一个图形按一定大小比例放大或缩小后,
点的坐标变化规律。
LEARNING OBJECTIVES
学习目标
1、理解位似图形的概念。
2、通过图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例
放大或缩小后,点的坐标变化规律。
01
3、了解平移、轴对称、旋转、位似的联系和区别,并能在复杂图形中找出这些变换。
01
情景引入
回想一下小孔成像的实验,你发现实物和所得的图像有什么关系吗?
01
情景引入
观看手机屏幕放大器,你发现手机屏幕和放大器所得图像有什么关系吗?
900×3-2400 =300(m)
答:这列火车长300米。
人教版小学数学五年级上册
第八单元 总复习
感 谢 你 的 聆 听
M E N T A L
H E A L T H
C O U N S E L I N G
讲解人: 时间:2020.6.1
P P T
指针停在红色区域的可能
性最大,停在黄色区域的
可能性最小。
指针停在蓝色区域的可
能性最大,停在红色区
域的可能性最小。
二、复习可能性
12. (P117“练习二十五”第12题)
两个都是正面,两个都是反面,
一个正面一个反面。
三、复习植树问题
常见类型:
①两端都栽的植树问题;
棵数=间隔数+1;
②两端都不栽的植树问题;
3、了解平移、轴对称、旋转、位似的联系和区别,并能在复杂图
形中找出这些变换。
02
重点
03
难点
通过图形的坐标的变化来表示图形的位似变换。
把一个图形按一定大小比例放大或缩小后,
点的坐标变化规律。
LEARNING OBJECTIVES
学习目标
1、理解位似图形的概念。
2、通过图形的坐标的变化来表示图形的位似变换,掌握把一个图形按一定大小比例
放大或缩小后,点的坐标变化规律。
01
3、了解平移、轴对称、旋转、位似的联系和区别,并能在复杂图形中找出这些变换。
01
情景引入
回想一下小孔成像的实验,你发现实物和所得的图像有什么关系吗?
01
情景引入
观看手机屏幕放大器,你发现手机屏幕和放大器所得图像有什么关系吗?
人教版数学九年级下册位似——在平面直角坐标系中画位似图形课件

经过位似变y
换还可以得到其 他图形吗?
5
A(4,4)
为位似中心,相似比
为2,将△AOC放大.
C(5,0)
O
5
x
①画出线段△AOC ②连接位似中心O,找到 相似比为2的对应点
探究1 当以原点为位似中心的两位似图形位 于原点同侧时,对应点的坐标有什么变化?
2 A′(8,8)
1 3
(2,1)
C′(10,0)
平移、轴对称、旋转、位似变换的坐标变化规律
平移变换 对应点的横坐标或纵坐标加上(或减去)平移的单位长度
以x 轴为对称轴,则对应点的横坐标相等,纵坐标互为相
轴对称变换 反数;以y 轴为对称轴,则对应点的纵坐标相等,横坐标互
为相反数
旋转变换 位似变换
一个图形绕原点旋转180° ,则旋转前后两个图形对应 点的横坐标与纵坐标都互为相反数
A′(8,-10), B′(12,0)
寄语:数学并不(-神2,秘-1,) 不是只有天才才能学好数学,只要通过努力,掌握适当的方法,人人都能学会数学。
规律:在平面直角坐标系中,如果以原点为位
似中心,新图形与原图形的相似比为k,那么当两图 形位于原点异侧时,与原图形上的点(x , y)对应的位 似图形上的点的坐标是(-kx , -ky).
(2,0)
规律:在平面直角坐标系中,如果以原点为位
似中心,新图形与原图形的相似比为k,那么当两图 形位于原点同侧时,与原图形上的点(x , y)对应的位 似图形上的点的坐标是(kx , ky).
探究2 当以原点为位似中心的两位似图形位 (3)会根据位似图形上的点的坐标变化的规律,在坐
目前已经学了哪些变换?有什么区别与联系? 课本第:50页 练习题1、2
人教版九年级下册数学 27.3 位似图形概念(共22张PPT)

B
A〞
在平面直角坐标系中,如果位似变换是以原点为 位似中心,相似比为k,那么位似图形对应点的坐 标乘以k或-k.
在平面直角坐标系中, △ABC三个顶点的坐标分别为 A(2,3),B(2,1),C(6,2),以原点O为位似中心,相似比为2将其放大.
放大后对应点的坐标分别是多少?
A′( 4 ,6 ), B′( 4 ,2 ), C′( 12 ,4 )
还有其他方法吗?
E
B
F
O
C
A D
如何把三角形ABC放大为原来的2倍?
E
B
O
C
F
D
A
D
B
O
C
F
A
E
(3)如果在射线AO,BO,CO上分别取D,E,F 使DO=OA,EO=OB,FO=OC,那么,结果又 会怎样呢?
B
D
O
C
F
A
E
结果会得到一个与△ABC全等的△DEF,.即它 们的位似比是1∶1.
在平面直角坐标系中,有两点A(6,3),B(6,0),以原点 O为位似中心,相似比为3:1,把线段AB缩小.
正向或反向
截取或延长
作业设计: . 1、(必做题)练习册第2,4,5题
2、(选做题)如图,以点P为位似中心,将五角星缩 小为原来的一半
●P
不知道自己缺点的人,一辈子都不会想要改善。成功的花,人们只惊慕她现时的明艳!然而当初她的芽儿,浸透了奋斗的泪泉,洒遍了牺牲的血雨。成功的条件在于勇气和 信乃是由健全的思想和健康的体魄而来。成功了自己笑一辈子,不成功被人笑一辈子。成功只有一个理由,失败却有一千种理由。从胜利学得少,从失败学得多。你生而有 前进,形如蝼蚁。你一天的爱心可能带来别人一生的感谢。逆风的方向,更适合飞翔。只有承担起旅途风雨,才能最终守得住彩虹满天只有创造,才是真正的享受,只有拚 活。知识玩转财富。志不立,天下无可成之事。竹笋虽然柔嫩,但它不怕重压,敢于奋斗、敢于冒尖。阻止你前行的,不是人生道路上的一百块石头,而是你鞋子里的那一 爱,不必呼天抢地,只是相顾无言。最值得欣赏的风景,是自己奋斗的足迹。爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。生活不可能像你想 不会像你想的那么糟。时间告诉你什么叫衰老,回忆告诉你什么叫幼稚。不要总在过去的回忆里缠绵,昨天的太阳,晒不干今天的衣裳。实现梦想往往是一个艰苦的坚持的 到位,立竿见影。那些成就卓越的人,几乎都在追求梦想的过程中表现出一种顽强的毅力。世界上唯一不变的字就是“变”字。事实胜于雄辩,百闻不如一见。思路决定出 细节决定成败,性格决定命运虽然你的思维相对于宇宙智慧来说只不过是汪洋中的一滴水,但这滴水却凝聚着海洋的全部财富;是质量上的一而非数量上的一;你的思维拥 所有过不去的都会过去,要对时间有耐心。人总会遇到挫折,总会有低潮,会有不被人理解的时候。如果你希望成功,以恒心为良友,以经验为参谋,以小心为兄弟,以希 个人不知道他要驶向哪个码头,那么任何风都不会是顺风。沙漠里的脚印很快就消逝了。一支支奋进歌却在跋涉者的心中长久激荡。上天完全是为了坚强你的意志,才在道 碍。拥有资源不能成功,善用资源才能成功。小成功靠自己,大成功靠团队。炫耀什么,缺少什么;掩饰什么,自卑什么。所谓正常人,只是自我防御比较好的人。真正的 防而又不受害。学习必须如蜜蜂一样,采过许多花,这才能酿出蜜来态度决定高度。外在压力增加时,就应增强内在的动力。我不是富二代,不能拼爹,但为了成功,我可 站在万人中央成为别人的光。人一辈子不长不短,走着走着,就进了坟墓,你是要轰轰烈烈地风光下葬,还是一把骨灰撒向河流山川。严于自律:不能成为自己本身之主人 他周围任何事物的主人。自律是完全拥有自己的内心并将其导向他所希望的目标的惟一正确的途径。生活对于智者永远是一首昂扬的歌,它的主旋律永远是奋斗。眼泪的存 伤不是一场幻觉。要不断提高自身的能力,才能益己及他。有能力办实事才不会毕竟空谈何益。故事的结束总是满载而归,就是金榜题名。一个人失败的最大原因,是对自 的信心,甚至以为自己必将失败无疑。一个人炫耀什么,说明内心缺少什么。一个人只有在全力以赴的时候才能发挥最大的潜能。我们的能力是有限的,有很多东西飘然于 之外。过去再优美,我们不能住进去;现在再艰险,我们也要走过去!即使行动导致错误,却也带来了学习与成长;不行动则是停滞与萎缩。你的所有不甘和怨气来源于你 你可以平凡,但不能平庸。懦弱的人只会裹足不前,莽撞的人只能引为烧身,只有真正勇敢的人才能所向披靡。平凡的脚步也可以走完伟大的行程。平静的湖面锻炼不出精 生活打造不出生活的强者。人的生命似洪水在奔流,不遇着岛屿、暗礁,难以激起美丽的浪花人生不怕重来,就怕没有将来。人生的成败往往就在于一念之差。人生就像一 为你在看别人耍猴的时候,却不知自己也是猴子中的一员!人生如天气,可预料,但往往出乎意料。人生最大的改变就是去做自己害怕的事情。如果不想被打倒,只有增加 你向神求助,说明你相信神的能力;如果神没有帮助你,说明神相信你的能力。善待自己,不被别人左右,也不去左右别人,自信优雅。活是欺骗不了的,一个人要生活得 象这杯浓酒,不经三番五次的提炼呵,就不会这样一来可口!生命不止需要长度,更需要宽度。时间就像一张网,你撒在哪里,你的收获就在哪里。世上最累人的事,莫过于 你感到痛苦时,就去学习点什么吧,学习可以使我们减缓痛苦。当世界都在说放弃的时候,轻轻的告诉自己:再试一次。过错是暂时的遗憾,而错过则是永远的遗憾!很多 结果,但是不努力却什么改变也没有。后悔是一种耗费精神的情绪后悔是比损失更大的损失,比错误更大的错误所以不要后悔。环境不会改变,解决之道在于改变自己。积 成功者的最基本要素。激情,这是鼓满船帆的风。风有时会把船帆吹断;但没有风,帆船就不能航行。即使道路坎坷不平,车轮也要前进;即使江河波涛汹涌,船只也航行 粹取出来的。浪费时间等于浪费生命。老要靠别人的鼓励才去奋斗的人不算强者;有别人的鼓励还不去奋斗的人简直就是懦夫。不要问别人为你做了什么,而要问你为别人 遥远的梦想和最朴素的生活,即使明天天寒地冻,金钱没有高贵,低贱之分。金钱在高尚人的手中,就会变得高尚;金钱在庸俗人手中,就会变得低级庸俗。涓涓细流一旦 大海也就终止了呼吸。漫无�
人教版数学九年级下册 . 位似课件-ppt1

练习.如图, △ABC三个顶 点坐标分别为 A(2,3)B(2,1), C(6,2),以点O 为位似中心, 相似比为2,将 △ABC放大,观 C″ 察对应顶点坐
标的变化,你 有什么发现?
6
4A
2 B
0
B″
A′
B′ C
4
8
C′ 12
A″
探究
如图,△ABC三个顶点坐 标分别为A(2,3),B( 2,1),C(6,2),以点 O为位似中心,相似比为2 ,将△ABC放大,观察对 应顶点坐标的变化,你有 什么发现?
4 A.(-2,3) B.(2,-3)C.(3,-2)或(-2,3) D.(-2,3)或(2,-3)
4.(5 分)某学习小组在讨论“变化的鱼”时,知道大鱼与小鱼是位似图形(如图所示),
则大鱼上的一点(a,b)对应小鱼上的点的坐标是 (-0.5a,-0.5b)_
.
人教版数学九年级下册 . 位似课件-ppt1(PPT优秀课件)
A. 2∶1 B.1∶ 2 C.1∶4 D.4∶1
人教版数学九年级下册 . 位似课件-ppt1(PPT优秀课件)
人教版数学九年级下册 . 位似课件-ppt1(PPT优秀课件)
8.如图,原点 O 是△ABC 和△A′B′C′的位似中心,点 A(1,0)与 A′(-2,0)是对应点, △ABC 的面积是3,则△A′B′C′的面积是_ 6 _.
人教版数学九年级下册 . 位似课件-ppt1(PPT优秀课件)
人教版数学九年级下册 . 位似课件-ppt1(PPT优秀课件)
思考题:
1.两个图形关于原点位似,且一对对应点的坐标分别为(3,-4),(-2,b),则 b 的的 取值为( C )
A.-9 B .9 C.8 D.-8
人教版九年级数学课件《位似图形的概念及画法》

在位置关系上还符合以下条件:(1)对应顶点的连线都经过同
一点;(2)对应边互相平行或共线.
判别两个图形位似的关键是寻找位似中心,位似中心可以
在两个图形的同侧、两个图形之间或两个图形内,还可以在
其中一个图形的边或顶点上.
人教版数学九年级下册
知识精讲
如何将一个图形放大或缩小,你有哪些方法?
利用位似,可以将一个图形放大或缩小.
(2)求所作的矩形的面积.
解: (2)设IK与CD交于N,,所作矩形的宽IJ=x,则IK=2x.
∵IK∥AB,
∴△CIK∽△CAB
∵CN、CD分别是△CIK、△CAB的高
∴ =
60− 2
即
= ,
60 80
解得x=24
∴该矩形的长为48,宽为24
∴S矩形IJLk=24×48=1152
的位似图形是(A )
A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR
达标检测
人教版数学九年级下册
5.如图,已知四边形ABCD,将图形各边放大到原来的三倍.
(你有几种方法)
解法一:四边形A'B'C'D'为所要求的图形.
达标检测
人教版数学九年级下册
5.如图,已知四边形ABCD,将图形各边放大到原来的三倍.
(你有几种方法)
解法四:四边形A'B'C'D'为所要求的图形.
人教版数学九年级下册
达标检测
6.一般在室外放映的电影胶片上每一个图片的规格
为:3.5cm×3.5cm,放映的银屏的规格为2m×2m,若影机的
光源距胶片20cm时,问银屏应在离镜头多远的地方,放映
一点;(2)对应边互相平行或共线.
判别两个图形位似的关键是寻找位似中心,位似中心可以
在两个图形的同侧、两个图形之间或两个图形内,还可以在
其中一个图形的边或顶点上.
人教版数学九年级下册
知识精讲
如何将一个图形放大或缩小,你有哪些方法?
利用位似,可以将一个图形放大或缩小.
(2)求所作的矩形的面积.
解: (2)设IK与CD交于N,,所作矩形的宽IJ=x,则IK=2x.
∵IK∥AB,
∴△CIK∽△CAB
∵CN、CD分别是△CIK、△CAB的高
∴ =
60− 2
即
= ,
60 80
解得x=24
∴该矩形的长为48,宽为24
∴S矩形IJLk=24×48=1152
的位似图形是(A )
A.四边形NPMQ
B.四边形NPMR
C.四边形NHMQ
D.四边形NHMR
达标检测
人教版数学九年级下册
5.如图,已知四边形ABCD,将图形各边放大到原来的三倍.
(你有几种方法)
解法一:四边形A'B'C'D'为所要求的图形.
达标检测
人教版数学九年级下册
5.如图,已知四边形ABCD,将图形各边放大到原来的三倍.
(你有几种方法)
解法四:四边形A'B'C'D'为所要求的图形.
人教版数学九年级下册
达标检测
6.一般在室外放映的电影胶片上每一个图片的规格
为:3.5cm×3.5cm,放映的银屏的规格为2m×2m,若影机的
光源距胶片20cm时,问银屏应在离镜头多远的地方,放映
人教版九年级下册数学 27.3 位似图形概念 (共24张PPT)
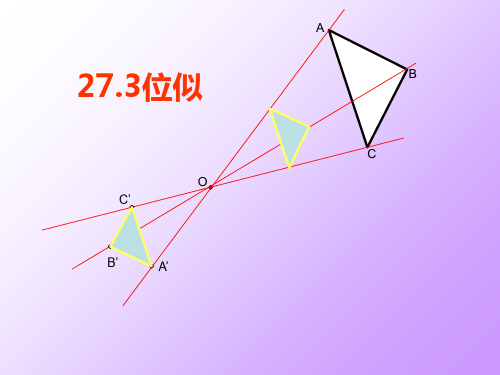
相似
对应点的连 线相交一点
对应边平行,(或 者在同一条直线上)
1. 判断下列各对图形是不是位似图形. (1)正五边形ABCDE与正五边形A′B′C′D′E′; 是 (2)等边三角形ABC与等边三角形A′B′C′. 是
思考:是否相似图形都是位似图形?
判断下面的正方形是不是位似图形?
A
D
不是
E
F
(1)
下面请欣赏如下图形的变换
下列图形中,每个图中的四边形ABCD和四 边形A′B′C′D′都是相似图形.分别观察这五个图,你 发现每个图中的两个四边形各对应点的连线有什么 特征?
1.位似图形的概念
如果两个图形不仅相似,而且每组对应点所 在的直线都经过同一点,对应边互相平行 (或者在同一条直线上),那么这样的两个 图形叫做位似图形,这个点叫做位似中心.此 时的相似比叫做位似比。
B
C
G
显然,位似图形是相似图形的特殊情形.相似图形不 一定是位似图形,可位似图形一定是相似图形
思考:位似图形有何性质?
2. 位似图形的性质 A〞(-2,-1),B(-2,0)
A〞(-2,-1),B(-2,0)
如何把三角形ABC放大为原来的2倍?
OA
你还有其从他第办法吗(?1试)试,看.(2)图中,我们可以看到,△OAB∽△O
以O为位似中心,求作△ABC的位似图形,并把△ABC的边长扩大到原来的两倍.
A′B′,则OA′
=
A〞(-2,-1),B(-2,0)
OB AB A′( -4 ,-6 ), B′( -4 ,-2 ), C′( -12 ,-4 )
AF AP AE EP FP
如在O何平B把 面′三直角角=形坐标AAB系C′中放,大B△′为A原BC来三.的从个2倍顶第?点的(坐标3)分别图为A中(2,3同),B(样2,1)可,C(6以,2),以看原点到O为AD位似=中心A,C相似=比为A2B画它=的位BC似图=形. DC
人教版数学九年级下册 27.3位似 课件
OA:OA'
1:4 ,那么
S :S 四边形ABCD
四边形A' B' C' D'
__1_:1_6__ .
课堂小结
位似
1.位似图形的概念. 2.位似与相似的关系. 3.位似图形的性质.
再见
似比又叫位似比.
A
位似中心:点O 相似比或位似比:EF FG HE
AB BC DA
ห้องสมุดไป่ตู้
E
B
O
F
HD
G
C
探究新知
结论: ①位似图形一定是相似图形. ②相似图形不一定是位似图形.
D'
C'
D
C
O
A'
A B'
B
探究新知
位似的特征: 1.位似是一种具有位置关系的相似. 2.位似图形是相似图形的特殊情形. 判断位似图形时,要注意首先它们必须是相似图形, 其次每一对对应点所在直线都经过同一点.
探究新知
①④对位应似线中段心有可可能能位平于行两,个也图可形能的共内线部.,也可能在两图形 ②的两公个共位顶似点图上形,的还位可似能中在心两只个有图一形个的.外部. ③⑤两每个组位对似应图点形到可位能似位中于心位的似距中离心之的比两都侧等,于也相可似能比位. 于 本位质似区中别心:的位一似侧多. 边形是具有特殊位置关系的相似多边形.
巩固新知
1.两个位似多边形中的对应角__相__等__,对应线段__成__比__例__, 对应顶 点的连线必经过___位__似__中__心___.
2.位似多边形上某一对对应点到位似中心的距离分别为5和10, 则它们的相似比为____1_:2_____.
3.四边形ABCD和四边形 A' B' C' D' 位似,O为位似中心,若
人教版第二学期数学九年级下 27.3 位似第1课时 位似图形的概念及画法课件(共20张PPT)
E′
D′
D
E
O
A
A′
B
C′
A
C
B′
C′
O
B
C
B′
A′
归纳:
1. 位似图形的对应角相等,对应边成比例,周长比
等于相似比,面积比等于相似比的平方;
2. 位似图形的对应点的连线相交于一点,即经过位似中心;
3. 位似图形的对应边互相平行或在同一条直线上;
4. 位似图形上任意一对对应点到位似中心的距离之比等
于相似比.
例2 如图所示,四边形ABCD 和四边形A′ B′ C′ D′位似,相似比1 = 2,四边
形A′ B′ C′D′和四边形A″ B″ C″D″位似,相似比2 = 1. 则四边形A″ B″ C″ D″
和四边形ABCD 是位似图形吗?如果是,请说明理由并求出相似比.
解:∵ 四边形ABCD 和四边形A′ B′ C′ D′位似,
E
OD;在射线OA、OB、OC、
H
A
OD上分别取点D、E、F,使
D
O
B
C
OE = 2OA , OF = 2OB , OG =
2OC , OH = 2OD;顺次连结E、
F、G、H,使正方形ABCD与
F
G
5.如图所示,四边形ABCD的一个位似图形是四边形A′ B′ C′ D′ ,
且A,B,C,D的对应点分别是A′ ,B′ ,C′ ,D′. 图中给出了AB的对应
似中心的位似图形,且
′
=
=
′
′
=
′
;五边形ABCDE 与五
边形A′ B′ C′ D′ E′是以点O 为位似中心的位似图形,且′ = ′ =
数学人教版九年级下册位似图形课件
思考:相似图形都是位似图形么?
判断下面的正方形是不是位似图形?
A D
不是
A’ (1) B C(B’) C’ D’
显然,位似图形是相似图形的特殊情形.位似图形一 定是相似图形,但相似图形不一定是位似图形。
思考:位似图形有何特征?
细心辨析 深化认识
位似的特征:
1.位似图形一定是相似形,反之相似形不一定是 位似图形。 2.判断位似图形时,要注意首先它们必须是相似 形,其次对应顶点的连线相交于一点。
细心辨析 归纳定义
位似图形的概念 如果两个图形不仅相似,而且对应顶点的连线相交 于一点,那么这样的两个图形叫做位似图形,这个点叫 做位似中心。这时的相似比又叫位似比。
明 确
相似 对应顶点的连线相交于一点
辨一辨
判断下列各组图形是不是位似图形.
(1)正五边形ABCDE与正五边形A′B′C′D′E′; 是 (2)等边三角形ABC与等边三角形A′B′C′。 是
归纳小结 自我完善
(1)本节课你学习了哪些知识? (2)举例说明如何利用位似,将一个图形放大或 缩小。
4. 下面的说法对吗?为什么? (1)分别在△ABC的边AB,AC上取点D,E,使DE∥BC, 那么△ADE是△ABC缩小后的图形。 √ (2)分别在△ABC的边AB,AC的延长线上取点D,E,使 DE∥BC,那么△ADE是△ABC放大后的图形。 √ (3)分别在△ABC的边AB,AC的反向延长线上取点 D,E,使DE∥BC,那么△ADE是△ABC缩小后的图形。 ×
A D B E C D A E D A E B C第 48 页练习 第 1,2 题。
B A
o
′
C
C
′
′
A B
5.若△ABC与△A’B’C’的相似比为:1:2,则 1:2 OA:OA’=( )。
人教版九年级数学下册27.3位似图形概念课件(共16张PPT)
3.相似图形一定位似。 4.位似图形不一定相似。
作△ABC与的位似图形△DEF
且位似比为1/2
即将△ABC的三边缩小为原来的1/2:
如图,任取一点O,连接AO,BO,CO,并取它们的中
点D,E,F;
△DEF就是所求
B E●
O
●
F
C
●
D
A
做一做:
任意画一个三角形,用上面的方法 亲自试一试.
课堂小结
这时两个相似图形的相似比又叫做它们的位似比. 3.相似图形一定位似。
AF AP AE EP FP 对应线段AB和A/B/是否平行?其它边呢?有哪些相似三角形?
对应边互相平行, 且位似比为1/2
= = = = 你发现每个图中的两个四边形各对应点的连线有什么特征? AD AC AB BC DC (5)△ABC与△A′B′C′
2.位似图形的性质 位似图形的对应点和位似中心在同一条直 线上,它们到位似中心的距离之比等于相 似比.(位似比)
1. 位似图形的概念
如果两个相似图形的每组对应点所在的直
线都交于一点,对应边互相平行,那么这样
(1)五边形ABCDE与五边形A′B′C′D′E′;
的两个图形叫做位似图形, 这个交点叫做位 显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
2.不是位似图形必定不相似。 2.位似图形上任意一对对应点到位似中心的距离之比等于位似比.
2.位似图形上任意一对对应点到位似中心的距离之比等于位似比.
(二)位似图形的性质
A A/ C
位似图形有以下性质:
1.位似图形的对应点和位似中心在同一条直线上
2.位似图形上任意一对对应点到位似中心的 距离之比等于位似比.
作△ABC与的位似图形△DEF
且位似比为1/2
即将△ABC的三边缩小为原来的1/2:
如图,任取一点O,连接AO,BO,CO,并取它们的中
点D,E,F;
△DEF就是所求
B E●
O
●
F
C
●
D
A
做一做:
任意画一个三角形,用上面的方法 亲自试一试.
课堂小结
这时两个相似图形的相似比又叫做它们的位似比. 3.相似图形一定位似。
AF AP AE EP FP 对应线段AB和A/B/是否平行?其它边呢?有哪些相似三角形?
对应边互相平行, 且位似比为1/2
= = = = 你发现每个图中的两个四边形各对应点的连线有什么特征? AD AC AB BC DC (5)△ABC与△A′B′C′
2.位似图形的性质 位似图形的对应点和位似中心在同一条直 线上,它们到位似中心的距离之比等于相 似比.(位似比)
1. 位似图形的概念
如果两个相似图形的每组对应点所在的直
线都交于一点,对应边互相平行,那么这样
(1)五边形ABCDE与五边形A′B′C′D′E′;
的两个图形叫做位似图形, 这个交点叫做位 显然,位似图形是相似图形的特殊情形,其相似比又叫做它们的位似比.
2.不是位似图形必定不相似。 2.位似图形上任意一对对应点到位似中心的距离之比等于位似比.
2.位似图形上任意一对对应点到位似中心的距离之比等于位似比.
(二)位似图形的性质
A A/ C
位似图形有以下性质:
1.位似图形的对应点和位似中心在同一条直线上
2.位似图形上任意一对对应点到位似中心的 距离之比等于位似比.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
过程与方法
• 经历位似图形性质的探索过程,进一步发 展学生的探究、交流能力、以及动手、动脑、 手脑和谐一致的习惯。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
情感态度与价值观
• 利用图形的位似解决一些简单的实际问题,并在此 过程中培养学生的数学应用意识,进一步培养学生动 手操作的良好习惯。 • 发展学生的合情推理能力和初步的逻辑推理能力。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
这些图形相 似吗?
这样放大或缩小,没有改变图形形状,经过 放大或缩小的图形,与原图是相似的。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
观察
它们相似的共 同点是什么?
其中相似图形的 共同点是什么?
知识要点
不仅相似,而且对应顶点的连线相交 于一点,对应边互相平行,像这样的两个图 形叫做位似图形(homothetic figures),这 个点叫做位似中心,这时的相似比又称为位 似比。
你还有其它方法吗?
如果依次在射线上PA,PB,PC,PD,PE,PF,PG 上取点A′,B′,C′,D′,E′,F′,G′呢?
A′
A
B′ C′
G′B G F′ C F
P●
DE
D′ E′
结果是一个向上的箭头. 新图形与原图形是位似图形,位似比是2∶1
位似变换的步骤
①确定位似中心,位似中心的位置可随意 选择;
教学目标
知识与能力
• 了解位似图形及其有关概念,了解位似与相 似的联系和区别,掌握位似图形的性质。 • 掌握位似图形的画法,能够利用作位似图 形的方法将一个图形放大或缩小。 • 掌握直角坐标系中图形的位似变化与对应点 坐标变化的规律。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
小练习
使新图形与原图形对应线段的比是2∶1.
在原图上取几个关键点A,B,C,D,E,F,G;图外任取一点P;
作射线AP,BP,CP,DP,EP,FP,GP;
在这些射线上依次取点A′,B′,C′,D′,E′,F′,G′,使
②确定原图形的关键点,如四边形有四个 关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以 判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图 形与所确定的位似中心的位置有关,并且同一 个位似中心的两侧各有一个符合要求的图形。
小练习
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
位似的作用 位似可以将一个图形放大或缩小。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
Байду номын сангаас小练习
请以坐标原点O为位似中心,作□ ABCD
的位似图形,并把它的边长放大3倍。
分析:根据位似图形上任意一对对应点到位似中 心的距离之比等于位似比,我们只要连结位似中心O
和□ ABCD的各顶点,并把线段延长(或反向延长)
到原来的3倍,就得到所求作图形的各个顶点。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
新课导入
这种相似有 什么特征?
相似图形
相似图形
这种相似有 什么特征?
相似图形
照相机把人物的影 像缩小到底片上
这种相似有 什么特征?
1. 在幻灯机放映图片的过程中,这些图片有 什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
作法:
1. 连结OA,OB,OC,OD. 2. 分别延长OA,OB,OC, OD至G,C,E,F,使
OG OC OE OF 3 OA OB OC OD
3. 依次连结GC,CE,EF,FG.
四边形GCEF就是所求作的四边形. 如果反向延长OA,OB,OC,OD,就得到四边形G’C’E’F’, 也是所求作的四边形.
位似图形
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
注意
✓ 位似是一种具有位置关系的相似。 ✓ 位似图形是相似图形的特殊情形。 ✓ 位似图形必定是相似图形,而相似图形 不一定是位似图形。 ✓ 两个位似图形的位似中心只有一个。 ✓ 两个位似图形可能位于位似中心的两侧, 也可能位于位似中心的一侧。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
位似图形的性质 ✓ 对应点与位似中心共线。 ✓ 不经过位似中心的对应边平行。 ✓ 位似图形上任意一对应点到位似中心的 距离之比等于位似比。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
PA′=2PA,PB′=2PB,PC′=2PC,PD′=2PD,PC′=2PC,PE′
=2PE,PF′=2PF,PG′=2PG;
E′
D′
A
B
P G ●
CF
DE
F′
C′
G′
B′
A′
顺次连接点A′, B′, C′, D′, E′, F′,G′,所得到的图形(向下的 箭头)就是符合要求的图形。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
位似多边形
如果两个图形不仅相似,而且每组对应顶 点所在的直线都经过同一个点,那么这样的两 个图形叫做位似图形,这个点叫做位似中心, 这时的相似比又称为位似比。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
教学重难点
• 位似图形的有关概念、性质与作图。 • 利用位似将一个图形放大或缩小。 • 直角坐标系中图形的位似变化与对应点 坐标的关系。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
• 经历位似图形性质的探索过程,进一步发 展学生的探究、交流能力、以及动手、动脑、 手脑和谐一致的习惯。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
情感态度与价值观
• 利用图形的位似解决一些简单的实际问题,并在此 过程中培养学生的数学应用意识,进一步培养学生动 手操作的良好习惯。 • 发展学生的合情推理能力和初步的逻辑推理能力。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
这些图形相 似吗?
这样放大或缩小,没有改变图形形状,经过 放大或缩小的图形,与原图是相似的。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
观察
它们相似的共 同点是什么?
其中相似图形的 共同点是什么?
知识要点
不仅相似,而且对应顶点的连线相交 于一点,对应边互相平行,像这样的两个图 形叫做位似图形(homothetic figures),这 个点叫做位似中心,这时的相似比又称为位 似比。
你还有其它方法吗?
如果依次在射线上PA,PB,PC,PD,PE,PF,PG 上取点A′,B′,C′,D′,E′,F′,G′呢?
A′
A
B′ C′
G′B G F′ C F
P●
DE
D′ E′
结果是一个向上的箭头. 新图形与原图形是位似图形,位似比是2∶1
位似变换的步骤
①确定位似中心,位似中心的位置可随意 选择;
教学目标
知识与能力
• 了解位似图形及其有关概念,了解位似与相 似的联系和区别,掌握位似图形的性质。 • 掌握位似图形的画法,能够利用作位似图 形的方法将一个图形放大或缩小。 • 掌握直角坐标系中图形的位似变化与对应点 坐标变化的规律。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
小练习
使新图形与原图形对应线段的比是2∶1.
在原图上取几个关键点A,B,C,D,E,F,G;图外任取一点P;
作射线AP,BP,CP,DP,EP,FP,GP;
在这些射线上依次取点A′,B′,C′,D′,E′,F′,G′,使
②确定原图形的关键点,如四边形有四个 关键点,即它的四个顶点;
③确定位似比,根据位似比的取值,可以 判断是将一个图形放大还是缩小;
④符合要求的图形不唯一,因为所作的图 形与所确定的位似中心的位置有关,并且同一 个位似中心的两侧各有一个符合要求的图形。
小练习
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
位似的作用 位似可以将一个图形放大或缩小。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
Байду номын сангаас小练习
请以坐标原点O为位似中心,作□ ABCD
的位似图形,并把它的边长放大3倍。
分析:根据位似图形上任意一对对应点到位似中 心的距离之比等于位似比,我们只要连结位似中心O
和□ ABCD的各顶点,并把线段延长(或反向延长)
到原来的3倍,就得到所求作图形的各个顶点。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
新课导入
这种相似有 什么特征?
相似图形
相似图形
这种相似有 什么特征?
相似图形
照相机把人物的影 像缩小到底片上
这种相似有 什么特征?
1. 在幻灯机放映图片的过程中,这些图片有 什么关系?
2. 幻灯机在哪儿呢?
3.我们能给这种有特殊位置的相似图形一个名称吗?
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
作法:
1. 连结OA,OB,OC,OD. 2. 分别延长OA,OB,OC, OD至G,C,E,F,使
OG OC OE OF 3 OA OB OC OD
3. 依次连结GC,CE,EF,FG.
四边形GCEF就是所求作的四边形. 如果反向延长OA,OB,OC,OD,就得到四边形G’C’E’F’, 也是所求作的四边形.
位似图形
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
注意
✓ 位似是一种具有位置关系的相似。 ✓ 位似图形是相似图形的特殊情形。 ✓ 位似图形必定是相似图形,而相似图形 不一定是位似图形。 ✓ 两个位似图形的位似中心只有一个。 ✓ 两个位似图形可能位于位似中心的两侧, 也可能位于位似中心的一侧。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
位似图形的性质 ✓ 对应点与位似中心共线。 ✓ 不经过位似中心的对应边平行。 ✓ 位似图形上任意一对应点到位似中心的 距离之比等于位似比。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
PA′=2PA,PB′=2PB,PC′=2PC,PD′=2PD,PC′=2PC,PE′
=2PE,PF′=2PF,PG′=2PG;
E′
D′
A
B
P G ●
CF
DE
F′
C′
G′
B′
A′
顺次连接点A′, B′, C′, D′, E′, F′,G′,所得到的图形(向下的 箭头)就是符合要求的图形。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
位似多边形
如果两个图形不仅相似,而且每组对应顶 点所在的直线都经过同一个点,那么这样的两 个图形叫做位似图形,这个点叫做位似中心, 这时的相似比又称为位似比。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
教学重难点
• 位似图形的有关概念、性质与作图。 • 利用位似将一个图形放大或缩小。 • 直角坐标系中图形的位似变化与对应点 坐标的关系。
人教版九年级数学下册27.3《位似》 课件 (共48张PPT)
