(完整版)多边形和圆的初步认识知识归纳及经典例题
九年级上册数学《圆》正多边形和圆知识点整理
正多边形和圆一、本节学习指导本节我们重点了解正多边形的各种概念和性质，在命题中正多边形经常和三角形、圆联合命题，部分地区也会以这部分综合题作为压轴题。
二、知识要点1、正多边形（1）、正多边形的定义各边相等，各角也相等的多边形叫做正多边形。
如：正六边形，表示六条边都相等，六个角也相等。
（2）、正多边形和圆的关系只要把一个圆分成相等的一些弧，就可以作出这个圆的内接正多边形，这个圆就是这个正多边形的外接圆。
（3）、正多边形的中心正多边形的外接圆的圆心叫做这个正多边形的中心。
（4）、正多边形的半径正多边形的外接圆的半径叫做这个正多边形的半径。
（5）、正多边形的边心距正多边形的中心到正多边形一边的距离叫做这个正多边形的边心距。
（6）、中心角正多边形的每一边所对的外接圆的圆心角叫做这个正多边形的中心角。
2、正多边形的对称性（1）、正多边形的轴对称性正多边形都是轴对称图形。
一个正n边形共有n条对称轴，每条对称轴都通过正n边形的中心。
（2）、正多边形的中心对称性边数为偶数的正多边形是中心对称图形，它的对称中心是正多边形的中心。
（3）、正多边形的画法先用量角器或尺规等分圆，再做正多边形。
24.3正多边形和圆一、填空题1． 在一个圆中，如果︒60的弧长是π，那么这个圆的半径r=_________.2． 正n 边形的中心角的度数是_______.3． 边长为2的正方形的外接圆的面积等于________.4． 正六边形的内切圆半径与外接圆半径的比等于_________.二、选择题5．正多边形的一边所对的中心角与该正多边形一个内角的关系是（ ）.（A ） 两角互余 （B ）两角互补 （C ）两角互余或互补 （D ）不能确定6．圆内接正三角形的边心距与半径的比是（ ）.（A ）2：1 （B ）1：2 （C ）4:3 （D ）2:37．正六边形的内切圆与外接圆面积之比是（ ）（A ）43 （B ）23 （C ）21 （D ）41 8．在四个命题：（1）各边相等的圆内接多边形是正多边形；（2）各边相等的圆外切多边形是正多边形；（3）各角相等的圆内接多边形是正多边形；（4）各角相等的圆外切多边形是正多边形，其中正确的个数为（ ）（A ）1 （B ）2 （C ）3 （D ）49．已知：如图48-1，ABCD 为正方形，边长为a ，以B 为圆心，以BA 为半径画弧，则阴影部分面积为（ ）.（A ）（1-π）a 2 （B ）1-π（C ）44π- （D ）44π-a 21. 3；2. n o360；3. ∏2；4. 2:3； DBABD。
(最新)多边形和圆的初步认识知识归纳及经典例题
多边形和圆的初步认识知识讲解
【要点梳理】
要点一、多边形及正多边形
1．定义：多边形是由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形．其中，各边相等、各角也相等的多边形叫
做正多边形．如下图：
要点诠释：
正多边形必须同时满足“各边相等”，“各角相等”两个条件，二者缺一不可；
2．相关概念：
顶点：每相邻两条边的公共端点叫做多边形的顶点．
边：组成多边形的各条线段叫做多边形的边．
内角：多边形相邻两边组成的角叫多边形的内角（可简称为多边形的角），一个n边形有n个内角.
外角：多边形的边与它的邻边的延长线组成的角叫做多边形
的外角.
对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的
对角线．
要点诠释：
(1)过n 边形的一个顶点可以引(n-3)条对角线，n 边形对角线的条数为(3)2
n n ．(2)过n 边形的一个顶点的对角线可以把
n 边形分成(n-2)个三角形．
类型一、多边形及正多边形1．如图，（1）从正六边形的顶点A 出发,可以画出
条对角线，分别用字母表示出来为
；（2）这些对角线把六边形分割成
个三角形.
【思路点拨】画出对角线，并按一定规律数出对角线的条数及分割成的三角形的个数即可.
【答案】（1）3，线段AC 、线段AD 、线段AE ；（2）4.E
A B C F
D。
第06讲 多边形和圆的初步认识(6类热点题型讲练)(解析版)--初中数学北师大版7年级上册
第06讲多边形和圆的初步认识(6类热点题型讲练)1.掌握多边形和正多边形的定义；2.掌握多边形的角平分线的规律；3.掌握圆的相关计算问题.知识点01多边形三角形、四边形、五边形、六边形等都是多边形，它们都是由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形.【说明】（1）内角：多边形相邻两边组成的角叫多边形的内角.（2）外角：多边形的边与它的邻边的延长线组成的角叫做多边形的外角.（3）连接多边形不相邻的两个顶点的线段，叫做多边形的对角线.（4）各边相等，各角也相等的多边形叫做正多边形，所以正多边形同时具有各边相等，各角相等的性质.知识点02多边形的对角线顶点3456n 从一个顶点出发的对角线的条数0123n-3对角线的总条数02592)3(-nn 分割成三角形的个数0234n-3知识点03圆（1）圆上任意两点A，B间的部分叫做圆弧，简称弧，记作A，读作“圆弧AB”或“弧AB”；（2）圆的周长公式：rCπ2=；圆的面积公式：2rSπ=.题型01多边形的概念与分类【典例1】（2023秋·全国·八年级专题练习）下列图形中，不是多边形的是（）A．B．C．D．【答案】C【分析】根据多边形的定义，逐项判断，即可求解．【详解】解：A、该图形是由4条线段首尾顺次连接而成的封闭图形，所以它是多边形．故本选项不符合题意；B、该图形是由5条线段首尾顺次连接而成的封闭图形，所以它是多边形．故本选项不符合题意；C、该图形是由线段、曲线首尾顺次连接而成的封闭图形，所以它不是多边形．故本选项符合题意；D、该图形是由5条线段首尾顺次连接而成的封闭图形，所以它是多边形．故本选项不符合题意；故选：C．【点睛】本题主要考查了多边形，熟练掌握由()3n n≥条线段首尾顺次连接而成的封闭图形是多边形是解题的关键．【变式1】（2023春·全国·八年级专题练习）如图所示的图形中，属于多边形的有（）A．3个B．4个C．5个D．6个【答案】A【分析】根据多边形定义，逐个验证即可得到答案．【详解】解：所示的图形中，第一个是三角形、第二个是四边形、第三个是圆、第四个是正六边形、第五个是正方体，∴属于多边形的有第一个、第二个、第四个，共有3个，故选：A．【点睛】本题考查多边形定义，熟记多边形定义是解决问题的关键．【变式2】（2023春·七年级单元测试）下列判断：（1）各边长相等的多边形是正多边形；（2）各角都相等的多边形是正多边形；（3）等边三角形是正多边形：（4）长方形是正多边形．其中正确的有（）A．1个B．2个C．3个D．4个【答案】A【分析】各个角都相等，各个边都相等的多边形叫做正多边形．依据正多边形的概念进行判断即可．【详解】解：（1）菱形各边相等，但不是正四边形，故说法错误；（2）长方形各角都相等，但不是正四边形，故说法错误；（3）等边三角形三条边都相等，三个角都相等，是正多边形，故说法正确；（4）长方形的四个角相等，但长与宽不一定相等，所以不一定是正多边形，故说法错误．故正确的有：1个．故说：A．【点睛】本题考查了正多边形的概念，各个角都相等，各个边都相等的多边形叫做正多边形．题型02多边形对角线的条数问题【典例2】（2023秋·八年级课时练习）已知过多边形的某一个顶点可以作2023条对角线（不是一共有2023条对角线），则这个多边形的边数是（）A．2023B．2024C．2025D．2026【答案】Dn-条对角线进行求解即可．【分析】根据从n边形的一个顶点出发可以引()3【详解】解：设这个多边形的边数为n．n-=，根据题意，得32023n=．解得2026题型03对角线分成三角形个数问题（1）从四边形的一个顶点出发，可以引1条对角线，将四边形分成故答案为：1，2，2；（2）从五边形的一个顶点出发，可以引2条对角线，将五边形分成故答案为：2，3，5；（3）从六边形的一个顶点出发，可以引3条对角线，将六边形分成题型04用七巧板拼图形A ．21dm4B ．23dm8C ．3123218÷⨯=（平方分米）答：阴影部分的面积为23dm 8．故选：B ．【答案】34/0.75【分析】根据七巧板中各部分面积的关系可得小三角形的面积为大正方形的三角形的面积的2倍，即可求解．【详解】∵图2是由边长为2的正方形分割制作的七巧板拼摆成的，∴大正方形面积4=，由图形可知，阴影部分面积为小三角形的面积与平行四边形的面积之和，即【答案】32【分析】利用七巧板的各边之间的关系即可求出积．【详解】由图可知“小狐狸”图案中阴影部分面积为图形∵正方形ABCD 的边长为∴AE DE DF FC ===∴ADC EDF S S S =-= 故答案为：32．题型05平面镶嵌【典例5】（2023春·广东佛山·八年级校考期末）在平面图形正三角形、正六边形、正四边形、正五边形中，能单独镶嵌平面的有（）种图形．A ．1B ．2C ．3D ．4．B．．．【点睛】本题考查了图形的密铺，一种图形能够密铺，则拼在同一顶点处的几个角恰好组成一个周角．题型06圆的周长和面积问题πB．4A．22R【答案】C【分析】根据图形的特征，四边形内角和为的面积．【详解】解：因为四边形内角和为【答案】4π【分析】根据铁环从原点O沿数轴滚动一周（无滑动）到达点【详解】∵铁环从原点O沿数轴滚动一周（无滑动）到达点【答案】大蚂蚁和小蚂蚁爬的路程一样长，见解析【分析】利用圆的周长公式分别求出大、小蚂蚁爬行的路程，然后比较即可．【详解】解：大圆的周长∴大圆的周长＝两个小圆的周长和，一、单选题1．（2023秋·全国·八年级专题练习）五边形经过一个顶点可以引（）条对角线．A．0B．1C．2D．3【答案】Cn-，进行计算即可．【分析】根据从一个n边形一个顶点出发，可以连的对角线的条数是3-=，【详解】解∶532∴五边形经过一个顶点可以引2条对角线．故选∶C．【点睛】此题主要考查了多边形的对角线，解答此类题目可以直接记忆：一个n边形一个顶点出发，可以n-．连的对角线的条数是32．（2023秋·河南周口·八年级校联考阶段练习）已知，一个多边形的边数恰好是从一个顶点出发的对角线条数的2倍，则这个多边形的边数是()A ．5B ．9C ．8D ．6【答案】D 【分析】设此多边形有n 条边，根据题意可得()23n n =-，解方程，即可求解．【详解】解：设此多边形有n 条边，由题意，得()23n n =-，解得6n =，故选：D ．【点睛】本题考查了多边形对角线条数问题，熟练掌握从n 边形的一个顶点出发的对角线条数为()3n -条，是解题的关键．3．（2023春·河南南阳·七年级统考期末）有足够多的如下4种边长相等的正多边形瓷砖图案进行平面镶嵌，则不能铺满地面的是（）A ．①②④B ．①②C ．①④D ．②③【答案】D 【分析】只需要计算各个选项中的一个顶点处的角是否能组合成一个周角即可得出答案.【详解】解：A 、若有一个正三角形、两个正方形、一个正六边形，则在一个顶点处的角的和为60902120360︒+︒⨯+︒=︒，能铺满地面，故①②④的正多边形瓷砖图案可以进行平面镶嵌；B 、若有三个正三角形、两个正方形，则在一个顶点处的角的和为603902360︒⨯+︒⨯=︒，能铺满地面，故①②的正多边形瓷砖图案可以进行平面镶嵌；C 、若有两个正三角形、两个正六边形，则在一个顶点处的角的和为6021202360︒⨯+︒⨯=︒，能铺满地面，故①④的正多边形瓷砖图案可以进行平面镶嵌；D 、由于正五边形的内角为108︒，正方形的内角为90︒，在一个顶点处不能构成一个周角，故不能铺满地面，故②③的正多边形瓷砖图案不可以进行平面镶嵌；故选：D .【点睛】本题考查了平面镶嵌，解决此类问题的关键是明确一个顶点处的角是否能组合成一个周角.4．（2023秋·河南南阳·七年级校联考期末）七巧板被西方人称为“东方魔板”．如图的两幅图是由同一副七巧板拼成的．已知七巧板拼成的正方形的边长为4cm ，则“一帆风顺”图中阴影部分的面积为（）A．28cm B．4cm【答案】C【分析】首先确定阴影部分的三角形在七巧板中所属的部分，再根据这个三角形与正方形边长的关系求出这个三角形的边长，便可以根据三角形的面积公式进行解答．【详解】由图可知“一帆风顺”图中阴影部分是正方形右下角的等腰直角三角形，A．54B．44C．35【答案】C【分析】根据一个n边形的对角线条数为()32n n-进行求解即可．【详解】解：一个四边形共有2条对角线，一个五边形共有一个十边形共有()10103352⨯-=条对角线，故C正确．故选：C．【点睛】本题主要考查了对角线条数问题，解题的关键是熟练掌握一个二、填空题【答案】猫和老鼠同时到达【分析】利用圆的周长公式即可求解．【详解】解：以AB为直径的半圆的长是：11．（2023春·上海·八年级专题练习）从一个多边形一边上的一点（不是顶点）出发，分别连接这个点与各个顶点，可以把这个多边形分割成若干个三角形，请你观察下图，并完成后面的填空.当多边形的边数是4时，可以把多边形分割成_______个三角形；当多边形的边数是5时，可以把多边形分割成_______个三角形；当多边形的边数是6时，可以把多边形分割成_______个三角形；……你能看出多边形边数与分割成的三角形的个数之间有什么规律吗？【答案】3,4,5,规律：多边形的边数比分割成的三角形的个数多1【分析】由相应图形得到分成的三角形的个数和多边形的边数的关系的规律即可．【详解】由图中可以看出：四边形被分为3个三角形，五边形被分为4个三角形，六边形被分成5个三角形，那么n 边形被分为（n -1）个三角形．∵n -(n -1)=1，∴多边形的边数比分割成的三角形的个数多1.【点睛】解决本题的难点是得到分成的三角形的个数和多边形的边数的关系．12．（2023秋·全国·八年级课堂例题）（1）如图①，O 为四边形ABCD 内一点，连接OA OB OC OD ，，，，可以得到几个三角形？它与边数有何关系？（2）如图②，点O 在五边形ABCDE 的边AB 上（不与端点重合），连接OC OD OE ，，，可以得到几个三角形？它与边数有何关系？（3）如图③，过点A 作六边形ABCDEF 的对角线，可以得到几个三角形？它与边数有何关系？（4）若是任意一个n （4n ≥，且n 为整数）边形，上述三种情况分别可以将n 边形分割成多少个三角形？【答案】（1）4个，它与边数相等．（2）4个，它等于边数减1．（3）4个，它等于边数减2．（4）若点在n 边形内部，则可以将n 边形分割成n 个三角形；若点在n 边形的边上（不与端点重合），则可以将n 边形分割成()1n -个三角形；若点为n 边形的顶点，则可以将n 边形分割成()2n -个三角形．【分析】（1）根据图形，求解即可；（2）依据题中的图形，求解即可；（3）依据题中的图形，求解即可；（4）根据前面三种情况求解即可．【详解】解：（1）由图形可得，可以得到4个三角形，它与边数相等；（2）可以得到4个三角形，它等于边数减1；（3）可以得到4个三角形，它等于边数减2；（4）由前面的性质可得，若点在n 边形内部，则可以将n 边形分割成n 个三角形；若点在n 边形的边上（不与端点重合），则可以将n 边形分割成()1n -个三角形；若点为n 边形的顶点，则可以将n 边形分割成()2n -个三角形．【点睛】此题考查了多边形的性质，解题的关键是理解题意，掌握多边形的有关性质．13．（2023春·广西百色·八年级统考期末）观察探究及应用；(1)观察下列图形并完成填空．如图①一个四边形有2条对角线；(2)分析探究：由凸n 边形的一个顶点出发，可做______条对角线，一个凸n 边形有(3)应用：一个凸十二边形有______条对角线．【答案】(1)9，14(2)()3n -，()132n n -(3)54【分析】（1）分别通过计数可得答案；（2）先探究从三角形到六边形的一个顶点出发作的对角线的数量，得到每种图形的对角线的总数量，再总。
4.5多边形和圆的初步认识
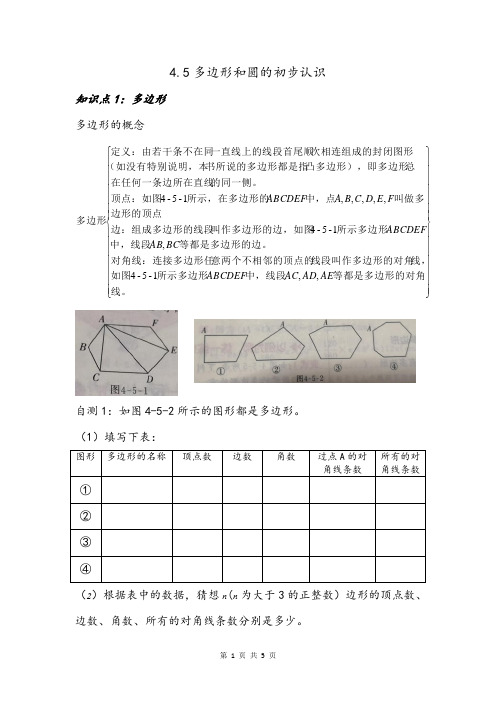
4.5多边形和圆的初步认识知识点1：多边形多边形的概念⎪⎪⎪⎪⎪⎪⎪⎭⎪⎪⎪⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧线。
等都是多边形的对角中，线段所示多边形如图线，线段叫作多边形的对角意两个不相邻的顶点的对角线：连接多边形任等都是多边形的边。
中，线段所示多边形叫作多边形的边，如图边：组成多边形的线段边形的顶点叫做多中，点所示，在多边形的顶点：如图的同一侧。
在任何一条边所在直线总凸多边形），即多边形书所说的多边形都是指（如没有特别说明，本次相连组成的封闭图形一直线上的线段首尾顺定义：由若干条不在同多边形AE AD AC ABCDEF BC AB ABCDEF F E D C B A ABCDEF ,,1-5-4,1-5-4,,,,,1-5-4自测1：如图4-5-2所示的图形都是多边形。
（1）填写下表：图形多边形的名称顶点数边数角数过点A 的对角线条数所有的对角线条数① ② ③ ④（2）根据表中的数据，猜想n (n 为大于3的正整数）边形的顶点数、边数、角数、所有的对角线条数分别是多少。
知识点2：正多边形各边相等、各角也相等的多边形叫做正多边形。
帮你理解〈〈〈〈〈（1）正多边形的定义中两个条件缺一不可，即要同时满足各边相等和各角相等，只有各边相等的多边形或只有各角相等的多边形都不是正多边形。
（2）正多边形按边数可分为正三角形、正方形、正五边形、正六边形、…、正n边形。
（3）多边形、正多边形都是平面图形。
自测2：我们学过的四边形有长方形和正方形，请问它们是正多边形吗？为什么？知识点3：圆圆：平面上，一条线段绕着它固定的一个端点旋转一周，另一个端点形成的图形叫圆，固定的端点称为圆心，这条线段称为半径。
弧：圆上任意两点之间的部分叫做圆弧，简称弧。
扇形：一条弧和经过这条弧的端点的两条半径组成的图形叫做扇形。
圆心角：顶点在圆心的角叫做圆心角。
自测3：圆的四条半径OA,OB,OC,OD把圆分为若干个扇形，其中扇形AOB,扇形BOC，扇形COD，扇形AOD在圆中所占的百分比如图4-5-3所示，如果OA=5cm,(1)求扇形AOB与扇形AOD的圆心角与面积，结果保留π；(2)求ABD的长度，结果保留π。
2024年北师大七年级数学上册 4.3 多边形和圆的初步认识(课件)
点 A， B， C， D， E
内角
多边形相邻两条边 组成的角
∠ EAB， ∠ ABC， ∠ BCD， ∠ CDE， ∠ DEA
对角线
连接多边形不相邻 两个顶点的线段
线段 AC，AD，BE ， BD， CE
知1－讲
图示
感悟新知
知1－讲
4. 正多边形：各边相等、各角也相等的多边形叫作正多边形 .
示 例
顶点在圆心的角叫作圆心角
如∠ AOB
知2－讲
感悟新知
知2－讲
1. 圆心角的度数： 因为一个周角为 360° ，所以将一个圆分 成的几个扇形的圆心角的度数之和等于 360° ，一个扇形 圆心角的度数 =360°× 这个扇形圆心角占周角的百分比 .
2. 扇形的面积： 半径为 R 的圆，其面积 S=π R2，将圆等分为 360 个小扇形，则每个圆心角为 1° 的小扇形的面积是
段组成，那么这个多边形叫作 n 边形 . 如三角形、四边形、
五边形……三角形是最简单的多边形 .
注意： 如无特别说明，本书所说的多边形都是指凸多边形，
即多边形总在其任意一条边所在直线的同一侧 .
感悟新知
知1－讲
2. 多边形的表示方法： 先写出多边形的名称，然后写出表示 它的各个顶点的大写字母，可以按顶点顺时针的顺序书写， 也可以按顶点逆时针的顺序书写 .
答案：C
感悟新知
知1－练
1-1.如图所示的图形中，属于多边形的有( A ) A.3 个 B.4 个 C.5 个 D.6 个
感悟新知
1-2.下列图形中一定是正多边形的是( B ) A. 三角形 B. 正方形 C. 长方形 D. 八边形
知1－练
感悟新知
知识点 2 圆和扇形及其相关概念
北师大七年级上-第12讲-多边形和圆的初步认识
多边形和圆的初步认识知识点一：多边形 1．定义：由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形是多边形． 2．分类：根据组成多边形的条数将其分为三角形、四边形、五边形、六边形…… 例 1 如图，下面图形是多边形的有____（填序号）．分析：根据多边形的定义及特征判断，①②⑤都有一部分曲线，不符合定义；⑥不是由线段首尾相连组成； ⑦不是封闭图形． 解：③④ 拓展 一些常见的多边形：变式训练 1.下列图形：①正方形；②三角形；③圆锥；④线段；⑤棱柱；⑥圆；⑦球；⑧长方形；⑨圆柱；⑩梯 形．其中，是平面图形的有 答案：⑧④①②⑧④ 知识点二：多边形的分割 1．三角形是特殊的多边形，其边数最少，也是生活中最常见的平面图形． 2．利用三角形研究多边形最常用的方法是将多边形进行分割，从而把多边形的问题转化成三角形来处理． 3．若多边形的边数为 n（n≥3），从这个多边形的一个顶点出发，能把这个多边形分割成（ n-2）个三角形． 例 2 在多边形中，连接不相邻的两个顶点的线段，叫做多边形的对角线．请你先画一画、数一数，如果从四 边形、五边形、六边形的一个顶点引对角线各有多少条？如果从每个顶点都引又各有对角线多少条？n 边形 （n,≥4，n 是整数）共有多少条对角线？ 分析：可以实际动手画一画，再数一数，然后从特殊到一般，找出多边形对角线的规律． 解：如下图所示： ；是多边形的有____．（只填序号）从一个顶点出发，四边形的一个顶点可引 4 -3 =1（条）对角线；五边形的一个顶点可引 5 -3 =2（条）对角 线；六边形的一个顶点可引 6-3 =3（条）对角线…… ∴n 边形的一个顶点可引（n-3）条对角线． 如果从每个顶点都引对角线，四边形有 4 个顶点，每个顶点引 4 -3 =1 条，四个顶点共可引 4 条．但在此过 程中，从顶点引过去，然后又从另一顶点引回来，故这四条对角线是两两重复的，结果实际上： 四边形有(4 3) 4 2 （条）对角线； 2(5 3) 5 5 （条）对角线； 2 (6 3) 6 六边形有 9 （条）对角线； 2 (n 3) n ∴n 边形有 条对角线． 2五边形有 如下图所示：拓展 (1)从一个顶点出发，连接不相邻的 顶点，此时可将 n 边形分割成（n -2）个三角形．(2)从多边形一边上的一点出发，连接各顶点，此时可将 n 边形分割成（n-1）个三角形．(3)从多边形内部的一点出发，连接各顶点， 此时可将 n 边形分割成 n 个三角形，变式训练 1．(1)若在 n 边形内部任意取一点 P，将 P 与各顶点连接起来，则可将多边形分割成 ________个三角形． (2)若点 P 取在多边形的一条边上（不是顶点），将 P 与 n 边形各顶点连接起来，则可将多边形分割成 ____个三角形． 2．用大小相同的实心点摆成如图所示的图案，按照这样的规律摆成的第 n 个图案中，共有实心点的个数为 ____答案：1.n n-1n 2 9n 2 (n 1)(n 2) n 2 9n 提示： 3(n 1) 2 2 22． 1．圆：(1)静态定义：平面上到定点的距离等于定长的所有点组成的图形叫圆. (2)描述性定义：平面上，一条线段绕着它固定的一个端点旋转一周，另一个端点形成的图形叫做知识点三：弧和扇形圆．定点叫做圆心，定长叫做半径2．弧：圆上两点 A、B 之间的部分叫做圆弧，简称弧．记作 AB，读作“圆弧 AB”或“弧 AB”． 3．扇形：由一条弧 AB 和经过这条弧的端点的两条半径 OA、08 所组成的图形叫做扇形。
中考数学复习----《正多边形与圆》知识点总结与练习题(含答案)
中考数学复习----《正多边形与圆》知识点总结与练习题（含答案）知识点总结1.正多边形与圆的关系把一个圆分成n（n是大于2的自然数）等份，依次连接各分点所得的多边形是这个圆的内接正多边形，这个圆叫做这个正多边形的外接圆。
2.正多边形的有关概念①中心：正多边形的外接圆的圆心叫做正多边形的中心。
②正多边形的半径：外接圆的半径叫做正多边形的半径。
③中心角：正多边形每一边所对的圆心角叫做正多边形的中心角。
④边心距：中心到正多边形的一边的距离叫做正多边形的边心距。
练习题1、（2022•长春）跳棋是一项传统的智力游戏．如图是一副跳棋棋盘的示意图，它可以看作是由全等的等边三角形ABC和等边三角形DEF组合而成，它们重叠部分的图形为正六边形．若AB＝27厘米，则这个正六边形的周长为厘米．【分析】根据对称性和周长公式进行解答即可．【解答】解：由图象的对称性可得，AM＝MN＝BN＝AB＝9（厘米），∴正六边形的周长为9×6＝54（厘米），故答案为：54．2、（2022•营口）如图，在正六边形ABCDEF中，连接AC，CF，则∠ACF＝度．【分析】设正六边形的边长为1，正六边形的每个内角为120°，在△ABC中，根据等腰三角形两底角相等得到∠BAC＝30°，从而∠CAF＝∠BAF﹣∠BAC＝120°﹣30°＝90°，过点B作BM⊥AC于点M，根据含30°的直角三角形的性质求出BM，根据勾股定理求出AM，进而得到AC的长，根据tan∠ACF＝＝＝即可得出∠ACF＝30°．【解答】解：设正六边形的边长为1，正六边形的每个内角＝（6﹣2）×180°÷6＝120°，∵AB＝BC，∠B＝120°，∴∠BAC＝∠BCA＝×（180°﹣120°）＝30°，∵∠BAF＝120°，∴∠CAF＝∠BAF﹣∠BAC＝120°﹣30°＝90°，如图，过点B作BM⊥AC于点M，则AM＝CM（等腰三角形三线合一），∵∠BMA＝90°，∠BAM＝30°，∴BM＝AB＝，∴AM＝＝＝，∴AC＝2AM＝，∵tan∠ACF＝＝＝，∴∠ACF＝30°，故答案为：30．3、（2022•呼和浩特）如图，从一个边长是a的正五边形纸片上剪出一个扇形，这个扇形的面积为（用含π的代数式表示）；如果将剪下来的扇形围成一个圆锥，圆锥的底面圆直径为．【分析】先求出正五边形的内角的度数，根据扇形面积的计算方法进行计算即可；扇形的弧长等于圆锥的底面周长，可求出底面直径．【解答】解：∵五边形ABCDE是正五边形，∴∠BCD＝＝108°，∴S扇形＝＝；又∵弧BD的长为＝，即圆锥底面周长为，∴圆锥底面直径为，故答案为：；．4、（2022•绥化）如图，正六边形ABCDEF和正五边形AHIJK内接于⊙O，且有公共顶点A，则∠BOH的度数为度．【分析】求出正六边形的中心角∠AOB和正五边形的中心角∠AOH，即可得出∠BOH的度数．【解答】解：如图，连接OA，正六边形的中心角为∠AOB＝360°÷6＝60°，正五边形的中心角为∠AOH＝360°÷5＝72°，∴∠BOH＝∠AOH﹣∠AOB＝72°﹣60°＝12°．故答案为：12．5、（2022•梧州）如图，四边形ABCD是⊙O的内接正四边形，分别以点A，O为圆心，取大1OA的定长为半径画弧，两弧相交于点M，N，作直线MN，交⊙O于点E，F．若OA 于2＝1，则BE⌒，AE，AB所围成的阴影部分面积为．【分析】连接OE、OB．由题意可知，∴△AOE为等边三角形，推出S阴影＝S扇形AOB﹣S弓形AOE﹣S△AOB＝S扇形AOB﹣（S扇形AOE﹣S△AOE）﹣S△AOB＝S扇形AOB﹣S扇形AOE+S△AOE ﹣S△AOB，即可求出答案．【解答】解：连接OE、OB，由题意可知，直线MN垂直平分线段OA，∴EA＝EO，∵OA＝OE，∴△AOE为等边三角形，∴∠AOE＝60°，∵四边形ABCD是⊙O的内接正四边形，∴∠AOB＝90°，∴∠BOE＝30°，∵S弓形AOE＝S扇形AOE﹣S△AOE，∴S阴影＝S扇形AOB﹣S弓形AOE﹣S△AOB＝S扇形AOB﹣（S扇形AOE﹣S△AOE）﹣S△AOB＝S扇形AOB﹣S扇形AOE+S△AOE﹣S△AOB＝S扇形BOE+S△AOE﹣S△AOB＝+﹣＝．故答案为：．6、（2022•宿迁）如图，在正六边形ABCDEF中，AB＝6，点M在边AF上，且AM＝2．若经过点M的直线l将正六边形面积平分，则直线l被正六边形所截的线段长是．【分析】设正六边形ABCDEF的中心为O，过点M、O作直线l交CD于点N，则直线l 将正六边形的面积平分，直线l被正六边形所截的线段长是MN，连接OF，过点M作MH ⊥OF于点H，连接OA，由正六边形的性质得出AF＝AB＝6，∠AFO＝∠AFE＝×＝60°，MO＝ON，进而得出△OAF是等边三角形，得出OA＝OF＝AF＝6，由AM＝2，得出MF＝4，由MH⊥OF，得出∠FMH＝30°，进而求出FH＝2，MH＝2，再求出OH＝4，利用勾股定理求出OM＝2，即可求出MN的长度，即可得出答案．【解答】解：如图，设正六边形ABCDEF的中心为O，过点M、O作直线l交CD于点N，则直线l将正六边形的面积平分，直线l被正六边形所截的线段长是MN，连接OF，过点M 作MH⊥OF于点H，连接OA，∵六边形ABCDEF是正六边形，AB＝6，中心为O，∴AF＝AB＝6，∠AFO＝∠AFE＝×＝60°，MO＝ON，∵OA＝OF，∴△OAF是等边三角形，∴OA＝OF＝AF＝6，∵AM＝2，∴MF＝AF﹣AM＝6﹣2＝4，∵MH⊥OF，∴∠FMH＝90°﹣60°＝30°，∴FH＝MF＝×4＝2，MH＝＝＝2，∴OH＝OF﹣FH＝6﹣2＝4，∴OM＝＝＝2，∴NO＝OM＝2，∴MN＝NO+OM＝2+2＝4，故答案为：4．。
多边形和圆的初步认识知识归纳及经典例题
多边形和圆的初步认识知识讲解【要点梳理】要点一、多边形及正多边形1. 定义：多边形是由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形.其中，各边相等、各角也相等的多边形叫做正多边形. 如下图：D/■人/E C E五边形正六边形要点诠释：正多边形必须同时满足“各边相等”，“各角相等”两个条件，二者缺一不可；2.相关概念：顶点：每相邻两条边的公共端点叫做多边形的顶点.边：组成多边形的各条线段叫做多边形的边.内角：多边形相邻两边组成的角叫多边形的内角（可简称为多边形的角），一个n边形有n个内角.夕卜角：多边形的边与它的邻边的延长线组成的角叫做多边形的外角.对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线.要点诠释:(1) 过n边形的一个顶点可以引(*3)条对角线，n边形对角线的条数为n(n 3).2(2) 过n边形的一个顶点的对角线可以把n边形分成(n- 2)个三角形. 类型一、多边形及正多边形G l.如图，(1)从正六边形的顶点A出发,可以画出___________________ 条对角线，分别用字母表示出来为_____________________ ; ( 2)这些对角线把六边形分割成__________ 个三角形.E D【思路点拨】画出对角线，并按一定规律数出对角线的条数及分割成的三角形的个数即可•【答案】(1) 3,线段AC线段AD线段AE; (2) 4.【总结升华】(1) n边形有n个顶点,n条边,n个内角.(2) 过n边形的每一个顶点有(n -3)条对角线,n边形总共n(n 3)条2 对角线•(3) n边形从一个顶点出发，分别连接这个顶点和其余各顶点，可以分割(n —2)个三角形.举一反三：【变式】(2015春?郑州期末)过多边形某个顶点的所有对角线，将这个多边形分成7个三角形，这个多边形是( )A .八边形B .九边形C.十边形 D .十一边形【答案】B若一个多边形的内角和等于720°则从这个多边形的一个顶点引出对角线条. 一个多边形除一个内角外其余内角的和为1510°，则这个多边形对角线的条数是( )A. 27B. 35C. 44D. 542.同学们在平时的数学活动中会遇到这样一个问题：把正方形纸片截去一个角后，还剩多少角，余下的图形是几边形，亲爱的同学们，你知道吗？【答案与解析】解：这个问题，我们可以用图来说明.按图（1）所示方式去截，不经过点B和D，还剩五个角，即得到一个五边形.按图（2）所示方式去截，经过点D（或点B）.不经过点B（或点D），还剩4个角，即得到一个四边形.按图（3）所示方式去截，经过点D、点B，则剩下3个角，即得到三角形.答：余下的图形是五边形或四边形或三角形.【总结升华】一个n边形剪去一个角后，可能是（n+1）边形，也可能是n边形，也可能是（n-1）边形，利用它我们可以解决一些具体问题. 举一反三：【变式】一个多边形共有20条对角线，则多边形的边数是（C ）.A.6B.7C.8D.9要点二、圆及扇形1. 圆的定义如图，在一个平面内，一条线段绕着它固定的一个端点旋转一周，另一个端点所形成的图形叫做圆，固定的端点叫做圆心，线段0A叫做半径.要点诠释:①圆心确定圆的位置，半径确定圆的大小；确定一个圆应先确定圆心，再确定半径，二者缺一不可.②圆是一条封闭曲线.2. 扇形（1）圆弧：圆上任意两点A, B间的部分叫做圆弧，简称弧，记作A B，读作“圆弧AB'或“弧AB'.如下图:（2）扇形的定义：如上图，由一条弧AB和经过这条弧的端点的两条半径OA 0B所组成的图形叫做扇形.要点诠释：圆可以分割成若干个扇形.（3）圆心角：顶点在圆心的角叫做圆心角.如上图，/ AOB是圆的一个圆心角，也是扇形OAB的圆心角.【典型例题】9. （2014?长宁区一模）下列说法中，结论错误的是（B ）A .直径相等的两个圆是等圆B .长度相等的两条弧是等弧C.圆中最长的弦是直径D .一条弦把圆分成两条弧，这两条弧可能是等弧10. （2015春?张掖校级月考）有下列四个说法：①半径确定了，圆就确定了；②直径是弦；③弦是直径；④半圆是弧，但弧不一定是半圆.其中错误说法的个数是（B ）A. 1B. 2C. 3D. 419. （2015春?定陶县期末）下列说法正确的是（④__________________ ）填序号.①半径不等的圆叫做同心圆；②优弧一定大于劣弧；③不同的圆中不可能有相等的弦；④直径是同一个圆中最长的弦03.如图是对称中心为点匚的正六边形.如果用一个含二角的直角三角板的角，借助点O （使角的顶点落在点O处），把这个正六边形的面积兀等分，那么左的所有可能的值是______________________________________________ .根据圆内接正多边形的性质可知，只要把此正六边形再化为正多边形即可，即可知：360- 30=12；【答360-60=6；360-120=3; 360-180=2.故n的所有可能的值是2, 3, 4, 6, 12.04.（2015?丰泽区校级质检）如图，MN为O O的弦，/ M=50 °则/ MON等于________ .【思路点拨】利用等腰三角形的性质可得/ N的度数，根据三角形的内角和定理可得所求角的度数.【答案】80°【解析】解：T OM=ON ,•••/ N= / M=50 °•••/ MON=180 °-Z M -Z N=80°故答案为80°【总结升华】考查圆的认识；利用圆的半径相等这个知识点是解决本题的突破点.360- 90=4；类型三、扇形C>5.将一个半径为3的圆形草坪分割成三个扇形，分别种植三种 花草，他们的圆心角的度数之比为2： 3： 4,求这三个圆心角的度数, 并尝试求他们的面积，你还能求他们的面积之比吗，你发现了什么 【思路点拨】考查扇形面积及圆心角的概念. 【答案与解析】 解：这三个圆心角的度数分别为:ooooo36080 ； 360120 ； 360160 .2342342 3 4圆的面积r 29 ,c 160 ’ 9 —— 4 .360这三个圆心角的面积之比为：2 :3 : 4 2： 发现：扇形的面积之比等于圆心角之比.【总结升华】一个扇形的面积与对应圆的面积比等于扇形圆心角的度 数n 与360的比, 即S 扇：S 圆=n ： 360,几个半径相等的扇形的面积比等于这几个扇形 的圆心角的比..一个扇形圆心角120°,以扇形的半径为边长画一个正方形,这个正方形的面积是16平方厘米.这个扇形的面积为多少？【思路点拨】由题意可知，这个扇形所在的圆的半径 r 就是这个正方 形的边长，即r 2 =边长2 = 120平方厘米. 【答案与解析】这三个圆心角的面积分别为：93602 ； 91203 ;3603: 4.解: 设扇形所在圆的半径为r，则r216，贝y：扇形的面积为：3.14 16 120 16.75 （平方厘米）. 360答这个扇形的面积为16.75平方厘米.：【总结升华】此题在求面积时用到了整体代换，此外注意扇形的面积的计算方法.。
多边形与圆初步认识
多边形与圆的初步认识一基础知识1多边形的概念；2正多边形的概念；3.凸n 边形的内角和公式及外角和定理；4.圆的概念；圆弧及弧长公式；弦的概念；圆心角与圆周角的概念；扇形及面积公式二典例分析1.（2011天津）如图，六边形ABCDEF 的六个内角都相等，若AB =1，BC =CD =3，DE =2，求这个六边形的周长2.（1）在⊙中，120°的圆心角所对的弧长为cm 80π，那么⊙O 的半径为________cm（2）已知扇形的周长为28cm ，面积为49cm 2，则它的半径为____________cm 。
（3）如果一个扇形的面积和一个圆面积相等，且扇形的半径为圆半径的2倍，这个扇形的中心角为______3.已知：在四边形ABCD中，如果，求各角的度数． 4. 已知四边形的一个外角等于与它不相邻的三个内角之和的14，求这个外角的度数． 5. 已知：一个多边形的内角和是，求这个多边形的边数.6.已知一个多边形的内角和是外角和的2倍，求此多边形的边数.7.（中招展示）（1）（12广东湛江）一个多边形的内角和是720°，这个多边形的边数是（ ）A ．4B ．5C ．6D 7（2）（12四川广安）如图7-1，四边形ABCD 中，若去掉一个60o 的角得到一个五边形，则∠1+∠2=_________度．（3）（12德阳）已知一个多边形的内角和是外角和的，则这个多边形的边数是 ．（4）（11山西）一个正多边形，它的每一个外角都等于45°，则该正多边形是（ ）A ．正六边形B ． 正七边形C ． 正八边形D ． 正九边形（5）（11四川眉山）若一个正多边形的每个内角为150°，则这个正多边形的边数是（ ）A ．12B ．11C ．10D ．9（6）（11广安）若凸边形的内角和为1260°，则从一个顶点出发引的对角线条数是________（7）（11湖北宜昌）如图7-7是圆锥的侧面展开图，其半径OA=3，圆心角∠AOB=l20°，则⌒AB 的 长为( ).A.π B.2π C.3π D.4π8（竞赛链接）（1） 在一个多边形中，除了两个内角外，其余内角之和为2002°，则这个多边形的 边数是 ．（2）在凸10边形的所有内角中，锐角的个数最多是（ ） A ．0 B ．1 C ．3 D ．5（3）凸n 边形中有且仅有两个内角为钝角，则n 的最大值是（ ）A ．4 B ．5 C ． 6 D ．7（4）一个凸多边形的每一内角都等于140°，那么从这个多边形的一个顶点出发的对角线的条数是( )A ．9条B ．8条C ．7条D ． 6条（5）已知148∠=，2∠的两边分别与1∠垂直，求2∠的大小 （6）①、②……是边长均大于2的三角形，四边形、……、凸n 边形，分别以它们的各顶点为圆心，以1为半径画弧与两邻边相交，得到3条弧，4条弧，……（1）图①中3条弧的弧长的和为______ 图②中4条弧的弧长的____（2）求图(n)中n 条弧的弧长的和（用n 表示）n （例1图） （7-1） （7-7）随堂练习1、用各种不同的方法把图形分割成三角形，至少可以分割成5个三角形的多边形是（）A.五边形B.六边形C.七边形D.八边形2、如图1，图中共有正方形（） A.12个 B.13个 C.15个 D.18个图1 图2 图3 图4 图53、如图2，图中三角形的个数为（）A.2 B.18 C.19 D. 204．如图3，已知一个圆，任意画出它的三条半径，能得到（）个扇形. A.4 B.5 C.6 D.85.我们熟悉的平面图形中的多边形有_____________等.它们是由一些_______同一条直线上的线段依次_______相连组成的_______图形.6．圆上两点之间的部分叫做_______，由一条_______和经过它的端点的两条_______所组成的图形叫做扇形. 7．如图4，用简单的平面图形画出三位携手同行的的小人物，请你仔细观察，图中共有三角形____个，圆_____个.8.如图5，你能数出_______个三角形，_______个四边形9. 平面内三条直线把平面分割成最少 ____ 块最多 ____ 块。
多边形和圆的初步认识知识点总结
多边形和圆的初步认识知识点总结多边形和圆的初步认识是几何学中的基本概念，以下是关于这两个概念的知识点总结：多边形的初步认识：1. 多边形的定义：由至少三条线段依次连接形成的闭合二维图形称为多边形。
2. 多边形的边数：多边形的边数可以是从三个到无数个不等，通常用字母n 表示多边形的边数。
3. 多边形的内角：多边形内部相邻两边之间的夹角称为内角。
所有内角之和为（n-2） 180度。
4. 多边形的外角：多边形的每一边与其外部的线之间的夹角称为外角。
所有外角之和为360度。
5. 多边形的对角线：连接多边形不相邻的两个顶点的线段称为对角线。
一个n边形有（n-3）条对角线。
6. 等边形：所有内角都相等的多边形称为等边形。
7. 正多边形：所有边和所有内角都相等的多边形称为正多边形。
圆的初步认识：1. 圆的定义：在同一平面内，线段OA绕它固定的一个端点O旋转一周，另一个端点A所形成的图形叫做圆。
其中，线段OA叫做半径，端点O叫做圆心，线段OA叫做弦。
2. 圆的基本性质：圆心到圆上任一点的距离（半径）都相等。
直径是圆中最长的弦，通过圆心的弦是直径。
弦中直径垂直平分弦，反过来，垂直平分弦的弦是直径。
3. 圆的周长：圆的周长C与半径r的关系为C = 2πr，其中π是一个常数（约等于）。
4. 圆的面积：圆的面积A与半径r的关系为A = πr^2。
5. 圆与圆的位置关系：根据两圆圆心距与两圆半径之和、差的关系，可以判断两圆的位置关系（外离、外切、相交、内切、内含）。
6. 圆的对称性：圆是中心对称图形，对称中心是圆心；同时，圆也是轴对称图形，对称轴是经过圆心的任意一条直线。
以上就是关于多边形和圆的初步认识的知识点总结，希望对你有所帮助。
正多边形与圆 知识点+例题+练习(非常好 分类全面)
§ 2.6 正多边形与圆一、概念知识点1 正多边形及其有关概念★正多边形：________相等、________也相等的多边形叫做正多边形.注：边数3n 的多边形必须同时满足“各边相等”和“各角相等”这两个条件，才能判定它是正多边形.例1 下列说法正确的是（）A.正三角形不是正多边形B.平行四边形是正多边形C.正方形是正多边形D.各角相等的多边形是正多边形知识点2 正多边形的对称性（重点）1.正多边形都是________图形.一个正n边形共有_______条对称轴，每一条对称轴都经过正n边形的_________.2.一个正多边形，如果有偶数条边，那么它是________________图形，也是_________________图形；如果有奇数条边，那么是_______________图形.注：（1）如果一个正多边形是中心对称图形，那么它的中心就是对称中心；（2）正n边形的内角和等于________________，每一个内角都等于___________________，每一个外角都等于_________________.知识点3 正多边形的判定例2 如图，在正∆ABC中，E,F,G,H,L,K分别是各边的三等分点，试说明六边形EFGHLK是正六边形.二、经典题型题型1 根据正多边形的性质求角例1 如图，正方形ABCD是O的内接正方形，点P是弧CD上不同于点C的任意一点，则∠BPC等于___________.题型2 利用正多边形的性质求图形的面积例 2 如图，正六边形内接于O，O的半径为10，则图中阴影面积_________.典例精讲：1． 下列边长为a 的正多边形与边长为a 的正方形组合起来，不能镶嵌成平面( ) 、(1)正三角形 (2)正五边形 (3)正六边形 (4)正八边形A ．(1)(2)B ．(2)(4)C ．(1)(3)D ．(1)(4)2. 若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r 3，r 4，r 6，则r 3：r 4：r 6等于( )A ．1:2:3B ．3:2:1C ．1:2:3D ． 3:2:13． 已知正六边形ABCDEF 内接于⊙O ，图中阴影部分的面积为312，则⊙O的半径为______________________．（第4题） （第5题）4．如图，正方形ABCD 内接于⊙O ，点E 在AD 上，则∠BEC= ．5．将一块正六边形硬纸片（图1），做成一个底面仍为正六边形且高相等的无盖纸盒（侧面均垂直于底面，见图2），需在每一个顶点处剪去一个四边形，例如图中的四边形AGA /H ，那么∠GA /H 的大小是 度．OB CDA EF E D C A O6．从一个半径为10㎝的圆形纸片上裁出一个最大的正方形，则此正方形的边长为 ．7.如图，若正方形A 1B 1C 1D 1内接于正方形ABCD 的内接圆，则AB B A 11的值为（ ）A ．21 B ．22 C ．41D ．42。
(完整版)北师大数学七年级上册第四章多边形和圆的初步认识
多边形和圆的初步认识知识讲解【学习目标】1．经历从现实世界中抽象出平面图形的过程，感受图形世界的丰富多彩；2. 在具体情景中认识多边形、正多边形、圆、扇形；3. 能根据扇形和圆的关系求扇形的圆心角的度数；4．在丰富的活动中发展有条理的思考和表达能力.【要点梳理】要点一、多边形及正多边形1．定义：多边形是由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形．其中，各边相等、各角也相等的多边形叫做正多边形．如下图：要点诠释：正多边形必须同时满足“各边相等”，“各角相等”两个条件，二者缺一不可；2．相关概念：顶点：每相邻两条边的公共端点叫做多边形的顶点．边：组成多边形的各条线段叫做多边形的边．内角：多边形相邻两边组成的角叫多边形的内角（可简称为多边形的角），一个n 边形有n个内角.外角：多边形的边与它的邻边的延长线组成的角叫做多边形的外角.对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线．要点诠释：(1)过n边形的一个顶点可以引(n-3)条对角线，n边形对角线的条数为(3)2n n．(2)过n边形的一个顶点的对角线可以把n边形分成(n-2)个三角形．要点二、圆及扇形1. 圆的定义如图，在一个平面内，一条线段绕着它固定的一个端点旋转一周，另一个端点所形成的图形叫做圆，固定的端点叫做圆心，线段OA 叫做半径.要点诠释：①圆心确定圆的位置，半径确定圆的大小；确定一个圆应先确定圆心，再确定半径，二者缺一不可.②圆是一条封闭曲线.2.扇形（1）圆弧：圆上任意两点A ，B 间的部分叫做圆弧，简称弧，记作AB ，读作“圆弧AB”或“弧AB”. 如下图：（2）扇形的定义：如上图，由一条弧AB 和经过这条弧的端点的两条半径OA ，OB 所组成的图形叫做扇形.要点诠释：圆可以分割成若干个扇形.（3）圆心角：顶点在圆心的角叫做圆心角. 如上图，∠AOB 是圆的一个圆心角，也是扇形OAB 的圆心角.【典型例题】类型一、多边形及正多边形1．如图，（1）从正六边形的顶点A 出发,可以画出 条对角线，分别用字母表示出来为 ；（2）这些对角线把六边形分割成 个三角形.【思路点拨】画出对角线，并按一定规律数出对角线的条数及分割成的三角形的个数即可.【答案】（1）3，线段AC 、线段AD 、线段AE ；（2）4. E A B CF D【总结升华】(1)n边形有n个顶点,n条边,n个内角.(2)过n边形的每一个顶点有(n－3)条对角线,n边形总共(3)2n n条对角线.(3)n边形从一个顶点出发,分别连接这个顶点和其余各顶点,可以分割（n－2）个三角形. 举一反三：【变式】（2016春•荣成市期中）从一个n边形的某个顶点出发，分别连接这个点与其他顶点可以把这个n边形分割成三角形个数是（）A．3个B．（n﹣1）个C．5个D．（n﹣2）个【答案】D2．同学们在平时的数学活动中会遇到这样一个问题：把正方形纸片截去一个角后，还剩多少角，余下的图形是几边形，亲爱的同学们，你知道吗?【答案与解析】解：这个问题，我们可以用图来说明．按图(1)所示方式去截，不经过点B和D，还剩五个角，即得到一个五边形．按图(2)所示方式去截，经过点D(或点B)．不经过点B(或点D)，还剩4个角，即得到一个四边形．按图(3)所示方式去截，经过点D、点B，则剩下3个角，即得到三角形．答：余下的图形是五边形或四边形或三角形．【总结升华】一个n边形剪去一个角后，可能是(n+1)边形，也可能是n边形，也可能是(n-1)边形，利用它我们可以解决一些具体问题．举一反三：【变式】一个多边形共有20条对角线，则多边形的边数是（）.A.6B.7C.8D.9【答案】C.3．如图是对称中心为点的正六边形．如果用一个含角的直角三角板的角，借助点（使角的顶点落在点处），把这个正六边形的面积等分，那么的所有可能的值是___________ __ .【答案】根据圆内接正多边形的性质可知，只要把此正六边形再化为正多边形即可，即可知：360÷30=12；360÷60=6；360÷90=4；360÷120=3；360÷180=2．故n的所有可能的值是2，3，4，6，12．类型二、圆4．（2015•丰泽区校级质检）如图，MN为⊙O的弦，∠M=50°，则∠MON等于．【思路点拨】利用等腰三角形的性质可得∠N的度数，根据三角形的内角和定理可得所求角的度数．【答案】80°．【解析】解：∵OM=ON，∴∠N=∠M=50°，∴∠MON=180°﹣∠M﹣∠N=80°，故答案为80°．【总结升华】考查圆的认识；利用圆的半径相等这个知识点是解决本题的突破点．【变式】如图,一根5m长的绳子,一端栓在柱子上,另一端栓着一只羊,请画出羊的活动区域.【答案】类型三、扇形5. 将一个半径为3的圆形草坪分割成三个扇形，分别种植三种花草，他们的圆心角的度数之比为2：3：4，求这三个圆心角的度数，并尝试求他们的面积，你还能求他们的面积之比吗，你发现了什么【思路点拨】考查扇形面积及圆心角的概念．【答案与解析】解：这三个圆心角的度数分别为： °°236080234⨯=++；°°3360120234⨯=++；°°4360160234⨯=++. 圆的面积29r ππ=，这三个圆心角的面积分别为：8092360ππ⨯=；12093360ππ⨯=；16094360ππ⨯=．这三个圆心角的面积之比为：2:3:4πππ=2：3：4． 发现：扇形的面积之比等于圆心角之比．【总结升华】一个扇形的面积与对应圆的面积比等于扇形圆心角的度数n 与360的比， 即S 扇：S 圆＝n ：360， 几个半径相等的扇形的面积比等于这几个扇形的圆心角的比．6.一个扇形圆心角120°，以扇形的半径为边长画一个正方形，这个正方形的面积是16平方厘米．这个扇形的面积为多少？【思路点拨】由题意可知，这个扇形所在的圆的半径r 就是这个正方形的边长，即r 2＝边长2＝120平方厘米．【答案与解析】解：设扇形所在圆的半径为r，则216r=，则：扇形的面积为：1203.141616.75360⨯⨯≈（平方厘米）.答：这个扇形的面积为16.75平方厘米．【总结升华】此题在求面积时用到了整体代换，此外注意扇形的面积的计算方法．【巩固练习】一、选择题1.下列几何图形中，平面图形的个数为（）个.①三角形，②圆，③圆柱，④圆锥，⑤正方体，⑥扇形.A.4B.5C.3D.62．从n边形的一个顶点出发共有对角线() .A．(n-2)条B．(n-3)条C．(n-1)条D．(n-4)条3．如图，图中四边形有() .A．3个B．5个C．2个D．6个4以已知点O为圆心，已知线段a为半径作圆，可以作（）.A．1个 B．2个 C．3个 D．无数个5（2016•重庆校级一模）从一个多边形的任何一个顶点出发都只有6条对角线，则它的边数是（）A．6 B．7 C．8 D．96 （2015•重庆校级模拟）如图，正四边形有2条对角线，正五边形有5条对角线，正六边形有9条对角线，则正十边形有（）条对角线．A．27 B．35 C．40 D．44二、填空题7．（2015春•龙口市期中）从多边形的一个顶点出发引对角线，可以把这个多边形分割成7个三角形，则该多边形为边形．8. 已知圆的半径，可以画____个圆；已知圆心，可以画____个圆；已知圆心和半径可以画_____个圆.9.一个圆的圆心决定这个圆的_________，圆的半径决定这个圆的_________．10.（2016•哈尔滨）一个扇形的圆心角为120°，面积为12πcm2，则此扇形的半径为cm．11.一个七边形的边数减少1，则它的对角线条数减少________，n边形的边数增加2，则对角线增加______．12.平面内到定点A的距离等于3cm的点组成的图形是 .三、解答题13.已知从n边形的一个顶点出发共有4条对角线，其周长为56，且各边长是连续的自然数，求这个多边形的各边长．14．已知多边形的边数恰好是从这个多边形的一个顶点出发的对角线条数的2倍，求此多边形的边数．15. （2014秋•腾冲县校级期末）如图，⊙A、⊙B、⊙C两两不相交，且半径都是0.5cm，求图中的三个扇形（即阴影部分）的面积之和．（友情提示：三个圆心角之间有何关系）【答案与解析】一、选择题1. 【答案】C；【解析】①⑥②为平面图形.2. 【答案】B；3. 【答案】A；【解析】四边形有：四边形ABCD,四边形ABOD，四边形ABCO.4. 【答案】A；【解析】以定点为圆心，定长为半径作圆，只能作一个，故选A.5. 【答案】D；【解析】设多边形有n条边，则n﹣3=6，解得n=9．6. 【答案】B二、填空题7. 【答案】九【解析】由题意可知，n﹣2=7，解得n=9．则这个多边形的边数为9，多边形为九边形．8. 【答案】无数；无数；1；【解析】圆心确定圆的位置，半径确定圆的大小，二者缺一不可．9. 【答案】位置，大小；10．【答案】6；【解析】设该扇形的半径为R ，则212012360ππR ⨯= ，解得R =6． 11.【答案】5，2n －1；【解析】七边形的对角线条数为：7(73)142⨯-=（条），七边形的边数减少1，即六边形的对角线条数为6(63)92⨯-=（条），相减得5条，所以一个七边形的边数减少1，它的对角线条数减少5条；同理n 边形的边数增加2，则对角线增加(2)(23)(3)2122n n n n n ++---=-(条) ． 12. 【答案】以A 为圆心3cm 为半径的圆.三、解答题13.【解析】解：由题意n -3＝4，n ＝7．设各边长为x -3，x -2，x -1，x ，x+1，x+2，x+3，则有： x -3+ x -2+ x -1+x+x+1+x+2+x+3＝56， 7x ＝56，x ＝8． ∴ 各边长为5，6，7，8，9，10，11．14.【解析】解：设多边形的边数为n ，根据题意，有：n ＝2(n -3)，解得n ＝6，故这个多边形的边数为6．15.【解析】解：∵∠A+∠B+∠C=180°∴答：图中的三个扇形面积之和为．。
七年级数学上册 4.5多边形和圆的初步认识含答案(pdf版)
７４ 君子成人之美，不成人之恶。
———《论语·颜渊》５ 多边形和圆的初步认识１．经历从现实世界中抽象出平面图形的过程，并能用美丽的图形打扮世界．２．在具体的情境中认识多边形、扇形、弧、圆心角等概念．３．在丰富的活动中发展有条理的思考，能从图形的变化中找出不变的规律． 夯实基础，才能有所突破……１．如图（１），小聪拿一张正方形的纸，沿虚线对折一次得到图（２），再对折一次得到图（３），然后用剪刀沿图（３）中的虚线剪去一个角，再打开后的形状为（ ）．（第１题）２．如图，在扇形统计图中，犃部分的圆心角为１５０°，犅部分的圆心角为１３５°，犆部分的圆心角为４５°，则犇部分的面积是圆面积的（ ）．（第２题）Ａ．１３６Ｂ．１２４Ｃ．１１２Ｄ．１６３．如图，在方格纸中有四个图形，其中面积相等的有（ ）．（第３题）Ａ．（１）和（２）Ｂ．（２）和（３）Ｃ．（２）和（４）Ｄ．（１）和（４）４．四边形不可能被分割成的三角形个数是（ ）．Ａ．１Ｂ．２Ｃ．３Ｄ．４５．下列说法中错误的是（ ）．Ａ．多边形是平面图形，平面图形不一定是多边形Ｂ．四边形由四条线段组成，但四条线段组成的图形不一定是四边形Ｃ．多边形是一个封闭图形，但封闭图形不一定是多边形Ｄ．多边形是三角形，但三角形不一定是多边形６．用水平线和竖直线将平面分成若干个边长为１的小正方形格子，小正方形的顶点叫格点，以格点为顶点的多边形叫格点多边形．设格点多边形的面积为犛，它各边上格点个数的和为狓．（第６题）（１）图中的格点多边形，其内部都只有１个格点，它们的面积与各边上格点个数的和狓的对应关系如下表，请写出犛与它各边上格点个数的和狓之间的关系式： ；多边形的序号①②③④…多边形的面积犛２２．５３４…各边上格点的个数和４５６８…（２）请你再画出一些格点多边形，使这些多边形内部都有而且只有２个格点．此时所画的各个多边形的面积犛与它各边上格点个数的和狓之间的关系式是 ；（３）请你继续探索，当格点多边形内部有且只有狀个格点时，猜想犛与它各边上格点个数的和狓之间的关系式是 ．７．如图，将６个相连的正方形分割成８个面积相等的图形，怎么分？画出分割线．（第７题） 课内与课外的桥梁是这样架设的。
2024年秋新北师大七年级数学上册 3 多边形和圆的初步认识(课件)
情境引入
观察图片，你能发现哪些熟悉的平面图形？与同伴进 行交流。
能发现圆、三角形、四边形、五边形、六边形等
探究新知
探究点1 多边形的初步认识
问题1 三角形、四边形、五边形、六边形等都是多边形。这些图 形是由什么样的线按怎样的方式组成的？如何对多边形进 行定义？
由若干条不在同一条直线上的线段首尾顺次相连组成 的封闭平面图形叫作多边形
圆心：固定的端点O
O
半径：线段OA
弧有两个端点，是一条曲线 圆弧：圆上任意两点 A，B 间的部
分叫做圆弧，简称弧，记作AB ，
读作“圆弧 AB ”或“弧 AB ”
扇形：由一条弧 AB 和经过这条弧 B
的端点的两条半径 OA，OB 所组成 的图形
圆心角：顶点在圆心的角
A
O
圆心角
例 将一个圆分割成三个扇形，它们的圆心角的度 数比为1:2:3，求这三个扇形的圆心角的度数。【教材 P129例题】
数关系 都是60° 都是90° 都是108° 都是120°都是135°
两个条件缺一不可 各边相等、各角也相等的多边形叫作正多边形
正三角形 正四边形 正五边形 正六边形 正八边形 （正方形）
【对应训练】
【教材 P130随堂练习第1题】
现实生活中有许多正多边形的实例，试举出两例。
解：如在生活中用正六边形的地板砖铺地面，六角 螺母的上下两个底面外轮廓是正六边形或用正多边 形设计图案。
四边形被分成两 五边形被分成三 六边形被分成四
个三角形
个三角形
个三角形
n边形可以分割成（n-2）个三角形
【对应训练】 如图，将多边形分割成三角形，图①中可分割出2个
三角形，图②中可分割出3个三角形，图③中可分割出4 个三角形……按照这种分割方式，n边形可以分割出多少 个三角形？
多边形和圆的初步认识_1
4条边,如图3所示.
第四章
多边形和圆的初步认识
知识要点基础练
综合能力提升练
拓展探究突破练
-10-
15.有一根长为32 cm的铁丝,请你按下列要求,弯成一个长方形或正方形,并分别计算它们的
面积.
( 1 )长为10 cm,宽为6 cm;
多边形和圆的初步认识
知识要点基础练
综合能力提升练
拓展探究突破练
-13-
18.观察、探索及应用.
( 1 )观察图形并填空:
一个四边形有2条对角线;
一个五边形有5条对角线;
一个六边形有 9 条对角线;
一个七边形有 14 条对角线.
( 2 )分析探索:由凸n边形的一个顶点出发,可作 ( n-3 ) 条对角线,凸n边形共有n个顶点,
( 2 )长为9 cm,宽为7 cm;
( 3 )边长为8 cm的正方形.
你会发现在长与宽的变化过程中,其面积有什么规律 根据这一规律,请将总长为100 m的篱
笆围成一个面积尽可能大的长方形或正方形.
解:( 1 )面积为60 cm2.
( 2 )面积为63 cm2.
( 3 )面积为64 cm2.
随着长与宽的差越来越小,其面积越来越大.将总长为100 m的篱笆围成一个边长为25 m的正
A.3
B.4
7.把一个圆分成四个扇形,四个扇形的面积分别占圆面积的10%,20%,30%,40%,则这四个扇
形的圆心角分别为 36°,72°,108°,144° .
第四章
多边形和圆的初步认识
知识要点基础练
综合能力提升练
拓展探究突破练
4.3多边形和圆的初步认识+同步练习2024-2025学年北师大版数学七年级上册
4.3多边形和圆的初步认识一、单选题1．如图，用对角线长为4的正方形，做了一套七巧板，拼成如图所示的一座桥，则桥中阴影部分的面积为（）A．2B．4C．6D．82．过一个多边形的一个顶点可引2021条对角线，则这个多边形的边数为（）A．2018B．2019C．2023D．20243．某中学新科技馆铺设地面，已有正方形地砖，现打算购买另一种正多边形地砖（边长与正方形的相等），与正方形地砖作平面镶嵌，则该学校可以购买的地砖形状是（）A．正五边形B．正六边形C．正八边形D．正十二边形4．一个n边形从一个顶点可引3条对角线．则n为（）A．4B．5C．6D．75．只使用下列正多边形中的一种铺满地面，这种正多边形可以是（）A．正五边形B．正六边形C．正七边形D．正八边形6．只用同一种正多边形铺满地面，不可以选择（）A．正六边形B．正五边形C．正四边形D．正三角形7．下列语句中，正确的是（）A．在同圆或等圆中，相等的圆心角所对的弧相等B．三点确定一个圆C．三角形的外心到三角形的三边距离相等D．长度相等的两条弧是等弧8．周长是18.84cm的圆，面积是（）平方厘米．A．50.24B．12.42C．25.12D．28.269．在多边形的一边上任取一点（不是顶点），将这个点与多边形的各顶点连接起来，可以将多边形分割成8个三角形，则该多边形的边数为（）A．8B．9C．10D．1110．用边长相等的两种正多边形地砖铺设地面，要求图形间既无缝隙又不重叠（平面镶嵌），下面选项中的两种正多边形不可以用来平面镶嵌的是（ ）A ．正三角形、正四边形B ．正三角形、正六边形C ．正四边形、正六边形D ．正四边形、正八边形二、填空题11．到定点的距离等于定长的所有点组成的图形是 ．12．小明用七巧板拼了一个对角线长为2的正方形，再用这副七巧板拼成一个长方形（如图所示），则长方形的周长为 ．13．如图，将四边形ABCD 沿BD 、AC 剪开，得到四个全等的直角三角形，已知，OA ＝4，OB ＝3，AB ＝5将这四个直角三角形拼为一个没有重叠和缝隙的四边形，则重新拼成的四边形的周长为 ．14．如图所示的圆可记作O ，图中半径有 条，分别是 ．15．若某个多边形从一个顶点出发的对角线最多可画9条，则这个多边形的边数为 ． 16．七巧板是中国传统智力玩具，现用以下方法制作一副七巧板：如图所示，取一张边长为20厘米的正方形纸板，联结对角线BD ；分别取BC CD 、中点E 、F ，联结EF ；过点A 作EF 垂线，分别交BD EF 、于G 、H 两点；分别取BG DG 、中点M 、N ，联结MH NF 、，沿图中实线剪开即可得到一副七巧板．其中四边形GHFN 的面积是 平方厘米．三、解答题17．三角形有几个顶点，几条边，几个内角？四边形有几个顶点，几条边，几个内角？……n 边形呢？18．如图，两个大小一样的传送轮连接着一条传送带，求这条传送带的长．19．（1）如图，线段AE上有三个点B，C，D，图中共有条线段；（2）如果线段上有n个点（包括线段的两个端点），则该线段上共有多少条线段？（3）n边形共有条对角线．20．用15.7米长的铁条做直径是50厘米的圆形铁环，可以做多少个？21．如图，点A，B，C在⊙O上，按要求作图：(1)过点A作⊙O的直径AD；(2)过点B作⊙O的半径；(3)过点C作⊙O的弦．22．例题：图（a）、（b）、（c）、（d）都称作平面图．(1)数一数每个图各有多少个顶点，多少条边，这些边围出了多少区域，将结果填人表中（其中（a）已填好）．(2)观察表，推断一个平面图的顶点数、边数、区域数之间有什么关系？(3)现已知某一平面图有999个顶点和999个区域，试根据（2）中推断出的关系，确定这个图有多少条边？。
北师大数学七年级上册第四章多边形和圆的初步认识(总结)
第03讲_多边形和圆的初步认识知识图谱多边形和圆的初步认识（北师版）知识精讲一．多边形1．多边形：由若干条不在同一直线上的线段首尾顺次相连组成的封闭平面图形，如三角形、四边形、五边形、六边形等．2．如下图，在多边形ABCDE 中，点A 、B 、C 、D 、E 是多边形的顶点，线段AB 、BC 、CD 、DE 、EA 是多边形的边；EAB ∠、ABC ∠、BCD ∠、CDE ∠、DEA ∠是多边形的内角（简称多边形的角）；AC 、AD 都是连接不相邻的两个顶点的线段，叫做多边形的对角线．3．正多边形：各边相等，各角也相等的多边形叫做正多边形．如下图，分别是正三角形、正四边形、正五边形、正六边形、正八边形．二．圆1．平面上，一条线段绕着它固定的一个端点旋转一周，另一个端点所形成的图形叫做圆； 2．固定的端点O 称为圆心，线段OA 称为半径；3．圆上任意两点AB 间的部分叫做圆弧，简称弧，记作AB ，读作“圆弧AB ”或“弧AB ”； 4．由一条弧AB 和经过这条弧的端点的两条半径OA 、OB 所组成的图形叫做扇形； 5．顶点在圆心的角叫做圆心角．三．扇形面积公式EDCBA BOA1．圆的周长公式：π2C D R π==2．扇形弧长公式：π180n Rl =（n 表示扇形圆心角度数值；R 表示半径）3．圆的面积公式：2πS R =4．扇形面积公式：2π360nS R =扇形（n 表示扇形圆心角度数值；R 表示半径）．三点剖析一．考点：1．多边形及对角线；2．圆和扇形．二．重难点：n 边形的对角线：一个顶点有()3n -条对角线，共有()32n n -条对角线．三．易错点：圆的周长面积计算公式计算错误．多边形及对角线例题1、 若从一个多边形的一个顶点出发，最多可以引10条对角线，则它是__________边形． 【答案】 13【解析】 从一个多边形的一个顶点出发，最多可以引()3n -条对角线，（n 为多边形边数）．本题中，设这个多边形是n 边形．代入公式，得310n -=，∴13n =．例题2、 把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是（ ） A.六边形 B.五边形 C.四边形 D.三角形 【答案】 A【解析】 剪去一个角的方法可能有三种：经过两个相邻顶点，则少了一条边；经过一个顶点和一边，边数不变；经过两条邻边，边数增加一条．例题3、 （1）若在n 边形内部任意取一点P ，将P 与各顶点连接起来，则可将多边形分割成__________ 个三角形． （2）若点P 取在多边形的一条边上（不是顶点），在将P 与n 边形各顶点连接起来，则可将多边形分割成__________ 个三角形．【答案】 （1）n （2）1n -【解析】 根据题中条件，画出简单图形，找出规律．（1）多边形内一点，可与多边形顶点连接n 条线段，构造出n 个三角形；（2）若P 点取在一边上，则可以与其他顶点连接出2n -条线段，可以分n 边形为()1n -个三角形． 随练1、 从一个n 边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n 的值是（ ） A.6 B.7 C.8 D.9 【答案】 C【解析】 根据从一个n 边形的某个顶点出发，可以引()3n -条对角线，把n 边形分为()2n -的三角形作答．设多边形有n 条边，则26n -=，解得8n =．故选C ． 随练2、 观察下面图形，并回答问题．（1）四边形有_______条对角线，五边形有_______条对角线，六边形有_______条对角线； （2）根据规律七边形有_______条对角线，n 边形有___________条对角线．【答案】 （1）2；5；9（2）14；()32n n - 【解析】 （1）四边形有2条对角线；五边形有5条对角线；六边形有9条对角线；（2）七边形有14条对角线，n 边形有()32n n -条对角线．圆和扇形例题1、 60°的圆心角所对的弧长为2πcm ，则此弧所在圆的半径为________． 【答案】 6cm【解析】 ∵l=180n rπ，∴r=180180260l n πππ⨯==6cm ． 例题2、 一个扇形的圆心角为135°，弧长为3πcm ，则此扇形的面积是________cm 2． 【答案】 6π【解析】 设扇形的半径为Rcm ，∵扇形的圆心角为135°，弧长为3πcm ， ∴135180R π⨯=3π，解得：R=4，所以此扇形的面积为21354360π⨯=6π（cm 2）．例题3、 在△ABC 中，∠C 为锐角，分别以AB ，AC 为直径作半圆，过点B ，A ，C 作BAC ，如图所示．若4AB =，2AC =，124S S π-=，则34S S -的值是__________．【答案】54π 【解析】 ∵4AB =，2AC =，∴132S S π+=，242S S π+=，∵124S S π-=，∴()()()()1324123432S S S S S S S S π+-+=-+-=∴3454S S π-=．随练1、 如图，O 的半径为1，分别以O 的直径AB 上的两个四等分点1O ，2O 为圆心，12为半径作圆，则图中阴影部分的面积为（ ）A.πB.12πC.14π D.2πS 4S 3S 2S 1【答案】 B【解析】 将下面阴影部分进行对称平移，根据半圆的面积公式列式计算即可求解．随练2、 如图，扇子的圆心角为α，余下扇形的圆心角为β，为了使扇子的外形美观，通常情况下α与β的比按黄金比例设计，若取黄金比为0.6，则α=__________度．【答案】 135【解析】 完整圆的周角是360︒，根据比例解出135α∠=︒．随练3、 一条弧所对的圆心角为135°，弧长等于半径为5cm 的圆的周长的3倍，则这条弧的半径为__________ cm ．【答案】 40【解析】 设弧所在圆的半径为r ，由题意得，135253180rππ=⨯⨯，解得40r cm =．故应填40．拓展1、 一个多边形，把一个顶点与其它各顶点连接起来，把这个多边形分成了12个三角形，则这个多边形的边数_______． 【答案】 14【解析】 从n 边形的一个顶点作对角线，把这个n 边形分成()2n -个三角形．根据题意可知，这个多边形的边数是12214+=．2、 若一个多边形截去一个角后，变成六边形，则原来多边形的边数可能是__________． 【答案】 5，6，7【解析】 如图可知，原来多边形的边数可能是5，6，7．3、 从一个n 边形的同一个顶点出发，分别连接这个顶点与其余各顶点，若把这个多边形分割成6个三角形，则n 的值是_______． 【答案】 8【解析】 设多边形有n 条边， 则n ﹣2=6， 解得n=8．4、 从一个多边形的一个顶点出发，一共可作10条对角线，则这个多边形的内角和是____度． 【答案】 1980【解析】 （13﹣2）•180=1980度，则这个多边形的内角和是1980度5、 如图，正方形ABCD 的边1AB =，BD 和AC 都是以1为半径的圆弧，则无阴影两部分的面积之差是_________βα【答案】12π- 【解析】 如图：正方形的面积1234S S S S =+++①；两个扇形的面积3122S S S =++②；②-①得：349036012112S S S S ππ⨯⨯-=-=-=-正方形扇形．6、 如图，扇形A 的圆心角的度数为__________．【答案】 144【解析】 根据题意，该扇形圆心角度数为：36040%144︒⨯=︒．7、 如下图中的五个半圆，两只小虫同时出发，以相同的速度从A 点到B 点，甲虫沿1ADA 、12A EA 、23A FA 、3A GB 路线爬行，乙虫沿ACB 路线爬行，则下列结论正确的是（ ）A.甲先到B 点B.乙先到B 点C.甲、乙同时到BD.无法确定 【答案】 C【解析】 ()1122331122AA A A A A A B AB ππ+++=⨯，因此甲虫走的四段半圆的弧长正好和乙虫走的大半圆的弧长相等，因此两个同时到B 点．故选C ．8、 如图，图1是由若干个相同的图形（图2）组成的美丽图案的一部分，图2中，图形的相关数据：半径OA ＝2cm ，∠AOB ＝120°．则图2的周长为________cm （结果保留π）．【答案】8π3【解析】 由图1得：AO OB AB +=的长的长的长 ∵半径OA ＝2cm ，∠AOB ＝120°则图2的周长为：240π28π1803⨯=． 9、 如图，将边长为3的正六边形铁丝框ABCDEF 变形为以点A 为圆心，AB 为半径的扇形（忽略铁丝的粗细），则所得扇形AFB （阴影部分）的面积为________．432140%AA 3A 2A 1GFE D CBA【答案】 18【解析】 ∵正六边形ABCDEF 的边长为3， ∵AB ＝BC ＝CD ＝DE ＝EF ＝FA ＝3， ∵BAF 的长＝3×6－3－3＝12， ∵扇形AFB （阴影部分）的面积1123182=⨯⨯=． 10、 如图，AB 为半圆的直径，且AB ＝2，半圆绕点B 顺时针旋转40°，点A 旋转到A′的位置，则图中阴影部分的面积为________（结果保留π）．【答案】49π 【解析】 ∵S 阴影＝S 扇形ABA′＋S 半圆－S 半圆 ＝S 扇形ABA′ 2452360π⨯=49=π．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
多边形和圆的初步认识知识讲解
【要点梳理】
要点一、多边形及正多边形
1．定义：多边形是由一些不在同一条直线上的线段依次首尾相连组成的封闭平面图形．其中，各边相等、各角也相等的多边形叫做正多边形．如下图：
要点诠释：
正多边形必须同时满足“各边相等”，“各角相等”两个条件，二者缺一不可；
2．相关概念：
顶点：每相邻两条边的公共端点叫做多边形的顶点．
边：组成多边形的各条线段叫做多边形的边．
内角：多边形相邻两边组成的角叫多边形的内角（可简称为多边形的角），一个n边形有n个内角.
外角：多边形的边与它的邻边的延长线组成的角叫做多边形的外角.
对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线．
要点诠释：
(1)过n 边形的一个顶点可以引(n -3)条对角线，n 边形对角线的条数
为(3)2
n n ． (2)过n 边形的一个顶点的对角线可以把n 边形分成(n -2)个三角形．
类型一、多边形及正多边形
1．如图，（1）从正六边形的顶点A 出发,可以画出 条对角
线，分别用字母表示出来为 ；（2）这些对角线把六
边形分割成 个三角形.
【思路点拨】画出对角线，并按一定规律数出对角线的条数及分割成
的三角形的个数即可.
【答案】（1）3，线段AC 、线段AD 、线段AE ；（2）4.
E A B C
F D
【总结升华】
(1)n边形有n个顶点,n条边,n个内角.
n n 条(2)过n边形的每一个顶点有(n－3)条对角线,n边形总共(3)
2对角线.
(3)n边形从一个顶点出发,分别连接这个顶点和其余各顶点,可以
分割（n－2）个三角形.
举一反三：
【变式】（2015春•郑州期末）过多边形某个顶点的所有对角线，将这个多边形分成7个三角形，这个多边形是（）
A．八边形B．九边形C．十边形D．十一边形
【答案】B
若一个多边形的内角和等于720°，则从这个多边形的一个顶点引出对角线条．
一个多边形除一个内角外其余内角的和为1510°，则这个多边形对角线的条数是（）
A．27 B．35 C．44 D． 54
2．同学们在平时的数学活动中会遇到这样一个问题：把正方形纸片截去一个角后，还剩多少角，余下的图形是几边形，亲爱的同学们，
你知道吗?
【答案与解析】
解：这个问题，我们可以用图来说明．
按图(1)所示方式去截，不经过点B和D，还剩五个角，即得到一个五边形．
按图(2)所示方式去截，经过点D(或点B)．不经过点B(或点D)，还剩4个角，即得到一个四边形．
按图(3)所示方式去截，经过点D、点B，则剩下3个角，即得到三角形．
答：余下的图形是五边形或四边形或三角形．
【总结升华】一个n边形剪去一个角后，可能是(n+1)边形，也可能是n边形，也可能是(n-1)边形，利用它我们可以解决一些具体问题．举一反三：
【变式】一个多边形共有20条对角线，则多边形的边数是（ C ）.
A.6
B.7
C.8
D.9
要点二、圆及扇形
1.圆的定义
如图，在一个平面内，一条线段绕着它固定的一个端点旋转一周，另一个端点所形成的图形叫做圆，固定的端点叫做圆心，线段OA叫
做半径.
要点诠释：
①圆心确定圆的位置，半径确定圆的大小；确定一个圆应先确定圆心，再确定半径，二者缺一不可.
②圆是一条封闭曲线.
2.扇形
（1）圆弧：圆上任意两点A，B间的部分叫做圆弧，简称弧，记作»AB，读作“圆弧AB”或“弧AB”. 如下图：
（2）扇形的定义：如上图，由一条弧AB和经过这条弧的端点的两条半径OA，OB所组成的图形叫做扇形.
要点诠释：圆可以分割成若干个扇形.
（3）圆心角：顶点在圆心的角叫做圆心角. 如上图，∠AOB是圆的一个圆心角，也是扇形OAB的圆心角.
【典型例题】
9．（2014•长宁区一模）下列说法中，结论错误的是（B）A．直径相等的两个圆是等圆
B．长度相等的两条弧是等弧
C．圆中最长的弦是直径
D．一条弦把圆分成两条弧，这两条弧可能是等弧
10．（2015春•张掖校级月考）有下列四个说法：①半径确定了，圆
就确定了；②直径是弦；③弦是直径；④半圆是弧，但弧不一定是
半圆．其中错误说法的个数是（B）
A．1 B． 2 C． 3 D． 4
19．（2015春•定陶县期末）下列说法正确的是（④）
填序号．
①半径不等的圆叫做同心圆；②优弧一定大于劣弧；
③不同的圆中不可能有相等的弦；④直径是同一个圆中最长
的弦
3．如图是对称中心为点的正六边形．如果用一个含角的直
角三角板的角，借助点（使角的顶点落在点处），把这个正六边
形的面积等分，那么的所有可能的值是___________ __ .
【答案】
根据圆内接正多边形的性质可知，只要把此正六边形再化为正多边
形即可，
即可知：360÷30=12；
360÷60=6；360÷90=4；
360÷120=3；360÷180=2．
故n的所有可能的值是2，3，4，6，12．
4．（2015•丰泽区校级质检）如图，MN为⊙O的弦，∠M=50°，则∠MON等于．
【思路点拨】利用等腰三角形的性质可得∠N的度数，根据三角形的内角和定理可得所求角的度数．
【答案】80°．
【解析】
解：∵OM=ON，
∴∠N=∠M=50°，
∴∠MON=180°﹣∠M﹣∠N=80°，
故答案为80°．
【总结升华】考查圆的认识；利用圆的半径相等这个知识点是解决本题的突破点．
类型三、扇形
5. 将一个半径为3的圆形草坪分割成三个扇形，分别种植三种花草，他们的圆心角的度数之比为2：3：4，求这三个圆心角的度数，并尝试求他们的面积，你还能求他们的面积之比吗，你发现了什么
【思路点拨】考查扇形面积及圆心角的概念．
【答案与解析】
解：这三个圆心角的度数分别为：
°°236080234⨯=++；°°3360120234⨯=++；°°4360160234
⨯=++. 圆的面积29r ππ=，
这三个圆心角的面积分别为：8092360ππ⨯
=；12093360
ππ⨯=；16094360ππ⨯=． 这三个圆心角的面积之比为：2:3:4πππ=2：3：4．
发现：扇形的面积之比等于圆心角之比．
【总结升华】一个扇形的面积与对应圆的面积比等于扇形圆心角的度数n 与360的比，
即S 扇：S 圆＝n ：360， 几个半径相等的扇形的面积比等于这几个扇形
的圆心角的比．
6.一个扇形圆心角120°，以扇形的半径为边长画一个正方形，这个正方形的面积是16平方厘米．这个扇形的面积为多少？
【思路点拨】由题意可知，这个扇形所在的圆的半径r 就是这个正方形的边长，即r 2＝边长2＝120平方厘米．
【答案与解析】。