随机变量及其概率习题
随机变量及其概率分布典型例题

概率与数理统计课件
天津科技大学理学院数学系
第8讲 随机变量及其概率分布习题课
第8讲 随机变量及其概率分布习题课
教学目的:通过对随机变量(一维,二维为主)及其概率分布的归纳总结, 及典型
知识要点回顾:
1. 一维随机变量及其分布函数. 2. 离散型随机变量及其概率分
5. 二维随机变量(X,Y)及其分布
函数F(x,y).
6. 二维随机变量的边际分布函
布列.
3. 连续型随机变量及其概率密
数及边际概率密度.
7. 随机变量的独立性. 8. 随机变量函数的分布.
度函数.
4. 常用的随机变量.
1 1
0 0
e
x y
dxdy 1 e1 .
2
随机变量及其概率分布典型例题解析
X \Y 7.设二维随机变量 X , Y 的联合概率分布为 1 2 1 1
5 20 3 20 2 20 3 20
返回
2
6 20 1 20
.求(1) X Y ; (2) X Y 的概率分布.
1 1 P X k 2 1 k 3. 3 ,故 P X k 3 ,即 F k 3 ,从而
5) 3 x 6时,F x dx
dx 0dx 1.
6
0 x
1
解
1) 1
f x, y dxdy
题的分析讲解,使学生对概部分内容有较深的理解与认识.
教学重点:随机变量(离散型,连续型),分布函数,六个重要的分布(两点, 二
随机变量及其分布列习题(含解析)
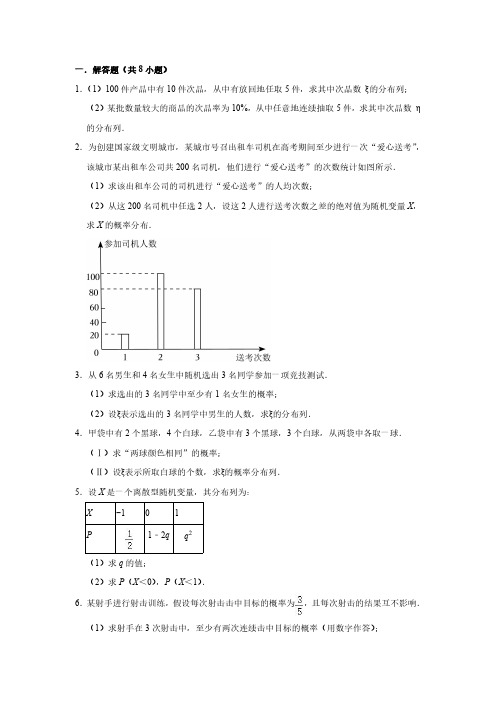
一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.2.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.参考答案与试题解析一.解答题(共8小题)1.(1)100件产品中有10件次品,从中有放回地任取5件,求其中次品数ξ的分布列;(2)某批数量较大的商品的次品率为10%,从中任意地连续抽取5件,求其中次品数η的分布列.【解答】解:(1)由题意知ξ的可能取值为0,1,2,3,4,5,每次取出次品的概率为:,相当于5次独立重复实验,ξ~B(5,),P(ξ=0)==0.59059,P(ξ=1)==0.32805,P(ξ=2)==0.07329,P(ξ=3)==0.0081,P(ξ=4)==0.00045,P(ξ=5)==0.00001,∴ξ的分布列为:ξ012345P0.590590.328050.07290.00810.000450.00001(2)由题意知η的可能取值为0,1,2,3,4,5,且η~B(5,0.1),∴η的分布列为:η012345P0.590590.328050.07290.00810.000450.000012.为创建国家级文明城市,某城市号召出租车司机在高考期间至少进行一次“爱心送考”,该城市某出租车公司共200名司机,他们进行“爱心送考”的次数统计如图所示.(1)求该出租车公司的司机进行“爱心送考”的人均次数;(2)从这200名司机中任选2人,设这2人进行送考次数之差的绝对值为随机变量X,求X的概率分布.【解答】解:(1)由统计图得200名司机中送考1次的有20人,送考2次的有100人,送考3次的有80人,∴该出租车公司的司机进行“爱心送考”的人均次数为;(2)从该公司任选两名司机,记“这两人中﹣人送考1次,另一人送考2次”为事件A,“这两人中一人送考2次,另一人送考3次“为事件B,“这两人中﹣人送考1次,另一人送考3次”为事件C,“这两人送考次数相同”为事件D,由题意知X的所有可能取值为0,1,2,,,,所以X的分布列为:X012P3.从6名男生和4名女生中随机选出3名同学参加一项竞技测试.(1)求选出的3名同学中至少有1名女生的概率;(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.【解答】解:(1)由意可知,选出的3名同学全是男生的概率为=,∴选出的3名同学中至少有1名女生的概率为P=1﹣=.(2)根据题意,ξ的可能取值为0,1,2,3,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,P(ξ=3)==,∴ξ的分布列为:ξ0123P4.甲袋中有2个黑球,4个白球,乙袋中有3个黑球,3个白球,从两袋中各取一球.(Ⅰ)求“两球颜色相同”的概率;(Ⅱ)设ξ表示所取白球的个数,求ξ的概率分布列.【解答】解:(I)从甲中取出黑球的概率为,取出白球的概率为,从乙中取出黑球的概率为,取出白球的概率为,故“两球颜色相同”的概率P=.(II)由题意可得,ξ所有可能取值为0,1,2,P(ξ=0)==,P(ξ=1)=,P(ξ=2)=,故ξ的分布列为:ξ012P5.设X是一个离散型随机变量,其分布列为:X−101P1﹣2q q2(1)求q的值;(2)求P(X<0),P(X<1).【解答】解:(1)依题意,得,解得或(舍去),所以.(2)由(1)得,,所以,.6.某射手进行射击训练,假设每次射击击中目标的概率为,且每次射击的结果互不影响.(1)求射手在3次射击中,至少有两次连续击中目标的概率(用数字作答);(2)求射手第3次击中目标时,恰好射击了4次的概率(用数字作答);(3)设随机变量ξ表示射手第3次击中目标时已射击的次数,求ξ的分布列.【解答】解:(1)设事件该射手第i次射击,击中目标为A i,i=1,2,3,则,所以,事件射手在3次射击中,至少有两次连续击中目标可表示为,因为事件,,A1A2A3互斥,所以又事件A1,A2,A3相互独立,所以==;(2)事件射手第3次击中目标时,恰好射击了4次等于事件前3次中恰好击中两次目标且第四次击中目标,又各次击中目标的概率为,所以前3次中恰有两次击中目标的概率为,第四次击中目标的概率为,所以事件射手第3次击中目标时,恰好射击了4次的概率;(3)由已知ξ的取值有3,4,5,⋅⋅⋅,n,⋅⋅⋅,又,,,⋅⋅⋅,,所以随机变量ξ的分布列为:ξ345…n…P……7.袋中有3个红球,4个黑球,从袋中任取4个球.(1)求红球个数X的分布列;(2)若取到一个红球得2分,取到一个黑球得1分,求得分不小于6分的概率.【解答】解:(1)由题意可得,X可能取值为0,1,2,3,P(X=0)=,P(X=1)=,P(X=2)=,P(X=3)=,故X的分布列为:X0123P(2)设得分为Y,则得分Y可以取4,5,6,7,分别对应4个黑球,3黑1红,2黑2红,1黑3红四种情况,P(Y≥6)=P(Y=6)+P(Y=7)=,故得分不小于6分的概率为.8.从5名男生和3名女生中任选2人去参加学校组织的“低碳杯”知识抢答赛,用ξ表示选出的女生的人数.(1)求随机变量ξ的分布列;(2)求事件“选出的2学生至少有一女生”的概率.【解答】解:(1)由题意得ξ的可能取值为0,1,2,P(ξ=0)==,P(ξ=1)==,P(ξ=2)==,∴随机变量ξ的分布列为:ξ012P(2)事件“选出的2学生至少有一女生”的概率为:P=P(ξ=1)+P(ξ=2)==.。
《概率论与数理统计》习题随机变量及其分布

第二章 随机变量及其分布一. 填空题1. 设随机变量X ~B(2, p), Y ~B(3, p), 若P(X ≥ 1) =95, 则P(Y ≥ 1) = _________. 解. 94951)1(1)0(=-=≥-==X P X P 94)1(2=-p , 31=p 2719321)0(1)1(3=⎪⎭⎫⎝⎛-==-=≥Y P Y P2. 已知随机变量X 只能取-1, 0, 1, 2四个数值, 其相应的概率依次为cc c c 162,85,43,21, 则c = ______. 解. 2,16321628543211==+++=c cc c c c 3. 用随机变量X 的分布函数F(x)表示下述概率: P(X ≤ a) = ________. P(X = a) = ________.P(X > a) = ________. P(x 1 < X ≤ x 2) = ________.解. P(X ≤ a) = F(a) P(X = a) = P(X ≤ a)-P(X < a) = F(a)-F(a -0) P(X > a) = 1-F(a) P(x 1 < X ≤ x 2) = F(x 2)-F(x 1)4. 设k 在(0, 5)上服从均匀分布, 则02442=+++k kx x 有实根的概率为_____.解. k 的分布密度为⎪⎩⎪⎨⎧=051)(k f 其它50≤≤kP{02442=+++k kx x 有实根} = P{03216162≥--k k } = P{k ≤-1或k ≥ 2} =535152=⎰dk 5. 已知2}{,}{kbk Y P k a k X P =-===(k = 1, 2, 3), X 与Y 独立, 则a = ____, b = ____, 联合概率分布_____, Z = X + Y 的概率分布为_____. 解. 116,132==++a a a a . 4936,194==++b b b b(X, Y)的联合分布为ab = 216α, 539=α α249)3()1()3,1()2(==-===-===-=abY P X P Y X P Z P α66)2,1()3,2()1(=-==+-===-=Y X P Y X P Z Pα251)1,1()2,2()3,3()0(=-==+-==+-====Y X P Y X P Y X P Z P α126)2,3()1,2()1(=-==+-====Y X P Y X P Z P α723)1()3()1,3()2(==-===-====abY P X P Y X P Z P6. 已知(X, Y)联合密度为⎩⎨⎧+=0)sin(),(y x c y x ϕ 其它4,0π≤≤y x , 则c = ______, Y 的边缘概率密度=)(y Y ϕ______.解.12,1)sin(4/04/0+==+⎰⎰c dxdy y x c ππ所以⎩⎨⎧++=0)sin()12(),(y x y x ϕ 其它4,0π≤≤y x当 40π≤≤y 时))4cos()(cos 12()sin()12(),()(4y y dx y x dx y x y Y +-+=++==⎰⎰∞+∞-πϕϕπ所以⎪⎩⎪⎨⎧+-+=0))4cos()(cos 12()(y y y Y πϕ 其它40π≤≤y7. 设平面区域D 由曲线2,1,01e x x y xy ====及直线围成, 二维随机变量(X, Y)在D 上服从均匀分布, 则(X, Y)关于X 的边缘密度在x = 2处的值为_______. 解. D 的面积 =2121=⎰e dx x. 所以二维随机变量(X, Y)的密度为: ⎪⎩⎪⎨⎧=021),(y x ϕ 其它D y x ∈),(下面求X 的边沿密度:当x < 1或x > e 2时0)(=x X ϕ当1 ≤ x ≤ e 2时 ⎰⎰===∞+∞-x X xdy dy y x x 102121),()(ϕϕ, 所以41)2(=X ϕ.8. 若X 1, X 2, …, X n 是正态总体N(μ, σ2)的一组简单随机样本, 则)(121n X X X nX +++=服从______. 解. 独立正态分布随机变量的线性函数服从正态分布.μ==⎪⎭⎫ ⎝⎛∑∑==n i i n i i X E n X n E 11)(11, nX D nX n D ni in i i 2121)(11σ==⎪⎭⎫ ⎝⎛∑∑==所以 ),(~2nN X σμ9. 如果(X, Y)的联合分布用下列表格给出,且X 与Y 相互独立, 则α = ______, β = _______.解.213161)1(,181)3(,91)2(,31)2(=+==+==+==++==Y P Y P Y P X P βαβα 132)3()2()1(=++==+=+=βαY P Y P Y P⎪⎪⎩⎪⎪⎨⎧+++=======+++=======)181)(31()3()2()3,2()91)(31()2()2()2,2(ββαβαβααY P X P Y X P Y P X P Y X P两式相除得βαβα=++18191, 解得 βα2=, 92,91==αβ.10. 设(X, Y)的联合分布律为则 i. Z = X + Y 的分布律 ______. ii. V = X -Y 的分布律______. iii. U= X 2 + Y -2的分布律_______. 解.二. 单项选择题1. 如下四个函数哪个是随机变量X 的分布函数(A)⎪⎪⎩⎪⎪⎨⎧=221)(x F 0022≥<≤--<x x x , (B) ⎪⎩⎪⎨⎧=1sin 0)(x x F ππ≥<≤<x x x 00(C) ⎪⎩⎪⎨⎧=1sin 0)(x x F 2/2/00ππ≥<≤<x x x , (D) ⎪⎪⎩⎪⎪⎨⎧+=1310)(x x F 212100≥<≤<x x x解. (A)不满足F(+∞) = 1, 排除(A); (B)不满足单增, 排除(B); (D)不满足F(1/2 + 0) = F(1/2), 排除(D); (C)是答案.2. ),4,2,0(!/)( ===-k k e c k X P k λλ是随机变量X 的概率分布, 则λ, c 一定满足 (A) λ > 0 (B) c > 0 (C) c λ > 0 (D) c > 0, 且 λ > 0解. 因为),4,2,0(!/)( ===-k k e c k X P k λλ, 所以c > 0. 而k 为偶数, 所以λ可以为负. 所以(B)是答案.3. X ~N(1, 1), 概率密度为ϕ(x), 则(A)5.0)0()0(=≥=≤X P X p (B)),(),()(+∞-∞∈-=x x x ϕϕ (C) 5.0)1()1(=≥=≤X P X p (D) ),(),(1)(+∞-∞∈--=x x F x F 解. 因为E(X) = μ = 1, 所以5.0)1()1(=≥=≤X P X p . (C)是答案.4. X, Y 相互独立, 且都服从区间[0, 1]上的均匀分布, 则服从区间或区域上的均匀分布的随机变量是(A) (X, Y) (B) X + Y (C) X 2 (D) X -Y解. X ~⎩⎨⎧=01)(x ϕ 其它10≤≤x , Y ~⎩⎨⎧=01)(y ϕ 其它10≤≤y . 所以(X, Y)~⎩⎨⎧=01),(y x ϕ其它1,0≤≤y x .所以(A)是答案.5. 设函数⎪⎪⎩⎪⎪⎨⎧=120)(xx F 1100>≤<≤x x x 则(A) F(x)是随机变量X 的分布函数. (B) 不是分布函数.(C) 离散型分布函数. (D)连续型分布函数.解. 因为不满足F(1 + 0) = F(1), 所以F(x)不是分布函数, (B)是答案.6. 设X, Y 是相互独立的两个随机变量, 它们的分布函数为)(),(y F x F Y X , 则Z = max(X, Y)的分布函数是(A) )(z F Z = max{)(),(z F z F Y X } (B) )(z F Z = max{|)(||,)(|z F z F Y X } (C) )(z F Z = )()(z F z F Y X (D) 都不是解. }{}),{max()()(z Y z X P z Y X P z Z P z F Z ≤≤=≤=≤=且 )()()()(z F z F z Y P z X P Y X =≤≤因为独立. (C)是答案.7. 设X, Y 是相互独立的两个随机变量, 其分布函数分别为)(),(y F x F Y X , 则Z = min(X, Y)的分布函数是(A) )(z F Z = )(z F X (B) )(z F Z = )(z F Y(C) )(z F Z = min{)(),(z F z F Y X } (D) )(z F Z = 1-[1-)(z F X ][1-)(z F Y ] 解. }{1}),{min(1)(1)()(z Y z X P z Y X P z Z P z Z P z F Z >>-=>-=>-=≤=且 )](1)][(1[1)](1)][(1[1z F z F z Y P z X P Y X ---=≤-≤--因为独立 (D)是答案.8. 设X 的密度函数为)(x ϕ, 而,)1(1)(2x x +=πϕ 则Y = 2X 的概率密度是(A))41(12y +π (B) )4(22y +π (C) )1(12y +π (D) y arctan 1π 解. )2()2(}2{)()(yF y X P y X P y Y P y F X Y =≤=≤=≤= )4(2)2(112121)2()2()]([)(22''y y y y F y F y X X Y Y +=⎪⎭⎫ ⎝⎛+⋅=⋅=⎪⎭⎫ ⎝⎛==ππϕϕ (B)是答案.9. 设随机变量(X, Y)的联合分布函数为⎩⎨⎧=+-0),()(y x e y x ϕ 其它0,0>>y x , 则2YX Z +=的分布密度是(A) ⎪⎩⎪⎨⎧=+-021)()(y x Z e Z ϕ 其它0,0>>y x (B) ⎪⎩⎪⎨⎧=+-0)(2y x Z e z ϕ 其它0,0>>y x(C) ⎩⎨⎧=-04)(2z Z ze Z ϕ 00≤>z z (D) ⎪⎩⎪⎨⎧=-021)(zZ eZ ϕ 00≤>z z解. 2YX Z +=是一维随机变量, 密度函数是一元函数, 排除(A), (B).21210=⎰∞+-dz e z , 所以(D)不是答案. (C)是答案. 注: 排除法做单项选择题是经常使用而且很有效的方法. 该题也可直接计算Z 的密度:当z < 0时0)(=z F Z当z ≥ 0时⎰⎰≤+=≤+=≤+=≤=zy x Z dxdy y x z Y X P z YX P z Z P z F 2),()2()2()()(ϕ =12222020+--=⎥⎦⎤⎢⎣⎡-----⎰⎰z z z xz y x e ze dx dy e e==)()('z F z ZZ ϕ⎩⎨⎧-042z ze 00≤>z z , (C)是答案.10. 设两个相互独立的随机变量X 和 Y 分别服从正态分布N(0, 1)和N(1, 1), 则下列结论正确的是(A) P{X + Y ≤ 0} = 1/2 (B) P{X + Y ≤ 1} = 1/2 (C) P{X -Y ≤ 0} = 1/2 (D) P{X -Y ≤ 1} = 1/2解. 因为X 和 Y 分别服从正态分布N(0, 1)和N(1, 1), 且X 和 Y 相互独立, 所以 X + Y ~ N(1, 2), X -Y ~ N(-1, 2) 于是P{X + Y ≤ 1} = 1/2, (B)是答案.11. 设随机变量X 服从指数分布, 则Y = min{X, 2}的分布函数是(A) 是连续函数 (B) 至少有两个间断点 (C) 是阶梯函数 (D) 恰好有一个间断点 解. 分布函数:))2,(m i n (1))2,(m i n ()()(y X P y X P y Y P y F Y >-=≤=≤= 当y ≥ 2时101))2,(m i n (1)(=-=>-=y X P y F Y 当0 ≤ y < 2时)2,(1))2,(m i n (1)(y y X y X P y F Y >>-=>-= ye y X P y X P λ--=≤=>-=1)()(1当y < 0时)2,(1))2,(m i n(1)(y y X y X P y F Y >>-=>-= 0)()(1=≤=>-=y X P y X P于是 ⎪⎩⎪⎨⎧-=-011)(yY e y F λ 0202<<≤≥y y y 只有y = 2一个间断点, (D)是答案.三. 计算题1. 某射手有5发子弹, 射击一次的命中率为0.9, 如果他命中目标就停止射击, 不命中就一直到用完5发子弹, 求所用子弹数X 的分布密度. 解. 假设X 表示所用子弹数. X = 1, 2, 3, 4, 5.P(X = i) = P(前i -1次不中, 第i 次命中) = 9.0)1.0(1⋅-i , i = 1, 2, 3, 4.当i = 5时, 只要前四次不中, 无论第五次中与不中, 都要结束射击(因为只有五发子弹). 所以 P(X = 5) = 4)1.0(. 于是分布律为2. 设一批产品中有10件正品, 3件次品, 现一件一件地随机取出, 分别求出在下列各情形中直到取得正品为止所需次数X 的分布密度.i. 每次取出的产品不放回; ii. 每次取出的产品经检验后放回, 再抽取; iii. 每次取出一件产品后总以一件正品放回, 再抽取.解. 假设A i 表示第i 次取出正品(i = 1, 2, 3, …) i.13)()1(1===A P X P1331210)()|()()2(11212⋅====A P A A P A A P X P1331221110)()|()|()()3(11223321⋅⋅====P P A P A P X P1331221111)()|()|()|()4(1122334⋅⋅⋅===A P A A P A A P A A P X Pii. 每次抽取后将原产品放回1310133)()()()()(11111---⎪⎭⎫⎝⎛====k k k k k A P A P A P A A A p k X P , (k = 1, 2, …)iii. 每次抽取后总以一个正品放回X 1 2 3 4p13101311133⋅ 1312132133⋅⋅ 1331321311⋅⋅⋅ 1310)()1(1===A P X P1331311)()|()()2(11212⋅====A P A A P A A P X P1331321312)()|()|()()3(112123321⋅⋅====A P A A P A A A P A A A P X P 1331321311)()|()|()|()4(1121231234⋅⋅⋅===A P A A P A A A P A A A A P X P3. 随机变量X 的密度为⎪⎩⎪⎨⎧-=01)(2x cx ϕ 其它1||<x , 求: i. 常数c; ii. X 落在)21,21(-内的概率. 解. πππϕ1,22|arcsin 21)(110112====-==⎰⎰-∞+∞-c c c x c dx xc dx x3162|a r c s i n 211))2/1,2/1((2/102/12/12=⋅==-=-∈⎰-ππππx x dxX P 4. 随机变量X 分布密度为i. 2102)(x x -⎪⎩⎪⎨⎧=πϕ 其它1||<x , ii. ⎪⎩⎪⎨⎧-=02)(x x x ϕ 其它2110≤≤<≤x x求i., ii 的分布函数F(x).解. i. 当x ≤ 1时 ⎰⎰∞-∞-===x xdt dt t x F 00)()(ϕ当-1< x < 1时 ⎰⎰∞--++-=-==x x x x xdt t dt t x F 21arcsin 1112)()(212πππϕ 当x ≥ 1时⎰⎰∞--=-==xdt t dt t x F 112)()(112πϕ所以 ⎪⎪⎩⎪⎪⎨⎧++-=121arcsin 110)(2x x xx F ππ 1111≥<<--≤x x xii. 当x < 0时 ⎰⎰∞-∞-===x xdt dt t x F 00)()(ϕ当0 ≤ x < 1时 ⎰⎰∞-===x x x t d t dt t x F 2)()(2ϕ当1 ≤ x < 2时 122)2()()(2110-+-=-+==⎰⎰⎰∞-x x dt t tdt dt t x F x xϕ当2 ≤ x 时 1)2()()(2110⎰⎰⎰∞-=-+==x dt t tdt dt t x F ϕ所以 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-+-=112220)(22x x x x F 221100≥<≤<≤<x x x x5. 设测量从某地到某一目标的距离时带有的随机误差X 具有分布密度函数⎪⎪⎭⎫ ⎝⎛--=3200)20(exp 2401)(2x x πϕ, -∞ < x < +∞ 试求: i. 测量误差的绝对值不超过30的概率;ii. 接连独立测量三次, 至少有一次误差的绝对值不超过30的概率.解. 因为⎪⎪⎭⎫ ⎝⎛--=3200)20(exp 2401)(2x x πϕ, -∞ < x < +∞, 所以X ~N(20, 402). i. {}⎭⎬⎫⎩⎨⎧<-<-=<<-=<25.0402025.13030)30|(|X P X P X P )25.1()25.0(-Φ-Φ=1)25.1()25.0()25.1(1()25.0(-Φ+Φ=Φ--Φ= 18944.05987.0-+== 0.4931.(其中Φ(x)为N(0, 1)的分布函数)ii. P(至少有一次误差的绝对值不超过30) = 1-P(三次误差的绝对值都超过30) =88.012.01)4931.0(13=-=- 6. 设电子元件的寿命X 具有密度为⎪⎩⎪⎨⎧=0100)(2x x ϕ 100100≤<x x问在150小时内, i. 三只元件中没有一只损坏的概率是多少? ii. 三只电子元件全损坏的概率是多少? iii. 只有一个电子元件损坏的概率是多少?解. X 的密度⎪⎩⎪⎨⎧=0100)(2x x ϕ 100100≤<x x . 所以31100)150(1501002==<⎰dx x X P . 令p = P(X ≥ 150) = 1-31= 32.i. P(150小时内三只元件没有一只损坏) =2783=p ii. P(150小时内三只元件全部损坏) =271)1(3=-piii. P(150小时内三只元件只有一只损坏) =943231213=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛c7. 对圆片直径进行测量, 其值在[5, 6]上服从均匀分布, 求圆片面积的概率分布. 解. 直径D 的分布密度为⎩⎨⎧=01)(d ϕ其它65≤≤d假设42D X π=, X 的分布函数为F(x).)()()(2x D P x X P x F ≤=≤=π当x ≤ 0时, F(x) = 0 当x > 0时⎭⎬⎫⎩⎨⎧≤≤-=≤=≤=πππx D xP x D P x X P x F 44)()()(2 当时即425,54ππ<<x xF(x) = 0 当时即πππ925,645≤≤≤≤x x⎭⎬⎫⎩⎨⎧≤≤-=≤=≤=πππx D xP x D P x X P x F 44)()()(2=54145-=⎰ππxdt x当 x > 9π时1)()(65===⎰⎰∞-dt dt t x F x ϕ所以 ⎪⎪⎩⎪⎪⎨⎧-=1540)(πxx F ππππ99425425>≤≤<x x x密度⎪⎩⎪⎨⎧==01)(')(x x F x πϕ 其它ππ9425≤≤x8. 已知X 服从参数 p = 0.6的0-1分布在X = 0, X = 1下, 关于Y 的条件分布分别为表1、表2所示表1 表2Y 1 2 3 Y 1 2 3 P(Y|X = 0)41 21 41 P(Y|X = 1) 21 61 31 求(X, Y)的联合概率分布, 以及在Y ≠ 1时, 关于X 的条件分布.解. X 的分布律为(X, Y)3.05321)1()1|1()1,1(=⋅=======X P X Y P Y X P 1.05361)1()1|2()2,1(=⋅=======X P X Y P Y X P2.05331)1()1|3()3,1(=⋅=======X P X Y P Y X P1.05241)0()0|1()1,0(=⋅=======X P X Y P Y X P2.05221)0()0|2()2,0(=⋅=======X P X Y P Y X P1.05241)0()0|3()3,0(=⋅=======X P X Y P Y X P所以Y 的分布律为5.06.03.0)1()1,0()1|0(==≠≠==≠=Y P Y X P Y X P5.06.03.0)1()1,1()1|1(==≠≠==≠=Y P Y X P Y X P所以9. 设随机变量X 与Y 相互独立, 并在区间[0, 9]上服从均匀分布, 求随机变量YXZ =的分布密度.解. X ~⎪⎩⎪⎨⎧=091)(x X ϕ 其它90≤≤x , Y ~⎪⎩⎪⎨⎧=091)(x Y ϕ 其它90≤≤y因为X, Y 相互独立, 所以(X, Y)联合密度为(X, Y)~⎪⎩⎪⎨⎧=0811),(y x ϕ 其它9,0≤≤y x , )()()(z X Y P z Z P z F Z ≤=≤= 当 z ≤ 0时0)(=z F Z 当 0 < z < 1时z z dxdy Xz Y P z X Y P z Z P z F D Z 219928181)()()()(1=⋅⋅==≤=≤=≤=⎰⎰ 当z ≥ 1时⎰⎰=≤=≤=≤=2811)()()()(D Z dxdy Xz Y P z X Y P z Z P z F zz 211)992181(811-=⋅-⋅=所以 ⎪⎪⎩⎪⎪⎨⎧==2'21210)()(zz F z Z Z ϕ 1100≥<<≤z z z 10. 设(X, Y)的密度为⎩⎨⎧--=0)1(24),(y x y y x ϕ 其它1,0,0<+>>y x y x求: i.)21|(),|(),(=x y x y x X ϕϕϕ, ii. )21|(),|(),(=y x y x y Y ϕϕϕ 解.i.⎰∞+∞-=dy y x x X ),()(ϕϕ当x ≤ 0 或 x ≥ 1时0),()(==⎰∞+∞-dy y x x X ϕϕ当0 < x < 1时310)1(4)1(24),()(x dy y x y dy y x x x X -=--==⎰⎰-∞+∞-ϕϕ所以 ⎩⎨⎧-=0)1(4)(3x x X ϕ 其它10<<x所以 ⎪⎩⎪⎨⎧---==0)1()1(6)(),()|(3x y x y x y x x y X ϕϕϕ 其它1,0,0<+>>y x y x 所以 ⎩⎨⎧-==0)21(24)21|(y y x y ϕ 其它210<<yii.⎰∞+∞-=dx y x y Y ),()(ϕϕ当y ≤ 0 或 y ≥ 1时0),()(==⎰∞+∞-dx y x y Y ϕϕ当0 < y < 1时210)1(12)1(24),()(y y dx y x y dx y x y y Y -=--==⎰⎰-∞+∞-ϕϕ所以 ⎩⎨⎧-=0)1(12)(2y y y Y ϕ 其它10<<y所以 ⎪⎩⎪⎨⎧---==0)1()1(2)(),()|(2y y x y y x y x Y ϕϕϕ其它1,0,0<+>>y x y x 所以 ⎩⎨⎧-==0)21(4)21|(x y x ϕ 其它210<<x。
离散型随机变量及其分布列练习题和答案

离散型变量强化1.每次试验的成功率为(01)p p <<,重复进行10次试验,其中前7次都未成功后3次都成功的概率为( )()A 33710(1)C p p - ()B 33310(1)C p p - ()C 37(1)p p - ()D 73(1)p p - 2.投篮测试中,每人投3次,至少投中2次才能通过测试,已知某同学每次投篮投中的概率为,且各次投篮是否投中相互独立,则该同学通过测试的概率为( )(A ) (B ) (C ) (D )3.甲、乙两队参加乒乓球团体比赛,甲队与乙队实力之比为3:2,比赛时均能正常发挥技术水平,则在5局3胜制中,甲打完4局才胜的概率为( )()A 23332()55C ⋅ ()B 22332()()53C ()C 33432()()55C ()D 33421()()33C 4.某地区气象台统计,该地区下雨的概率是154,刮三级以上风的概率为152,既刮风又下雨的概率为101,则在下雨天里,刮风的概率为( )A.2258 B.21 C.83 D.43 5.从4名男生和2名女生中任选3人参加演讲比赛,设随机变量ξ表示所选3人中女生的人数,则P (ξ≤1)等于( ).6.一袋中有5个白球,3个红球,现从袋中往外取球,每次任取一个记下颜色后放回,直到红球出现10次时停止,设停止时共取了ξ次球,则==)12(ξP ( ) A.2101012)85()83(⋅C B.83)85()83(29911⨯C C.29911)83()85(⋅C D. 29911)85()83(⋅C 7.袋中有5个球,3个白球,2个黑球,现每次取一个,无放回地抽取两次,第二次抽到白球的概率为( ) A.53 B.43 C.21 D. 1038.6位同学参加百米短跑初赛,赛场有6条跑道,已知甲同学排在第一跑道,则乙同学排在第二跑道的概率( ) A 52 B.51 C.92 D. 73 9.一个袋中有9张标有1,2,3,…,9的票,从中依次取两张,则在第一张是奇数的条件下第二张也是奇数的概率( ) A.52 B.51 C.21 D. 7310.位于坐标原点的一个质点P 按下述规则移动:质点每次移动一个单位;移动的方向为向上或向右,并且向上向右的概率都是21,质点P 移动5次后位于点(2,3)的概率是( )A.3)21( B.525)21(C C.335)21(C D.53525)21(C C 11.若样本数据1x ,2x ,⋅⋅⋅,10x 的标准差为8,则数据121x -,221x -,⋅⋅⋅,1021x -的标准差为( )(A )8 (B )15 (C )16 (D )3212.设某项试验的成功率是失败率的2倍,用随机变量ξ描述一次试验的成功次数,则)0(=ξP 等于( ) B. 21 C. 31 D.32 解答题13.种植某种树苗,成活率为90%,现在种植这种树苗5棵,试求:⑴全部成活的概率; ⑵全部死亡的概率;⑶恰好成活3棵的概率; ⑷至少成活4棵的概率14.某高中共派出足球、排球、篮球三个球队参加市学校运动会,它们获得冠军的概率分别为12,13,23.(1)求该高中获得冠军个数X 的分布列;(2)若球队获得冠军,则给其所在学校加5分,否则加2分,求该高中得分η的分布列.15.实力相等的甲、乙两队参加乒乓球团体比赛,规定5局3胜制(即5局内谁先赢3局就算胜出并停止比赛). 试分别求甲打完3局、4局、5局才能取胜的概率;(2)求按比赛规则甲获胜的概率.16.某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.(1)求顾客抽奖1次能获奖的概率;(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为X ,求X 的分布列.。
Ch2随机变量及其概率分布习题

3 设某人买一种数字型体育彩票,每一注号码中大奖的概率为107 。
(1) 若每期买一注,共买了 n 期,求没有中大奖的概率; (2)若每期买 10 注(号码全不同),共买了 n 期,求没有中大奖的概率。
解:(1)没有中大奖的概率是 p1 1107 n ;
(2)每一期没有中大奖的概率是 p
(2)求 PX 2.5 的值。
解 由题意可判断各次抽样结果是相互独立的,停止时已检查了 X 件产品,说明第 X 次抽
样才有可能抽到不合格品。 X 的取值有 1、2、3、4、5,有
P( X k) p(1 p)k1, k 1, 2,3, 4 ,
P( X 5) (1 p)4 ;
(2) P(X 2.5) P( X 1) P( X 2) p p(1 p) p(2 p) 。
(2)求诊断正确的概率; (3)此人被诊断为有病的概率。
解 (1)用 X 表示诊断此人有病的专家的人数, X 的取值有 1、2、3、4、5。在此人有病
的条件下,诊断此人有病的概率为:
P( X 3) P( X 3) P( X 4) P( X 5) C53 (1 0.1)3 0.12 C54 (1 0.1)4 0.1 C55 (1 0.1)5 0.991
Y 取每一值的概率分布为:
p y 0 p1 , p y 1 1 p1 p2 , p y 2 1 p1 1 p2 p3 , p y 3 1 p1 1 p2 1 p3 . 6. 从一批不合格频率为 p 0 p 1 的产品中随机抽查产品。如果查到不合格品就停止检
查,且最多查 5 件产品。设停止时已检查了 X 件产品。 (1)求 X 的概率分布律;
解 (1)用 X 表示男婴的个数,则 X 可取值有 0、1、2、3,至少有 1 名男婴的概率可表
概率论与数理统计随机变量及其分布习题课

01 排列及其逆序数
解 以X表示此人外出时电话铃响的次数, 由题意知X~π(2t), t表示外出的总时间,则X的的分布律为
当t=10/60=1/6时, (1)
,故所求概率为
(2)设外出最长时间为t(单位:h), 因为X~π(2t),
3
01 排列及其逆序数
因此无电话打进的概率为
,
要使
即
,
解之得
0.3466小时约为21分钟,因此,某人应控制外出时间小
16
01 排列及其逆序数
ꢀ例8 设随机变量
,记
, 则A. p随着 μ的增加而增加
C. p随着μ的增加而减少
B. p随着 σ的增加而增加 D. p随着σ的增加而减少
解
因为 为单调增函数, p σ
,
所以 随着 的增加而增加
应选B.
17
01 排列及其逆序数
ꢀ例9 测量某距离时,随机误差X(单位:cm)具有密度函数:
则性。
6
01 排列及其逆序数 ꢀ例3 设随机变量X的概率密度为 为X的分布函数, 求 解 由题意知,X的分布函数为
因此,
F(x)
7
01 排列及其逆序数 ꢀ例4 设某加油站每周补给一次油,如果这个加油站每 周的销售量(单位:千升)为一随机变量,其密度函数为
试问该加油站的储油罐需要多大,才能把一周内断油的概 率控制在5%以下?
,求
解 当y≤0时,Y的密度函数为 当y>0时,Y的分布函数为
的分布. ;
对上式两边关于y求导,得
20
01 排列及其逆序数 即
这是伽玛分布
的概率密度函数.
21
01 排列及其逆序数
ꢀ例11 设电流I是一个随机变量,它均匀分布在9A~11A 之间.若此电流通过2Ω的电阻,在其上消耗的功率W=2I2, 求W的概率密度.
概率论与数理统计+第二章+随机变量及其分布+练习题答案

滨州学院《概率论与数理统计》(公共课)练习题第二章 随机变量及其分布一、填空题 10.712设一本书的各页的印刷错误个数X 服从泊松分布律.已知有一个和两个印刷错误的页数相同,则随意抽查的4页中无印刷错误的概率p = 0.0003 .3⎪⎪⎩⎪⎪⎨⎧≥<≤<≤<=≤=.若,;,若;,若;,若 3 1 324544 21 51 1 0 }{)(x x x x x X x F P 4{}12525.032)05.0()02(25.0=-=---=<≤F F X P . 例2.11设随机变量X 的概率密度函数为⎪⎩⎪⎨⎧≤≤≤≤=其它06310)(9231x x x f ;若k 使得32)(=≥k X P ,则k 的取值范围是 . 【[1,3]】例2.13 设X 服从二项分布),(p n B ,且已知)2()1(===X P X P ,)3(2)2(===X P X P ,则)4(=X P = . 【24310】 例2.14若随机变量X 服从正态分布)0)(,(2>σσμN ,且二次方程042=++X y y 无实根的概率是21,则=μ . 【4】2.22 (1)24310;(2)4;(3)2922;(4)649;(5))0(2)1(ln 221)(+∞<<--=y y Y I e y y f π〖选择题〗1 [ C ]2 [ C ]3 [ C ]例2.1 【C 】例2.2 【A 】 例2.3 【B 】例2.5 【A 】例2.16设随机变量X ,Y 相互独立均服从正态分布)4,1(N , 若概率21)1(=<-bY aX P ,则(A)1,2==b a(B) 2,1==b a(C) 1,2=-=b a(D) 2,1-==b a 【A 】例2.18 设X 为随机变量, 若矩阵⎪⎪⎪⎭⎫ ⎝⎛--=01020232X A 的特征根全为实数的概率为0.5, 则(A)X 服从区间[0,2]上的均匀分布 (B) X 服从二项分布B(2, 0.5) (C) X 服从参数为1的指数分布 (D) X 服从标准正态分布 【A 】2.23 (1)A ;(2)B ;(3)C ;(4)C ;(5)B 解答题〗 〖解答题〗例2.30解 不妨假设正立方体容器的边长为1.引进事件:{}0==X A ,即事件A 表示“小孔出现在容器的下底面”.由于小孔出现在正立方体的6个侧面是等可能的,易见 61)(=A P .从而,{}61===)(0A X P P.对于任意x <0,显然()=x F 0;而()610=F .由于小孔出现的部位是随机性,可见对于任意)75.0,0(∈x ,有(){}{}.641646100xx x X X x F +=+=≤<+≤=P P 该式中4x 表示容器的四个侧面x 以下的总面积,而容器6个侧面的总面积为6.对于任意x ≥0.75,显然()1=x F.于是,最后得()⎪⎪⎩⎪⎪⎨⎧≥<≤+<=.若若若 75.0 , 1 , 75.00 , 641, 0 , 0 x x x x x F例2.31(分布函数)解 因X 服从指数分布,且21==λX E (百小时),故分布参数λ=0.5,故X的分布函数为()⎩⎨⎧≤>-=-.,若;,若0 0 0 e 15.0x x x G x 易见,{}1.0min ,X Y=.设)(y F 是Y 的分布函数,则对于y <0,)(y F =0;对于y >0.1,)(y F =1;对于1.00≤≤y ,有{}{}.,y y G y X y X y Y y F 5.0e 1)(}1.0 min{}{)(--==≤=≤=≤=P P P 于是,{}.10 min ,X Y=的分布函数为()⎪⎩⎪⎨⎧≥<≤-<=-.,若,若,,若 1.0 1 , 1.00 e 1 0 0 5.0y y y y F y例2.33解 试验次数X 是一随机变量.为求X 的概率分布,引进事件:j B ={第j 次试验成功}(j =1,2,…,n ).显然P(j B ) = p .而由于试验的独立性,知事件n B B B ,,,21 …相互独立.设试验进行到成功或n 次为止,则X 的可能值为1,2,…,n 且1}1{B X==;对于2≤k ≤n-1,.;;;,111111112111)(}{ )(}1{)12()(}{}{ }{------======-≤≤=======k n k k k n k k q B B n X p B X n k pq B B B k X B B B n X B B B k X P P P P P P于是,X 的概率分布为有限几何分布:⎪⎪⎭⎫ ⎝⎛---1121321~n n q pq pq pq pn n X . 例2.35解 以ν表示抽到的30件产品中不合格品的件数,则ν服从参数为(30,0.02)的二项分布:.;;4545.0}0{1}1{3340.002.098.030}1{5455.098.0}0{2930==-=≥=⨯⨯=====ννννP P P P1) 不合格品不少于两件的概率.1205.002.098.03098.01}1{}0{1}2{2930=⨯⨯--==-=-=≥=ννναP P P2) 在已经发现一件不合格品的条件下,不合格品不少于两件的条件概率{}.2652.0}1{}2{}1{}2,1{12≈≥≥=≥≥≥=≥≥=νννννννβP P P P P 例2.36解 由条件知每台设备出现故障的概率为0.08.以ν表示10台设备中同时出现故障的台数,则ν服从参数为(10,0.08)的二项分布.需要安排的值班人数k 应满足条件:95.0}{≥≤k νP .需要对不同的k 进行试算.首先,设k =1和k =2,相应得{}{}{}{}{}{}.,95.09599.008.092.008.092.01092.021281.008.092.01092.010128210910910≥≈⨯⨯+⨯⨯+==+≤=≤≈⨯⨯+==+==≤C ννννννP P P P P P因此,至少需要安排2个人值班.例2.37解 设X ——一周5个工作日停用的天数;Y ——一周所创利润.X 服从参数为(5,0.2)的二项分布.因此,有.,,,057.0205.0410.0328.01}3{205.08.02.010}2{410.08.02.05}1{328.08.0}0{3245=---=≥=⨯⨯===⨯⨯=====X X X X P P P P一周所创利润Y 是X 的函数:⎪⎪⎩⎪⎪⎨⎧≥-====3.,若2,,若1,,若,,若X X X X Y 2 2 7 0 10 ⎪⎪⎭⎫ ⎝⎛-328.0410.0205.0057.010722~Y . 例2.38(二项分布)解 设n ——至少出现一件不合格品所要生产产品的件数,则n 件产品中不合格品的件数n ν服从参数为(n ,0.01)的二项分布;按题意,n 应满足条件., 0729.29899.0ln 05.0ln 95.099.01}0{1}1{≈≥≥-==-=≥n nn n ννP P 于是,为至少出现一件不合格品的概率超过95%,最少需要298.0729×3≈895分,将近14小时55分.例3.41解 由条件知X +Y 是一日内到过该商店的顾客的人数,服从参数为λ的泊松分布.设X ——一日内到过该商店的顾客中购货的人数.由条件知,在一日内有n 个顾客到过该商店的条件下,购货人数的条件概率分布为{}().;),2,1,0(1m n m p p C n Y X m X mn m m n ≥=-==+=- P由全概率公式可见,对于m =0,1,2,…,有{}{}{}()[]()()()()[]()()[]()()().p mp mk km m n mn m mn nmn mm nmn n mn mm nmn m p m p p k m p p m n m p n p p C n p p Cn Y X n Y X m Xm X λλλλλλλλλλλλλλλ---∞=-∞=--∞=--∞=--∞===-=--=-=⎥⎦⎤⎢⎣⎡-==+=+===∑∑∑∑∑e ! e e ! 1!1e!1!1e!!1ee ! 110P P P于是,一日内到过该商店的顾客中购货的人数X 服从参数为p λ的泊松分布.同理,Y 服从参数为)1(p -λ的泊松分布.例2.44 解 以()t ν表示t =90天内售出的电冰箱台数.可以假设()t ν服从参数为t λ的泊松分布.由条件知()λν77E ==56,从而λ=8(台).这样,()t ν服从参数为t λ=8t 的泊松分布: (){}()() ,2,1,0 e !88===-k k t k t tkνP .随机变量X 的可能值为自然数m =0,1,2,….记t a λ=.由全概率公式,有{}(){}(){}()()()()()()()(), pa m pa a a m k k a m m n mn ammn a n m n m m nmn m pa m pa k qa m pa m n qa m pan a q p C n a n a m X m X ---∞=-∞=--∞=--∞====-=======∑∑∑∑e !e e ! ! e!! e ! e ! 0ννP P P 其中6.390805.0=⨯⨯==t p pa λ.因此返修件数X 服从参数为3.6的泊松分布:{}() ,2,1,0 e !6.36.3===-m m m X m P .例2.47解 由条件知{}{}{}{},⎪⎭⎫ ⎝⎛--≈⎥⎦⎤⎢⎣⎡--⎪⎭⎫ ⎝⎛--=⎭⎬⎫⎩⎨⎧-≤-≤--=≤≤-=≤-≤--=≤--=>-=310821)36(310821310823108310812011 1 025.0a a a X a X a a X a a a X a a X ΦΦΦP P P P P其中()x Φ是标准正态分布函数.由熟知的事实()975.096.1=Φ,可见.;;94.5696.131082 0.975031082≈≈-≈⎪⎭⎫⎝⎛-a a a Φ 例2.48 解 由条件知()210,0~N X.设ν为100次独立重复测量中事件{}6.19 >X 出现的次数,则{}05.096.1106.19 =⎭⎬⎫⎩⎨⎧>=>=X X p P P .易见ν服从参数为(100 , 0.05)的二项分布,近似服从参数为5的泊松分布.因此{}{}{}{}{}().87.05.125115.125105.095.0299100 05.095.010095.012101313555529899100≈++-=---≈⨯⨯⨯-⨯⨯--==-=-=-=<-=≥=----e e e e ννννναP P P P P 〖证明题〗例2.52(分布函数)证明 只需验证)()()(21x bF x aF x F +=满足分布函数的三条基本性质.由条件知a 和b 非负且a +b =1.由于)(1x F 和)(2x F 都是分布函数,可见对于任意,有1)()()(021=+≤+=≤b a x bF x aF x F对于任意实数21x x <,由于)2,1)(()(21=≤i x F x F i i ,可见,)()()()()()(2222112111x F x bF x aF x bF x aF x F =+≤+=即)(x F 单调不减.由)(1x F 和)(2x F 的右连续性,可见)(x F 也右连续.最后,.;1)(lim )(lim )(lim 0)(lim )(lim )(lim 2121=+==+=+∞→+∞→+∞→-∞→-∞→-∞→x F b x F a x F x F b x F a x F x x x x x x于是)()()(21x bF x aF x F +=也是分布函数.例2.53(分布函数) 证明 指数分布函数为)0(e 1)(≥-=-x x F x λ设}{P )(y Y y G ≤=为Y=)(X F 的分布函数.由于分布函数)(x F 的值域为(0,1),可见当0≤y时0)(=y G ;当1≥y 时1)(=y G .设10<<y ,有.y y F y X y y Y y G X =⎪⎭⎫⎝⎛--=⎭⎬⎫⎩⎨⎧--≤=≤-=≤=-)1ln(1)1ln(1}e 1{}{)(λλλP P P 于是,)(y G 是区间(0,1)上的均匀分布函数,从而Y=例2.4 【π2=C ;5)arctan 2(πe】例2.6 连续型随机变量X 的分布函数为:x B A x F arctan )(+=,∞<<∞-x试求:(1)常数A 、B ;(2))11(<<-X P ;(3)随机变量X 的概率密度.【(1)π1,21==B A ;(2)21;(3))1(12x +π】 例2.7 设随机变量X 具有对称的密度函数,即)()(x f x f =-,证明对任意的0>a ,有(1)⎰-=-=-adx x f a F a F 0)(21)(1)((2)1)(2)|(|-=<a F a X P (3) ))(1(2)|(|a F a X P -=>问题3: 已知实际背景, 求随机变量的分布律与分布函数(或密度函数)例2.8 一袋中装有4个球,球上分别记有号码1,2,3,4。
概率论与数理统计 第三章 二维随机变量及其概率分布 例题

1.甲乙两人独立地进行两次射击,命中率分别为0.2、0.5,把X、Y分别表示甲乙命中的次数,求(X,Y)联合分布律。
2.袋中有两只白球,两只红球,从中任取两只以X、Y表示其中黑球、白球的数目,求(X,Y)联合分布律。
3.设,且P{}=1,求(,)的联合分布律,并指出,是否独立。
4.设随机变量X的分布律为Y=,求(X,Y)联合分布律。
5.设(X,Y)的概率分布为且事件{X=0}与{X+Y=1}独立求a,b。
6. 设某班车起点上车人数X服从参数λ(λ>0)的泊松分布,每位乘客中途下车的概率为P (0<P<1)相互独立。
以Y表示中途下车的人数。
(1)求在发车时有n个人的情况下,中途m个人下车的概率;(2)求(X,Y)联合分布律。
7. 设二维随机变量(X,Y)联合分布函数F(x.y)=A(B+arctan) (C+arctan)。
(1)A、B、C (2)(X,Y)的联合密度f(x,y) (3)(X,Y)的边缘密度,概率论与数理统计第三章二维随机变量及其概率分布例题8.设f(x,y)=为二维随机变量(X,Y)的联合密度函数,求:其它(1)C的值(2), (3)P{X+Y1}并判别X与Y是否独立。
为(X,Y)的密度函数,求:9.设f(x,y)=其它(3)P{X>1/2|Y>0}为(X,Y)的密度函数,求10. 设f(x,y)=其它11. 设f(x,y)=为(X,Y)的密度函数,求()的联合分布其它函数。
12.设X,Y独立,均服从(0,1)上的均匀分布,Z的密度函数。
13. 设f(x,y)=()为(X,Y)的密度函数,Z=X+Y,求的密度函其它数。
概率论与数理统计第三章二维随机变量及其概率分布例题14.设X,Y独立,X~N(μ,),Y~V(-π,π),Z=X+Y,求,结果用Φ( x)表示。
15.设(X,Y)的联合密度函数为f(x,y)=,Z=X+Y,求Z的概率密度。
为(X,Y)的密度函数,Z=X+2Y,求的密度函数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
习题二 一、填空题1. 已知随机变量X 只能取-1, 0, 1, 2四个数值, 其相应的概率依次为cc c c 162,85,43,21, 则c = 2______. 解. 2,16321628543211==+++=c cc c c c2. 某射手每次命中目标的概率为,若独立射击了三次,则三次中命中目标次数为k 的概率==)(k X P 3,2,1,0,)2.0()8.0(33=-k C k k k .3. 设X 服从参数为p 的两点分布,则X 的分布函数为 ⎪⎩⎪⎨⎧≥<≤-<=1 ,110 ,10 ,0)(x x p x x F .4. 设随机变量X ~B (2, p ), Y ~B (3, p ), 若95)1(=≥X P , 则)1(≥Y P = 19/27 . 解. 94951)1(1)0(=-=≥-==X P X P 94)1(2=-p , 31=p 2719321)0(1)1(3=⎪⎭⎫ ⎝⎛-==-=≥Y P Y P . 5. 设随机变量X 服从泊松分布,且)2()1(===X P X P ,则==)4(X P 223e -. 6. 已知连续型随机变量X 的分布函数为⎩⎨⎧≤>+=-0 ,00,)(2x x Be A x F x ,则=A 1 ,=B 1- ,=<<)221(x P 41---e e ,=)(x f⎩⎨⎧≤>-0 ,00,22x x e x . 7. 设随机变量X 的概率密度函数⎩⎨⎧∈=其它 ,0]2,0[ ,)(x Ax x f , 则=A ,)(x F =⎪⎪⎩⎪⎪⎨⎧>≤≤<2,120 ,4,02x x xx ; =≤)21|(|x P116.8. 设随机变量X 的概率密度为⎪⎩⎪⎨⎧∈∈=其它若若 ,0]6,3[ ,9/2]1,0[ ,3/1)(x x x f ,若k 使得32)(=≥k X P , 则k 的取值范围是13k ≤≤.9. 某公共汽车站有甲,乙,丙三人,分别等1,2,3路车,设每人等车的时间(分钟)都服从[0,5]上的均匀分布,则三人中至少有两人等车时间不超过2分钟的概率为.10. 设k 在(0, 5)上服从均匀分布, 则02442=+++k kx x 有实根的概率为___3/5__.解. k 的分布密度为⎪⎩⎪⎨⎧=051)(k f 其它50≤≤k .P{02442=+++k kx x 有实根} = P{03216162≥--k k }= P{k -1或k 2} =535152=⎰dk . 11. 设),(~2σμN X 则X Y μσ-=服从的分布为 )1,0(~N Y .12. 设),(~2σμN X 则Y aX b =+服从的分布为 ),(22σ+μa b a N . 13. 若随机变量X ~),2(2σN ,且P (2<X <4)=, 则P (X <0)= . 14.设)2,3(~2N X ,若)()(c X p c X p ≥=<,则=c 3 . 15. 设随机变量X 和2X Y =的概率分布分别为12210120.10.20.3X Pp p --30140.60.2Y Pp则123,,p p p 分别为,,.16. 设随机变量X 服从(0,2)上的均匀分布,则随机变量2X Y =在(0,4)内的概率密度)(y f Y 为 ⎪⎩⎪⎨⎧<<=其它,)( ,040 41y y y f Y 。
二、选择题1. 随机变量X 的分布律为:01230.10.30.40.2X P()F x 为其分布函数,则(2)F =( C )。
(A)0.2;(B)0.4;(C)0.8;(D)1.2. 如下四个函数哪个不能成为随机变量X 的分布函数 (B )(A) 10, 01/3, 01; 1/2, 121, 2x x F xx x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩()(B) 20, 0 ();ln , 0x F x x x x ≤⎧⎪=⎨>⎪⎩ 2330, 01, 0(C) ()/4, 02 ; (D) ().0, 01, 2x x e x F x x x F x x x -<⎧⎧-≥⎪=≤<=⎨⎨<⎩⎪≥⎩解. (A)不满足F(+) = 1, 排除(A); (B)不满足单增, 排除(B); (D)不满足F(1/2 + 0) = F(1/2), 排除(D); (C)是答案.3. 设函数 ⎩⎨⎧∈=其它,0],[ ,sin )(b a x x x f , )(x f 可能是某个随机变量的概率密度函数,区间[]b a ,是(A )。
(A) ;,]20[π (B) ];22[ππ,- (C) ];,0[π (D) ).2,0(π4.设随机变量X 服从参数为λ的泊松分布,且},2{}1{===X P X P 则}2{>X P 的值为( B ).(A) 2-e ; (B) 251e-; (C) 241e-; (D) 221e-. 5. 每张奖券中尾奖的概率为110,某人购买了20张号码杂乱的奖券,设中尾奖的张数为ξ,则ξ服从( A )分布。
(A) 二项; (B) 泊松; (C) 指数; (D) 正态.6.连续型随机变量X 的密度函数)(x f 必满足条件( D ). (A)1)(0≤≤x f ;(B))(x f 为偶函数; (C) )(x f 单调不减 ;(D)()1f x dx +∞-∞=⎰.7.设随机变量X 的密度函数为X x F x f x f x f 是且)(),()(),(=-的分布函数,则对任意实数a 有(B )(A) ;)(1)(0⎰-=-adx x f a F (B);)(21)(0⎰-=-a dx x f a F (C) ;)()(a F a F =- (D).1)(2)( -=-a F a F8.设X的密度函数为01()0,x f x ≤≤=⎪⎩其他,则1{}4P X >为( A ).(A)78;(B)14⎰;(C) 141-⎰; (D)32. 9.设A,B 为随机事件,,0)(=AB P 则( B ).(A).φ=AB(B) AB 未必是不可能事件(C) A 与B 对立 (D) P(A)=0或P(B)=0 10.设X 服从]5,1[上的均匀分布,则( D ). (A)4}{ab b X a P -=≤≤ (B)43}63{=<<X P (C) 1}40{=<<X P(D)21}31{=≤<-X P 11.设X 服从参数为91的指数分布,则=<<}93{X P ( C ). (A))93()99(F F -;(B))11(913ee -; (C) ee 113-;(D)⎰-939dx ex .12.设随机变量~(0,1)X N , X 的分布函数为()x Φ,则{||2}P X >的值为( A )。
(A )2[1(2)]Φ-; (B )2(2)1Φ-; (C );2(2)Φ- (D )12(2)Φ-.13.设),4,(~μN X 则( C ). (A))1,0(~4N X μ-; (B) 21}0{=≤X P ; (C) )1(1}2{Φ-=>-μX P ;(D) 0≥μ.14.若)1,1(~N X ,记其密度函数为)(x f ,分布函数为)(x F ,则(C ). (A){0}{0}P X P X ≤=≥; (B))(1)(x F x F --=; (C) {1}{1}P X P X ≤=≥;(D))()(x f x f -=.15. 设随机变量X ~),2, (σμN 则随σ的增大,概率)|(|σμ<-X P (C ) (A) 单调增大; (B) 单调减少; (C) 保持不变; (D) 增减不变.16. 设随机变量X 服从正态分布Y N ),,(211σμ服从正态分布 ),,(222σμN 且 }1{}1{21<-><-μμY P X P ,则必有(A ).(A )12;σσ< (B )12;σσ> (C )12;μμ< (D ).21μμ>17.设随机变量X 的分布函数为),(x F 则随机变量12+=X Y 的分布函数)(y G 是(A ).111(A) ()(); (B) ()(1);22211(C) ()2()1; (D) ()().22G y F y G y F y G y F y G y F y =-=+=+=-18. 设随机变量X 的密度函数是21(), 2 (1)X f x Y X x π==+则的密度函数是(B ).(A );)41(1)(2y y f Y +=π (B );)4(2)(2y y f Y +=π (C );)1(1)(2y y f Y +=π (D ).1)(arctgy y f Yπ=三、解答题1. 设在15只同类型零件中有2只是次品,在其中取三次,每次任取一只,作不放回抽样,以X 表示取出次品的只数,求X 的分布律。
解:任取三只,其中新含次品个数X 可能为0,1,2个。
3522)0(315313===C C X P 3512)1(31521312=⨯==C C C X P 351)2(31511322=⨯==C C C X P 再列为下表X : 0, 1, 2 P :351,3512,3522 566530.0}4{}3{=≥=>X P X P2. 袋中有6个球,分别标有数字1,2,2,2,3,3,从中任取一个球,令X 为取出的球的号码,试求X 的分布律及分布函数。
解 X 的分布列为P61 21 31由分布函数的计算公式得X 的分布函数为 ⎪⎪⎪⎩⎪⎪⎪⎨⎧≥<≤<≤<=3 ,132 ,3221 ,611,0)(x x x x x F3. 已知离散型随机变量X 的分布律为:(1)0.2,(2)0.3P X P X ====,(3)0.5P X ==,试写出X 的分布函数。
解X 的分布律为1230.20.30.5X P所以X 的分布函数为0,1,0.2,12,()0.5,23,1,3.x x F x x x <⎧⎪≤<⎪=⎨≤<⎪⎪≥⎩4. 某射手有5发子弹, 射击一次的命中率为, 如果他命中目标就停止射击, 不命中就一直到用完5发子弹, 求所用子弹数X 的分布律. 解. 假设X 表示所用子弹数. X = 1, 2, 3, 4, 5.P (X = i ) = P (前i -1次不中, 第i 次命中) = 9.0)1.0(1⋅-i , i = 1, 2, 3, 4.当i =5时, 只要前四次不中, 无论第五次中与不中, 都要结束射击(因为只有五发子弹). 所以P(X = 5) =+5)1.0(9.0)1.0(4⋅4)1.0(=. 于是分布律为5. 设一批产品中有10件正品, 3件次品, 现一件一件地随机取出, 分别求出在下列各情形中直到取得正品为止所需次数X 的分布律.(i ). 每次取出的产品不放回; (ii ). 每次取出的产品经检验后放回, 再抽取; (iii) . 每次取出一件产品后总以一件正品放回, 再抽取. 解. 假设A i 表示第i 次取出正品(i = 1, 2, 3, …) (i). 13)()1(1===A P X P1331210)()|()()2(11212⋅====A P A A P A A P X P 1331221110)()|()|()()3(11223321⋅⋅====A P A A P A A P A A A P X P 1331221111)()|()|()|()4(1122334⋅⋅⋅===A P A A P A A P A A P X P(ii). 每次抽取后将原产品放回1310133)()()()()(11111---⎪⎭⎫⎝⎛====k k k k k A P A P A P A A A p k X P ΛΛ, (k = 1, 2, …)(iii).13)()1(1===A P X P 1331311)()|()()2(11212⋅====A P A A P A A P X P1331321312)()|()|()()3(112123321⋅⋅====A P A A P A A A P A A A P X P 1331321311)()|()|()|()4(1121231234⋅⋅⋅===A P A A P A A A P A A A A P X P6.一实习生用一台机器接连生产了三个同种零件,第i 个零件是不合格品的概率1(1,2,3)1i p i i ==+,以X 表示三个零件中合格品的个数,求X 的分布律。
