2018高考数学复习:随机事件的概率
2018年高考数学总复习 11.1 随机事件的概率

如何选择各自的路径.
-21-
考点一
考点二
考点三
解 (1)由已知共调查了100人,其中40分钟内不能赶到火车站的有
12+12+16+4=44人.
故用频率估计相应的概率为
44 100
=0.44.
(2)选择L1的有60人,选择L2的有40人,故由调查结果得频率如下表.
所用时间(分钟) 10~20 20~30 30~40 40~50 50~60
⑤频率是概率的近似值,概率是频率的稳定值.
其中正确的是( B )
A.①②③④
B.①④⑤
C.①②③④⑤ D.②③
解析:由概率的相关定义知①④⑤正确.
知识梳理 考点自测
-10-
4.甲、乙两人下棋,两人下成和棋的概率是12,甲获胜的概率是13, 则甲不输的概率为( A )
A.56
B.25
C.16
D.13
选择 L1 的频率2
0.2
选择 L2 的频率 0
0.1
0.4
0.4
0.1
(3)A1,A2分别表示甲选择L1和L2时,在40分钟内赶到火车站; B1,B2分别表示乙选择L1和L2时,在50分钟内赶到火车站. 由(2)得P(A1)=0.1+0.2+0.3=0.6,P(A2)=0.1+0.4=0.5,P(A1)>P(A2), 故甲应选择L1;P(B1)=0.1+0.2+0.3+0.2=0.8,P(B2)=0.1+0.4+0.4 =0.9,P(B2)>P(B1),故乙应选择L2.
事件,A∪B A∩B=⌀,且A∪B=Ω ,则称事件 A 与事件 (Ω 为必然
(完整word版)2018年高考数学总复习概率及其计算
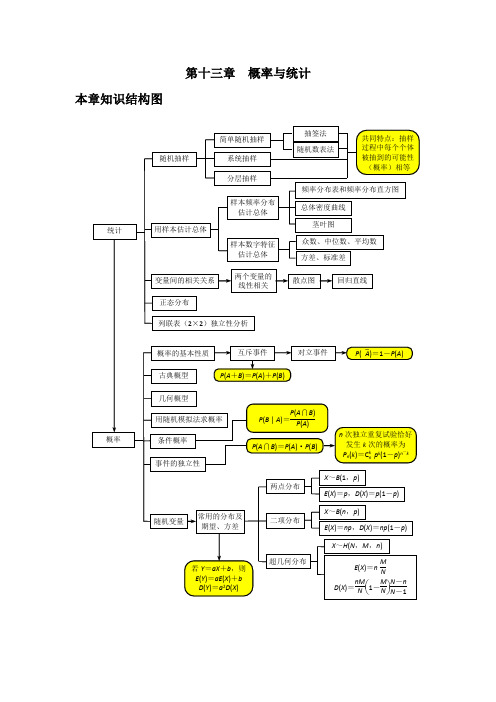
第十三章概率与统计本章知识结构图第一节 概率及其计算考纲解读1.了解随机事件发生的不确定性、频率的稳定性、概率的意义、频率与概率的区别。
2.了解两个互斥事件的概率的加法公式。
3.掌握古典概型及其概率计算公式。
4.了解随机数的意义,能运用模拟方法估计概率。
5.了解几何概型的意义。
命题趋势探究1.本部分为高考必考内容,在选择题、填空题和解答题中都有渗透。
2.命题设置以两种概型的概率计算及运用互斥、对立事件的概率公式为核心内容,题型及分值稳定,难度中等或中等以下。
知识点精讲一、必然事件、不可能事件、随机事件在一定条件下:①必然要发生的事件叫必然事件; ②一定不发生的事件叫不可能事件;③可能发生也可能不发生的事件叫随机事件。
二、概率在相同条件下,做次重复实验,事件A 发生次,测得A 发生的频率为,当很大时,A 发生的频率总是在某个常数附近摆动,随着的增加,摆动幅度越来越小,这时就把这个常数叫做A 的概率,记作。
对于必然事件A ,;对于不可能事件A ,=0.三、基本事件和基本事件空间在一次实验中,不可能再分的事件称为基本事件,所有基本事件组成的集合称为基本事件空间。
四、两个基本概型的概率公式1、古典概型条件:1、基本事件空间含有限个基本事件 2、每个基本事件发生的可能性相同()(A)=()A card P A card =Ω包含基本事件数基本事件总数2、几何概型条件:每个事件都可以看作某几何区域Ω的子集A ,A 的几何度量(长度、面积、体积或时间)记为Aμ.()P A =AμμΩ。
五、互斥事件的概率1、互斥事件在一次实验中不能同时发生的事件称为互斥事件。
事件A 与事件B 互斥,则()()()P A B P A P B =+ 。
2、对立事件事件A,B 互斥,且其中必有一个发生,称事件A,B 对立,记作B A =或A B =。
()()1P A p A =- 。
3、互斥事件与对立事件的联系对立事件必是互斥事件,即“事件A ,B 对立”是”事件A ,B 互斥“的充分不必要条件。
2018届高考数学二轮复习 随机事件的概率专题

随机事件的概率专题[基础达标](20分钟40分)一、选择题(每小题5分,共25分)1.设事件A,B,已知P(A)=15,P(B)=13,P(A∪B)=815,则A,B之间的关系一定为()A.两个任意事件B.互斥事件C.非互斥事件D.对立事件B【解析】因为P(A)+P(B)=15+13=815=P(A∪B),所以A,B一定是互斥事件.2.某小组有5名男生和4名女生,从中任选4名同学参加“教师节”演讲比赛,则下列每对事件是对立事件的是()A.恰有2名男生与恰有4名男生B.至少有3名男生与全是男生C.至少有1名男生与全是女生D.至少有1名男生与至少有1名女生C【解析】“恰有2名男生”与“恰有4名男生”是互斥事件,但不是对立事件,排除A;“至少有3名男生”与“全是男生”可以同时发生,不是对立事件,排除B;“至少有1名男生”与“全是女生”不可能同时发生,且必有一个发生,是对立事件,C正确;“至少有1名男生”与“至少有1名女生”可以同时发生,不是对立事件,排除D.3辽宁舰”是中国人民解放军海军第一艘可以搭载固定翼飞机的航空母舰,在“辽宁舰”的飞行甲板后部有四条拦阻索,降落的飞行员须捕捉钩挂上其中一条,则为“成功着陆”,舰载机白天挂住第一条拦阻索的概率为18%,挂住第二条、第三条拦阻索的概率为62%,捕捉钩未挂住拦阻索需拉起复飞的概率约为5%,现有一架歼-15战机白天着舰演练20次,则其被第四条拦阻索挂住的次数约为()A.5B.3C.1D.4B【解析】由题意可知舰载机被第四条拦阻索挂住的概率为1-18%-62%-5%=15%,故其被第四条拦阻索挂住的次数约为20×0.15=3.41,2,3,4,5,6的6个球(小球除编号外完全相同),甲先从袋中摸出一个球,记下编号后放回,乙再从袋中摸出一个球,记下编号,则甲、乙两人所摸出球的编号不同的概率是()A.15B.16C.56D.3536C【解析】设a,b分别为甲、乙摸出球的编号.由题意,摸球试验共有n=6×6=36种不同结果,满足a=b的基本事件共有6种,所以摸出编号不同的概率P=1-636=56.5费者对网上购物的满意情况,某公司随机对4500名网上购物消费者进行了调查(每名消费者限选一种情况回答),统计结果如表:根据表中数据,估计在网上购物的消费者群体中对网上购物“比较满意”或“满意”的概率是()A.715B.25C.1115D.1315C【解析】由题意,n=4500-200-2100-1000=1200,所以对网上购物“比较满意”或“满意”的人数为1200+2100=3300,由古典概型公式可得对网上购物“比较满意”或“满意”的概率为=33004500=1115.二、填空题(每小题5分,共15分)690分及以上的概率是0.18,在80~89分的概率是0.51,在70~79分的概率是0.15,在60~69分的概率是0.09,60分以下的概率是0.07,小明考试及格(60分及以上)的概率为.0.93【解析】“小明考试及格”与“小明考试不及格”是对立事件,所以小明考试及格的概率是1-0.07=0.93.710环,9环,8环的概率分别为0.24,0.28,0.19,那么,在一次射击训练中,该射手射击一次不够9环的概率为.0.48【解析】在某射手一次射击中,击中10环,9环,8环的概率分别是0.24,0.28,0.19,所以该射手在一次射击中不够9环的概率P=1-0.24-0.28=0.48.8.某篮球队员在比赛中每次罚球的命中率相同,且在两次罚球中至多命中一次的概率为1625,则该队员每次罚球的命中率为.3 5【解析】设该队员每次罚球的命中率为p,利用对立事件的概率公式得1-p2=1625,解得p=35.[高考冲关](25分钟45分)1.(5分8个小区A,B,C,D,E,F,G,H和市中心O的整齐方格形道路网,每个小方格均为正方形,如图所示.某人从道路网中随机地选择一条最短路径,由小区A前往小区H,则他经过市中心O的概率为()A.13B.23C.14D.34B【解析】由题意知,此人从小区A前往小区H的所有最短路径为A→B→C→E→H,A→B→O→E→H,A→B→O→G→H,A→D→O→E→H,A→D→O→G→H,A→D→F→G→H,共6条.记“此人经过市中心O”为事件M,则M包含的基本事件为A→B→O→E→H,A→B→O→G→H,A→D→O→E→H,A→D→O→G→H,共4个,所以P(M)=46=23,即他经过市中心O的概率为23.2.(5分)盒中装有分别标着1到80号的大小相同的小球80个,从中随机摸出一个球.则摸出的球既不是3的倍数又不是4的倍数的概率为()A.1740B.2340C.12D.1320C【解析】设事件A为“摸出的球是3的倍数”,事件B为“摸出的球是4的倍数”,则A+B表示摸出的球是3或4的倍数,表示摸出的球既不是3的倍数又不是4的倍数.试验的总事件数为80,A所包含的试验分别有摸出的球号为3,6,9,…,78,共有26种;B所包含的试验分别有摸出的球号为4,8,12,…,80,共有20种,但12,24,36,48,60,72重复了,所以A+B所包含的试验总数为26+20-6=40种,则所包含的试验总数为80-40=40种,故P(A+B)=4080=12.3.(5分)如果事件A和B是互斥事件,且A∪B发生的概率是0.64,事件B发生的概率是事件A发生的概率的3倍,则事件A发生的概率为.0.16【解析】设事件A发生的概率为P,则事件B发生的概率为3P,又事件A 和B是互斥事件,且A∪B发生的概率是0.64,则P+3P=0.64,P=0.16.4.(5分1个红球和2个黑球,乙盒内有外形和质地相同的2个红球和2个黑球.现从甲、乙两个盒内各取1个球,则取出的2个球中恰有1个红球的概率是.12【解析】从甲乙两个盒中各取1个球,共有3×4=12种不同取法,其中从甲盒取出红球、乙盒取出黑球的结果有2种;从乙盒取出红球、甲盒取出黑球的结果有4种,故所求概率为212+412=12.5.(12分)袋中有12个小球,分别为红球、黑球、黄球、绿球,从中任取一球,得到红球的概率是13,得到黑球或黄球的概率是512,得到绿球或黄球的概率也是512,求得到黑球、黄球和绿球的概率分别是多少?【解析】从袋中任取一球,记事件“得到红球”“得到黑球”“得到黄球”“得到绿球”分别为A,B,C,D,则事件A,B,C,D彼此互斥,∴P(B+C)=P(B)+P(C)=512,P(D+C)=P(D)+P(C)=512,P(B+C+D)=P(B)+P(C)+P(D)=1-P(A)=1-13=23,解得P(B)=14,P(C)=16,P(D)=14.∴得到黑球、黄球和绿球的概率分别是14,16,14.6.(13分)某人抛掷一枚硬币,出现正反面的概率都是12,构造数列{a n},使得a n=1(当第n次出现正面时),-1(当第n次出现反面时),记S n=a1+a2+a3+…+a n(n∈N*).(1)若抛掷4次,求S4=2的概率;(2)已知抛掷6次的基本事件总数是N=64,求前两次均出现正面且2≤S6≤4的概率.【解析】(1)S4=2,需4次中有3次正面1次反面.设其概率为P1,再设正面向上为a,反面向上为b.则基本事件空间为Ω={aaaa,aaab,aaba,abaa,baaa,bbbb,bbba,bbab,babb,abbb,aabb,bbaa,baab,abba,abab,baba},则n=16,n1=4,所以P1=416=14.(2)6次中前两次均出现正面,且要使2≤S6≤4,则后4次中有2次正面2次反面或3次正面1次反面,设概率为P2,则n=64,由(1)知n2=10,所以P2=1064=532.。
2018届高考数学一轮复习随机事件的概率课件人教A版(30张)

3.事件的关系与运算 定义 符号表示 如果事件 A 发生,则事件 B 一定 包含 发生,这时称事件 B⑧________ B⊇A 或 A⊆B) 包含关系 ⑨______( 事件 A(或称事件 A 包含于事件 B) 若某事件发生当且仅当 A 发生或 并事件 事件 B 发生,称此事件为事件 A A∪B(或 A+B) 10__________( 并事件 或和 (和事件) 与事件 B 的○ 事件)
二、必明 3●个易误点 1.正确区别互斥事件与对立事件的关系:对立事件是互斥 事件的特殊情况,但互斥事件不一定是对立事件,“互斥”是 “对立”的必要不充分条件. 2.从集合的角度看,几个事件彼此互斥,是指由各个事件 所含的结果组成的集合彼此不相交, 事件 A 的对立事件- A 所含的 结果组成的集合, 是全集中由事件 A 所含的结果组成的集合的补 集. 3.需准确理解题意,特留心“至多„„”,“至少„„”, “不少于„„”等语句的含义.
解析:①②④⑤为随机事件,③为不可能事件.要注意函数 1 -1 a y=x 随 a 的取值不同,有可能不过(0,0),如 y=x =x ,所以是 随机事件. 答案:C
2.(2017· 揭阳模拟)把红、黑、蓝、白 4 张纸牌随机地分给 甲、乙、丙、丁四个人,每人分得 1 张,事件“甲分得红牌”与 事件“乙分得红牌”是( ) A.对立事件 B.不可能事件 C.互斥事件但不是对立事件 D.以上答案都不对
[知识重温] 一、必记 4●个知识点 1.随机事件和确定事件 (1)在条件 S 下,①____________ 一定会发生 的事件,叫做相对于条件 S 的必然事件,简称必然事件. 一定不会发生 的事件,叫做相对于条 (2)在条件 S 下,②_______________ 件 S 的不可能事件,简称不可能事件. (3)必然事件和不可能事件统称为相对于条件 S 的确定事件, 简称确定事件. 可能发生也可能不发生 的事件, (4)在条件 S 下, ③______________________ 叫做相 对于条件 S 的随机事件,简称随机事件.
最新-2018届高三数学一轮复习 181 随机事件的概率课件

答案:A
4.从编号为1,2,3,4,5,6,7,8,9,10的10个形状大小相同的球中,任取3个球,则这3个 球编号之和为奇数的概率是________. 解析:解法一:任取3个球有 种结果,编号之和为奇数的结果数为 .
结果,故所求概率为=
解法二:10个球的编号中,恰好有5个奇数和5个偶数,从中任取3个球,3个球 编号之和为奇数与3个球编号之和为偶数的机会是均等的,故所求概率为 答案: .
(5,1)、(5,2)、(5,3)、(5,4)、(5,5)、(5,6)、(6,1)、(6,2)、(6,3)、(6,4)、
(6,5)、(6,6).其中点数和为6的有(1,5)、(2,4)、(3,3)、(4,2)、(5,1)共5
种.由于每个基本事件都是等可能的,所以“所得点数和为6”的概率为
.
变式2:将甲、乙两颗骰子先后各抛一次,a、b分别表示抛掷甲、乙两颗骰子所 出现的点数. (1)若点P(a,b)落在不等式组表示的平面区域的事件记为A,求事件A的 概率; (2)若点P(a,b)落在直线x+y=m(m为常数)上,且使此事件的概率最 大,求m的值.
提示:事件的频率与概率有本质上的区别,不可混为一谈.频率是随着试验次
数的改变而改变的,概率却是一个常数,它是频率的科学抽象,不是频率的极
限,只是在大量重复试验中事件出现频率本事件: 一次试验连同其中可能出现的每一个结果 称为一个基本事件. (2)等可能性事件的概率:如果一次试验由n个基本事件组成,而且所有结果出现 的可能性 都相等,那么每一个基本事件的概率都是 果有m个,那么事件A的概率:P(A)= . ,如果某个事件A包含的结
解析:易知①③④正确,②错误.
答案:C
2.在正方体上任选3个顶点连成三角形,则所得的三角形是直角非等腰三角 形的概率为( A. B. ) C. D.
2018高考文科数学一轮复习 随机事件的概率

考点一 随机事件的频率与概率
解题的关键是根据统计图表分析满足条件的事件发生 的频数,计算频率,用频率估计概率.
例 1、某电子商务公司随机抽取 1 000 名网络购物者进行调 查.这 1 000 名购物者 2015 年网上购物金额(单位:万元)均在 区间[0.3,0.9]内,样本分组为:[0.3,0.4),[0.4,0.5),[0.5,0.6), [0.6,0.7),[0.7,0.8),[0.8,0.9],购物金额的频率分布直方图如 下:
件 B 的交事件(或积事件)
名称
定义
符号 表示
互斥 若 A∩B 为不可能事件,那么称 A∩B
事件 事件 A 与事件 B 互斥
=∅
若 A∩B 为 不可能事件,A∪B 对立
为 必然事件 ,那么称事件 A 与事 事件
件 B 互为对立事件
对立事件与互斥事件有什么关系?
事件互斥,它们未必对立;反之,两个事件 对立,它们一定互斥.也就是说,两个事件对立 是这两个事件互斥的充分而不必要条件。
(1)P(A),P(B),P(C); (2)1 张奖券的中奖概率; (3)1 张奖券不中特等奖且不中一等奖的概率.
三、古典概型
(1)基本事件的特点 ①任何两个基本事件是互斥的。
②任何事件(除充分也不必要条件
(2)在 5 张电话卡中,有 3 张移动卡和 2 张联通卡,从中任取 2
张,若事件“2 张全是移动卡”的概率是130,那么概率是
7 10
的事
件是 A.至多有一张移动卡
B.恰有一张移动卡
(A)
C.都不是移动卡
D.至少有一张移动卡
练习:《新坐标》P149.例1、变式训练1
50 随机事件的概率-2018年高考数学(理)考点一遍过含解析
(1)了解随机事件发生的不确定性和频率的稳定性,了解概率的意义,了解频率与概率的区别。
(2)了解两个互斥事件的概率加法公式。
一、随机事件及其概率1.事件的分类2.频率与概率(1)事件的频率:在相同的条件S 下重复n 次试验,观察某一事件A 是否出现,称n 次试验中事件A 出现的次数An 为事件A 出现的频数,称事件A 出现的比例()A n n fA n 为事件A 出现的频率. (2)事件的概率:对于给定的随机事件A ,由于事件A 发生的频率()f A随着试验次数的增加稳定在某个常数上,把这个常数n记作()P A,称为事件A的概率,因此可以用()n f A来估计概率()P A。
注意:频率是事件A发生的次数与试验总次数的比值,与试验次数有关。
概率是一个确定的数,是客观存在的,与试验做没做、做多少次完全无关。
二、事件间的关系及运算=B∅B∅且=A B U=注意:互斥事件与对立事件都是指两个事件的关系,互斥事件是不可能同时发生的两个事件,而对立事件除要求这两个事件不同时发生外,还要求必须有一个发生。
因此,对立事件一定是互斥事件,而互斥事件未必是对立事件。
三、概率的基本性质1.由于事件的频数总是小于或等于试验的次数,所以频率在0~1之间,从而任何事件的概率都在0~1之间,即0()1≤≤.必然P A事件的概率为1,不可能事件的概率为0.2.当事件A与事件B互斥时,()()()=+,该公式为概率P A B P A P B的加法公式。
当一个事件包含多个结果且各个结果彼此互斥时,要用到概率加法公式的推广,即()()()1212()n n P A A A P A P A P A =+++.3.若事件A 与事件B 互为对立事件,则A B 为必然事件,1()P A B =。
再由加法公式得()()1P A P B +=.考向一 由频率估计随机事件的概率随机事件在一次试验中是否发生虽然不能事先确定,但是在大量重复试验的情况下,随机事件的发生呈现一定的规律性,因而,可以从统计的角度,通过计算事件发生的频率去估算事件发生的概率。
2018年高考数学(人教A版)一轮复习课件:10.1随机事件的概率
(1)作出B地区用户满意度评分的频率分布直方图,并通 过此图比较两地区满意度评分的平均值及分散程 度.(不要求计算出具体值,给出结论即可)
(2)根据用户满意度评分,将用户的满意度评分分为三 个等级: 满意度评分 低于70分 70分到89分 不低于90分
满意度等级
不满意
满意
非常满意
估计哪个地区的用户的满意度等级为不满意的概率大, 说明理由.
事件A出现的频率.
(2)概率:对于给定的随机事件A,如果随着试验次数的 增加,事件A发生的频率fn(A)稳定在某个常数上,把这 P(A) 称为事件A的概率. 个常数记作_____,
3.事件的关系与运算
名称 包含
关系 相等 关系
条件 A发生⇒B
发生
结论
包含 事件 事件B_____ 包含于 A(事件A_______ 事件B)
【解析】(1)B地区用户满意度评分的频率分布直方图
通过两地区用户满意度评分的频率分布直方图可以看 出,B地区用户满意度评分的平均值高于A地区用户满意 度评分的平均值;B地区用户满意度评分比较集中,而A 地区用户满意度评分比较分散.
(2)A地区用户的满意度等级为不满意的概率大.理由如 下: 记CA表示事件:“A地区用户的满意度等级为不满 意”;CB表示事件:“B地区用户的满意度等级为不满 意”.
【解析】(1) 42 0.07.
600
(2) 52 8 0.1.
600
答案:(1)0.07 (2)0.1
2.(必修3P124T6改编)袋中装有9个白球,2个红球,从中 任取3个球,则①恰有1个红球和全是白球;②至少有1个 红球和全是白球;③至少有1个红球和至少有2个白球; ④至少有1个白球和至少有1个红球.在上述事件中,是 对立事件的为________.
(完整word版)2018年高考数学总复习概率及其计算
第十三章概率与统计本章知识结构图统计概率第一节概率及其计算考纲解读1. 了解随机事件发生的不确定性、频率的稳定性、概率的意义、频率与概率的区别。
2. 了解两个互斥事件的概率的加法公式。
3. 掌握古典概型及其概率计算公式。
4. 了解随机数的意义,能运用模拟方法估计概率。
5. 了解几何概型的意义。
命题趋势探究1. 本部分为高考必考内容,在选择题、填空题和解答题中都有渗透。
2. 命题设置以两种概型的概率计算及运用互斥、 对立事件的概率公式为核心内容,题型及分值稳定,难度中等或中等以下。
知识点精讲一、 必然事件、不可能事件、随机事件在一定条件下:① 必然要发生的事件叫必然事件; ② 一定不发生的事件叫不可能事件; ③ 可能发生也可能不发生的事件叫随机事件。
二、 概率在相同条件下,做次重复实验,事件 A 发生次,测得 A 发生的频率为,当很大时,A 发生的频率总是在某个常数附近摆动, 随着的增加,摆动幅度越来越小,这时就把这个常数叫 做A 的概率,记作。
对于必然事件A,;对于不可能事件 A, =0.三、 基本事件和基本事件空间在一次实验中,不可能再分的事件称为基本事件, 所有基本事件组成的集合称为基本事件空间。
四、 两个基本概型的概率公式1、古典概型条件:1、基本事件空间含有限个基本事件2、每个基本事件发生的可能性相同P AA 包含基本事件数 =card (A) 基本事件总数=card ()2、几何概型条件:每个事件都可以看作某几何区域的子集A ,A 的几何度量(长度、面积、体积或时间)记为五、互斥事件的概率1互斥事件在一次实验中不能同时发生的事件称为互斥事件。
事件A与事件B互斥,则P AUB P A P B2、对立事件事件A,B互斥,且其中必有一个发生,称事件A,B对立,记作B A或A B。
P A 1 p A。
3、互斥事件与对立事件的联系对立事件必是互斥事件,即“事件A, B对立”是”事件 A B互斥“的充分不必要条件。
2018高考数学试题分类汇编 随机事件的概率、古典概型、几何概型 解析版
随机事件的概率、古典概型、几何概型一、选择题1.(2018·全国卷II高考理科·T8)我国数学家陈景润在哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数可以表示为两个素数的和”,如30=7+23.在不超过30的素数中,随机选取两个不同的数,其和等于30的概率是()A.错误!未找到引用源。
B.错误!未找到引用源。
C.错误!未找到引用源。
D.错误!未找到引用源。
【命题意图】本题考查了概率的有关概念以及数学建模能力.【解析】选C.不超过30的素数有2,3,5,7,11,13,17,19,23,29共10个,其中和为30的有7+23,11+19,13+17.所以随机选取两个数,和为30的概率为错误!未找到引用源。
=错误!未找到引用源。
.2.(2018·全国卷II高考文科·T5)从2名男同学和3名女同学中任选2人参加社区服务,则选中的2人都是女同学的概率为()A.0.6B.0.5C.0.4D.0.3【命题意图】本题考查古典概型的有关知识,难度较小.【解析】选D.用1,2代表两名男同学,A,B,C代表三名女同学,则选中的两人可以为12,1A,1B,1C,2A,2B,2C,AB,AC,BC共10种,全是女同学有AB,AC,BC 共3种,所以概率P=错误!未找到引用源。
=0.3.3.(2018·全国Ⅲ高考文科·T5)若某群体中的成员只用现金支付的概率为0.45,既用现金支付也用非现金支付的概率为0.15,则不用现金支付的概率为 ()A.0.3B.0.4C.0.6D.0.7【命题意图】考查统计与概率知识中的事件的运算,意在考查对立事件、概率的加法公式,培养学生的实际应用能力、逻辑推理能力,体现了数学抽象、数学建模、数学运算、数据分析的数学素养.【解析】选B.方法一:画Venn图,如图设只用非现金支付(不用现金支付)的概率为x,则0.45+0.15+x=1,解得x=0.4,所以不用现金支付的概率为0.4.方法二:记“用现金支付”为事件A,“用非现金支付”为事件B,则“只用非现金支付(不用现金支付)”为事件B-(A∩B),由已知,P(A)=0.45+0.15=0.6,P(A∩B)=0.15,又P(A∪B)=P(A)+P(B)-P(A∩B)=0.6+P(B)-0.15=1,所以P(B)=0.55,P(B-(A∩B))=P(B)-P(A∩B)=0.55-0.15=0.4.4.(2018·全国卷I高考理科·T10)如图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成,三个半圆的直径分别为直角三角形ABC的斜边BC,直角边AB,AC,△ABC的三边所围成的区域记为Ⅰ,黑色部分记为Ⅱ,其余部分记为Ⅲ,在整个图形中随机取一点,此点取自Ⅰ,Ⅱ,Ⅲ的概率分别记为p1,p2,p3,则()A.p1=p2B.p1=p3C.p2=p3D.p1=p2+p3【解析】选A.方法一:取AB=AC=2,则BC=2错误!未找到引用源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)设 C 表示事件“投保车辆中新司机获赔 4 000 元”,由 已知, 样本车辆中车主为新司机的有 0. 1×1 000=100(辆), 而赔付金额为 4 000 元的车辆中,车主为新司机的有 0.2×120=24(辆),所以样本车辆中新司机车主获赔金额为 24 4000 元的频率为 =0.24,由频率估计概率得 P(C)=0.24. 100 [规律方法] 频率是个不确定的数, 在一定程度上频率可以
A=B __________
若某事件发生 当且仅当事件A ________________, 并事件 发生或事件B发生 ___________________则称此 (和事件) 事件为事件A与事件B的并事件 (或和事件)
A∪B __________ (或A+B)
定义
符号表示
若某事件发生 当且仅当事件A发生 _________ A∩B 交事件 ____________________, 且事件B发生 _ (或 AB (积事件) __________________则称此事件为 _______) 事件A与事件B的交事件(或积事件) 互斥 事件 不可能 若A∩B为__________ 事件,那么称 A∩B=∅ 事件A与事件B互斥 不可能 若A∩B为__________ 事件,A∪B A∩B=∅且 必然事件 为_______________,那么称事件A A∪B=Ω 与事件B互为对立事件
解:(1)由于事件 C“至多订一种报纸”中有可能“只订甲 报纸”, 即事件 A 与事件 C 有可能同时发生, 故A与C不 是互斥事件.
(2) 事件 B“至少订一种报纸”与事件 D“一种报纸也不 订”是不可能同时发生的,故 B 与 D 是互斥事件.由于事 件 B 不发生可导致事件 D 一定发生, 且事件 D 不发生会导 致事件 B 一定发生,故 B 与 D 还是对立事件. (3)事件 B“至少订一种报纸”中有这些可能:“只订甲报 纸”、“只订乙报纸” 、 “订甲、乙两种报纸” ,事件 C“至 多订一种报纸”中有这些可能: “一种报纸也不订”、 “只 订甲报纸”、“只订乙报纸”,由于这两个事件可能同时 发生,故 B 与 C 不是互斥事件. (4)由(3)的分析, 事件 D“一种报纸也不订”是事件 C 的一 种可能,即事件 C 与事件 D 有可能同时发生,故 C 与 D 不是互斥事件.
1 1-P(B) . 件.P(A∪B)=______ ,P(A)=__________
考点一
随机事件的关系
一个均匀的正方体玩具的各个面上分别标有数字 1,2,3,4,5,6.将这个玩具向上抛掷 1 次,设事件 A 表示向上的一面出现奇数点,事件 B 表示向上的一面出现 的点数不超过 3,事件 C 表示向上的一面出现的点数不小 于 4,则( D ) A.A 与 B 是互斥而非对立事件 B.A 与 B 是对立事件 C.B 与 C 是互斥而非对立事件 D.B 与 C 是对立事件 [解析] A∩B={出现点数 1 或 3},事件 A,B 不互斥更不
[解]
(1)设 A 表示事件“赔付金额为 3 000 元”, B 表示事
件“赔付金额为 4 000 元”,以频率估计概率得 150 120 P(A)= =0.15,P(B)= =0.12. 1 000 1 000 由于投保金额为 2 800 元, 赔付金额大于投保金额对应的情 形是赔付金额为 3 000 元和 4 000 元,所以其概率为 P(A)+P(B)=0.15+0.12=0.27.
对立;B∩C=∅,B∪C=Ω,故事件 B,C 是对立事件.
[规律方法] 对互斥事件要把握住不能同时发生, 而对于对 立事件除不能同时发生外,其并事件应为必然事件,这些 也可类比集合进行理解,具体应用时,可把所有试验结果 写出来,看所求事件包含哪些试验结果,从而断定所给事 件的关系.
1.某城市有甲、乙两种报纸供居民们订阅, 记事件 A 为“只订甲报纸”,事件 B 为“至少订一种报 纸”,事件 C 为“至多订一种报纸”,事件 D 为“一种报 纸也不订”.判断下列每对事件是不是互斥事件;如果是, 再判断它们是不是对立事件. (1)A 与 C;(2)B 与 D;(3)B 与 C;(4)C 与 D.
随机事件的概率
1.概率与频率 (1)在相同的条件 S 下重复 n 次试验,观察某一事件 A 是否 出现,称 n 次试验中事件 A 出现的次数 nA 为事件 A 出现 nA 的频数,称事件 A 出现的比例 fn(A)=__________ 为事件 A n 出现的频率. (2)对于给定的随机事件 A,由于事件 A 发生的频率 fn(A) 随 着 试 验 次 数 的 增 加 稳 定 于 概 率 P(A) , 因 此 可 以 用 频率fn(A) 来估计概率 P(A). __________
考点二
随机事件的频率与概率
某保险公司利用简单随机抽样方法,对投保车辆进行 抽样,样本车辆中每辆车的赔付结果统计如下:
赔付金额(元) 车辆数(辆) 0 500 1 000 2 000 3 000 4 000 130 100 150 120
(1)若每辆车的投保金额均为 2 800 元,估计赔付金额大于 投保金额的概率; (2)在样本车辆中,车主是新司机的占 10%,在赔付金额为 4 000 元的样本车辆中, 车主是新司机的占 20%, 估计在已 投保车辆中,新司机获赔金额为 4 000 元的概率.
对立 事件
3.概率的几个基本性质 0__________ ≤P(A)≤1 . (1)概率的取值范围: 1 (2)必然事件的概率:P(A)=______ . 0 (3)不可能事件的概率:P(A)=_______ . (4)概率的加法公式 P(A)+P(B) . 如果事件 A 与事件 B 互斥,则 P(A∪B)=____________ (5)对立事件的概率 若事件 A 与事件 B 互为对立事件,则 A∪B 为必然事
2.事件的关系与运算定义ຫໍສະໝຸດ 符号表示包含 关系
发生 如果事件A__________ ,则事 一定发生 件B __________,这时称事件B ___________ B⊇A(或A⊆B) _ 包含事件A(或称事件A包含于事
件B) A⊇B 若B⊇A且__________ ,那么称 事件A与事件B相等
相等 关系
