2021届辽宁沈阳市中考数学模拟试卷
2021年辽宁省沈阳市中考数学学业水平模拟试卷(含解析)
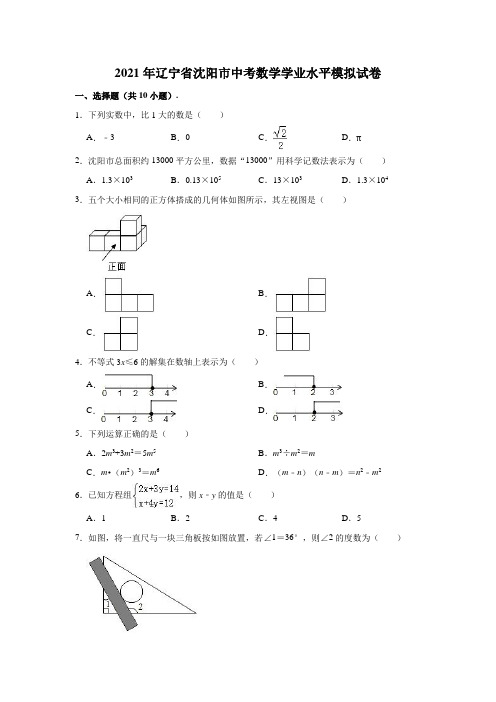
2021年辽宁省沈阳市中考数学学业水平模拟试卷一、选择题(共10小题).1.下列实数中,比1大的数是()A.﹣3B.0C.D.π2.沈阳市总面积约13000平方公里,数据“13000”用科学记数法表示为()A.1.3×103B.0.13×105C.13×103D.1.3×104 3.五个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.4.不等式3x≤6的解集在数轴上表示为()A.B.C.D.5.下列运算正确的是()A.2m3+3m2=5m5B.m3÷m2=mC.m•(m2)3=m6D.(m﹣n)(n﹣m)=n2﹣m2 6.已知方程组,则x﹣y的值是()A.1B.2C.4D.57.如图,将一直尺与一块三角板按如图放置,若∠1=36°,则∠2的度数为()A.126°B.136°C.120°D.144°8.方程x2﹣2x﹣1=0根的情况是()A.有两个相等的实数根B.只有一个实数根C.没有实数根D.有两个不相等的实数根9.一次函数y=﹣x+5的图象经过()A.一、二、三象限B.一、二、四象限C.一、三、四象限D.二、三、四象限10.如图,已知线段AB,分别以A,B为圆心,大于AB同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是()A.AB平分∠CAD B.CD平分∠ACB C.AB⊥CD D.AB=CD二、填空题(每小题3分,共18分)11.因式分解:a3+2a2+a=.12.不等式组的解集是.13.若某正六边形的边长是4,则该正六边形的边心距为.14.如图,在平面直角坐标系中,点B的坐标为(﹣3,1).反比例函数y=(k>0)的图象经过点A.∠AOB=90°,AB=10,则k的值为.15.如图,在△ABC中,点D在边BC上,AB=AD,点E,点F分别是AC,BD的中点,EF=2.5.则AC的长为.16.如图,四边形ABCD中,AD∥BC,∠C=90°.点E在边BC上,AD=BE=2,DC=3,BC=5,点M在射线DC上,连接BM,当直线BM与直线AE的夹角等于45°时,线段DM的长为.三、解答题(第17小题6分,第18、19小题各8分,共22分)17.计算:3tan30°+(﹣)﹣2﹣(π﹣2021)0+|2﹣|.18.在创建“文明校园”活动中,某校甲、乙两班共有5名学生被评为“文明学生”.甲班一名男生、一名女生,乙班三名女生.现要从甲、乙两班各随机抽取一名“文明学生”作为学校文明礼仪值周生,请用列表法或画树状图法求抽取的两名学生性别相同的概率(甲班男生用A表示,女生用B表示;乙班三名女生分别用b1,b2,b3表示).19.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点A作AE⊥BD,垂足为点E,过点C作CF⊥BD,垂足为点F.(1)求证:AE=CF;(2)若∠AOE=74°,∠EAD=3∠CAE,直接写出∠BCA的度数.四、(每小题8分,共16分)20.某校体育组以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球,乒乓球、跳绳及其他项目(每位同学仅选一项).根据调查数据绘制了两幅不完整的统计图.根据统计图提供的信息,解答下列问题:(1)本次共调查了名学生;(2)请根据以上信息直接补全条形统计图;(3)扇形统计图中的m的值是,乒乓球所对应的扇形的圆心角的度数是°;(4)若该校有1200名学生,根据抽样调查的结果.请估计该校有多少名学生最喜爱乒乓球项目.21.四月是辽宁省“全民阅读月”,某校阅览室需购买一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多8元,已知学校用15000元购买科普类图书的数量与用12000元购买文学类图书的数量相同,求文学类图书和科普类图书平均每本的价格.五、(本题10分)22.如图,AB是⊙O的直径,点C在⊙O上,AD⊥CE于点D,AC平分∠BAD.(1)求证:EC是⊙O的切线;(2)若AD=4,cos∠CAB=,直接写出⊙O的半径的长.六、(本题10分)23.在平面直角坐标系中,直线AB与x轴负半轴交于点A,与y轴交于点B,点B坐标为(0,),AB=7,点C在x轴上(点C在点A的右侧),AC=5,动点P从点B 出发,以每秒1个单位长度的速度沿BC运动,动点Q从点A出发,以每秒3个单位长度的速度沿射线AC运动,两点同时出发,当点P到达点C时,两点同时停止运动.设运动时间为t秒(t>0).(1)如图,当点Q在线段AC上时.①求点C的坐标;②当△CPQ是等腰三角形时,求t的值;(2)是否存在时刻t,使得PQ⊥AB,若存在,直接写出t的值;若不存在,说明理由.七、(本题12分)24.四边形ABCD是正方形,点F在射线CD上,以点A,点F为顶点作正方形AEFG(点A,E,F,G按顺时针方向排列),连接DE,BG.(1)如图1,点F在线段CD上,求证:DE=BG;(2)如图2,点F在线段CD上,连接AF.①求证:FC=BG;②直接写出线段AD,DF,BG之间的数量关系;(3)当DF=1,以点A,E,D,F为顶点的四边形的面积等于5时,直接写出此时BG 的长.八、(本题12分)25.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点B(0,3),动点E和点F在x轴上方抛物线上,点E在点P的右侧,EP∥x轴.分别过点E,点F作EH⊥x轴于点H,FG⊥x轴于点G.(1)求抛物线的表达式,并直接写出抛物线的顶点C的坐标;(2)设点E的横坐标为a,四边形EFGH的周长为L,求L的最大值;(3)在(2)的条件下,连接CF,CE,OE.点P在x轴下方抛物线上,点P到CF的距离记为h1,点P到OE的距离记为h2,当=时,①直接写出点P的坐标;②将△CFE沿射线CF平移,平移后的三角形记为△C'F'E′,在平移过程中,当△C'F′E′三边所在直线最后一次经过点P时,直接写出平移的距离.参考答案一、选择题(下列各题的备选答案中,只有一个答案是正确的每小题2分,共20分)1.下列实数中,比1大的数是()A.﹣3B.0C.D.π解:显然﹣3<1,0<1.∵1<<2,∴<<1.∵3<π<4,∴π>1.故选:D.2.沈阳市总面积约13000平方公里,数据“13000”用科学记数法表示为()A.1.3×103B.0.13×105C.13×103D.1.3×104解:13000用科学记数法表示为:1.3×104.故选:D.3.五个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.解:从左边看第一层是两个小正方形,第二层右边一个小正方形,故选:C.4.不等式3x≤6的解集在数轴上表示为()A.B.C.D.解:不等式解得:x≤2,表示在数轴上,如图所示,.故选:B.5.下列运算正确的是()A.2m3+3m2=5m5B.m3÷m2=mC.m•(m2)3=m6D.(m﹣n)(n﹣m)=n2﹣m2解:A.2m3+3m2=5m5,不是同类项,不能合并,故错误;B.m3÷m2=m,正确;C.m•(m2)3=m7,故错误;D.(m﹣n)(n﹣m)=﹣(m﹣n)2=﹣n2﹣m2+2mn,故错误.故选:B.6.已知方程组,则x﹣y的值是()A.1B.2C.4D.5解:∵2x+3y﹣(x+4y)=x﹣y=14﹣12=2,∴x﹣y=2,故选:B.7.如图,将一直尺与一块三角板按如图放置,若∠1=36°,则∠2的度数为()A.126°B.136°C.120°D.144°解:∵∠1=36°,∴∠3=90°﹣36°=54°,∵AB∥CD,∴∠4=∠3=54°,∴∠2=180°﹣54°=126°,故选:A.8.方程x2﹣2x﹣1=0根的情况是()A.有两个相等的实数根B.只有一个实数根C.没有实数根D.有两个不相等的实数根解:∵△=(﹣2)2﹣4×(﹣1)=8>0,∴方程有两个不相等的实数根.故选:D.9.一次函数y=﹣x+5的图象经过()A.一、二、三象限B.一、二、四象限C.一、三、四象限D.二、三、四象限解:∵y=﹣x+5中k<0,∴一次函数图像经过第二四象限,∵b>0,∴一次函数图像经过二四一象限.故选:B.10.如图,已知线段AB,分别以A,B为圆心,大于AB同样长为半径画弧,两弧交于点C,D,连接AC,AD,BC,BD,CD,则下列说法错误的是()A.AB平分∠CAD B.CD平分∠ACB C.AB⊥CD D.AB=CD解:由作图知AC=AD=BC=BD,∴四边形ACBD是菱形,∴AB平分∠CAD、CD平分∠ACB、AB⊥CD,不能判断AB=CD,故选:D.二、填空题(每小题3分,共18分)11.因式分解:a3+2a2+a=a(a+1)2.解:a3+2a2+a,=a(a2+2a+1),…(提取公因式)=a(a+1)2.…(完全平方公式)故答案为:a(a+1)2.12.不等式组的解集是﹣4≤x<2.解:解不等式x﹣2<0,得:x<2,解不等式2x+8≥0,得:x≥﹣4,则不等式组的解集为﹣4≤x<2.13.若某正六边形的边长是4,则该正六边形的边心距为2.解:如图所示,连接OB、OC,过O作OG⊥BC于G,∵此多边形是正六边形,∴△OBC是等边三角形,∴∠OBG=60°,∴边心距OG=OB•sin∠OBG=4×=2故答案为:2.14.如图,在平面直角坐标系中,点B的坐标为(﹣3,1).反比例函数y=(k>0)的图象经过点A.∠AOB=90°,AB=10,则k的值为27.解:∵点B的坐标为(﹣3,1).∴OB==,∵∠AOB=90°,AB=10,∴OA===3,作AD⊥x轴于D,BE⊥x轴于E,∵∠BOE+∠AOD=90°=∠AOD+∠OAD,∴∠BOE=∠OAD,∵∠BEO=∠ADO=90°,∴△BOE∽△OAD,∴====3,∴OD=3BE=3,AD=3OE=9,∴A(3,9),∵反比例函数y=(k>0)的图象经过点A,∴k=3×9=27,故答案为27.15.如图,在△ABC中,点D在边BC上,AB=AD,点E,点F分别是AC,BD的中点,EF=2.5.则AC的长为5.解:连接AF.∵AB=AD,F是BD的中点,∴AF⊥BD,又∵E是AC的中点,∴EF=AC(直角三角形斜边上的中线等于斜边的一半),∴AC=2EF,∵EF=2.5,∴AC=5.故答案为:5.16.如图,四边形ABCD中,AD∥BC,∠C=90°.点E在边BC上,AD=BE=2,DC=3,BC=5,点M在射线DC上,连接BM,当直线BM与直线AE的夹角等于45°时,线段DM的长为或13.解:如图1中,当点M在线段DC上时,∠BNE=∠ABC=45°,∵∠AEB=∠BEN,∴△EBN∽△EAB,∴EB2=EN•AE,设DM=x,∴4=,解得:x=,如图2,当点M在线段DC的延长线上时,∠ANB=∠ABE=45°,∵∠BAE=∠NAB,∴△BNA∽△EBA,∴AB2=AE•AN,设DM=x,∴,解得:x=13,综上所述,可知DM的长为或13.故答案为:或13.三、解答题(第17小题6分,第18、19小题各8分,共22分)17.计算:3tan30°+(﹣)﹣2﹣(π﹣2021)0+|2﹣|.解:原式=3×+9﹣1+2﹣=+9﹣1+2﹣=10.18.在创建“文明校园”活动中,某校甲、乙两班共有5名学生被评为“文明学生”.甲班一名男生、一名女生,乙班三名女生.现要从甲、乙两班各随机抽取一名“文明学生”作为学校文明礼仪值周生,请用列表法或画树状图法求抽取的两名学生性别相同的概率(甲班男生用A表示,女生用B表示;乙班三名女生分别用b1,b2,b3表示).解:画树状图如图:共有6个等可能的结果,抽取的两名学生性别相同的结果有3个,∴抽取的两名学生性别相同的概率为=.19.如图,在平行四边形ABCD中,对角线AC,BD相交于点O,过点A作AE⊥BD,垂足为点E,过点C作CF⊥BD,垂足为点F.(1)求证:AE=CF;(2)若∠AOE=74°,∠EAD=3∠CAE,直接写出∠BCA的度数.【解答】(1)证明:∵四边形ABCD是平行四边形,∴OA=OC,∵AE⊥BD,CF⊥BD,∴∠AEO=∠CFO=90°,∵∠AOE=∠COF,∴△AEO≌△CFO(AAS),∴AE=CF.(2)解:∵AE⊥BD,∴∠AEO=90°,∵∠AOE=74°,∴∠EAO=90°﹣∠AOE=16°,∵∠EAD=3∠CAE,∴∠EAD=3×16°=48°,∴∠DAC=∠DAE﹣∠EAO=48°﹣16°=32°,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠BCA=∠DAC=32°.四、(每小题8分,共16分)20.某校体育组以“我最喜爱的体育项目”为主题对全校学生进行随机抽样调查,调查的运动项目有:篮球、羽毛球,乒乓球、跳绳及其他项目(每位同学仅选一项).根据调查数据绘制了两幅不完整的统计图.根据统计图提供的信息,解答下列问题:(1)本次共调查了120名学生;(2)请根据以上信息直接补全条形统计图;(3)扇形统计图中的m的值是30,乒乓球所对应的扇形的圆心角的度数是72°;(4)若该校有1200名学生,根据抽样调查的结果.请估计该校有多少名学生最喜爱乒乓球项目.解:(1)本次调查的学生总人数为12÷10%=120(名),故答案为:120;(2)“其他”人数为120×15%=18(人),“乒乓球”人数为120﹣(36+30+12+18)=24(人),补全图形如下:(3)篮球对应的百分比m%=×100%=30%,即m=30,乒乓球所对应的扇形的圆心角的度数是360°×=72°,故答案为:30、72;(4)估计该校最喜爱乒乓球项目的学生人数为1200×=240(名).21.四月是辽宁省“全民阅读月”,某校阅览室需购买一批图书,其中科普类图书平均每本的价格比文学类图书平均每本的价格多8元,已知学校用15000元购买科普类图书的数量与用12000元购买文学类图书的数量相同,求文学类图书和科普类图书平均每本的价格.解:设文学类图书平均每本的价格为x元,则科普类图书平均每本的价格为(x+8)元,依题意得:=,解得:x=32,经检验,x=32是原方程的解,且符合题意,∴x+8=40.答:文学类图书平均每本的价格为32元,科普类图书平均每本的价格为40元.五、(本题10分)22.如图,AB是⊙O的直径,点C在⊙O上,AD⊥CE于点D,AC平分∠BAD.(1)求证:EC是⊙O的切线;(2)若AD=4,cos∠CAB=,直接写出⊙O的半径的长.【解答】(1)证明:连接OC.∵OA=OC,∴∠OAC=∠OCA,∵AC平分∠DAB,∴∠CAD=∠CAB,∴∠DAC=∠ACO,∴AD∥OC,∵AD⊥DE,∴OC⊥DE,∴直线EC是⊙O的切线;(2)解:∵AB是直径,∴∠ACB=90°,∵AD⊥CD,∴∠ADC=∠ACB=90°,∵∠DAC=∠CAB,∴△DAC∽△CAB,∴,∵AD=4,cos∠CAB=,设AC=4x,AB=5x,∴,∴x=,∴AB=,即⊙O的半径的长为.六、(本题10分)23.在平面直角坐标系中,直线AB与x轴负半轴交于点A,与y轴交于点B,点B坐标为(0,),AB=7,点C在x轴上(点C在点A的右侧),AC=5,动点P从点B 出发,以每秒1个单位长度的速度沿BC运动,动点Q从点A出发,以每秒3个单位长度的速度沿射线AC运动,两点同时出发,当点P到达点C时,两点同时停止运动.设运动时间为t秒(t>0).(1)如图,当点Q在线段AC上时.①求点C的坐标;②当△CPQ是等腰三角形时,求t的值;(2)是否存在时刻t,使得PQ⊥AB,若存在,直接写出t的值;若不存在,说明理由.解:(1)①∵B(0,),∴OB=,在Rt△AOB中,AO===,∵AC=5,∴OC=OA=AC=﹣5=,∴C(﹣,0).②∵△CPQ是等腰三角形,∠PCQ是钝角,∴只有CQ=CP,∵tan∠BCO===,∴∠BCO=60°,∴∠CBO=30°,∴BC=2OC=3,∵CQ=5﹣3t,CP=3﹣t,∴5﹣3t=3﹣t,∴t=1.(2)如图,过点P作PJ⊥OA于J.∵PQ⊥AB,∴∠ABO+∠BAO=90°,∠BAO+∠QPJ=90°,∴∠PQJ=∠ABO,∴tan∠PQJ=tan∠ABO,∴=,∴=,∴t=1.96.七、(本题12分)24.四边形ABCD是正方形,点F在射线CD上,以点A,点F为顶点作正方形AEFG(点A,E,F,G按顺时针方向排列),连接DE,BG.(1)如图1,点F在线段CD上,求证:DE=BG;(2)如图2,点F在线段CD上,连接AF.①求证:FC=BG;②直接写出线段AD,DF,BG之间的数量关系;(3)当DF=1,以点A,E,D,F为顶点的四边形的面积等于5时,直接写出此时BG 的长.【解答】(1)证明:如图1,∵四边形ABCD,四边形EFGC都是正方形,∴AD=AB,∠DAB=90°,∵四边形AEFG是正方形,∴AE=AG,∠EAG=90°,∵∠EAD=∠EAG﹣∠DAG,∠GAB=∠DAB﹣∠DAG,∴∠EAD=∠GAB,∴∠BCE=∠DCG,∴△EAD≌△GAB(SAS),∴DE=BG;(2)①证明:连接AC,∵四边形ABCD是正方形,∴BC=BA,∠CBA=90°,在Rt△ABC中,tan∠CAB=1,∴∠CBA=45°,∴AC==AB,∵四边形AEFG是正方形,∴AG=FG,∠FGA=90°,在Rt△AGF中,tan∠FAG==1,∴∠FAG=45°,∴AF==AG,∴∠FAC=∠FAG﹣∠CAG,∠GAB=∠CAB﹣∠CAG,∴∠FAC=∠GAB,,∴△CFA∽△BGA,∴,∴FC=BG;②AD=DF+BG.理由如下:∵FC=BG,CD=DF+CF,∴CD=DF+BG,∵四边形ABCD是正方形,∴AD=CD,∴AD=DF+BG;(3)解:①如图3,当点F在线段CD上时,设DE=BG=x,则FC=x,∴DC=AD=x+1,过点E作EM⊥AD于点M,∵∠AEF=∠ADF=90°,∴A,E,D,F四点共圆,∴∠AFE=∠EDM=45°,∴EM=x,∴S△ADE=×x,S△ADF=AD×DF=x,∴=5,解得x=,x=﹣3(舍去),∴BG=;②如图4,当点F在线段CD的延长线上时,连接AC,∵S四边形AEFD=S△AEF+S△ADF,设AD=a,∴AF2=DF2+AD2=1+a2,∴S=a=5,解得a=﹣1+2(负值舍去),∴AD=﹣1+2,∴CF=2,由(2)知△CFA∽△BGA,∴=,∴BG==.综合以上可得BG的长为或.八、(本题12分)25.如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A(﹣1,0)和点B(0,3),动点E和点F在x轴上方抛物线上,点E在点P的右侧,EP∥x轴.分别过点E,点F作EH⊥x轴于点H,FG⊥x轴于点G.(1)求抛物线的表达式,并直接写出抛物线的顶点C的坐标;(2)设点E的横坐标为a,四边形EFGH的周长为L,求L的最大值;(3)在(2)的条件下,连接CF,CE,OE.点P在x轴下方抛物线上,点P到CF的距离记为h1,点P到OE的距离记为h2,当=时,①直接写出点P的坐标;②将△CFE沿射线CF平移,平移后的三角形记为△C'F'E′,在平移过程中,当△C'F′E′三边所在直线最后一次经过点P时,直接写出平移的距离.解:(1)将点A(﹣1,0),B(0,3)代入y=﹣x2+bx+c,得解得,∴抛物线的表达式为y=﹣x2+2x+3,顶点为(1,4).(2)∵EH⊥x轴,FG⊥x轴,EF∥x轴,∴四边形EFGH是矩形,∴EF=GH,EH=FG,∴点E,F关于对称轴x=1对称,∴设点E(a,﹣a2+2a+3)则点F(2﹣a,﹣a2+2a+3),∴EF=2a﹣2,EH=﹣a2+2a+3,∴L=2(EF+EH)=﹣2a2+8a+2=﹣2(a﹣2)2+10,∵﹣2<0,∴当a=2时,L有最大值,最大值为10.(3)①如图,连接PF,CP,OP,PE,过点P作PN⊥EF交EF的延长线于N,过点C作CM⊥PN于M,连接BM.设P(x0,y0).由(2)可知,a=2,∴E(2,3),F(0,3),C(1,4),∴CF=,OE=,∵S△PCF=S△PCM﹣S△PMB﹣S△CMB=(x0﹣y0+3),∴h1=,同法h2=,∵,且,如图,x0>3或x0<﹣1,y0<0,解得:,∴P(﹣4,﹣21).②令x=﹣4代入l CF:y=x+3中,y=﹣1,∴(﹣4,﹣21)不过点P,若直线CE平移后过点P,设平移后直线解析式为:y=﹣x+b,代入(﹣4,﹣21),得b=﹣25,此时平移距离为,若直线EF平移后过点P,设F'(f,﹣21),代入l CF:y=x+3中,得f=﹣24,∴平移距离为,∴直线最后一次经过点P时,平移的距离为24.。
2021年辽宁省沈阳市中考数学模考试卷解析版

15.(3分)为了节省材料,某农场主利用围墙(围墙足够长)为一边,用总长为60m的篱笆围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等,则BC长为15m时,能围成的矩形区域ABCD的面积最大.
解:如图,
∵三块矩形区域的面积相等,
∴矩形AEFD面积是矩形BCFE面积的2倍,
2021年辽宁省沈阳市中考数学模考试卷解析版
一、选择题(本大题共10小题,共20.0分)
1.(2分)﹣8的相反数是( )
A.﹣8B.8C. D.
解:由相反数的定义可知,﹣8的相反数是﹣(﹣8)=8.
故选:B.
2.(2分)如图是由五个小正方体搭成的几何体,它的左视图是( )
A. B.
C. D.
解:从左面可看到从左往右2列小正方形的个数为:2,1,故选A.
=a(b+2)(b﹣2),
故答案为:a(b+2)(b﹣2)
12.(3分)若反比例函数 的图象在每一个象限中,y随着x的增大而减小,则m的取值范围是 .
解:∵在每个象限内,y随着x的增大而减小,
∴2m﹣1>0,
∴m .
故答案为:m .
13.(3分)不等式组 的解集是﹣1≤x<3.
解:
∵由不等式①,得x≥﹣1,
∴当x 15(m)时,S有最大值,最大值为: 152 15 (m2)
故答案为:15m.
16.(3分)如图,矩形ABCD中,P为AB上一动点(P与A,B不重合),将△BPC沿CP翻折至△B1PC,BP1与AD相交于点E,CB1与AD相交于点F,连接BB1交AD于Q,若EQ=8,QF=5,BC=20 ,则B1F的长=5,折痕CP的长= .
故∠OBA=60°,
辽宁省沈阳市2021版中考数学模拟试卷A卷

辽宁省沈阳市2021版中考数学模拟试卷A卷姓名:________ 班级:________ 成绩:________一、选择题 (共10题;共20分)1. (2分)下列说法错误的有()①无限小数是无理数;②无理数都是带根号的数;③只有正数才有平方根;④3的平方根是;⑤﹣2是(﹣2)2的平方根.A . 1个B . 2个C . 3个D . 4个2. (2分)同时抛掷两枚质地均匀的正方体骰子,骰子的六个面上分别刻有l到6的点数,下列事件中为不可能事件的是()A . 点数之和为12B . 点数之和小于3C . 点数之和为13D . 点数之和大于4且小于83. (2分)下列生活中的运动,属于平移的是()A . 电梯的升降B . 夏天电风扇中运动的扇叶C . 汽车挡风玻璃上运动的刮雨器D . 跳绳时摇动的绳子4. (2分)下列说法正确的是()A . 要了解全市居民对环境的保护意识,采用全面调查的方式B . 若甲组数据的方差S2甲 =0.1,乙组数据的方差S2乙 =0.2,则甲组数据比乙组稳定C . 随机抛一枚硬币,落地后正面一定朝上D . 若某彩票“中奖概率为1%”,则购买100张彩票就一定会中奖一次5. (2分) (2019八上·杭州期末) 若三角形三个内角度数比为2:3:4,则这个三角形一定是()A . 锐角三角形B . 直角三角形C . 钝角三角形D . 不能确定6. (2分)某件商品原价是a元,连续两次降价15%后是()A . (a-2×15%)元B . (a-2×15%a)元C . 2a(1-15%)元D . a(1-15%)元7. (2分) (2017八上·宁河月考) 过多边形的一个顶点可以引出6条对角线,则多边形的边数是()A . 7B . 8C . 9D . 108. (2分)下列说法正确的有()①4是x﹣3>1的解;②不等式x﹣2<0的解有无数个;③x>5是不等式x+2>3的解集;④x=3是不等式x+2>1的解;⑤不等式x+2<5有无数个正整数解.A . 1个B . 2个C . 3个D . 4个9. (2分)若一个直角三角形的三边长分别为a,b,c,且a2=9,b2=16,则c2为()A . 25B . 7C . 7或25D . 9或1610. (2分)用白铁皮做罐头盒,每张铁皮可制盒身25个,或制盒底40个,一个盒身与两个盒底配成一套罐头盒.现在又有36张白铁皮.设用x张制作盒身,y张制作盒底可以使盒身和盒底正好配套,则所列方程组正确的()A .B .C .D .二、填空题 (共6题;共15分)11. (1分)计算 a a a+(a ) +(-2a ) =________12. (1分)从﹣4、3、5这三个数中,随机抽取一个数,记为a,那么,使关于x的方程x2+4x+a=0有解,且使关于x的一次函数y=2x+a的图象与x轴、y轴围成的三角形面积恰好为4的概率________.13. (1分)如图所示,当________时,有CE∥AB成立.(只需要写出一个条件即可)14. (1分)(2017·吉安模拟) “一带一路”国际合作高峰论坛于2017年5月14日至15日在北京举行,中国预计为丝路基金新增资金1000亿人民币,1000亿用科学记数法表示为________.15. (1分) (2017七下·石城期末) 已知AB∥x轴,A点的坐标为(﹣3,2),并且AB=4,则B点的坐标为________.16. (10分)(2020·灯塔模拟) 如图,△AB C中,BC=AC,∠ACB=90°,将△ABC绕着点C顺时针旋转α(0≤α≤90°),得到△EFC,EF与AB、AC相交于点D、H,FC与AB相交于点G..(1)求证:△GBC≌△HEC;(2)在旋转过程中,当α是多少度时四边形BCED可以是某种特殊的平行四边形?并说明理由.三、解答题 (共11题;共95分)17. (10分)计算下列各题:(1)计算:(﹣1)﹣2+|2﹣|+2cos30°;(2)先化简,再求值:(1﹣)÷ ,其中x= +1.18. (5分) (2019八上·朝阳期中) 作出已知图形△ABC 关于给定直线 l 的对称图形△A'B'C'.19. (5分)计算:+.20. (5分)某中学开展“阳光体育一小时”活动,根据学校实际情况,决定开设A:踢毽子;B:篮球;C:跳绳;D:乒乓球四种运动项目.为了解学生最喜欢哪一种运动项目,随机抽取了一部分学生进行调查,并将调查结果绘制成如下两个统计图.请结合图中的信息解答下列问题:(1)本次共调查了多少名学生?(2)请将两个统计图补充完整.(3)若该中学有1200名学生,喜欢篮球运动项目的学生约有多少名?21. (20分) (2019九上·西安开学考) 解方程:(1)(2)(3)(4)22. (5分) (2019九上·鼓楼期中) 如图,点D为△ABC边AB上一点,请用尺规作图在AC边上找一点E,使得(保留作图痕迹,不写作法),并说明理由.23. (5分)一次函数的图像经过(1,2),求反比例函数的解析式。
2021年辽宁省沈阳市中考数学模拟试卷解析版

2021年辽宁省沈阳市中考数学模拟试卷解析版一.选择题(共10小题,满分20分,每小题2分)1.(2分)如果a 表示有理数,那么下列说法中正确的是( )A .+a 和﹣(﹣a )互为相反数B .+a 和﹣a 一定不相等C .﹣a 一定是负数D .﹣(+a )和+(﹣a )一定相等解:A 、+a 和﹣(﹣a )互为相反数;错误,二者相等;B 、+a 和﹣a 一定不相等;错误,当a =0时二者相等;C 、﹣a 一定是负数;错误,当a =0时不符合;D 、﹣(+a )和+(﹣a )一定相等;正确.故选:D .2.(2分)我国倡导的“一带一路”地区覆盖的总人口为4400000000人,这个数用科学记数法表示为( )A .44×108B .4.4×108C .4.4×109D .44×1010解:4 400 000 000用科学记数法表示为:4.4×109,故选:C .3.(2分)如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )A .B .C .D .解:从上面看第一排是三个小正方形,第二排右边是一个小正方形,故选:B .4.(2分)下列说法中,正确的是( )A .为检测某市正在销售的酸奶质量,应该采用普查的方式B .若两名同学连续六次数学测试成绩的平均分相同,则方差较大的同学的数学成绩更稳定C .抛掷一个正方体骰子,朝上的面的点数为偶数的概率是12D .“打开电视,正在播放广告”是必然事件解:A .测某市正在销售的酸奶质量,应该采用抽查的方式,此选项错误;B .若两名同学连续六次数学测试成绩的平均分相同,则方差较小的同学的数学成绩更稳定,此选项错误;C .抛掷一个正方体骰子,朝上的面的点数为偶数的概率是12,此选项正确;D .“打开电视,正在播放广告”是随机事件,此选项错误;故选:C .5.(2分)在下列运算中,正确的是( )A .(x ﹣y )2=x 2﹣y 2B .(a +2)(a ﹣3)=a 2﹣6C .(a +2b )2=a 2+4ab +4b 2D .(2x ﹣y )(2x +y )=2x 2﹣y 2解:A 、(x ﹣y )2=x 2﹣2xy +y 2,故本选项错误;B 、(a +2)(a ﹣3)=a 2﹣a ﹣6,故本选项错误;C 、(a +2b )2=a 2+4ab +4b 2,故本选项正确;D 、(2x ﹣y )(2x +y )=4x 2﹣y 2,故本选项错误;故选:C .6.(2分)某车间需加工一批零件,车间20名工人每天加工零件数如表所示:每天加工零件数4 5 6 78 人数 3 6 5 42 每天加工零件数的中位数和众数为( )A .6,5B .6,6C .5,5D .5,6解:由表知数据5出现了6次,次数最多,所以众数为5;因为共有20个数据,所以中位数为第10、11个数据的平均数,即中位数为6+62=6,故选:A .7.(2分)若△ABC ∽△ADE ,若AB =6,AC =4,AD =3,则AE 的长是( )。
2021年辽宁省沈阳市中考数学名校模考试卷(附答案解析)
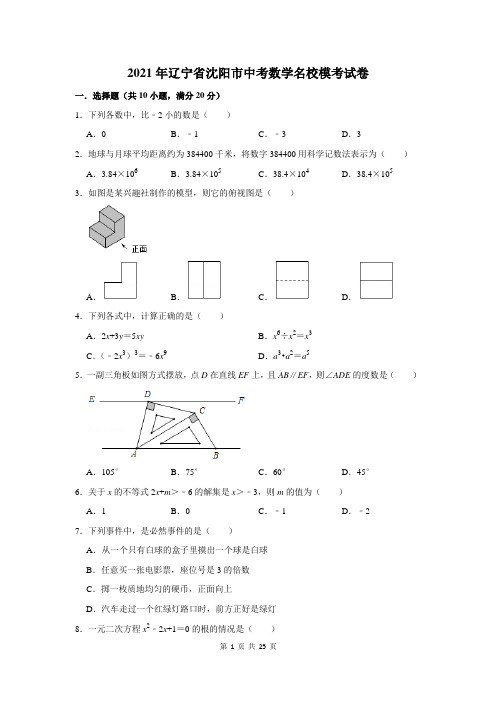
2021年辽宁省沈阳市中考数学名校模考试卷一.选择题(共10小题,满分20分)1.下列各数中,比﹣2小的数是()A.0B.﹣1C.﹣3D.32.地球与月球平均距离约为384400千米,将数字384400用科学记数法表示为()A.3.84×106B.3.84×105C.38.4×104D.38.4×1053.如图是某兴趣社制作的模型,则它的俯视图是()A.B.C.D.4.下列各式中,计算正确的是()A.2x+3y=5xy B.x6÷x2=x3C.(﹣2x3)3=﹣6x9D.a3•a2=a55.一副三角板如图方式摆放,点D在直线EF上,且AB∥EF,则∠ADE的度数是()A.105°B.75°C.60°D.45°6.关于x的不等式2x+m>﹣6的解集是x>﹣3,则m的值为()A.1B.0C.﹣1D.﹣27.下列事件中,是必然事件的是()A.从一个只有白球的盒子里摸出一个球是白球B.任意买一张电影票,座位号是3的倍数C.掷一枚质地均匀的硬币,正面向上D.汽车走过一个红绿灯路口时,前方正好是绿灯8.一元二次方程x2﹣2x+1=0的根的情况是()A .有两个不相等的实数根B .有两个相等的实数根C .没有实数根D .无法确定9.已知一次函数y =(k +1)x +b 的图象与x 轴负半轴相交,且函数值y 随自变量x 的增大而增大,则k ,b 的取值情况为( ) A .k >﹣1,b >0B .k >﹣1,b <0C .k <﹣1,b >0D .k <﹣1,b <010.如图,矩形ABCD 绕着点A 顺时针旋转60°得到矩形AEFG ,若BC =3,且E 恰好落在CD 上,则CF̂的长为( )A .53πB .√2πC .√3πD .√213π 二.填空题(共6小题,满分18分,每小题3分)11.(3分)长和宽分别是a ,b 的长方形的周长为16,面积为9,则a 2b +ab 2的值为 . 12.(3分)解方程组{ax +by =2cx −7y =8时,一学生把c 看错而得到{x =−2y =2,而正确的解是{x =3y =−2,那么a +b ﹣c = .13.(3分)某鸡腿生产公司的质检人员从两批鸡腿中各随机抽取了6个,记录相应的质量(g )如表,若甲、乙两个样本数据的方差分别为S 甲2、S乙2,则S甲2S乙2(填“>“、“=”、“<”)质量 70 71 72 73 甲 1 4 1 0 乙32114.(3分)如图,△ABC 和△BOD 都是等腰直角三角形,∠ACB =∠BDO =90°,且点A 在反比例函数y =kx (k ≠0)的图象上,若OB 2﹣AB 2=8,则k 的值为 .。
2021年辽宁省沈阳市中考数学模拟试卷及答案解析

第 1 页 共 28 页
2021年辽宁省沈阳市中考数学模拟试卷
一.选择题(共10小题,满分20分,每小题2分)
1.如果a 表示有理数,那么下列说法中正确的是( )
A .+a 和﹣(﹣a )互为相反数
B .+a 和﹣a 一定不相等
C .﹣a 一定是负数
D .﹣(+a )和+(﹣a )一定相等
2.我国倡导的“一带一路”地区覆盖的总人口为4400000000人,这个数用科学记数法表示
为( )
A .44×108
B .4.4×108
C .4.4×109
D .44×1010
3.如图是由6个完全相同的小正方体组成的几何体,其俯视图为( )
A .
B .
C .
D .
4.下列说法中,正确的是( )
A .为检测某市正在销售的酸奶质量,应该采用普查的方式
B .若两名同学连续六次数学测试成绩的平均分相同,则方差较大的同学的数学成绩更稳定
C .抛掷一个正方体骰子,朝上的面的点数为偶数的概率是12
D .“打开电视,正在播放广告”是必然事件
5.在下列运算中,正确的是( )
A .(x ﹣y )2=x 2﹣y 2
B .(a +2)(a ﹣3)=a 2﹣6
C .(a +2b )2=a 2+4ab +4b 2
D .(2x ﹣y )(2x +y )=2x 2﹣y 2
6.某车间需加工一批零件,车间20名工人每天加工零件数如表所示:
每天加工零件
数
4 5 6 7 8 人数 3 6 5 4 2 每天加工零件数的中位数和众数为( )。
2021年沈阳市中考数学模拟试卷及答案解析
2021年沈阳市中考数学模拟试卷一、选择题(本大题共10小题,每小题2分,共20分)1.下列各数中最大的数是()A.5B.C.πD.﹣82.随着“一带一路”建设的不断发展,我国已与多个国家建立了经贸合作关系,去年中哈铁路(中国至哈萨克斯坦)运输量达8200000吨,将8200000用科学记数法表示为()A.8.2×105B.82×105C.8.2×106D.82×1073.如图是某几何体的三视图,该几何体是()A.三棱柱B.三棱锥C.圆锥D.圆柱4.不等式x+1≥2的解集在数轴上表示正确的是()A.B.C.D.5.下列计算正确的是()A.x4+x4=2x8B.x3•x2=x6C.(x2y)3=x6y3D.(x﹣y)(y﹣x)=x2﹣y26.点P(4,3)关于y轴的对称点所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限7.已知点A(﹣2,y1),B(﹣4,y2)都在反比例函数y=(k>0)的图象上,则y1,y2的大小关系()A.y1>y2B.y1<y2C.y1=y2D.无法确定8.如图,分别过矩形ABCD的顶点A、D作直线l1、l2,使l1∥l2,l2与边BC交于点P,若∠1=38°,则∠BPD为()A.162°B.152°C.142°D.128°9.某同学5次数学小测验的成绩分别为(单位:分):90,85,90,95,100,则该同学这5次成绩的众数是()A.90 分B.85 分C.95 分D.100 分10.已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论正确的是()A.当x<2时,y随x增大而增大B.a+b+c<0C.抛物线过点(﹣4,0)D.4a+2b+c=0二、填空题(每题3分,共18分)11.(3分)分解因式:x4﹣2x2y2+y4=.12.(3分)如图,每个小正方形边长为1,则△ABC边AC上的高BD的长为.13.(3分)如图,正方形ABCD中,点E为对角线AC上一点,且AE=AB,则∠BEA的度数是度.。
【中考冲刺】2021年辽宁省沈阳市中考数学模拟试卷(附答案)
25.如图1,抛物线y=ax2+bx+ 与x轴交于点A(﹣1,0),C(3,0),点B为抛物线顶点,连接AB,BC,AB与y轴交于点D,连接CD.
【详解】
解:∵反比例函数y= 的图象在每一象限内,y随x的增大而减小,
∴k﹣1>0,
解得:k>1,
故选:A.
【点睛】
本题考查了反比例函数的图象和性质,能熟记反比例函数的性质是解此题的关键.
5.D
【分析】
根据二次函数图象的平移规律(左加右减,上加下减)进行解答即可.
【详解】
抛物线y= x2向左平移1个单位,再向上平移2个单位得y= (x+1)2+2.
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )
A.1B.2C.3D.4
二、填空题
11.已知△ABC∽△ ,AD和 是它们的对应中线,若AD=8, =6,则△ABC与△ 的周长比是_____.
12.已知关于x的一元二次方程(a﹣2)x2+2x+1=0有两个不相等的实数根,则a的取值范围是_____.
21.如图,一次函数的图象y=ax+b(a≠0)与反比例函数 (k≠0)的图象交于点A( ,4),点B(m,1).
(1)求这两个函数的表达式;
(2)若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,点P是反比例函数图象上的一点,当S△OCP:S△BCD=1:3时,请直接写出点P的坐标.
2021年辽宁省沈阳市中考数学模拟试卷解析版
第 1 页 共 15 页 2021年辽宁省沈阳市中考数学模拟试卷解析版
一.选择题(共10小题,满分20分)
1.下列各对数中,互为相反数的是( )
A .﹣2与3
B .﹣(+3)与+(﹣3)
C .4与﹣4
D .5与15 解:A 、只有符号不同的两个数互为相反数,故A 错误;
B 、都是﹣3,故B 错误;
C 、只有符号不同的两个数互为相反数,故C 正确;
D 、互为倒数,故D 错误;
故选:C .
2.如图是某兴趣社制作的模型,则它的俯视图是( )
A .
B .
C .
D .
解:该几何体的俯视图是:由两个长方形组成的矩形,且矩形的之间有纵向的线段隔开. 故选:B .
3.壮丽七十载,奋进新时代.2019年10月1日上午庆祝中华人民共和国成立70周年大会在
北京天安门广场隆重举行,超20万军民以盛大的阅兵仪式和群众游行欢庆共和国70华诞,其中20万用科学记数法表示为( )
A .20×104
B .2×105
C .2×104
D .0.2×106
解:20万=200000=2×105.
故选:B .
4.如图,直线a ,b 被直线c 所截,a ∥b ,若∠2=45°,则∠1等于( )
A .125°
B .130°
C .135°
D .145°。
2021年辽宁省沈阳市中考数学模拟卷解析版
第 1 页 共 20 页2021年辽宁省沈阳市中考数学模拟卷解析版一.选择题(共10小题,满分20分)1.在实数√7,112,0,π2,√25,1.414中,有理数有( ) A .1 个B .2 个C .3 个D .4 个 解:在实数√7,112,0,π2,√25,1.414中,有理数有:112,0,√25,1.414共4个. 故选:D .2.地球的表面积约为510000000km 2,将510000000用科学记数法表示为( )A .0.51×109B .5.1×108C .5.1×109D .51×107 解:510000000=5.1×108,故选:B .3.如图所示的几何体,上下部分均为圆柱体,其主视图是( )A .B .C .D .解:∵该几何体上下部分均为圆柱体,∴其主视图为矩形,故选:C .4.在平面直角坐标系中,点A (1,﹣2)关于x 轴对称的点的坐标为( )A .(1,2)B .(﹣1,2)C .(2,1)D .(﹣1,﹣2) 解:点A (1,﹣2)关于x 轴对称的点的坐标为:(1,2).故选:A .5.下列运算正确的是( )A .a 2•a 3=a 6B .2a 2+a 2=3a 4C.(﹣2a2)3=﹣2a6D.a4÷(﹣a)2=a2解:A、原式=x5,所以A选项的计算错误;B、原式=3a2,所以B选项的计算错误;C、原式=﹣8a6,所以C选项的计算错误;D、原式=a4÷a2=a2,所以D选项的计算正确.故选:D.6.如图所示,将一块直角三角板的直角顶点O放在直尺的一边CD上,如果∠AOC=23°,那么∠BOD=()A.67°B.57°C.77°D.23°解:∵∠AOC=23°,∴∠BOD=180°﹣23°﹣90°=67°.故选:A.7.下列事件中是随机事件的是()A.校运会上立定跳远成绩为10米B.在只装有5个红球的袋中,摸出一个红球C.慈溪市明年五一节是晴天D.在标准大气压下,气温3°C时,冰熔化为水解:“校运会上立定跳远成绩为10米”是不可能事件,因此选项A不符合题意;“在只装有5个红球的袋中,摸出一个红球”是必然事件,因此选项B不符合题意;“慈溪市明年五一节是晴天”可能发生,也可能不发生,是随机事件,因此选项C符合题意;“在标准大气压下,气温3°C时,冰熔化为水”是必然事件,因此选项D不符合题意;故选:C.8.在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是()第2 页共20 页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021届辽宁沈阳市中考数学模拟试卷
一、选择题(下列各题的备选答案中,只有一个答案是正确的.每小题2分,共20分)1.下列各数中是无理数的是()
A.0B.C.D.
【解答】解:0是整数,属于有理数;是分数,属于有理数;是无理数;,是整数,属于有理数.
故选:C.
2.如图是由五个相同的小立方块搭成的几何体,这个几何体的左视图是()
A.B.
C.D.
【解答】解:从左面看易得上面一层中间有1个正方形,下面有3个正方形.
故选:C.
3.“弘扬雷锋精神,共建幸福沈阳”,幸福沈阳需要830万沈阳人共同缔造,将数据830万用科学记数法可以表示为()万.
A.83×10B.8.3×102C.8.3×103D.0.83×103
【解答】解:830万=8.3×102万.
故选:B.
4.下列运算正确的是()
A.2m3+3m2=5m5B.m3÷(﹣m)2=m
C.m•(m2)3=m6D.(m+n)(n﹣m)=m2﹣n2
【解答】解:A.2m3与3m2不是同类项,所以不能合并,故本选项不合题意;
B.m3÷(﹣m)2=m,正确;
C.m•(m2)3=m7,故本选项不合题意;
D.(m+n)(n﹣m)=n2﹣m2,故本选项不合题意.
故选:B.
5.在平面直角坐标系中,点B的坐标是(4,﹣1),点A与点B关于x轴对称,则点A的坐标是()
A.(4,1)B.(﹣1,4)C.(﹣4,﹣1)D.(﹣1,﹣4)【解答】解:∵点B的坐标是(4,﹣1),点A与点B关于x轴对称,
∴点A的坐标是:(4,1).
故选:A.
6.如果m=﹣1,那么m的取值范围是()
A.0<m<1B.1<m<2C.2<m<3D.3<m<4
【解答】解:∵2<<3,
∴1<﹣1<2,
∵m=﹣1,
∴1<m<2,
故选:B.
7.已知△ABC∽△A′B′C′,AD和A'D'是它们的对应中线,若AD=10,A'D'=6,则△ABC与△A'B'C'的面积比是()
A.5:3B.25:9C.3:5D.9:25
【解答】解:∵△ABC∽△A′B′C′,AD和A'D'是它们的对应中线,AD=10,A'D'=6,
∴两三角形的相似比为:5:3,
则△ABC与△A'B'C'的面积比是:25:9.
故选:B.
8.顺次连接对角线相等的四边形的各边中点,所形成的四边形是()A.平行四边形B.菱形C.矩形D.正方形
【解答】解:菱形,理由为:
如图所示,∵E,F分别为AB,BC的中点,
∴EF为△ABC的中位线,
∴EF∥AC,EF=AC,。
