等厚干涉
光的等厚干涉公式

光的等厚干涉公式在我们探索物理世界的奇妙旅程中,光的等厚干涉公式就像是一把神奇的钥匙,能打开一扇通往微观世界奥秘的大门。
先来说说啥是光的等厚干涉。
想象一下,你拿着一块平整的玻璃片,在上面滴上一小滴透明的液体,然后把另一块玻璃片轻轻地盖上去。
这时候,你会发现两片玻璃接触的地方,液膜的厚度不是处处相等的。
而光在通过这样厚度不均匀的液膜时,就会发生等厚干涉现象。
那光的等厚干涉公式到底是啥呢?它就是:2nh + λ/2 = mλ 。
这里的 n 是介质的折射率,h 是薄膜的厚度,λ 是入射光的波长,m 是干涉条纹的级数。
我记得有一次在课堂上给学生们讲解这个公式的时候,有个调皮的小家伙举起手说:“老师,这公式看起来好复杂,感觉像个解不开的谜题。
”我笑着回答他:“别着急,咱们一步步来,就像玩解谜游戏一样。
” 于是,我拿出事先准备好的实验器材,现场给他们演示了光的等厚干涉实验。
在实验中,我让一束平行光垂直照射到涂有油膜的玻璃板上,同学们通过显微镜清晰地看到了明暗相间的条纹。
我指着那些条纹说:“你们看,这就是光在跟我们‘说话’,通过这些条纹,再结合我们的公式,就能听懂它的‘语言’啦。
”接下来,我们就开始深入理解这个公式。
比如说,当我们知道了入射光的波长、介质的折射率,还有观察到的干涉条纹级数,就能算出薄膜的厚度。
这在实际生活中可有大用处呢!就拿检测精密零件的表面平整度来说吧。
工人师傅们可以利用光的等厚干涉原理,快速准确地判断零件表面是否平整。
如果干涉条纹均匀分布,那就说明表面比较平整;要是条纹弯曲或者疏密不均,那可就意味着表面存在瑕疵。
再比如说,在制造光学仪器的时候,这个公式能帮助工程师们精确控制镜片之间的距离和镀膜的厚度,从而提高仪器的性能和精度。
回到我们的学习中,理解和掌握这个公式可不能靠死记硬背。
得通过多做实验、多观察现象,才能真正把它装进我们的知识口袋里。
总之,光的等厚干涉公式虽然看起来有点复杂,但只要我们用心去探索、去实践,就能发现它其实就像一个贴心的小助手,能帮助我们解决很多实际问题,让我们更加深入地了解光的奇妙世界。
等厚干涉实验

平凸透镜
平凸透镜与平板玻璃组合成牛顿环实验样
品。
平凸透镜
平板玻璃返回ຫໍສະໝຸດ 劈尖两块光学平玻璃重叠在一起,在一端插入一
薄纸片,制成实验样品。
平板玻璃
薄纸片
平板玻璃
返回
实验内容
1.用牛顿环测透镜的曲率半径 2.用劈尖干涉法测薄纸片的厚度
实验公式 1.牛顿环 2.劈尖
返回目录页
1.牛顿环
在空气厚度为e的地方,
返回
数据处理
数据记录 曲率半径计算 不确定度评定
返回目录页
数据记录表格
1.牛顿环
次数 1 2 3 4 C15 C5 C’15 C’5 D15 D5
单位:mm
56
下一页
2.劈尖干涉
次数 0 1 2 3 4 5 Xi
△X
L始 L末 L
单位:mm
返回
2
2
曲率半径计算 R Dm Dn
4(m n)
空气隙的等厚干 涉条纹是一组明暗相间 的同心环。该干涉条纹 最早被牛顿发现,所以 称为牛顿环(Newton -ring)
牛顿环
返回
劈尖干涉
L
将两块光学平玻璃重叠 在一起,在一端插入一 薄纸片,则在两玻璃板 间形成一空气劈尖
当一束平行单色光垂直 d’ 入射时,由空气层上下
表面反射的光将在空气 层上表面处发生干涉, 形成一组平行于交棱的 明暗相间、等间距的直 条纹。
返回
测量薄纸片厚度
•由于相邻条纹之间的距离很小,为了减小测
量误差,通常测量n条干涉暗条纹之间的距
离。取n=10,横向改变显微镜筒位置,使叉 丝与某级暗纹重合读取X0 ,继续朝同一方向 移 动 叉 丝 , 每 隔 10 条 暗 纹 依 次 读 取 X1 , X2, … ,X5。 •测量交棱到纸边的距离L,重复测5次。
等厚干涉
薄膜倾角: 薄膜倾角:α 入射角: 入射角:i1 折射角: 折射角:i2
7
1 [cos(α + 2i2 ) + cos(α )] λ δ = n2 (d1 + d 2 )[ 2 ]− cos α cos(α + i2 ) 2
(B)
17
工件水平放置
参见:崔宏滨、李永平、段开敏,光学,科学出版社,北京, 参见:崔宏滨、李永平、段开敏,光学,科学出版社,北京,2008年7月,第118页 年 月 页 郑少波、赵清,物理光学基础,国防工业出版社,北京, 郑少波、赵清,物理光学基础,国防工业出版社,北京,2009年8月,P35 年 月
λ
2
4
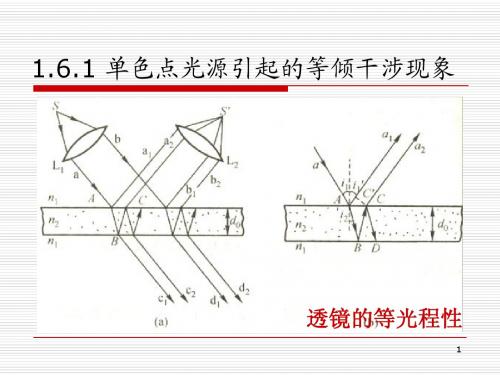
一、单色点光源所引起的等厚干涉条纹
D
C
M
A d1
d2
薄膜倾角: 薄膜倾角:α 入射角:i1 入射角: 折射角:i2 折射角:
δ = n2 ( AB + BC ) − n1CD −
A’
N
B
C’
λ
2
5
AB = d1 / cos(α + i2 )
D C
M
BC = d 2 / cos(α + i2 )
2
∆d0 α ≈ sinα ≈ tanα = ∆x
∴d02 −d01 = ∆d0 ≈α∆x
15
α∆x =
由此可得:
λ
2
60 180 (2)浸入油中后,条纹间距变为
λ 550×10−6 ∆x = = ≈ 0.158(m ) m 2 α 2× 6 × π
等厚干涉的原理特点应用

等厚干涉的原理、特点和应用1. 等厚干涉的原理等厚干涉是一种光学干涉现象,指的是光线在具有两个或多个等厚介质间传播时发生的干涉效应。
它基于菲涅尔(Fresnel)原理,即光线在介质边界上发生反射和折射的规律,导致光线的相位差引起干涉现象。
2. 等厚干涉的特点•等厚等相位线:等厚干涉的最显著特点是产生一系列彼此平行的等厚等相位线。
在等厚干涉图上,等厚线呈现为彩虹色的同心圆。
•颜色分布规律:等厚干涉中,不同颜色的环呈现特定的分布规律。
通常,中心为黑白交替的暗环,向外围逐渐过渡为彩虹色的明亮环。
•相位差的影响:等厚干涉的颜色变化与光线在相邻等厚介质中的相位差有关。
相位差的大小决定了干涉环的颜色与宽度。
3. 等厚干涉的应用3.1 表面形貌测量等厚干涉可用于表面形貌测量,通过观察干涉图案的等厚等相位线变化,可以推断出被测表面的形状和曲率。
这被广泛应用于光学元件的制造、光学仪器的校准以及微小器件的表面测量。
3.2 涂层薄膜分析等厚干涉也可以用于涂层薄膜的分析。
由于不同材料的折射率不同,涂层的厚度会导致光线的相位差,从而形成干涉图案。
通过观察和分析这些干涉图案,可以测量涂层薄膜的厚度、折射率和均匀性等参数。
3.3 正交偏光干涉等厚干涉可与正交偏光干涉相结合,用于材料的应力分析。
通过在光路中加入一个用于改变光线偏振方向的偏光片,可以观察到具有不同偏振方向的光线在材料中传播产生的干涉图案。
通过分析多组干涉图案,可以推断材料中的应力分布和应力状态。
3.4 光学显微镜等厚干涉技术在光学显微镜中得到了广泛应用。
基于等厚干涉的光学显微镜可以实现高分辨率的成像,对于材料的微观结构和表面形貌进行观察和分析。
在生物学、材料科学和纳米科技等领域中,该技术被广泛用于微观结构与性能的研究。
结论等厚干涉作为一种光学干涉现象,通过光线的相位差引起干涉图案的形成,具有等厚等相位线、颜色分布规律等特点。
其重要应用包括表面形貌测量、涂层薄膜分析、正交偏光干涉和光学显微镜等领域。
等厚干涉原理

等厚干涉原理
干涉原理是光学中的一个基本原理,描述了当两束光波相遇时,它们的干涉现象。
在干涉实验中,我们通常会使用一对光栅或两个狭缝来产生干涉效应。
干涉现象的产生源于光波的波动性质。
等厚干涉是其中一种干涉现象,它指的是当两个处于同一平面上的玻璃或空气薄膜之间被光所填充时,光在两个界面之间的反射和折射所引起的干涉现象。
等厚干涉主要是由于光在介质中传播速度不同而引起的。
当入射光波垂直于两个界面时,会发生垂直入射等厚干涉。
在这种情况下,入射光波在第一个界面上发生反射,并在第二个界面上发生折射,然后再次反射回来。
这两束光波具有不同的光程差,这会导致干涉现象的出现。
干涉现象的强度取决于光的波长、介质的折射率以及两个界面的厚度差。
根据等厚条件,当两个界面之间的厚度差等于光的波长的整数倍时,我们就会观察到明纹或暗纹。
等厚干涉广泛应用于光学领域,例如在干涉测量中,我们可以利用等厚干涉现象来测量薄膜的厚度或者根据干涉纹的形态来判断介质的性质。
此外,等厚干涉还可以用于图像处理和光学元件的设计等方面。
总之,等厚干涉原理是一种重要的光学现象,通过研究光的波
动性质,我们可以深入理解光的行为,并将其应用于实际生活和科学研究中。
等厚干涉

n =1
n
L
d
b
b'
b' λ ∆e = b 2
b
d=
1 λ λ ≈ ⋅ = 3 2 6
λ L
2n b ⋅
1. 用劈尖干涉法可检测工件表面缺陷,当波长为 λ 的 用劈尖干涉法可检测工件表面缺陷, 单色平行光垂直入射时, 单色平行光垂直入射时,若观察到的干涉条纹如图 所示, 所示,每一条纹弯曲部分的顶点恰好与其左边条纹 的直线部分的连线相切, 的直线部分的连线相切,则工件表面与条纹弯曲处 对应的部分 A)凸起, (A)凸起,且高度为 λ 4 (B)凸起,且高度为 λ 2 )凸起, (C)凹陷,且深度为 λ 2 )凹陷, (D)凹陷,且深度为 λ 4 )凹陷, 平玻璃
(2)将牛顿环置于 n>1 ) 的液体中,条纹如何变? 的液体中,条纹如何变? 未置于的液体中
R r
r = kRλ
k = r 2 Rλ
r = k , Rλ n 置于的液体中
k = r n Rλ
, 2
k, > k
4.应用 4.应用
(1)测量透镜的曲率半径
R
r
rk = kR λ
2
rk + m = ( k + m ) Rλ
二、等厚干涉
(一)劈尖干涉 1.干涉实现 干涉实现 平行光垂直入射到劈尖上 平行光垂直入射到劈尖上 i=0 垂直入射
θ
玻璃
n
e
空气
δ = 2e n
2
2 2 − n1 sin i
+λ 2
n1 n1
空气劈尖n=1 空气劈尖
δ = 2e + λ 2
θ ≈ 10−4 ~ 10 −5 rad
等厚干涉的工作原理和应用

等厚干涉的工作原理和应用工作原理等厚干涉是一种光学干涉现象,它基于光线在介质中传播时的干涉效应。
在等厚干涉中,当光线通过一块具有等厚的透明介质时,光线会发生干涉,形成明暗条纹。
这些明暗条纹的出现是由于光线在通过介质时以不同的相位到达观察者的眼睛。
等厚干涉的原理等厚干涉的原理基于光线传播过程中的两个基本原理:光的波动性和叠加原理。
光的波动性是指光可以被看作是波动的电磁场。
光线在介质中传播时,会发生折射和反射,这些过程都可以看作是波动的电磁场沿特定方向的传播。
叠加原理是指当两个或多个波相遇时,它们会叠加在一起形成一个新的波。
在等厚干涉中,当光线从不同路径通过透明介质时,它们会叠加在一起形成明暗条纹。
发生等厚干涉的条件等厚干涉发生的条件包括:1.光源必须是连续的、单色的光源。
单色光指的是波长相同的光,例如激光器发射的光。
2.介质必须是透明的、具有相同的厚度。
只有具有相同厚度的介质才能使光线以相同的相位到达观察者的眼睛。
3.光线必须以一定的角度穿过介质。
当光线以特定角度穿过介质时,才会发生干涉。
应用等厚干涉在光学测量中的应用等厚干涉在光学测量中有广泛的应用,其中包括:1.表面形貌测量。
通过观察等厚干涉条纹的形态变化,可以测量表面的形貌和形变,从而利用这些信息进行表面质量评估和产品检测。
2.薄膜厚度测量。
等厚干涉可以用来测量透明材料的薄膜厚度,例如涂层、薄膜和玻璃等。
通过分析等厚干涉条纹的间距,可以计算出薄膜的厚度。
3.材料折射率测量。
等厚干涉可以用来测量材料的折射率,即光线在材料中的传播速度。
通过分析等厚干涉条纹的位置和形态变化,可以计算出材料的折射率。
等厚干涉在光学成像中的应用等厚干涉在光学成像中也有一些重要的应用,包括:1.厚度图像生成。
通过观察等厚干涉条纹的形态和分布,可以生成物体的厚度图像。
这对于材料的质量控制和产品的检测非常有价值。
2.目标定位和跟踪。
等厚干涉可以用来定位和跟踪目标。
通过观察等厚干涉条纹的变化,可以精确确定目标的位置和运动状态。
等厚干涉_实验报告

一、实验目的1. 观察和分析等厚干涉现象;2. 学习利用干涉现象测量平凸透镜的曲率半径;3. 掌握读数显微镜的使用方法。
二、实验原理等厚干涉是薄膜干涉的一种,当薄膜层的上下表面有一很小的倾角时,从光源发出的光经上下表面反射后在上表面附近相遇时产生干涉,并且厚度相同的地方形成同一干涉条纹,这种干涉就叫等厚干涉。
牛顿环是等厚干涉的一个最典型的例子,其原理如下:牛顿环装置由一块曲率半径较大的平凸透镜放在一块光学玻璃平板上构成。
平凸透镜的凸面与玻璃平板之间的空气层厚度从中心到边缘逐渐增加。
当平行单色光垂直照射到牛顿环上时,经空气层上、下表面反射的两光束存在光程差,它们在平凸透镜的凸面相遇后,将发生干涉。
从透镜上看到的干涉花样是以玻璃接触点为中心的一系列明暗相间的圆环,称为牛顿环。
根据干涉原理,当空气层厚度为d时,两束相干光的光程差为ΔL = 2nd +(λ/2),其中n为空气折射率,λ为入射光的波长。
当ΔL为整数倍的波长时,产生明环;当ΔL为奇数倍的半波长时,产生暗环。
根据牛顿环的干涉条件,可以推导出牛顿环的半径与平凸透镜的曲率半径R之间的关系。
三、实验仪器与器材1. 牛顿环仪2. 读数显微镜3. 钠光灯4. 秒表5. 记录本四、实验步骤1. 将牛顿环仪放置在平稳的工作台上,调整读数显微镜使其对准牛顿环仪的中心。
2. 打开钠光灯,调整其亮度,使光线垂直照射到牛顿环仪上。
3. 观察牛顿环现象,记录明暗环的位置和数量。
4. 使用读数显微镜测量明暗环的半径,记录数据。
5. 重复实验步骤,取平均值。
五、数据处理1. 根据实验数据,计算明环和暗环的半径。
2. 根据牛顿环的干涉条件,推导出平凸透镜的曲率半径R的表达式。
3. 代入实验数据,计算平凸透镜的曲率半径R。
六、实验结果与分析1. 实验过程中观察到牛顿环现象,明暗环以接触点为中心,内疏外密。
2. 通过测量明暗环的半径,计算出平凸透镜的曲率半径R。
3. 实验结果与理论计算值基本一致,说明实验方法可靠。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
红线对应薄膜厚度相同的位置。
劈角由小变大时,条纹由疏变密,反之亦然
三、劈尖的应用(50页 1.10)1、测量细丝直径、微小夹角
¾
例: 两玻璃片夹一细丝,两片之间形成一个空气薄膜,n 2=1,光垂直入射,i 1≈i 2=0。
∵有额外光程差,∴d 0=0 处为暗条纹。
¾
如何测小角度α呢?
已知d ,通过测量L ,可计算:α≈d/L 。
α
λ
Δ22n x ≈
2
02n d λ
Δ=
如何求细丝直径d ?
=(m-1)λ/2
假如一共有m 条,则d =(m-1)Δd 0射,看反射光的干涉条纹。
加热,膨胀,表面上升,条纹有什么变化?
待测材料膨胀后,空气膜变薄,如图所示,虚线
所需要的光程差值,即该处为一若条纹的最大变形线度为O
B
A A O 为心的圆,所以条纹是以点为心的一组同心圆,叫做牛顿环。
)
(干涉相消⋅⋅⋅=2,1,0j r B
A A
3、条纹位置
此时反射光中看到的O 点是暗点。
¾
有额外光程差时,()()⋅⋅⋅=λ
+=
2,1,0j n R
21j 2r 2
()⋅⋅⋅=λ=
2,1,0j n R
2j
2r 2
条纹位置是由圆形条
纹的半径r决定。
亮条纹半径为:
暗条纹半径为:¾
没有额外光程差时,亮(暗)条纹半径为?
此时反射光中看到的O 点是亮点。
4、条纹级次分布、条纹密度
条纹级次:内低外高条纹密度:内疏外密
条纹向中间收缩,中心条纹被吞没。
条纹向外扩展,中心有条纹冒出。
与等倾条纹的变化情况相反。
透镜上移时:透镜下移时:r
B
A ′
A O
5、在透射光中亦可观察到牛顿环。
动画
2
λ+例题:
已知:半径为4cm 的平凸透镜,凸面向下,放在平玻璃板上,
透镜和平板的折射率均为1.5,用波长为500nm 的平行光垂直照射,观察反射光的干涉条纹。
求:(1)若透镜边缘恰为暗纹,且共有17条暗纹(若圆心
为暗点,也算是一条暗纹),求透镜凸面的曲率半径,和透镜边缘处两反射光的光程差;
(2)若透镜向上平移两个波长,干涉条纹如何变化?
(如果有额外光程差,要求取。
)。
