圆内接四边形拔高练习题
中考数学总复习 圆内接四边形专项练习题

中考数学总复习圆内接四边形专项练习题例题1:如图,已知四边形ABCD内接于⊙O,OC∥AD,∠DAB=60°,∠ADC=106°.求∠OCB及弧DC的度数.练:如图,四边形ABCD是⊙O的内接四边形,AB∥DC,∠BAD的平分线交⊙O于点P,交DC的延长线于点E,若∠BAD=86°,则∠PCE= °,⌒ADC的度数为例题2,如图,四边形ABCD是⊙O的内接四边形,弧AB=弧AD,∠BCD=120°,连接AC,DE⊥AC于点E,连接BE,若∠BED=150°,AC=37 ,求DE的长.练:如图,四边形ABCD是⊙O的内接四边形,AB=BD,BM⊥AC于点M,已知AC=11,CD=7,求CM的长.例3.如图,在△ABC中,AB=AC,在△ABC的外侧作直线AP,点B与点D关于AP轴对称,连接BD,CD,CD与AP交于点E. 求证:∠1=∠2.练:如图,在△ABC内有一点D,使得DA=DB=DC,若∠DAB=20°,则∠ACB= °.例题2,如图,E是正方形ABCD的边AB上的一点,过点E作DE的垂线交∠ABC的外角平分线于点F.求证:EF=DE.练:如图,锐角△ABC中,BD,CE是高线,DG⊥CE于点G,EF⊥BD于点F.求证:FG∥BC6.如图,已知△ABC,∠C=90°,将△ABC绕点A顺时针旋转x度(α为锐角),得到△ADE,连接BE,CD,延长CD交BE于点F.(1)用含有x的代数式表示∠ACD的度数为;(2)求证:点B,C,A,F四点共圆.(3)求证:点F为BE的中点.7.如图,在△ABC中,∠BAC=45°,AD是BC边上的高,且BD=6,CD=2.求AD的长度,课后习题:1.如图,⊙O内接四边形ABCD中,点E在BC延长线上,∠A+∠BOD=150°,则∠DCE= °2.如图,四边形ABCD是⊙O的内接四边形,∠A与∠C的度数之比为2:3,且弧AD的度数为100°,则弧AB的度数°3,如图,∠DAE是⊙O的内接四边形ABCD的一个外角,且DB=DC.AC是直径,若∠ACB=52°,则∠DAE= °4.如图,在平行四边形ABCD中,AD=2,∠A=120°,CF⊥AB于F,连接DF交CB延长线于E,连接AE,则△AEF的面积为5.如图,已知P为长方形内一点,S△P AB=5, S△PBC=12, 则S△PBD=6.如图,在菱形ABCD中,∠A=110°,点E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=()7.已知如图,四边形ABCD中,AB∥CD,AB=AC=AD=5,BC=6,求BD的长.8.如图,已知△ABC中,AH是高线,AT是角平分线,且TD⊥AB于点D,TE⊥AC于点E.求证:∠AHD=∠AHE.。
初中数学:圆内接四边形练习(含答案)

初中数学:圆内接四边形练习(含答案)知识点 1 圆内接四边形的性质——圆内接四边形的对角互补1.2016·丽水如图3-6-1,四边形ABCD为⊙O的内接四边形.已知∠ BCD=110°,则∠BAD=_______ °.2.已知四边形ABCD内接于⊙ O,且∠ A∶∠C=1∶2,则∠A=_____ °.图3-6-23.如图3-6-2,四边形ABCD是⊙ O的内接四边形,且∠ ABC=115°,那么∠ AOC=4.如图3-6-3,AB是半圆O的直径,C,D 是AB上两点,∠ ADC=120°,则∠ BAC=图3-6-3图3-6-45.如图3-6-4,点A,B,C,D都在⊙ O上,∠ B=90°,AD=3,CD=2,则⊙ O的直径是____ .6.在圆内接四边形ABCD中,∠ A∶∠ B∶∠ C=2∶3∶6,求∠ D的度数.CD.7.如图3-6-5,四边形ABCD内接于⊙ O,AD∥BC,求证:AB=图3-6-5知识点 2 圆内接四边形的性质的推论——圆内接四边形的外角等于其内对角8.2017·嵊州市模拟如图3-6-6,点A,B,C,D在圆O上,点 E 在AD的延长线上,若∠ ABC=60°,则∠ CDE的度数为( )A.30°B.45°C.60°D.70°9.如图3-6-7,四边形ABCD内接于⊙ O,点E在BC的延长线上,若∠ BOD=120°,则∠DCE=___ °.10.如图3-6-8 所示,已知A,B,C,D是⊙O上的四点,延长DC,AB相交于点 E. 若BC=BE.求证:△ ADE是等腰三角形.图3-6-6图3-6-811.如图3-6-9,△ ABC 内接于⊙ O ,∠ OBC =40°,则∠ A 的度数为 ( ) A .80° B .100° C .110° D .130°12.如图 3-6-10,在平面直角坐标系中, ⊙C 过原点 O ,且与两坐标轴分别交于点 A ,B , 点 A 的坐标为(0,3),M 是O ︵B 上一点,且在第三象限内.若∠BMO =120°,则⊙C 的半径为 ()A .6B .5C .3 2D .313.如图 3-6-11,已知四边形 ABCD 内接于半径为 4的⊙O 中,且∠C =2∠A ,则 BD =图 3- 6- 11图 3-6-1014.如图3-6-12,在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,求四边形ABCD的面积.图3-6-1215.(1) 已知:如图3-6-13①,四边形ABCD内接于⊙ O,延长BC至点E,则∠A+∠ BCD =180°,∠ DCE=∠A.(2) 依已知条件和(1) 中的结论:如图②,若点 C 在⊙O外,且A,C两点分别在直线BD的两侧.试确定∠ A+∠ BCD 与180°的大小关系;如图③,若点 C 在⊙O内,且A,C两点分别在直线BD的两侧.试确定∠ A+∠ BCD与180°的大小关系.(3) 如图3-6-14,四边形ABCD内接于⊙ O,∠DAB=130°,连结OC,P 是半径OC上任意一点,连结DP,BP,则∠ BPD的度数可能为_____ (写出一个即可).图3-6-14详解详析1.702.60 [解析]∵四边形ABCD内接于⊙ O,∴∠A+∠C=180°.又∵∠A∶∠C=1∶2,∠A=60°.3.130 [解析]∵四边形ABCD是⊙ O的内接四边形,且∠ ABC=115°,∴∠ ADC=180 -∠ ABC=180°-115°=65°,∴∠AOC=2∠ADC=2×65°=130°.4.305. 136.解:∵四边形ABCD是圆内接四边形,∴∠ A+∠ C=180°,∠ B+∠D=180°.∵∠ A∶∠ B∶∠ C=2∶3∶6,设∠ A=2α,∠ B=3α,∠ C=6α,则2α+6α=180°,∴α =22.5 °,∴∠ B=3α =67.5 °,∴∠ D=180°-∠ B=112.5 °.7.证明:∵ AD∥BC,∴∠ A+∠ B=180°.∵四边形ABCD内接于⊙ O,∴∠ A+∠ C=180°,∴∠ B=∠ C,∴ AC=BD,∴AC-AD=BD-AD,即AB=CD,∴AB=CD.8.C [解析]∵四边形ABCD为圆O的内接四边形,∴∠ABC+∠ADC=180°.∵∠CDE+∠ADC=180°,∠ ABC=60°,∴∠CDE=∠ABC=60°.故选 C.9.60 [解析]∵∠BOD=120°,∴∠BAD=60°. 又∠ BAD+∠ BCD=180 =180°,∴∠ DCE=∠ BAD=60°.10.证明:∵ BC=BE,∴∠ E=∠ BCE.∵四边形ABCD是圆内接四边形,∴∠ A+∠ DCB=180°.∵∠BCE+∠DCB=180°,∴∠ A=∠ BCE,则∠ A=∠E,∴AD=DE,∴△ ADE是等腰三角形.11.D [解析]如图,连结OC.∵OB=OC,∴∠OCB=∠OBC=40∴∠ BOC=100∵∠ 1+∠ BOC=360°,,∠DCE+∠ BCD∴∠ 1=260°.1∵∠A=2∠1,∴∠A=130°.故选 D.12.D [解析]∵四边形ABMO内接于⊙ C,∴∠BMO+∠BAO=180°. ∵∠ BMO=120°,∴∠BAO=60°.又∵AO⊥BO,A(0,3),∴AB=2AO=6,∴⊙C的半径为 3.故选 D.13.4 3 [解析]连结OD,OB,过点O作OF⊥BD,垂足为F,∴DF=BF,∠DOF=∠BOF.∵ 四边形ABCD内接于⊙O,∴∠A+∠C=180°.∵∠C =2∠A,∴∠A=60°,∴∠BOD =120°,∴∠ BOF=60°. ∵OB=4,∴ BF=2 3,∴ BD=2BF=4 3.14.解:如图,过点A作AE⊥BC于点E,AF⊥CD于点 F.∵∠ADF+∠ABC=180°(圆内接四边形的对角互补),∠ ABE+∠ ABC=180∴∠ ADF=∠ ABE.在△ AEB与△ AFD中,∠ABE=∠ADF,∠AEB=∠AFD,AB=AD,∴△ AEB≌△ AFD,∴四边形ABCD的面积=四边形AECF的面积,AE=AF. 又∵∠ E=∠AFC=90°,AC=AC,∴Rt△AEC≌Rt△AFC.∵∠ACD=60°,∠AFC=90°,∴∠ CAF=30°.∵AC=1,∴ CF=21,AF=23,15.解:(2) 如图①,连结DE.∵∠ A+∠ BED=180°,∠ BED>∠ BCD,∴∠ A+∠ BCD<180°.如图②,延长DC交⊙ O于点E,连结BE.∵∠ A+∠ E=180°,∠ BCD>∠E,∴∠ A+∠ BCD>180 (3) 答案不唯一,如80∴四边形ABCD的面积=2S△ ACF=12×21CF×AF=11。
专题2.2 圆周角(专项拔高卷)学生版

2023-2024学年苏科版数学九年级上册同步专题热点难点专项练习专题2.2 圆周角(专项拔高卷)考试时间:90分钟试卷满分:100分难度:0.52姓名:___________班级:___________考号:___________题号一二三总分得分评卷人得分一.选择题(共10小题,满分20分,每小题2分)1.(2分)(2022秋•成武县校级期末)如图,点A、B、C、D、E都是⊙O上的点,=,∠D=128°,则∠B的度数为()A.128°B.126°C.118°D.116°2.(2分)(2023•遵义模拟)如图点A,B,C在⊙O上,OA⊥OB,则∠ACB的度数为()A.45°B.50°C.55°D.90°3.(2分)(2023•岷县校级三模)如图,在⊙O中,AB是直径,弦AC=5,∠BAC=∠D.则AB的长为()A.5 B.10 C.5D.104.(2分)(2022秋•邯山区校级期末)将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上.点A,B的读数分别为85°,31°,则∠ACB的度数是()A.28°B.27°C.26°D.56°5.(2分)(2023•泸县校级模拟)如图,四边形ABCD内接于⊙O,AE⊥CB交CB的延长线于点E,若BA平分∠DBE,AD=7,CE=5,则AE=()A.3 B.C.D.6.(2分)(2023•封开县一模)已知:如图OA,OB是⊙O的两条半径,且OA⊥OB,点C在⊙O上,则∠ACB 的度数为()A.45°B.40°C.35°D.50°7.(2分)(2022秋•高邑县期末)将量角器按如图所示的方式放置在三角形纸板上,使点C在半圆上,点A、B的读数分别为86°、30°,则∠ACB的大小为()A.56°B.34°C.29°D.28°8.(2分)(2023•梁溪区模拟)如图,已知四边形ABCD内接于⊙O,=,AD、BC的延长线相交于点E,AF为直径,连接BF.若∠BAF=32°,∠E=40°,则∠CBF的度数为()A.16°B.24°C.12°D.14°9.(2分)(2022秋•九龙坡区校级月考)如图,AB是⊙O的直径,C,D是⊙O上的点,且OC∥BD,AD分别与BC,OC相交于点E,F,有下列结论:①AD⊥BD;②∠AOC=∠AEC;③BC平分∠ABD;④AF=DF;⑤BD =2OF;⑥△CEF≌△BED.其中一定成立的是()A.②④⑤⑥B.①③④⑤C.②③④⑥D.①③⑤⑥10.(2分)(2021•汉阳区校级模拟)如图,AB是半圆O的直径,将半圆沿弦BC折叠,折叠后的圆弧与AB 交于点D,再将弧BD沿AB对折后交弦BC于E,若E恰好是BC的中点,则BC:AB=()A.B.C.D.评卷人得分二.填空题(共10小题,满分20分,每小题2分)11.(2分)(2023•浑江区一模)如图,四边形ABCD内接于⊙O,若∠B=108°,则∠D的度数为.12.(2分)(2023春•兴宁区校级期中)如图,已知⊙O的直径AB=2,点P是弦BC上一点,连接OP,∠OPB=45°,PC=1,则弦BC的长为.13.(2分)(2023•宁江区三模)如图,点A,B,C,D,E都是⊙O上的点,AC=AE,∠D=128°,则∠B =°.14.(2分)(2023•阜新一模)如图,点A,B,C,D,E都在⊙O上,∠BAC=15°,∠CED=30°,则∠BOD =.15.(2分)(2023春•青山区校级月考)如图,四边形ABCD内接于⊙O,AD、BC的延长线相交于点E,AB、DC的延长线相交于点F.若∠A=55°,∠F=30°,则∠E=°.16.(2分)(2023•二道区校级模拟)如图,四边形ABCD内接于⊙O,延长CO交⊙O于点E,连接BE,若∠A=100°,∠E=60°,则∠OCD的大小为°.17.(2分)(2022秋•盘山县期末)如图,AB是⊙O的直径,∠BCD=34°,则∠ABD的度数为.18.(2分)(2022秋•沈河区校级期末)如图,已知以BC为直径的⊙O,A为弧BC中点,P为弧AC上任意一点,AD⊥AP交BP于D,连CD.若BC=6,则CD的最小值为.19.(2分)(2022秋•大丰区期中)如图,△ABC中,AD⊥BC,∠B=45°,∠C=30°.以AD为弦的圆分别交AB、AC于E、F两点.点G在AC边上,且满足∠EDG=120°.若CD=4+2,则△DEG的面积的最小值是.20.(2分)(2021秋•斗门区期末)如图,点D为边长是4的等边△ABC边AB左侧一动点,不与点A,B 重合的动点D在运动过程中始终保持∠ADB=120°不变,则四边形ADBC的面积S的最大值是.评卷人得分三.解答题(共8小题,满分60分)21.(6分)(2022秋•新抚区期末)如图,已知AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连接AC、OC、BC.(1)若∠ACO=25°,求∠BCD的度数.(2)若EB=4cm,CD=16cm,求⊙O的半径.22.(6分)(2022秋•常州期末)如图,在△ABC中,∠ACB=90°,AB=5,BC=3,点D在AB的延长线上,且BD=3,过点D作DE⊥AD,交AC的延长线于点E,以DE为直径的⊙O交AE于点F.(1)求⊙O的半径;(2)连接CD,交⊙O于点G,求证:G是CD的中点.23.(8分)(2023•安徽二模)如图,已知:AB是⊙O的直径,点C在圆上,AB=10,AC=6,点C、E分别在AB两侧,且E为半圆AB的中点.(1)求△ABC的面积;(2)求CE的长.24.(8分)(2022秋•烟台期末)如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E.(1)求证:∠BCO=∠D;(2)若CD=4,OE=1,求⊙O的半径.25.(8分)(2022秋•蜀山区校级期末)如图,以AB为直径的⊙O经过△ABC的顶点C,AE,BE分别平分∠BAC和∠ABC,AE的延长线交⊙O于点D,连接BD,CD.(1)求证:DB=DE;(2)若,,求BC的长.26.(8分)(2023•方城县模拟)如图,已知四边形ABCD内接于圆O,AC为圆O的直径,∠BAC=∠ADB.(1)试说明△ABC的形状;(2)若,.①求CD的长度;②将△ABD沿BD所在的直线折叠,点A的对应点是A′,连接BA′、CA′,直接写出∠BA′C的度数.27.(8分)(2023•遵义一模)如图,AB是⊙O的直径,C是⊙O上的一点,且OC⊥AB于点O,点D是的中点,连接AD交OC于M,连接BD,CD.(1)∠DAB的度数为度.(2)求证:DC=DM;(3)过点C作CE⊥AD于点E,若BD=,求ME的长.28.(8分)(2022•芙蓉区模拟)如图,AB=4,点P是⊙O上一点(不与点A、B重合),PC平分∠APB交⊙O于点C,交AB于点D,∠BAC=60°.(1)连接OA,OB,求∠AOB的度数;(2)求DC•PC的值;(3)若设AP+BP=x,△PAB的面积为y,求y关于x的函数解析式,并写出自变量x的取值范围.。
(完整)圆内接四边形拔高练习题

圆内接四边形一.选择题1.如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA、CB分别交半圆于点D,E 若△CDE的面积与四边形ABED的面积相等,则∠C等于()A.30°B.40°C.45°D.60°二.填空题2.如图,四边形ABCD中,AB=AC=AD,若∠CAD=76°,则∠CBD=_________度.3.如图,在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边形的面积为_________.三.解答题4.已知:⊙O的直径AB和弦CD,且AB⊥CD于E,F为DC延长线上一点,连接AF交⊙O于M.求证:∠AMD=∠FMC.5.如图1,已知△ABC,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.(1)求证:DE=DC.(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系.6.设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C 及D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.7.已知:如图1,四边形ABCD内接于⊙O,AC⊥BD于点P,OE⊥AB于点E,F为BC 延长线上一点.(1)求证:∠DCF=∠DAB;(2)求证:;(3)当图1中点P运动到圆外时,即AC、BD的延长线交于点P,且∠P=90°时(如图2所示),(2)中的结论是否成立?如果成立请给出你的证明,如果不成立请说明理由.8.如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.9.如图,圆内接四边形ABCD的两组对边延长线分别交于E、F,∠AEB、∠AFD的平分线交于P点.求证:PE⊥PF.10.如图,P是等边△ABC外接圆上任意一点,求证:PA=PB+PC.。
非学科数学学培训 圆内第四大定理之圆内接四边形(资料附答案)

自学资料一、圆内接四边形【知识探索】1.如果一个多边形的所有顶点都在同一个圆上,这个多边形叫做圆内接多边形.这个圆叫做这个多边形的外接圆.2.圆内接四边形的对角互补.【错题精练】例1.如图,四边形ABCD的对角线CA平分∠BCD且AD=AB,AE⊥CB于E,点O为四边形ABCD的外接圆的圆心,下列结论:①OA⊥DB;②CD+CB=2CE;③∠CBA−∠DAC=∠ACB;④若∠DAB= 90∘,则CD+CB=√3CA.其中正确的结论()第1页共25页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训A. ①③④;B. ①②④;C. ②③④;D. ①②③.【答案】D,例2.如图,等腰△ABC内接于⊙O,已知AB=AC,∠ABC=30∘,BD是⊙O的直径,如果CD=4√33则AD=.【答案】4.的值是例3.如图,正方形ABCD和正△AEF都内接于⊙O,EF与BC、CD分别相交于点G、H,则EFGH ()A. ;B. ;C. ;D. 2.【答案】C例4.如图,两正方形彼此相邻且内接于半圆,若小正方形的面积为16cm2,则该半圆的半径为第2页共25页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训().A. cmB. 9 cmC. cmD. cm【解答】C【答案】C例5.如图,四边形ABCD内接于⊙O,BC=CD,∠C=2∠BAD.(1)求∠BOD的度数;(2)求证:四边形OBCD是菱形;(3)若⊙O的半径为r,∠ODA=45∘,求△ABD的面积(用含r的代数式表示).【解答】(1)解:∠A+∠C=180,∠C=2∠A,∴∠A=60∘,∴∠BOD=2∠A=120∘(2)证明:连接OB,OC,OD,可以得出△BOC是等边三角形,∴OB=OC=OD=CD,∴四边形OBCD是菱形;(3)解:过D做DH⊥AB与H,∵DH=√62r,BH=√62r,AH=√22r,∴S△ABD=3+√34r2.第3页共25页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训【答案】(1)∠BOD=2∠A=120∘;(2)略;(3)S△ABD=3+√3r2.4例6.如图,已知四边形ABCD内接于圆,对角线AC与BD相交于点E,F在AC上,AB=AD,∠BFC=∠BAD=2∠DFC.(1)若∠DFC=40∘,求∠CBF的度数;(2)求证:CD⊥DF.【解答】(1)解:∵∠ADB=∠ACB,∠BAD=∠BFC,∴∠ABD=∠FBC,又∵AB=AD,∴∠ABD=∠ADB,∴∠CBF=∠BCF,∵∠BFC=2∠DFC=80°,∴∠CBF=50∘;(2)证明:令∠CFD=α,则∠BAD=∠BFC=2α,∵四边形ABCD是圆的内接四边形,∴∠BAD+∠BCD=180°,即∠BCD=180∘−2α,又∵AB=AD,∴∠ACD=∠ACB,∴∠ACD=∠ACB=90∘−α,∴∠CFD+∠FCD=α+(90∘−α)=90°,∴∠CDF=90°,即CD⊥DF.【答案】(1)∠CBF=50∘;(2)CD⊥DF.例7.如图,在圆内接四边形ABCD中,CD为∠BCA的外角的平分线,F为弧AD上一点,BC=AF,延长DF与BA的延长线交于E.第4页共25页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训(1)求证:△ABD为等腰三角形.(2)求证:AC⋅AF=DF⋅FE.【解答】(1)证明:∵四边形ABCD是圆O的内接四边形,∴∠DCB+∠DAB=180∘,∵∠MCD+∠DCB=180∘,∴∠MCD=∠DAB,∵CD为∠BCA的外角的平分线,∴∠MCD=∠ACD,∵∠DCA和∠DBA都对弧AFD,∴∠DCA=∠DBA,∴∠DAB=∠DBA,∴DB=DA,∴△ABD为等腰三角形.(2)证明:由(1)知AD=BD,BC=AF,则弧AFD=弧BCD,弧AF=弧BC,∴∠BDC=∠ADF,弧CD=弧DF,CD=DF①∴∠BDC+∠BDA=∠ADF+∠BDA,即∠CDA=∠BDF,而∠FAE+∠BAF=∠BDF+∠BAF=180∘,∴∠FAE=∠BDF=∠CDA,同理∠DCA=∠AFE∴在△CDA与△FAE中,∠CDA=∠FAE,∠DCA=∠AFE,∴△CDA∽△FAE,∴即CD⋅EF=AC⋅AF,又由①有AC⋅AF=DF⋅EF.【答案】(1)略;(2)略.例8.如图,△ABC是⊙O的内接三角形,AC=BC,D为⊙O中弧AB上一点,延长DA至点E,使CE=CD.(1)求证:AE=BD;(2)若AC⊥BC,求证:AD+BD=CD.第5页共25页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训【答案】例9.(1)已知:如图1,四边形ABCD内接于⊙O,延长BC至E.求证:∠A+∠BCD=180°,∠DCE=∠A.(2)依已知条件和(1)中的结论:①如图2,若点C在⊙O外,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系;②如图3,若点C在⊙O内,且A、C两点分别在直线BD的两侧.试确定∠A+∠BCD与180°的大小关系.第6页共25页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【解答】【答案】见解析例10.如图1,已知△ABC,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.(1)求证:DE=DC.(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC 的延长线于点G.试探究线段DF、DG的数量关系.【答案】(1)证明:∵四边形ABDE内接于⊙O,第7页共25页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训第8页共25页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【解答】第9页共25页自学七招之智慧树神拳:知识内容体系化,思维导图来助力非学科培训第10页共25页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【答案】【举一反三】1.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE.若∠D=78∘,则∠EAC=度.【答案】27.2.如图,四边形ABCD是菱形,⊙O经过点A、C、D,与BC相交于点E,连接AC、AE,若∠D=78∘,则∠EAC=()A. 37°;B. 32°;C. 21°;D. 18.5°.【答案】C.3.已知,如图:AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°.给出以下四个结论:①∠EBC=22.5°;②AE=2EC;③劣弧AE是劣弧DE的2倍;④DE=DC.其中不正确结论的序号是()A. ①B. ④C. ③D. ②【解答】【答案】D4.如图,已知四边形ABEC内接于⊙O,点D在AC的延长线上,CE平分∠BCD交⊙O于点E,则下列结论中一定正确的是()A. AB=AEB. AB=BEC. AE=BED. AB=AC【解答】【答案】C5.已知△ABC.(1)如图,AC⊥AB,点D为BC上一点,∠ABD=∠BAD,∠EAC=∠CAD,求证:AE∥BC.(2)如图,点P是BC上一点,且∠APC<90°,以AP为一边作正方形APMN,若NC⊥BC,则∠ACB= °,并证明你的结论.【答案】6.已知如图,四边形ABCD内接于⊙O,直径AF⊥BC于点H,AD与BC的延长线交于点E,连接BD.(1)若BC=8,FH=2,求⊙O得半径长;(2)若∠EDC=70∘,求∠ADB的度数.【解答】(1)解:由垂径定理得BH=4,OH=r−2,由勾股得:r=5;(2)解:连接AC,由垂径定理得:AB=AC,∴∠ABC=∠ACB,∵∠EDC=70∘,∴∠ABC=∠ACB=70∘,∵∠ADB=∠ACB,∴∠ADB=70∘.【答案】(1)5;(2)70°.7.如图,在半径为5的扇形AOB中,∠AOB=90°,点C是弧AB上的一个动点(不与点A、B重合)OD⊥BC,OE⊥AC,垂足分别为D、E.(1)当BC=6时,求线段OD的长;(2)在△DOE中是否存在长度保持不变的边?如果存在,请指出并求其长度;如果不存在,请说明理由.【答案】8.如图,⊙M交x轴于B、C两点,交y轴于A,点M的纵坐标为2.B(-3,0),C(,0))(1)求⊙M的半径;(2)若CE⊥AB于H,交y轴于F,求证:EH=FH.(3)在(2)的条件下求AF的长.【答案】9.如图,△ABC中,E、F分别是AB、AC上的点.①AD平分∠BAC,②DE⊥AB,DF⊥AC,③AD⊥EF.以此三个中的两个为条件,另一个为结论,可构成三个命题,即:(1)试判断上述三个命题是否正确(直接作答);(2)请证明你认为正确的命题.【解答】【答案】见解析10.已知△ABC中,AB=AC,以AB为直径的圆O交BC于D,交AC于E,(1)如图①,若AB=6,CD=2,求CE的长;(2)如图②,当∠A为锐角时,使判断∠BAC与∠CBE的关系,并证明你的结论;(3)若②中的边AB不动,边AC绕点A按逆时针旋转,当∠BAC为钝角时,如图③,CA的延长线与圆O相交于E.请问:∠BAC与∠CBE的关系是否与(2)中你得出的关系相同?若相同,请加以证明,若不同,请说明理由.【解答】【答案】见解析11.我们学过圆内接三角形,同样,四个顶点在圆上的四边形是圆内接四边形,下面我们来研究它的性质.(I)如图(1),连接AO、OC,则有.∴,同理∠BAD+∠BCD=180°,即圆内接四边形对角(相对的两个角)互补.(II)在图(2)中,∠ECD是圆内接四边形ABCD的一个外角,请你探究外角∠DCE与它的相邻内角的对角(简称内对角)∠A的关系,并证明∠DCE与∠A的关系.(III)应用:请你应用上述性质解答下题:如图(3)已知ABCD是圆内接四边形,F、E分别为BD、AD延长线上的点,如果DE平分∠FDC,求证:AB=AC.【解答】【答案】见解析1.如图,已知⊙O中,直径MN=10,正方形ABCD的四个顶点分别在半径OM、OP以及⊙O上,并且∠POM=45∘,试求AB的长.【解答】解:∵ABCD是正方形,∴∠DCO=90∘.∵∠POM=45∘,∴∠CDO=45∘.∴CD=CO.∴BO=BC+CO=BC+CD.∴BO=2AB.连接AO,∵MN=10,∴AO=5.在Rt△ABO中,AB2+BO2=AO2,AB2+(2AB)2=52,解得:AB=√5,则AB的长为√5.【答案】√5.2.如图所示,⊙O的直径AB长为6,弦AC长为2,∠ACB的平分线交⊙O于点D,求四边形ADBC的面积.【解答】解:∵AB是直径,∴∠ACB=∠ADB=90∘.在Rt△ABC中,AB=6,AC=2,∴BC=√AB2−AC2=√62−22=4√2.∵∠ACB的平分线交⊙O于点D,∴∠DCA=∠BCD.∴.∴AD=BD.∴在Rt△ABD中,AD=BD=3√2,AB=6.∴四边形ADBC的面积=S△ABC+S△ABD=12AC⋅BC+12AD⋅BD=12×2×4√2+12×3√2×3√2=9+4√2.故四边形ADBC的面积是9+4√2.【答案】9+4√2.3.(2015秋•嵊泗县期中)如图①、②、③,正三角形ABC、正方形ABCD、正五边形ABCDE分别是⊙O的内接三角形、内接四边形、内接五边形,点M、N分别从点B、C开始,以相同的速度在⊙O上逆时针运动.(1)求图①中∠APN的度数(写出解题过程);(2)写出图②中∠APN的度数和图③中∠APN的度数;(3)试探索∠APN的度数与正多边形边数n的关系(直接写答案)【解答】【答案】。
浙教版九年级数学上册《3.6圆内接四边形》同步练习题带答案
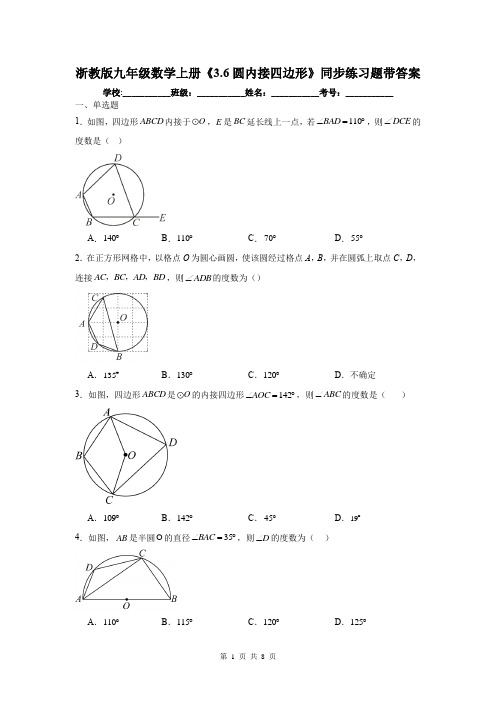
浙教版九年级数学上册《3.6圆内接四边形》同步练习题带答案学校:___________班级:___________姓名:___________考号:___________一、单选题1.如图,四边形ABCD 内接于O ,E 是BC 延长线上一点,若110BAD ∠=︒,则DCE ∠的度数是( )A .140︒B .110︒C .70︒D .55︒2.在正方形网格中,以格点O 为圆心画圆,使该圆经过格点A ,B ,并在圆弧上取点C ,D ,连接AC BC AD BD ,,,,则ADB ∠的度数为()A .135︒B .130︒C .120︒D .不确定3.如图,四边形ABCD 是O 的内接四边形142AOC ∠=︒,则ABC ∠的度数是( )A .109︒B .142︒C .45︒D .19︒4.如图,AB 是半圆O 的直径35BAC ∠=︒,则D ∠的度数为( )A .110︒B .115︒C .120︒D .125︒5.如图,点A ,B ,C 、D 四点均在O 上68AOD ∠=︒,AO DC ∥则B ∠的度数为( )A .62︒B .56︒C .34︒D .54︒6.如图,四边形ABCD 内接于O ,AB=BC ,连接OA ,OB .若60AOB ∠=︒,则D ∠=( )A .40︒B .60︒C .45︒D .30︒7.如图,四边形ABCD 内接于O ,如果它的一个外角64DCE ∠=︒,那么BOD ∠=( )A .128︒B .100︒C .120︒D .132︒8.如图,四边形ABCD 内接于O ,点C 是BD 的中点40A ∠=︒,则CBD ∠的度数为( )A .20︒B .25︒C .30°D .35︒9.若等腰ABC 内接于O ,AB=AC ,100BOC ∠=︒则ABC 底角的度数为( ) A .65︒B .25︒C .65︒或25︒D .65︒或35︒10.如图,AB 是O 的弦,OC AB ⊥交O 于点C ,点D 是O 上一点,连接BD ,CD .若25CDB ∠=︒,则ACB ∠的度数为( )A .100︒B .155︒C .130︒D .125︒二、填空题11.如图,点A ,B ,C 在O 上,若128AOB ∠=︒,则C ∠= .12.如图,点A ,B ,C ,D 在O 上,若25CAD ∠=︒,55ABD ∠=︒则ADC ∠= 度.13.已知半径为2的O 中,弦2AB =,则弦AB 所对的圆周角P ∠= .14.如图,在O 中,AB 为直径,点C 为圆上一点,将劣弧沿弦AC 翻折交AB 于点D ,连接CD .如果6AD =,2DB =则AC 的长为 .15.如图,O 过四边形ABCD 的四个顶点,已知90ABC ∠=︒,BD 平分ABC ∠,1,2AB BC ==则BD = .三、解答题16.如图,在O 的内接四边形ABCD 中AB CD = AB CD ∥. 求证:四边形ABCD 是矩形.17.(1)如图1,在等边三角形ABC 中,AB=6,点D 是线段BC 上的一点,CD=4,连接AD ,将线段AD 绕点A 逆时针旋转60︒后得到AE ,连接CE 、DE .求CE 的长(2)如图2,ABC 是等边三角形,且点A ,B ,C 三点都在O 上,点D 是BC 上任一点,求证:DB DC DA +=.18.O 的半径OA ⊥弦BC ,点D 在O 上(不与点A 、B 、C 重合) 70AOC ∠=︒.(1)如图,当点D 在优弧BC 上时,求ADB ∠的度数;(2)若点D 在劣弧BC 上,则ADB ∠的度数为________.19.如图,在ABC 中90A B α∠=︒∠=,,点D ,E 分别在AB ,BC 上,线段DE 绕点D 顺时针旋转得到DF ,其中旋转角1802EDF α∠=︒-,此时点F 恰好落在AC 上,过点D ,E ,F 的圆交BC 于点G ,连接GF .(1)若35α=︒,求BGF ∠的度数; (2)求证:BE GF =.题号 1 2 3 4 5 6 7 8 9 10 答案 BAADB BAACC11.116︒ 12.100 13.30︒或150︒ 14.14153216证明:⊥AB CD = AB CD ∥⊥四边形ABCD 是平行四边形 180A D ∠+∠=︒ ⊥AD BC ∥ ⊥180A B ∠+∠=︒ ⊥B D ∠=∠⊥四边形ABCD 是O 的内接四边形 ⊥180B D ∠+∠=︒ ⊥90B D ∠=∠=︒⊥平行四边形ABCD 是矩形.17.解:(1)在等边ABC 中,AB=6,点D 是线段BC 上的一点,CD=4 ⊥6AC BC AB === 60BAC ∠=︒⊥642BD BC CD =-=-=将AD 绕点A 逆时针旋转60︒后得到AE ⊥AD AE = 60DAE ∠=︒ ⊥BAD DAC DAC CAE ∠+∠=∠+∠ ⊥BAD CAE ∠=∠ 在ABD △和ACE △中AD AE BAD CAE AB AC =⎧⎪∠=∠⎨⎪=⎩⊥()SAS ABD ACE ≌ ⊥2CE BD ==;(2)证明:如图,将ACD 绕点A 顺时针旋转60︒得到ABE⊥ACD ABE ∠=∠ DC BE = ⊥180ACD ABD ∠+∠=︒ ⊥180ABE ABD ∠+∠=︒ ⊥D 、B 、E 三点共线由旋转得:60DAE ∠=︒ AD AE = ⊥ADE 是等边三角形 ⊥AD DE = ⊥DE BD BE =+ ⊥DB DC DA +=. 18.(1)解:连接OB⊥半径OA ⊥弦BC ⊥AB AC =⊥70AOB AOC ∠=∠=︒ ⊥1352ADB AOB ∠=∠=︒ (2)解:当点D 在AB 上时由(1)知⊥135AD B ∠=︒⊥四边形1ADBD 是圆的内接四边形 ⊥1180145ADB AD B ∠=︒-∠=︒ 当点D 在AC 上时则1352ADB AOB ∠=∠=︒综上,ADB ∠的度数为145︒或35︒. 故答案为:145︒或35︒. 19.(1)解:⊥35α=︒ ⊥()180235110EDF ∠=-⨯︒=︒⊥18070BGF EDF ∠=︒-∠=︒; (2)证明:连接DG⊥()1802EDF α∠=-︒ ⊥1802EGF EDF α∠=︒-∠= ⊥DE DF = ⊥DE DF =⊥12EGD FGD EGF α∠=∠=∠=⊥B α∠= ⊥B FGD ∠=∠⊥180GED GFD ∠+∠=︒ 又⊥180GED BED ∠+∠=︒ ⊥GFD BED ∠=∠ ⊥()AAS BDE GDF ≌ ⊥BE GF =.。
九年级下册圆形拔高习题(较难及难题)(含解析)(可编辑修改word版)

九年级下册圆形拔高习题(较难及难题)(含解析)(可编辑修改word版)九年级下册圆形拔高习题(中等及较难)一、选择题1、如图,Rt△ABC 中,AB⊥BC,AB=6,BC=4,P 是△ABC 内部的一个动点,且满足∠PAB=∠PBC,则线段 CP 长的最小值为( )A .B .2C .D .2、如图,⊙O 是△ABC 的外接圆,∠BOC=3∠AOB,若∠ACB=20°,则∠BAC 的度数是( )A .120°B .80°C .60°D .30°3、如图,AB 为⊙O的直径,点C 在⊙O上,若∠OCA=50°,AB=4,则的长为( )A . πB . πC . πD . π4、如图所示,AB 是⊙O的直径,点 C 为⊙O外一点,CA,CD 是⊙O的切线,A,D 为切点,连接 BD,AD.若∠ACD=30°,则∠DBA的大小是( )B .30°C .60°D .75°5、如图,圆 O 是Rt△ABC的外接圆,∠ACB=90°,∠A=25°,过点 C 作圆 O 的切线,交 AB 的延长线于点 D,则∠D的度数是 ( )A .25°B .40°C .50°D .65°6、如图,在⊙O中,AB 是直径,点 D 是⊙O上一点,点 C 是弧AD 的中点,弦CE⊥AB于点 E,过点 D 的切线交 EC 的延长线于点 G,连接 AD,分别交 CE、CB 于点 P、Q,连接 AC.给出下列结论:①∠BAD=∠ABC;②AD=CB;③点 P 是△ACQ的外心;④GP=GD;⑤CB∥GD.其中正确结论的序号是()A.①②④B.②③⑤C.③④D.②⑤7、一个直角三角形的斜边长为8,内切圆半径为1,则这个三角形的周长等于( )A .21B .20C .19D .188、如图,△ABC 是圆O 的内接三角形,且AB≠AC,∠ABC 和∠ACB 的平分线,分别交圆 O 于点 D ,E ,且 BD=CE ,则∠A 等于()B .60°C .45°D .30°9、如图,半径为 5 的⊙O 中,弦 AB ,CD 所对的圆心角分别是∠AOB,∠COD.已知AB=8,∠AOB+∠COD=180°,则弦CD 的弦心距等于()B .3D .4 A .C .10、如图,AB 是半圆 O 的直径,AC 为弦,OD⊥AC 于 D ,过点 O 作OE∥AC 交半圆 O 于点 E ,过点 E 作EF⊥AB 于 F ,若AC=4,则 OF 的长为( )D .411、如图,正方形 ABCD 的边长为 1,将长为 1 的线段 QR 的两端放在正方形相邻的两边上同时滑动.如果点Q 从点A 出发,按A→B→C→D→A 的方向滑动到A 停止,同时点R 从点B 出发,按B→C→D→A→B 的方向滑动到 B 停止,在这个过程中,线段 QR 的中点 M 所经过的路线围成的图形面积为()A. B.4-πC .πD .A .1B .C .2二、填空题12、如图,点 C 在以AB 为直径的半圆上,AB=4,∠CBA=30°,点D 在AO 上运动,点 E 与点D 关于AC 对称:DF⊥DE于点D,并交 EC 的延长线于点 F,下列结论:①CE=CF;②线段EF 的最小值为;③当 AD=1 时,EF 与半圆相切;④当点D 从点A 运动到点O 时,线段EF 扫过的面积是4.其中正确的序号是.13、如图,P 是等边三角形ABC 内一点,将线段AP 绕点A 顺时针旋转60°得到线段AQ,连接BQ.若PA=6,PB=8,PC=10,则四边形APBQ 的面积为.14、已知正三角形的面积是cm,则正三角形外接圆的半径是cm.15、如图,四边形ABCD 为⊙O的内接四边形,已知∠C=∠D,则AB 与CD 的位置关系是.16、如图,四边形 ABCD 内接于⊙O,AB 是直径,过 C 点的切线与 AB 的延长线交于 P 点,若∠P=40°,则∠D 的度数为.三、解答题17、如图,圆心角∠AOB=120°,弦AB=2 cm.(1)求⊙O的半径 r;(2)求劣弧的长(结果保留π).18、在△ABC 中,CE,BD 分别是边 AB,AC 上的高,F 是 BC 边上的中点.(1)指出图中的一个等腰三角形,并说明理由.(2)若∠A=x°,求∠EFD的度数(用含 x 的代数式表达).(3)猜想∠ABC和∠EDA的数量关系,并证明.19、如图,直线 AB 经过⊙O上的点 C,直线 AO 与⊙O交于点E 和点D,OB 与OD 交于点F,连接DF,DC.已知OA=OB,CA=CB,DE=10,DF=6.(1)求证:①直线 AB 是⊙O的切线;②∠FDC=∠EDC;(2)求CD 的长.20、如图,AB 是⊙O 的直径,点 C、D 在⊙O 上,∠A=2∠BCD,点 E 在 AB 的延长线上,∠AED=∠ABC(1)求证:DE 与⊙O相切;(2)若BF=2,DF= ,求⊙O的半径.21、如图,在△ABC中,∠C=90°,∠BAC的平分线交 BC 于点D,点O 在AB 上,以点 O 为圆心,OA 为半径的圆恰好经过点D,分别交 AC,AB 于点E,F.(1)试判断直线 BC 与⊙O的位置关系,并说明理由;(2)若BD=2 ,BF=2,求阴影部分的面积(结果保留π).22、如图1,在△ABC 中,点D 在边BC 上,∠ABC:∠ACB:∠ADB=1:2:3,⊙O 是△ABD 的外接圆.(1)求证:AC 是⊙O的切线(2)当BD 是⊙O的直径时(如图 2),求∠CAD的度数.23、如图,AB 为⊙O的直径,点E 在⊙O上,C 为的中点,过点C 作直线CD⊥AE于D,连接AC,BC.(1)试判断直线 CD 与⊙O的位置关系,并说明理由;(2)若AD=2,AC= ,求AB 的长。
圆的内接四边形(拔高训练)(有答案)

第3课时圆内接四边形重点:圆内接四边形对角互补。
习题精练1、下列关于圆内接四边形叙述正确的有()①在圆内部的四边形叫圆内接四边形;②圆内接四边形的对角相等;③圆内接四边形中不相邻的两个内角互补;④圆内接四边形的一个外角等于它的相邻内角的对角。
A、1个B、2个C、3个D、4个2、如图所示,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是()A、80°B、120°C、100°D、90°3、四边形ABCD内接于⊙O,则∠A:∠B:∠C:∠D的值可以是()A、1:2:3:4B、1:3:2:4C、1:4:2:3D、1:2:4:34、如图,四边形ABCD内接于⊙O,DA=DC,∠CBE=50°,则∠DAC的大小为()A、130°B、100°C、65°D、50°5、如图,A、B、C在⊙O上,∠AOB=22.5°,则∠ACB的度数是_________.6、如图,正方形ABCD 的四个顶点分别在⊙O 上,点P 为CD⌒ 上不同于点C 、D 的任意一点,则∠DPC 的度数是_________.7、如图,四边形ABCD 内接于⊙O ,∠DAE 是四边形ABCD 的一个外角,且AD 平分∠CAE 。
求证:DB=DC 。
拓展提升8、如图,四边形ABCD 为⊙O 的内接四边形,延长AB 与DC 相交于点G ,AO ⊥CD ,垂足为E ,连接BD ,∠GBC=50°,则∠DBC 的度数为( )A 、50°B 、60°C 、80°D 、90°第8题 第9题9、如图,在△ABC 中,∠ACB=90°,过B 、C 两点的⊙O 交AC 于点D ,交AB 于点E ,连接EO 并延长交⊙O 于点F ,连接BF ,CF ,若∠EDC=135°,22=CF ,则22BE AB +的值为( )A 、8B 、12C 、16D 、2010、如图,在⊙O 的内接五边形ABCDE 中,∠CAD=35°,则∠B+∠E=_______°.11、如图,AB ,CD 是⊙O 的弦,AB ⊥CD ,BE 是⊙O 的直径,若AC=3,则DE=________.12、如图,正方形ABCD 内接于⊙O ,在劣弧AB 上取一点E ,连接DE ,BE ,过点D 作DF//BE 交⊙O 于点F ,连接BF ,AF ,且AF 与DE 相交于点G ,求证:(1)四边形EBFD 是矩形;(2)DG=BE 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆内接四边形
一.选择题
1.如图,AB是半圆的直径,O是圆心,C是半圆外一点,CA、CB分别交半圆于点D,E 若△CDE的面积与四边形ABED的面积相等,则∠C等于()
A.30°B.40°C.45°D.60°
二.填空题
2.如图,四边形ABCD中,AB=AC=AD,若∠CAD=76°,则∠CBD=_________度.
3.如图,在圆内接四边形ABCD中,AB=AD,AC=1,∠ACD=60°,则四边形的面积为_________.
三.解答题
4.已知:⊙O的直径AB和弦CD,且AB⊥CD于E,F为DC延长线上一点,连接AF交⊙O于M.求证:∠AMD=∠FMC.
5.如图1,已知△ABC,AB=AC,以边AB为直径的⊙O交BC于点D,交AC于点E,连接DE.
(1)求证:DE=DC.
(2)如图2,连接OE,将∠EDC绕点D逆时针旋转,使∠EDC的两边分别交OE的延长线于点F,AC的延长线于点G.试探究线段DF、DG的数量关系.
6.设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C 及D、E,直线EB及CD分别交MN于P、Q.
求证:AP=AQ.
7.已知:如图1,四边形ABCD内接于⊙O,AC⊥BD于点P,OE⊥AB于点E,F为BC 延长线上一点.
(1)求证:∠DCF=∠DAB;
(2)求证:;
(3)当图1中点P运动到圆外时,即AC、BD的延长线交于点P,且∠P=90°时(如图2所示),(2)中的结论是否成立?如果成立请给出你的证明,如果不成立请说明理由.
8.如图,已知ABCD是圆O的内接四边形,AB=BD,BM⊥AC于M,求证:AM=DC+CM.
9.如图,圆内接四边形ABCD的两组对边延长线分别交于E、F,∠AEB、∠AFD的平分线交于P点.求证:PE⊥PF.
10.如图,P是等边△ABC外接圆上任意一点,求证:PA=PB+PC.。
