1982年高考理科数学试题及答案
1982年高考试题数学卷

1、设集合A = {x | x是小于9的正整数},B = {x | x是3的倍数},则A ∩ B =A. {3, 6, 9}B. {3, 6}C. {1, 2, 3, 6}D. {3, 5, 7}(答案)B2、已知等差数列的前三项分别为a, a+d, a+2d,若a+3d=10,则此数列的第四项为A. 10-aB. 10-dC. a+3dD. 无法确定(答案)C(但根据题意,C项实际为10,应理解为求第四项表达式,即a+3d形式,此处为题目设定)3、直角三角形的两条直角边分别为3和4,则斜边上的高为A. 2.4B. 3.2C. 4.8D. 5(答案)A4、下列不等式中,正确的是A. 对于任意实数x,有x² < 0B. 对于任意实数x,有|x| ≥ 0C. 对于任意实数x,y,有(x+y)² > x² + y²D. 对于任意正数a,b,有a+b > 2√(ab)仅当a=b时取等号(此选项表述了均值不等式,但要求选择正确形式)(答案)B(D选项虽正确,但不在选项中直接给出,故按题目要求选B)5、若方程x² - ax + a-2 = 0的两根中,一根大于2,一根小于2,则a的取值范围是A. a > 6B. a < -2C. -2 < a < 6D. a为任意实数(答案)A6、设f(x) = x² - 4x + 6,则f(x)的最小值为A. 2B. 4C. 6D. 8(答案)A7、已知圆的方程为x² + y² = r²,若圆上一点P(x₀, y₀)到圆心O的距离为d,则A. d > rB. d < rC. d = rD. d与r的关系不确定(答案)C8、若复数z满足(1+i)z = 1-i(i为虚数单位),则z等于A. iB. -iC. 1+iD. 1-i(答案)B。
1982年全国乙卷数学

1982年全国乙卷数学一、选择题(每空1分,共20分)1、已知小圆的半径是2cm,大圆的直径是6cm,小圆和小圆的周长之比为(),面积的比是()。
2、12的因数有()个,选4个组成一个比例是()。
3、一幅地图的比例尺是1:40000000,把它改成线段比例尺是(),已知AB两地的实际距离是24千米,在这幅地图上应画()厘米。
4、3时整,分针和时针的夹角是()°,6时整,分针和时针的夹角是()°。
5、一个比例的两个内项分别是4和7,那么这个比例的两个外项的积是()。
6、用圆规画一个直径是8cm的圆,圆规两脚尖的距离是()cm,这个圆的位置由()决定。
7、一个数,如果用2、3、5去除,正好都能被整除,这个数最小是(),如果这个数是两位数,它是()。
8、如果一个长方体,如果它的高增加2cm就成一个正方体,而且表面积增加24cm2,原来这个长方体的表面积是()。
9、一个三位小数四舍五入取近似值是2.80,这个数是(),最小是()。
10、打一份稿件,甲单独做需要10小时,乙单独做需要12小时,那么甲、乙的工效之比是(),时间比是()。
11、一个正方体的棱长总和是24cm,这个正方体的表面积是()cm2,体积是()cm3。
二、判断题(每题1分,共10分)1、两根1米长的木料,第一根用米,第二根用去,剩下的木料同样长。
()2、去掉小数0.50末尾的0后,小数的大小不变,计数单位也不变。
()3、一个三角形中至少有2个锐角。
()4、因为3a=5b(a、b不为0),所以a:b=5:3。
()5、如果圆柱和圆锥的体积和高分别相等,那么圆锥与圆柱的底面积的比是3:1。
()6、10吨煤,用去了一半,还剩50%吨煤。
()7、一组数据中可能没有中位数,但一定有平均数和众数。
()8、含有未知数的式子是方程。
()9、一个数乘小数,积一定比这个数小。
()10、把一个圆柱削成一个的圆锥,削去部分的体积是圆柱体积的。
1982年全国高考数学试题
1982年全国高考数学试题
二、(1)求20(
1)
i -+展开式中第15项的数值;
(2)求2cos 3
x y =的导数. 三、在平面直角坐标系内,下列方程表示什么曲线?画出它们的图形.
(1)211
3230634
x x -=;
(2)1cos 2sin x y ϕϕ
=+⎧⎨=⎩.
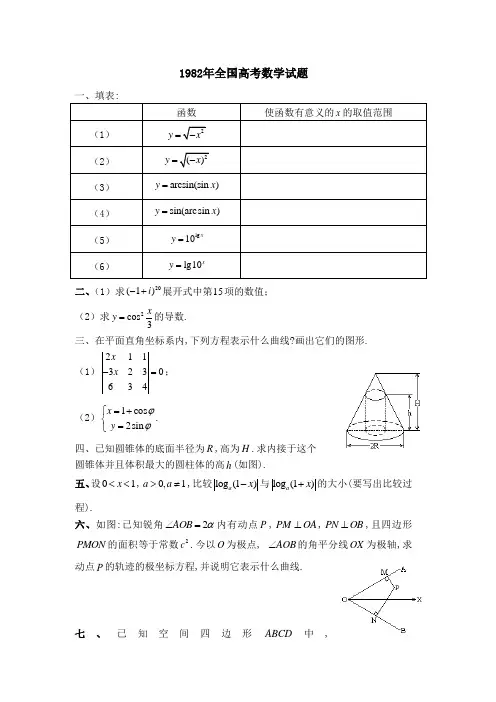
四、已知圆锥体的底面半径为R ,高为H .求内接于这个
圆锥体并且体积最大的圆柱体的高h (如图).
五、设01x <<,0,1a a >≠,比较log (1)a x -与log (1)a x +的大小(要写出比较过程).
六、如图:已知锐角2AOB α∠=内有动点P ,PM OA ⊥,PN OB ⊥,且四边形PMON 的面积等于常数2c .今以O 为极点, AOB ∠的角平分线OX 为极轴,求动点P 的轨迹的极坐标方程,并说明它表示什么曲线.
七、已知空间四边形ABCD 中,
AB BC =,CD DA =,,,,M N P Q 分别是边AB ,BC ,CD ,DA 的中点(如图).求证: MNPQ 是一个矩形.
八、抛物线22y px =的内接三角形有两边与抛物线22x qy =相切,证明这个三角形的第三边也与22x qy =相切.
九、附加题:计入总分.
已知数列1a ,2a ,…, n a ,…和数列1b ,2b ,…, n b ,…,其中1a p =,1b q =, 1n n a pa -=,11n n n b qa rb --=+,(,,p q r 是已知常数,且0q ≠,0p r >>). (1)用,,,p q r n 表示n b ,并用数学归纳法加以证明;
(2
)n A
B C D M N P Q。
一九八二年高考数学试卷

一、选择题(每题5分,共50分)1. 下列各数中,无理数是()A. √4B. √9C. √16D. √252. 若a,b,c成等差数列,且a+b+c=12,则a²+b²+c²的值为()A. 36B. 48C. 60D. 723. 下列函数中,定义域为实数集R的是()A. y=√xB. y=x²C. y=1/xD. y=|x|4. 已知函数f(x)=2x-3,若f(x+1)=f(x),则x的值为()A. 0B. 1C. 2D. 35. 在△ABC中,角A、B、C的对边分别为a、b、c,若a=5,b=7,c=8,则cosA 的值为()A. 1/2B. 1/3C. 1/4D. 1/56. 下列方程中,无解的是()A. 2x+3=0B. x²-4=0C. x²+x+1=0D. x²-2x+1=07. 下列命题中,正确的是()A. 若a+b=0,则a=0且b=0B. 若a²+b²=0,则a=0或b=0C. 若a²+b²=0,则a=0且b=0D. 若a²+b²=0,则a=0或b=08. 下列函数中,y=f(x)在x=0处的导数存在的是()A. y=x²B. y=x³C. y=x⁴D. y=x9. 下列不等式中,正确的是()A. a²+b²≥2abB. a²+b²≤2abC. a²+b²>2abD. a²+b²<2ab10. 若log₂x+log₂y=1,则x+y的值为()A. 2B. 4C. 8D. 16二、填空题(每题5分,共50分)1. 已知等差数列{an}的第一项为a₁,公差为d,求第n项an的表达式。
2. 已知函数f(x)=x²-4x+3,求f(x)的对称轴方程。
1982年普通高等学校招生全国统一考试理科数学试题及答案

1982年普通高等学校招生全国统一考试数学(理科)一.(本题满分6分) 填表:解:见上表二.(本题满分9分)1.求(-1+i)20展开式中第15项的数值; 2.求3cos 2xy =的导数解:1.第15项T 15=.38760)()1(6201461420-=-=-C i C2..32sin 31)3(3sin 3cos 2)3)(cos 3(cos 2x x x x x xy -='-='=' 三.(本题满分9分)在平面直角坐标系内,下列方程表示什么曲线?画出它们的图形1.;0436323112=-y x2.⎩⎨⎧φ=φ+=.sin 2,cos 1y x解:1.得2x-3y-6=0图形是直线2.化为,14)1(22=+-y x 图形是椭圆四.(本题满分12分)已知圆锥体的底面半径为R ,高为H求内接于这个圆锥体并且体积最大的圆柱体的高h (如图) 解:设圆柱体半径为r 高为h 由△ACD ∽△AOB 得.RrH h H =- 由此得),(h H HR r -=圆柱体体积.)()(2222h h H HR h r h V -π=π= 由题意,H >h >0,利用均值不等式,有.)(,3,,2.274274224232222最大时因此当时上式取等号当原式h V H h h h H H R H H R h h H h H H R ==-π=⋅π⋅≤⋅-⋅-⋅π⋅=Y XAB 2R(注:原“解一”对h 求导由驻点解得) 五.(本题满分15分)的大小与比较设|)1(log ||)1(log |,1,0,10x x a a x a a +-≠><<(要写出比较过程) 解一:当a >1时,.|)1(log ||)1(log |,1,0,10.|)1(log ||)1(log |,0)1(log ,110 ,10).1(log |)1(log ||)1(log |),1(log |)1(log |),1(log |)1(log |,10.|)1(log ||)1(log |,0)1(log ,110,1).1(log )]1(log )1([log |)1(log ||)1(log |),1(log |)1(log |),1(log |)1(log |222222x x a a x x x x x a x x x x x x x a x x x x a x x x x x x x x x a a a a a a a a a a a a a a a a a a a a a a a a +>-≠><<+>-∴>-∴<-<<<-=+--+-=+-=-<<+>-∴>--∴<-<>--=++--=+--+=+--=-总有时因此当时当解二:|)1(log |)1(log )1(log |)1(log ||)1(log |1x x x x x x a a a a -=+-=+-+,110,11<-<>+x x|)1(log ||)1(log |,1|)1(log ||)1(log |,10)1(log ,110,11)1(log 111log 11log )1(log 212212111x x x x x x x x xx x x a a a a x x x x x +>-∴>+->∴<-<-<>+--=-+=-=--=+++++即原式原式 六.(本题满分16分)如图:已知锐角∠AOB=2α内有动点P ,PM ⊥OA ,PN ⊥OB ,且四边形PMON 的面积等于常数c 2今以O 为极点,∠AOB 的角平分线OX 为极轴,求动点P的轨迹的极坐标方程,并说明它表示什么曲线解:设P 的极点坐标为(ρ,θ)∴∠POM=α-θ,∠NOM=α+θ, OM=ρcos(α-θ),PM=ρsin(α-θ), ON=ρcos(α+θ),PN=ρsin(α+θ), 四边形PMON 的面积.2sin 2.2sin 2)sin (cos sin ,cos .2sin 22cos 2cos 2sin 2)](2sin )(2[sin 4)]sin()cos()sin()[cos(2:,)]sin()cos()sin()[cos(221212222222222222222α=-α=θ-θρθρ=θρ=α=θρ=θαρ=θ+α+θ-αρ=θ+αθ+α+θ-αθ-αρθ+αθ+α+θ-αθ-αρ=⋅+⋅=c y x c y x c c c c P PN ON PM OM S 即为化为直角坐标方程上式用即用和差化积公式化简得用倍角公式化简得的轨迹的极坐标方程是动点依题意这个方程表示双曲线由题意,动点P 的轨迹是双曲线右面一支在∠AOB 内的一部分七.(本题满分16分)AO已知空间四边形ABCD 中AB=BC ,CD=DA ,M ,N ,P ,Q 分别是边AB ,BC ,CD ,DA 的中点(如图)求证MNPQ 是一个矩形证:连结AC ,在△ABC 中,∵AM=MB ,CN=NB ,∴MN ∥AC在△ADC 中,∵AQ=QD ,CP=PD , ∴QP ∥AC ∴MN ∥QP同理,连结BD 可证MQ ∥NP∴MNPQ 是平行四边形 取AC 的中点K ,连BK ,DK ∵AB=BC ,∴BK ⊥AC ,∵AD=DC ,∴DK ⊥AC 因此平面BKD 与AC 垂直∵BD 在平面BKD 内,∴BD ⊥AC ∵MQ ∥BD ,QP ∥AC ,∴MQ ⊥QP ,即∠MQP 为直角故MNPQ 是矩形 八.(本题满分18分)抛物线y 2=2px 的内接三角形有两边与抛物线x 2=2qy 相切,证明这个三角形的第三边也与x 2=2qy 相切解:不失一般性,设p>0,q>0.又设y 2=2px 的内接三角形顶点为A 1(x 1,y 1),A 2(x 2,y 2),A 3(x 3,y 3) 因此y 12=2px 1,y 22=2px 2 ,y 32=2px 3BP C Y x 2=2qy y 2=2px X其中y 1≠y 2 , y 2≠y 3 , y 3≠y 1 .依题意,设A 1A 2,A 2A 3与抛物线x 2=2qy 相切,要证A 3A 1也与抛物线x 2=2qy 相切因为x 2=2qy 在原点O 处的切线是y 2=2px 的对称轴,所以原点O 不能是所设内接三角形的顶点即(x 1,y 1),(x 2,y 2),(x 3,y 3),都不能是(0,0);又因A 1A 2与x 2=2qy 相切,所以A 1A 2不能与Y 轴平行,即x 1≠x 2 , y 1≠-y 2,直线A 1A 2的方程是),(112121x x x x y y y y ---=- ).(2))((1212122122x x p y y y y y y -=+-=-(1)0)(2.0)2(4)4(,2,0242.2212122121221221212121222121212121=++=+++-=∆==+-+-=+++=∴y y y y q p y y y qy y y pq qy x A A y y y qy x y y pqx qy x A A y y y y x y y py A A 化简得上面二次方程的判别式相切与抛物线由于交点的横坐标满足与抛物线方程是同理由于A 2A 3与抛物线x 2=2qy 相切,A 2A 3也不能与Y 轴平行,即 x 2≠x 3, y 2≠-y 3,同样得到(2) 0)(2p 32322=++y y y y q由(1)(2)两方程及y 2≠0,y 1≠y 3,得y 1+y 2+y 3=0.由上式及y 2≠0,得y 3≠-y 1,也就是A 3A 1也不能与Y 轴平行今将y 2=-y 1-y 3代入(1)式得:(3) 0)(2p 13132=++y y y y q(3)式说明A 3A 1与抛物线x 2=2qy 的两个交点重合,即A 3A 1与抛物线x 2=2qy 相切所以只要A 1A 2,A 2A 3与抛物线x 2=2qy 相切,则A 3A 1也与抛物线x 2=2qy 相切九.(附加题,本题满分20分,计入总分)已知数列 ,21,,n a a a 和数列,,,,21 n b b b 其中111,,-===n n pa a q b p a).0,0,,,(),2(11>>≠≥+=--r p q r q p n rb qa b n n n 且是已知常数1.用p,q,r,n 表示b n ,并用数学归纳法加以证明; 2.求.lim22nn n n b a b +∞→解:1.∵a 1=p, a n =p a n-1,∴a n =p n . 又b 1=q,b 2=q a 1+rb 1=q(p+r), b 3=q a 2+rb 2=q(p 2+pq+r 2),… 设想.)()(121rp r p q rr ppq b n n n n n n --=+++=---用数学归纳法证明:当n=2时,,)()(222r p r p q r p q b --=+=等式成立;设当n=k 时,等式成立,即,)(r p r p q b k k k --=则b k+1=q a k +rb k =,)()(11rp r p q r p r p rq qp k k k k k--=--+++即n=k+1时等式也成立所以对于一切自然数n ≥2,rp r p q b n n n --=)(都成立.)(lim ,0)(,,10,])(1[)(])(1[lim,,)()()(lim,0,)()()(limlim.222222222222222222q r p qb a b p rn p r prq r p p rq p r p q r p p r p q r p r p r p q p r p r p q ba b n n n n n n n n n n nnn n n n nn n n n nnn n +-=+∴→∞→<<-+--=-+--=>>--+--=+∞→∞→∞→∞→∞→时故当原式分子分母同除以原式。
高考理科数学试题及答案

1982年普通高等学校招生全国统一考试数学(理科)一.(本题满分6分) 填表:解:见上表二.(本题满分9分)1.求(-1+i)20展开式中第15项的数值; 2.求3cos 2xy =的导数解:1.第15项T 15=.38760)()1(6201461420-=-=-C i C 2..32sin 31)3(3sin 3cos 2)3)(cos 3(cos 2x x x x x xy -='-='=' 三.(本题满分9分)在平面直角坐标系内,下列方程表示什么曲线?画出它们的图形1.;0436323112=-y x Y2.⎩⎨⎧φ=φ+=.sin 2,cos 1y x解:1.得2x-3y-6=0图形是直线2.化为,14)1(22=+-y x 图形是椭圆四.(本题满分12分)已知圆锥体的底面半径为R ,高为H求内接于这个圆锥体并且体积最大的圆柱体的高h (如图)解:设圆柱体半径为r 高为h由△ACD ∽△AOB 得.RrH h H =- 由此得),(h H HR r -=圆柱体体积.)()(2222h h H HR h r h V -π=π= 由题意,H >h >0,利用均值不等式,有.)(,3,,2.274274224232222最大时因此当时上式取等号当原式h V H h h h H H R H H R h h H h H H R ==-π=⋅π⋅≤⋅-⋅-⋅π⋅=(注:原“解一”对h 求导由驻点解得)五.(本题满分15分)的大小与比较设|)1(log ||)1(log |,1,0,10x x a a x a a +-≠><<(要写出比较过程)A2R解一:当a >1时,.|)1(log ||)1(log |,1,0,10.|)1(log ||)1(log |,0)1(log ,110 ,10).1(log |)1(log ||)1(log |),1(log |)1(log |),1(log |)1(log |,10.|)1(log ||)1(log |,0)1(log ,110,1).1(log )]1(log )1([log |)1(log ||)1(log |),1(log |)1(log |),1(log |)1(log |222222x x a a x x x x x a x x x x x x x a x x x x a x x x x x x x x x a a a a a a a a a a a a a a a a a a a a a a a a +>-≠><<+>-∴>-∴<-<<<-=+--+-=+-=-<<+>-∴>--∴<-<>--=++--=+--+=+--=-总有时因此当时当ΘΘ解二:|)1(log |)1(log )1(log |)1(log ||)1(log |1x x x x x x a a a a -=+-=+-+Θ,110,11<-<>+x x Θ|)1(log ||)1(log |,1|)1(log ||)1(log |,10)1(log ,110,11)1(log 111log 11log )1(log 212212111x x x x x x x x xx x x a a a a x x x x x +>-∴>+->∴<-<-<>+--=-+=-=--=+++++即原式原式Θ 六.(本题满分16分)如图:已知锐角∠AOB=2α内有动点P ,PM ⊥OA ,PN ⊥OB ,且四边形PMON 的面积等于常数c 2今以O 为极点,∠AOB 的角平分线OX 为极轴,求动点P的轨迹的极坐标方程,并说明它表示什么曲线解:设P 的极点坐标为(ρ,θ)∴∠POM=α-θ,∠NOM=α+θ,AOM=ρcos(α-θ),PM=ρsin(α-θ), ON=ρcos(α+θ),PN=ρsin(α+θ), 四边形PMON 的面积.2sin 2.2sin 2)sin (cos sin ,cos .2sin 22cos 2cos 2sin 2)](2sin )(2[sin 4)]sin()cos()sin()[cos(2:,)]sin()cos()sin()[cos(221212222222222222222α=-α=θ-θρθρ=θρ=α=θρ=θαρ=θ+α+θ-αρ=θ+αθ+α+θ-αθ-αρθ+αθ+α+θ-αθ-αρ=⋅+⋅=c y x c y x c c c c P PN ON PM OM S 即为化为直角坐标方程上式用即用和差化积公式化简得用倍角公式化简得的轨迹的极坐标方程是动点依题意这个方程表示双曲线由题意,动点P 的轨迹是双曲线右面一支在∠AOB 内的一部分七.(本题满分16分)已知空间四边形ABCD 中AB=BC ,CD=DA ,M ,N ,P ,Q 分别是边AB ,BC ,CD ,DA 的中点(如图)求证MNPQ 是一个矩形证:连结AC ,在△ABC 中,∵AM=MB ,CN=NB ,∴MN ∥AC 在△ADC 中,∵AQ=QD ,CP=PD , ∴QP ∥AC ∴MN ∥QPBP C同理,连结BD 可证MQ ∥NP∴MNPQ 是平行四边形取AC 的中点K ,连BK ,DK ∵AB=BC ,∴BK ⊥AC ,∵AD=DC ,∴DK ⊥AC BKD 与AC 垂直∵BD 在平面BKD 内,∴BD ⊥AC ∵MQ ∥BD ,QP ∥AC ,∴MQ ⊥QP ,即∠MQP 为直角故MNPQ 是矩形八.(本题满分18分)抛物线y 2=2px 的内接三角形有两边与抛物线x 2=2qy 相切,证明这个三角形的第三边也与x 2=2qy 相切解:不失一般性,设p>0,q>0.又设y 2=2px 的内接三角形顶点为A 1(x 1,y 1),A 2(x 2,y 2),A 3(x 3,y 3)因此y 12=2px 1,y 22=2px 2 ,y 32=2px 3其中y 1≠y 2 , y 2≠y 3 , y 3≠y 1 .依题意,设A 1A 2,A 2A 3与抛物线x 2=2qy 相切,要证A 3A 1也与抛物线x 2=2qy 相切因为x 2=2qy 在原点O 处的切线是y 2=2px 的对称轴,所以原点O 不能是所设内接三角形的顶点即(x 1,y 1),(x 2,y 2),(x 3,y 3),都不能是(0,0);又因A 1A 2与x 2=2qy 相切,所以A 1A 2不能与Y 轴平行,即Yx 2=2qyy 2=2pxx 1≠x 2 , y 1≠-y 2,直线A 1A 2的方程是),(112121x x x x y y y y ---=- ).(2))((1212122122x x p y y y y y y -=+-=-Θ(1)0)(2.0)2(4)4(,2,0242.2212122121221221212121222121212121=++=+++-=∆==+-+-=+++=∴y y y y q p y y y qy y y pq qy x A A y y y qy x y y pqx qy x A A y y y y x y y py A A 化简得上面二次方程的判别式相切与抛物线由于交点的横坐标满足与抛物线方程是同理由于A 2A 3与抛物线x 2=2qy 相切,A 2A 3也不能与Y 轴平行,即 x 2≠x 3, y 2≠-y 3,同样得到(2) 0)(2p 32322=++y y y y q由(1)(2)两方程及y 2≠0,y 1≠y 3,得y 1+y 2+y 3=0.由上式及y 2≠0,得y 3≠-y 1,也就是A 3A 1也不能与Y y 2=-y 1-y 3代入(1)式得:(3) 0)(2p 13132=++y y y y q(3)式说明A 3A 1与抛物线x 2=2qy 的两个交点重合,即A 3A 1与抛物线x 2=2qy 相切所以只要A 1A 2,A 2A 3与抛物线x 2=2qy 相切,则A 3A 1也与抛物线x 2=2qy 相切九.(附加题,本题满分20分,计入总分)已知数列ΛΛ,21,,n a a a 和数列,,,,21ΛΛn b b b 其中111,,-===n n pa a q b p a).0,0,,,(),2(11>>≠≥+=--r p q r q p n rb qa b n n n 且是已知常数1.用p,q,r,n 表示b n ,并用数学归纳法加以证明; 2.求.lim22nn n n b a b +∞→解:1.∵a 1=p, a n =p a n-1,∴a n =p n . 又b 1=q,b 2=q a 1+rb 1=q(p+r), b 3=q a 2+rb 2=q(p 2+pq+r 2),… 设想.)()(121rp r p q rr ppq b n n n n n n --=+++=---Λ用数学归纳法证明:当n=2时,,)()(222r p r p q r p q b --=+=等式成立; 设当n=k 时,等式成立,即,)(r p r p q b k k k --=则b k+1=q a k +rb k =,)()(11rp r p q r p r p rq qp k k k k k--=--+++ 即n=k+1时等式也成立所以对于一切自然数n ≥2,rp r p q b n n n --=)(都成立.)(lim ,0)(,,10,])(1[)(])(1[lim,,)()()(lim ,0,)()()(limlim.222222222222222222q r p qb a b p rn p r prq r p p rq p r p q r p p r p q r p r p r p q p r p r p q ba b n n n n n n n n n n nnn n n n nn n n n nnn n +-=+∴→∞→<<-+--=-+--=>>--+--=+∞→∞→∞→∞→∞→时故当原式分子分母同除以原式ΘΘ(注:专业文档是经验性极强的领域,无法思考和涵盖全面,素材和资料部分来自网络,供参考。
1982年高考理科数学试题及答案
1982年普通高等学校招生全国统一考试数学(理科)一.(本题满分6分) 填表:解:见上表二.(本题满分9分)1.求(-1+i)20展开式中第15项的数值; 2.求3cos 2xy =的导数解:1.第15项T 15=.38760)()1(6201461420-=-=-C i C 2..32sin 31)3(3sin 3cos 2)3)(cos 3(cos 2x x x x x xy -='-='=' 三.(本题满分9分)在平面直角坐标系内,下列方程表示什么曲线?画出它们的图形1.;0436323112=-y x2.⎩⎨⎧φ=φ+=.sin 2,cos 1y x解:1.得2x-3y-6=0图形是直线2.化为,14)1(22=+-y x 图形是椭圆四.(本题满分12分)已知圆锥体的底面半径为R ,高为H求内接于这个圆锥体并且体积最大的圆柱体的高h (如图)解:设圆柱体半径为r 高为h由△ACD ∽△AOB 得.RrH h H =- 由此得),(h H HR r -=圆柱体体积.)()(2222h h H HR h r h V -π=π= 由题意,H >h >0,利用均值不等式,有.)(,3,,2.274274224232222最大时因此当时上式取等号当原式h V H h h h H H R H H R h h H h H H R ==-π=⋅π⋅≤⋅-⋅-⋅π⋅=Y XAB 2R(注:原“解一”对h 求导由驻点解得)五.(本题满分15分)的大小与比较设|)1(log ||)1(log |,1,0,10x x a a x a a +-≠><<(要写出比较过程)解一:当a >1时,.|)1(log ||)1(log |,1,0,10.|)1(log ||)1(log |,0)1(log ,110 ,10).1(log |)1(log ||)1(log |),1(log |)1(log |),1(log |)1(log |,10.|)1(log ||)1(log |,0)1(log ,110,1).1(log )]1(log )1([log |)1(log ||)1(log |),1(log |)1(log |),1(log |)1(log |222222x x a a x x x x x a x x x x x x x a x x x x a x x x x x x x x x a a a a a a a a a a a a a a a a a a a a a a a a +>-≠><<+>-∴>-∴<-<<<-=+--+-=+-=-<<+>-∴>--∴<-<>--=++--=+--+=+--=-总有时因此当时当解二:|)1(log |)1(log )1(log |)1(log ||)1(log |1x x x x x x a a a a -=+-=+-+,110,11<-<>+x x|)1(log ||)1(log |,1|)1(log ||)1(log |,10)1(log ,110,11)1(log 111log 11log )1(log 212212111x x x x x x x x xx x x a a a a x x x x x +>-∴>+->∴<-<-<>+--=-+=-=--=+++++即原式原式 六.(本题满分16分)如图:已知锐角∠AOB=2α内有动点P ,PM ⊥OA ,PN ⊥OB ,且四边形PMON 的面积等于常数c 2今以O 为极点,∠AOB 的角平分线OX 为极轴,求动点P的轨迹的极坐标方程,并说明它表示什么曲线解:设P 的极点坐标为(ρ,θ)∴∠POM=α-θ,∠NOM=α+θ, OM=ρcos(α-θ),PM=ρsin(α-θ), ON=ρcos(α+θ),PN=ρsin(α+θ), 四边形PMON 的面积.2sin 2.2sin 2)sin (cos sin ,cos .2sin 22cos 2cos 2sin 2)](2sin )(2[sin 4)]sin()cos()sin()[cos(2:,)]sin()cos()sin()[cos(221212222222222222222α=-α=θ-θρθρ=θρ=α=θρ=θαρ=θ+α+θ-αρ=θ+αθ+α+θ-αθ-αρθ+αθ+α+θ-αθ-αρ=⋅+⋅=c y x c y x c c c c P PN ON PM OM S 即为化为直角坐标方程上式用即用和差化积公式化简得用倍角公式化简得的轨迹的极坐标方程是动点依题意这个方程表示双曲线由题意,动点P 的轨迹是双曲线右面一支在∠AOB 内的一部分七.(本题满分16分)AO已知空间四边形ABCD 中AB=BC ,CD=DA ,M ,N ,P ,Q 分别是边AB ,BC ,CD ,DA 的中点(如图)求证MNPQ 是一个矩形证:连结AC ,在△ABC 中,∵AM=MB ,CN=NB ,∴MN ∥AC 在△ADC 中,∵AQ=QD ,CP=PD , ∴QP ∥AC ∴MN ∥QP同理,连结BD 可证MQ ∥NP∴MNPQ 是平行四边形取AC 的中点K ,连BK ,DK ∵AB=BC ,∴BK ⊥AC ,∵AD=DC ,∴DK ⊥AC BKD 与AC 垂直∵BD 在平面BKD 内,∴BD ⊥AC ∵MQ ∥BD ,QP ∥AC ,∴MQ ⊥QP ,即∠MQP 为直角故MNPQ 是矩形八.(本题满分18分)抛物线y 2=2px 的内接三角形有两边与抛物线x 2=2qy 相切,证明这个三角形的第三边也与x 2=2qy 相切解:不失一般性,设p>0,q>0.又设y 2=2px 的内接三角形顶点为A 1(x 1,y 1),A 2(x 2,y 2),A 3(x 3,y 3)因此y 12=2px 1,y 22=2px 2 ,y 32=2px 3BP C Y x 2=2qy y 2=2px X其中y 1≠y 2 , y 2≠y 3 , y 3≠y 1 .依题意,设A 1A 2,A 2A 3与抛物线x 2=2qy 相切,要证A 3A 1也与抛物线x 2=2qy 相切因为x 2=2qy 在原点O 处的切线是y 2=2px 的对称轴,所以原点O 不能是所设内接三角形的顶点即(x 1,y 1),(x 2,y 2),(x 3,y 3),都不能是(0,0);又因A 1A 2与x 2=2qy 相切,所以A 1A 2不能与Y 轴平行,即x 1≠x 2 , y 1≠-y 2,直线A 1A 2的方程是),(112121x x x x y y y y ---=- ).(2))((1212122122x x p y y y y y y -=+-=-(1)0)(2.0)2(4)4(,2,0242.2212122121221221212121222121212121=++=+++-=∆==+-+-=+++=∴y y y y q p y y y qy y y pq qy x A A y y y qy x y y pqx qy x A A y y y y x y y py A A 化简得上面二次方程的判别式相切与抛物线由于交点的横坐标满足与抛物线方程是同理由于A 2A 3与抛物线x 2=2qy 相切,A 2A 3也不能与Y 轴平行,即 x 2≠x 3, y 2≠-y 3,同样得到(2) 0)(2p 32322=++y y y y q由(1)(2)两方程及y 2≠0,y 1≠y 3,得y 1+y 2+y 3=0.由上式及y 2≠0,得y 3≠-y 1,也就是A 3A 1也不能与Y y 2=-y 1-y 3代入(1)式得:(3) 0)(2p 13132=++y y y y q(3)式说明A 3A 1与抛物线x 2=2qy 的两个交点重合,即A 3A 1与抛物线x 2=2qy 相切所以只要A 1A 2,A 2A 3与抛物线x 2=2qy 相切,则A 3A 1也与抛物线x 2=2qy 相切九.(附加题,本题满分20分,计入总分)已知数列 ,21,,n a a a 和数列,,,,21 n b b b 其中111,,-===n n pa a q b p a).0,0,,,(),2(11>>≠≥+=--r p q r q p n rb qa b n n n 且是已知常数1.用p,q,r,n 表示b n ,并用数学归纳法加以证明; 2.求.lim22nn n n b a b +∞→解:1.∵a 1=p, a n =p a n-1,∴a n =p n . 又b 1=q,b 2=q a 1+rb 1=q(p+r), b 3=q a 2+rb 2=q(p 2+pq+r 2),… 设想.)()(121rp r p q rr ppq b n n n n n n --=+++=---用数学归纳法证明:当n=2时,,)()(222r p r p q r p q b --=+=等式成立; 设当n=k 时,等式成立,即,)(r p r p q b k k k --=则b k+1=q a k +rb k =,)()(11rp r p q r p r p rq qp k k k k k--=--+++ 即n=k+1时等式也成立所以对于一切自然数n ≥2,rp r p q b n n n --=)(都成立.)(lim ,0)(,,10,])(1[)(])(1[lim,,)()()(lim ,0,)()()(limlim.222222222222222222q r p qb a b p rn p r prq r p p rq p r p q r p p r p q r p r p r p q p r p r p q ba b n n n n n n n n n n nnn n n n nn n n n nnn n +-=+∴→∞→<<-+--=-+--=>>--+--=+∞→∞→∞→∞→∞→时故当原式分子分母同除以原式微信红包群/q1Ia61tgTO67。
1982年高考数学全国卷(理科)及其参考答案-推荐下载
H2 2
2
当 H h h,时上式取等号,因此当h H 时,V (h)最大.
2
(注:原“解一”对 h 求导由驻点解得 ) 新疆 王新敞 奎屯
五.(本题满分 15 分)
新疆
王新敞
奎屯
奎屯
A
Dc
h BE
O
H 2 27 27
3
设0 x 1, a 0, a 1,比较 | loga (1 x) | 与 | loga (1 x) | 的大小 (要写出比 较过程)
原式
| 1,即
|
六.(本题满分 16 分)
log a log a
如图:已知锐角 ∠AOB=2α 内有动点 P,PM⊥OA,PN⊥OB,且四边 形 PMON 的面积等于常数 c2 今
新疆 王新敞
奎屯
以 O 为极点,∠AOB 的角平分
(1 (1
log1 x
x) x)
| |
| log1x (1 x) |
1982 年高考数学全国卷(理科)及其参考答案
一.(本题满分 6 分)
填表:
1
2
3
4
5
6
解:见上表 新疆 王新敞 奎屯
二.(本题满分 9 分)
函
y x2
y (x)2
y arcsin(sin x)
y sin(arcsin x)
y 10lg x
y lg10 x
1.求(-1+i)20 展开式中第 15 项的数值;
2.求 y cos2 x
解:1.第
15
3
项
新疆
的导数 王新敞
T15=
历年理科数学重点题1982
历年理科数学重点题单选题(共5道)1、已知函数,若,则的最小值为()A6B8C9D122、对大于1的自然数m的三次幂可用奇数进行以下方式的“分裂”,233343…仿此,若2015会在m3的“分裂”数中,则m的值为().A44B45C46D473、设复数z1,z2在复平面内的对应点关于虚轴对称,z1=2+i,则z1z2=( )A-5B5C-4+iD-4-i4、已知函数,若,则的最小值为()A6B8C9D125、是函数的导函数,的图象如图所示,则的图象最有可能的是()ABCD多选题(共5道)6、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)7、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)8、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)9、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)10、已知函数,若互不相等,且,则的取值范围是()ABCD填空题(本大题共4小题,每小题____分,共____分。
)简答题(共5道)11、、、(1)若的值;(2)若12、、、(1)若的值;(2)若13、把函数的图像向右平移a()个单位,得到的函数的图像关于直线对称.(1)求a的最小值;(2)当a取最小值,求函数在区间上的值域14、已知函数(1)求的最小正周期和值域;(2)在中,角所对的边分别是,若且,试判断的形状。
15、如图,四棱锥中,底面为梯形,底面,,,,.书面表达(共5道)16、车身总重量大于40公斤等指标)上了牌照,算是给予它们临时合法的出行身份,但是牌照有效期到今年2月底止,这也就是说,从今年3月1日起,该市城区4万多辆超标电动车已被禁行,违者将受到严厉的处罚。
82年高考数学(理科)第五题的多种解法
,
.
。
、
: l
取
` U s
La 十 P ) = 一气
。
扩 互 二一 一
l 件
一
户为半 圆 上 一 动点
积
。
,
问 尸 位 于何
处 时多 边 形 A C 尸 D B 有 最 大 面
.
:
T、 / 、
~
〔
~ 二
工
_
_ _
勺l 苛
` . 毖
澎了
百一
乙
尸
分 析 ( l ) 从求 函 数 极值 的 一
/
/
l
。
凡、
:
,
,
《
四 川 招生通讯 》 增
1 10 9 。
( 1+
1
.
劣
)
:
卜1
.
0
9。
(
l+
一
劣
)
,
刊 以 下简称
主 要 解法 一
增刊 》
本文 以下 再 介 绍 几种
而
< 1 0
二
一
< z x
万
蕊>ቤተ መጻሕፍቲ ባይዱ
“
1+
差值 比 较 法 。 [ 解一 ] ! 10 9 ( 1 一 劣 )
:
、
, 0 9·
一
( )! 卜 一 丛 卜 戛 续且 { 」 然 续止
一 般方 法
题 的 技巧
列 方 程 的 思 想方法
点
。
;
而
“
刀= ( a
,
+
,
刀) 一
a
使 学 生 提高 了 解
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1982年普通高等学校招生全国统一考试数学(理科)一.(本题满分6分) 填表:解:见上表二.(本题满分9分)1.求(-1+i)20展开式中第15项的数值; 2.求3cos 2xy =的导数解:1.第15项T 15=.38760)()1(6201461420-=-=-C i C 2..32sin 31)3(3sin 3cos 2)3)(cos 3(cos 2x x x x x xy -='-='=' 三.(本题满分9分)在平面直角坐标系内,下列方程表示什么曲线?画出它们的图形1.;0436323112=-y x2.⎩⎨⎧φ=φ+=.sin 2,cos 1y x解:1.得2x-3y-6=0图形是直线2.化为,14)1(22=+-y x 图形是椭圆四.(本题满分12分)已知圆锥体的底面半径为R ,高为H求内接于这个圆锥体并且体积最大的圆柱体的高h (如图)解:设圆柱体半径为r 高为h由△ACD ∽△AOB 得.RrH h H =- 由此得),(h H HR r -=圆柱体体积.)()(2222h h H HR h r h V -π=π= 由题意,H >h >0,利用均值不等式,有.)(,3,,2.274274224232222最大时因此当时上式取等号当原式h V H h h h H H R H H R h h H h H H R ==-π=⋅π⋅≤⋅-⋅-⋅π⋅=Y XAB 2R(注:原“解一”对h 求导由驻点解得)五.(本题满分15分)的大小与比较设|)1(log ||)1(log |,1,0,10x x a a x a a +-≠><<(要写出比较过程)解一:当a >1时,.|)1(log ||)1(log |,1,0,10.|)1(log ||)1(log |,0)1(log ,110 ,10).1(log |)1(log ||)1(log |),1(log |)1(log |),1(log |)1(log |,10.|)1(log ||)1(log |,0)1(log ,110,1).1(log )]1(log )1([log |)1(log ||)1(log |),1(log |)1(log |),1(log |)1(log |222222x x a a x x x x x a x x x x x x x a x x x x a x x x x x x x x x a a a a a a a a a a a a a a a a a a a a a a a a +>-≠><<+>-∴>-∴<-<<<-=+--+-=+-=-<<+>-∴>--∴<-<>--=++--=+--+=+--=-总有时因此当时当解二:|)1(log |)1(log )1(log |)1(log ||)1(log |1x x x x x x a a a a -=+-=+-+,110,11<-<>+x x|)1(log ||)1(log |,1|)1(log ||)1(log |,10)1(log ,110,11)1(log 111log 11log )1(log 212212111x x x x x x x x xx x x a a a a x x x x x +>-∴>+->∴<-<-<>+--=-+=-=--=+++++即原式原式 六.(本题满分16分)如图:已知锐角∠AOB=2α内有动点P ,PM ⊥OA ,PN ⊥OB ,且四边形PMON 的面积等于常数c 2今以O 为极点,∠AOB 的角平分线OX 为极轴,求动点P的轨迹的极坐标方程,并说明它表示什么曲线解:设P 的极点坐标为(ρ,θ)∴∠POM=α-θ,∠NOM=α+θ, OM=ρcos(α-θ),PM=ρsin(α-θ), ON=ρcos(α+θ),PN=ρsin(α+θ), 四边形PMON 的面积.2sin 2.2sin 2)sin (cos sin ,cos .2sin 22cos 2cos 2sin 2)](2sin )(2[sin 4)]sin()cos()sin()[cos(2:,)]sin()cos()sin()[cos(221212222222222222222α=-α=θ-θρθρ=θρ=α=θρ=θαρ=θ+α+θ-αρ=θ+αθ+α+θ-αθ-αρθ+αθ+α+θ-αθ-αρ=⋅+⋅=c y x c y x c c c c P PN ON PM OM S 即为化为直角坐标方程上式用即用和差化积公式化简得用倍角公式化简得的轨迹的极坐标方程是动点依题意这个方程表示双曲线由题意,动点P 的轨迹是双曲线右面一支在∠AOB 内的一部分七.(本题满分16分)AO已知空间四边形ABCD 中AB=BC ,CD=DA ,M ,N ,P ,Q 分别是边AB ,BC ,CD ,DA 的中点(如图)求证MNPQ 是一个矩形证:连结AC ,在△ABC 中,∵AM=MB ,CN=NB ,∴MN ∥AC 在△ADC 中,∵AQ=QD ,CP=PD , ∴QP ∥AC ∴MN ∥QP同理,连结BD 可证MQ ∥NP∴MNPQ 是平行四边形取AC 的中点K ,连BK ,DK ∵AB=BC ,∴BK ⊥AC ,∵AD=DC ,∴DK ⊥AC BKD 与AC 垂直∵BD 在平面BKD 内,∴BD ⊥AC ∵MQ ∥BD ,QP ∥AC ,∴MQ ⊥QP ,即∠MQP 为直角故MNPQ 是矩形八.(本题满分18分)抛物线y 2=2px 的内接三角形有两边与抛物线x 2=2qy 相切,证明这个三角形的第三边也与x 2=2qy 相切解:不失一般性,设p>0,q>0.又设y 2=2px 的内接三角形顶点为A 1(x 1,y 1),A 2(x 2,y 2),A 3(x 3,y 3)因此y 12=2px 1,y 22=2px 2 ,y 32=2px 3BP C Y x 2=2qy y 2=2px X其中y 1≠y 2 , y 2≠y 3 , y 3≠y 1 .依题意,设A 1A 2,A 2A 3与抛物线x 2=2qy 相切,要证A 3A 1也与抛物线x 2=2qy 相切因为x 2=2qy 在原点O 处的切线是y 2=2px 的对称轴,所以原点O 不能是所设内接三角形的顶点即(x 1,y 1),(x 2,y 2),(x 3,y 3),都不能是(0,0);又因A 1A 2与x 2=2qy 相切,所以A 1A 2不能与Y 轴平行,即x 1≠x 2 , y 1≠-y 2,直线A 1A 2的方程是),(112121x x x x y y y y ---=- ).(2))((1212122122x x p y y y y y y -=+-=-(1)0)(2.0)2(4)4(,2,0242.2212122121221221212121222121212121=++=+++-=∆==+-+-=+++=∴y y y y q p y y y qy y y pq qy x A A y y y qy x y y pqx qy x A A y y y y x y y py A A 化简得上面二次方程的判别式相切与抛物线由于交点的横坐标满足与抛物线方程是同理由于A 2A 3与抛物线x 2=2qy 相切,A 2A 3也不能与Y 轴平行,即 x 2≠x 3, y 2≠-y 3,同样得到(2) 0)(2p 32322=++y y y y q由(1)(2)两方程及y 2≠0,y 1≠y 3,得y 1+y 2+y 3=0.由上式及y 2≠0,得y 3≠-y 1,也就是A 3A 1也不能与Y y 2=-y 1-y 3代入(1)式得:(3) 0)(2p 13132=++y y y y q(3)式说明A 3A 1与抛物线x 2=2qy 的两个交点重合,即A 3A 1与抛物线x 2=2qy 相切所以只要A 1A 2,A 2A 3与抛物线x 2=2qy 相切,则A 3A 1也与抛物线x 2=2qy 相切九.(附加题,本题满分20分,计入总分)已知数列 ,21,,n a a a 和数列,,,,21 n b b b 其中111,,-===n n pa a q b p a).0,0,,,(),2(11>>≠≥+=--r p q r q p n rb qa b n n n 且是已知常数1.用p,q,r,n 表示b n ,并用数学归纳法加以证明; 2.求.lim22nn n n b a b +∞→解:1.∵a 1=p, a n =p a n-1,∴a n =p n . 又b 1=q,b 2=q a 1+rb 1=q(p+r), b 3=q a 2+rb 2=q(p 2+pq+r 2),… 设想.)()(121rp r p q rr ppq b n n n n n n --=+++=---用数学归纳法证明:当n=2时,,)()(222r p r p q r p q b --=+=等式成立; 设当n=k 时,等式成立,即,)(r p r p q b k k k --=则b k+1=q a k +rb k =,)()(11rp r p q r p r p rq qp k k k k k--=--+++ 即n=k+1时等式也成立所以对于一切自然数n ≥2,rp r p q b n n n --=)(都成立.)(lim,0)(,,10,])(1[)(])(1[lim,,)()()(lim ,0,)()()(limlim.222222222222222222q r p qb a b p r n prprq r p p r q p r p q r p p r p q r p r p r p q p r p r p q ba b n n n n n n n n n n nnn n n n nn n n n nnn n +-=+∴→∞→<<-+--=-+--=>>--+--=+∞→∞→∞→∞→∞→时故当原式分子分母同除以原式。
