带余除法初步知识点
苏教版二年级下册第1单元有余数的除法知识点及易错题
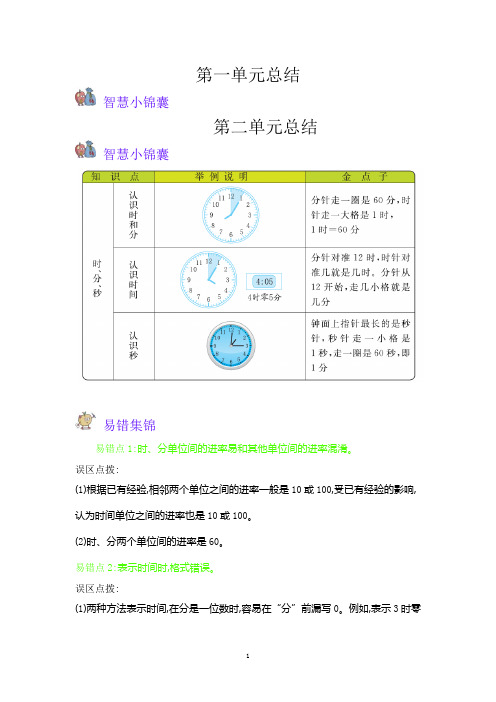
第一单元总结智慧小锦囊第二单元总结智慧小锦囊易错集锦易错点1:时、分单位间的进率易和其他单位间的进率混淆。
误区点拨:(1)根据已有经验,相邻两个单位之间的进率一般是10或100,受已有经验的影响,认为时间单位之间的进率也是10或100。
(2)时、分两个单位间的进率是60。
易错点2:表示时间时,格式错误。
误区点拨:(1)两种方法表示时间,在分是一位数时,容易在“分”前漏写0。
例如,表示3时零5分时,在冒号后面直接写5,如:3:5。
(2)时间的表示方法有两种:一种是用汉字描述,如3时零5分,几时就在“时”前写几,多少分就在“分”前写多少;另一种是用数字表示,如3:15,前面是时,后面是分,分是两位数,如果小于10时,几分,就在后面一位写几,前面的0不能省略。
如3时零5分,可以写作:3:05。
第三单元总结智慧小锦囊易错集锦易错点1:方向混淆。
误区点拨:(1)根据方向标来确定平面图的方向,平面图一般是按上北、下南、左西、右东制成的。
(2)东和南之间是东南,东和北之间是东北,西和南之间是西南,西和北之间是西北。
东南和西北相对,东北和西南相对。
易错点2:观测点不清。
误区点拨:(1)辨别方向时找准观测点是关键,因为物体的位置关系是相对的。
如:①甲在乙的哪一面,是以乙作为观测点。
②甲的哪一面是乙,是以甲作为观测点。
(2)观测的位置不同,观测点也会变化,要灵活找准观测点。
易错集锦易错点1:计算结果出错。
误区点拨:(1)计算有余数的除法时,会出现由于乘法口诀掌握不熟练而使商变大或变小,余数变大等错误。
(2)要熟记乘法口诀。
商和除数相乘的积应小于被除数,而且最接近被除数,余数要比除数小。
当余数大于或等于除数时,说明商小了,可以把商再调大。
易错点2:有余数的除法的意义。
误区点拨:(1)有余数的除法,在把被除数平均分时,要一直分到剩下的部分不够再分为止。
(2)余数要比除数小。
易错点3:忘写余数或忽略余数。
误区点拨:(1)由于初步接触有余数的除法,计算时会忘写余数或忽略余数。
除法的整除与余数知识点总结

除法的整除与余数知识点总结除法是数学中的一种基本运算,它涉及到整除和余数的概念。
在本文中,我将对除法的整除与余数进行知识点的总结,帮助读者更好地理解和应用这一概念。
一、整除的定义与性质整除是指一个数能够被另一个数整除,即没有余数。
对于两个整数a和b,若存在一个整数c,使得a = b * c,我们说a能够被b整除,记作b|a。
下面是整除的一些重要性质:1. 任何数都可以被1整除,即1|a,其中a为任意整数。
2. 任何整数a能够被自身整除,即a|a。
3. 若a能够被b整除,并且b能够被c整除,则a也能够被c整除,即若b|a且c|b,则c|a。
4. 若a能够被b整除,并且b不为0,则a/b是整数,即若b|a且b≠0,则a/b为整数。
这些性质在解题和证明中经常应用,对于理解整除概念起到重要作用。
二、余数的定义与应用余数是指在进行除法运算时,被除数除以除数后所剩下的未被整除的部分。
对于两个整数a和b,其中a为被除数,b为除数,我们用符号a%b表示a除以b的余数。
下面是余数的一些重要性质:1. 若a能够被b整除,则a%b等于0。
2. 余数不可为负数,即对于任意整数a,a%b的值在0到b-1之间。
3. 若a>b,则a%b的值小于b。
余数在解决问题时具有广泛的应用,例如:1. 判断一个数的奇偶性:若一个整数a%2的余数为0,则a为偶数,否则为奇数。
2. 进行模运算:模运算是指将一个数除以另一个数的余数,常用符号为a≡b(mod m)表示a和b对模m同余,也即a% m = b% m。
3. 判断能否整除:若余数为0,则被除数能够被除数整除。
通过了解余数的定义和应用,我们能够更好地理解和利用除法运算。
三、应用举例为了加深对整除与余数的理解,下面举两个具体的例子进行说明。
例1:判断一个数是否能够被5整除。
解析:我们只需要判断这个数的个位上的数字是否是0或5,如果是,则这个数能够被5整除。
例如,对于数字155,它的个位数字为5,所以能够被5整除。
余数知识点总结

余数知识点总结一、余数的定义在进行整数除法时,如果被除数不能被除数整除,我们就会得到一个余数。
例如,当我们用10除以3时,商是3,余数是1,因为10除以3得到3余1。
一般来说,对于任意的整数a和b(b不为0),都存在唯一的整数q和r,使得a=bq+r,其中q是商,r是余数。
二、余数的性质1. 余数的范围余数r的范围是0到b-1。
这是因为如果r=b-1,那么a=bq+r=bq+(b-1)=(q+1)b-1。
所以当r大于等于b时,我们可以用b来替换掉r,而商q则加1。
所以余数r必然小于b。
2. 余数的相等性如果两个整数a和b除以同一个整数m得到相同的余数,那么它们的差也一定能被m整除,即如果a%m=b%m,则(a-b)%m=0。
3. 余数的加法性两个整数a和b的余数之和等于它们的和的余数,即(a+b)%m=(a%m+b%m)%m。
4. 余数的乘法性两个整数a和b的余数之积等于它们的积的余数,即(a*b)%m=(a%m*b%m)%m。
5. 余数的幂运算如果要计算a的n次幂的余数,我们可以先计算a%m的n次幂的余数,然后再对m取余。
即a^n%m=(a%m)^n%m。
6. 余数的倒数两个整数a和b互素,即它们的最大公约数是1,那么a在模b意义下一定有倒数。
即对于方程ax≡1 mod b,一定存在整数x满足条件。
三、余数的应用1. 余数的运算余数在算术运算中有着广泛的应用,可以用于简化复杂的运算。
例如在大数运算中,我们往往会对结果取模,以减小结果的数值大小,提高运算效率。
2. 余数的模运算模运算是指对一个数除以另一个数后得到的余数。
在计算机科学中,模运算常常被用于实现循环、加密和散列等操作。
例如在密码学中,模运算可以用于加解密算法中的步骤之一。
3. 余数的逆元余数的逆元是指在模意义下存在的一个数,使得与它相乘后得到的余数是1。
余数的逆元在密码学和数论中有着重要的应用,例如在RSA算法中,逆元的存在性是保证算法有效性的关键。
小学奥数考点知识精讲之5-5-2 带余除法(二)

1. 能够根据除法性质调整余数进行解题2. 能够利用余数性质进行相应估算3. 学会多位数的除法计算4.根据简单操作进行找规律计算带余除法的定义及性质 1、定义:一般地,如果a 是整数,b 是整数(b ≠0),若有a ÷b =q ……r ,也就是a =b ×q +r ,0≤r <b ;我们称上面的除法算式为一个带余除法算式。
这里:(1)当0r =时:我们称a 可以被b 整除,q 称为a 除以b 的商或完全商(2)当0r ≠时:我们称a 不可以被b 整除,q 称为a 除以b 的商或不完全商一个完美的带余除法讲解模型:如图这是一堆书,共有a 本,这个a 就可以理解为被除数,现在要求按照b 本一捆打包,那么b 就是除数的角色,经过打包后共打包了c 捆,那么这个c 就是商,最后还剩余d 本,这个d 就是余数。
这个图能够让学生清晰的明白带余除法算式中4个量的关系。
并且可以看出余数一定要比除数小。
2、余数的性质⑴ 被除数=除数⨯商+余数;除数=(被除数-余数)÷商;商=(被除数-余数)÷除数;⑵ 余数小于除数.3、解题关键理解余数性质时,要与整除性联系起来,从被除数中减掉余数,那么所得到的差就能够被除数整除了.在一些题目中因为余数的存在,不便于我们计算,去掉余数,回到我们比较熟悉的整除性问题,那么问题就会变得简单了.模块一、带余除法的估算问题【例 1】 修改31743的某一个数字,可以得到823的倍数。
问修改后的这个数是几?【考点】带余除法的估算问题 【难度】3星 【题型】解答【解析】 本题采用试除法。
823是质数,所以我们掌握的较小整数的特征不适用,31743÷823=38……469,于是31743除以823可以看成余469也可以看成不足(823-469=)354,于是改动某位数字使得得到的新数比原来大354或354+823n 也是满足题意的改动.有n =1时,354+823:1177,n =2时,354+823×2=2000,所以当千位增加2,即改为3时,有修改后的五位数33743为823的倍数.【答案】33743例题精讲知识点拨教学目标5-5-2.带余除法(二)【例 2】 有48本书分给两组小朋友,已知第二组比第一组多5人.如果把书全部分给第一组,那么每人4本,有剩余;每人5本,书不够.如果把书全分给第二组,那么每人3本,有剩余;每人4本,书不够.问:第二组有多少人?【考点】带余除法的估算问题 【难度】3星 【题型】解答【关键词】小学数学夏令营【解析】 由48412÷=,4859.6÷=知,一组是10或11人.同理可知48316÷=,48412÷=知,二组是13、14或15人,因为二组比一组多5人,所以二组只能是15人,一组10人.【答案】10【例 3】 一个两位数除以13的商是6,除以11所得的余数是6,求这个两位数.【考点】带余除法的估算问题 【难度】3星 【题型】解答【解析】 因为一个两位数除以13的商是6,所以这个两位数一定大于13678⨯=,并且小于13(61)91⨯+=;又因为这个两位数除以11余6,而78除以11余1,这个两位数为78583+=.【答案】83【例 4】 在小于1000的自然数中,分别除以18及33所得余数相同的数有多少个?(余数可以为0)【考点】带余除法的估算问题 【难度】3星 【题型】解答【解析】 我们知道18,33的最小公倍数为[18,33]=198,所以每198个数一次.1~198之间只有1,2,3,…,17,198(余0)这18个数除以18及33所得的余数相同,而999÷198=5……9,所以共有5×18+9=99个这样的数.【答案】99【例 5】 托玛想了一个正整数,并且求出了它分别除以3、6和9的余数.现知这三余数的和是15.试求该数除以18的余数.【考点】带余除法的估算问题 【难度】3星 【题型】解答【关键词】圣彼得堡数学奥林匹克【解析】 除以3、6和9的余数分别不超过2,5,8,所以这三个余数的和永远不超过25815++=,既然它们的和等于15,所以这三个余数分别就是2,5,8.所以该数加1后能被3,6,9整除,而[3,6,9]18=,设该数为a ,则181a m =-,即18(1)17a m =-+(m 为非零自然数),所以它除以18的余数只能为17.【答案】17模块二、多位数的余数问题【例 6】 2000"2"2222个除以13所得余数是_____.【考点】多位数的余数问题 【难度】3星 【题型】填空【解析】 方法一、我们发现222222整除13,2000÷6余2,所以答案为22÷13余9。
小学奥数精讲:带余除法(同余式和同余方程)知识点及典型例题

小学奥数精讲:带余除法(同余式和同余方程)一、基本性质的复习1、带余数除法算式:a÷b=q……r(a、b、q、r 均为整数) 从中我们应该得到:(1)b>r 除数大于余数(2)a-r=b×q 被除数减去余数则会出现整除关系,则带余数问题就可以转化为整数问题。
2、余数的性质:(1)可加性:和的余数等于余数的和。
即:两数和除以m 的余数等于这两个数分别除以m 的余数和。
例:7÷3=2……1 5÷3=1……2,则(7+5)÷3 的余数就等于(1+2)÷3 的余数0。
(2)可减性:差的余数等于余数的差。
即:两数差除以m 的余数等于这两个数分别除以m 的余数差。
例:17÷3=5……2 5÷3=1……2,则(17-5)÷3 的余数就等于(2-2)÷3 的余数0。
(3)可乘性:积的余数等于余数的积。
即:两数积除以m 的余数等于这两个数分别除以m 的余数积。
例:64÷7=9……1 45÷7=6……3,则(64×45)÷3 的余数就等于(1×3)÷7 的余数3。
二、同余式在生活中,若两个自然数 a 和 b 都除以同一个除数m 时,余数相同该如何表示呢?在代数中我们称之为同余。
即:a 与b 同余于模m。
意思就是自然数a 和b 关于m 来说是余数相同的。
用同余式表达为:a≡b(modm).注:若a 与b 同余于模m,则a 与b 的差一定被m 整除。
(余数的可减性)三、例题。
例1、当2011 被正整数N 除时,余数为16,请问N 的所有可能值有多少个?例2、(1)求多位数1234567891011…20102011除以9的余数?(2)将1开始到103的连续奇数依次写成一个多位数:a=135791113…9799101103,则数a共有多少位?数a除以9 的余数为几?(3)一个多位数1234567……979899,问除以11 的余数是多少?例3、(1)用一个数除200 余5,除300 余1,除400 余10,求这个数?(2)甲、乙、丙、丁四个旅行团分别有游客69 人,85 人、93 人、97 人。
数论之余数问题

数论之余数问题余数问题是数论知识板块中另一个内容丰富,题目难度较大的知识体系,也是各大杯赛小升初考试必考的奥数知识点,所以学好本讲对于学生来说非常重要。
许多孩子都接触过余数的有关问题,并有不少孩子说“遇到余数的问题就基本晕菜了!”余数问题主要包括了带余除法的定义,三大余数定理(加法余数定理,乘法余数定理,和同余定理),及中国剩余定理和有关弃九法原理的应用。
知识点拨:一、带余除法的定义及性质:一般地,如果a是整数,b是整数(b≠0),若有a〔b=q……r,也就是a=b〓q+r,0≤r<b;我们称上面的除法算式为一个带余除法算式。
这里:r=时:我们称a可以被b整除,q称为a除以b的商或完全商(1)当0r≠时:我们称a不可以被b整除,q称为a除以b的商或不完全商(2)当0一个完美的带余除法讲解模型:如图,这是一堆书,共有a本,这个a就可以理解为被除数,现在要求按照b本一捆打包,那么b就是除数的角色,经过打包后共打包了c捆,那么这个c就是商,最后还剩余d本,这个d就是余数。
这个图能够让学生清晰的明白带余除法算式中4个量的关系。
并且可以看出余数一定要比除数小。
二、三大余数定理:1.余数的加法定理a与b的和除以c的余数,等于a,b分别除以c的余数之和,或这个和除以c的余数。
例如:23,16除以5的余数分别是3和1,所以23+16=39除以5的余数等于4,即两个余数的和3+1.当余数的和比除数大时,所求的余数等于余数之和再除以c的余数。
例如:23,19除以5的余数分别是3和4,故23+19=42除以5的余数等于3+4=7除以5的余数,即2.2.余数的乘法定理a与b的乘积除以c的余数,等于a,b分别除以c的余数的积,或者这个积除以c所得的余数。
例如:23,16除以5的余数分别是3和1,所以23〓16除以5的余数等于3〓1=3。
当余数的和比除数大时,所求的余数等于余数之积再除以c的余数。
例如:23,19除以5的余数分别是3和4,所以23〓19除以5的余数等于3〓4除以5的余数,即2.3.同余定理若两个整数a、b被自然数m除有相同的余数,那么称a、b对于模m同余,用式子表示为:a≡b ( mod m ),左边的式子叫做同余式。
五年级数学带余除法(含答案)

带余除法知识框架带余除法的定义及性质1、定义:一般地,如果a是整数,b是整数(b≠0),若有a÷b=q……r,也就是a=b×q+r,0≤r<b;我们称上面的除法算式为一个带余除法算式。
这里:(1)当0r=时:我们称a可以被b整除,q称为a除以b的商或完全商(2)当0r≠时:我们称a不可以被b整除,q称为a除以b的商或不完全商一个完美的带余除法讲解模型:如图这是一堆书,共有a本,这个a就可以理解为被除数,现在要求按照b本一捆打包,那么b就是除数的角色,经过打包后共打包了c捆,那么这个c就是商,最后还剩余d本,这个d就是余数。
这个图能够让学生清晰的明白带余除法算式中4个量的关系。
并且可以看出余数一定要比除数小。
2、余数的性质⑴被除数=除数⨯商+余数;除数=(被除数-余数)÷商;商=(被除数-余数)÷除数;⑵余数小于除数.3、解题关键理解余数性质时,要与整除性联系起来,从被除数中减掉余数,那么所得到的差就能够被除数整除了.在一些题目中因为余数的存在,不便于我们计算,去掉余数,回到我们比较熟悉的整除性问题,那么问题就会变得简单了.例题精讲【例 1】某数被13除,商是9,余数是8,则某数等于。
【考点】除法公式的应用【难度】1星【题型】填空【关键词】2009年,希望杯,第七届,四年级,复赛,第2题,5分【解析】125【答案】125【巩固】一个三位数除以36,得余数8,这样的三位数中,最大的是__________。
【考点】除法公式的应用【难度】1星【题型】填空【关键词】2008年,希望杯,第六届,四年级,复赛,第3题【解析】因为最大的三位数为999,999362727⨯+=÷=,所以满足题意的三位数最大为:36278980【答案】980【例 2】除法算式÷□□=208中,被除数最小等于。
【考点】除法公式的应用【难度】1星【题型】填空【关键词】2007年,第5届,希望杯,4年级,初赛,4题【解析】本题的商和余数已经知道了,若想被除数最小,则需要除数最小即可,除数最小是819+=,所以本题答案为:20×(8+1)+8=188.【答案】188【巩固】计算口÷△,结果是:商为10,余数为▲。
初中余数知识点总结

初中余数知识点总结在学习余数的概念时,我们需要了解四则运算、整数的概念、两个整数的相对大小的比较、除法时商和余数的关系等。
这是一系列基本数学概念和技能的纽带,是数学教学中重要的知识点之一。
概述:余数是指一个数被另一个数除后得到的剩余部分。
例如 15除以4等于3余3。
余数的概念:在算术中,除法运算是划分的过程。
除法中划分得到的相等的几份就是商。
而最后剩下的一份就是余数。
当我们用一个数除另一个数时,有时会有余数。
例如,当12 ÷ 5时,商是2,余数是2;而当13 ÷ 4时,商是3,余数是1。
取模运算和余数:取模运算即求余数的运算。
它是计算机领域常用的一种数学运算符号。
如果说 a 除以 b 可以得到商 c 和余数 r,那么 r = a % b。
小数和余数:小数是再除法时出现的一种特殊的余数形式。
例如 7 ÷ 2 = 3.5,其中3是商数,0.5是余数,但是以小数的形式存在。
正整数的除法:当一个正整数(除数)除不尽一个大于零的整数(被除数)时,结果和余数都是一个非负整数。
这就是正整数的除法。
负整数的除法:当一个负整数(除数)除不尽一个大于零的整数(被除数)时,结果和余数都是一个与除数同号的整数。
但是当被除数是负数时,结果和余数可能会有很多种情况。
需要合理的确定符号。
同余关系:同余关系是指两个数的差能整除一个数的性质。
例如13和5模6是同余关系,因为13-5=8,8可以整除6。
余数的性质:(1)余数与除数的关系:不管是正负整数,被除数总能写成“商×除数+余数”的形式。
(2)余数的大小:余数永远小于除数,但可以等于0。
余数运算:余数的运算是对余数进行特定的运算。
例如,对余数做加法、减法、乘法、除法等运算。
余数的应用:余数可以用在取模运算、排列组合、密码学、数据校验等领域。
本文将详细介绍余数相关的概念和运算,以及余数的一些基本性质、应用和相关知识点。
一、余数的概念余数是指一个数被另一个数除后得到的剩余部分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1.除法算式13÷2=6… …1中13是(),2是(),6是(),1是()。
1.(单选题)10÷3=3……1,其中10是________
A、除数
B、被除数
C、商
D、余数
2.(单选题)10÷3=3……1,其中1是_______
A、除数
B、被除数
C、商
D、余数
例2.除数是9,被除数是62,商是()?余数是()?
1.49里面最多有_________个9。
2.49除以9,余数是________。
例3.有32本书,最少拿出()本后就可以平均分给5个小朋友?
1.4根小棒可摆成一个正方形,用19根小棒摆这样的4个正方形(没有公共边),问还剩________根。
2.在一个余数是8的除法算式中,除数最小是_________。
例4.39里面有几个6,还余几?
1.被除数是57,除数是7,余________?
2.8的5倍里最多有_________个9。
例5.一辆汽车上有4个轮子和1个备用胎,现在有38个轮子,能装几辆这样的汽车,还剩几个轮子?
1.食堂买来40袋面粉。
如果每天吃6袋,最后一天还剩________袋?
2.小刚买来20条金鱼,送给小明4条,小刚再把剩下的平均放在3个鱼缸,最后还剩_________条?
例6.10里面最多有()个4;28里面最多有()个6;32里面最多有()个7;43里面最多有()个8.
1.□÷8=5……△,当△最大时,□应该是________。
2.有32本书,最少拿出_______本后,剩下的书就可以平均分给5个小朋友。
