实验-图像增强和图像分割实验
遥感图像增强实验报告
遥感图像增强实验报告1. 实验目的和内容实验目的：（1）遥感图像的空间域增强：通过直接改变图像中的单个像元及相邻像元的灰度值来增强图像，是图像增强技术的基本组成部分，包括点运算和邻域运算。
（2）遥感图像的频率域增强：通过对频率域的调整对遥感图像进行平滑和锐化，平滑主要是保留图像的低频部分抑制高频部分，锐化则保留图像的高频部分而削弱低频部分。
（3）遥感图像的彩色增强：将黑白图像转换成彩色图像，使地物的差别易于分辨，突出图像的有用信息，从而提高对图像的解译和分析能力。
实验内容：（1）遥感图像的空间域增强：点运算—直方图均衡化、灰度拉伸、任意拉伸，邻域运算—图像平滑、图像锐化。
（2）遥感图像的频率域增强：定义FFT，反向FFT，再进行对比。
（3）遥感图像的彩色增强：多波段影像—彩色合成、单波段影像—伪彩色增强、色彩空间变换、遥感数据融合。
2. 图像处理方法和流程A.遥感图像的空间域增强1.直方图均衡化(1)在主窗口中打开can_tmr.img文件。
(2)以gray形式显示一个波段。
(3)Display窗口>enhance>equalization2.灰度拉伸(1)Display窗口>enhance>interactive stretching(2)弹出的对话框>stretch_type>linear(3)在STRETCH对应的两个文本框中输入需要拉伸的范围，然后单击对话框上的APPLY按钮，图像显示为线性拉伸后的效果。
3.任意拉伸（1）弹出的对话框>stretch_type>Arbitary，在output histogram中单击绘制直方图，右键结束（2）点击apply，结果如图所示4.图像平滑（1）均值平滑，在主窗口中打开can_tmr.img文件。
主窗口>enhance>filter>smooth[3*3]。
结果如图所示（2）中值平滑，在主窗口中打开can_tmr.img文件。
图像处理实验报告
图像处理实验报告图像处理实验报告一、引言图像处理是计算机科学与工程领域的一个重要研究方向，它涉及到对数字图像进行获取、处理、分析和显示等一系列操作。
本实验旨在通过使用图像处理技术，对一幅给定的数字图像进行处理和分析，以探索图像处理的原理和应用。
二、实验目的本实验有以下几个目的：1. 理解图像处理的基本概念和原理；2. 掌握图像处理的常用技术和方法；3. 熟悉图像处理软件的使用。
三、实验步骤1. 图像获取在本实验中，我们选择了一张风景图作为实验对象。
该图像是通过数码相机拍摄得到的，保存在计算机中的文件格式为JPEG。
我们使用图像处理软件将该图像导入到程序中，以便进行后续的处理和分析。
2. 图像预处理在进行图像处理之前，我们需要对图像进行预处理。
预处理的目的是去除图像中的噪声、平滑图像的边缘等。
我们使用了均值滤波和中值滤波两种常用的图像平滑方法。
通过对比两种方法的效果，我们可以选择合适的方法来进行图像预处理。
3. 图像增强图像增强是指通过一系列的操作，使得图像在视觉上更加鲜明、清晰、易于观察。
在本实验中，我们使用了直方图均衡化和灰度拉伸两种图像增强方法。
直方图均衡化通过对图像的像素值进行变换，使得图像的直方图更加均匀，从而增强图像的对比度。
灰度拉伸则是通过对图像的像素值进行线性变换，将图像的灰度范围拉伸到更广的范围内，从而增强图像的细节。
4. 图像分割图像分割是将图像分成若干个互不重叠的区域，每个区域具有一定的意义和特征。
在本实验中，我们使用了阈值分割和边缘检测两种图像分割方法。
阈值分割是指通过设置一个合适的阈值，将图像中的像素分为两个类别。
边缘检测则是通过检测图像中的边缘信息，将图像分割为不同的区域。
5. 图像特征提取图像特征提取是指从图像中提取出具有一定意义和特征的信息。
在本实验中，我们选择了纹理特征和颜色特征两种常用的图像特征提取方法。
纹理特征提取通过对图像的纹理进行分析，提取出图像的纹理特征。
遥感实验三(图像分割)2010
卷积滤波
卷积（Convolutions）滤波是通过消除特定的空间频率来使图像增强，根据增强类型（低频、中频和高频）不同可分为低通滤波、带通滤波和高通滤波。此外还可以增强图像某些方向特征的方向滤波等。它们的核心部分是卷积核。ENVI提供很多卷积核，包括高通滤波（High Pass）、低通滤波（Low Pass）、拉普拉斯算子（Laplacian）、方向滤波（Directional）、高斯高通滤波（Gaussian High Pass）、高斯低通滤波（Gaussian Low Pass）、中值滤波（Median）、Sobel、Roberts，还可以自定义卷积核。具体操作如下：
下面对ENVI中各种滤波作一个简单的说明，如表5.1。
表5.1 各种滤波说明
滤波
说明
高通滤波器（High Pass）
高通滤波在保持图像高频信息的同时，消除了图像中的低频成分。它可以用来增强纹理、边缘等信息。高通滤波通过运用一个具有高中心值的变换核来完成（周围通常是负值权重）。ENVI默认的高通滤波器使用3×3的变换核（中心值为“8”，周围像元值为“-1”），高通滤波卷积核的维数必须是奇数。
二、实验内容
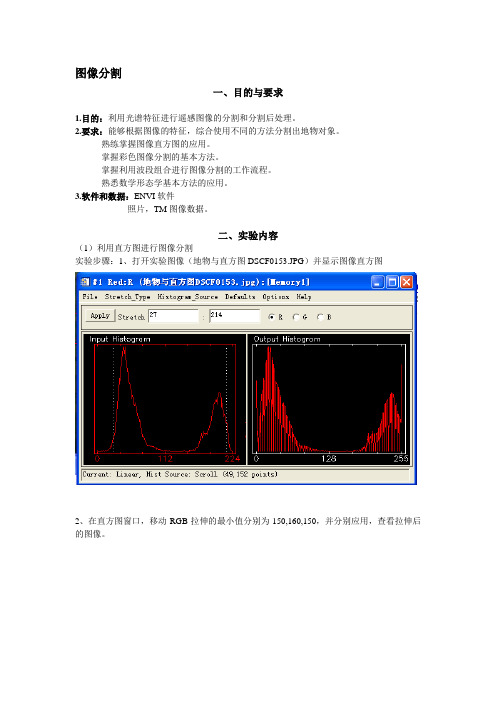
（1）利用直方图进行图像分割
实验步骤：1、打开实验图像（地物与直方图DSCF0153.JPG）并显示图像直方图
2、在直方图窗口，移动RGB拉伸的最小值分别为150,160,150，并分别应用，查看拉伸后的图像。
原图：
最小值150的拉伸：
最小值160的拉伸：
去除天空的操作：（菜单—basictools—bandmath）
3)Editable Kernel
卷积核中各项的值。在文本框中双击鼠标可以进行编辑，选择File->Save Kernel或者Restore Kernel，可以把卷积核保存为文件（.ker）或者打开一个卷积核文件。
matlab数字图像处理实验报告
《数字图像处理实验报告》实验一图像的增强一.实验目的1.熟悉图像在MATLAB下的读写、输出；2.熟悉直方图；3.熟悉图像的线性指数等；4.熟悉图像的算术运算和几何变换。
二.实验仪器计算机、MATLAB软件三.实验原理图像增强是指根据特定的需要突出图像中的重要信息，同时减弱或去除不需要的信息。
从不同的途径获取的图像，通过进行适当的增强处理，可以将原本模糊不清甚至根本无法分辨的原始图像处理成清晰的富含大量有用信息的可使用图像。
其基本原理是：对一幅图像的灰度直方图，经过一定的变换之后，使其成为均匀或基本均匀的，即使得分布在每一个灰度等级上的像素个数．f=H等或基本相等。
此方法是典刑的图像空间域技术处理，但是由于灰度直方图只是近似的概率密度函数，因此，当用离散的灰度等级做变换时，很难得到完全平坦均匀的结果。
频率域增强技术频率域增强是首先将图像从空间与变换到频域，然后进行各种各样的处理，再将所得到的结果进行反变换，从而达到图像处理的目的。
常用的变换方法有傅里叶变换、DCT变换、沃尔什-哈达玛变换、小波变换等。
假定原图像为f(x，y)，经傅立叶变换为F(u，v)。
频率域增强就是选择合适的滤波器H(u,v)对F(u,v)的频谱成分进行处理，然后经逆傅立叶变换得到增强的图像。
四.实验内容及步骤1.图像在MATLAB下的读写、输出；实验过程：>> I = imread('F:\image\');figure;imshow(I);title('Original Image');text(size(I,2),size(I,1)+15, ...'', ...'FontSize',7,'HorizontalAlignment','right');Warning: Image is too big to fit on screen; displaying at 25% > In imuitools\private\initSize at 86In imshow at 1962.给定函数的累积直方图。
物理实验技术中的数据可视化与图像处理方法
物理实验技术中的数据可视化与图像处理方法引言：在物理实验中，收集和分析数据是非常重要的，而数据可视化和图像处理技术则为我们提供了更好地理解和解释这些数据的方法。
通过数据可视化和图像处理，我们可以直观地展示实验结果，并提取有用的信息。
本文将探讨在物理实验中常用的数据可视化和图像处理方法。
一、数据可视化方法1. 直方图直方图是一种常用的数据可视化方法。
它通过将数据分成一系列连续的区间，并统计每个区间内的数据出现的频率，然后绘制成柱状图的方式显示。
直方图可以有效地展示数据的分布情况，帮助我们发现数据的规律和异常点。
2. 折线图折线图是一种通过连接数据点来展示数据变化趋势的方法。
它常用于展示随时间变化的数据。
在物理实验中，我们可以将实验过程中的数据绘制成折线图，以帮助分析实验结果。
3. 散点图散点图是一种用点表示数据，并以坐标轴表示变量之间关系的可视化方法。
在物理实验中，我们可以用散点图来展示两个变量的关系，例如实验探测到的电压和电流之间的关系。
二、图像处理方法1. 图像增强图像增强是指通过一系列的处理步骤，改善图像质量的方法。
在物理实验中，图像增强可以提高图像的对比度、亮度等属性，从而更清晰地显示实验结果。
2. 图像去噪在物理实验中，由于各种因素的影响，图像常常会受到噪声的干扰。
图像去噪是一种通过处理方法将噪声从图像中消除的技术。
常见的图像去噪方法有中值滤波、均值滤波等。
3. 图像分割图像分割是将图像分成多个区域的过程，它可以帮助我们提取感兴趣的目标或边缘。
在物理实验中，图像分割可以用于分析实验结果中的不同区域的特性。
4. 特征提取特征提取是从图像中提取出具有代表性的信息的过程。
在物理实验中，我们常常需要从实验结果的图像中提取出与实验参数相关的特征，例如颜色、形状等。
结论：数据可视化和图像处理在物理实验中起到了非常重要的作用。
通过合理地运用这些技术，我们可以更好地展现实验结果，并从中获得有用的信息。
希望本文的介绍对读者在物理实验中的数据可视化和图像处理方面有所启发。
DIP课程实验
Digital Image Processing Homework课程实验实验题目（任选其中两个完成，欢迎多选）：∙实验1: 图像增强∙实验2: 图像分割与边缘检测∙实验3: 图像几何变换∙实验4: 图像特征与理解∙实验5: 图像压缩与编码∙实验6: 图像复原∙实验7: 图像频域处理∙实验8: 图像数学形态学处理实验1：图像增强一、实验目的：学会常用图像增强与平滑的算法。
二、实验要求：1．直方图计算与显示，直方图拉伸与均衡；2．灰度变换算法；3．燥声去除算法；4．图象锐化算法。
三、实验步骤：1．利用工具（如ACDSee、PhotoShop）将JPG图像文件转换为BMP图像文件；2．根据BMP格式，将图像内容读入内存数组；3．调用各种算法处理读入的图像；4．注意不同处理方法对边缘的影响。
四、实验图像：Sample1-1.jpg（原始图像）Sample1-2.jpg（加噪声后的图像）实验2：图像分割与边缘检测一、实验目的：学会常用图像分割与边缘检测算法。
二、实验要求：1．用灰度阈值法、区域生长与聚合算法实现图象分割；2．用梯度算子检测图像中的边缘；3．用Sobel算子检测图像中的边缘；4．实现投影法和差影算法。
三、实验步骤：1．利用工具（如ACDSee、PhotoShop）将JPG图像文件转换为BMP图像文件；2．根据BMP格式，将图像内容读入内存数组；3．调用算法；4．比较处理结果。
四、实验图像：Sample2-1.jpg Sample2-2.jpg实验3：图像几何变换1、Image Printing Program Based on Halftoning (Pattern 半影调法，图案法)The following figure shows ten shades of gray approximated by dot patterns. Each gray level is represented by a 3 x 3 pattern of black and white dots. A 3 x 3 area full of black dots is the approximation to gray-level black, or 0. Similarly, a 3 x 3 area of white dotsrepresents gray level 9, or white. The other dot patterns are approximations to gray levels in between these two extremes. A gray-level printing scheme based on dots patterns such as these is called "halftoning" Note that each pixel in an input image will correspond to 3 x 3 pixels on the printed image, so spatial resolution will be reduced to 33% of the original in both the vertical and horizontal direction. Size scaling as required in (a) may furtherreduce resolution, depending on the size of the input image.(a) Write a halftoning computer program for printing gray-scale images based on the dotpatterns just discussed. Your program must be able to scale the size of an input image so that it does not exceed the area available in a sheet of size A4 (21.6 x 27.9 cm). Yourprogram must also scale the gray levels of the input image to span the full halftoning range.(b) Write a program to generate a test pattern image consisting of a gray scale wedge ofsize 256 x 256, whose first column is all 0's, the next column is all 1's, and so on, with the last column being 255's. Print this image using your gray-scale printing program.(c) Print iamges Sample4-1.jpg, Sample4-2.jpg and Sample4-3.jpg using your gray-scaleprinting program.2、Reducing the Number of Gray Levels in an Image （二值化）(a) Write a computer program capable of reducing the number of gray levels in a image from 256 to 2, in integer powers of 2. The desired number of gray levels needs to be a variable input to your program.(b) Download the image Sample4-4.jpg and run your program.3、Zooming and Shrinking Images by Pixel Replication （基于像素插补的放大缩小） (a) Write a computer program capable of zooming and shrinking an image by pixelreplication （插补）. Assume that the desired zoom/shrink factors are integers. You may ignore aliasing effects.(b) Download the image Sample4-5.jpg and use your program to shrink the image from 1024 x 1024 to 256 x 256 pixels.(c) Use your program to zoom the image in (b) back to 1024 x 1024. Explain the reasons for their differences.4、Zooming and Shrinking Images by Bilinear Interpolation （基于双线性插值的放大缩小）(a) Write a computer program capable of zooming and shrinking an image by bilinear interpolation. The input to your program is the desired size of the resulting image in the horizontal and vertical direction. You may ignore aliasing effects.(b) Download the image Sample4-5.jpg and use your program to shrink this image from 1024 x 1024 to 256 x 256 pixels.(c) Use your program to zoom the image in (b) back to 1024 x 1024. Explain the reasonsfor their differencesSample4-1.jpgSample4-2.jpgSample4-3.jpgSample4-4.jpgSample4-5.jpg实验4：图像特征与理解实验5：图像压缩与编码一、实验目的：掌握数字图像的基本压缩与编码技术。
图像处理
医学图像处理实验喻罡实验一图像增强实验实验目的：掌握图像增强的算法实验内容：(1)图像的点操作、邻域操作算法(2)图像的直方图处理算法实验工具：Matlab7.1实验步骤：(1)读入图像用Matlab函数实现图像读入(2)实现图像点操作运算(如gamma校正，对数校正等)(3)实现图像的邻域处理(均值滤波，拉普拉斯滤波)(4)实现直方图均衡处理实验过程及分析：(1)、读入，Matlab读入图像只需imread(‘image.jpg/bmp…’)语句，显示部分用到imshow(image)即可。
(2)、伽马变换代码如下RGB=imread('赫本_3.jpg');f=rgb2gray(RGB); %彩图转灰度图c=1;p=2;s=c*f.^p; %伽马变换表达式imshow(s);title('伽马校正')因为所用的p>1其效果是压缩暗像素值，扩展亮像素值，与原图相比，可见图像亮的更亮，暗的变得稀薄了。
对数校正代码如下：RGB=imread('赫本_3.jpg');f=rgb2gray(RGB);f=im2double(f); %uint8图像转为double型c=2;s=c.*log(1+f); %对数计算表达式imshow(b);title('对数图像');对数变换增强低灰度级、抑制高灰度级，两图相比，亮处更亮，暗处变淡。
因为低灰度级被扩展了，相当于被平滑了，高灰度级被抑制，相当于被浓缩了。
(3)均值滤波代码如下RGB=imread('赫本_3.jpg');f=rgb2gray(RGB);f=im2double(f);[m,n]=size(s); %将阵列s的行数返回到m中，列数返回到n中for i=2:m-1for j=2:n-1h(i,j)=f(i-1,j-1)+f(i-1,j)+f(i-1,j+1)+f(i,j-1)+f(i,j)+f(i,j+1)+f(i+1,j-1)+f(i+1,j)+f(i+1,j+1 );g(i,j)=h(i,j)/9; %滤波函数表达式endendimshow(g);title('均值滤波')均值滤波所用的滤波器是3x3的矩阵且，阵元都等于1。
matlab图像处理综合实验实验报告
《数字图像处理》实验报告学院：专业：班级：姓名：学号：实验一实验名称：图像增强实验目的：1.熟悉图像在Matlab下的读入，输出及显示；2.熟悉直方图均衡化；3.熟悉图像的线性指数等；4.熟悉图像的算术运算及几何变换.实验仪器：计算机，Matlab软件实验原理：图像增强是为了使受到噪声等污染图像在视觉感知或某种准则下尽量的恢复到原始图像的水平之外，还需要有目的性地加强图像中的某些信息而抑制另一些信息，以便更好地利用图像。
图像增强分频域处理和空间域处理，这里主要用空间域的方法进行增强。
空间域的增强主要有：灰度变换和图像的空间滤波。
图像的直方图实际上就是图像的各像素点强度概率密度分布图，是一幅图像所有像素集合的最基本统计规律，均衡化是指在每个灰度级上都有相同的像素点过程。
实验内容如下：I=imread('E:\cs.jpg');%读取图像subplot(2,2,1),imshow(I),title('源图像')J=rgb2gray(I)%灰度处理subplot(2,2,2),imshow(J) %输出图像title('灰度图像') %在原始图像中加标题subplot(2,2,3),imhist(J) %输出原图直方图title('原始图像直方图')0100200几何运算：I=imread('E:\cs.jpg');%subplot(1,2,1),imshow(I); theta = 30;K = imrotate(I,theta); subplot(1,2,2),imshow(K)对数运算：I=imread('E:\dog.jpg');subplot(2,2,1),imshow(I),title('源图像') J=rgb2gray(I)%灰度处理subplot(2,2,2),imshow(J),title('灰度变换后图像') J1=log(1+double(J));subplot(2,2,3),imshow(J1,[]),title('对数变换后') 指数运算:I=imread('E:\dog.jpg'); f=double(I); g=(2^2*(f-1))-1 f=uint8(f); g=uint8(g);subplot(1,2,1);subimage(f),title('变换一') subplot(1,2,2);subimage(g),title('变换二')加法运算：clc;clear all;close all; i = imread('E:\dog.jpg');j = imnoise(i,'gaussian',0,0.02);subplot(1,3,1),imshow(i),title('图一') subplot(1,3,2),imshow(j),title('图二') k=zeros(242,308); for p=1:100j = imnoise(i,'gaussian',0,0.02); j1 = im2double(j); k = k + j1; end k=k/100;subplot(1,3,3),imshow(k),title('图三')变换一200400600100200300400500变换二200400600100200300400500实验二实验名称：图像变换实验目的：（1）进一步对matlab的了解和使用；（2）学习如何在matlab中对数字图像的处理；实验原理：图像和其他信号一样，既能在空间域处理，也能在频率域处理。
结合图像增强和肤色分割的人脸检测新方法
Ｋｅ ｙ ｗｏ ｄ ： ｆ ｃ ｅｅ ｔ ｎ； ａ ｅ ｅ ａ ｃ ｍｅ ｔ ｓ ｉ ｅ ｍ ｅ ｔ Ａｄ Ｂｏ ｓ ａ ｇ ｒ ｈ ｒ ｓ ａ ｅ ｄ ｔ ｃ ｉ ｉ ｇ ｎ ｎ ｅ ｎ ； ｋ ｎ ｓ ｇ ｎ ； ａ ｏ ｔ ｌ ｏ ｉ ｍ ｏ ｍ ｈ ｔ
摘 要 ： 色图像 中通常存在 噪音 、 糊 、 彩 模 背景等 问题 ， 影响到人脸 检测 的结果。提 出一种 Ａ ａ ｏｓ 法结合 图像增 强和肤 直接 ｄＢ ｏｔ 算 色分割 的人脸检 测新 方法 。对输 入 图像进行 平滑 、 锐化 图像增强操作 ， 较好地 消除噪声干扰和增 强 图像 的边缘信 息； 利用肤 色分 割， 将肤 色区域 和 背景有效地 区分开 ； 候选 区域用 ＡｄＢ ｏｔ 法精 确地 定位 出人脸 位置 。实验结 果证 明 ， 在 ａ ｏ ｓ算 该方 法对 “ 漏检 ” 和
ｐ ｒｍｅ ｔ ｉｌ ｓ ａｅ ｔ ａ ｉ ｔ ｏ ａ ｅ ｅ ｍｐ ｏ ｅ ｎ ｏ ｔ ｅ ｐ ｏ ｌｍ ｆ ｌａ ｅ ｅ ｔ ｎ ａ ｄ ｅ ｒ ｒ ｄ ｔｃ ｉｎ． ｅ ｉ ｎ ｓ ｌ ｔ ｔ ｔ ｔ ｓ ｍｅ ｈ ｄ ｈ ｓ ａ ｂ Ｒ ｒ ｉ ｒ ｖ ｍｅ ｔ ｔ ｒ ｂ ｅ ｏ ｅ ｋ ｄ ｔ ｃｉ ｎ ｒｏ ｅｅ ｔ ｕ ｒ ｈ ｈ ｈ ｏ ｏ
ｆ ｃ ｅ ｅ ｔ ｎ ｒ ｓ ｌ ． ｉ ｐ ｐ ｒ ｐ ｔ ｏ ｗａ ｄ ａ ｎ ｗ ｔ ｏ ｉｈ ｃ ｍｂ ｎ ｓ ｉ ｇ ｎ ａ ｃ ｍｅ ｔ ａ ｄ ｓ ｉ ｅ ｍｅ ｔ ｗｉ ａ ａ ｅ ｄ ｔ ｃｉ ｅ ｕ ｔ Ｔｈ ｓ ａ ｅ ｕ ｓ ｆ ｒ ｒ ｅ ｍｅｈ ｄ ｗｈ ｃ ｏ ｏ ｓ ｉ ｅ ｍａ ｅ ｅ ｈ ｎ ｅ ｎ ｎ ｋ ｎ ｓ ｇ ｎ ｔ Ａｄ — ｈ
遥感影像处理实验报告(3篇)
第1篇一、实验背景与目的随着遥感技术的不断发展，遥感影像已成为获取地球表面信息的重要手段。
遥感影像处理是对遥感影像进行一系列技术操作，以提高影像质量、提取有用信息的过程。
本实验旨在通过实践操作，让学生掌握遥感影像处理的基本原理和常用方法，提高学生对遥感影像数据的应用能力。
二、实验内容与步骤本次实验主要包括以下内容：1. 数据准备：获取实验所需的遥感影像数据，包括光学影像、红外影像等。
2. 影像预处理：对原始遥感影像进行辐射校正、几何校正、图像增强等处理。
3. 影像分割：对预处理后的影像进行分割，提取感兴趣的目标区域。
4. 影像分类：对分割后的影像进行分类，识别不同的地物类型。
5. 结果分析：对分类结果进行分析，评估分类精度。
三、实验步骤1. 数据准备- 获取实验所需的遥感影像数据，包括光学影像、红外影像等。
- 确保影像数据具有较好的质量和分辨率。
2. 影像预处理- 辐射校正：对原始遥感影像进行辐射校正，消除大气、传感器等因素对影像辐射强度的影响。
- 几何校正：对原始遥感影像进行几何校正，消除地形起伏、地球曲率等因素对影像几何形状的影响。
- 图像增强：对预处理后的影像进行图像增强，提高影像对比度、清晰度等。
3. 影像分割- 选择合适的分割方法，如基于阈值分割、基于区域生长分割、基于边缘检测分割等。
- 对预处理后的影像进行分割，提取感兴趣的目标区域。
4. 影像分类- 选择合适的分类方法，如监督分类、非监督分类等。
- 对分割后的影像进行分类，识别不同的地物类型。
5. 结果分析- 对分类结果进行分析，评估分类精度。
- 分析分类结果中存在的问题，并提出改进措施。
四、实验结果与分析1. 影像预处理结果- 经过辐射校正、几何校正和图像增强处理后，遥感影像的质量得到显著提高，对比度、清晰度等指标明显改善。
2. 影像分割结果- 根据实验所采用的分割方法，成功提取了感兴趣的目标区域，分割效果较好。
3. 影像分类结果- 通过选择合适的分类方法，对分割后的影像进行分类，成功识别了不同的地物类型。
光学遥感算法实验报告
一、实验目的本次实验旨在通过光学遥感图像处理，掌握光学遥感图像的基本处理方法，包括图像预处理、图像增强、图像分割等，并熟悉常用的光学遥感图像处理算法，提高对光学遥感图像的分析和处理能力。
二、实验内容1. 实验环境（1）软件：ENVI 5.3（2）硬件：计算机2. 实验步骤（1）数据准备首先，准备一幅光学遥感图像，本实验选用的是一幅Landsat 8卫星影像。
（2）图像预处理对图像进行预处理，包括辐射校正、几何校正等。
（3）图像增强对图像进行增强，提高图像的视觉效果，便于后续处理。
本实验采用直方图均衡化、对比度拉伸等方法。
（4）图像分割对图像进行分割，提取目标区域。
本实验采用阈值分割、区域生长等方法。
（5）结果分析对分割结果进行分析，评估算法性能。
三、实验结果与分析1. 图像预处理经过辐射校正和几何校正后，图像质量得到提高，细节更加清晰。
2. 图像增强通过直方图均衡化和对比度拉伸，图像视觉效果得到明显改善。
3. 图像分割（1）阈值分割采用Otsu方法进行阈值分割，得到初步的目标区域。
但该方法存在一定局限性，如噪声干扰、目标区域内部亮度不均匀等。
（2）区域生长采用区域生长方法对图像进行分割，得到较为准确的目标区域。
区域生长方法具有以下优点：- 可以较好地处理噪声干扰；- 可以处理目标区域内部亮度不均匀的问题；- 可以根据需要设置生长参数，提高分割精度。
4. 结果分析通过对比阈值分割和区域生长两种方法，发现区域生长方法在处理光学遥感图像时具有更好的性能。
区域生长方法可以较好地处理噪声干扰和目标区域内部亮度不均匀等问题，提高分割精度。
四、实验结论1. 光学遥感图像预处理、增强和分割是光学遥感图像处理的重要环节。
2. 直方图均衡化、对比度拉伸等方法可以有效提高图像视觉效果。
3. 区域生长方法在处理光学遥感图像时具有较好的性能，可以提高分割精度。
4. 通过本次实验，掌握了光学遥感图像处理的基本方法，提高了对光学遥感图像的分析和处理能力。
数字图像处理实验报告
数字图像处理实验报告引言数字图像处理是一门研究如何对图像进行数字化处理的学科，它的应用广泛，涵盖了图像的获取、增强、压缩、分割等多个方面。
本次实验旨在探索数字图像处理的基本原理和常用技术，并通过实践操作加深对数字图像处理的理解。
实验目的1.学习掌握数字图像处理的基本原理；2.熟悉常用的数字图像处理工具和方法；3.实践应用数字图像处理技术解决实际问题。
实验环境在本次实验中，我们使用了以下环境和工具：- 操作系统：Windows 10 - 编程语言：Python - 图像处理库：OpenCV实验步骤步骤一：图像获取与显示首先，我们需要获取一张待处理的图像，并对其进行显示。
在Python中，我们可以使用OpenCV库来实现图像的读取和显示。
以下是示例代码：import cv2# 读取图像image = cv2.imread('image.jpg')# 显示图像cv2.imshow('Image', image)cv2.waitKey(0)cv2.destroyAllWindows()步骤二：图像增强图像增强是数字图像处理中常用的技术之一，旨在改善图像的质量和可视化效果。
常见的图像增强技术包括灰度转换、直方图均衡化、滤波器等。
以下是示例代码：import cv2# 读取图像image = cv2.imread('image.jpg')# 灰度转换gray_image = cv2.cvtColor(image, cv2.COLOR_BGR2GR AY)# 直方图均衡化equalized_image = cv2.equalizeHist(gray_image)# 高斯滤波器blurred_image = cv2.GaussianBlur(equalized_image, (5, 5), 0)# 边缘增强enhanced_image = cv2.Canny(blurred_image, 100, 20 0)# 显示图像cv2.imshow('Enhanced Image', enhanced_image)cv2.waitKey(0)cv2.destroyAllWindows()步骤三：图像压缩图像压缩是数字图像处理中的重要话题，旨在减少图像的存储空间和传输带宽。
图像增强实验报告
图像增强实验报告篇一：图像处理实验报告——图像增强实验报告学生姓名：刘德涛学号:2010051060021指导老师：彭真明日期：2013年3月31日一、实验室名称：光电楼329、老计算机楼309机房二、实验项目名称：图像增强三、实验原理：图像增强是为了使受到噪声等污染图像在视觉感知或某种准则下尽量的恢复到原始图像的水平之外，还需要有目的性地加强图像中的某些信息而抑制另一些信息，以便更好地利用图像。
图像增强分频域处理和空间域处理，这里主要用空间域的方法进行增强。
空间域的增强主要有：灰度变换和图像的空间滤波。
1.灰度变换灰度变换主要有线性拉伸、非线性拉伸等。
灰度图像的线性拉伸是将输入图像的灰度值的动态范围按线性关系公式拉伸到指定范围或整个动态范围。
令原图像f(x,y)的灰度变化范围为[a,b]，线性变换后图像g(x,y)的范围为[a',b']，线性拉伸的公式为：b'?a'g(x,y)?a?[f(x,y)?a] b?a灰度图像的非线性拉伸采用的数学函数是非线性的。
非线性拉伸不是对图像的灰度值进行扩展，而是有选择地对某一灰度范围进行扩展，其他范围的灰度值则可能被压缩。
常用的非线性变换：对数变换和指数变换。
对数变换的一般形式：g(x,y)?a?ln[f(x,y)?1] blnc指数变换的一般形式：g(x,y)?bc[f(x,y)?a]?1（a,b,c用于调整曲线的位置和形状的参数。
）2.图像的空间滤波图像的空间滤波主要有图像的空域平滑和锐化。
图像的平滑是一种消除噪声的重要手段。
图像平滑的低频分量进行增强，同时抑制高频噪声，空域中主要的方法有领域平均、中值滤波、多帧相加平均等方法。
图像锐化能使图像的边缘、轮廓处的灰度具有突变特性。
图像的锐化主要有微分运算的锐化，包括梯度法和拉普拉斯法算子。
四、实验目的：1．熟悉和掌握利用Matlab工具进行数字图像的读、写、显示等数字图像处理基本步骤。
数字图像处理四个实验
数字图像处理实验指导书目录实验一MATLAB数字图像处理初步实验二图像的代数运算实验三图像增强-空间滤波实验四图像分割实验五形态学运算3实验一 MATLAB数字图像处理初步一、实验目的与要求1．熟悉及掌握在MATLAB中能够处理哪些格式图像。
2．熟练掌握在MATLAB中如何读取图像。
3．掌握如何利用MATLAB来获取图像的大小、颜色、高度、宽度等等相关信息。
4．掌握如何在MATLAB中按照指定要求存储一幅图像的方法。
5．图像间如何转化。
二、实验原理及知识点1、数字图像的表示和类别一幅图像可以被定义为一个二维函数f(x,y),其中x和y是空间(平面)坐标，f 在任何坐标处(x,y)处的振幅称为图像在该点的亮度。
灰度是用来表示黑白图像亮度的一个术语，而彩色图像是由单个二维图像组合形成的。
例如，在RGB彩色系统中，一幅彩色图像是由三幅独立的分量图像(红、绿、蓝)组成的。
因此，许多为黑白图像处理开发的技术适用于彩色图像处理，方法是分别处理三副独立的分量图像即可。
图像关于x和y坐标以及振幅连续。
要将这样的一幅图像转化为数字形式，就要求数字化坐标和振幅。
将坐标值数字化成为取样；将振幅数字化成为量化。
采样和量化的过程如图1所示。
因此，当f的x、y分量和振幅都是有限且离散的量时，称该图像为数字图像。
作为MATLAB基本数据类型的数值数组本身十分适于表达图像，矩阵的元素和图像的像素之间有着十分自然的对应关系。
图1 图像的采样和量化根据图像数据矩阵解释方法的不同，MA TLAB把其处理为4类：亮度图像(Intensity images)二值图像(Binary images)索引图像(Indexed images)RGB图像(RGB images)(1) 亮度图像一幅亮度图像是一个数据矩阵，其归一化的取值表示亮度。
若亮度图像的像素都是uint8类或uint16类，则它们的整数值范围分别是[0，255]和[0，65536]。
实验六指导书 图像分割
实验六图像分割一、实验目的利用光谱特征进行遥感图像的分割和分割后处理。
二、实验内容1、利用直方图进行图像分割2、提取指定颜色的对象3、去除图片的背景噪声4、提取厦门市TM遥感影像中的水体信息5、提取线性地物信息6、图像形态学基本方法三、实验条件电脑、ENVI软件。
厦门市TM遥感影像、实验数据四、实验步骤1.利用直方图进行图像分割图像：地物与直方图DSCF0153.JPG打开图像，并显示图像的直方图在直方图窗口，移动RGB拉伸的最小值分别为150，160，150，并分别应用，查看拉伸后的图像。
使用下面的表达式去除天空，其中，b1，b2，b3对应图像的R，G，B通道，b4对应原始图像。
b4*(1-b1 lt 150)* (b2 lt 160) * (b3 lt 150)2.彩色图像的分割（1）提取图像中的兰花关闭所有打开的窗口和文件图像：兰花.jpg要求：将兰花从图像分割出来主要操作：利用直方图，查看当前像素值工具比较兰花在各个通道上的灰度值的差异，确定兰花与周围物体最大的通道或通道的组合。
提示：兰花是蓝色的。
表达式：（b1 gt b2)* (b1 gt b3)，其中b1是蓝通道，b2，b3对应绿和红通道。
（2）去除背景噪声，提取图像中的娃娃关闭所有打开的窗口和文件图像：娃娃.jpg选择“波段“作为直方图数据来源，进行图像拉伸。
思考以下问题①直方图有什么特征？②任意对RGB波段进行拉伸，图像发生了什么变化？③按照如下设置进行图像拉伸，R：154~184,G:8~100,B:0~160,图像发生了什么变化？④如何去除背景中的噪声？步骤：使用float（b1）/ float（b2）对通道R和G进行代数运算，产生图像m1；对于m1图像，使用b1 gt 0.98进行代数运算，产生图像m2；使用原始图像的RGB作为b1（在变量与波段匹配的对话框中，点击按钮Map Variable to input file），使用m2作为b2，进行代数运算b1*b2，产生新的图像m3，按照R，G，B顺序合成显示。
数字图像处理实验(全完整答案)
实验一常用MATLAB图像处理命令一、实验目得1、熟悉并掌握ＭAＴLＡB工具得使用;2、实现图像得读取、显示、代数运算与简单变换。
二、实验环境MAＴLAB ６。
５以上版本、ＷIN XP或WＩN2000计算机三、常用函数●读写图像文件1 imrｅadimreａd函数用于读入各种图像文件,如:ａ=imread(＇ｅ:\ｗ0１。
tif')2 imｗrｉtｅiｍｗriｔe函数用于写入图像文件,如:imｗrｉtｅ(a,’e:＼w02。
ｔif’,’tｉf')３imfiｎｆｏimfｉnｆｏ函数用于读取图像文件得有关信息,如:ｉmfｉnfo('e:\ｗ０1、tif’)●图像得显示1imａｇeｉmagｅ函数就是MATLAB提供得最原始得图像显示函数,如:ａ=[1,2,3,4;４,5,6,７;８,9,10,１１,1２］;imaｇｅ(a);2 imsｈowimshow函数用于图像文件得显示,如:i＝ｉmreａｄ('e:＼w0１、tiｆ');iｍshow(ｉ);tiｔｌe(‘原图像’)％加上图像标题3 cｏlｏrbaｒｃolorbａr函数用显示图像得颜色条,如:i＝imread(’e:\w01。
ｔif');iｍshow(i);ｃｏｌoｒbar;4 fｉｇurefｉgure函数用于设定图像显示窗口,如:fｉｇｕrｅ(1); /fiｇure(2);5 suｂｐｌoｔ把图形窗口分成多个矩形部分,每个部分可以分别用来进行显示、Ｓubpｌｏｔ(m,n,ｐ)分成ｍ＊ｎ个小窗口,在第ｐ个窗口中创建坐标轴为当前坐标轴,用于显示图形、6 ｐｌoｔ绘制二维图形pｌｏt(y)Plot(ｘ,ｙ)ｘy可以就是向量、矩阵。
图像类型转换１ｒgb２gray把真彩图像转换为灰度图像i=ｒgb2gｒａｙ(ｊ)2 iｍ２bw通过阈值化方法把图像转换为二值图像I=im2bw(ｊ,lｅvel)Lｅｖel表示灰度阈值,取值范围０～１(即0.n),表示阈值取自原图像灰度范围得n%3 imresize改变图像得大小Ｉ=imrｅsize(j,［m n］)将图像j大小调整为m行ｎ列图像运算１ｉmadd两幅图像相加,要求同样大小,同种数据类型Z＝imadd(x,y)表示图像x＋ｙ2 imsｕbstraｃt两幅图像相减,要求同样大小,同种数据类型Z=imsubｔract(x,ｙ) 表示图像ｘ-y3 immultiｐlｙZ=iｍmulｔｉplｙ(x,y) 表示图像x＊y4 imdivｉｄeZ=ｉmdｉvidｅ(ｘ,y) 表示图像x/y四、实验内容(请将实验程序填写在下方合适得位置,实验图像结果拷屏粘贴)1、读入一幅RGＢ图像,变换为灰度图像与二值图像,并在同一个窗口内分成三个子窗口来分别显示ＲGＢ图像与灰度图像,注上文字标题。
数字图像处理实验书
数字图像处理实验实验指导书图像处理实验<一）直方图灰度变换是图像增强的一种重要手段，使图像对比度扩展，图像更加清晰，特征更加明显。
灰度级的直方图给出了一幅图像概貌的描述，通过修改灰度直方图来得到图像增强。
1、灰度直方图<1）计算出一幅灰度图像的直方图clearclose allI=imread('004.bmp'>。
imhist(I>title('实验一<1）直方图'>。
<2）对灰度图像进行简单的灰度线形变换，figuresubplot(2,2,1>imshow(I>。
title('实验2-灰度线性变换'>。
subplot(2,2,2>histeq(I>。
<3）看其直方图的对应变化和图像对比度的变化。
原图像 f(m,n> 的灰度范围 [a,b] 线形变换为图像 g(m,n>,灰度范围[a’,b’]公式：g(m,n>=a’+(b’-a’>* f(m,n> /(b-a>figuresubplot(2,2,1>imshow(I>J=imadjust(I,[0.3,0.7],[0,1],1>。
title(' 实验一<3）用g(m,n>=a’+(b’-a’>* f(m,n> /(b-a>进行变换 '>。
b5E2RGbCAPsubplot(2,2,2>imshow(J>subplot(2,2,3>imshow(I>J=imadjust(I,[0.5 0.8],[0,1],1>。
subplot(2,2,4>imshow(J>(4> 图像二值化 <选取一个域值，(5> 将图像变为黑白图像）figuresubplot(2,2,1>imshow(I>J=find(I<150>。
图像处理实验报告
图像处理实验报告第一次实验课：绘制直方图f=imread('bld.tif');imshow(f)imhist(f)原图像：直方图：第二次实验课：图像增强f=imread('hua.jpg');imshow(f)g=gscale(f);figure,imshow(g)原图像：处理后的图像：第三次实验课：图像平滑f=imread('noisy.jpg');imshow(f)f1=imnoise(f,'salt & pepper',0.1);figure,imshow(f1)f2=medfilt2(f1);figure,imshow(f2)imwrite(f2,'w.tif')原图像：加噪声后的图像：平滑后的图像：第四次实验课：图像分割f=imread('bld.tif');imshow(f)[gc,t]=edge(f,'canny');figure,imshow(gc)tt =0.0188 0.0469[gc,t]=edge(f,'canny',[0.04 0.10]); figure,imshow(gc)[gc,t]=edge(f,'canny',[0.04 0.10],1.5); figure,imshow(gc)原图像：线检测后得到如下图像：第五次实验课：彩色图像处理f=imread('iris.tif');imshow(b)fr=f(:,:,1);fg=f(:,:,2);fb=f(:,:,3);w=fspecial('disk',3.5);fr_f=imfilter(fr,w,'replicate');fg_f=imfilter(fg,w,'replicate');fb_f=imfilter(fb,w,'replicate');f1=cat(3,fr_f,fg_f,fb_f);原图像：处理后图片为：第六次实验课：形态学处理f=imread('calculator.tif');imshow(f)se=strel('line',55,0);f0=imopen(f,se);f1=imsubtract(f,f0);figure,imshow(f1)原图像：处理后图像：第七次实验课：频域处理f=imread('periodic.jpg');[m,n]=size(f)sig=30;h=lpfilter('gaussian',m,n,sig);F=fft2(double(f));G=h.*F;figure,imshow(abs(G),[])x=real(ifft2(G));figure,imshow(x,[])原图像：处理后图像：f=imread('noise.jpg'); imshow(f)g=fft2(f);s=abs(g);figure,imshow(double(s))figure,imshow(double(s),[])h=fftshift(g);figure,imshow(double(abs(g)),[]) figure,imshow(double(abs(h)),[]) ss=log(1+s);figure,imshow(double(ss),[])原图像：处理后图像：。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验一图像增强和图像分割实验（1）分别用图中给出的直线和曲线作为增强函数进行增强，比较它们的效果并讨论其特点。
线性变换对指数变换图片1 图片2实验步骤：1.在MATLAB中编写灰度图像的线性变换点运算程序图片1处理程序I=imread('图片1.png');%读入原图像I=im2double(I);%转换数据类型为double[M,N]=size(I);figure(1);imshow(I);%显示原图像title('原图像');figure(2);I=rgb2gray(I);L-1%转化为灰度图像[H,x]=imhist(I,64); stem(x,(H/M/N),'.'); title('原图像');%tan=30`a=sqrt(3)/3;b=0;y=a.*I+b;figure(3);imshow(y);title('tan=30'); figure(4);[H,x]=imhist(y,64); stem(x,(H/M/N),'.'); title('tan=30');%tan=45`a=1;b=0;y=a.*I+b; figure(5);imshow(y);title('tan=45'); figure(6);[H,x]=imhist(y,64); stem(x,(H/M/N),'.'); title('tan=45');%tan=60`a=sqrt(3);b=0;y=a.*I+b;figure(7);imshow(y);title('tan=60'); figure(8);[H,x]=imhist(y,64); stem(x,(H/M/N),'.'); title('tan=60');实验结果如下图所示：原图像图片1的原图像tan=30图片1的30度线性变换图像tan=45图片1的45度线性变换图像tan=60图片1的60度线性变换图像原图像tan=30原图像的直方图 30度变换后直方图tan=4545度变换后的直方图 60度变换后直方图图片2处理程序参考图片1处理程序。
图片2实验结果如图所示：原图像图片2原图像tan=3030度变换后图像tan=4545度变换后图像tan=6060度变换后图像2. 实验结果分析由实验结果可以看出，当按照30度线性变换后图像变暗，按照45度变换后图像没有任何改变，按照60度变换后图像变亮，由变换后的直方图可以确认像素点的变化。
由以上分析可以得出，当线性变换函数的斜率大于1时，图像的对比度将增大；当线性变换的斜率小于时，图像的对比度将减小；当线性变换函数的斜率等于1时，图像的对比度不变，只是像素点整体的移动。
虽然线性变换可以改变对比度，但是对图像的细节部分增强有限。
1. 在MATLAB 中编写灰度图像的对指数点运算程序 图片1对数处理程序：I=imread('图片1.png'); %读入原图像I=im2double(I); %转换数据类型为double I=rgb2gray(I); figure(1);imshow(I); %显示原图像title('原图像'); figure(3);[H,x]=imhist(I,64);stem(x,(H/M/N),'.'); title('原图像'); figure(2); y=log(I+1); imshow(I);title('对数变换'); figure(4);[H,x]=imhist(y,64); stem(x,(H/M/N),'.'); title('对数变换');实验结果如下图所示：原图像对数变换图片1直方图 图片1对数变换直方图对数变换对数变换后图像图片1指数处理程序：I=imread('图片1.png'); %读入原图像I=im2double(I); %转换数据类型为double I=rgb2gray(I); [M,N]=size(I); figure(1);imshow(I); %显示原图像 title('原图像');figure(3);[H,x]=imhist(I,64); stem(x,(H/M/N),'.'); title('原图像'); figure(2);imshow(imadjust(I,[],[],3)); figure(4);[H,x]=imhist(imadjust(I,[],[],4),64); stem(x,(H/M/N),'.'); title('指数变换');实验结果如下图所示：原图像指数变换图片1直方图 指数变换后直方图图片1指数变换后图像图片2对指数处理程序参考图片1处理程序。
对指数处理结果如图所示：指数变换图片2指数变换后图像原图像指数变换图片2直方图 指数变换后直方图对数变换对数变换后直方图对数变换图片2对数变换后图像2.实验结果分析A、对数变换采用对数变换，当函数自变量为低值时，曲线斜率很高；自变量为高值时，曲线斜率变小。
由变换后图像和直方图可以得出，对数变换是增强图像中较暗的细节，从而可用来扩展被压缩的高值图像中较暗的像素。
B、指数变换对数变换采用的是伽玛变换（γ>1），同理图像的高灰度区域对比度得到增加。
因为伽玛变换变换不是线性变换，不仅可以改变图像的对比度，还能够增强细节，从而带来整体图像效果的增强和改善。
（2）分别用Roberts算子、Sobel算子、LoG算子和Canny算子进行边缘检测，比较它们的效果并讨论其特点；图片3 图片4实验步骤：1.在MATLAB中编写检测程序I=imread('图片3.png');bw1=edge(I,'roberts');bw2=edge(I,'sobel');bw3=edge(I,'log');bw4=edge(I,'canny');figure(1);imshow(I);title('原图像');figure(2);imshow(bw1);title('roberts');figure(3);imshow(bw2);title('sobel');figure(4);imshow(bw3);title('log');figure(5);imshow(bw4);title('canny');实验结果如图所示：roberts图片3经过roberts算子检测的图像sobel图片3经过sobel算子检测的图像log图片3经过LoG算子检测的图像canny图片3经过canny算子检测的图像图片4处理程序参考图片3处理程序。
实验结果如下图所示：roberts sobelroberts处理后图像 sobel处理后图像logcannyLoG处理后图像 canny处理后图像2.实验结果分析由实验结果可以看出：Roberts利用局部差分算子寻找边缘，边缘定位精度较高，但是容易丢失一部分边缘，同时由于图像没经过平滑处理，因此不具备抑制噪声的能力，所以对含噪声少的图像的处理效果较好；Sobel算子考虑了邻域信息，相当于对图像先做加权平滑处理，然后再做微分运算，虽然能够对噪声有抑制效果，但不能完全排除检测结果中出现的虚假边缘。
对边缘定位准确，但检测出的边缘容易出现多像素宽度；LoG算子即高斯-拉普拉斯算子，克服了拉普拉斯抗噪声比较差的缺点，但在抑制噪声的同时也可能将原有的比较尖锐的边缘也平滑掉，造成这些尖锐的边缘无法被检测到，但是相对于Roberts算子和Sobel算子处理结果稍好;Canny算子：在图像边缘检测中，抑制噪声和边缘精确定位是无法同时瞒足的，Canny算子在力图在抗干扰和精确定位之间寻求最佳的折中方案。
由图像处理结果可以看出，效果较前三者边缘更细腻、清楚。
从边缘定位的精度看：Roberts算子和LoG算子定位精度更高。
从对不同方向边缘的敏感性而言：Sobel算子检测斜向阶跃边缘效果较好；Roberts算子检测水平和垂直边缘效果较好；LoG算子不具备边缘方向检测能力；Soberl算子可以提供最精确的边缘方向估计。
从去噪能力看：Roberts算子和LoG算子虽然定位精度较高，但受噪声影响大。
从总体效果来衡量，Canny算子给出了一种边缘定位精确性和抗噪声干扰性的较好折中。
（3）采用不同阈值化方法（固定阈值、迭代阈值、Otsu 阈值等）对图像进行分割，比较它们的效果并讨论其特点；图片5 图片6实验步骤： 1. 固定阈值：I=imread('图片5.png');figure(1);imshow(I);title('原图像'); figure(2);imhist(I);title('直方图'); i=1;j=1; for i=1:1:256 for j=1:1:256 if (I(i,j)<=129)I(i,j)=0; else I(i,j)=255; end end endfigure(3);imshow(I);title('129阈值');直方图50100150200250129阈值图片5直方图 取129阈值分割图片6处理过程参考图片5。
实验结果如图所示：直方图05010015020025083图片6直方图取83阈值分割2.迭代阈值：I=imread('图片5.png');ZMAX=max(max(I)); %取出最大灰度值ZMIN=min(min(I)); %取出最小灰度值TK=(ZMAX+ZMIN)/2;bcal=1;ISIZE=size(I); %读出图像大小while(bcal)iForeground=0; %定义前景和背景数 iBackground=0;ForegroundSum=0;%定义前景和背景灰度总和BackgroundSum=0;for i=1:ISIZE(1)for j=1:ISIZE(2)tmp=I(i,j);if(tmp>=TK)iForeground=iForeground+1;ForegroundSum=ForegroundSum+double(tmp); %前景灰度值elseiBackground=iBackground+1; BackgroundSum=BackgroundSum+double(tmp);endendendZO=ForegroundSum/iForeground;%计算前景和背景的平均值ZB=BackgroundSum/iBackground;TKTmp=uint8(ZO+ZB)/2;if(TKTmp==TK )bcal=0;elseTK=TKTmp;end%当阈值不再变化的时候，说明迭代结束enddisp(strcat('迭代后的阀值：',num2str(double(TK))));%显示最终阈值newI=im2bw(I,double(TK)/255);figure(1);imshow(I);title('原始图像');figure(2);imshow(newI);title('迭代法分割')实验结果：迭代后的阀值：128迭代法分割图片5迭代分割图片6处理过程同上，实验结果如图所示：迭代后的阀值：104迭代法分割图片6迭代分割3. Otsu 阈值：I = imread('图片5.png'); level = graythresh(I); BW = im2bw(I,level);figure(1);imshow(I);title('原图像'); figure(2); imshow(BW);title('otsu');实验结果：Level=0.5137otsuOtsu 阈值分割图片6处理过程同上，实验结果如下： Level=0.4039；otsuOtsu 阈值分割4.实验结果分析固定阈值：由图片5和图片6的处理结果看出，固定阈值适合具有明显双峰的图像，但是当两个峰值相差很远时不适用，而且容易受到噪声的干扰，进而导致阈值的选取误差。