加法与减法的关系,乘法与除法的关系
四则运算的相同点和不同点

四则运算的相同点和不同点
四则运算指的是加法、减法、乘法和除法这四种基本运算。
它们的相同点和不同点如下:
相同点:
1. 都是基本的数学运算方法,用于计算数值之间的关系。
2. 都可以用于解决实际生活中的问题,比如计算购物费用、计算面积等。
3. 都遵循一定的运算规则,如加法和乘法都满足交换律和结合律。
不同点:
1. 运算符不同:加法使用"+"运算符,减法使用"-"运算符,乘法使用"*"运算符,除法使用"/"运算符。
2. 运算对象不同:加法和减法可以对两个数进行运算,乘法可以对两个或多个数进行运算,除法需要一个被除数和一个除数进行运算。
3. 运算规则不同:加法满足交换律和结合律,减法和除法不满足交换律和结合律,乘法满足交换律和结合律但不满足分配律。
4. 运算结果不同:加法的结果是两个数的和,减法的结果是两个数的差,乘法的结果是两个数的积,除法的结果是两个数的商。
四年级数学PPT1(加减法的意义和各部分间的关系、乘除法的意义和各部分间的关系)

(2)有12枝花,每3枝插一瓶,可以插几瓶? 12 ÷ 3 = 4(瓶)
除数 商 (3)有12枝花,平均插到4个花瓶里,每个花瓶插几枝?
12 ÷4 = 3(枝)
除数 商
已知两个因数的积与其中一个因数,求另一个因数的 运算,叫做除法
在除法中已知的积叫做被除数,其中的一个因数叫 除数,所求的结果叫做商
3. 直接写出得数
24+0=24 0+504=504 13-13= 0 70-0= 70 0×8= 0 392×0=0 0÷9= 0 0÷36= 0
① 一个数加上零,还得原数。 ② 被减数等于减数,差是零。 ③ 一个数和0相乘,仍得0。 ④ 0除以一个非零的数,还得零。
(176)-56=120
被减数=差+减数
( )= 56+120 =176
483加上我得数是792 483+(309)=792
加数=和-另一个加数 ( )=792-483 =309
巩固新知
一: 利用加、减法各部分间的关系写出另外两个等式
203+147=350
203=350-147 147=350-203
在加法中,相加的两个数叫加数,加得的数叫做和
(2) 西宁到拉萨的铁路全长 1956千米,其中西宁到格尔木 长814千米。格尔木到拉萨的铁 路长多少千米?
1956
(3) 西宁到拉萨的铁路全长1956
千米,其中格尔木到拉萨长1142
千米。西宁到格尔木的铁路长多少
千米?
1956
西宁
格尔木
拉萨
814
西宁
格尔木
括号可以改变运算顺序,运算顺序不同,计算结果也不同
2
乘、除法的意义和各部分间的关系
人教四年级数学下册:四则运算(一)教学教案

四则运算(一)教学教案加数的运算工,叫做减法。
在减法中,差=被减数-减数,减数=被减数-差,被减数=减数+差。
3、加、减法之间的关系:减法是加法的逆运算。
考点题库一1.(重点题)列竖式计算,并用加、减法各部分间的关系进行验算。
1325+4786= 验算:3043-684= 验算:2.(难点题)填一填。
309 + = 456 - =3.(辨析题)判断。
1 5 3 6 6 72 + 6 7 2 的验算方法只有一种: + 1 53 6 。
2 2 0 8 2 2 0 8( )4.(变式题)根据122-48=74写一道加法算式和一道减法算式。
123 764 200129319 2852、列式解答:12÷3=4(瓶) 12÷4=3(枝) 答:可以插4瓶。
答:每个花瓶插3枝。
3、明确除法的意义并探索乘、除法之间的关系: 比较问题一中的乘法算式:3×4=12 12 ÷ 3 = 4 12 ÷ 4 = 3 被除数 除数 商 (积) (因数) (因数) 4、探究有余数除法各部分间的关系:3×5+2=17 商×除数+余数=被除数 17 ÷ 5 = 3 …… 2 (17-2)÷5=3 (被除数-余数)÷除数=商 (被除数) (除数) (商) (余数) (17-2)÷3=5 (被除数-余数)÷商=除数 归纳总结 1、乘法的意义和各部分的关系:求几个相同加数的和的简便运算,叫做乘法。
在乘法中,积=因数×因数,因数=积÷另一个因数。
2、除法的意义和各部分的关系:已知两个因数的积与其中一个因数,求另一 个因数的运算,叫做除法。
在没有余数的除法中,商=被除数÷除数,除数=被除数÷商,被除数=商×除数。
在有余数的除法中,被除数=商×除数+余数,商=(被除数-余数)÷除数,除 数=(被除数-余数)÷商。
加、减、乘、除法的意义及关系式

加法的意义:把两个数合并成一个数的运算减法的意义:已知两个加数的和与其中一个加数,求另一个加数的运算乘法的意义:求几个相同加数和的简便运算除法的意义:已知两个因数的积与其中一个因数,求另一个因数的运算加、减法的关系式:一个加数=和-另一个加数;被减数=差+减数;减数=被减数-差乘、除法关系式:一个因数=积÷另一个因数;被除数=商×除数;被除数=商×除数+余数;除数=被除数÷商加法交换律:两个数相加,交换加数的位置,和不变。
这叫做加法交换律。
用字母表示:a+b=b+a加法结合律三个数相加,先把前两个数相加,或先把后两个数相加,和不变。
这叫做加法结合律。
用字母表示:(a+b)+c=a+(b+c)减法的性质:从一个数里连续减去两个数,可以减去这两个数的和,也可以先减去第二个数,再减去第一个数。
用字母表示:a-b-c=a-(b+c)a-b-c=a-c-b a-(b+c)= a-b-c乘法交换律两个数相乘,交换因数的位置,积不变。
这叫做乘法交换律。
用字母表示:a×b=b×a乘法结合律三个数相乘,先把前两个数相乘,或先把后两个数相乘,积不变。
这叫做乘法结合律。
用字母表示:(a×b)×c=a×(b×c)乘法分配律两个数的和与一个数相乘,可以先把它们与这个数分别相乘,再把积相加,结果不变。
这叫做乘法分配律。
用字母表示:(a+b)×c=a×c+b×c除法的性质:一个数连续除以两个数,可以除以这两个数的积,也可以先除以第一个除数,再除以第二个除数.用字母表示:a÷b÷c=a÷(b×c)=a÷c÷b a÷(b×c)= a÷b÷c。
第5讲 用加减法、乘除法关系来求未知数(学生)

第5讲用加减法、乘除法关系来求未知数一、加减法加法各部分间的关系是:和= 加数十加数,一个加数= 和-另一个加数减法各部分间的关系是:差= 被减数-减数,减数= 被减数-差,被减数= 减数+差应用加减法各部分间的关系,可以验算加减法是否正确,也可以求加减法算式中的未知数。
在列含有未知数x的等式解答文字题和应用题时,第一步“设”所求的未知数为x,第二步按照题意列出含有未知数x的等式;第三步解出未知数是多少,要注意的是求出的x所代表的数不写单位名称:最后再写出答案。
例1求x+15=40中的未知数x例2求未知数x(1)x+38=51 (2) 45+x=62例327加上什么数得70?例4 什么数加上49得71?例5求未知数x(1)x-48=35 (2) 135-x=98例6求未知数x(1)x-29=43 (2)64-x=48例7 80减去一个数得49,这个数是多少?例8一个数减去42得33,这个数是多少?例9牧场养的肉牛比奶牛多16头,肉牛有94头,奶牛有多少头?例10 丁丁买了一支钢笔和一支圆珠笔一共花了22元,一支钢笔是15元,那么一支圆珠笔是多少元?二、乘除法乘法各部分间的关系是:积=被乘数×乘数(因数×因数)一个因数=积÷另一个因数除法各部分间的关系是:商=被除数÷除数,除数=被除数÷商,被除数=除数×商。
应用乘除法各部分间的关系,可以验算乘除法是否正确,也可以求乘除法算式中的未知数。
怎样才能正确、迅速地求出未知数x呢?我们可以采用“一看,二想,三求,四验”的方法来求未知数x。
一看:看题目中的未知数x是什么数;二想:就是想一想根据哪一种关系式,就要运用已学过的乘除法各部分之间的关系,求出题目中的未知数x;三求:由想到的要运用的关系式来计算出x的值;四验:就是把求出的x值代入原来的式子,算一算等号两边是否相等。
例1求x×5=40中的未知数x。
数的运算

浓缩: 和除以差,商是多少?
和
÷
差
( 45 + 39 ) ÷( 62—58 )
————浓缩式分析法
1 (3) 一个数加上它的 2 是75,求这个数。 1 代入为:一个数加上这个数的 2 是75,求这个数。 1 一个数 + 这个数的 2 = 75
解:设这个数为X。 X + 1 — 2 X=75 ————代入式分析法
(4) 用84与40的差去除160与720的和,商是多少? 用84与40的差去除160与720的和,商是多少? 浓缩为:差除和,商是多少? 颠倒为:和除以差,商是多少? 和 ÷ 差
( 160 +720 ) ( 84 - 40 ) ÷ ————颠倒式分析法
解答文字题的关键:
正确理解数字名词和术语(如:和、商、积、差、除、
另一个因数的运算,叫除法。
整数 加法 减法
小数
分数
把两个数合并成一个数的运算. 已知两个数的和与其中的一个加数,求另一个 加数的运算. 求几个相同加数的和 的简便运算
一个数与小数 相乘,可以看 作是求这个数 的十分之、百 分之几…… 是 多少。 一个数与分数相 乘,可以看作是求 这个数的几分之几 是多少。
)
(5)已知a是一个真分数,b是一个假分数,在下列算式中答案一定大于1的算式
是( )
A 、a÷b (6)已知
÷
B、a×b =4, ÷
C 、b-a
D、a+b 少( )
=3 , =1/4.那么 比
A 、1/3
B、1/4
C 、3/4
D、1/12
200的4/5是多少?
200减少它的3/5是多少?
800增加1/8是多少? 800增加1/8,增加了多少?
加减乘除法的意义和各部分之间的关系复习汇编

一:加法的意义和各部分之间的关系 1、什么叫做加法?
237+498= 735
把两个数合并成一个数的运算,叫 做加法
2、加法各部分之间的关系 735-237= 498 237+498= 735 735-498= 237 和 加 加 数 数
加数+加数=和 一个加数=和-另一个加数
二、减法的意义和各部分之间的关系 1、什么叫做减法? 237+498= 735 735-237= 498 735-498= 237
注意:0 不能作除数。例如,5÷ 0 不可能 得到商,因为找不到一个数同0 相乘得到5。 0能不能作除数 0÷ 0 不可能得到一个确定的商,因为任何 数同0 相乘都得0。
整数加法式计算法则:
相同数位对齐,从低位 加起,哪一位上的数相加 满十,就向前一位进一。
整数减法竖式计算法则:
相同数位对齐,从低位减起, 哪一位上的数不够减,就从它 的前一位退一作十,和本位上 的数合并在一起,再减。
已知两个数的和与其中的一个加数, 求另一个加数的运算,叫做减法。
减法是加法的逆运算
2、减法各部分之间的关系
735-498= 237 被 减 差 减 数 数 735-237= 498
237+498= 735
被减数- 减数=差 被减数= 减数+ 差 减数= 被减数- 差
加数+ 加数=和 一个加数= 和- 另一个加数
减法 99-0= 99 89-89= 0
一个数减去0还得原数。 被减数等于减数,差是0。
乘法 67679×0= 0 0×9999= 0
一个数乘0,还得原数。
0除以一个非零的数,还得0。
除法 0÷76= 0
四年级数学下册(原卷)人教版 第一单元《四则运算》单元复习
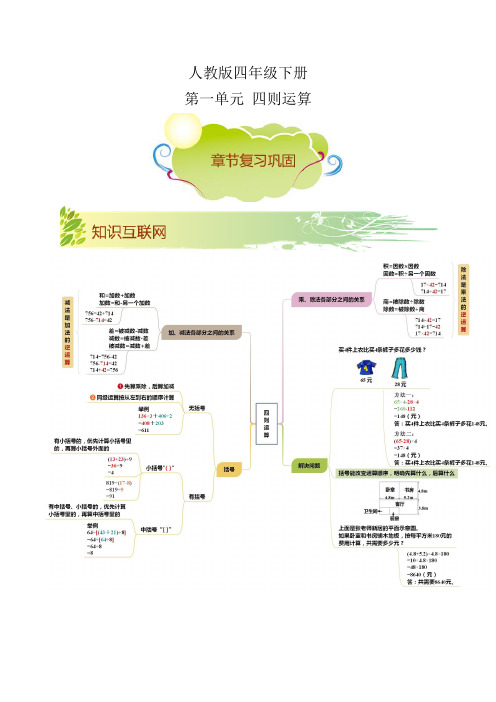
人教版四年级下册第一单元四则运算知识点一:.加、减法的意义和各部分间的关系1.加、减法的意义(1)把两个数合并成一个数的运算,叫做加法。
在加法中,相加的两个数叫做加数,加得的数叫做和。
(2)已知两个数的和与其中的一个加数,求另一个加数的运算,叫做减法。
在减法中,已知的和叫做被减数,减号后面的数叫做减数,减得的数叫做差。
(3)减法是加法的逆运算。
2.加、减法各部分间的关系(1)加法各部分间的关系:和=加数+加数,加数=和一另一个加数。
(2)减法各部分间的关系:差=被减数一减数,减数=被减数-差,被减数=减数+差。
(3)由加、减法各部分间的关系,我们可以根据一个加法算式写出两个减法算式,也可以根据一个减法算式写出一个加法算式和一个减法算式。
知识点二:.乘、除法的意义和各部分间的关系1.乘、除法的意义(1)求几个相同加数的和的简便运算,叫做乘法。
在乘法中,相乘的两个数叫做因数,乘得的数叫做积。
(2)已知两个因数的积与其中一个因数,求另一个因数的运算,叫做除法。
在除法中,已知的积叫做被除数,其中一个因数叫做除数,求出的另一个因数叫做商。
(3)除法是乘法的逆运算。
2.乘、除法各部分间的关系(1)乘法各部分间的关系:积=因数×因数因数=积÷另一个因数(2)除法各部分间的关系:商=被除数÷除数除数=被除数÷商被除数=商×除数3.有关0的运算(1)一个数加上0,还得原数;一个数减去0,还得原数;被减数等于减数,差是0;一个数和0相乘,仍得0;0除以一个非0的数,还得0。
(2)注意:0不能作除数。
知识点三:括号1.四则运算我们学过的加、减、乘、除四种运算统称四则运算。
2.有括号的混合运算的顺序(1)一个算式里,有小括号的要先算小括号里面的,再算小括号外面的。
(2)一个算式里,既有小括号,又有中括号,要先算小括号里面的,再算中括号里面的。
3.解决租车、租船等最省钱问题解决此类问题时,可以先假设(如假设全租大船,或假设全租小船),然后再根据计算结果进行调整。
