直线与圆的位置关系2--浙教版
浙教版九年级数学(全一册)课件第2章 直线与圆的位置关系 切线长定理

A
P O
B
A
O.
O1
P
B
直径所对的圆周角是直角.
新课讲解
1 切线长的定义
1.切线长的定义:
经过圆外一点作圆的切
A
线,这点和切点之间的线段的
长叫做切线长.
O P
2.切线长与切线的区别在哪里?
①切线是直线,不能度量.
②切线长是线段的长,这条线段的两个端点分别 是圆外一点和切点,可以度量.
新课讲解
2 切线长定理
平分两条切线的夹角. 几何语言:
PA、PB分别切⊙O于A、B
B PA = PB ∠OPA=∠OPB
注意: 切线长定理为证明线段相等、角相等提供了新的方 法.
新课讲解
拓展结论 A
PA、PB是⊙O的两条切线,A、B
为切点,直线OP交⊙O于点D、E,
E OCD
P
交AB于C.
(1)写出图中所有的垂直关系;
AP=4, ∠APB= 40 ° ,则∠APO= 20,P°B= 4 .
A P
O
A P
O
B 第1题
B 第2题
2.如图,PA、PB是⊙O的两条切线,切点为A、B,∠P= 50 °,点
C是⊙O上异于A、B的点,则∠ACB= 65 °或1.15 °
随堂练习
3.PA、PB是⊙O的两条切线,A,B是切点,OA=3. (1)若AP=4,则OP= 5 ;
(2)若∠BPA=60 °,则OP= 6 .
A
O
P
B
课堂总结
切线长 切线长 定理
三角形 内切圆
原理 作用
图形的轴对称性
提供了证线段和 角相等的新方法
辅助线
有关概念
浙教版数学九年级下册2.1《直线与圆的位置关系》教学设计2

浙教版数学九年级下册2.1《直线与圆的位置关系》教学设计2一. 教材分析《直线与圆的位置关系》是浙教版数学九年级下册2.1的内容,本节课主要探讨直线与圆的位置关系,包括相切和相交两种情况。
通过本节课的学习,学生能够理解直线与圆的位置关系的概念,掌握判断直线与圆位置关系的方法,以及会运用直线与圆的位置关系解决实际问题。
二. 学情分析九年级的学生已经学习了直线、圆的基本知识,对图形的直观感知和空间想象能力有一定的基础。
但直线与圆的位置关系较为抽象,需要学生具有较强的逻辑思维能力和综合运用知识的能力。
因此,在教学过程中,要注重启发学生的思维,引导学生主动探究,提高学生的动手实践能力。
三. 教学目标1.理解直线与圆的位置关系的概念,掌握判断直线与圆位置关系的方法。
2.能够运用直线与圆的位置关系解决实际问题。
3.培养学生的空间想象力,提高学生的逻辑思维能力和综合运用知识的能力。
四. 教学重难点1.教学重点:直线与圆的位置关系的概念,判断直线与圆位置关系的方法。
2.教学难点:直线与圆的位置关系的应用,解决实际问题。
五. 教学方法1.情境教学法:通过生活中的实例,引导学生感受直线与圆的位置关系,激发学生的学习兴趣。
2.启发式教学法:在教学过程中,引导学生主动探究,培养学生的思维能力。
3.实践操作法:让学生通过动手实践,加深对直线与圆位置关系的理解。
4.小组合作学习:鼓励学生分组讨论,培养学生的团队协作能力。
六. 教学准备1.教学课件:制作精美的教学课件,辅助教学。
2.实例素材:收集生活中的直线与圆的位置关系的实例,用于导入和巩固环节。
3.练习题:准备相应的练习题,用于巩固和拓展环节。
七. 教学过程1.导入(5分钟)利用生活中的实例,如自行车轮子、地球仪上的经纬线等,引导学生感受直线与圆的位置关系,激发学生的学习兴趣。
同时,提出问题,引导学生思考直线与圆的位置关系。
2.呈现(10分钟)通过课件展示直线与圆的位置关系的概念,以及判断直线与圆位置关系的方法。
【浙教版】九年级数学下册:2.1直线与圆的位置关系第3课时切线的性质

第2章直线与圆的位置关系2.1 直线与圆的位置关系第3课时切线的性质知识点切线的性质1.下列说法中,正确的是( )A.圆的切线垂直于经过切点的半径B.垂直于切线的直线必经过切点C.垂直于切线的直线必经过圆心D.垂直于半径的直线是圆的切线2.如图2-1-23所示,AB是⊙O的弦,BC与⊙O相切于点B,连结OA,OB,若∠ABC =70°,则∠A的度数为( )A.15° B.20° C.30° D.70°2-1-232-1-243.如图2-1-24,P是⊙O外一点,PA是⊙O的切线,PO=26 cm,PA=24 cm,则⊙O 的周长为( )A.18π cm B.16π cmC.20π cm D.24π cm4.如图2-1-25,AC是⊙O的切线,切点为C,BC是⊙O的直径,AB交⊙O于点D,连结OD.若∠BAC=55°,则∠COD的度数为( )A.70° B.60° C.55° D.35°2-1-252-1-265.如图2-1-26,在以O为圆心的两个同心圆中,大圆的弦AB切小圆于点C.若∠AOB =120°,则大圆半径R与小圆半径r之间满足( )A.R=3r B.R=3rC.R=2r D.R=2 2r6.如图2-1-27,已知AB是⊙O的直径,C是AB延长线上一点,BC=OB,CE是⊙O 的切线,切点为D,过点A作AE⊥CE,垂足为E,则CD∶DE的值是( )A.12B.1 C.2 D.3图2-1-272-1-287.如图2-1-28所示,PA,PB是⊙O的切线,切点分别为A,B,点C在⊙O上.如果∠ACB=70°,那么∠P的度数是________.8.如图2-1-29所示,已知AB是⊙O的切线,A为切点,OB交⊙O于点C,AB=3 cm,BC=1 cm,求⊙O的半径.图2-1-299.2017·常德如图2-1-30,已知AB是⊙O的直径,CD与⊙O相切于点C,BE∥CO.(1)求证:BC是∠ABE的平分线;(2)若DC=8,⊙O的半径OA=6,求CE的长.图2-1-3010.如图2-1-31所示,PA 和PB 是⊙O 的切线,A ,B 是切点,AC 是⊙O 的直径.已知∠P =40°,则∠ACB 的大小是( )A .60°B .65°C .70°D .75°11.课本课内练习第2题变式在半径为13的⊙O 中,CD 是⊙O 的一条弦,AB 是⊙O 的切线,且AB ∥CD ,若AB 和CD 之间的距离为18,则弦CD 的长为________.2-1-312-1-3212.如图2-1-32所示,在△ABC 中,BC =4,以点A 为圆心,2为半径的⊙A 与BC 相切于点D ,交AB 于点E ,交AC 于点F ,且∠EAF =80°,则图中阴影部分的面积是________.13.2017·温州一模如图2-1-33,点C 在以AB 为直径的⊙O 上,过点C 作⊙O 的切线交AB 的延长线于点E ,AD ⊥CE 于点D ,连结AC ,BC .(1)求证:AC 平分∠BAD ;(2)若tan ∠CAD =34,AD =8,求⊙O 的直径AB 的长.图2-1-3314.2017·衢州如图2-1-34,AB 为半圆O 的直径,C 为BA 延长线上一点,CD 切半圆O 于点D ,连结OD .作BE ⊥CD 于点E ,交半圆O 于点F .已知CE =12,BE =9.(1)求证:△COD ∽△CBE ; (2)求半圆O 的半径r .图2-1-3415.如图2-1-35,AB 为⊙O 的直径,直线CD 切⊙O 于点D ,AM ⊥CD 于点M ,BN ⊥CD 于点N .(1)求证:∠ADC =∠ABD ; (2)求证:AD 2=AM ·AB ;(3)若AM =185,sin ∠ABD =35,求线段BN 的长.图2-1-35。
直线和圆的位置关系课件(浙教版)

A
CB QH
数学知识: 直线与圆的三种位置关系.
直线与圆的位置关系的判定方法. 根据已知条件作与直线相切的圆. 生活与数学.
思想方法:
分类互逆思想.
1.作业本 2.课本P50组(4)(5)
希望大家如这旭日, 朝气蓬勃!
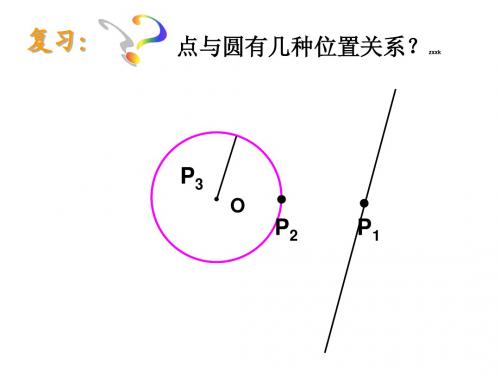
1.设⊙O的半径为4,点O到直线a的距离为d,
1、已知⊙O的半径为5cm,O到直线a的距离 为3cm,则⊙O与直线a的位置关系是_相_交___。 直线a与⊙O的公共点个数是_两_个__。
2、已知⊙O的半径是4cm,O到直线a的距离 是4cm,则⊙O与直线a的位置关系是相__切_ 。
3、已知⊙O的半径为6cm,O到 直线a的距离为7cm,则直线a与 ⊙O的公共点个数是_零___。
若⊙O与直线a至多只有一个公共点,则d为 ( C )
A、d≤4 B、d<4 C、d≥4 D、d=4 2.设⊙P的半径为4cm,直线l上一点A到圆心的距离为
4cm,则直线l与⊙O的位置关系是( D )
A、相交 B、相切 C、相离 D、相切或相交
3.已知⊙A的直径为6,点A的坐标为(-3,-4),
则⊙A与X轴的位置关系是_相__离__, ⊙A与Y轴的位置关系是_相__切___。
4、已知⊙O的直径是6cm, O到直线a的距离是4cm, 则⊙O与直线a的位置关系是相_离__ _。
在码头A的北偏东60°方向有一个海岛, 离该岛中心P的15海里范围内是一个暗礁区。货船 从码头A由西向东方向航行,行驶了18海里到达B, 这时岛中心P在北偏东30°方向。若货船不改变航 向,问货船会不会进入暗礁区?
.O .A
1.若A为⊙O上的一点,则过点A的直线与⊙O相切( × ) 变:若A为⊙O内一点呢? 过点A的直线与 ⊙O必相交
3.1 直线与圆的位置关系 课件2(数学浙教版九年级下册)
· O
(3) l
· O
l
· O
l 相离 (4) 相交 (5)
· O ?
相切
· O
相交
l
l
(5)
· O ?
l
· ·
如果,公共点的个数不好判断, 该怎么办? “直线和圆的位置关系”能否像 “点和圆的位置关系”一样进行数 量分析?
Z..x..x..k
A
B
如图,O为直线l外 一 点,OT⊥l,设OT=d, 请以O为圆心,r为半径画圆,r分别满足下列条 件:⑴ d < r ,⑵d=r,⑶ d > r 。
3 (2)d= 2 , r=3 ;∵ d < r∴直线l与⊙O相交 2 3 ( 3) d= 3 , r = 5 ; ∵d> r∴直线l与⊙O相离
√ 5 ,r=2 √ 5; ( 4) d= 2 ∵d=r∴直线l与⊙O相切
在△ABC中,∠C=900 , AC=3cm, BC=4cm,设⊙C的半径为r,请根据r的下列值, 判断直线AB与⊙C的位置关系,并说明理由。 (1) r=2cm; (2) r=2.4cm (3) r=3cm
O
d T
l
直线与圆的位置关系的性质:
O
r l
O
O
r d T l d T l
d T
圆心O与 直线的距 离关系 直线与圆 的位置关 系:
d<r
d=r
d>r
相离
相交
相切
设⊙O的半径为r,圆心O到直线l的距离为d. 根据下列条件判断直线l与⊙O的位置关系. (1)d=4,r=3;
∵d> r∴直线l与⊙O相离
AC 3OC, BC OC AC BC AB 100 3OC OC 100
浙教版九年级数学(全一册)课件第2章 直线与圆的位置关系 切线的性质与判定

★应用格式 OA为⊙O的半径 BC ⊥ OA于A
BC为⊙O的切线
新课讲解
B
O
A
C
新课讲解 判一判: 下列各直线是不是圆的切线?如果不是,请说明为什么?
O.
A l
(1)
(1)不是,因为没
有垂直.
O.
O
A
l
B
(2)
A
l
(3)
(2),(3)不是,因为没有经过半径的
外端点A.
注意:在此定理中,“经过半径的外端”和“垂直于 这条半径”,两个条件缺一不可,否则就不是圆的切线.
分析:根据切线的判定定理,要 证明AC是⊙O的切线,只要证明
A
E
F
由点O向AC所作的垂线段OF是
⊙O的半径就可以了,而OE是 B
O
C
⊙O的半径,因此只需要证明
OF=OE.
新课讲解
证明:连结OE ,OA, 过O 作OF ⊥AC.
∵⊙O 与AB 相切于E , ∴OE ⊥ AB.
又∵△ABC 中,AB =AC ,
的直径为6. 求证:直线AB是⊙O的切线.
作垂直 O
AC B
AC B
对比思考
新课讲解
2 切线的性质定理
思考:如图,如果直线l是⊙O 的切线,点A为切点,那么OA 与l垂直吗?
★切线性质 圆的切线垂直于经过切点的半径.
★应用格式 ∵直线l是⊙O 的切线,A是切点, ∴直线l ⊥OA.
O
A
l
新课讲解
性 质 有1个公共点
有切线时常用辅助线 添加方法: 见切线,连切点,得垂直.
d=r
情景引入
砂轮上打磨工件时飞出的火星
1 切线的判定定理
浙教版数学九年级下册《2.1 直线与圆的位置关系》教学设计
浙教版数学九年级下册《2.1 直线与圆的位置关系》教学设计一. 教材分析浙教版数学九年级下册第2.1节“直线与圆的位置关系”是本册教材中的重要内容,为学生提供了直线与圆位置关系的理论基础。
这部分内容是在学生已经掌握了圆的基本概念、直线的斜率、方程等知识的基础上进行学习的,为后续解析几何的学习打下基础。
本节课的主要内容有:直线与圆的位置关系的判定,直线与圆相交、相切的条件,以及直线与圆的位置关系的应用。
这些内容不仅涉及到数学理论,还包含了丰富的数学思想,对提高学生的数学素养具有重要意义。
二. 学情分析九年级的学生已经具备了一定的数学基础,能够理解和掌握一些基本的数学概念和原理。
但是,对于直线与圆的位置关系的理解和运用,还需要通过实例和操作来进一步巩固。
此外,学生对于数学证明的过程和方法还需要进一步指导和培养。
三. 教学目标1.知识与技能:使学生掌握直线与圆的位置关系的判定方法,能够运用直线与圆的位置关系解决一些实际问题。
2.过程与方法:通过观察、操作、证明等过程,培养学生的观察能力、动手能力和逻辑思维能力。
3.情感态度与价值观:激发学生对数学的兴趣,培养学生的团队合作意识,提高学生解决实际问题的能力。
四. 教学重难点1.重点:直线与圆的位置关系的判定,直线与圆相交、相切的条件。
2.难点:直线与圆的位置关系的证明和应用。
五. 教学方法1.引导法:通过问题引导,让学生自主探究直线与圆的位置关系。
2.演示法:通过几何画板的演示,让学生直观地理解直线与圆的位置关系。
3.讨论法:让学生分组讨论,培养学生的团队合作意识和解决问题的能力。
4.练习法:通过大量的练习题,巩固学生对直线与圆位置关系的理解和运用。
六. 教学准备1.教具:几何画板、黑板、粉笔。
2.学具:笔记本、练习本、尺子、圆规、橡皮擦。
3.课件:直线与圆的位置关系的动画演示、例题讲解。
七. 教学过程1.导入(5分钟)通过提问方式引导学生回顾圆的基本概念、直线的斜率和方程等知识,为新课的学习做好铺垫。
浙教版数学九年级下册2.1《直线与圆的位置关系》说课稿1
浙教版数学九年级下册2.1《直线与圆的位置关系》说课稿1一. 教材分析《直线与圆的位置关系》是浙教版数学九年级下册第2章第1节的内容。
本节课主要介绍了直线与圆的位置关系,包括相切、相交和相离三种情况,并学习了如何判断直线与圆的位置关系。
教材通过实例和问题,引导学生探究和发现直线与圆的位置关系,培养学生的空间想象能力和解决问题的能力。
二. 学情分析九年级的学生已经学习了平面几何的基础知识,对图形的性质和判定有一定的了解。
但是,对于直线与圆的位置关系的理解和应用,部分学生可能会感到困难。
因此,在教学过程中,需要关注学生的学习情况,针对性地进行辅导和指导。
三. 说教学目标1.知识与技能目标:学生能够理解直线与圆的位置关系的概念,学会判断直线与圆的位置关系。
2.过程与方法目标:学生通过观察、操作和思考,培养空间想象能力和解决问题的能力。
3.情感态度与价值观目标:学生能够积极参与课堂活动,克服困难,增强对数学学习的信心和兴趣。
四. 说教学重难点1.教学重点:直线与圆的位置关系的概念和判断方法。
2.教学难点:直线与圆的位置关系的理解和应用。
五. 说教学方法与手段1.教学方法:采用问题驱动法、案例教学法和合作学习法。
2.教学手段:利用多媒体课件和实物模型进行教学。
六. 说教学过程1.导入:通过实例展示直线与圆的位置关系,引发学生的兴趣和思考。
2.新课导入:介绍直线与圆的位置关系的概念和判断方法。
3.案例分析:分析具体案例,让学生理解和掌握直线与圆的位置关系的判断方法。
4.课堂练习:学生自主完成练习题,巩固所学知识。
5.应用拓展:学生分组讨论,探索直线与圆的位置关系在实际问题中的应用。
6.总结:对本节课的内容进行总结,强调直线与圆的位置关系的重要性和应用价值。
七. 说板书设计板书设计如下:直线与圆的位置关系八. 说教学评价教学评价主要包括学生的课堂参与度、作业完成情况和课堂表现等方面。
通过观察学生的学习情况和反馈,了解学生对直线与圆的位置关系的理解和掌握程度,及时进行教学调整和改进。
九年级数学下册 2.1 直线与圆的位置关系 切线的性质课件 (新版)浙教版
点C的切线的垂线,垂足为D,交BC的延长线于点E。连
结AC。
E
根据上述操作及已知条件,在图中
D
找出一些相等的线段和角,并证明
C
你所得到的结论。
A
O
B
O D
∵⊙O与AB相切于点C
E
∴OC⊥AB
A
C
B
∴∠ACD=∠COE=900-∠OCE
ACD1COD 2
1、如图:PA,PC分别切圆O于点A,C两点,B为圆O上与 A,C不重合的点,若∠P=50°,求∠ABC的度数。
C
O
B
O
P
A
AC
B
2、如图,已知:AB与⊙O相切于点C ,OA=OB,⊙O的
的理由
圆的切线垂直于经过切点的半径 T
C
O
A
B
B
O
A
P
l
2、如图,AT切⊙O于点A,AB⊥AT,交⊙O于点B,BT
交⊙O于点C。已知∠B=300,AT= 3 。求⊙O的直径
和弦BC的长。经过切点垂直于切线的直线必经过圆心
3.如图,AB切⊙O于点B,割线ACD经过圆心O,若
∠BCD=700, 则∠A的度数为( B )
经过切点的半径垂直于圆的切线
O
A
已知直线AT切⊙O于点A(切 点),连结OA,则OA是半径.
T 问:
②过点A作AT的垂线,垂线 过点O吗?
O
A
经过切点垂直于切线的直线必经过圆心
一般地,
P
O
圆的切线有如下的性质:
T A
经过切点的半径垂直于圆的切线 (判定垂直)
经过切点垂直于切线的直线必经过圆心(判定半径或直径)
浙教版九年级下册2.1.3直线和圆的位置关系课件(共21张PPT)
3.AB是⊙O的直径,AE平分∠BAC交⊙O于点E,过点E 作⊙O的切线交AC于点D,试判断△AED的形状,并 说明理由.
练一练
4、如图,∠APC=50°,PA、PC、DE都为⊙O的切线,
则∠DOE为 65° 。 变式:改变切线DE的位置,
C D
则∠DOE= 6;5°
CD
F
O
P
F
E
O
P
A
E
A
归纳:只要∠APC的大小不变,∠DOE也不变.
切线的性质3、4、5可归纳为:已知直线满 足a、过圆心,b、过切点,c、垂直于切线中任 意两个,便得到第三个结论。
试一试
1、如图,直线l切⊙O于点P,弦AB∥l,请说明 AP=PB
的理由
圆的切线垂直于经过切点的半径 T
C
O
A
B
BOA
P
l
2、如图,AT切⊙O于点A,AB⊥AT,交⊙O于点B,BT
交⊙O于点C。已知∠B=300,AT= 3 。求⊙O的直径
如图,直线AB与⊙O相切于点C,射线AO交⊙O于点D,E, 连结CD,CE.
1)求证: ∠ACD=∠AEC
2)找出图中的一对相似三角形,并说明理由。
E O
D
A
C
B
弦切角
弦切角定义:
顶点在圆上,一边与圆相交,另一边与 圆相切的角叫弦切角.
C
∠BAC的特征:
(1) 顶点在圆上;
B
(2) 一边和圆相交; A B (3) 一边和圆相切。
练一练
练习1、判别下列图形中的角是不是弦切角, 并说明理由。(图中AB与圆相切于A)( D)
A
B
C
D
弦切角
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
直线与圆的位置关系有下面的性质: 如果⊙O的半径为r,圆心O到直线l 的距离为d,那么 (1)d<r 直线l 与⊙O相交
(2)d=r
(3)d > r
直线l 与⊙O相切
直线l 与⊙O相离
O
请按照下述步骤作图:
A
如图,在⊙O上任取一点A,连结OA,,过点A作直线l⊥O距离和圆的半径有什么关系? 相等 相切 d=r (2)直线l 和⊙ O的位置有什么关系?根据什么?
(3)由此你发现了什么?
一般地,有以下直线与圆相切的判定定理: 经过半径的外端并且垂直这条 半径的直线是圆的切线 几何语言表示:
∵l⊥OA 且OA为圆O的半径 ∴ l是⊙O的切线
2.如图,OP是⊙O的半径,∠POT=60°,
Q S O P
OT交⊙O于S点.
(1)过点P作⊙O的切线. (2)过点P的切线交OT于Q,判断S是不 是OQ的中点,并说明理由.
请任意画一个圆,并在这个圆所在的平面内任意取一点P. (1)过点P是否都能作这个圆的切线? 点在圆内不能作切线 点在圆上
(2)点P在什么位置时,能作并且只能作一条切线?
A
D
B
3、如图,AB是⊙O的直径,BC切⊙O于点 B,连结OC,过A作AD∥OC,交⊙O于点 D,连结DC。求证:CD是⊙O的切线。
A O B D
C
数控切割机 / 数控型材切割机 数控激光切管机 数控全自动切割机
yrk910qox
列车上有人问我,为什么要回来?你是第一个离开了再回来的人。 我没说。
(2)若∠C=30°,CD=10cm,求⊙O的半径. C
D E A O B
2、如图,在Rt△ABC中,∠ACB=Rt∠,CD⊥AB于 点D。 (1)求证:BC是△ADC的外接圆的切线; (2) △BDC的外接圆的切线是哪一条?为什么? (3)若AC=5,BC=12,以C为圆心作圆C,使圆C与 AB相切,则圆C的半径是多少? C
y(km)
600 500 400
D A
30°
B C
300
200 100 0
P
100
200 300 400 500 600 700
X(km)
1.如图,Q在⊙O上,分别根据下列条件,判定直线PQ与⊙O是否 相切: Q
(1)OQ=6,OP=10,PQ=8
(2)∠O=67.3°,∠P=22°42′
O
P T
我终于知道,在一段关系里,最伤人的不是时间,也不是距离。是我忘了的你还记得,而我想起时,你却不见了。
我终于不会再忘记她,因为这里的时间永远不会变,我选择留在自己的时间里,假装她还没有离开。 如果有一天你不画画了,也许还可以尝试写作。 我写的东西估计不会有人看。 不见得。 不,长安,我们都是遵从内心真实感受的人,写下的无非也只是某个时刻的片段式感受,太过私人化和碎片化,难以引起读者 的共鸣。 这样想来也是。太过忠于内心的感受,无法迎合热潮。
O l A
问:如何过圆上一个已知点做圆的切线呢?
做一做:
A O
B
如图AB是⊙O的直径,请分别过A,B作⊙O的切线.
例1.已知:如图A是⊙O外一点,AO的延长线交⊙O于点C,点B
在圆上,且AB=BC,∠A=30°. 求证:直线AB是⊙O的切线 B C A
证明:连结OB
∵OB=OC,AB=BC,∠A=30°
(3)点P在什么位置时,能作两条切线?这两条切线有什么特性? 点在圆外 (4)能作多于2条的切线吗? 相等 不能
切线的判定定理:
经过半径的外端并且垂直这条半径的直线是圆的切线
这个定理不仅可以用来判定圆的切线,还可以依据它来画切线. 在判定切线的时候,如果已知点在圆上,则连半径是常用的辅助线
1、如图,已知AB是⊙O的直径,⊙O过BC的中点D,且DE⊥AC. (1)求证:DE是⊙O的切线.
O
∴∠OBC=∠C=∠A=30° ∴∠AOB=∠C+ ∠OBC =60° ∵∠ABO=180°-(∠AOB+∠A) =180°-(60°+30°) =90° ∴AB⊥OB ∴AB为⊙O的切线
例2.如图,台风P(100,200)沿北偏东30°方向移动,受 台风影响区域的半径为200km,那么下列城市 A(200,380),B(600,480),C(550,300),D(370,540)中, 哪些受到这次台风的影响,哪些不受到台风的影响?
