必修2直线与圆的位置关系
人教A版数学必修2课件：4.2.1直线与圆的位置关系
仿照点和圆位置关系的 判定，怎样判断直线和 圆的位置关系呢？
二、直线与圆的位置关系的判定：
方法1：定义法 判断方法： (1)△＞0 直线与圆相交； 方法2：几何法
圆心到直线的距离d与 (3)△＜0 直线与圆相离. 直线与圆没有交点 半径r的大小关系
(d△ >r= ) 0 直线与圆相切； 1、相离 (2)
2 2
交于A, B两点.
x y 5 0 若弦长 A B 最大，则直线l的方程是2 ___________; x 2y 5 0 若弦长 A B 最短，则直线l的方程是___________.
【总一总★成竹在胸】
一、直线与圆的位置关系； 二、直线与圆的位置关系的判定； 三、直线与圆相交时弦长的求法。
(1)几何法：用弦心距d，半径r及 半弦构成直角三角形的三边
AB r d , d为弦心距，r为半径 2
2 2 2
y r
B
A
d O
x
(2)代数法：用弦长公式
AB 1 k x1 x2 1 k x1 x2 4x1 x2
2 2 2
1.直线x+y-2=0与圆x2+y2=2的位置关
相切 系为________ 2.直线x-y-2=0与圆(x-1)2+(y-1)2=1的
相离 位置关系为________
3.直线x+2y-1=0和圆x2-2x+y2-y+1=0 相交 的位置关系为________
直线和圆相交时, 如何来求弦长呢？
三、直线与圆相交时弦长的求法：
1 1 AB 1 y1 y2 1 k k
2
2Leabharlann y1 y2 2
高中数学必修二-直线与圆的位置关系
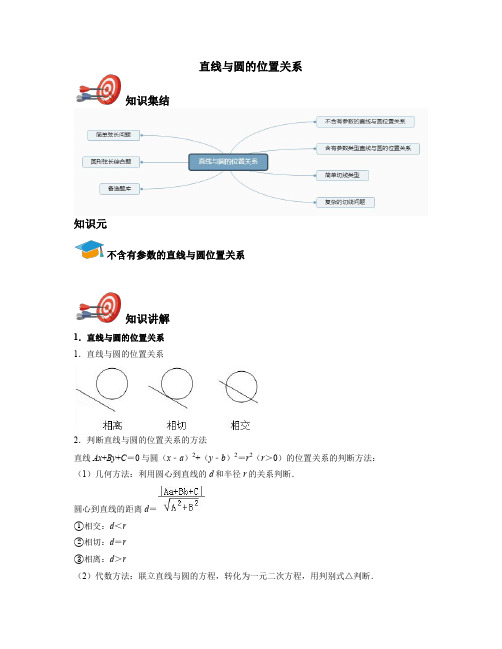
直线与圆的位置关系知识集结知识元不含有参数的直线与圆位置关系知识讲解1．直线与圆的位置关系1．直线与圆的位置关系2．判断直线与圆的位置关系的方法直线Ax+By+C＝0与圆（x﹣a）2+（y﹣b）2＝r2（r＞0）的位置关系的判断方法：（1）几何方法：利用圆心到直线的d和半径r的关系判断．圆心到直线的距离d＝①相交：d＜r②相切：d＝r③相离：d＞r（2）代数方法：联立直线与圆的方程，转化为一元二次方程，用判别式△判断．由消元，得到一元二次方程的判别式△①相交：△＞0②相切：△＝0③相离：△＜0．例题精讲不含有参数的直线与圆位置关系例1.已知点P在单位圆x2+y2=1上运动，P到直线3x﹣4y﹣10=0与x=3的距离分为d1、d 2，则d1+d2的最小值是．例2.点P是直线x+y﹣2=0上的动点，点Q是圆x2+y2=1上的动点，则线段PQ长的最小值为．例3.经过圆x2+y2﹣2x+2y=0的圆心且与直线2x﹣y=0平行的直线方程是（）A．2x﹣y﹣3=0B．2x﹣y﹣1=0C．2x﹣y+3=0D．x+2y+1=0含有参数类型直线与圆的位置关系知识讲解1．直线与圆的位置关系1．直线与圆的位置关系2．判断直线与圆的位置关系的方法直线Ax+By+C＝0与圆（x﹣a）2+（y﹣b）2＝r2（r＞0）的位置关系的判断方法：（1）几何方法：利用圆心到直线的d和半径r的关系判断．圆心到直线的距离d＝①相交：d＜r②相切：d＝r③相离：d＞r（2）代数方法：联立直线与圆的方程，转化为一元二次方程，用判别式△判断．由消元，得到一元二次方程的判别式△①相交：△＞0②相切：△＝0③相离：△＜0．例题精讲含有参数类型直线与圆的位置关系例1.已知△ABC的三边长为a，b，c，满足直线ax+by+2c=0与圆x2+y2=4相离，则△ABC是（）A．直角三角形B．锐角三角形C．钝角三角形D．以上情况都有可能例2.直线ax﹣y+a=0（a≥0）与圆x2+y2=9的位置关系是（）A．相交B．相切C．相离D．相切或相离例3.圆x2+y2+4x﹣2y﹣1=0上存在两点关于直线ax﹣2by+2=0（a＞0，b＞0）对称，则的最小值为（）A．8B．9C．16D．18简单切线类型知识讲解1．圆的切线方程圆的切线方程一般是指与圆相切的直线方程，特点是与圆只有一个交点，且过圆心与切点的直线垂直切线．圆的切线方程的类型：（1）过圆上一点的切线方程：对于这种情况我们可以通过圆心与切点的连线垂直切线求出切线的斜率，继而求出直线方程（2）过圆外一点的切线方程．这种情况可以先设直线的方程，然后联立方程求出他们只有一个解（交点）时斜率的值，进而求出直线方程．例题精讲简单切线类型例1.设点A为圆（x﹣1）2+y2=1上的动点，PA是圆的切线，且|PA|=1，则P点的轨迹方程为（）A．y2=2x B．（x﹣1）2+y2=4C．y2=﹣2x D．（x﹣1）2+y2=2例2.已知圆的方程是x2+y2=1，则经过圆上一点M（1，0）的切线方程是（）A．x=1B．y=1C．x+y=1D．x﹣y=1例3.'已知圆C的方程为x2+y2﹣2x+4y﹣3=0，直线l：x﹣y+t=0．若直线l与圆C相切，求实数t的值.'简单弦长问题知识讲解弦长问题一、求直线与圆相交时的弦长有三种方法(1)交点法：将直线方程与圆的方程联立，求出交点A，B的坐标，根据两点间的距离公式|AB|＝求解．(2)弦长公式：如图所示，将直线方程与圆的方程联立，设直线与圆的两交点分别是A(x1，y1)，B(x2，y2)，则|AB|＝＝|x1－x2|＝|y1－y2|(直线l的斜率k存在)．(3)几何法：如图，直线与圆C交于A，B两点，设弦心距为d，圆的半径为r，弦长为|AB|，则有()2＋d2＝r2，即|AB|＝2.通常采用几何法较为简便。
高一数学直线与圆的位置关系1
讨论：能否根据两个圆的公共点的个数 判断两圆的位置关系？ 方法：联立两圆的方程构成方程组；再 根据方程组的解的个数判断两圆的位置 关系。
典例讲解
例1、 已知：
圆C1：x2＋y2＋2x＋8y－8＝0，
圆C2：x2＋y2－4x－4y－2＝0， 判断圆C1与圆C2的位置关系.
知识探究（三）
若两圆C1：x2+y2+D1x+E1y+F1=0
和圆C2：x2+y2+D2x+E2y+F2=0相
交，则其公共弦所在直线的方程 (D1-D2)x+(E1-E2)y+F1-F2=0 是 ：
知识探究（四）
若圆O：x2+y2+Dx+Ey+F=0和直线
Ax+By+C=0有公共点，则经过它
们的交点的圆系方程是：
x y Dx Ey F ( Ax By c ) 0
与圆
x y 6 y 28 0
2 2
的交点的圆的方程。
作业： 教材：P130 练习
P133习题9、10、11
《学海》第四章第4课时
；
/macd/ macd指标详解 ； 2019.1
就照我说的办.娜塔莎,听从你政委姐姐的话,注意,要好好瞄准敌人的观察口！" 李小克还记得自己给妻子的承诺,作为副师长要给全师负责,不会愚蠢的像个下级连长帅兵猛攻.但是杀红了眼睛谁在乎,再者时间非常宝贵！它些承诺暂且放在一边战机稍纵即逝. 因为胳膊的伤刚好,还不能 疯狂的抱着冲锋枪一通扫射,卖力气的活儿由属下负责,此刻的他就是监军的存在. 此刻,一部分德军被叶甫根尼的营狠狠拖住,一部分依靠着装甲列车战斗.李小克率领二百多人从街道迂回,他们遭遇了轻微的抵
人教版高中数学必修2《直线与圆的位置关系》教案
四、教学过程设计
解析几何就是用代数方法研究几何图形，当然也要研究几何图形的位置关系，直线与直线的位置关系已经研究清楚，这节课我们研究直线与圆的位置关系。
1．问题情境
问题1．直线与圆的位置关系有几种？在平面几何中，我们怎样判断直线与圆的位置关系呢？
师生活动：学生解答，解释出错原因。
6．课堂小结
问题9判断直线与圆的位置关系有哪些方法?
问题10当直线与圆相交时,如何求弦长?
设计意图：巩固所学知识，培养学生归纳概括能力．
师生活动：学生思考，教师引导时应涉及到“如何求弦长”以及判断直线与圆的位置关系有几种方法？它们的步骤是什么？
人教版高中数学必修2《直线与圆的位置关系》教案这篇文章共11261字。
（2）通过消元，得到一个一元二次方程；
（3）求出其判别式△的值；
（4）判断△的符号：
若△＞0，则直线与圆相交；
若△＝0，则直线与圆相切；
若△＜0，则直线与圆相离．
4．例题示范
例1如图，已知直线：和圆心为的圆，
（1）判断直线与圆的位置关系；
（2）如果相交，求它们交点的坐标．
设计意图：通过例题巩固判断直线与圆的位置关系方法，关注量与量之间的关系．使学生体验用坐标法研究直线与圆的位置关系的想法与结论．
4．当直线与圆有公共点时，能通过联解方程组得出直线与圆的公共点的坐标．
5．当直线与圆相交时，会求圆的弦长，以及能解决与弦长相关的简单问题．
6．通过直线与圆的位置关系的代数化处理，使学生进一步认识到坐标系是联系“数”与“形”的桥梁，从而更深刻地体会坐标法思想．
教学应对
三、教学问题诊断
学生版 高中数学必修2直线与圆的位置关系知识点总结经典例题与习题
高中数学必修2 直线与圆的位置关系【一】、圆的定义及其方程．（1）圆的定义：平面内与定点距离等于定长的点的集合(轨迹)叫做圆，定点叫做圆心，定长就是半径；（圆心是定位条件，半径是定型条件） （2）圆的标准方程： ；圆心),(b a圆的一般方程：)04(02222>-+=++++F E D F Ey Dx y x ；圆心 ，半径为 ；【二】、点与圆的位置关系（仅以标准方程为例，其他形式，则可化为标准式后按同样方法处理）设),(00y x P 与圆222)()(r b y a x =-+-；若P 到圆心之距为d ； ①P 在在圆C 外 ； ②P 在在圆C 内 ； ③P 在在圆C 上 ； 【三】、直线与圆的位置关系：设直线0:=++C By Ax l 和圆222)()(:r b y a x C =-+-，圆心C 到直线l 之距为d ，由直线l 和圆C 联立方程组消去x （或y ）后，所得一元二次方程的判别式为∆，则它们的位置关系如下：相离 ；相切 ；相交 ； 注意：这里用d 与r 的关系来判定，称为几何法，只有对圆才实用，也是最简便的方法；利用∆判定称为代数法，对讨论直线和二次曲线的位置关系都适应。
【四】、两圆的位置关系：（1）代数法：解两个圆的方程所组成的二元二次方程组；若方程组有两组不同的实数解，则两圆相交；若方程组有两组相同的实数解，则两圆相切；若无实数解，两圆相离。
（2）几何法：设圆1O 的半径为1r ，圆2O 的半径为2r①两圆外离 ； ②两圆外切 ； ③两圆相交 ； ④两圆内切 ⑤两圆内含 ；（五）已知圆C ：(x-a)2+(y-b)2=r 2(r>0)，直线L ：Ax+By+C=01．位置关系的判定：判定方法1：联立方程组得到关于x(或y)的方程(1)△>0相交；(2)△=0相切；(3)△<0相离。
判定方法2：若圆心(a，b)到直线L的距离为d(1)d<r相交；(2)d=r相切；(3)d>r相离。
高考数学第四章圆与方程4.2.1直线与圆的位置关系课件新人教A版必修2
3.研究圆的切线问题时要注意切线的斜率是否存在.过一点求圆的切线方 程时，要考虑该点是否在圆上.当点在圆上时，切线只有一条；当点在圆 外时，切线有两条.
返回
编后语
• 同学们在听课的过程中，还要善于抓住各种课程的特点，运用相应的方法去听，这样才能达到最佳的学习效果。 • 一、听理科课重在理解基本概念和规律 • 数、理、化是逻辑性很强的学科，前面的知识没学懂，后面的学习就很难继续进行。因此，掌握基本概念是学习的关键。上课时要抓好概念的理解，
|1＋4－5＋ 5|
圆心 C 到直线 AB 的距离 d＝|CP|＝
12＋22 ＝1.
在 Rt△ACP 中，|AP|＝ r2－d2＝2，故直线被圆截得的弦长|AB|＝4.
解析答案
数学思想
数形结合思想
例 4 直线 y＝x＋b 与曲线 x＝ 1－y2有且只有一个交点，则 b 的取值范
围是( ) A.|b|＝ 2 C.－1≤b＜1
线的距离等于
12－222＝0，即圆心(1，2)位于直线 kx－y＝0 上.
于是有k－2＝0，即k＝2，
因此所求直线方程是2x－y＝0.
解析答案
课堂小结 1.判断直线和圆的位置关系的两种方法中，几何法要结合圆的几何性质 进行判断，一般计算较简单.而代数法则是通过解方程组进行消元，计算 量大，不如几何法简捷. 2.一般地，在解决圆和直线相交时，应首先考虑圆心到直线的距离，弦长 的一半，圆的半径构成的直角三角形.还可以联立方程组，消去 y，组成 一个一元二次方程，利用方程根与系数的关系表达出弦长 l＝
返回
题型探究
重点突破
题型一 直线与圆的位置关系的判断 例1 已知直线方程mx－y－m－1＝0，圆的方程x2＋y2－4x－2y＋1＝0. 当m为何值时，圆与直线 (1)有两个公共点； (2)只有一个公共点； (3)没有公共点.
人教版高中数学必修2第四章《4.2直线、圆的位置关系：4.2.1 直线与圆的位置关系》教学PPT
1)若AB和⊙O相离, 则 d > 5cm ; 2)若AB和⊙O相切, 则 d = 5cm ; 3)若AB和⊙O相交,则 0cm≤ d < 5cm.
例1、如图，已知直线l:3x+y-6=0和圆心为C 的圆x2+y2-2y-4=0，判断直线l与圆的位置关 系；如果相交，求它们的交点坐标。
相交
△＞0
r ＞d
O
x
当-2 2<b<2 2 时，⊿>0, 直线与圆相交；
当b=2 2或 b=-2 2 时, ⊿=0, 直线与圆相切；
当b>2 2或b<-2 2 时，⊿<0，直线与圆相离。
㈠方法探索
y 解法二(利用d与r的关系)：圆x2+y2=4的圆心为（0，0）,半径为r=2
00b b
圆心到直线的距离为 d
(3)△＜0 直线与圆径相r离的. 大小关系 直线与圆没有交点
方法3：代数性质
2、相切 (d=r)
直线与圆有一个交点
3、相交 (d<r)
直线与圆有两个交点
设圆 C∶(x-a)2+(y-b)2=r2， 直线L的方程为 Ax+By+C=0，
(x-a)2+(y-b)2=r2
Ax+By+C=0
练习与例题
1、已知圆的直径为13cm，设直线和圆心的距离为d ： 1)若d=4.5cm ,则直线与圆 相交, 直线与圆有___2_个公共点. 2)若d=6.5cm ,则直线与圆__相__切__, 直线与圆有___1_个公共点. 3)若d= 8 cm ,则直线与圆__相__离__, 直线与圆有___0_个公共点.
最新人教版高中数学必修2第四章《直线与圆的位置关系》
4．2.1 直线与圆的位置关系1．知道直线与圆的位置关系的分类．2．能根据方程，判断直线和圆的位置关系． 3．能够解决有关直线和圆的位置关系的问题．直线A x ＋B y ＋C ＝0与圆(x －a)2＋(y －b)2＝r 2的位置关系及判断【做一做】 直线3x ＋4y ＋12＝0与圆(x －1)＋(y ＋1)＝9的位置关系是( ) A ．过圆心 B ．相切 C ．相离 D ．相交答案：两 一 零 ＜ ＝ ＞ ＞ ＝ ＜ 【做一做】 D代数法与几何法的比较剖析：代数法的运算量较大，几何法的运算量较小，并且也简单、直观．受思维定式的影响，看到方程就想解方程组，自然就想到代数法．【例】 若直线4x －3y ＋a ＝0与圆x 2＋y 2＝100：①相交；②相切；③相离，试分别求实数a 的取值范围．解法一：(代数法)由方程组⎩⎪⎨⎪⎧4x －3y ＋a ＝0，x 2＋y 2＝100，消去y ，得25x 2＋8a x ＋a 2－900＝0.则Δ＝(8a)2－4×25(a 2－900)＝－36a 2＋90 000.①当直线和圆相交时，Δ＞0，即－36a 2＋90 000＞0，解得－50＜a ＜50； ②当直线和圆相切时，Δ＝0，解得a ＝50或a ＝－50； ③当直线和圆相离时，Δ＜0，解得a ＜－50或a ＞50. 解法二：(几何法)圆x 2＋y 2＝100的圆心为(0,0)，半径r ＝10，则圆心到直线4x －3y ＋a ＝0的距离d ＝|a|32＋42＝|a|5.①当直线和圆相交时，d<r ，即|a|5<10，所以－50＜a ＜50；②当直线和圆相切时，d ＝r ，即|a|5＝10，所以a ＝50或a ＝－50；③当直线和圆相离时，d>r ，即|a|5>10，所以a ＜－50或a ＞50.处理直线与圆的位置关系的代数法和几何法，都具有普遍性，都要熟练掌握．由这两种解法可看到，几何法比代数法运算量要小，也比较简单、直观．题型一：直线与圆的相交问题【例1】 过点(－4,0)作直线l 与圆x 2＋y 2＋2x －4y －20＝0交于A ，B 两点，如果|AB|＝8，求直线l 的方程．反思：(1)讨论直线与圆的相交问题时，通常情况下不求出交点坐标．利用半径、半弦和弦心距组成的直角三角形，由勾股定理能解决弦长问题．(2)解答本题时易出现漏掉x ＋4＝0的错误结果，导致这种错误的原因是对直线点斜式方程存在的条件理解不透，从而思维不严密，分类不完整．题型二：直线与圆的相切问题【例2】 求经过点(1，－7)且与圆x 2＋y 2＝25相切的直线方程．反思：解决直线与圆的相切问题时，通常利用圆心到切线的距离等于半径来解决．答案：【例1】 解：将圆的方程配方得(x ＋1)2＋(y －2)2＝25，由圆的性质可得，圆心到直线l 的距离d ＝(25)2－⎝⎛⎭⎫822＝3.当l 的斜率不存在时，x ＝－4满足题意．当l 的斜率存在时，设方程为y ＝k (x ＋4)，即kx －y ＋4k ＝0.由点到直线的距离公式，得3＝|－k －2＋4k |1＋k 2，解得k ＝－512.所以直线l 的方程为5x ＋12y ＋20＝0.综上所述，直线l 的方程为x ＋4＝0或5x ＋12y ＋20＝0.【例2】 解：(1)当直线斜率不存在时，其方程为x ＝1，不与圆相切；(2)当直线斜率存在时，设斜率为k ，则切线方程为y ＋7＝k (x －1)，即kx －y －k －7＝0.∴|－k －7|k 2＋(－1)2＝5，解得k ＝43或k ＝－34.∴所求切线方程为y ＋7＝43(x －1)或y ＋7＝－34(x －1)，即4x －3y －25＝0或3x ＋4y ＋25＝0.1．(2011·山东济南一模)若圆C 的半径为1，圆心在第一象限，且与直线4x －3y ＝0和x 轴都相切，则该圆的标准方程是( )A ．(x －2)2＋(y －1)2＝1B ．(x －2)2＋(y ＋1)2＝1C ．(x ＋2)2＋(y －1)2＝1D ．(x －3)2＋(y －1)2＝1 2．圆x 2＋y 2－2x ＋4y －20＝0截直线5x －12y ＋c ＝0所得的弦长为8，则c 的值是( ) A ．10 B ．10或－68 C ．5或－34 D ．－683．直线l：3x－4y－5＝0被圆x2＋y2＝5所截得的弦长为__________．4．(2011·北京丰台高三期末)过点(－3,4)且与圆(x－1)2＋(y－1)2＝25相切的直线方程为__________．5．已知一个圆C与y轴相切，圆心C在直线l1：x－3y＝0上，且在直线l2：x－y＝0上截得的弦长为C的方程．答案：1．A 2.B 3.4 4.4x－3y＋24＝05．解：∵圆心C在直线l1：x－3y＝0上，∴可设圆心为C(3t，t)．又∵圆C与y轴相切，∴圆的半径为r＝|3t|.再由弦心距、半径、弦长的一半组成的直角三角形，可得2＋2＝|3t|2，解得t＝±1.∴圆心为(3,1)或(－3，－1)，半径为3.故所求圆的方程为(x－3)2＋(y－1)2＝9或(x＋3)2＋(y＋1)2＝9.。
高一数学人教版A版必修二课件：4.2.1 直线与圆的位置关系
解析答案
(3)直线l经过点P(5,5)，且和圆C：x2＋y2＝25相交于A、B两点，截得的 弦长为4 5 ，求l的方程.
什么是学习力
什么是学习力-你遇到这些问题了 吗
总是
比别人
学得慢
一看就懂 一做就错 看得懂，但不会做
总是 比别人学得差 不会举一反三
什么是学习力-含义
管理知识的能力 （利用现有知识
解决问题）
学习知识的能力 （学习新知识
速度、质量等）
长久坚持的能力 （自律性等）
什么是学习力-常见错误学习方 式
案例式
位置关系 公共点个数
相交 相切 相离 2个 1个 0个
判 几何法：设圆心到直线的距离d＝|Aa＋Bb＋C|
A2＋B2 定
方 法
代数法： Ax＋By＋C＝0， 由 x－a2＋y－b2＝r2
消元得到一元二次方程的判别式Δ
_d_<_r_ _d_＝__r _Δ_>_0_ Δ_＝__0_
_d_>_r_ Δ__<_0_
|k＋1| 即 k2＋1≤1， 解得k≤0.
解析答案
规律与方法
1.直线与圆位置关系的两种判断方法比较 (1)若直线和圆的方程已知或圆心到直线的距离易表达，则用几何法 较为简单. (2)若直线或圆的方程中含有参数，且圆心到直线的距离较复杂，则 用代数法较简单. 2.过一点的圆的切线方程的求法 (1)当点在圆上时，圆心与该点的连线与切线垂直，从而求得切线的 斜率，用直线的点斜式方程可求得圆的切线方程.
高中数学必修2圆与圆的位置关系
λ=-7
2.过点M（2，-2）以及圆x2+y2-6x=0 与x2+y2=4圆交点的圆的方程
直线与圆的位置关系圆和圆的位置关系 两圆的位 置关系 外离 图形 d与R， 公切线 r的关系 的条数
公切线长
d>R+r
4
外切
相交 内切
d=R+r
R-r<d<R+r
3
2 1
d=R-r
0≤d<R-r
内含
0
结束 返回 下一页
•
P130练习
• 练习
• 点M在圆心为C1的圆x2+y2+6x-2y+1=0上, 点N在圆心为C2的圆x2+y2+2x+4y+1=0上, 求 |MN| 的最大值. y
M
c1
O
x
c2
N
1.已知C1:x2+y2=9,C2: (x-2)2+y2=r2，若C1与C2内切， 求r的值 2.已知C1:x2+y2=9,C2: (x-5)2+y2=r2，若C1与C2内切， 求r的值
R O1 r O2 R O1 r O2
R O1
r O2
外离
外切
相交
|O1O2|>|R+r|
R
|O1O2|=|R+r|
R
|R-r|<|O1O2|<|R+r|
R
O 1 O 2r
O 1 O 2r
O 1 O 2r
内切
内含
同心圆
(一种特殊的内含)
|O1O2|=|R-r|
0≤|O1O2|<|R-r|
|圆系方程 ▲经过圆C1:x2+y2+D1x+E1y+F1=0和 C2:x2+y2+D2x+E2y+F2=0的交点的圆可设为 x2+y2+D1x+E1y+F1+λ(x2+y2+D2x+E2y+F2)=0 ▲当 λ=-1时，表示经过两相交圆两交点的直线方程
高中数学必修2直线与圆的位置关系知识题型总结
直线与圆的位置关系一、点与圆的位置关系设),(00y x P 与圆222)()(r b y a x =-+-；若P 到圆心之距为d ；①P 在在圆C 外22020)()(r b y a x r d >-+-⇔>⇔； ②P 在在圆C 内22020)()(r b y a x r d <-+-⇔<⇔； ③P 在在圆C 上22020)()(r b y a x r d =-+-⇔=⇔；二、直线与圆的位置关系：设直线0:=++C By Ax l 和圆222)()(:r b y a x C =-+-，位置关系的判定：判定方法1：联立方程组 得到关于x(或y)的方程(1)△>0相交； (2)△=0相切； (3)△<0相离。
判定方法2：若圆心(a ，b)到直线L 的距离为d (1)d<r 相交； (2)d=r 相切；(3)d>r 相离。
利用∆判定称为代数法，对讨论直线和二次曲线的位置关系都适应。
三、两圆的位置关系：（1）代数法：解两个圆的方程所组成的二元二次方程组；若方程组有两组不同的实数解，则两圆相交；若方程组有两组相同的实数解，则两圆相切；若无实数解，两圆相离。
（2）几何法：设圆1O 的半径为1r ，圆2O 的半径为2r①两圆外离2121||r r O O +>⇔；4条公切线②两圆外切2121||r r O O +=⇔；3条公切线③两圆相交212112||||r r O O r r +<<-⇔；2条公切线④两圆内切||||1221r r O O -=⇔；1条公切线⑤两圆内含||||1221r r O O -<⇔；没有公切线四、两圆公共弦所在直线方程圆1C ：221110x y D x E y F ++++=，圆2C ：222220x y D x E y F ++++=，则()()()1212120D D x E E y F F -+-+-=为两相交圆公共弦方程. 补充说明：① 若1C 与2C 相切，则表示其中一条公切线方程； ② 若1C 与2C 相离，则表示连心线的中垂线方程.五、圆系问题过两圆1C ：221110x y D x E y F ++++=和2C ：222220x y D x E y F ++++=交点的圆系方程为()22221112220x y D x E y F x y D x E y F λ+++++++++=（1λ≠-） 补充：① 上述圆系不包括2C ；② 2）当1λ=-时，表示过两圆交点的直线方程（公共弦）③ 过直线0Ax By C ++=与圆220x y Dx Ey F ++++=交点的圆系方程为()220x y Dx Ey F Ax By C λ+++++++=六、 过一点作圆的切线的方程：(1) 过圆外一点的切线： ①k 不存在，验证是否成立②k 存在，设点斜式方程，用圆心到该直线距离=半径，即 ⎪⎩⎪⎨⎧+---=-=-1)()(2110101R x a k y b R x x k y y 求解k ，得到切线方程【一定两解】例1. 经过点P(1，—2)点作圆(x+1)2+(y —2)2=4的切线，则切线方程为 。
人教版数学必修2课件-直线与圆的位置关系
有解，则直线与圆有公共点： 有一组解，则直线与圆相切； 有两组解，则直线与圆相交；
小 结：
1. 利用直线与圆的位置直观特征导出几 何判定： 比较圆心到直线的距离d与圆的半径r.
2. 看直线与圆组成的方程组有无实数解:
有解，则直线与圆有公共点： 有一组解，则直线与圆相切； 有两组解，则直线与圆相交；
例4. 一艘轮船在沿直线返回港口的途中，
接到气象台的台风预报: 台风中心位于轮
船正西70km处，受影响的范围是半径长
为30km的圆形区域. 已知港口位于台风中
心正北40km处， 如果这艘轮船不
y 港口
改航线，那么
它是否会受到台
风的影响？
O
轮船 x
小 结：
设直线l：Ax＋By＋C＝0， 圆C：(x－a)2＋(y－b)2＝r2，
无解，则直线与圆相离.
例2.直线y＝x与圆x2＋(y－1)2＝r2相切， 求r的值.
例3. 已知过点M(－3, －3)的直线l被 圆x2＋y2＋4y－21＝0所截得的弦长 为 4 5, 求直线l的方程.
练习.
已知直线l：3x y 2 3 0， 圆C：x2 y2 4，
求直线l被圆C截得的弦长.
(2) 圆心到直线的距离与半径的关系:
Aa Bb C d
A2 B2
a. 如果d＜r，直线与圆相交； b. 如果d＝r，直线与圆相切； c. 如果d＞r，直线与圆相离.
2. 在初中我们怎样判断直线与圆的位置 关系？现在，如何用直线和圆的方程 判断它们之间的位置关系？
讲授新课
例1. 已知直线l: 3x＋y－6＝0和圆心为 C的圆x2＋y2－2y－4＝0，判断直线l 与圆的位置关系；如果相交，求出它 们交点的坐标.
《直线与圆的位置关系》课件8 (北师大版必修2)
(2) 当 r = 2.4cm时, 有 d = r, 因此C和AB相切
(3) 当 r = 3cm时, 有 d < r, 因此C和AB相交
想一想
你能用直线和圆的位置关系的
相关知识解答生活实例吗？
知识迁移
思考：学完本节课后有什么收获？能否进 行类比延伸呢？（可从运动变化的关系、 学习方面、人与人的关系、个人与集体的 关系、人与环境的关系等方面进行思考）
o r d
l
o r d
l
(性质） (1) 直线L和O相离 （判定） (性质） (2) 直线L和O相切 （判定） (性质） (3) 直线L和O相交 （判定）
d>r
d=r
d<r
说一说
两 判定直线 与圆的位置关系的方法有____种：
（1）根据定义，由________________ 的个数来判断； 直线 与圆的公共点
直线和圆的位置关系实践作业
4.做一做(A层同学选做）
搜集或自己制作一个直线和圆的位置关系的教学小 课件。
作法建议：软件可任意选用如 powerpoint,authorware,flash等。
直线和圆的位置关系实践作业
（分层作业）
想一 想 （ABC层）
看一看 做一做 （ABC层）（AB层选做）（A层选做）
2.写一写 (ABC层同学做）
（1）整理直线和圆的位置关系的概念、判定和性质。 （2）整理例题变式，总结形成文字命题，并对结果 给予解答。
直线和圆的位置关系实践作业
3.看一看(AB层同学选做）
请搜集直线和圆的位置关系在我们生活与其它学 科中的应用。 建议资料来源:(1)教科书，(2)图书馆资料，(3)互 联网等。
直线和圆的位置关系实践作业
2019年最新-人教版高中数学必修二直线与圆的位置关系(公式及技巧)
2．已知：如图，PT切⊙O于点T，PA交⊙O于A、B两点且 与直径CT交于点D，CD＝2，AD＝3，BD＝6，则PB＝ ________.
解析：由AD·BD＝CD·TD，得TD＝9，又由
得PB(PB＋9)＝(PB＋6)2－92，则PB＝15. 答案：15
3.如图，已知EB是半圆O的直径，A是BE延长线上一点，AC
解析：∵∠CAE＝∠EAB，∠EAB＝∠ACB， ∴∠ACB＝∠CAE＝∠EAB. 又∵CB⊥AD，∴∠ACB＝∠CAE＝∠EAB＝30°. 又∵AE＝2，∴AB＝ 3,AC2 3,BC＝3. 答案：
6．如图，EB、EC是⊙O的两条切线，B、C是切点，A、D 是⊙O上两点，如果∠E＝46°，∠DCF＝32°，则∠A 的度数是________．
３，能创编动作表现歌（乐）曲，准 确地唱 歌。
教学重点：用柔和的声音演唱歌曲。
教学难点：能创编动作表现歌曲。
教学准备：录音机，电子琴
教学内容及过程：
一 开始部分：
１ 听音乐问好！
２ 复习歌曲。
３ 复习柯尔文手势。
二 基本部分：
１、表演《布谷》
a 完整地感受歌曲的旋律，课题是学 生跟着 音乐拍 手、拍 腿，感 受歌曲 的节拍 。然后 听歌曲 录音， 用手指 点歌词 ，想一 想哪些 音长？
(1)可利用圆内接四边形对角互补来证明A，P，O，M四 点共圆； (2)利用(1)所得结论即可求得∠OAM＋∠APM的大小．
证明：连结OP，OM，如图(1)所示．因为AP与⊙O相切 于点P，所以OP⊥AP.因为M是⊙O的弦BC的中点，所以 OM⊥BC.于是∠OPA+∠OMA=180°.由圆心O在∠PAC的 内部，可知四边形APOM的对角互补，所以A，P，O， M四点共圆．
圆与圆的位置关系教案必修2
圆与圆的位置关系教案必修2直线和圆有公共点时,叫做直线和圆相切.这时直线叫做圆的切线,的公共点叫做切点.直线和圆没有公共点时,叫做直线和圆相离.一起看看圆与圆的位置关系教案必修2!欢送查阅!圆与圆的位置关系教案必修2 1由直线与圆的公共点的个数,得出以下直线和圆的三种位置关系：(1)相交：直线与圆有两个公共点时,叫做直线和圆相交.这时直线叫做圆的割线.(2)相切：直线和圆有公共点时,叫做直线和圆相切.这时直线叫做圆的切线,的公共点叫做切点.(3)相离：直线和圆没有公共点时,叫做直线和圆相离.直线与圆的位置关系的数量特征1、迁移：点与圆的位置关系(1)点P在⊙O内dr.2、归纳概括：假如⊙O的半径为r,圆心O到直线l的间隔为d,那么(1)直线l和⊙O相交dr.练习题：1.直线L上的一点到圆心的间隔等于⊙O的半径，那么L 与⊙O的位置关系是A.相离B.相切C.相交D.相切或相交2.圆的的弦长为12cm，假如直线与圆相交，且直线与圆心的间隔为d，那么A.d<6cmB.6cmC.d≥6cmD.d>12cm3.P是⊙O外一点，PA、PB切⊙O于点A、B，Q是优弧AB 上的一点，设∠APB=α，∠AQB=β，那么α与β的关系是A.α=βB.α+β=90°C.α+2β=180°D.2α+β=180°4.在⊙O中，弦AB和CD相交于点P，假设PA=4，PB=7，CD=12，那么以PC、PD的长为根的一元二次方程为A.x2+12x+28=0B.x2-12x+28=0C.x2-11x+12=0D.x2+11x+12=0圆与圆的位置关系教案必修2 2教学目的(1)掌握圆的标准方程，能根据圆心坐标和半径纯熟地写出圆的标准方程，也能根据圆的标准方程纯熟地写出圆的圆心坐标和半径.(2)掌握圆的一般方程，理解圆的一般方程的构造特征，纯熟掌握圆的标准方程和一般方程之间的互化.(3)理解参数方程的概念，理解圆的参数方程，可以进展圆的普通方程与参数方程之间的互化，能应用圆的参数方程解决有关的简单问题.(4)掌握直线和圆的位置关系，会求圆的切线.(5)进一步理解曲线方程的概念、熟悉求曲线方程的方法.教学建议教材分析^p(1)知识构造(2)重点、难点分析^p①本节内容教学的重点是圆的标准方程、一般方程、参数方程的推导，根据条件求圆的方程，用圆的方程解决相关问题.②本节的难点是圆的一般方程的构造特征，以及圆方程的求解和应用.教法建议(1)圆是最简单的曲线.这节教材安排在学习了曲线方程概念和求曲线方程之后，学习三大圆锥曲线之前，旨在熟悉曲线和方程的理论，为后继学习做好准备.同时，有关圆的问题，特别是直线与圆的位置关系问题，也是解析几何中的根本问题，这些问题的解决为圆锥曲线问题的解决提供了根本的思想方法.因此教学中应加强练习，使学生确实掌握这一单元的知识和方法.(2)在解决有关圆的问题的过程中屡次用到配方法、待定系数法等思想方法，教学中应多总结.(3)解决有关圆的问题，要经常用到一元二次方程的理论、平面几何知识和前边学过的解析几何的根本知识，老师在教学中要注意多复习、多运用，培养学生运算才能和简化运算过程的意识.(4)有关圆的内容非常丰富，有很多有价值的问题.建议适中选择一些内容供学生研究.例如由过圆上一点的切线方程引申到切点弦方程就是一个很有价值的问题.类似的还有圆系方程等问题.圆与圆的位置关系教案必修2 3教学目的：(1)掌握圆的一般方程及其特点.(2)能将圆的一般方程转化为圆的标准方程，从而求出圆心和半径.(3)能用待定系数法，由条件求出圆的一般方程.(4)通过本节课学习，进一步掌握配方法和待定系数法.教学重点：(1)用配方法，把圆的一般方程转化成标准方程，求出圆心和半径.(2)用待定系数法求圆的方程.教学难点：圆的一般方程特点的研究.教学用具：计算机.教学方法：启发引导法，讨论法.教学过程：【引入】前边已经学过了圆的标准方程把它展开得任何圆的方程都可以通过展开化成形如①的方程【问题1】形如①的方程的曲线是否都是圆?师生共同讨论分析^p ：假如①表示圆，那么它一定是某个圆的标准方程展开整理得到的.我们把它再写成原来的形式不就可以看出来了吗?运用配方法，得②显然②是不是圆方程与是什么样的数亲密相关，详细如下：(1)当时，②表示以为圆心、以为半径的圆;(2)当时，②表示一个点 ;(3)当时，②不表示任何曲线.总结：任意形如①的方程可能表示一个圆，也可能表示一个点，还有可能什么也不表示.圆的一般方程的定义：当时，①表示以为圆心、以为半径的圆，此时①称作圆的一般方程.即称形如的方程为圆的一般方程.【问题2】圆的一般方程的特点，与圆的标准方程的异同.(1) 和的系数一样，都不为0.(2)没有形如的二次项.圆的一般方程与一般的二元二次方程③相比拟，上述(1)、(2)两个条件仅是③表示圆的必要条件，而不是充分条件或充要条件.圆的一般方程与圆的标准方程各有千秋：(1)圆的标准方程带有明显的几何的影子，圆心和半径一目了然.(2)圆的一般方程表现出明显的代数的形式与构造，更合适方程理论的运用.【实例分析^p 】例1：以下方程各表示什么图形.(1) ;(2) ;(3) .学生演算并答复(1)表示点(0，0(2)配方得，表示以为圆心，3为半径的圆;(3)配方得，当、同时为0时，表示原点(0，0当、不同时为0时，表示以为圆心，为半径的圆.例2：求过三点，，的圆的方程，并求出圆心坐标和半径.分析^p ：由于学习了圆的标准方程和圆的一般方程，那么此题既可以用标准方程求解，也可以用一般方程求解.解：设圆的方程为因为、、三点在圆上，那么有解得：，，所求圆的方程为可化为圆心为，半径为5.请同学们再用标准方程求解，比拟两种解法的区别.【概括总结】通过学生讨论，师生共同总结：(1)求圆的方程多用待定系数法.其步骤为：由题意设方程(标准方程或一般方程根据条件列出关于待定系数的方程组;解方程组求出系数，写出方程.(2)如何选用圆的标准方程和圆的一般方程.一般地，易求圆心和半径时，选用标准方程;假如给出圆上点，可选用一般方程.下面再看一个问题：例3：经过点作圆的割线，交圆于、两点，求线段的中点的轨迹.解：圆的方程可化为，其圆心为，半径为2.设是轨迹上任意一点.∵∴即化简得点在曲线上，并且曲线为圆内部的一段圆弧.【练习稳固】(1)方程表示的曲线是以为圆心，4为半径的圆.求、、的值.(结果为4，-6，-3)(2)求经过三点、、的圆的方程.分析^p ：用圆的一般方程，代入点的坐标，解方程组得圆的方程为 .(3)课本第79页练习1，2.【小结】师生共同总结：(1)圆的一般方程及其特点.(2)用配方法化圆的一般方程为圆的标准方程，求圆心坐标和半径.(3)用待定系数法求圆的方程.【作业】课本第82页5，6，7，8.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
d
| Aa Bb C | A2 B 2
例1 如图4.2-2，已知直线l：3x+y-6=0和圆心 为C的圆 x 2 y 2 2 y 4 0 ，判断直线l与圆的位 置关系。
2 2 解法 ：圆 x y 2 y 4 0可化为
其圆心C 到直线l的距离 | 3 0 1 6 | 5 d 5. 10 32 12
Company Logo
巩固练习
1.已知直线l：y＝x+6,圆Ｃ: x2 y2－2 y 4 0. 试判断直线l与圆Ｃ有无公共点,有几个公共点．
解: 圆Ｃ的圆心坐标是(０,１),半径长r = 圆心到直线y＝x +6的距离
d 5 2 2
5 ，
5.
所以直线l与圆Ｃ无公共点．
Company Logo
巩固练习 2.判断直线４x－３y=50与圆 x y 100的 位置关系．如果相交，求出交点坐标．
2 2
解：因为圆心O（0,0）到直线４x－３y=50的距离
| 0 0 50 | d 10. 5 而圆的半径长是10，所以直线与圆相切.
Company Logo
4.2.1直线与圆的位置关系
知识回顾
1
直线方程的一般式
Ax+By+C=0(A,B不同时为零)
2
圆的标准方程 (x-a)2+(y-b)2=r2
圆心为(a,b) ,半径为r. 圆的一般方程：
24Biblioteka 2 Dx Ey F 0, 其中D2 E 2 4F 0. y x
圆心为
D E , 2 2
所以，直线l与圆相交
x 2 ( y 1) 2 ， 5 的坐标为（0，1）,半径长为 5 ,点C（0，1）
y
l B
C● O
A
x
思考：求它们交点的坐标.？
巩固练习 2.判断直线３x＋４y＋２＝０与圆 x y －2x 0 的位置关系．
2 2
2 2 2 2 ( x 1) y 1. x y － 2 x 0 解: 方程 经过配方,得 圆心坐标是(１,０),半径长r =1．
1 2 2 D E 4F ,半径为 2
.
位置 d与 r 图形 交点 个数
相离
相切
相交
d>r
d r
d= r
r
d<r
r
d
d
0个
1个
2个
一般地,已知直线Ax+By+C=0(A,B不同时 2 2 2 x a y b r 为零)和圆 ,则圆心(a,b)到
此直线的距离为
| 3 0 2| 圆心到直线３x＋４y＋２＝０的距离 d 1. 5
因为d=r，所以直线３x＋４y＋２＝０与圆相切．
归纳小结
直线与圆的位置关系的判断方法有两种：
①代数法
通过直线方程与圆 的方 程所组成的方程组 成的方 程组,根据解的个数 来研究, 两个解相交。 一个解相切， 没有解相离。 ②几何法 由圆心到直线的 距离d与 半径r的大小来判 断: d<r时,直线与 圆相 交; d=r时,直线与 圆相切; d>r时,直线与 圆相离．