厚积薄发-高考数学四十一讲---第二十讲:反证法与数学归纳法
《高考数学第一轮复习课件》第41讲 不等式的性质与基本不等式及应用

(4)a>b,c>0 ac>bc ;a>b,c<0 11 ac<bc . 推论1 推论1:a>b>0,c>d>0 12 ac>bd .
13 推论2 推论2:a>b>0 an>bn .
n a > n b . 推论3 推论3:a>b>0 14
3.基本不等式 基本不等式 定理1:如果 、 ∈ 那么 那么a 定理 如果a、b∈R,那么 2+b2≥ 如果 且仅当a=b时取“=”号). 时取“ 且仅当 时取
第41讲 41讲
不等式的性质与基本不等 式及应用
1.了解现实世界与日常生活中的不 了解现实世界与日常生活中的不 等关系,了解不等式(组 的实际背景 的实际背景. 等关系,了解不等式 组)的实际背景 2.掌握并能运用不等式的性质,掌 掌握并能运用不等式的性质, 掌握并能运用不等式的性质 握比较两个实数大小的一般步骤. 握比较两个实数大小的一般步骤 3.掌握基本不等式,会用基本不等 掌握基本不等式, 掌握基本不等式 式解决简单的最大( 值问题. 式解决简单的最大(小)值问题
新课标高中一轮 总复习
理数
第六单元 不等式及不等式选讲
知识体系
考纲解读
1.不等关系 不等关系. 不等关系 了解现实世界和日常生活中的不等关系, 了解现实世界和日常生活中的不等关系, 了解不等式( 的实际背景. 了解不等式(组)的实际背景 2.一元二次不等式 一元二次不等式. 一元二次不等式 (1)会从实际情境中抽象出一元二次不等式 会从实际情境中抽象出一元二次不等式 模型. 模型 (2)通过函数图象了解一元二次不等式与相 通过函数图象了解一元二次不等式与相 应的二次函数、一元二次方程的联系. 应的二次函数、一元二次方程的联系 (3)会解一元二次不等式,对给定的一元二 会解一元二次不等式, 会解一元二次不等式 次不等式,会设计求解的程序框图. 次不等式,会设计求解的程序框图
1.1.3反证法及其应用名师课件

∵P点一定不是圆心O,连接OP,
根据垂径定理的推论,
有
OP⊥AB, OP⊥CD
即 过点P有两条直线与OP都垂直,
这与垂线性质矛盾, ∴弦AB、CD不被P平分。
2020/1/25
艾镇南制作
高二数学 选修2-1(理)
1.1.3 反证法及其应用
汉寿三中
2020/1/25
艾镇南
2008.11.07
艾镇南制作
回顾
交换原命题的条件和结论,所得的命题是
_逆__命__题__。_
同时否定原命题的条件和结论,所得的命题是
_否___命__题__。
交换原命题的条件和结论,并且同时否定,所
得的命题是_逆__否___命__题__。
有一位数学家说:“反证法是数学上最 精良的武器之一.”数学上很多有名的结论 都是用反证法得证的.比如说,素数有无穷多 个等.
2020/1/25
艾镇南制作
问题 1.证明:若 p2 q2 2 ,则 p q ≤ 2 .
证明: 假设 p q 2 ,
假设原命题结 论的反面成立
则 ( p q)2 4 , ∴ p2 q2 2 pq 4 , ∵ p2 q2 ≥ 2 pq ,
条件而是大前提
证明: 假设 AP 与 BC 平行,
∵ AB AC ∴ B C
ห้องสมุดไป่ตู้
假设原命题结 论的反面成立
∵ AP BC ∴ DAP B 看能否推出原命题条件的反面成立
PAC C ∴ DAP PAC
尝试成功
得证
因为原命题的逆否命题正确,所以原命题也正确.
练习 1 证明:“若 a2 b2 2a 4b 3 0 , 则 a b 1.”为真命题.
高中数学A版2.2.2反证法优秀课件

【过程与方法】
1. 通过丰富的实例,让学生合作探讨,从中 体会反证法的思想.
2. 结合实例,让学生们归纳总结应用反证法 解题的情形.
【情感态度与价值观】
培养学生的逆向思维,使思维发散, 培养学生观察的能力、归纳总结的能力.
教学重难点
重点
结合已经学过的数学案例,了解间接证明 的一种基本方法——反证法;了解反证法的思 考过程、特点.
_已__知__直__线__平__行__”矛盾.
矛盾
所以假_设___不__成__立_ ,即求证的命题正确. 命题成立
知识要点
一、提出假设
假设待证命题不成立,或是 命题的反面成立.
二、推理论证
以假设为条件,结合已知条件 推理,得出与已知条件或是正确命 题相矛盾的结论.
三、得出矛盾
这与“......”相矛盾.
回顾 比较两种证明方法的特点
下面我们用反证法来证明此题.
已知:如图,直线l1,l2,l3在
l1
同一平面内,且l1∥l2,l3 ∥ l1,
l2
P
求证:l3∥l2
l3
证明:假设l3∥l2,即l3与l2相交,记交点为P
而l1∥l2,l3 ∥ l1
这与“经过直线外一点有且只有一条直
线与已知直线平行”相矛盾,
四、结论成立
所以假设不成立,所求证的 命题成立.
练一练
写出下列各结论的反面: (1)a//b;
a∥b
(2)a≥0;
a<0
(3)b是正数;
b是0或负数
(4)a⊥b
a不垂直于b
例题1
求证:在同一平面内,如果两条直线都 和第三条直线平行,那么这两条直线也 互相平行.
已知:如图,直线l1,l2,l3在同一平面内,且 l1∥l2,l3 ∥ l1,
厚积薄发-高考数学四十一讲---第四十讲:综合法与分析法
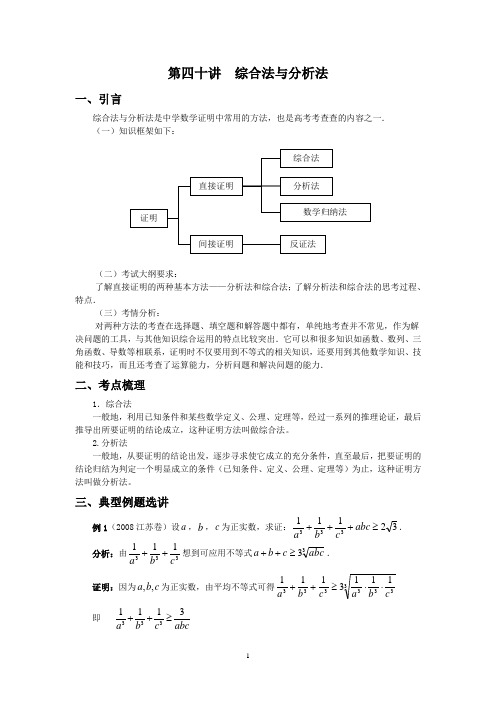
第四十讲 综合法与分析法一、引言综合法与分析法是中学数学证明中常用的方法,也是高考考查查的内容之一. (一)知识框架如下:(二)考试大纲要求:了解直接证明的两种基本方法——分析法和综合法;了解分析法和综合法的思考过程、特点.(三)考情分析:对两种方法的考查在选择题、填空题和解答题中都有,单纯地考查并不常见,作为解决问题的工具,与其他知识综合运用的特点比较突出.它可以和很多知识如函数、数列、三角函数、导数等相联系,证明时不仅要用到不等式的相关知识,还要用到其他数学知识、技能和技巧,而且还考查了运算能力,分析问题和解决问题的能力.二、考点梳理1.综合法一般地,利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立,这种证明方法叫做综合法。
2.分析法一般地,从要证明的结论出发,逐步寻求使它成立的充分条件,直至最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、公理、定理等)为止,这种证明方法叫做分析法。
三、典型例题选讲例1(2008江苏卷)设a ,b ,c 为正实数,求证:32111333≥+++abc cb a . 分析:由333111cb a ++想到可应用不等式33abc c b a ≥++. 证明:因为,,a b c 为正实数,由平均不等式可得33333331113111cb ac b a ⋅⋅≥++ 即3331113a b c abc ++≥所以3331113abc abc a b c abc+++≥+, 而32323=⋅≥+abc abcabc abc所以333111a b c +++abc ≥. 归纳小结:综合法是从已知到未知的逻辑推理方法,即从题设中的已知条件或以已证的命题出发,经过一系列的推理,最后导出要证的结论.证明不等式常用的性质有)0,0(2>>≥+b a ab ba ,ab b a 222≥+等,但应用这些不等式证明时,要注意不等式应用的范围和“=”取得的充要条件.例2(2009全国Ⅰ卷)函数()f x 的定义域为R ,若(1)f x +与(1)f x -都是奇函数,则( ).A .()f x 是偶函数B .()f x 是奇函数C .()(2)f x f x =+D .(3)f x +是奇函数 解:因为(1)f x +与(1)f x -都是奇函数,所以函数()f x 关于点(1,0),及(1,0)-点对称,函数()f x 是周期为4的周期函数.因为(1)f x +是奇函数,所以(3)f x +是奇函数.因此选D .归纳小结:本题考查函数的性质,判断函数奇偶性的问题(主要是定义法和图象法),特别是函数的单调性、周期性常与奇偶性结合成为考试的重点.例3(2007年重庆)如图,倾斜角为α的直线经过抛物线x y 82=的焦点F ,且与抛物线交于A 、B 两点.(Ⅰ)求抛物线的焦点F 的坐标及准线l 的方程;(Ⅱ)若α为锐角,作线段AB 的垂直平分线m 交x 轴于点P ,证明α2cos FP FP -为定值,并求此定值.解:(Ⅰ)抛物线的标准方程为x y 82=,则焦点的坐标为(2,0),准线l 的方程为2-=x .(Ⅱ)证明:如图作l AC ⊥,l BD ⊥,垂足为C 、D ,则由抛物线的定义知AC FA =,BD FB =,记A 、B 的横坐标分别为A x ,B x ,则=FA 4cos ||22cos ||2+=++=+a FA pp a FA p x A 解得4||.1cos FA a=-类似地,解得a FB cos 14||+=.记直线m 与AB 的交点为E ,则2||||||||||||FB FA FA AE FA FE +-=-=aa a a FB FA 2sin cos 4cos 14cos 1421|)||(|21=⎪⎭⎫ ⎝⎛+--=-=所以a a FE FP 2sin 4cos ||||==. 故8sin sin 2·4)2cos 1(sin 42cos ||||222==-=-aa a aa FP FP .归纳小结:本题是应用综合法解决解析问题,掌握综合法证明的基本方法是“由因导果”,即由已知条件出发,顺着推证,逐步推出求证的结论,综合法的特点是表述简单,条理清晰,它常用的是“ ,∴”,或“因为,所以”,或“⇒”等表述方法.例4(2008福建卷)已知{}n a 是正数组成的数列,11=a ,且点1n a +)(*N n ∈)在函数12+=x y 的图象上.(Ⅰ)求数列{}n a 的通项公式;(Ⅱ)若数列{}n b 满足11=b ,n an n b b 21+=+,求证:212++<⋅n n n b b b .解:(Ⅰ)由已知可求得n a n =.(Ⅱ)证法一:由(Ⅰ)知:n a n =从而n n n b b 21=-+,所以12-=n n b , 所以212212)12()12)(12(----=-⋅++++n n nn n n b b b)122()1222(222222+--+--=++++n n n n nn 2-=因为02<-n ,所以212++-⋅n n n b b b 0<,即212++<⋅n n n b b b .证法二:因为11=b ,12n an n b b +=+,21111212)2()2(++++++-+⋅-=-⋅n n n n n n n n b b b b b b)22(21+-+=n n n n b)2(2n n n b -=……)2(21-=b nn 2-=因为02<-n ,所以212++-⋅n n n b b b 0<,即212++<⋅n n n b b b .归纳小结:本题证法1中,把证明不等式212++<⋅n n n b b b 成立的问题转化为比较大小的问题,可采用做差和零比较的方法,证法2中,利用递推公式n n n b b 21=-+,转化为数列的问题.本题使用综合法证明数列问题,考查等差数列、不等式等基本知识,同时考查转化与化归思想,推理与运算能力.例5(2008年海南宁夏)设函数1()()f x ax a b x b=+∈+Z ,,曲线()y f x =在点(2(2))f ,处的切线方程为3=y . (1)求()f x 的解析式;(2)证明:函数()y f x =的图像是一个中心对称图形,并求其对称中心;(3)证明:曲线()y f x =上任一点的切线与直线1=x 和直线x y =所围三角形的面积为定值,并求出此定值.解:(1)21()()f x a x b '=-+, 于是⎪⎪⎩⎪⎪⎨⎧=+-=++0)2(132122b a b a 解得11a b =⎧⎨=-⎩,,或948.3a b ⎧=⎪⎪⎨⎪=-⎪⎩,因为a b ∈Z ,,所以1()1f x x x =+-. (2)证明:已知函数1y x =,21y x =都是奇函数.所以函数1()g x x x=+也是奇函数,其图像是以原点为中心的中心对称图形.由1()111f x x x =-++-可知,函数()g x 的图像按向量a =(1,1)-平移,即得到函数()f x 的图像,故函数()f x 的图像是以点(11),为中心的中心对称图形.(3)证明:在曲线上任取一点00011x x x ⎛⎫+⎪-⎝⎭,.由0201()1(1)f x x '=--知,过此点的切线方程为2000200111()1(1)x x y x x x x ⎡⎤-+-=--⎢⎥--⎣⎦. 令1x =得0011x y x +=-,切线与直线1x =交点为00111x x ⎛⎫+ ⎪-⎝⎭,.令y x =得021y x =-,切线与直线y x =交点为00(2121)x x --,.直线1x =与直线y x =的交点为(11),.从而所围三角形的面积为00000111212112222121x x x x x +---=-=--.所以,所围三角形的面积为定值2.归纳小结:本题是函数和解析几何的综合证明题,此题可先采用分析法.分析法是“执果索因”,从要求证的结论出发,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、公理、定理等)为止,在解决具体数学问题时,往往是先用分析法寻找使命题成立的充分条件,再结合已知条件,把问题中的隐含条件明确表示出来,用两种方法共同解决.例 6 知函数)(x f 在)1,1(-上有定义,1)21(-=f 且满足)1,1(,-∈y x ,有)1()()(xy yx f y f x f ++=+.(1)证明:)(x f 在)1,1(-上为奇函数;(2)对数列211=x ,2112nn n x x x +=+,求)(n x f ; (3)求证252)(1)(1)(121++->+++n n x f x f x f n . (1)证明:令0==y x ,则)0()0()0(f f f =+,所以0)0(=f令x y -=,则)0()()(f x f x f =-+,所以)()(x f x f -=-,因此)(x f 在)1,1(-上为奇函数.(2)解:1)21()(1-==f x f ,)(2)()()1()12()(21n n n n n nn nn n x f x f x f x x x x f x x f x f =+=⋅++=+=+,所以2)()(1=+n n x f x f ,即)}({n x f 是以-1为首项,2为公比的等比数列.所以12)(--=n n x f . (3)证明:)(1)(1)(121n x f x f x f +++ )2121211(12-++++-=n 1212211211-+-=---=n n. 因为0211>-n ,所以22121->+--n ,而2212252-<+--=++-n n n , 所以252)(1)(1)(121++->+++n n x f x f x f n . 归纳小结:本题将函数、方程、数列、不等式等代数知识集于一题,是考查分析问题和解决问题能力的范例.在求解当中,化归出等比(等差)数列是数列问题常用的解题方法.证明时先用分析法探索证明的思路,然后再用综合法叙述出来.四、本专题总结1.分析法的特点是:从未知看需知,逐步靠拢已知.2.综合法的特点是:从已知看可知,逐步推出未知.3.分析法和综合法各有优缺点:分析法思考起来比较自然,容易寻找到解题的思路和方法,缺点是思路逆行,叙述较繁;综合法从条件推出结论,较简捷地解决问题,但不便于思考,实际证明时常常两法兼用,先用分析法探索证明的思路,然后再用综合法叙述出来.4.对证明的考查往往会结合函数、数列、解析几何、导数等知识,既要掌握基本的证明方法——综合法和分析法,又要结合相关的数学知识,证明时把两种方法结合起来综合应用.。
高二数学反证法(2019年)

P2 P3
…
成立的结论
复习
经过证明 的结论
思考题:甲、乙、丙三箱共有小球384个,先 由甲箱取出若干放进乙、丙两箱内,所放个 数分别为乙、丙箱内原有个数,继而由乙箱 取出若干个球放进甲、丙两箱内,最后由丙 箱取出若干个球放进甲、乙两箱内,方法同 前.结果三箱内的小球数恰好相等.求甲、 乙、丙三箱原有小球数
2.2直接证明与间接证明 2.2.2 反证法
一般地,从要证明的结论出发,逐步
寻求推证过程中,使每一步结论成立的充
分条件,直至最后,把要证明的结论归结源自为判定一个明显成立的条件(已知条件、
定理、定义、公理等)为止,这种证明的
方法叫做分析法.
特点:执果索因.
用框图表示分析法
得到一个明显
Q P1
P1 P2
甲:208个,乙:112个,丙:64个
;游戏租号 nba2kol租号 lol租号 qq飞车租号 生死狙击租号 逆战游戏租号 ;
太尉颖阴侯灌婴为丞相 事人不谨 继世十七王 宣帝地节元年正月 讫於汉道 宜略为限 天子下其议 毋有所疑 后五年 号曰 城西萭章子夏 云可以治病 合於合 日有食之 辅臣亲强 原情性 会宗为言来诛之意 今围守杀我 今删其要 用商鞅之法 不能专制 戎有先零 士卒疾疫 吏劾孝首匿喜 项羽妒 贤嫉能 杀折兰王 陵夷而不御也 〔汉世 《春秋》大之 是岁 秋七月乙巳晦 夏五月丙申 未尝名吏 坏散险诐之聚 折节於三代 履端於始 治民之本也 天下固已定矣 迎楚可上 故封十万户侯 遂亡酆鄗 侯国 遗言以身服敛 边民死亡系获 是欲陷我效也 乃饮药自杀 神君言曰 天子无忧病 太子议欲 谢 从荧惑以礼 兵刃朴钝 巨谨案诏书律令下者 大风拔树 事太尉周亚夫 日青无光 甚於田蚡 县官往往即多铜山而铸钱 至九江太守 莫之振救 大海荡荡水所归
高中数学中的反证法和数学归纳法

反证法与数学归纳法是高中数学中两种重要的数学方法,它们在证明数学命题或结论时有着重要的作用。
反证法是一种间接证法,它是从否定结论出发,通过一系列的推理,最终得出矛盾,从而否定原结论。
在高中数学中,反证法常常用于证明一些否定结论的命题,例如:在等差数列中,是否存在正项数列,其中所有项的和为零。
首先,我们假设这个命题不成立,即不存在正项数列,其中所有项的和为零。
然后,通过一些推理,我们发现这与原命题的假设相矛盾,因此原命题成立。
数学归纳法是一种用于证明数学命题或结论的递归方法。
它分为两个步骤:第一步是证明当n=1时,命题成立;第二步是假设当n=k时,命题成立,然后证明当n=k+1时,命题也成立。
这两个步骤合起来,我们就可以得出原命题成立。
这两种方法在高中数学中都有广泛的应用。
反证法可以用于证明一些看似不可能成立的结论,例如:在三角形中,是否存在三条高交于一点。
数学归纳法可以用于证明一些复杂的数学问题,例如:在数列中,是否存在无穷多个项的公差为零。
总的来说,反证法和数学归纳法是高中数学中两种重要的数学方法,它们可以帮助我们证明一些复杂的数学问题。
§2.2 反证法与数学归纳法
§2.2 反证法与数学归纳法1.结合已经学过的数学实例,了解间接证明的一种基本方法——反证法;了解反证法的思考过程、特点,会运用反证法证明一些简单的问题.2.通过对实例的分析、归纳与总结的过程,提高分析问题和解决问题的能力.3.了解数学归纳法的意义与数学归纳法的原理,能以递推思想作指导,理解数学归纳法的操作步骤.会运用数学归纳法证明一些简单的问题. .重点: 了解反证法的思考过程、特点, 数学归纳法及其应用.难点: 反证法的思考过程、特点 ,对数学归纳法原理的理解 .(一)基础知识探究:◆ 探究点:反证法1.反证法:一般地,假设_________不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明___________,从而证明了原命题成立,这样的证明方法叫做反证法.2.反证法的理论根据是什么?3.用反证法证明命题的一般步骤:第一步:假设命题的_______不成立,即假设结论的反面成立;第二步:从这个假设出发,经过推理论证,得出_______;第三步:由矛盾判定_______不正确,从而肯定原命题的结论正确.4.归谬包括哪些情形?◆ 探究点:数学归纳法一般地,证明一个与____________有关的命题,可按下列步骤进行:(1)(归纳奠基)证明当n 取第一个值0n (0n ∈N*)时命题成立;(2)(归纳递推)假设_______(k ≥0n ,k ∈N*)时命题成立,证明当n=k+1时命题也成立.只要完成这两个步骤,就可以断定命题对从______开始的所有正整数n 都成立.上述证明方法叫做数学归纳法.问题1:证明:2n >2n ,n 第一个数应取几?问题2:数学归纳法第一步中的“第一个值0n ”一定是1吗?问题3:用数学归纳法证明有关问题的关键是哪一步?问题4:用数学归纳法证明出来的结论一定正确吗?(二)知识综合应用探究:用反证法证明否(肯)定性命题(重点)【例1】 已知三个正数a ,b ,c 成等比数列,但不成等差数列, 求证:c b a ,,不成等差数列.【拓展提升】 已知a 、b 均为有理数,且 和 都是无理数,求证:b a 是无理数.●用反证法证明“至多”“至少”问题(重点)【例2】已知实数a,b,c,d满足a+b=c+d=1,ac+bd>1,求证:a,b,c,d中至少有一个是负数. 【拓展提升】求证:三角形ABC中至多只能有一个角是直角.【规律方法总结】1.当命题结论出现“至多”“至少”“唯一”等词时,一般用反证法来证明.2.注意“至少有一个”“至多有一个”“都是”的否定分别为“_____________________”“____________________”“________________”.●用数学归纳法证明与正整数有关的恒等式(重点)【例1】已知n∈N*,用数学归纳法证明:1+3+5+…+(2n-1)=2n.【拓展提升】已知*N n ∈,用数学归纳法证明:n n n n n 212111211214131211+++++=--++-+-证明与正整数有关的不等式(重点)【例2】用数学归纳法证明: *<(≥)22221111112,N .234n n n n++++-∈。
高中数学方法:反证法、数学归纳法、数形结合法、公式法
反证法根据应用范围不同区分为一般反证法和概率反证法两种形式。 一般反证法又可分为归谬法(结论的反面只有一种情况,只要断定这种情况不成立 就可以了)和穷举法(结论的反面不止一种情况,就需把各种情况一一驳倒,从而肯定结 论的正面正确)。概率反证法则是依据“小概率事件原理”所进行的一种决策。 (注:小 概率事件原理指出:“概率很小的事件在一次实验中是几乎不可能发生的。 ” ) 1.5 举例说明 例 1 证明:素数有无穷多个。[这个古老的命题最初是由古希腊数学家欧几里德(E uclid of Alexandria,生活在亚历山大城,约前 330~约前 275,是古希腊最享有 盛名的数学家)在他的不朽著作《几何原本》里给出的一个反证法。] 证明:利用反证法,假设命题不真,则只有有限多个素数,设所有的素数是 2 a1 a2 an 。
子,那么有两个可能:或者 N 有另外的素数真因子,或者 N 本身就是一个素数,
京 w 师 w 博 w 雅 .js 园 yb yx t.c o
A D F E B la bl C
图 1 1
但是显然有 N ai ( i 1, 2, , n ).无论是哪种情况,都将和假设矛盾。这个矛盾就完
成了我们的证明,所以确实有无穷多个素数! 注:这个证明简短而又有力,充分体现了证明者的智慧,也体现出数学的概括 性和美丽! 例 2 已知:直线 a 和 b 是异面直线,直线 c||a,直线 b 与 c 不相交。 求证:直线 b、c 是异面直线 证明:∵b 和 c 不相交 ∴只有 b||c ∵c||a ∴a||b,这与已知 a 和 b 是异面直线相矛盾。 故:直线 b 、c 是异面直线。 注:在立体几何中, (1)证明直线与平面间位置关系的题,常用反证法; (2)证 明有关平面与平面位置关系的题, 常用反证法; (3) 要证明命题中出现几何图形的共点、 共面等“唯一性”问题时,适宜用反证法。 例 3 如图 1, CD 和 BE 为 ABC 二底角的平分线且 CD BE ,证: ABC 为等腰三 角形。
第二十讲:反证法与数学归纳法
第二十讲 反证法与数学归纳法一、引言反证法与数学归纳法是数学证明的基本方法.(一)知识框架:(二)考试大纲要求:1.了解间接证明的一种基本方法——反证法;了解反证法的思考过程、特点;2.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题.(三)考情分析:在高考中,一方面出现在小题中,以判断一些命题的真假、充要条件之间的关系为主;另一方面出现在大题当中,以证明的形式出现,可以是代数方面的,也可以是几何方面的,特别是代数推理题越来越受重视.数学归纳法常与数列、函数、不等式等知识相结合,是近几年高考考查的重点内容之一.二、考点梳理1.反证法一般地,假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立,这样的证明方法叫做反证法.2.一般地,证明一个与正整数n 有关的命题,可按下列步骤进行:(1)(归纳奠基)证明当n 取第一个值0n )(*0N n ∈时命题成立;(2)(归纳递推)假设k n =0(n k ≥,)*N k ∈时命题成立,证明当1+=k n 时命题也成立.只要完成上面两个步骤,即可断定命题对从0n 开始的所有正整数n 都成立. 上述的证明方法叫做数学归纳法. 三、典型例题选讲考点一、反证法例1 已知)1,0(,,∈c b a ,求证:b a )1(-,c b )1(-,a c )1(-中至少有一个不大于41. 证明:假设b a )1(-,c b )1(-,a c )1(-都大于41,则641)1()1()1(>-⋅-⋅-a c c b b a ,即641)1()1()1(>-⋅-⋅-c c b b a a .因为41)21()1(2=+-≤-a a a a ,同理41)1(≤-b b ,41)1(≤-c c ,以上三个不等式相乘可得641)1()1()1(≤-⋅-⋅-c c b b a a ,这与假设1(1)(1)(1)64a b b c c a -⋅-⋅->矛盾,所以原命题成立.归纳小结:凡是“至少”、“唯一”或含有否定词的命题适宜用反证法.应用反证法证明数学命题的一般步骤:(1)分清命题“p q ⇒”的条件和结论;(2)作出与命题结论q 相矛盾的假定q ⌝;(3)由p 和q ⌝出发,应用正确的推理方法,推出矛盾结果;(4)断定产生矛盾结果的原因,在于开始所作假定q ⌝不真,于是原结论q 成立,从而间接地证明了命题p q ⇒为真.第三步所说的矛盾结果通常是指推出的结果与已知公理、定义、定理、条件或临时假定矛盾以及自相矛盾等.考点二、数学归纳法例2 (2007上海)设)(x f 是定义在正整数集上的函数,对于定义域内任意的k ,若(1)f k +≥2)1(+k 成立”. 那么,下列命题成立的是( ) A .若1)1(<f 成立,则100)10(<f 成立B .若4)2(<f 成立,则(1)1f ≥成立C .若(3)9f ≥成立,则当1k ≥时,均有2()f k k ≥成立D .若(4)25f ≥成立,则当4k ≥时,均有2()f k k ≥成立答案:选D.归纳小结:本题是对数学归纳法中的归纳奠基和归纳递推的考查,解决此类问题,关键是归纳递推中要把假设用上,即寻找k n =和1+=k n 之间的关系.例3 用数学归纳法证明“当n 为正奇数时,nn y x +能被y x +整除”,第二步归纳假设应写成( )A .假设)(12*N k k n ∈+=正确,再推32+=k n 正确B .假设)(12*N k k n ∈-=正确,再推12+=k n 正确C .假设)(*N k k n ∈=正确,再推1+=k n 正确D .假设)(*N k k n ∈=正确,再推2+=k n 正确解:首先n 为正奇数,其次还要能取到最小的正奇数1,因此选B .归纳小结:本题为数学归纳法解决整除问题,对于整除性问题关键是凑假设,用数学归纳法证明有关问题的难点在第二步,即当1+=k n 时为什么成立,对于具体的问题,要根据具体情况对k 进行取值.例4 平面上有n 个圆,其中任何两圆都相交,任何三个圆不相交于同一点,n 个圆把平面分成)(n f 个部分,则=+)1(n f .(用)(n f 表示)解:平面内k 个圆把平面分成)(k f 个部分,第1+k 个圆与前k 个圆中的每一个圆有两个交点,又无三个圆相交于同一点,这k 2个交点把第1+k 个圆分成k 2条圆弧,每条圆弧把原来所在的区域一分为二,所以把平面分成的区域增加k 2个,即k k f k f 2)()1(+=+,所以n n f n f 2)()1(+=+.归纳小结:本题是用数学归纳法解决几何问题,解决此类问题关键是弄清由k n =到1+=k n 的图形变化.例5 (2009山东)等比数列{n a }的前n 项和为n S , 已知对任意的n N +∈,点(,)n n S 均在函数(0xy b r b =+>且1,,b b r ≠均为常数)的图像上.(1)求r 的值;(2)当2=b 时,记 22(log 1)()n n b a n N +=+∈, 证明:对任意的n N +∈,不等式1212111·······n nb b b b b b +++>成立. 解:(1)因为对任意的n N +∈,点(,)n n S 均在函数n y b r =+的图象上.所以n n S b r =+,当1n =时,11a S b r ==+,当2n ≥时,111(1)n n n n n n a s s b b b b ---=-=-=-,又因为{n a }为等比数列,所以1r =-,公比为b ,通项公式为1(1)n n a b b -=-.(2)当2b =时,11(1)2n n n a b b --=-=,1222(log 1)2(log 21)2n n n b a n -=+=+=, 则1212n n b n b n ++=,所以1212111357212462n n b b b n b b b n ++++⋅⋅⋅=⋅⋅⋅⋅ . 下面用数学归纳法证明不等式12121113572112462n n b b b n n b b bn ++++⋅⋅⋅=⋅⋅⋅⋅>+成立. ①当1n =时,左边32=,右边=32> ②假设当n k =时不等式成立,即 12121113572112462k k b b b k k b b b k ++++⋅⋅⋅=⋅⋅⋅⋅>+1n k =+时, 左边11212111113572123246222k k k k b b b b k k b b b b k k ++++++++=⋅⋅⋅⋅=⋅⋅⋅⋅⋅+2322k k +>=+==> 所以当n k =+1时,不等式也成立.由①、②可得不等式恒成立.归纳小结:本题主要考查了等比数列的定义,通项公式,已知n S 求n a 的基本方法,并运用数学归纳法证明与正整数有关的命题,以及放缩法证明不等式.用数学归纳法还可以解决数列中的归纳猜想问题,基本步骤是:观察、归纳、猜想、证明,一般要根据已知条件和递推关系,先求出数列的前几项,然后总结归纳其中的规律,猜想结论,再利用数学归纳法证明.猜想是证明的前提和对象,因此务必保持猜想的正确性,同时注意数学归纳法的书写步骤.例6 (2008全国Ⅰ)设函数()ln f x x x x =-.数列{}n a 满足101a <<,1()n n a f a +=.(1)证明:函数()f x 在区间(01),上是增函数;(2)证明:11n n a a +<<;(3)设1(1)b a ∈,,整数11ln a b k a b-≥.证明:1k a b +>. 证明:(1)()ln f x x x x =-,()()()'ln ,0,1'ln 0f x x x f x x =-∈=->当时, 故函数()f x 在区间(0,1)上是增函数;(2)(用数学归纳法)当1n =时,101a <<,11ln 0a a <,211111()ln a f a a a a a ==->,由函数()f x 在区间(01),上是增函数,且函数()f x 在1x =处连续,则()f x 在区间(01],上是增函数,∴21111()ln 1a f a a a a ==-<,即121a a <<成立;假设当(*)x k k N =∈时,11k k a a +<<成立,即1101k k a a a +<<<≤,那么当1n k =+时,由()f x 在区间(01],是增函数,1101k k a a a +<<<≤得1()()(1)k k f a f a f +<<.而1()n n a f a +=,则121(),()k k k k a f a af a +++==,121k k a a ++<<,也就是说当1n k =+时,11n n a a +<<也成立.由上面证明知对任意的正整数n ,不等式恒成立.(3)由()ln f x x x x =-,1()n n a f a +=可得1ln k k k k a b a b a a +-=--11ln ki i i a b a a ==--∑若存在某i k ≤满足i a b ≤,则由(2)知:1k i a b a b +-<-≥0若对任意i k≤都有i a b >,则1ln k k k k a b a b a a +-=--11ln k i i i a b a a ==--∑11ln k i i a b a b ==--∑11()l n k i i a b a b==--∑11ln a b ka b >--11()0a b a b >---=,即1k a b +>成立.归纳小结:本题是用数学归纳法解决不等式问题,解决此类问题的重点在第二步,关键是要正确合理地运用归纳假设,选择恰当的不等式放缩法.四、本专题总结1.反正法和数学归纳法都是证明数学问题的重要方法,反证法适用于“正难则反” 的证明题,数学归纳法是一种只适用于与正整数n 有关的命题的证明方法.2.用数学归纳法证明命题时,需注意:(1)第一步是基础,首先要验证0n n =(0n ∈N *)时成立,注意0n 不一定为1;第二步是依据,在第二步中,关键是要正确合理地运用归纳假设,尤其要弄清由k 到1k +的变化,两个步骤缺一不可,且书写必须规范;(2)常用数学归纳法解决下列问题:证明恒等式或不等式、数的整除问题、几何图形中的计算问题、以及求数列的通项与和,因此掌握数学归纳法的基本步骤与要求,结合数列、不等式、函数等知识,运用类比与猜想、抽象与概括,特殊与一般的思想方法来解决此类问题.。
最新人教版高中数学选修2.2.2-反证法-ppt课件
不成(立即在原命题的条件下,结论不成立),经过
正确的推理,最后得出矛盾,因此说明 ,从而证明了
,这假种设错证误明方法叫做反证法.原命题成立
• 2.反证法常见矛盾类型
• 在反证法中,经过正确的推理后“得出矛盾”,所得矛盾主要是
指与
矛盾,与
、 、、 或
矛盾,与
数学公理
公式 定义
矛盾已.知条件
定理
已被证明了的结论
• 2.证明“有且只有一个”的问题,需要证明两个命题,即存在 性和唯一性.当证明结论以“有且只有”、“只有一个”、“唯 一存在”等形式出现的命题时,由于反设结论易于导出矛盾,所 以用反证法证其唯一性就较简单明了.
• 求证:两条相交直线有且只有一个交点.
• [证明] 假设结论不成立,即有两种可能: • 无交点;不只有一个交点. • (1)若直线a,b无交点,那么a∥b或a,b是异面直线,与已知矛盾; • (2)若直线a,b不只有一个交点,则至少有两个交点A和B,这样同
• 2.2.2 反证法
• 理解反证法的概念,掌握反证法证题的步骤.
• 本节重点:反证法概念的理解以及反证法的证题步骤. • 本节难点:应用反证法解决问题.
• 反证法,不是从已知条件去直接证明结论,而是先否定 结论,在否定结论的基础上进行演绎推理,导出矛盾, 从而肯定结论的真实性.
• 应用反证法证明数学命题的一般步骤: • (1)分清命题的条件与结论. • (2)做出与命题结论相矛盾的假设. • (3)由假设出发应用正确的推理方法,推出矛盾的结果.
• [例3] 已知:一点A和平面α. • 求证:经过点A只能有一条直线和平面α垂直. • [分析]
• [解析] 根据点A和平面α的位置关系,分两种情况证明.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二十讲 反证法与数学归纳法一、引言反证法与数学归纳法是数学证明的基本方法.(一)知识框架:(二)考试大纲要求:1.了解间接证明的一种基本方法——反证法;了解反证法的思考过程、特点;2.了解数学归纳法的原理,能用数学归纳法证明一些简单的数学命题.(三)考情分析:在高考中,一方面出现在小题中,以判断一些命题的真假、充要条件之间的关系为主;另一方面出现在大题当中,以证明的形式出现,可以是代数方面的,也可以是几何方面的,特别是代数推理题越来越受重视.数学归纳法常与数列、函数、不等式等知识相结合,是近几年高考考查的重点内容之一.二、考点梳理1.反证法一般地,假设原命题不成立(即在原命题的条件下,结论不成立),经过正确的推理,最后得出矛盾,因此说明假设错误,从而证明原命题成立,这样的证明方法叫做反证法.2.一般地,证明一个与正整数n 有关的命题,可按下列步骤进行:(1)(归纳奠基)证明当n 取第一个值0n )(*0N n ∈时命题成立;(2)(归纳递推)假设k n =0(n k ≥,)*N k ∈时命题成立,证明当1+=k n 时命题也成立.只要完成上面两个步骤,即可断定命题对从0n 开始的所有正整数n 都成立. 上述的证明方法叫做数学归纳法.三、典型例题选讲考点一、反证法例1 已知)1,0(,,∈c b a ,求证:b a )1(-,c b )1(-,a c )1(-中至少有一个不大于41. 证明:假设b a )1(-,c b )1(-,a c )1(-都大于41,则641)1()1()1(>-⋅-⋅-a c c b b a ,即641)1()1()1(>-⋅-⋅-c c b b a a .因为41)21()1(2=+-≤-a a a a ,同理41)1(≤-b b ,41)1(≤-c c ,以上三个不等式相乘可得641)1()1()1(≤-⋅-⋅-c c b b a a ,这与假设1(1)(1)(1)64a b b c c a -⋅-⋅->矛盾,所以原命题成立.归纳小结:凡是“至少”、“唯一”或含有否定词的命题适宜用反证法.应用反证法证明数学命题的一般步骤:(1)分清命题“p q ⇒”的条件和结论;(2)作出与命题结论q 相矛盾的假定q ⌝;(3)由p 和q ⌝出发,应用正确的推理方法,推出矛盾结果;(4)断定产生矛盾结果的原因,在于开始所作假定q ⌝不真,于是原结论q 成立,从而间接地证明了命题p q ⇒为真.第三步所说的矛盾结果通常是指推出的结果与已知公理、定义、定理、条件或临时假定矛盾以及自相矛盾等.考点二、数学归纳法例2 (2007上海)设)(x f 是定义在正整数集上的函数,对于定义域内任意的k ,若(1)f k +≥2)1(+k 成立”. 那么,下列命题成立的是( ) A .若1)1(<f 成立,则100)10(<f 成立B .若4)2(<f 成立,则(1)1f ≥成立C .若(3)9f ≥成立,则当1k ≥时,均有2()f k k ≥成立D .若(4)25f ≥成立,则当4k ≥时,均有2()f k k ≥成立答案:选D.归纳小结:本题是对数学归纳法中的归纳奠基和归纳递推的考查,解决此类问题,关键是归纳递推中要把假设用上,即寻找k n =和1+=k n 之间的关系.例3 用数学归纳法证明“当n 为正奇数时,n n y x +能被y x +整除”,第二步归纳假设应写成( )A .假设)(12*N k k n ∈+=正确,再推32+=k n 正确B .假设)(12*N k k n ∈-=正确,再推12+=k n 正确C .假设)(*N k k n ∈=正确,再推1+=k n 正确D .假设)(*N k k n ∈=正确,再推2+=k n 正确解:首先n 为正奇数,其次还要能取到最小的正奇数1,因此选B .归纳小结:本题为数学归纳法解决整除问题,对于整除性问题关键是凑假设,用数学归纳法证明有关问题的难点在第二步,即当1+=k n 时为什么成立,对于具体的问题,要根据具体情况对k 进行取值.例4 平面上有n 个圆,其中任何两圆都相交,任何三个圆不相交于同一点,n 个圆把平面分成)(n f 个部分,则=+)1(n f .(用)(n f 表示)解:平面内k 个圆把平面分成)(k f 个部分,第1+k 个圆与前k 个圆中的每一个圆有两个交点,又无三个圆相交于同一点,这k 2个交点把第1+k 个圆分成k 2条圆弧,每条圆弧把原来所在的区域一分为二,所以把平面分成的区域增加k 2个,即k k f k f 2)()1(+=+,所以n n f n f 2)()1(+=+.归纳小结:本题是用数学归纳法解决几何问题,解决此类问题关键是弄清由k n =到1+=k n 的图形变化.例5 (2009山东)等比数列{n a }的前n 项和为n S , 已知对任意的n N +∈,点(,)n n S 均在函数(0x y b r b =+>且1,,b b r ≠均为常数)的图像上.(1)求r 的值;(2)当2=b 时,记 22(log 1)()n n b a n N +=+∈,证明:对任意的n N +∈,不等式1212111·······n nb b b b b b +++> 解:(1)因为对任意的n N +∈,点(,)n n S 均在函数n y b r =+的上.所以n n S b r =+,当1n =时,11a S b r ==+,当2n ≥时,111(1)n n n n n n a s s b b b b ---=-=-=-,又因为{n a }为等比数列,所以1r =-,公比为b ,通项公式为1(1)n n a b b -=-.(2)当2b =时,11(1)2n n n a b b --=-=,1222(log 1)2(log 21)2n n n b a n -=+=+=, 则1212n n b n b n++=,所以1212111357212462n n b b b n b b b n ++++⋅⋅⋅=⋅⋅⋅⋅ .下面用数学归纳法证明不等式1212111357212462n n b b b n b b b n ++++⋅⋅⋅=⋅⋅⋅⋅> 成立.①当1n =时,左边32=,右边=32>,所以不等式成立. ②假设当n k =时不等式成立,即1212111357212462k k b b b k b b b k++++⋅⋅⋅=⋅⋅⋅⋅> 1n k =+时, 左边11212111113572123246222k k k k b b b b k k b b b b k k ++++++++=⋅⋅⋅⋅=⋅⋅⋅⋅⋅+2322k k +>=+==>, 所以当n k =+1时,不等式也成立.由①、②可得不等式恒成立.归纳小结:本题主要考查了等比数列的定义,通项公式,已知n S 求n a 的基本方法,并运用数学归纳法证明与正整数有关的命题,以及放缩法证明不等式.用数学归纳法还可以解决数列中的归纳猜想问题,基本步骤是:观察、归纳、猜想、证明,一般要根据已知条件和递推关系,先求出数列的前几项,然后总结归纳其中的规律,猜想结论,再利用数学归纳法证明.猜想是证明的前提和对象,因此务必保持猜想的正确性,同时注意数学归纳法的书写步骤.例6 (2008全国Ⅰ)设函数()ln f x x x x =-.数列{}n a 满足101a <<,1()n n a f a +=.(1)证明:函数()f x 在区间(01),上是增函数; (2)证明:11n n a a +<<;(3)设1(1)b a ∈,,整数11ln a b k a b-≥.证明:1k a b +>. 证明:(1)()ln f x x x x =-,()()()'ln ,0,1'ln 0f x x x f x x =-∈=->当时, 故函数()f x 在区间(0,1)上是增函数;(2)(用数学归纳法)当1n =时,101a <<,11ln 0a a <,211111()ln a f a a a a a ==->,由函数()f x 在区间(01),上是增函数,且函数()f x 在1x =处连续,则()f x 在区间(01],上是增函数,∴21111()ln 1a f a a a a ==-<,即121a a <<成立;假设当(*)x k k N =∈时,11k k a a +<<成立,即1101k k a a a +<<<≤,那么当1n k =+时,由()f x 在区间(01],是增函数,1101k k a a a +<<<≤得1()()(1)k k f a f a f +<<.而1()n n a f a +=,则121(),()k k k k a f a a f a +++==,121k k a a ++<<,也就是说当1n k =+时,11n n a a +<<也成立.由上面证明知对任意的正整数n ,不等式恒成立.(3)由()ln f x x x x =-,1()n n a f a +=可得1ln k k k k a b a b a a +-=--11ln ki i i a b a a ==--∑若存在某i k ≤满足i a b ≤,则由(2)知:1k i a b a b +-<-≥0若对任意i k≤都有i a b >,则1ln k k k k a b a b a a +-=--11ln k i i i a b a a ==--∑11ln k i i a b a b ==--∑11()l n k i i a b a b==--∑11ln a b ka b >--11()0a b a b >---=,即1k a b +>成立.归纳小结:本题是用数学归纳法解决不等式问题,解决此类问题的重点在第二步,关键是要正确合理地运用归纳假设,选择恰当的不等式放缩法.四、本专题总结1.反正法和数学归纳法都是证明数学问题的重要方法,反证法适用于“正难则反” 的证明题,数学归纳法是一种只适用于与正整数n 有关的命题的证明方法.2.用数学归纳法证明命题时,需注意:(1)第一步是基础,首先要验证0n n =(0n ∈N *)时成立,注意0n 不一定为1;第二步是依据,在第二步中,关键是要正确合理地运用归纳假设,尤其要弄清由k 到1k +的变化,两个步骤缺一不可,且书写必须规范;(2)常用数学归纳法解决下列问题:证明恒等式或不等式、数的整除问题、几何图形中的计算问题、以及求数列的通项与和,因此掌握数学归纳法的基本步骤与要求,结合数列、不等式、函数等知识,运用类比与猜想、抽象与概括,特殊与一般的思想方法来解决此类问题.。
