第十七章 量子物理基础习题解
量子物理17
A ν0 = h
光电效应、 康普顿效应 证明了光的 波粒二象性。
ε = hν
p= h
λ
3.康普顿效应 从光子与电子发生弹性碰撞,能量、动 量守恒推导。
4.德布罗意物质波 5. 波函数物理意义:
h E λ= ν= p h E2 = p2c2 + m02c4
Ψ|2 = Ψ ⋅ Ψ * 表示 t 时刻在(x, y, z)处 概率密度。 单位体积内出现的概率 即概率密度 概率密度 波函数的标准条件:单值、有限、连续。 归一化条件:
2. 用频率为ν1的单色光照射某一种金属时,测得光电子的最大 的单色光照射某一种金属时, 动能为E 的单色光照射另一种金属时, 动能为 K1 ;用频率为ν2的单色光照射另一种金属时,测得光电 子的最大动能为E 如果E 子的最大动能为 K2 ;如果 K1 > EK2 ,那么 : (A) ν1一定大于 ν2 ) (B) ν1一定小于 ν2 ) (C) ν1一定等于 ν2 ) (D) ν1可能大于也可能小于 ν2 ) [ D ]
3.玻尔氢原子理论的成功和局限性是什么? 答:成功:从理论上解释了氢原子光谱的实验规律,并从 理论上算出里德伯常量. 玻尔首先提出了原子系统能量量子化的概念和角动量量 子化的假设. 玻尔创造性的提出了定态、跃迁等重要概念 玻尔创造性的提出了定态、跃迁等重要概念,为近代量子 物理的建立奠定了基础.
局限性:由于未能预见微观粒子的波粒二象性,虽然提出正 确的量子假设,但未能完全脱离经典理论的影响,仍采用经 典理论的思想和处理方法,因此不能正确说明氢原子内部的 微观粒子运动.
15. 根据玻尔理论, 氢原子在 n=5轨道上的动量矩 与第一激发态的轨道上动量矩之比为 (A) 5/2 (C) 5/4 (B) 5/3 (D) 5 [A ] 轨道动量矩 第一激发态 n=2
习题解答(光学篇和量子物理篇)

第14章习题解答1.某单色光从空气射入水中,其频率、波速、波长是否变化?怎样变化?解: υ不变,为波源的振动频率;nn 空λλ=变小;υλn u =变小.2.什么是光程? 在不同的均匀介质中,若单色光通过的光程相等时,其几何路程是否相同?其所需时间是否相同?在光程差与相位差的关系式2πϕδλ∆=中,光波的波长要用真空中波长,为什么?解:nr δ=.不同媒质若光程相等,则其几何路程定不相同;其所需时间相同,为t C δ∆=.因为δ中已经将光在介质中的路程折算为光在真空中所走的路程。
3.在杨氏双缝实验中,作如下调节时,屏幕上的干涉条纹将如何变化?试说明理由。
(1)使两缝之间的距离变小;(2)保持双缝间距不变,使双缝与屏幕间的距离变小; (3)整个装置的结构不变,全部浸入水中;(4)光源作平行于1S 、2S 连线方向的上下微小移动; (5)用一块透明的薄云母片盖住下面的一条缝。
解: 由λdDx =∆知,(1)条纹变疏;(2)条纹变密;(3)条纹变密;(4)零级明纹在屏幕上作相反方向的上下移动;(5)零级明纹向下移动.4.在空气劈尖中,充入折射率为n 的某种液体,干涉条纹将如何变化? 解:干涉条纹将向劈尖棱边方向移动,并且条纹间距变小。
5.当将牛顿环装置中的平凸透镜向上移动时,干涉图样有何变化?解:透镜向上移动时,因相应条纹的膜厚k e 位置向中心移动,故条纹向中心收缩。
6.杨氏双缝干涉实验中,双缝中心距离为0.60mm ,紧靠双缝的凸透镜焦距为2.5m ,焦平面处有一观察屏。
(1)用单色光垂直照射双缝,测得屏上条纹间距为2.3mm ,求入射光波长。
(2)当用波长为480nm 和600nm 的两种光时,它们的第三级明纹相距多远? 解:(1)由条纹间距公式λdDx =∆,得 332.3100.6105522.5x d nm D λ--∆⋅⨯⨯⨯===(2)由明纹公式Dx k d λ=,得92132.5()3(600480)10 1.50.610D x k mm d λλ--∆=-=⨯⨯-⨯=⨯ 7.在杨氏双缝实验中,双缝间距d =0.20mm ,缝屏间距D =1.0m 。
量子物理基础习题

17-1 在加热黑体过程中,其单色辐出度的峰值波长是由μm 69.0变化到μm 50.0,求总辐出度改变为原来的多少倍?解:由 4)(T T M B σ=,b T m =λ 得 63.3)5.069.0()()()(442112===m m B B T M T M λλ17-2解:(1)m 10898.21010898.21073--⨯=⨯==T b m λ (2)J 1086.610898.21031063.61610834---⨯=⨯⨯⨯⨯===λνch h E 17-3解:(1)4)(T T M B σ=,K 17001067.5001.0/6.473)(484=⨯==-σT M T B(2)m 1070.1170010898.263--⨯=⨯==T b m λ (3)162)()()(441212===T T T M T M B B ,2612W/m 10578.7001.06.47316)(16)(⨯=⨯==T M T M B B17-4 钾的光电效应红限波长为μm 62.00=λ。
求:(1)钾的逸出功;(2)在波长nm 330=λ的紫外光照射下,钾的截止电压。
解:(1)eV 2J 1021.31062.01031063.61968340=⨯=⨯⨯⨯⨯===---λνch h A (2)A h mv eU a -==ν221 V 76.11060.11021.3103301031063.619199834=⨯⨯-⨯⨯⨯⨯=-=-=----eA ch eA h U a λν17-5 铝的逸出功为eV 2.4。
今用波长为nm 200的紫外光照射到铝表面上,发射的光电子的最大初动能为多少?截止电压为多大?铝的红限波长是多大?解:(1)eV 2J 1023.3106.12.4102001031063.621191998342≈⨯=⨯⨯-⨯⨯⨯⨯=-=-=----A c h A h mv λν (2)221mv eU a =,V 2eV2==eU a (3)Hz 10014.11063.6106.12.41534190⨯=⨯⨯⨯==--h A νnm 296m 1096.210014.1103715800=⨯=⨯⨯==-νλc17-6 在光电效应实验中,对某金属,当入射光频率为Hz 102.215⨯时,截止电压为V 6.6,入射光频率为Hz 106.415⨯时,截止电压为V 5.16。
大学物理 第十七章 量子力学基础3

e2
运用球坐标系
1 2 1 ( r ) (sin ) 2 2 r r r r sin 1 2 2m e2 2 2 2 (E ) 0 2 r sin 40 r
17
将 分离变量为
( r, , ) R( r )( )( )
科学家简介——尼尔斯· 玻尔
6
尼尔斯· 玻尔
尼尔斯· 玻尔(Bohr,Niels)1885年10月 7日生于丹麦首都哥本哈根,父亲是哥本 哈根大学的生理学教授.从小受到良好 的家庭教育.1903年进入哥本哈根大学 学习物理,1909年获科学硕士学位, 1911年获博士学位.大学二年级时研究 水的表面张力问题,自制实验器材,通 过实验取得了精确的数据,并在理论方 面改进了物理学家瑞利的理论,研究论 文获得丹麦科学院的金奖章.
23
在不同的状态中,电子在各处出现的概率是不一样 的.如果用疏密不同的点子表示电子在各个位臵出现的概 率,画出图来,就像云雾一样,可以形象地称做电子云. 注意:1)电子云是几率云,只知电子在何处出现的几 率大小,要问电子在何处,答曰;“云深不知处” 2)电子没有确定的轨道,所谓“轨道”只是电子出现几 率最大的地方。 对于基态 n 1.l 0, ml 0
14
m
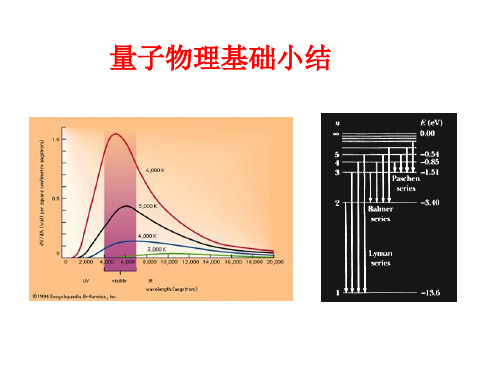
E(eV)
0(电离态) -0.54 -0.85 -1.51
布喇开系
帕邢系 巴耳末系
5 4
3
2
-3.39
赖曼系
1 氢原子中电子的能级
15
-13.6(基态)
玻尔把当时人们持极大怀疑的普朗克--爱因斯坦 的量子化与表面上毫不相干的光谱实验巧妙地结合起 来,解释了近30年的光谱之谜--巴耳末与里德伯的公 式,并首次算出里德伯常数。 在表面上完全不同的事物之间寻找它们的内在联系, 这永远是自然科学的一个令人向往的主题。 玻尔能成功解释氢原子光谱的规律性,但不能解 释复杂光谱规律等问题。产生这种缺陷的原因是玻尔 的原子模型是牛顿力学概念和量子化条件的混合物。 1922年,玻尔因为对原子结构和原子放射性的 研究而获诺贝尔物理奖。
高中物理人教版选修3-5练习:第十七章 第1、2节 能量量子化 光的粒子性 课下作业 含解析

A.热的物体向外辐射电磁波,冷的物体只吸收电磁波B.温度越高,物体辐射的电磁波越强C.辐射强度按波长的分布情况只与物体的温度有关,与材料种类及表面状况无关D.常温下我们看到的物体的颜色就是物体辐射电磁波的颜色解析:一切物体都不停地向外辐射电磁波,且温度越高,辐射的电磁波越强,A错误,B正确;选项C是黑体辐射的特性,C错误;常温下看到的物体的颜色是反射光的颜色,D错误。
答案:B2.如图1所示,一验电器与锌板用导线相连,用紫外线光源照射锌板时,验电器指针发生了偏转,下列判断正确的是( ) A.此时锌板带正电B.紫外线越强,验电器的指针偏角越大图1C.改用红外线照射锌板,验电器的指针一定会偏转D.将一不带电的金属小球与锌板接触,则验电器指针偏角会减小解析:用紫外线照射锌板,锌板发生了光电效应,即锌板有电子逸出,锌板带正电,A正确;紫外线越强,即单位时间打在锌板上的光子越多,逸出的电子越多,锌板所带的电荷量越多,验电器的指针偏角越大,B正确;由于红外线的频率比紫外线的频率小,因此不一定能发生光电效应,验电器指针不一定会发生偏转,C错误;将一不带电的金属小球与锌板接触,锌板将部分电荷转移给金属小球,验电器指针的偏角将减小,D正确。
答案:ABD3.光子有能量,也有动量,动量p=,它也遵守有关动量的规律。
如图2所示,真空中,有“∞”字形装置可绕通过横杆中点的竖直轴OO′在水平面内灵活地转动,其中左边是圆形黑纸片(吸收光子),右边是和左边大小、质量相同的圆形白纸片(反射光子)。
当用图2平行白光垂直照射这两个圆面时,关于装置开始时转动情况(俯视)的下列说法中正确的是( ) A.顺时针方向转动B.逆时针方向转动C.都有可能D.不会转动解析:根据动量定理Ft=mvt-mv0,由光子的动量变化可知黑纸片和光子之间的作用力小于白纸片和光子之间的作用力,所以装置开始时逆时针方向转动,B选项正确。
答案:B4.分别用波长为λ和λ的单色光照射同一金属板,发出的光电子的最大初动能之比为1∶2。
大学物理下大物量子17分解

hc
= 1.61013 J
h
5.35 10 22 (kg m s 1 )
光子质量: 由 h
hc
mc 2
h m 1.78 10 30 (kg ) c
大学物理
§17.3 康普顿效应
一、实验规律
二、 Compton 的解释
三、吴有训对研究康普顿效应的贡献
大学物理
遵守能量守恒定律和动量守恒定律
P0 P Pe h 0 m0 c h Ee
2
h
j
P 散射光子
Pe
反冲电子
P0 h 0
•利用相对论能量与动量关系
E P c m c
2 e 2 2 e
2 4 0
h P c
•得出结果
0 h (1 cosj ) m0c
•解释在散射线中还有原波长的成分 如果光子与石墨中被原子核束缚得很紧的电 子发生碰撞(内层电子) 相当于光子和整个原子碰撞(m0是原子质量)
这样 散射光的能量(波长)几乎不改变
从而散射线中还有与原波长相同的射线 原子序数愈大的散射体原波长的成分愈多
3.康普顿散射实验的意义
大学物理
支持了“光量子”概念 进一步证实 了 = h 首次在实验上证实了爱因斯坦提出的 “光量子具有动量”的假设 P = E/c = h/c = h/
T m = b
b = 2.897103m k.
大学物理
例1. 假定恒星表面的行为和黑体表面一样,测得 太阳和北极星辐射波谱的峰值波长分别为:
m 510nm, m 350nm, 试估计太阳和北极 星的表面温度及每单位表面上单位时间内辐 射出的总能量。
2020-2021学年高二人教版物理选修3-5学案:第十七章 1 能量量子化 Word版含解析

第十七章波粒二象性1能量量子化一、黑体与黑体辐射1.热辐射(1)热辐射:我们周围的一切物体都在以电磁波的形式向外辐射能量,而且辐射强度与物体的温度相关,所以物理上把这种辐射称为热辐射.(2)热辐射的基本规律:物体以电磁波的形式向外辐射能量,而且在不同温度下辐射强度按电磁波波长有不同的分布.2.黑体辐射(1)黑体物体在辐射电磁波的同时,还会吸收和反射外界射来的电磁波.如果一个物体能全部吸收外来的电磁波而不产生反射,我们称之为绝对黑体,简称黑体.(2)黑体辐射黑体表面向外辐射电磁波,这个过程叫做黑体辐射.黑体辐射的状况只与黑体的温度有关,与材料的种类及表面状况无关,能反映具有普遍意义的热辐射规律,是研究热辐射的理想模型.在火炉旁边有什么感觉?投入炉中的铁块颜色怎样变化?说明了什么问题?提示:在火炉旁会感到热,这是由于火炉不断地向外辐射能量.投入炉中的铁块依次呈现暗红、赤红、橘红等颜色,直至成为黄白色,这表明同一物体热辐射的强度与温度有关.二、黑体辐射的实验规律1.黑体辐射的实验规律随着温度的升高,一方面,各种波长的辐射强度都有增加,另一方面,辐射强度的最大值向波长短的方向移动.2.黑体辐射实验规律的理论解释(1)维恩公式:德国物理学家维恩从热学理论推出的公式,只在短波部分与实验相符;(2)瑞利公式:英国物理学家瑞利从经典电磁理论推出的公式,只在长波部分与实验相符;且根据瑞利公式,当波长趋于零时,辐射本领将会趋于无穷大,这显然与客观事实不符.由于高频范围的辐射是在紫外波段,故而被当时的科学家称为“紫外灾难”.你认为现实生活中存在理想的黑体吗?提示:现实生活中不存在理想的黑体,实际的物体都能辐射红外线(电磁波),也都能吸收和反射红外线(电磁波),绝对黑体不存在,是理想化的模型.三、能量子1.能量子微观世界里的能量是一份一份的,其中不可分的最小值ε叫做能量子,ε=hν,式中的ν是电磁波的频率,h是普朗克常量,h=6.626×10-34J·s.2.量子化宏观世界里的能量是连续的,微观世界里的能量是不连续的,不是任意值,是量子化的,或者说是分立的.考点一对黑体和黑体辐射的理解(1)对黑体的理解:绝对的黑体实际上是不存在的,但可以用某装置近似地代替.如图所示,如果在一个空腔壁上开一个小孔,那么射入小孔的电磁波在空腔内表面会发生多次反射和吸收,最终不能从空腔射出,这个小孔就成了一个绝对黑体.(2)对黑体辐射的理解:任何物体都具有不断辐射、吸收、反射电磁波的本领.辐射出去的电磁波在各个波段是不同的,也就是具有一定的谱分布.这种谱分布与物体本身的特性及其温度有关,因而被称为热辐射.(3)一般物体与黑体的比较:热辐射特点吸收、反射特点一般物体辐射电磁波的情况与温度有关,与材料的种类及表面状况有关既吸收又反射,其能力与材料的种类及入射波长等因素有关黑体辐射电磁波的强度按波长的分布只与黑体的温度有关完全吸收各种入射电磁波,不反射①在任何温度下,任何物体都会发射电磁波,并且其辐射强度按波长的分布情况随物体的温度而有所不同,这是热辐射的一种特性.在室温下,大多数物体辐射的是不能引起视觉的波长较长的电磁波——红外光;但当物体被加热到500 ℃左右时,开始发出暗红色的可见光.随着温度的不断上升,辉光逐渐亮起来,而且热辐射中较短波长的成分越来越多,即能引起视觉的电磁波越来越多,大约在 1 500 ℃时变成明亮的白炽光.这说明同一物体在一定温度下所辐射的能量在不同光谱区域的分布是不均匀的,而且温度越高光谱中与能量最大的辐射相对应的频率也越高.②在一定温度下,不同物体所辐射的光谱成分有显著的不同.例如,将钢加热到约800 ℃时,就可观察到明亮的红色光,但在同一温度下,熔化的水晶却不辐射可见光.【例1】(多选)下列叙述正确的是()A.一切物体都在辐射电磁波B.一般物体辐射电磁波的情况只与温度有关C.黑体辐射电磁波的强度按波长的分布只与黑体温度有关D.黑体能够完全吸收入射的各种波长的电磁波根据热辐射的定义及黑体辐射的实验规律直接判断即可.【答案】ACD【解析】根据热辐射的定义,A正确;因为一般物体辐射电磁波的情况除与温度有关外,还与材料种类和表面状况有关,而黑体辐射只与黑体的温度有关,故B错误,C正确;根据黑体的定义知D正确.总结提能黑体同其他物体一样也在辐射电磁波,黑体的辐射规律最为简单,黑体辐射强度只与温度有关.下列描绘两种温度下黑体辐射强度与波长关系的图中,符合黑体辐射规律的是(A)解析:根据黑体辐射的规律,温度越高,辐射强度越大,辐射出的波频率高的比例增大,即波长小的波比例增大,故选A.考点二能量量子化1.能量子:超越牛顿的发现(1)普朗克的量子化假设:①能量子:振动着的带电微粒的能量只能是某一最小能量值ε的整数倍.例如,可能是ε或2ε、3ε……当带电微粒辐射或吸收能量时,也是以这个最小能量值为单位一份一份地辐射或吸收的.这个不可再分的最小能量值ε叫做能量子;②能量子公式:ε=hν,ν是电磁波的频率,h是一个常量,称为普朗克常量,其值h=6.63×10-34J·s;③能量的量子化:在微观世界中能量不能连续变化,只能取分立值,这种现象叫做能量的量子化.(2)能量子假说的实验证实:普朗克公式与实验结果比较,发现它与实验结果“令人满意地相符”.如图所示,曲线是根据普朗克的公式作出的,小圆代表实验值.(3)普朗克的能量子假说的意义:普朗克的能量子假说,使人类对微观世界的本质有了全新的认识,对现代物理学的发现产生了革命性的影响.2.能量的量子化微观粒子的能量与宏观世界的能量的认识不同.例如,一个宏观的弹簧振子,把小球推离平衡位置后开始振动,能量为E.第二次我们可以把它推得稍远一些,使它振动的能量稍多一些,例如1.2E 或1.3E.推得更远,能量更大.弹簧振子的能量不是某一个最小值的整数倍.只要在弹性限度内,我们可以把小球推到任何位置,其能量可以是任何值.即对弹簧振子的能量,我们说能量值是连续的;而普朗克的假说则认为,微观粒子的能量是量子化的,或说微观粒子的能量是分立的.【例2】 一盏电灯发光功率为100W ,假设它发出的光向四周均匀辐射,光的平均波长λ=6.0×10-7m ,在距电灯10 m 远处,以电灯为球心的球面上,1m 2的面积每秒通过的光子(能量子)数约为( )A .2×1017B .2×1016C .2×1015D .2×10231.每个光子的能量是多少?2.电灯每秒钟产生的光能是多少,这些光能包含多少个光子? 【答案】 A【解析】 光是电磁波,辐射能量也是一份一份进行的,100 W 灯泡每秒产生光能E =100J ,设电灯每秒发出的光子数为n ,E =nhν=nh cλ,在以电灯为球心的球面上,1m 2的面积每秒通过的光子(能量子)数n ′=n 4πr 2, n ′=Eλ4πr 2hc =100×6.0×10-74×3.14×102×6.63×10-34×3×108≈2×1017(个).总结提能 此类题一定要注意空间想象能力,并把画面想象出来.同时要注意关键字眼,如“每秒”“1 m 2”的理解.太阳光垂直射到地面上时,地面上1 m 2接收的太阳光的功率是1.4 kW ,其中可见光部分约占45%.(1)假设认为可见光的波长约为0.55μm ,日地间距离R =1.5×1011 m .普朗克常量h =6.6×10-34J·s ,估算太阳每秒辐射出的可见光光子数为多少?(2)若已知地球的半径为6.4×106 m ,估算地球接收的太阳光的总功率. 答案:(1)4.9×1044个 (2)1.8×1014 kW解析:(1)设地面上垂直阳光的每平方米面积上每秒接收的可见光光子数为n ,则有P ×45%=nh cλ.解得:n =0.45λP hc =0.45×0.55×10-6×1.4×1036.6×10-34×3×108 个·m -2=1.75×1021 个·m -2. 则所求可见光光子数N =n ·4πR 2=1.75×1021×4×3.14×(1.5×1011)2=4.9×1044(个). (2)地球接收阳光的总功率P 地=P πr 2=1.4×3.14×(6.4×106)2 kW ≈1.8×1014 kW.重难疑点辨析 黑体温度的计算方法自然界中的物体由于具有一定的温度,会不断向外辐射电磁波,这种辐射因与温度有关,称为热辐射.热辐射具有如下特点:(1)辐射的能量中包含各种波长的电磁波;(2)物体温度越高,单位时间从物体表面单位面积上辐射的能量越大;(3)在辐射的总能量中,各种波长所占的百分比不同.处于一定温度的物体在向外辐射电磁能量的同时,也要吸收由其他物体辐射的电磁能量,如果它处在平衡状态,则能量保持不变.若不考虑物体表面性质对辐射与吸收的影响,我们定义一种理想的物体,它能100%地吸收入射到其表面的电磁辐射,这样的物体称为黑体.单位时间内从黑体表面单位面积辐射的电磁波的总能量与黑体热力学温度的四次方成正比,即P 0=σT 4,其中常量σ=5.67×10-8 W/(m 2·K 4).【典例】 在下面的问题中,把研究对象都简单地看作黑体.有关数据及数学公式:太阳半径R s =696 000 km ,太阳表面温度T =5 770 K ,火星半径r =3 395 km ,球面积公式S =4πR 2,其中R 为球半径.(1)太阳热辐射能量的绝大多数集中在波长为2×10-7~1×10-5 m 范围内,求相应的频率范围.(2)每小时从太阳表面辐射的总能量为多少?(3)火星受到来自太阳的辐射可以认为垂直射到面积为πr 2(r 为火星半径)的圆盘上,已知太阳到火星的距离约为太阳半径的400倍,忽略其他天体及宇宙空间的辐射,试估算火星的平均温度.【解析】 (1)由ν=cλ,得ν1=3.00×1082×10-7 Hz=1.5×1015 Hz.ν2=3.00×1081×10-5Hz =3×1013Hz.所以,辐射频率范围是3×1013~1.5×1015 Hz. (2)每小时从太阳表面辐射的总能量为E =4πσR 2s T 4t ,代入数据得E =1.38×1030 J.(3)设火星表面温度为T ′,太阳到火星的距离为d ,火星单位时间吸收来自太阳的辐射能量为P入=4πR 2s σT 4·πr 24πd 2,d =400R s .所以P 入=πσT 4r 24002. 火星单位时间向外辐射电磁波能量为 P 出=4πσr 2T ′4,火星处于平衡状态 P 入=P 出,即πσT 4r 24002=4πσr 2T ′4得T ′=T800=204 K. 【答案】 (1)3×1013~1.5×1015 Hz (2)1.38×1030 J (3)204 K热辐射与温度之间有着密切的关系.热辐射的光谱是连续光谱,辐射光谱的性质与温度有关.在室温下,大多数物体辐射不可见的红外光.但当物体被加热到500 ℃左右时,开始发出暗红色的可见光.随着温度的不断上升,辉光逐渐亮起来,而且波长较短的辐射越来越多.大约在1 500 ℃时就会变成明亮的白炽光.这说明同一物体在一定温度下所辐射的能量,在不同光谱区域的分布是不均匀的,而且温度越高,光谱中与能量最大的辐射相对应的频率也越高.现在的汽车大灯、LED 灯等都标有“色温”,色温越高,越偏向蓝色,色温越低,越偏向红色.1.黑体辐射电磁波的波长分布的影响因素是( A ) A .温度B .材料C.表面状况D.以上都正确解析:根据黑体辐射电磁波的波长分布的决定因素知,其只与温度有关.2.以下宏观概念,是“量子化”的是(D)A.木棒的长度B.物体的质量C.物体的动量D.学生的个数解析:所谓“量子化”应该是不连续的,一份一份的.故正确选项为D.3.(多选)黑体辐射的实验规律如图所示,由图可知(AC)A.随温度升高,各种波长的辐射强度都有增加B.随温度降低,各种波长的辐射强度都有增加C.随温度升高,辐射强度的极大值向波长较短的方向移动D.随温度降低,辐射强度的极大值向波长较短的方向移动解析:根据黑体辐射的实验规律和题图知,A正确,B错误;温度升高时,辐射强度的极大值向波长较短的方向移动,C正确,D错误.4.(多选)关于对普朗克能量子假说的认识,下列说法正确的是(BC)A.振动着的带电微粒的能量只能是某一能量值εB.带电微粒辐射或吸收的能量只能是某一最小能量值的整数倍C.能量子与电磁波的频率成正比D.这一假说与现实世界相矛盾,因而是错误的解析:根据普朗克能量子假说知,A错误,B、C正确;普朗克能量子假说反映的是微观世界的特征,不同于宏观世界,D错误.5.在自然界生态系统中,蛇与老鼠和其他生物通过营养关系构成食物链,在维持生态平衡方面发挥着重要作用.蛇是老鼠的天敌,它是通过接收热辐射来发现老鼠的.假设老鼠的体温约37 ℃,它发出的最强的热辐射的波长为λmax.根据热辐射理论,λmax与辐射源的绝对温度T的关系近似为Tλmax=2.90×10-3 m·K.(1)老鼠发出最强的热辐射的波长为(B)A.7.8×10-5 m B.9.4×10-6 mC.1.16×10-4 m D.9.7×10-8 m(2)老鼠发出的最强热辐射属于(C)A.可见光波段B.紫外波段C.红外波段D.X射线波段莘莘学子,最重要的就是不要去看远方模糊的,而要做手边清楚的事。
大学物理17章答案

第17章 量子物理基础17.1 根据玻尔理论,计算氢原子在n = 5的轨道上的动量矩与其在第一激发态轨道上的动量矩之比.[解答]玻尔的轨道角动量量子化假设认为电子绕核动转的轨道角动量为2π==n n hL mvr n ,对于第一激发态,n = 2,所以L 5/L 2 = 5/2.17.2设有原子核外的3p 态电子,试列出其可能性的四个量子数.[解答] 对于3p 态电子,主量子数为n = 3,角量子数为 l = 1,磁量子数为 m l = -l , -(l - 1), …, l -1, l ,自旋量子数为 m s = ±1/2.3p 态电子的四个可能的量子数(n ,l ,m l ,m s )为(3,1,1,1/2),(3,1,1,-1/2),(3,1,0,1/2),(3,1,0,-1/2),(3,1,-1,1/2),(3,1,-1,-1/2) .17.3 实验表明,黑体辐射实验曲线的峰值波长λm 和黑体温度的乘积为一常数,即λm T = b = 2.897×10-3m·K .实验测得太阳辐射波谱的峰值波长λm = 510nm ,设太阳可近似看作黑体,试估算太阳表面的温度.[解答]太阳表面的温度大约为392.8971051010λ--⨯==⨯m b T = 5680(K).17.4 实验表明,黑体辐射曲线和水平坐标轴所围成的面积M (即单位时间内从黑体单位表面上辐射出去的电磁波总能量,称总辐射度)与温度的4次方成正比,即M = σT 4,其中σ =5.67×10-8W·m -2·K -4.试由此估算太阳单位表面积的辐射功率(太阳表面温度可参见上题).[解答]太阳单位表面积的辐射功率大约为M = 5.67×10-8×(5680)4 = 5.9×107(W·m -2).17.5宇宙大爆炸遗留在宇宙空间的均匀背景辐射相当于3K 黑体辐射.求:(1)此辐射的单色辐射强度在什么波长下有极大值?(2)地球表面接收此辐射的功率是多少?[解答](1)根据公式λm T = b ,可得辐射的极值波长为λm = b/T = 2.897×10-3/3 = 9.66×10-4(m).(2)地球的半径约为R = 6.371×106m ,表面积为 S = 4πR 2.根据公式:黑体表面在单位时间,单位面积上辐射的能量为 M = σT 4,因此地球表面接收此辐射的功率是P = MS = 5.67×10-8×34×4π(6.371×106)2= 2.34×109(W).17.6 铝表面电子的逸出功为6.72×10-19J,今有波长为λ = 2.0×10-7m 的光投射到铝表面上.试求:(1)由此产生的光电子的最大初动能;(2)遏止电势差;(3)铝的红限波长.[解答](1)光子的能量为E = hν = hc/λ,根据爱因斯坦光电效应方程hν = E k + A,产生的光电子的最大初动能为E k= hν - A= 6.63×10-34×3×108/2.0×10-7-6.72×10-19= 3.23×10-19(J).(2)遏止电势差的公式为eU s = E k,遏止电势差为U s = E k/e = 3.23×10-19/1.6×10-19=2.0(V).(3)铝的红限频率为ν0= A/h,红限波长为λ0= c/ν0= hc/A= 6.63×10-34×3×108/6.72×10-19= 2.96×10-7(m).17.7 康普顿散射中入射X射线的波长是λ = 0.70×10-10m,散射的X 射线与入射的X射线垂直.求:(1)反冲电子的动能E K ;(2)散射X 射线的波长;(3)反冲电子的运动方向与入射X 射线间的夹角θ.[解答](1)(2)根据康普顿散射公式得波长变化为21222sin 2 2.42610sin 24ϕπλΛ-∆==⨯⨯= 2.426×10-12(m),散射线的波长为λ` = λ + Δλ = 0.72426×10-10(m).反冲电子的动能为`k hchcE λλ=-34834810106.6310310 6.63103100.7100.7242610----⨯⨯⨯⨯⨯⨯=-⨯⨯= 9.52×10-17(J).(3)由于 /`tan /`hc hc λλθλλ==,0.70.96650.72426==,所以夹角为θ = 44°1`.17.8 求波长分别为λ1 = 7.0×10-7m 的红光;λ2 = 0.25×10-10m 的X 射线的能量、动量和质量.[解答]X 射线的能量为E = h ν = hc/λ,动量为 p = h/λ;由E = hc/λ = mc 2,得其质量为m = h/cλ.对于红光来说,能量为348176.6310310710E --⨯⨯⨯=⨯= 2.84×10-19(J),动量为34176.6310710p --⨯=⨯= 9.47×10-25(kg·m·s -1),质量为341876.6310310710m --⨯=⨯⨯⨯= 3.16×10-36(kg).对于X 射线来说,能量为3482106.63103100.2510E --⨯⨯⨯=⨯= 7.956×10-15(J),动量为342106.63100.2510p --⨯=⨯= 2.652×10-23(kg·m·s -1),质量为3428106.63103100.2510m --⨯=⨯⨯⨯= 8.84×10-32(kg).17.9 处于第四激发态上的大量氢原子,最多可发射几个线系,共几条谱线?那一条波长最长.[解答]第四激发态的氢原子处于第5个能级,最多可发射四个线系.(1)能级5到4,1条谱线;(2)能级5和4到3,2条谱线;(3)能级5、4和3到2,3条谱线;(3)能级5、4、3和2到1,4条谱线.共10条谱线.从能级5跃迁到4发射的光谱频率最小,波长最长.17.10 设氢原子中电子从n = 2的状态被电离出去,需要多少能量.[解答]氢原子能级公式为4222018n me E h n ε=-,当n =1时,基态能级的能量为412208me E h ε=-≈-2.18×10-18(J) = -13.6(eV),因此 12n E E n =.当电子从n 能级跃迁到m 能级时放出(正)或吸收(负)光子的能量为12211()n m E E E E n m ∆=-=-.电离时,m 趋于无穷大.当电子从n = 2的能级电离时要吸收能量 221113.6()2E ∆=--∞= -3.4(eV),因此需要3.4eV 的能量.17.11 质量为m 的卫星,在半径为r 的轨道上环绕地球运动,线速度为v .(1)假定玻尔氢原子理论中关于轨道角动量的条件对于地球卫星同样成立.证明地球卫星的轨道半径与量子数的平方成正比,即r = Kn 2,(式中K 是比例常数);(2)应用(1)的结果求卫星轨道和下一个“容许”轨道间的距离,由此进一步说明在宏观问题中轨道半径实验上可认为是连续变化的(利用以下数据作估算:普朗克常数h = 6.63×10-34J·s ,地球质量M = 6×1024kg ,地球半径R = 6.4×103km ,万有引力常数G =6.7×10-11N·m 2·kg -2.[解答](1)卫星绕地球运动的向心力是万有引力22Mm mv G r r =;根据玻尔理论,角动量为mvr = nh /2π.将前式乘以mr 3得2222()()4nh GMm r mvr π==,所以 222224h n r Kn GMm π==,即:卫星的轨道半径与量子数的平方成正比.(2)假设卫星质量m = 100kg ,比例系数为2224h K GMm π=342211242(6.6310)4 6.710610(100)π--⨯=⨯⨯⨯⨯⨯ = 2.77×10-87.可见:比例系数很小.当r = R 时,地球表面的量子数为460 4.810n ⨯.可见:地球表面处的量子数很大.地面以上的量子数设为n `,(n` = 1,2,3,…),则总量子数可表示为两个量子数之和:n =n 0 + n`.轨道间的距离为Δr = K [(n 0 + n` + 1)2 - (n 0 + n`)2]= K [2(n 0 + n`) + 1].由于n 0>>1,所以Δr = 2Kn 0 + 2Kn`.设n` = kn 0,即:取地面以上的量子数为地球表面量子数的倍数,有n = (k + 1)n 0,则r = Kn 02(k + 1)2,Δr = 2Kn 0(k + 1) = 2.66×10-40(k + 1).这说明:当地面以上的量子数按k + 1成倍地增加时,半径将按k + 1的平方的规律增加,而轨道之间的距离只按k + 1的一次方的规律增加;由于Δr 的系数很小,所以轨道间距是非常非常小的,因此可认为轨道半径是连续变化的.17.12 电子和光子各具有波长2.0×10-10m ,它们的动量和总能量各是多少?[解答]它们的动量都为34106.6310210h p λ--⨯==⨯= 3.315×10-24(kg·m·s -1).根据公式E 2 = p 2c 2 + m 02c 4,电子的总能量为E ==3×108×[(3.315×10-24)2+ (9.1×10-31×3×108)2]1/2=8.19×10-14(J).光子的静止质量为零,总能量为E = cp= 3×108×3.315×10-24 = 9.945×10-16(J).17.13 室温下的中子称为热中子T = 300K ,试计算热中子的平均德布罗意波长.[解答]中子热运动的平均速度为=v其中k为玻尔兹曼常数k= 1.38×10-23J·K-1,m p是电子的质量m p= 1.675×10-27kg,可得平均速度为v= 2.509×104(m·s-1),平均动量为=np m v= 4.2×10-27(kg·m·s-1).平均德布罗意波长为/λ=h p= 1.58×10-10(m) = 0.158(nm).17.14 一束动量是p的电子,通过缝宽为a的狭缝,在距离狭缝为R 处放置一屏,屏上电子衍射图样中央最大的宽度是多少?[解答]根据动量和位置的不确定关系Δp x·Δx≧h,其中位置不确定量为Δx = a,动量的不确定量为Δp x = p sinθ.设电子衍射图样的中央最大半宽度为w,则sinθ = w/R,可得wp a hR⋅≥,宽度为22hRwpa≥.[注意]如果将h改为ћ/2,则宽度为2w≧ћR/pa.两者相差很小.17.15 一宽度为a的一维无限深势阱,试用不确定关系估算阱中质量为m的粒子最低能量为多少?[解答]粒子坐标的不确定范围是Δx ≦a ,动量的不确定范围是Δp ≧h /Δx ≧h /a .这也就是动量p 的范围.因此能量为E = p 2/2m ≧ h 2/2ma 2,最低能量可估计为E min = h 2/2ma 2.17.16 设有一宽度为a 的一维无限深势阱,粒子处于第一激发态,求在x = 0至x = a /3之间找到粒子的几率?[解答]粒子在一维无限深势阱中的定态波函数为(0)(),(1,2,3,...)πψ≤≤==n x a n x x n a ,Ψ(x ) = 0,(x < 0,x > a ).当粒子处于第一激发态时,n = 2,在x = 0至x = a /3之间被发现的几率为/3220|()|d ψ⎰a x x /32022sin d π=⎰a x x a a23== 0.391.17.17 设粒子在宽度为a 的一维无限深势阱运动时,其德布罗意波在阱内形成驻波,试利用这一关系导出粒子在阱中的能量计算式.[解答]当粒子在势阱中形成稳定驻波时,势阱宽度必然为半波长的整数倍,即n (λ/2) = a ,(n = 1,2,3,…).根据德布罗意假设 λ = h/p ,可得粒子的动量为2λ==h nhp a 能量为 222228==p h E n m ma .17.18假定对某个粒子动量的测定可精确到千分之一,试确定这个粒子位置的最小不确定量.(1)该粒子质量为5×10-3kg ,以2m·s -1的速度运动;(2)该粒子是速度为1.8×108m·s -1的电子.[解答]粒子的动量为 p = mv ,动量的不确定量为 Δp = p /1000,根据动量和位置的不确定关系Δp ·Δx ≧ћ/2,位置的不确定量为 Δx = ћ/2Δp .(1)100024h x p mv π∆≥=∆h3431000 6.631045102-⨯⨯=π⨯⨯⨯= 5.276×10-30(m).(2)100024h x p mv π∆≥=∆h343181000 6.631049.110 1.810--⨯⨯=π⨯⨯⨯⨯= 3.22×10-10(m).17.19设有某线性谐振子处于第一激发态,其波函数为2221ψ-=a x .式中a =,k 为常数,则该谐振子在何处出现的概率最大?[解答]第一激发态的概率为22221||a xw e ψ-==,对x 求导得222222d (2)]d a x a x w xe x a x e t --=+-2222(1)a xx x a e -=-,令d w /d t = 0,得概率最大的位置为x = ±1/a .17.20一维运动的粒子,处于如下的波函数所描述的状态,(0);()0,(0).x Axe x x x λψ-⎧>=⎨<⎩式中λ > 0,A 为常数.(1)将此波函数归一化;(2)求粒子位置的概率分布函数;(3)粒子在在何处出现的概率最大?[解答](1)归一化得222201||d d x x A xe x λψ∞∞--∞==⎰⎰ 22201d 2x A x e λλ∞--=⎰2222001{2d }2x x A x e xe x λλλ∞∞---=-⎰222012()d 2xA x e λλ∞--=-⎰ 22220012(){d }2xx A xe e x λλλ∞∞---=--⎰22323012()24xA A e λλλ∞--==,所以A =2λ3/2 .归一化波函数为3/22,(0);()0,(0).x xe x x x λλψ-⎧>=⎨<⎩([注]利用Γ函数的性质可简化积分过程.10()d n x n x e x∞--Γ=⎰,当n 为整数时,Γ(n ) = (n - 1)!.设y = 2λx ,则d x = d y /2λ,可得22331001d ()d 2x y x ex y e y λλ∞∞---=⎰⎰ 3311()(3)2()22λλ=Γ=,可以得出同一结果.)(2)粒子坐标的几率分布函数为32224,(0);()|()|0,(0).x x e x w x x x λλψ-⎧>==⎨<⎩(3)利用上一题的方法求导可得几率最大的位置为x = 1/λ.17.21 设有某一维势场如下:0,(0);,(0,).≤≤⎧=⎨<>⎩x LVV x x L该势场可称为有限高势阱,设粒子能量E < V0,求E所满足的关系式.[解答]粒子运动的薛定谔方程为222()0mE Vψψ∇+-=h.在三个区域的方程为210122d2()0,(0);dmE V xxψψ+-=<h22222d20,(0);dmE x Lxψψ+=<<h230322d2()0,().dmE V x Lxψψ+-=>h设1k=h,2k=h,则得221112d0,(0);dk xxψψ-=<(1)222222d0,(0);dk x Lxψψ+=<<(2)223132d0,().dk x Lxψψ-=>(3)方程的通解为ψ1(x) = A1exp(k1x) + B1exp(-k1x),(x<0);(4)ψ2(x ) = A 2cos(k 2x ) + B 2sin(k 2x ),(0<x <L );(5)ψ3(x) = A 3exp(k 1x ) + B 3exp(-k 1x ),(x >L ).(6)当x →-∞时,ψ1有限,所以B 1 = 0;当x →∞时,ψ3有限,所以A 3 = 0.当x = 0时,ψ1(0) = ψ2(0),可得A 1 = A 2; (7)同时ψ1`(0) = ψ2`(0),可得k 1A 1 = k 2B 2. (8)当x = L 时,ψ2(L ) = ψ3(L ),ψ2`(L ) = ψ3`(L ),可得A 2cos k 2L +B 2sin k 2L = B 3exp(-k 1L );(9)-k 2A 2sin k 2L + k 2B 2cos k 2L = -k 1B 3exp(-k 1L )(10)将(9)乘以k 1加(10)得k 1A 2cos k 2L + k 1B 2sin k 2L-k 2A 2sin k 2L + k 2B 2cos k 2L = 0.即 (k 1A 2 + k 2B 2)cos k 2L = (k 2A 2 - k 1B 2)sin k 2L ,亦 122222212t a n k A k B k L k A k B +=-. (11)由(7)和(8)得k 1A 2 = k 2B 2,即 B 2 = k 1A 2/k 2, (12)(12)代入(11)式得12222212tan kk k L k k =-,即0t a n =h (13)这就是总能量满足的关系式.17.22 原子内电子的量子态由n 、l 、m l 、m s 四个量子数表征,当n 、l 、m l 一定时,不同的量子态数目为多少?当n 、l 一定时,不同量子态数目为多少?当n 一定时,不同量子态数目为多少?[解答]当n 、l 、m l 一定时,m s 只取两个值,所以量子态数目为2. 当n 、l 一定时,m l 有(2l + 1)种不同取值,所以量子态数目为2(2l + 1).当n 一定时,l 从0到(n - 1)共有n 种不同取值,量子态数目为1110002(21)421n n n l l l l l ---===+=+∑∑∑2(1)4222n n n n -=⨯+=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十七章 量子物理基础17–1 用辐射高温计测得炉壁小孔的辐射出射度为22.8W/cm 2,则炉内的温度为 。
解:将炉壁小孔看成黑体,由斯特藩—玻耳兹曼定律()4T T M B σ=得炉内的温度为3484410416.11067.5108.22)(⨯=⨯⨯==-σT M T B K17–2 人体的温度以36.5︒C 计算,如把人体看作黑体,人体辐射峰值所对应的波长为 。
解:由维恩位移定律b T =m λ得人体辐射峰值所对应的波长为33m 10363.95.30910898.2⨯=⨯==-Tb λnm 17–3 已知某金属的逸出功为A ,用频率为1ν的光照射该金属刚能产生光电效应,则该金属的红限频率0ν= ,遏止电势差Uc = 。
解:由爱因斯坦光电效应方程W m h +=2m 21v ν,A W =,当频率为1ν刚能产生光电效应,则0212m =v m 。
故红限频率 h A /0=ν遏止电势差为()01011ννννν-=-=-=eh e h e h e W e h U c 17–4 氢原子由定态l 跃迁到定态k 可发射一个光子,已知定态l 的电离能为0.85eV ,又已知从基态使氢原子激发到定态k 所需能量为10.2eV ,则在上述跃迁中氢原子所发射的光子的能量为 eV 。
解:氢原子的基态能量为6.130-=E eV ,而从基态使氢原子激发到定态k 所需能量为E ∆=10.2eV ,故定态k 的能量为eV 4.32.106.130-=+-=∆+=E E E k又已知eV 85.0-=l E ,所以从定态l 跃迁到定态k 所发射的光子的能量为eV 55.2=-=k l E E E17–5 一个黑体在温度为T 1时辐射出射度为10mW/cm 2,同一黑体,当它的温度变为2T1时,其辐射出射度为[ ]。
A .10mW/cm 2B .20mW/cm 2C .40mW/cm 2D .80mW/cm 2E .160mW/cm 2解:由斯特藩—玻耳兹曼定律,黑体的总辐射能力和它的绝对温度的四次方成正比,即()4T T M B σ=故应选(E )。
17–6 量子力学中的波函数模的平方表示[ ]。
A .粒子出现的概率B .粒子出现的概率密度C .粒子在空间的位置坐标D .粒子在空间的动量密度解:量子力学中的波函数模的平方*2||ψψψ=表示的是粒子在空间出现的概率密度,而粒子在V d 出现的概率为V d ||2ψ。
因此应选(B )。
17–7 一个处于4f 态的电子,它的轨道角动量的大小为[ ]。
A . 2B . 3C . 6D . 32E . 54解:电子处于4f 态,4表示其所处能级,f 代表其角动量量子数为3。
所以角动量为)13(3)1(+=+=l l L 32=故应选(D )。
17–8 如果一个电子被限制在原子核的尺度范围内,它的动量的不确定度最接近的值是[ ]。
A .200 eV/cB .200 KeV/cC .200 MeV/cD .200GeV/c解:由测不准关系2≥∆⋅∆p x 近似取 =∆⋅∆p x ,原子核的尺度为1510~-x ∆m ,动量不确定度为M eV/c 219eV/c 106.110310054.11010054.1198191534=⨯⨯⨯⨯=⨯=∆=∆----x p 。
选(C )。
17–9 已知一粒子在一维矩形无限深势阱中运动,其波函数为)(,2π3cos 1)(a x a a x a x ≤≤-=ψ 那么粒子在a x 65=处出现的概率密度为[ ]。
A .a 21 B .a 21 C .a 1 D .a1 解:粒子在一维矩形无限深势阱中任意点的概率密度为ax a x x 2π3cos 1)*()(2=ψψ 在a x 65=处出现的概率密度为 a a a a x x a x 21652π3cos 1*)()(265=⎪⎭⎫ ⎝⎛⨯==ψψ 故答案应选(A )。
17–10 当用钠光灯发现的波长为589.3nm 的黄光照射某一光电池时,需要0.300V 的负电势差才能遏止所有向阳极运动的光电子。
如果用波长为400nm 的光照射这个光电池,截止电压多大?板极材料的逸出功多大?解(1)求对应于2λ的截止电压U 2。
根据爱因斯坦光效方程和光电子的最大初动能与截止电压的关系,得,W eU W m h +=+=121121v ν W eU W m h +=+=222221v ν 两式相减得 )(2121U U e h h -=-νν即)(112121U U e hc -=⎪⎪⎭⎫ ⎝⎛-λλ由此导出⎪⎪⎭⎫ ⎝⎛-+=211211λλe hc U U 将已知数和常量代入,得V 3.12=U(2)求极板材料的逸出功。
由W m h +=21121v ν 得1.80eV J 1089.21911=⨯=-=-eU hc A λ17–11 试计算氢原子中巴耳末系的最短波长和最长波长各是多少?解:根据巴耳末系的波长公式,其最长波长应是n=3→n=2跃迁的光子,即)3121(10097.1)3121(122722max -⨯=-=R λnm 3.656m 1056.67max =⨯=-λ最短波长应是n=∞→n=2跃迁的光子,即4/10097.121172min ⨯==Rλ nm 4.346min =λ17–12 原则上讲,玻尔理论也适用于太阳系:太阳相当于核,行星相当于电子,而万有引力相当于库仑力。
其角动量是量子化的,即 n L =,而且其运动服从经典理论。
(1)求出行星绕太阳运动的允许半径的公式;(2)太阳的质量为 2.0×1030kg ,地球的质量为5.98×1024kg ,地球运行半径实际上是1.50×1011m ,和此半径对应的量子数n 多大?(3)地球实际的轨道和它的下一个较大的可能轨道的半径差值多大?解:(1)设行星的质量为m ,太阳的质量为M ,行星绕太阳运动的半径为R ,并将其视为绕太阳的圆周运动,则行星绕太阳运动的角动量为RGmM mR mR L ==v 故有n RGmM mR = 所以行星绕太阳运动的允许半径为 M Gm n R 222 =, ,3,2,1=n (1)(2)由(1)式得和地球半径对应的量子数n 为11301134241050.1100.21067.61005.11098.5⨯⨯⨯⨯⨯⨯⨯==--GMR m n =2.54×1074(3)由(1)式得地球实际的轨道和它的下一个较大的可能轨道的半径差值为n M Gm n R ∆=∆222 633048211682741017.1100.21098.51067.61005.11054.22---⨯=⨯⨯⨯⨯⨯⨯⨯⨯⨯=17–13 一个调频广播电台的播出频率为98.1MHz ,天线的辐射功率为4100.5⨯W ,求天线每秒钟辐射的光子数。
解:设天线每秒钟辐射的光子数为n ,由νnh E =得天线每秒钟辐射的光子数为s /107.7101.981063.6100.5296344⨯=⨯⨯⨯⨯==-νh E n 17–14 计算动能为300eV 的电子的德布罗意波长。
解: 已知常数s J 10626.634⋅⨯=-h ,kg 1011.931-⨯=m ,J 10602.1eV 119-⨯=。
由mP E k 22=,k mE P 2= 因此k mE h P h 2==λnm 08.710602.13001011.9210626.6193134=⨯⨯⨯⨯⨯⨯---17–15 求波长为450nm 的单色光子的能量和动量。
解:光子的能量为eV 76.2J 1042.410450100.31063.6199834=⨯=⨯⨯⨯⨯===---λνεhc h 光子的动量为 s /m kg 1047.1104501063.627934⋅⨯=⨯⨯==---λhp17–16 质量为0.01kg 的子弹和质量为kg 1011.931-⨯,运动速度都为1000m/s ,若速度的不确定程度为其运动速度的1%,求它们位置的不确定程度;它们能否用经典力学处理?解:子弹位置的不确定度为:m 1063.6%1100001.01063.633341--⨯=⨯⨯⨯=∆=∆v m h x 可以认为位置和动量能同时确定,所以可以用经典力学处理。
电子位置的不确定程度为:m 103.7%110001011.91063.65313422---⨯=⨯⨯⨯⨯=∆=∆v m h x 远远超过在原子和分子中的电子离原子核的距离,不能用经典力学处理。
17–17 求下列波函数归一化常数和概率密度。
⎪⎩⎪⎨⎧<<≥≤=-)0(,πsin ,0(,0)(i a x x a Ae a x x x Et )ψ 解:利用归一化条件可得⎰∞∞-x x d |)(|2ψ⎰=a x a x A 022d πsin 122==a A 所以归一化常数A 为 aA 2= 概率密度为2||)(ψρ=x ⎪⎩⎪⎨⎧<<≥≤=)0( , πsin 2),0( , 02a x a x a a x x 17–18 有一微观粒子,沿x 方向运动,其波函数为+∞<<-∞+=x xA x (,i 1)(ψ,A 为正常数) (1)将此波函数归一化;(2)求粒子的概率密度函数;(3)求找到粒子概率最大的位置。
解:(1)1πarctan d 1d |)(|22222===+=∞∞-∞∞-∞∞-⎰⎰A x Ax x A x x ψ 所以归一化常数 π1=A 归一化后的波函数为)(,i 11π1)(+∞<<-∞+=x xx ψ (2)求粒子的几率密度函数 )1(π1||)(22x x +==ψρ(3)对几率密度函数求导,并令其为零,即0)1(π2d )(d 22=+-=x x x x ρ 可得0=x 时概率密度最大,即找到粒子概率最大位置。
17–19 一质量为M 、能量为E 的粒子在一维势场V (x )中波函数为⎪⎪⎭⎫ ⎝⎛-=2exp )(22x b A x ψ,波函数中A 和b 为实常量。
如果当x = 0时,势场0)(=x V 。
计算粒子的能量E 和势场V (x)。
解:由一维薛定谔方程ψψ)(d d 2222V E x M -=- (1) 将题给波函数代入,得⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛---2exp )(2exp )1(222222222x b V E x b x b b M (2) 由于x = 0时,势场0)(=x V ,代入上式得M b E 222 =(3) 将(3)式代回(2)式,得M x b x V 2)(242 =。
