第二章 相交线、平行线练习题
北师大版七年级下册数学 第二章 相交线与平行线 同步基础练习

七年级下册数学(北师大版)-第二章-相交线与平行线-同步基础练习(含答案)一、单选题1. ( 2分) 如果一个角的补角是120°,那么这个角的余角是()A.150°B.90°C.60°D.30°2.下列说法:①在同一平面内,不相交的两条线段叫做平行线;②过一点,有且只有一条直线平行于已知直线;③两条平行直线被第三条直线所截,同位角相等;④同旁内角相等,两直线平行.正确的个数有()个.A.1B.2C.3D.43. ( 2分) 如图,点B是△ADC的边AD的延长线上一点,DE△AC,若△C=50°,△BDE=60°,则△CDA 的度数等于()A.70°B.100°C.110°D.120°4. ( 2分) △α的补角是它的3倍,则△α等于()A.45°B.60°C.90°D.120°5. ( 2分) 下列说法中正确的是()A.旋转一定会改变图形的形状和大小B.两条直线被第三条直线所截,同位角相等C.在同一平面内,过一点有且只有一条直线与已知直线垂直D.相等的角是对顶角6. ( 2分) 如图,直线a、b被直线c所截,现给出下列四个条件:①△1=△5,②△1=△7,③△2+△3=180°,④△4=△7,其中能判定a△b的条件的序号是( )A.①②B.①③C.①④D.③④7. ( 2分) 图中,△1与△2是对顶角的是()A. B. C. D.8. ( 2分) 如图,下列结论中,正确的是()A.△DAC与△ACB是一对同位角B.若△DAC=△ACB,则AB△CDC.△D与△DAC是一对同旁内角D.若△D=△B,则AD△BC9. ( 2分) 画一条线段的垂线,垂足在()A.线段上B.线段的端点C.线段的延长线上D.以上都有可能二、填空题10. ( 1分) 如图,直线,将含有角的三角板ABC的直角顶点C放在直线m上,若,则的度数为________11. ( 2分) 如图,若△________=△________,则AD△BC.12. ( 5分) 指出图中各对角的位置关系:(1)△C和△D是________角;(2)△B和△GEF是________角;(3)△A和△D是________角;(4)△AGE和△BGE是________角;(5)△CFD和△AFB是________角.13.如图,直线m△n,△ABC为等腰三角形,△BAC=90°,则△1=________度.14. ( 1分) 一个角是它的余角的2倍,则这个角的补角的度数是________° .15. ( 1分) 如图,已知CD平分△ACB,DE△AC,△1=30°,则△2=________°.三、解答题16. ( 5分) 完成下面的证明。
北师大版七年级数学下册第二章 相交线与平行线练习(含答案)

第二章 相交线与平行线一、单选题1.如图,直线,AB CD 相交于点,50,O AOC OE AB ︒∠=⊥,则DOE ∠的大小是( )A .40︒B .50︒C .70︒D .90︒2.如图CD⊥AB,⊥C=90°,线段AC 、BC 、CD 中最短的是( )A .ACB .BC C .CD D .不能确定 3.如图,下列说法正确的是( )A .A ∠与⊥1与是内错角B .A ∠与2∠是同旁内角C .⊥1与2∠是内错角D .A ∠与3∠是同位角4.下列说法正确的是( )A .一条直线的平行线有且只有一条B .经过一点有且只有一条直线与已知直线平行C .经过一点有两条直线与已知直线平行D .过直线外一点有且只有一条直线与已知直线平行5.如图,能判定EB ⊥AC 的条件是( )A .⊥C =⊥ABEB .⊥A =⊥EBDC .⊥C =⊥ABCD .⊥A =⊥ABE 6.如图,点E 在AD 的延长线上,下列条件中能判断AB ⊥CD 的是( )A .⊥3=⊥4B .⊥1=⊥2C .⊥C =⊥CDED .⊥C +⊥ADC =180° 7.AF 是BAC ∠的平分线,//,DF AC 若70,BAC ∠=︒则1∠的度数为( )A .17.5B .35C .55D .708.如图,直线,a b 被直线,c d 所截,1110,270,360︒︒︒∠=∠=∠=,则4∠的大小是( )A .60︒B .70︒C .110︒D .120︒ 9.下列对尺规作图步骤的描述不准确的是( )A .作ABC ∠,使ABC αβ∠=∠+∠B .作AOB ∠,使2AOB α∠=∠C .以点A 为圆心,线段a 的长为半径作弧D .以点O 为圆心作弧10.如图,已知直线AB 、CD 被直线AC 所截,AB⊥CD ,E 是平面内任意一点(点E 不在直线AB 、CD 、AC 上),设⊥BAE=α,⊥DCE=β.下列各式:⊥α+β,⊥α﹣β,⊥β﹣α,⊥360°﹣α﹣β,⊥AEC 的度数可能是( )A .⊥⊥⊥B .⊥⊥⊥C .⊥⊥⊥D .⊥⊥⊥⊥二、填空题 11.如图,直线AB 、CD 相交于点O ,OA 平分⊥EOC ,⊥EOC=80°,则⊥BOD=_____.12.如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是___.13.如图,已知AB ,CD ,EF 互相平行,且⊥ABE =70°,⊥ECD =150°,则⊥BEC =________°.14.如图,AB //CD BED 110BF ,,∠=平分ABE DF ∠,平分CDE ∠,则BFD ∠= ______ .三、解答题15.如图,直线AB ,CD 相交于点O ,OE AB ⊥,垂足为O .(1)直接写出图中AOC ∠的对顶角为 ,BOD ∠的邻补角为 ; (2)若:1:2BOD COE ∠∠=,求AOD ∠的度数.16.如图,已知四边形ABCD ,AB⊥CD ,点E 是BC 延长线上一点,连接AC 、AE ,AE 交CD 于点F ,⊥1=⊥2,⊥3=⊥4.证明:(1)⊥BAE=⊥DAC;(2)⊥3=⊥BAE;(3)AD⊥BE.17.如图,已知AB⊥CD,⊥B=60°,CM平分⊥ECB,⊥MCN=90°,求⊥DCN的度数.18.如图,已知BC⊥GE,AF⊥DE,点D在直线BC上,点F在直线GE上,且⊥1=50°.(1)求⊥AFG的度数;(2)若AQ平分⊥FAC,交直线BC于点Q,且⊥Q=18°,则⊥ACB的度数为______°.(直接写出答案)答案1.A2.C3.D4.D5.D6.B7.B8.A9.D10.D11.40°12.内错角13.4014.12515.(1)⊥AOC 的对顶角为:⊥BOD⊥BOD 的邻补角为:⊥BOC ,⊥AOD(2)⊥:1:2BOD COE ∠∠=设⊥BOD=x,则⊥COE=2x⊥OE⊥AB⊥⊥EOB=90°⊥⊥COE+⊥BOD=90°,即x+2x=90°解得:x=30°⊥⊥BOD=⊥COA=30°⊥⊥AOD=150°16.证明:(1)⊥⊥1=⊥2,⊥⊥1+⊥CAE=⊥2+⊥CAE,即⊥BAE=⊥DAC;(2)⊥AB⊥CD,⊥⊥4=⊥BAE,⊥⊥3=⊥4,⊥⊥3=⊥BAE;(3)⊥⊥3=⊥BAE,⊥BAE=⊥DAC,⊥⊥3=⊥DAC,⊥AD⊥BE.17.⊥AB⊥CD,⊥⊥B+⊥BCE=180°,⊥BCD=⊥B,⊥⊥B=60°,⊥⊥BCE=120°,⊥BCD=60°,⊥CM平分⊥BCE,⊥⊥ECM=12⊥BCE=60°,⊥⊥MCN=90°,⊥⊥DCN=180°-60°-90°=30°.18.(1)⊥BC⊥EG,⊥⊥E=⊥1=50°.⊥AF⊥DE,⊥⊥AFG=⊥E=50°;(2)作AM⊥BC,⊥BC⊥EG,⊥AM⊥EG,⊥⊥FAM=⊥AFG=50°.⊥AM⊥BC,⊥⊥QAM=⊥Q=18°,⊥⊥FAQ=⊥FAM+⊥QAM=68°.⊥AQ平分⊥FAC,⊥⊥QAC=⊥FAQ=68°,⊥⊥MAC=⊥QAC+⊥QAM=86°.⊥AM⊥BC,⊥⊥ACB=⊥MAC=86°故答案为:86。
北师大版七年级下册数学第二章相交线与平行线测试题(附答案)

北师大版七年级下册数学第二章相交线与平行线测试题(附答案)北师大版七年级下册数学第二章相交线与平行线测试题(附答案)一、单选题1.如图,已知直线l1∥l2,将一块直角三角板ABC按如图所示方式放置,若∠1=39°,则∠2等于()A。
39° B。
45° C。
50° D。
51°2.如图.直线a∥b,直线L与a、b分别交于点A,B,过点A作AC⊥b于点C.若∠1=50°,则∠2的度数为()A。
130° B。
50° C。
40° D。
25°3.如图,三点共线A、B、C,D、E、F三点共线,且AD∥CF,BE∥CD,下列结论错误的是()A。
∠ABE=∠XXX∠ABE=∠CDEC。
∠ABE=∠XXX∠ABE=∠BDF4.如图,平行线AB∥CD,EF⊥CD,垂足为G,图中∠AGE=()A。
90° B。
45° C。
30° D。
60°5.如图,互余的角有()A。
1个 B。
2个 C。
3个 D。
4个6.如图,AB∥CD,EF∥GH,则下列等式正确的是()A。
∠AEF=∠GHF B。
∠AEF=∠HGFC。
∠XXX∠GHF D。
∠XXX∠HGF7.已知同一平面内的三条直线AB,CD,EF,AB∥CD,CD∥EF,则下列结论错误的是()A。
AB∥EF B。
AB∥CD C。
EF∥CD D。
AB∥EF8.如果a<b,且a+b=5c,如果c<a,b<c,比a与b 的和的3倍少2,那么a与b的位置关系是()A。
a<b B。
a>b C。
a=b D.无法确定9.如图,已知AB∥CD,AE=2cm,EC=3cm,则图中互相平行的线段是()A。
AB//CD B。
AE//DC C。
BE//CD D。
AB//EC10.如图,AB∥CD,点E在直线AD上,且∠AEC=34°,则∠BED的大小为()A。
北师大版七年级下册第二章-平行线与相交线同步练习题(含答案)

第二章平行线与相交线同步练习题2.1 两条直线的位置关系一、选择题(共18小题)3.如图,在方格纸上给出的线中,平行的有()8.一个角的余角是它的补角的,则这个角为(). B .C .D .11.(2007•济南)已知:如图,AB ⊥CD ,垂足为O ,EF 为过点O 的一条直线,则∠1与∠2的关系一定成立的是( )A . 相等B . 互余C . 互补D . 互为对顶角12.(2003•杭州)如图所示立方体中,过棱BB 1和平面CD 1垂直的平面有( )A . 1个B . 2个C . 3个D . 0个13.(2006•大连)如图,∠PQR 等于138°,SQ ⊥QR ,QT ⊥PQ .则∠SQT 等于( )15.如图,已知0A ⊥m ,OB ⊥m ,所以OA 与OB 重合,其理由是( )16.如图,∠BAC=90°,AD⊥BC,则下列的结论中正确的个数是()①点B到AC的垂线段是线段AB;②线段AC是点C到AB的垂线段;③线段AD是点D到BC的垂线段;④线段BD是点B到AD的垂线段.A.1个B.2个C.3个D.4个17.如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,其依据是()二、填空题(共12小题)19.已知∠1=43°27′,则∠1的余角是_________ ,补角是_________ .20.若一个角的余角是30°,则这个角的补角为_________ °.21.两个角互余或互补,与它们的位置_________ (填“有”或“无”)关.22.一个角的补角是它的余角的4倍,则这个角等于_________ 度.23.若∠α和∠β互为余角,并且∠α比∠β大20°,∠β和∠γ互为补角,则∠α= _________ ,∠β= _________ ,那么,∠γ﹣∠α= _________ .24.如图,已知∠COE=∠BOD=∠AOC=90°,则图中与∠B0C相等的角为_________ ,与∠BOC互补的角为_________ ,与∠BOC互余的角为_________ .25.如图,直线AB,CD相交于点O,∠EOC=60°,OA平分∠EOC,那么∠BOD的度数是_________ .26.(2006•宁波)如图,直线a⊥b,∠1=50°,则∠2= _________ 度.27.如图,点A,B,C在一条直线上,已知∠1=53°,∠2=37°,则CD与CE的位置关系是_________ .28.老师在黑板上随便画了两条直线AB,CD相交于点0,还作∠BOC的平分线OE和CD的垂线OF(如图),量得∠DOE 被一直线分成2:3两部分,小颖同学马上就知道∠AOF等于_________ .29.如图,∠ADB=90°,则AD _________ BD;用“<”连接AB,AC,AD,结果是_________ .30.如图,已知BA⊥BD,CB⊥CD,AD=8,BC=6,则线段BD长的取值范围是_________ .三、解答题(共9小题)31.已知一个角的补角加上10°后等于这个角的余角的3倍,求这个角的余角.32.如图所示,直线a,b,C两两相交,∠1=2∠3,∠2=80°,求∠4的度数.33.如图,直线AB,CD相交于点O,且∠1=∠2.(1)指出∠1的对顶角;(2)若∠2和∠3的度数比是2:5,求∠4和∠AOC的度数.34.如图,直线AB,EF相交于点O,∠AOE=30°,∠BOC=2∠AOC,求∠DOF的度数.35.如图,两条笔直的街道AB,CD相交于点0,街道OE,OF分别平分∠AOC,∠BOD,请说明街道EOF是笔直的.36.如图,OA⊥OB,OB平分∠MON,若∠AON=120°,求∠AOM的度数.37.如图,一辆汽车在直线形公路AB上由A向B行驶,M,N是分别位于公路AB两侧的两所学校.(1)汽车在公路上行驶时,噪声会对两所学校教学都造成影响,当汽车行驶到何处时,分别对两所学校影响最大?请在图上标出来.(2)当汽车从A向B行驶时,在哪一段上对两学校影响越来越大?在哪一段上对两学校影响越来越小?在哪一段上对M学校影响逐渐减小而对N学校影响逐渐增大?38.如图,直线AB,CD相交于O点,OM⊥AB于O.(1)若∠1=∠2,求∠NOD;(2)若∠BOC=4∠1,求∠AOC与∠MOD.2.1 两条直线的位置关系同步练习参考答案与试题解析一、选择题(共18小题)3.如图,在方格纸上给出的线中,平行的有()解:根据方格纸上给出的线可以看出a∥c,c∥b,a∥b,故选:C.本题考查了平行线的判定,熟练掌握网格结构是解题的关键.8.一个角的余角是它的补角的,则这个角为()A.60°B.45°C.30°D.90°先设出这个角,根据题中的数量关系列方程解答.解:设这个角是x,列方程得:90°﹣x=(180°﹣x).解得x=45°.故选B.列方程时一定明确“余角是它的补角的”,不能误为(90°﹣x)=180°﹣x..B.C.D.11.(2007•济南)已知:如图,AB⊥CD,垂足为O,EF为过点O的一条直线,则∠1与∠2的关系一定成立的是()12.(2003•杭州)如图所示立方体中,过棱BB1和平面CD1垂直的平面有()A.1个B.2个C.3个D.0个13.(2006•大连)如图,∠PQR等于138°,SQ⊥QR,QT⊥PQ.则∠SQT等于()A.42°B.64°C.48°D.24°本题是对有公共部分角的性质的考查,解决此类问题的关键是正确画出图形.解:因为过一个钝角的顶点作这个角两边的垂线,所以两个直角的和是180°,而两条垂线的夹角为40°,所以此钝角为140度.故选A.解决此类问题的关键是正确的画出图形.15.如图,已知0A⊥m,OB⊥m,所以OA与OB重合,其理由是()16.如图,∠BAC=90°,AD⊥BC,则下列的结论中正确的个数是()①点B到AC的垂线段是线段AB;②线段AC是点C到AB的垂线段;③线段AD是点D到BC的垂线段;④线段BD是点B到AD的垂线段.A.1个B.2个C.3个D.4个17.如图,把水渠中的水引到水池C,先过C点向渠岸AB画垂线,垂足为D,再沿垂线CD开沟才能使沟最短,其依据是()A.垂线最短二、填空题(共12小题)19.已知∠1=43°27′,则∠1的余角是46°33′,补角是136°33′.20.若一个角的余角是30°,则这个角的补角为120 °.21.两个角互余或互补,与它们的位置无(填“有”或“无”)关.22.一个角的补角是它的余角的4倍,则这个角等于60 度.23.若∠α和∠β互为余角,并且∠α比∠β大20°,∠β和∠γ互为补角,则∠α= 55°,∠β= 35°,那么,∠γ﹣∠α= 90°.24.如图,已知∠COE=∠BOD=∠AOC=90°,则图中与∠B0C相等的角为∠DOE ,与∠BOC互补的角为∠AOD ,与∠BOC互余的角为∠COD,∠AOB .25.如图,直线AB,CD相交于点O,∠EOC=60°,OA平分∠EOC,那么∠BOD的度数是30°.根据角平分线的定义求出∠AOC,再根据对顶角相等的性质解答即可.解:∵∠EOC=60°,OA平分∠EOC,∴∠AOC=∠EOC=×60°=30°,∴∠BOD=∠AOC=30°.故答案为:30°.本题考查了对顶角相等的性质,角平分线的定义,是基础题,准确识图是解题的关键.26.(2006•宁波)如图,直线a⊥b,∠1=50°,则∠2= 40 度.27.如图,点A,B,C在一条直线上,已知∠1=53°,∠2=37°,则CD与CE的位置关系是互相垂直.28.老师在黑板上随便画了两条直线AB,CD相交于点0,还作∠BOC的平分线OE和CD的垂线OF(如图),量得∠DOE 被一直线分成2:3两部分,小颖同学马上就知道∠AOF等于45°.29.如图,∠ADB=90°,则AD ⊥BD;用“<”连接AB,AC,AD,结果是AD<AC<AB .30.如图,已知BA⊥BD,CB⊥CD,AD=8,BC=6,则线段BD长的取值范围是6<BD<8 .三、解答题(共9小题)31.已知一个角的补角加上10°后等于这个角的余角的3倍,求这个角的余角.32.如图所示,直线a,b,C两两相交,∠1=2∠3,∠2=80°,求∠4的度数.33.如图,直线AB,CD相交于点O,且∠1=∠2.(1)指出∠1的对顶角;(2)若∠2和∠3的度数比是2:5,求∠4和∠AOC的度数.34.如图,直线AB,EF相交于点O,∠AOE=30°,∠BOC=2∠AOC,求∠DOF的度数.35.如图,两条笔直的街道AB,CD相交于点0,街道OE,OF分别平分∠AOC,∠BOD,请说明街道EOF是笔直的.对顶角、邻补角.根据对顶角相等可得∠AOC=∠BOD,再根据角平分线的定义可得∠1=∠AOC,∠2=∠BOD,从而得到∠1=∠2,再根据AB是笔直的街道可得∠2+∠AOF=180°,求出∠1+∠AOF=180°,从而得解.解:∵∠AOC和∠BOD是对顶角,∴∠AOC=∠BOD,∵OE,OF分别平分∠AOC,∠BOD,∴∠1=∠AOC,∠2=∠BOD,∴∠1=∠2,∵AB是笔直的街道,∴∠2+∠AOF=180°,∴∠1+∠AOF=180°,即∠EOF=180°,∴EOF是一条直线,即街道EOF是笔直的.本题考查了对顶角相等的性质,角平分线的定义,是基础题,求出∠EOF=180°是解题的关键.36.如图,OA⊥OB,OB平分∠MON,若∠AON=120°,求∠AOM的度数.37.如图,一辆汽车在直线形公路AB上由A向B行驶,M,N是分别位于公路AB两侧的两所学校.(1)汽车在公路上行驶时,噪声会对两所学校教学都造成影响,当汽车行驶到何处时,分别对两所学校影响最大?请在图上标出来.(2)当汽车从A向B行驶时,在哪一段上对两学校影响越来越大?在哪一段上对两学校影响越来越小?在哪一段上对M学校影响逐渐减小而对N学校影响逐渐增大?(2)此题说明时要分3段A到E;由F向B,由E向F分别说明对两学校的影响情况.解:(1)如图所示:过M作ME⊥AB,过N作NF⊥AB,当汽车行驶到点E处时,对M学校影响最大;当汽车行驶到点F处时,对N学校影响最大;(2)由A向E行驶时,对两学校影响逐渐增大;由F向B行驶时,对两学校的影响逐渐减小;由E向F行驶时,对M学校影响逐渐减小而对N学校影响逐渐增大.此题主要考查了应用与设计作图,以及垂线段的性质,关键是正确画出图形.38.如图,直线AB,CD相交于O点,OM⊥AB于O.(1)若∠1=∠2,求∠NOD;(2)若∠BOC=4∠1,求∠AOC与∠MOD.39.如图,点O为直线AB上一点,OC为一射线,OE平分∠AOC,OF平分∠BOC.(1)若∠BOC=50°,试探究OE,0F的位置关系;(2)若∠BOC为任意角α(0°<α<180°),(1)中OE,OF的位置关系是否仍成立?请说明理由.由此你发现什么规律?位置关系.解:(1)OE⊥OF;∵∠BOC=50°,∴∠AOC=180°﹣50°=130°,∵OE平分∠AOC,OF平分∠BOC,∴∠EOC=∠AOC=65°,∠COF=∠COB=25°,∴∠EOF=65°+25°=90°,∴OE⊥OF;(2)∵∠BOC=α,∴∠AOC=180°﹣α,∵OE平分∠AOC,OF平分∠BOC,∴∠EOC=∠AOC=90°﹣,∠COF=∠COB=,∴∠EOF=90°﹣+α=90°,∴OE⊥OF.规律:邻补角的角平分线互相垂直.2.2 探索直线平等的条件一、填空题:(每题5分,共20分)1、如图1,∠1和∠2是直线_______和直线________被直线_____所截得的同位角,∠2和∠3是直线_____和直线________被直线______所截得的__________角。
北师大版七年级数学下册第二章《相交线与平行线》考试卷附解析版)
(3)利用上述结论解决问题:如图已知 , 和 的平分线相交于 , ,求 的度数.
22.实验证明,平面镜反射光线的规律是:射到平面镜上的光线和被反射出的光线与平面镜所夹的锐角相等.
(1)如图,一束光线 射到平面镜 上,被 反射到平面镜 上,又被 反射,若被 反射出的光线 与光线 平行,且 ,则 _________, ________.
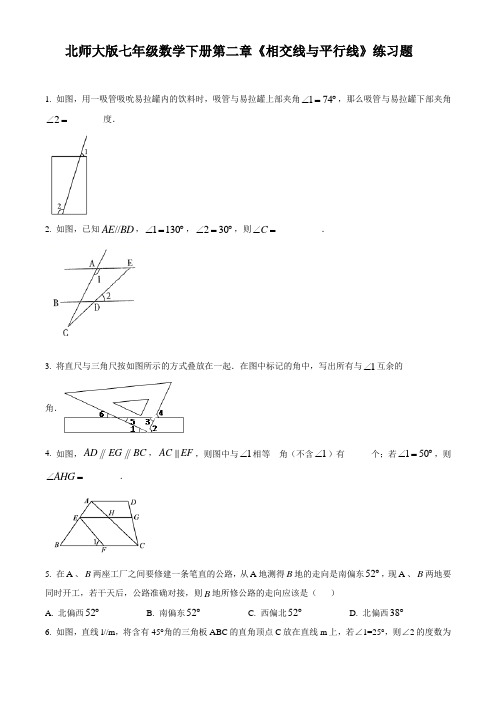
4.如图, , ,则图中与 相等 角(不含 )有______个;若 ,则 ________.
5.在 、 两座工厂之间要修建一条笔直的公路,从 地测得 地的走向是南偏东 ,现 、 两地要同时开工,若干天后,公路准确对接,则 地所修公路的走向应该是( )
A.北偏西 B.南偏东 C.西偏北 D.北偏西
6.如图,直线l//m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为()
【答案】95°
【解析】
【详解】如图,作EF∥AB,则EF∥CD,
∴∠ABE+∠BEF=180°,∵∠ABE=120°,∴∠BEF=60°,
∵∠DCE=∠FEC=35°,∴∠BEC=∠BEF+∠FEC=95°.
故答案为95°.
点睛:本题关键在于构造平行线,再利用平行线的性质解题.
13.某人在练车场上练习驾驶汽车,两次拐弯后的行驶方向与原来的方向相反,则这两次拐弯的角度可能是________.①第一次向左拐 ,第二次向右拐 ;②第一次向右拐 ,第二次向左拐 ;③第一次向右拐 ,第二次向左拐 ;④第一次向左拐 ,第二次向左拐 .
A. 20°B. 25°C. 30°D. 35°
【答案】A
【解析】
【详解】如图,过点B作BD//l,
平行线与相交线练习题

平行线与相交线练习题一、选择题1. 在同一平面内,两条不相交的直线叫做平行线。
以下哪组直线不满足平行线的定义?A. 直线a和直线b在平面内,且直线a与直线b不相交B. 直线c和直线d在平面内,但直线c与直线d相交C. 直线e和直线f在不同平面内D. 直线g和直线h在平面内,且直线g与直线h相交2. 根据平行线的性质,以下说法正确的是:A. 平行线之间的距离处处相等B. 平行线可以相交C. 平行线可以重合D. 平行线之间的夹角是锐角3. 如果直线a与直线b平行,直线b与直线c相交,那么直线a与直线c的关系是:A. 平行B. 相交C. 重合D. 无法确定4. 在同一平面内,两条直线的位置关系有几种?A. 1种B. 2种C. 3种D. 4种5. 两条平行线被第三条直线所截,同位角相等。
以下哪个选项不能说明两条直线平行?A. 同位角相等B. 内错角相等C. 同旁内角互补D. 同旁内角相等二、填空题6. 如果直线m和直线n在同一平面内且不相交,那么直线m和直线n 是_________。
7. 两条直线相交成90度角,这两条直线叫做_________。
8. 根据平行线的性质,如果直线a和直线b平行,那么直线a和直线b之间的距离在任何位置都是_________。
9. 平行线的性质之一是,如果两条平行线被第三条直线所截,那么一组内错角的度数之和等于_________。
10. 如果直线a和直线b相交,且直线a和直线c平行,那么直线b 和直线c的关系是_________。
三、判断题11. 平行线永远不会相交。
()12. 两条平行线之间的距离处处相等。
()13. 如果两条直线相交,它们就不可能平行。
()14. 两条直线相交所形成的四个角中,如果有一个角是直角,那么其他三个角也是直角。
()15. 平行线的性质可以用于证明其他几何命题。
()四、解答题16. 已知直线AB和直线CD相交于点O,直线EF平行于直线AB,请说明直线EF与直线CD的位置关系。
第二章平行线与相交线的单元测试题及答案
第(3)题1234A BC D EF第(5)题1234a b c 12ab c 第(2)题第(10)??ABCDE第二章《平行线与相交线》测验题(时间;60分钟 满分100分)班级 姓名 成绩 一、填空题:(每空2分,共30分)1.同一平面内,两条直线的位置关系有 、 两种。
2.如图,在直线a 、b 被直线c 所截,若∠1=∠2 ,则 ∥ ,根据是 .3.如图,直线AB 、CD 被直线EF 所截,∠1=∠2,那么∠3与∠4的关系是 4.若a ∥b,b ∥c, 则a 与c 的关系是 ,理由是 .5.如图,直线a ∥b ,∠1=30°,那么∠2= ;∠3= ;∠4= 6.平行公理是:经过 一点, 一条直线与这条直线平行。
7.如图,在A 、B 两点之间要架设一条铁路,从A 处测得公路的走向是南偏东42°,如果A 、B 两处同时开工,那么,在B 处应按∠β=______度施工,以保证公路准确接通。
8.如图,直线AB ∥CD ,EF ⊥CD ,垂足为F ,射线FN 交 AB 于M ,∠NMB=136°,则∠EFN=第(8)题A B CDE FN MA B CD9.如图,AB ∥CD ,直线EF 分别交AB 、CD 于E 、F 点,EG 平分∠BEF ,若∠1=72°,则∠2= °10.如图,AB ∥CD ,若∠ABE=120°,∠DCE=35°,则∠BEC= 。
1.下列说法中,正确的是( ) A .没有公共点的两线段一定平行B .如果直线a 与直线b 相交,直线b 与c 相交,那么,直线a 与c 也一定相交第(8)题第(10)题第(4)题4321D CB A E DC B A C .在同一平面内,两条直线不相交就一定平行D .不相交的两条直线,就是平行线 2.下列说法不正确的是( )A .同位角相等,两直线平行B .过一点有且只有一条直线与已知直线平行C .两直线平行,内错角相等D .同旁内角互补,两直线平行3.如图,已知:∠1=∠2,那么下列结论正确的是( ) A .∠C=∠D B .AD ∥BC C .AB ∥CDD .∠3=∠44.如图,AD ⊥BC 于D ,DE ∥AC ,那么∠C 与∠ADE 的关系是( )A .互余B .互邻C .相等D .互补5.两条直线被第三条直线所截,有一对同旁内角互补,则这一对同旁内角的平分线( ) A .平行 B .垂直 C .平行或垂直 D .平行或垂直或在同一平面上三、填写理由:(每题10分,共20分) 1. 如右上图, ∵CE ∥AB (已知)∴∠ECD=∠ ( )又∵EF ∥BC (已知)∴∠CEF+∠ECD=180°( ) ∴∠ABD+∠CEF= (等量代换) 2. 已知:如图,AB ∥CD ,∠ABC=∠ADC ,求证:AD ∥BC证明: ∵AB ∥CD ( )∴∠1= ( )又 ∵∠ABC=∠ADC ( ) ∴∠ABC -∠1=∠ADC -∠2即:∠3=∠4∴AD ∥ ( )A B C D 1234第(3)题A B CD E FD C B A FECBA四、解答题:(共35分)1.(9分)如图,DC ∥AB ,DB 平分∠ABC ,∠A=72°∠CBA=30°, 求:(1)∠CDB 的度数(2)∠ADB 的度数。
北师大版七年级数学下册第二章《相交线与平行线》单元同步练习题(含答案)
北师大版七年级数学下册第二章《相交线与平行线》同步练习题(含答案)一、选择题1、如图,将一张长方形纸条折叠,如果∠2比∠1大6°,则∠2的度数为( ) A .108°B .114°C .118°D .122°2、如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为( ) A .90°-αB .90°+αC .90°-α2D .90°+α23、如图,在长方形纸片ABCD 中,在AD 边上取一点E ,沿BE 折叠,使点C ,D 分别落在点C 1,D 1处,且点A 刚好落在C 1D 1上.若∠ABC 1=45°,则∠BED =( ) A .112.5°B .135°C .125°D .100.5°4、如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB ,CD ,若CD ∥BE ,∠1=40°,则∠2的度数是( ) A .90°B .100°C .105°D .110°5、如图,已知AB ∥DE ,∠1=30°,∠2=35°,则∠BCE 的度数为( ) A .70°B .65°C .35°D .5°6、如图,直线AB ∥CD ,AE ⊥CE 于点E.若∠EAB =120°,则∠ECD 的度数是( ) A .120°B .100°C .150°D .160°二、填空题7、如图,将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处.若∠AEH =30°,则∠EFC等于______.8、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG=______.度,再沿BF折叠成图c.则图中的∠CFE=______度.9、已知:如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD=______度.10、如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=______.11、如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=______.12、如图是我们生活中经常接触的小刀,刀片的外壳是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=______.三、解答题13、如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D 在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?14、问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.(1)按小明的思路,易求得∠APC的度数为______度;(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P 在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;(3)在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系.15、已知AM∥CN,点B为平面内一点,AB⊥BC于点B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD.若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.参考答案一、选择题1、如图,将一张长方形纸条折叠,如果∠2比∠1大6°,则∠2的度数为(D) A .108°B .114°C .118°D .122°2、如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为(C) A .90°-αB .90°+αC .90°-α2D .90°+α23、如图,在长方形纸片ABCD 中,在AD 边上取一点E ,沿BE 折叠,使点C ,D 分别落在点C 1,D 1处,且点A 刚好落在C 1D 1上.若∠ABC 1=45°,则∠BED =(A) A .112.5°B .135°C .125°D .100.5°4、如图,将一条对边互相平行的纸带进行两次折叠,折痕分别为AB ,CD ,若CD ∥BE ,∠1=40°,则∠2的度数是(B) A .90°B .100°C .105°D .110°5、如图,已知AB ∥DE ,∠1=30°,∠2=35°,则∠BCE 的度数为(B) A .70°B .65°C .35°D .5°6、如图,直线AB ∥CD ,AE ⊥CE 于点E.若∠EAB =120°,则∠ECD 的度数是(C) A .120°B .100°C .150°D .160°二、填空题7、如图,将长方形ABCD沿EF折叠,点D落在AB边上的H点处,点C落在点G处.若∠AEH =30°,则∠EFC等于105°.8、如图a是长方形纸带,∠DEF=15°,将纸带沿EF折叠成图b,则∠AEG=150度,再沿BF折叠成图c.则图中的∠CFE=135度.9、已知:如图,AB∥EF,∠ABC=75°,∠CDF=135°,则∠BCD=30度.10、如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=140°.11、如图,AB∥CD,∠BED=110°,BF平分∠ABE,DF平分∠CDE,则∠BFD=125°.12、如图是我们生活中经常接触的小刀,刀片的外壳是一个直角梯形,刀片上、下是平行的,转动刀片时会形成∠1和∠2,则∠1+∠2=90°.三、解答题13、如图,在Rt△AOB和Rt△COD中,∠AOB=∠COD=90°,∠B=40°,∠C=60°.点D 在边OA上,将图中的△COD绕点O按每秒10°的速度沿顺时针方向旋转一周,当旋转了多少秒时,边CD恰好与边AB平行?解:分两种情况:当两三角形在点O的同侧时,如图1,设CD与OB相交于点E.∵AB∥CD,∴∠CEO=∠B=40°.∵∠C=60°,∴∠OOE=180°-60°-40°-80°.∴∠DOE=∠COD-∠COE=10°.∴旋转角∠AOD=∠AOB+∠DOE=90°+10°=100°.∵每秒旋转10°,∴旋转的时间为100÷10=10(秒).当两三角形在点O的异侧时,如图2,延长BO与CD相交于点E.∵AB∥CD,∴∠CEO=∠B=40°.∵∠C=60°,∴∠COE=180°-60°-40°=80°.∴旋转角为360°-∠COE=360°-80°=280°.∵每秒旋转10°,∴旋转的时间为280÷10=28(秒).综上所述,当旋转了10秒或28秒时,边CD恰好与边AB平行.14、问题情境:如图1,AB∥CD,∠PAB=130°,∠PCD=120°,求∠APC的度数.小明的思路是:过P作PE∥AB,通过平行线性质来求∠APC.(1)按小明的思路,易求得∠APC的度数为110度;(2)问题迁移:如图2,AB∥CD,点P在射线OM上运动,记∠PAB=α,∠PCD=β,当点P 在B,D两点之间运动时,问∠APC与α,β之间有何数量关系?请说明理由;(3)在(2)的条件下,如果点P在B,D两点外侧运动时(点P与点O,B,D三点不重合),请直接写出∠APC与α,β之间的数量关系.图1 图2解:∠APC=α+β.理由:过点P作PE∥AB交AC于点E,∵AB∥CD,∴AB∥PE∥CD.∴α=∠APE,β=∠CPE.∴∠APC=∠APE+∠CPE=α+β.(3)如图3,当P在BD延长线上时,∠CPA=α-β;如图4,当P在DB延长线上时,∠CPA=β-α.图3 图415、已知AM∥CN,点B为平面内一点,AB⊥BC于点B.(1)如图1,直接写出∠A和∠C之间的数量关系;(2)如图2,过点B作BD⊥AM于点D,∠BAD与∠C有何数量关系,并说明理由;(3)如图3,在(2)问的条件下,点E,F在DM上,连接BE,BF,CF,BF平分∠DBC,BE平分∠ABD.若∠FCB+∠NCF=180°,∠BFC=5∠DBE,求∠EBC的度数.解:(1)∠A+∠C=90°(2)过点B作BG∥DM,∵BD⊥AM,∴∠ABD+∠BAD=90°,DB⊥BG,即∠ABD+∠ABG=90°.又∵AB⊥BC,∴∠CBG+∠ABG=90°.∴∠ABD=∠CBG.∵AM∥CN,BG∥AM,∴CN∥BG.∴∠C=∠CBG.∴∠ABD=∠C.∴∠C+∠BAD=90°.(3)过点B作BG∥DM,∵BF平分∠DBC,BE平分∠ABD,∴∠DBF=∠CBF,∠DBE=∠ABE,由(2)可得∠ABD=∠CBG.∴∠ABF=∠GBF.设∠DBE=α,∠ABF=β,则∠ABE=α,∠ABD=2α=∠CBG,∠GBF=β=∠AFB,∠BFC =5∠DBE=5α,∴∠AFC=5α+β.∵∠AFC+∠NCF=180°,∠FCB+∠NCF=180°,∴∠FCB=∠AFC=5α+β.在△BCF中,由∠CBF+∠BFC+∠BCF=180°,可得(2α+β)+5α+(5α+β)=180°.①由AB⊥BC,可得β+β+2α=90°.②由①②联立方程组,解得α=9°.∴∠ABE=9°.∴∠EBC=∠ABE+∠ABC=9°+90°=99°.。
第二章-相交线与平行线练习题(带解析)
第二章 相交线与平行线练习题(带解析)1、如图,直线a 、b 、c 、d ,已知c⊥a,c⊥b,直线b 、c 、d 交于一点,若∠1=500,则∠2等于【 】(1)(2)(5)(6)(7) 2、如图,AB⊥BC,BC⊥CD,∠EBC=∠BCF,那么,∠ABE 与∠DCF 的位置与大小关系是 ( ) 3、如果两个角的一边在同一直线上,另一边互相平行,那么这两个角只能( )A .相等B .互补C .相等或互补D .相等且互补4、下列说法中,为平行线特征的是( )①两条直线平行,同旁内角互补; ②同位角相等, 两条直线平行;③内错角相等, 两条直线平行; ④垂直于同一条直线的两条直线平行.A .①B .②③C .④D .②和④5、如图,AB∥CD∥EF,若∠ABC=50°,∠CEF=150°,则∠BCE=( )A .60°B .50°C .30°D .20°6、如图,如果AB∥CD,则角α、β、γ之间的关系为( )A .α+β+γ=360°B .α-β+γ=180°C .α+β-γ=180°D .α+β+γ=180°7、如图,由A 到B 的方向是( )8、如图,由AC∥ED,可知相等的角有( )(8) (9)A .6对B .5对C .4对D .3对9、如图,直线AB 、CD 交于O ,EO⊥AB 于O ,∠1与∠2的关系是( )A.互余B.对顶角C.互补 D.相等10、若∠1和∠2互余,∠1与∠3互补,∠3=120°,则∠1与∠2的度数分别为( )A .50°、40°B .60°、30°C .50°、130°D .60°、120°11、下列语句正确的是( )A .一个角小于它的补角B .相等的角是对顶角C .同位角互补,两直线平行D .同旁内角互补,两直线平行12、图中与∠1是内错角的角的个数是( )A .600B .500C .400D .300A .是同位角且相等B .不是同位角但相等;C .是同位角但不等D .不是同位角也不等 A .南偏东30° B .南偏东60° C .北偏西30° D .北偏西60°A.2个B.3个C.4个D.5个13、如图,直线AB和CD相交于点O,∠AOD和∠BOC的和为202°,那么∠AOC的度数为( )A.89°B.101°C.79°D.110°14、如图,∠1和∠2是对顶角的图形的个数有( )A.1个B.2个C.3个D.0个15、如图,直线a、b被直线c所截,现给出下列四个条件:①∠1=∠5,②∠1=∠7,③∠2+∠3=180°,④∠4=∠7,其中能判定a∥b的条件的序号是( )A.①②B.①③C.①④D.③④分卷II分卷II 注释评卷人得分二、填空题(注释)16、如图,∠ACD=∠BCD,DE∥BC交AC于E,若∠ACB=60°,∠B=74°,则∠EDC=___°,∠CDB=____°。
第二章 相交线与平行线单元测试卷(二)及答案解析
第二章相交线与平行线单元测试卷(二)一.选择题(共10小题)1.下列说法中正确的个数是()①过两点有且只有一条直线;②两直线相交只有一个交点;③0的绝对值是它本身④射线AB和射线BA是同一条射线.A.1个B.2个C.3个D.4个2.如图,直线a,b相交于点O,若∠1等于30°,则∠2等于()A.60°B.70°C.150°D.170°3.如图,三条直线a、b、c相交于一点,则∠1+∠2+∠3=()A.360°B.180°C.120°D.904.如图,AO⊥BO,垂足为点O,直线CD经过点O,下列结论正确的是()A.∠1+∠2=180°B.∠1﹣∠2=90°C.∠1﹣∠3=∠2 D.∠1+∠2=90°5.如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,这样做的理由是()A.两点之间,线段最短B.垂线段最短C.过一点可以作无数条直线D.两点确定一条直线6.如图,AC⊥BC,CD⊥AB,下列结论中,正确的结论有()①线段CD的长度是C点到AB的距离;②线段AC是A点到BC的距离;③AB>AC>CD;④线段BC是B到AC的距离;⑤CD<BC<AB.A.2个B.3个C.4个D.5个7.如图,∠ACB=90°,CD⊥AB,垂足为D,则点B到直线CD的距离是指()A.线段BC的长度B.线段CD的长度C.线段AD的长度D.线段BD的长度8.下列说法正确的有()①两点之间的所有连线中,线段最短;②相等的角叫对顶角;③过一点有且只有一条直线与已知直线平行;④过一点有且只有一条直线与已知直线垂直;⑤两点之间的距离是两点间的线段;⑥在同一平面内的两直线位置关系只有两种:平行或相交.A.1个B.2个C.3个D.4个9.下列各组线中一定互相垂直的是()A.对顶角的平分线B.同位角的平分线C.内错角的平分线D.邻补角的平分线10.如图,AB∥EF,设∠C=90°,那么x、y和z的关系是()A.y=x+z B.x+y﹣z=90°C.x+y+z=180°D.y+z﹣x=90°二.填空题(共8小题)11.如图,直线a、b相交于点O,将量角器的中心与点O重合,发现表示60°的点在直线a上,表示138°的点在直线b上,则∠1=°.12.已知一个角的两边分别垂直于另一个角的两边,且这两个角的差是30°,则这两个角的度数分别是.13.如图所示,想在河的两岸搭建一座桥,搭建方式最短的是,理由是.14.两条直线被第三条直线所截,∠2是∠3的同旁内角,∠1是∠3的内错角,若∠2=4∠3,∠3=2∠1,则∠1的度数是.15.如图,用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是.16.如图,点D在△ABC的边AC的延长线上,DE∥BC,若∠A=65°,∠B=40°,则∠D的度数为.17.如图,若要说明AC∥DE,则可以添加的条件是.18.若∠A与∠B的两边分别平行,且∠A比∠B的5倍少20°,则∠A的度数为.三.解答题(共3小题)19.直线AB∥CD,直线EF分别交AB、CD于点A、C,CM是∠ACD的平分线,CM交AB于点N.(1)如图①,过点A作AC的垂线交CM于点M,若∠MCD=55°,求∠MAN的度数;(2)如图②,点G是CD上的一点,连接MA、MG,∠MGD+∠EAB=180°,MC平分∠AMG.①∠AMG和∠EAB满足怎么样的数量关系时EC⊥AM?②若∠AMG=36°,求∠ACD的度数.20.如图,直线EF分别与直线AB、CD交于M,N两点,∠1=55°,∠2=125°,求证:AB∥CD【要求写出每一步的理论依据】.21.已知直线l1∥l2,直线l3与l1、l2分别交于C、D两点,点P是直线l3上的一动点,如图①,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有∠3+∠1=∠2这一相等关系?试说明理由;如图②,当动点P在线段CD之外且在CD的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由.参考答案与试题解析一.选择题(共10小题)1.【解答】解:①过两点有且只有一条直线,故①正确;②两直线相交只有一个交点,故②正确;③0的绝对值是它本身,故③正确;④射线AB和射线BA的端点不同,延伸方向也不同,不是同一条射线,故④错误.故选:C.2.【解答】解:∵∠1+∠2=180°,且∠1=30°,∴∠2=150°.故选:C.3.【解答】解:因为对顶角相等,所以∠1+∠2+∠3=×360°=180°.故选:B.4.【解答】解:∵如图,AO⊥BO,∴∠AOB=90°.A、∠1+∠3=180°,只有当∠2=∠3时,等式∠1+∠2=180°才成立,故本选项不符合题意.B、∠1=180°﹣∠3,则∠1﹣∠2=180°﹣∠3﹣∠2=90°,故本选项符合题意.C、∠1>90°,∠2+∠3=90°,则∠1≠∠3+∠2,即∠1﹣∠3=∠2,故本选项不符合题意.D、∠2+∠3=90°,只有当∠1=∠3时,等式∠1+∠2=90°才成立,故本选项不符合题意.故选:B.5.【解答】解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,∴过点A作AH⊥PQ于点H,这样做的理由是垂线段最短.故选:B.6.【解答】解:①线段CD的长度是C点到AB的距离,正确;②线段AC的长度是A点到BC的距离,错误;③AB>AC>CD,正确;④线段BC的长度是B到AC的距离,错误;⑤CD<BC<AB,正确;故选:B.7.【解答】解:∵BD⊥CD于D,∴点B到直线CD的距离是指线段BD的长度.故选:D.8.【解答】解:①两点之间的所有连线中,线段最短,故①正确.②相等的角不一定是对顶角,故②错误.③经过直线外一点有且只有一条直线与已知直线平行,故③错误.④同一平面内,过一点有且只有一条直线与已知直线垂直,故④错误.⑤两点之间的距离是两点间的线段的长度,故⑤错误.⑥在同一平面内,两直线的位置关系只有两种:相交和平行,故⑥正确.综上所述,正确的结论有2个.故选:B.9.【解答】解:A、对顶角的平分线在同一直线上,故本选项错误;B、两条平行线被第三条直线所截,同位角的平分线互相平行,故本选项错误;C、两条平行线被第三条直线所截,内错角的平分线互相平行,故本选项错误;D、邻补角的平分线互相垂直,故本选项正确.故选:D.10.【解答】解:过C作CM∥AB,延长CD交EF于N,则∠CDE=∠E+∠CNE,即∠CNE=y﹣z∵CM∥AB,AB∥EF,∴CM∥AB∥EF,∴∠ABC=x=∠1,∠2=∠CNE,∵∠BCD=90°,∴∠1+∠2=90°,∴x+y﹣z=90°.故选:B.二.填空题(共8小题)11.【解答】解:根据题意得:∠1=138°﹣60°=78°,故答案为:7812.【解答】解:∵一个角的两边分别垂直于另一个角的两边,∴这两个角相等或互补.又∵这两个角的差是30°,∴这两个角互补.设一个角为x,则另一个角为x+30°,根据题意可知:x+x+30°=180°.解得:x=75°,x+30°=75°+30°=105°.故答案为:75°、105°.13.【解答】解:∵PM⊥MN,∴由垂线段最短可知PM是最短的,故答案为:PM,垂线段最短.14.【解答】解:如图,设∠1=x°,则∠3=2x°,∠2=4∠3=8x°,∵∠1+∠2=180°,∴x°+8x°=180°,解得:x=20,∴∠1=20°.故答案为:20°.15.【解答】解:用直尺和三角尺作出直线AB、CD,得到AB∥CD的理由是同位角相等,两直线平行;故答案为:同位角相等,两直线平行.16.【解答】解:如图所示:∵∠A+∠B+∠ACB=180°,∠A=65°,∠B=40°,∴∠ACB=180°﹣∠A﹣∠B=108°﹣65°﹣40°=75°,又∵DE∥BC,∴∠ACB=∠D,∴∠D=75°.故答案为75°,17.【解答】解:由题可得,当∠A=∠EDB时,AC∥DE,(同位角相等,两直线平行)当∠A+∠ADE=180°时,AC∥DE,(同旁内角互补,两直线平行)当∠C=∠CDE时,AC∥DE,(内错角相等,两直线平行)故答案为:∠A=∠EDB(答案不唯一).18.【解答】解:设∠B=x,则∠A=5x﹣20°,由题意x=5x﹣20°,或x+5x﹣20°=180°,解得x=5°或()°,∴∠A=5°或()°故答案为5°或()°.三.解答题(共3小题)19.【解答】解:(1)∵CM是∠ACD的平分线,∠MCD=55°,∴∠ACD=2∠MCD=110°,又∵AB∥CD,∴∠BAC=180°﹣110°=70°,又∵AM⊥EF,∴∠MAN=90°﹣70°=20°;(2)①当∠AMG=∠EAB=90°时EC⊥AM,理由如下:∵CM是∠ACD的平分线,MC平分∠AMG,∴∠ACM=∠GCM,∠AMC=∠GMC,又∵CM=CM,∴△AMC≌△GMC(ASA),∴∠CGM=∠CAM,∵EC⊥AM,∴∠CGM=∠CAM=90°,∴∠MGD=90°,∵∠MGD+∠EAB=180°,∴∠EAB=∠BAF=90°,∵AB∥CD,∴∠ACG=90°,∴∠AMG=360°﹣90°﹣90°﹣90°=90°;②∵MC平分∠AMG且∠AMG=36°,∴∠CMG=18°,∵MC平分∠ACG,∴∠MCG=∠ACG,∵∠CAB+∠EAB=180°,∠MGD+∠EAB=180°,∴∠BAC=∠MGD,∵AB∥CD,∴∠BAC+∠ACD=180°,设∠ACD=α,则∠MCG=∠ACD=α,∠BAC=∠MGD=180°﹣α,∵∠MGD是△CMG的外角,∴∠MGD=∠CMG+∠MCG,即180°﹣α=α+18°,解得α=108°,∴∠ACD=108°.20.【解答】证明:∵∠1=55°(已知),∴∠CNM=55°(对顶角相等),∵∠2=125°(已知),∴∠CNM+∠2=180°(等式的性质),∴AB∥CD(同旁内角互补,两直线平行).21.【解答】解:(1)∠3+∠1=∠2成立,理由如下:如图①,过点P作PE∥l1,∴∠1=∠AEP,∵l1∥l2,∴PE∥l2,∴∠3=∠BPE,∵∠BPE+∠APE=∠2,∴∠3+∠1=∠2;(2)∠3+∠1=∠2不成立,新的结论为∠3﹣∠1=∠2,理由为:如图②,过P作PE∥l1,∴∠1=∠APE,∵l1∥l2,∴PE∥l2,∴∠3=∠BPE,∵∠BPE﹣∠APE=∠2,∴∠3﹣∠1=∠2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 相交线、平行线
1. 如图,已知:CE=DF ,AC=BD ,∠1=∠2。
求证:∠A=∠B 。
B
2. 如图,已知:AB//CD ,AB=CD ,求证:AC 与BD 互相平分。
3. 已知:如图,E 、F 分别是AB 和CD 上的点,DE 、AF 分别交BC 于G 、H ,∠A=∠D ,∠1=∠2,求证:∠B=∠C 。
2 A
B
E
C
F
D H
G 1
4. 已知:如图,在∆ABC 中,∠=︒C 90,AC=BC ,BD 平分∠CBA ,DE AB ⊥于E
,求证:AD+DE=BE 。
5. 如图,已知:AB//CD ,求证:∠B+∠D+∠BED=360︒(至少用三种方法)
E
A
B
C
D
【试题答案】
1. 证明:
∠=∠∴∠=∠=∴+=+==∠=∠=∴≅∴∠=∠⎧⎨⎪
⎩
⎪12(已知)
(等角的补角相等)(已知)即在和中,
(已知)(已证)(已证)()
(全等三角形的对应角相等)
ECB FDA AC BD AC CD BD CD AD BC
ADF BCE DF CE FDA ECB AD BC ADF BCE SAS A B ∆∆∆∆
2. 证明: AB CD //(已知)
∴∠=∠∠=∠∠=∠=∠=∠∴≅∴==⎧⎨⎪
⎩
⎪BAO DCO ABO CDO ABO CDO BAO DCO AB CD ABO CDO ABO CDO ASA AO CO BO DO ,(两直线平行,内错角相等)在和中
(已证)(已知)
(已证)()
,(全等三角形对应边相等)
∆∆∆∆
即AC 与BD 互相平分。
3. 证明: ∠=∠12(已知) ∠=∠∴∠=∠∴∴∠=∠12AHB AHB AF ED D AFC (对顶角相等)(等量代换)
(同位角相等,两直线平行)(两直线平行,同位角相等)
//
又 ∠=∠A D (已知)
∴∠=∠∴∴∠=∠A AFC AB CD B C (等量代换)
(内错角相等,两直线平行)(两直线平行,内错角相等)// 4. 证明: BD CBA 平分(已知)∠ ∴∠=∠⊥∴∠=︒∠=︒EBD CBD DE AB DEB C (角平分线的定义)(已知)
(垂直的定义)(已知)
9090
∴∠=∠DEB C (等量代换) 在∆∆DEB DCB 和中
∠=∠∠=∠=∴≅⎧⎨⎪
⎩
⎪DEB C EBD CBD DB DB DEB DCB AAS (已证)(已证)
(公共边)
()
∆∆ ∴==+==∴+=DE DC BE BC AD DC AC BC AD DE BE ,(全等三角形的对应边相等)(已知)(等量代换)
5. 证明:(1)连结BD 。
AB CD ABD CDB BED ABD CDB BED ABE CDE BED //(已知)
(两直线平行,同旁内角互补)(三角形内角和为)即∴∠+∠=︒∠+∠+∠=︒︒∴∠+∠+∠+∠+∠=︒∠+∠+∠=︒
1801218018012360360
(2)延长DE 交AB 延长线于F 。
AB CD F D ABE FEB F BED FBE F ABE CDE BED
//(已知)
(两直线平行,同旁内角互补),
(三角形一个外角等于和它不相邻的两个内角的和)∴∠+∠=︒∠=∠+∠∠=∠+∠∴∠+∠+∠180
=∠+∠+∠+∠+∠
FEB F CDE FBE F
=︒+︒
=︒
180180360 (3)过点E 作EF//AB ,
AB CD //
∴AB EF CD ////(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠+∠=︒
∠+∠=︒∴∠+∠+∠+∠=︒+︒=︒∴∠+∠+∠=︒
B BEF D DEF B BEF D DEF B D BED 180180180180360360(两直线平行,同旁内角互补)。
