时移加尺度变换证明
拉普拉斯变换的基本性质

d
f d
(t t
)
e
st
d
t
0
d
f (t) dt
lsimest
d
t
0
所以
lim
t 0
f (t)
f
(0 )
lim sF(s) s
信号与系统
九.初值定理和终值定理
终值定理证明
根据初值定理证明时得到的公式
sF(s)
f (0 )
d f (t) estd t 0 d t
lim sF(s)
ω02
信号与系统
五.时域微分定理
若 L f (t) F(s)
则
L
d
f (t) d t
sF (s)
f
(0 )
证明: f (t) estd t f (t) est [sf (t) est ]d t
0
00
f (0) sF(s)
推广:
L
d
f 2 (t)
dt2
ssF (s)
例:求图示信号的拉普拉斯变换
f (t) 1
解:
0
2
4
t
f (t) 1 t u(t) u(t 2) ( 1 t 2)u(t 2) u(t 4)
2
2
求导得
df (t) 1 u(t) u(t 2) 1 u(t 2) u(t 4)
dt 2
2
df (t) dt
F1(s)
1 1 e2s 2s
证明: L f (t) eαt
f (t) eαtestd t F(s α)
0
例:求 eαt cos ω0t 的拉氏变换
解:已知
: L cos(ω0t )u(t )
傅里叶变换性质证明

傅里叶变换性质证明性质一:线性性质F[a*f(t)+b*g(t)]=a*F[f(t)]+b*F[g(t)]其中F表示傅里叶变换。
这个性质的证明非常简单,我们只需将傅里叶变换的定义代入到等式中即可。
性质二:时移性质时移性质指的是时域上的移动会导致频域上的相位变化。
设F[f(t)]表示函数f(t)的傅里叶变换,则有:F[f(t - a)] = e^(-2πiaω) * F[f(t)]其中a是常数,ω是角频率。
这个性质的证明可以通过将f(t-a)展开成泰勒级数,并代入傅里叶变换的定义进行推导得到。
性质三:频移性质频移性质指的是频域上的移动会导致时域上的相位变化。
设F[f(t)]表示函数f(t)的傅里叶变换,则有:F[e^(2πiaω0) * f(t)] = F[f(t - a)]其中a是常数,ω0是角频率。
这个性质的证明可以利用傅里叶变换的定义以及欧拉公式进行推导。
性质四:尺度变换性质尺度变换性质指的是时域上的信号缩放会导致频域上的信号压缩。
设F[f(t)]表示函数f(t)的傅里叶变换,则有:F[f(a*t)]=,a,^(-1)*F[f(t/a)]其中a是常数。
这个性质的证明可以通过将f(a*t)展开成泰勒级数,并代入傅里叶变换的定义进行推导得到。
性质五:卷积定理卷积定理是傅里叶变换中最重要的性质之一、它指出卷积在频域上等于两个函数的傅里叶变换的乘积。
设f(t)和g(t)是两个函数,f(t)*g(t)表示它们的卷积,F[f(t)]和F[g(t)]表示它们的傅里叶变换,则有:F[f(t)*g(t)]=F[f(t)]*F[g(t)]其中*表示卷积,乘法表示两个函数的傅里叶变换的乘积。
这个性质的证明可以通过将卷积展开成积分形式,然后利用傅里叶变换的定义进行推导得到。
以上是傅里叶变换的几个重要性质及其证明。
这些性质使得傅里叶变换具有很强的分析和应用能力,在信号处理、图像处理、通信等领域得到广泛应用。
这些性质的正确性和证明对于理解和应用傅里叶变换非常重要。
傅里叶变换性质傅里叶变换的性质证明

F ( ) R ( ) j X ( ) R () jX () F * ()
五.时移特性
若 f(t) F (),
则 f(t t0 ) F ()e j t0 ;
若 F ()F ()ej() 则 f ( t t 0 ) F () e j ( ) t 0
utF 直流 12
余下部 f2(t)分 u(t)1 21 2sgtn),( utj1
f2t微f分 2tt1, f2(t)j1
ut
f1 t
dut f1t
1
dt
1 2
1
o
t
o
t
o
t
2.频域微分性质
若 f(t) F (),则 t( t f ) jF d d
或 j t( t f ) d F d
显然
R ftc ostdt
X
fts
intdt
R R
关于 的奇函数
X X
F F
已 F f t 知 F
F f t F
证明
当 F 1 a 0 时 ,设 f(a a b b t)t e j x t,d 则 tt x b ,d t 1 d x
aa
F 1 f(x )e j axeja ba 1d xa1Faejab
2 E ej24 E 2 E e j2 j2 F 2 F
F 1 2 2 E e j 2 4 E 2 E e j 2
122 E ej2 2 e j2
2 E 2 e j 4 e j 4 2 2 E 2 2 jsi4 n 2
2
对压 所 2 : f缩 2 有 t 5 E S a e j 5 2
信号与系统 第3章-3

解 若直接按定义求图示信号的频谱,会遇到形如te-jωt的繁 复积分求解问题。而利用时域积分性质,则很容易求解。 将f(t)求导,得到图 3.5-5(b)所示的波形f1(t),将f1(t)再求导, 得到图 3.5-5(c)所示的f2(t), 显然有
第3章 连续信号与系统的频域分析
f 2 (t ) = f (t ) = f " (t )
ω )为各频率点
上单位频带中的信号能量,所以信号在整个频率范围的全部
W = ∫ G (ω )dω
0
∞
式中
G (ω ) =
1
π
F ( jω )
2
第3章 连续信号与系统的频域分析 表 3.2 傅里叶变换的性质
第3章 连续信号与系统的频域分析
3.6 周期信号的傅里叶变换
设f(t)为周期信号,其周期为T,依据周期信号的傅里叶级数分 析, 可将其表示为指数形式的傅里叶级数。即
f ( −t ) ↔ F ( − jω )
也称为时间倒置定理 倒置定理。 倒置定理
第3章 连续信号与系统的频域分析
若已知f(t) ↔ F(jω ),求f(at - b)的傅立叶变换。
此题可用不同的方法来求解。 解 此题可用不同的方法来求解。
第3章 连续信号与系统的频域分析
(2) 先利用尺度变换性质,有 先利用尺度变换性质,
第3章 连续信号与系统的频域分析 2. 时移性 时移性 若f(t) ←→ F(jω), 且t0为实常数(可正可负),则有
f ( t − t0 ) ↔ F ( jω ) e
此性质可证明如下
− jω t 0
F [ f (t − t 0 )] = ∫− ∞ f (t − t 0 )e 令τ = t − t 0
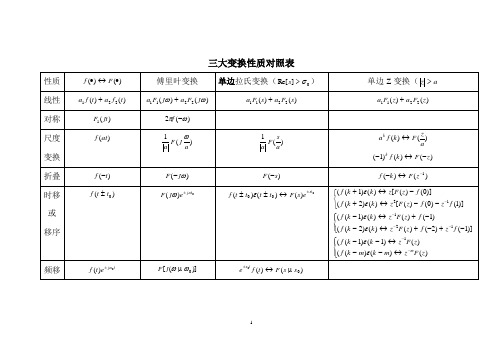
信号分析三大变换性质
sa a)2
w02
e at
sin
w0t (t)
(s
w0 a)2
w02
Rs[s] a Rs[s] a
7
t
s
时域
f1 (t) f2 (t)
F1 ( j) F2 ( j)
F1 (s) F2 (s)
kf (k) zF(z) k 2 f (k) z d [z d F(z)]
dz dz
f (k)
km
zm
z
F () m1
d
f (k) F () d
与收敛域有关 收敛域以圆为界 因果:圆外复平面 反因果:园内复平面 双边:圆环状复平面
k f (i) f (k) (k) z F (z)
i
z 1
f (0 ) lim f (t) lim sF (s)
t 0
s
F (s)是 真 分 式
f (0) Lim F (z) z
f (1) Lim z 2[F (z) f (0) f (1)z 1 ] z
m1
f (m) Lim z m[F (z) f (k)z k ]
z
k 0
3
终值
f () lim f (t) lim sF (s)
t
s0
F (s)所 有 极 点 在 左 半 平 面 ,
( f (k 1) (k) z1F (z) f (1) ( f (k 2) (k) z2F (z) f (2) z1 f (1)]
( f (k 1) (k 1) z1F (z)
(
f
(k
3.5傅立叶变换的性质与应用

线性与对称性
例4. 求:
1 F t
(ω ≠ 0)
解: 由符号函数的傅立叶变换对: 由符号函数的傅立叶变换对: Sgn(t)
2 jω
2 ∴ 2π Sgn(ω) = 2π Sgn(ω) jt
1 则 jπ Sgn(ω) : t
脉冲展缩与频带的关系
尺度特性 信号在时域中的扩展或压缩, 信号在时域中的扩展或压缩,将影响频谱的波形 若 f (t ) F ( jω ) 则
h(t ) H ( jω )
Y f ( jω ) = H ( jω ) F ( jω )
卷积定理
利用卷积定理证明时移特性: 利用卷积定理证明时移特性:
f (t t0 ) = f (t ) * δ (t t0 ) F ( jω )e jω t0
利用卷积定理证明频移特性: 利用卷积定理证明频移特性:
0
Aτ 4π τ
ω
τ
4
τ
4
τ
等效脉宽与等效频宽
F ( jω ) =
∫
∞
∞
f ( t )e
jω t
dt
1 ∞ jω t f (t ) = ∫∞ F ( jω)e dω 2π
∫
∞
∞
f ( t )d t = F (0)
F (0 ) B B
f f
∫
= 1
∞
∞
F ( jω )dω = f (0)
等效脉宽
1 ω f ( at ) F( j ) a a
(a ≠ 0)
若 a > 1: 时域压缩,则频域展宽; 若 : 时域压缩,则频域展宽; 若 0 < a < 1: 时域展宽,则频域压缩. 若 : 时域展宽,则频域压缩. 若 a = -1: 若 :
信号翻转、尺度变换和时移的注意事项和关键点?

信号翻转、尺度变换和时移的注意事项和关键点?信号处理中,常常需要进行信号翻转、尺度变换和时移等操作。
这些操作是信号处理的基础,对于信号处理的正确性和精度有着至关重要的影响。
下面将对这些操作的注意事项和关键点进行详细说明。
一、信号翻转信号翻转是将信号中的数据按照时间轴进行翻转的操作。
信号翻转常用于滤波器的设计、频域分析等场合。
在进行信号翻转时需要注意以下事项:1、翻转位置的选择信号翻转的位置对于信号处理的结果具有重要的影响。
一般情况下,我们选择对信号的中心位置进行翻转,以保证翻转前后信号的长度和对称性。
2、翻转后的信号类型进行信号翻转后,信号的类型可能会发生变化。
例如,实数信号翻转后可能变成虚数信号。
因此,在进行信号翻转时需要确认翻转后信号的类型是否符合要求。
3、异常情况的处理在进行信号翻转时,可能会遇到一些异常情况,例如翻转位置超出信号范围等情况。
在这种情况下,需要根据具体情况进行异常处理,以避免程序异常终止。
二、尺度变换尺度变换是指将信号中的数据按照比例进行缩放的操作。
尺度变换经常用于信号压缩、扩展等场合。
在进行尺度变换时需要注意以下事项:1、比例系数的选择尺度变换的比例系数决定了变换后信号的幅度和长度。
因此,在进行尺度变换时,需要根据具体需求合理选择比例系数。
2、信号类型的变化尺度变换后信号的类型可能会发生变化,例如实数信号可能变成复数信号。
在进行尺度变换时需要注意变换后信号的类型是否符合要求。
3、异常情况的处理在进行尺度变换时,可能会遇到一些异常情况,例如比例系数为零等情况。
在这种情况下,需要根据具体情况进行异常处理,以保证程序的正确性和稳定性。
三、时移时移是将信号中的数据在时间轴上进行平移的操作。
时移常用于信号对齐、滤波器设计等场合。
在进行时移操作时需要注意以下事项:1、平移位置的选择时移操作的平移位置决定了平移后信号的相对位置。
一般情况下,我们选择相对于信号开始位置进行平移。
2、平移量的选择时移操作的平移量决定了平移后信号的时间延迟或超前程度。
信号与系统 拉普拉斯变换的基本性质

L
f
(at
b)u(at
b)
1
F
(
s
)
sb
ea
(a 0,b 0)
aa
信号与系统
四.s 域平移
若 L f (t) F(s)
则 L f (t) eαt F (s α)
证明:
L f (t) eαt
f (t) eαtestd t f (t) e(αs)td t F (s α)
sF (s)
f
(0 )
证明: f (t) estd t f (t) est [sf (t) est ]d t
0
0
0
推广:
f (0) sF(s)
L
d
f 2 (t)
dt2
s
L
d
f (t)
dt
f
(0 )
ssF(s)
f
(0 )
f
(0 )
s2F (s) sf (0 ) f (0 )
s0
f
(0
)
lim
s0
d f (t) estd t 0 d t
f
(0
)
lim
t
f
(t)
f (0 )
lim f (t) t
信号与系统
九.初值定理和终值定理
例:确定下列拉普拉斯变换所对应的时域因果信号的初值和终值
I(s) s 2 s(s 2)
H(s)
s2
8 10s
169
V(s)
2s3 10 s3 (s 1)
t0 0
证明:
L f (t t0 )u(t t0 )
0
f
(t
t0 )u(t
