第3章 第3讲 导数的应用(二)
合集下载
导数及其应用PPT课件

解:(1)
4.已知a>0,n为正整数。 (1)设y=(x-a)n, 证明y’=n(x-a)n-1; (2)设fn(x)=xn-(x-a)n , 对任意n≥a,证明:
小
求函数单调区间的步骤:
求函数极值的步骤:
结
(1)求导函数f ’(xቤተ መጻሕፍቲ ባይዱ; (2)求方程f ’(x)=0的根;(3)检查f ’(x)在 方程根左右的符号,如果左正右负,那么f(x)在这个根处 取得最大值,如果左负右正,那么f(x)在这个根处取得最 小值。 求闭区间上函数的最值的方法:
y
极大值
极大值
x0
极小值
0
x
极小值
显然在极值处函数的导数为0.
【知识在线】:
1.函数y=2x3+4x2+1的导数是_____________. 2.函数y=f(x)的导数y/>0是函数f(x)单调递增的 (B )
A.充要条件
C.必要不充分条件
B.充分不必要条件
D.既不充分也不必要条件
(0,2) 单调递增区 3.函数y=x2 (x-3),则f(x)的单调递减区间是_____, (-∞,0) , (2,+∞) 。 间为______________
x
f(x)
极大值 极小值
由此可得,函数在x=- ,处取得极大值2+ 2
在x= ,处取得极小值2- 2 .草图如图
y
∵a>0,显然极大值必为正,
故只要看极小值的正负即可。
-
0
x
y
方程x3-3ax+2=0有惟一的实根;
-
0 y
x
方程x3-3ax+2=0有二个不同的实根 (其中有一个为二重根);
2020版高中数学第三章导数及其应用3.2.3导数的四则运算法则(第2课时)课件新人教B版

题目类型二、求导法则的灵活运用
求下列函数的导数: (1)y=(2x2+3)(3x-2); (2)y=x-sin2x·cos2x.
解:由函数的和(或差)与积的求导法则,可得 (1)解法一:y′=(2x2+3)′(3x-2)+(2x2+3)(3x-2)′= 4x(3x-2)+(2x2+3)·3 =18x2-8x+9. 解法二:∵y=(2x2+3)(3x-2)=6x3-4x2+9x-6, ∴y′=18x2-8x+9. (2)∵y=x-sin2x·cos2x=x-12sinx, ∴y′=1-12cosx.
(2)∵y=
x·1x-
x+
1x-1=-
1
x2
+
1
x2
,
∴y′=-12
1
x2
-12
3
x2
=- 1 2
x(1+1x).
题目类型三、求导法则的综合应用
求曲线 y=x+ x在点(1,2)处的切线在 x 轴上的
截距.
1
解:∵y=f(x)=x+ x=x+ x 2 ,
∴f′(x)=1+12
x
1 2
=1+21 x,∴f′(1)=32,
[点评] 熟练掌握导数运算法则,再结合给定函数本 身的特点,才能准确有效地进行求导运算,在解决问 题时才能做到举一反三,触类旁通.
求下列函数的导数: (1)y=x22+x33; (2)y=x3·10x; (3)y=cosx·lnx; (4)y=sixn2x.
解:(1)y=x22+x33=2x-2+3x-3, y′=-4x-3-9x-4. (2)y′=(x3)′·10x+x3·(10x)′ =3x2·10x+x3·10x·ln10. (3)y′=(cosx)′·lnx+cosx·(lnx)′ =-sinx·lnx+coxsx. (4)y′=x2′·sinsxi-n2xx2·sinx′ =2x·sinsxi-n2xx2cosx.
高等数学(理工科)课件第3章导数的应用

0
0
极
f (x) ↗ 大
值
极大值 f (1) 10,
极
↘
小
↗
值
极小值 f (3) 22.
高等数学应用教程 3.2.1 函数的极值及其求法
解法2 f ( x) 3x2 6x 9 3( x 1)(x 3) f (x) 6x 6 6(x 1)
令 f ( x) 0, 得驻点 x1 1, x2 3. 由于 f (1) 12 0, 则 f (1) 10为极大值 由于 f (3) 12 0, 则 f (3) 22为极小值
1、求出函数 f(x)所有的临界点(驻点和不可导点);
2、计算各临界点的函数值和区间端点的函数值;
3、比较各函数值的大小,其中最大的就是函数 f(x)在区 间[a, b]上的最大值,最小的就是函数 f(x)在区间[a, b] 的最小值.
高等数学应用教程 3.2.2 函数的最大值与最小值 例3
高等数学应用教程 3.2.2 函数的最大值与最小值
2
arctan
1 n
n
( n 为正整数)?
高等数学应用教程
二、 型未定式
定理3.3.2 如果函数 f (x)和g (x)满足:
2)
f
( x)、g ( x)
,在
o
U(x0 )
内可导,且
f (x)
3) lim
A
xx0 g(x)
则 lim f (x) lim f (x) A
xx0 g(x) xx0 g(x)
高等数学应用教程
3.1 函数的单调性与凹凸性
3.1 函数的单调性与凹凸性
上面图形的形状可以通过导数的知识加以 研究解决,为此先介绍拉格朗日中值定理
第三章中值定理与导数的应用课件
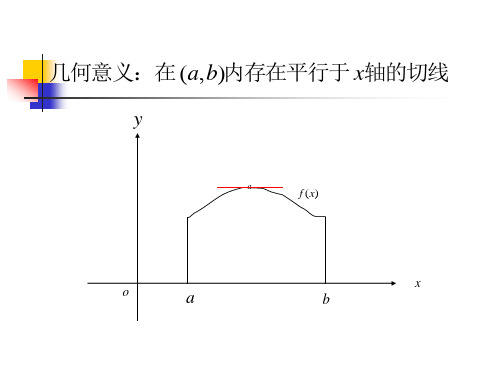
那么在(a,b)内至少有一点 使等式
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
f (b) f (a) f ' ( ) 成立 F (b) F (a) F ' ( )
例1:验证罗尔定理对函数y ln sin x在区间
[
6
,
5
6
]的正确性
解:y ln sin x在[ , 5 ]上连续
66
y ln sin x在( , 5 )上可导
66
lim 2 cos3x 3 1 x0 3 cos2x 2
例6:求
lim
x
xn ex
(n 0, 0)
解:lim xn lim n xn1 lim n (n 1) xn2
e e x x x
x x
2 ex
lim n! 0
x n ex
例7:求 lim x sin x
且f ( ) ln 1 f (5 )
6
2
6
又
y'
c os x
ctgx
令
0
x
(
, 5 )sin x源自2 662罗尔定理正确
例2:证明arctgx arcctgx
2
证 : (arctgx arcctgx)' 1 1 0 1 x2 1 x2
arctgx arcctgx c
取x 1 c c
若f (x)是一般的函数,且它存在直到n 1 阶的导数,那么
n
f (x)
f (k) (a) (xa)k ?
k 0 k!
泰勒(Taylor)中值定理
泰勒(Taylor)中值定理 如果函数 f ( x)在含有 x0 的某个开区间(a, b)内具有直到(n 1)阶的导数,则
当 x在(a, b)内时, f ( x)可以表示为( x x0 )的一个
2018高考数学(理)大一轮复习课件:第三章 导数及其应用 第二节 导数与函数的单调性

1 由曲线y=f(x)在点(1,f(1))处的切线垂直于直线y= 2 x, 3 5 知f′(1)=-4-a=-2,解得a=4.
x2-4x-5 x 5 3 所以f(x)=4+4x-ln x-2,则f′(x)= , 4x2 令f′(x)=0,解得x=-1或x=5, 因x=-1不在f(x)的定义域(0,+∞)内,故舍去. 当x∈(0,5)时,f′(x)<0,故f(x)在(0,5)内为减函数; 当x∈(5,+∞)时,f′(x)>0,故f(x)在(5,+∞)内为增 函数. 所以函数f(x)的单调递增区间为(5,+∞),单调递减区 间为(0,5).
值对不等式解集的影响进行分类讨论.
求函数的单调区间
[例2] x a 3 已知函数f(x)= 4 + x -ln x- 2 ,其中a∈R,且曲
1 线y=f(x)在点(1,f(1))处的切线垂直于直线y= 2 x,求函数f(x) 的单调区间.
[解]
1 a 1 对f(x)求导得f′(x)=4-x2-x,
第二节 导数与 函数的 单调性
本节主要包括2个知识点: 1.利用导数讨论函数的单调性或求函数的单调区间; 2.利用导数解决函数单调性的应用问题.
突破点(一)
基础联通
利用导数讨论函数的单调性或求函数的单调区间
抓主干知识的“源”与“流”
1.函数的单调性与导数的关系 函数y=f(x)在某个区间内可导: (1)若f′(x)>0,则f(x)在这个区间内 单调递增 ; (2)若f′(x)<0,则f(x)在这个区间内 单调递减 ; (3)若f′(x)=0,则f(x)在这个区间内是 常数函数 .
考点贯通
抓高考命题的“形”与“神”
证明或讨论函数的单调性
判断函数单调性的三种方法
导数的应用教学课件ppt

乘法法则
对于两个函数f(x)和g(x),其导数分别为f'(x)和g'(x),则两函数积的导数为(fg)'(x)=f'(x)g(x)+f(x)g'(x)。
幂法则
对于一个函数f(x),其导数为f'(x),则(x^n)'=nx^(n-1)。
导数计算的常见问题与解决方案
常见问题
在导数计算中,容易出现一些错误,如符号错误、运算错误 、化简错误等。
导数可以用来求函数的极值、单调区间、凹凸区间等
导数在其他领域中的应用
导数可以用来解决物理、经济、工程等领域中的一些问题,如物体运动时的加速 度、经济学中的边际效应、工程中的曲率等等
02
导数的计算
极限与导数
极限的定义
极限是函数在某一变化过程中, 某个变量的变化趋势,通常用符 号lim表示。
导数的定义
与其他学生或老师交流讨论,及时解决学习中遇 到的问题。
THANKS
导数的深入研究
1
深入理解导数的定义和计算方法,包括高阶导 数和复合函数的导数。
2
研究导数在函数性质、曲线形状、极值等方面 的应用,以及在实际问题中的应用。
3
探讨导数在数学中的地位和作用,以及与其他 数学分支的联系。
导数在未来的应用前景
分析导数在金融、经济、工程等领域 的应用前景,例如最优化问题、供应 链管理、计算机图形学等。
导数的应用教学课件ppt
xx年xx月xx日Biblioteka contents目录
• 导数的概念及背景 • 导数的计算 • 导数在函数性质研究中的应用 • 导数在几何中的应用 • 导数在实际问题中的应用 • 导数的进一步探讨与展望
01
对于两个函数f(x)和g(x),其导数分别为f'(x)和g'(x),则两函数积的导数为(fg)'(x)=f'(x)g(x)+f(x)g'(x)。
幂法则
对于一个函数f(x),其导数为f'(x),则(x^n)'=nx^(n-1)。
导数计算的常见问题与解决方案
常见问题
在导数计算中,容易出现一些错误,如符号错误、运算错误 、化简错误等。
导数可以用来求函数的极值、单调区间、凹凸区间等
导数在其他领域中的应用
导数可以用来解决物理、经济、工程等领域中的一些问题,如物体运动时的加速 度、经济学中的边际效应、工程中的曲率等等
02
导数的计算
极限与导数
极限的定义
极限是函数在某一变化过程中, 某个变量的变化趋势,通常用符 号lim表示。
导数的定义
与其他学生或老师交流讨论,及时解决学习中遇 到的问题。
THANKS
导数的深入研究
1
深入理解导数的定义和计算方法,包括高阶导 数和复合函数的导数。
2
研究导数在函数性质、曲线形状、极值等方面 的应用,以及在实际问题中的应用。
3
探讨导数在数学中的地位和作用,以及与其他 数学分支的联系。
导数在未来的应用前景
分析导数在金融、经济、工程等领域 的应用前景,例如最优化问题、供应 链管理、计算机图形学等。
导数的应用教学课件ppt
xx年xx月xx日Biblioteka contents目录
• 导数的概念及背景 • 导数的计算 • 导数在函数性质研究中的应用 • 导数在几何中的应用 • 导数在实际问题中的应用 • 导数的进一步探讨与展望
01
高中数学第三章导数及其应用3.2导数的计算课件新人教A版选修1_1

④ 紧跟老师的推导过程抓住老师的思路。老师在课堂上讲解某一结论时,一般有一个推导过程,如数学问题的来龙去脉、物理概念的抽象归纳、语 文课的分析等。感悟和理解推导过程是一个投入思维、感悟方法的过程,这有助于理解记忆结论,也有助于提高分析问题和运用知识的能力。
⑤ 搁置问题抓住老师的思路。碰到自己还没有完全理解老师所讲内容的时候,最好是做个记号,姑且先把这个问题放在一边,继续听老师讲后面的 内容,以免顾此失彼。来自:学习方法网
x2
-
1
1
x2
.
22
(2)y′=(
ln
x
)′=
(ln
x)x
x ln
x
=
1 x
x
ln
x
x
x2
x2
= 1 ln x . x2
(3)y=tan x; (4)y=3xex-2x+e.
解:(3)y′=( sin x )′= (sin x)cos x sin x(cos x)
cos x
cos2 x
课堂探究 素养提升
题型一 利用导数公式求函数的导数
【例 1】 求下列函数的导数:
(1)y=x8;(2)y=
5
x2
;(3)y=4x;(4)y= log1
2
x;(5)y=sin(x+
π 2
);(6)y=sin
π 3
.
解:(1)y′=(x8)′=8x8-1=8x7.
(2)y′=(
5
x2
)′=(
2
x 5 )′=
编后语
老师上课都有一定的思路,抓住老师的思路就能取得良好的学习效果。在上一小节中已经提及听课中要跟随老师的思路,这里再进一步论述听课时如何 抓住老师的思路。
⑤ 搁置问题抓住老师的思路。碰到自己还没有完全理解老师所讲内容的时候,最好是做个记号,姑且先把这个问题放在一边,继续听老师讲后面的 内容,以免顾此失彼。来自:学习方法网
x2
-
1
1
x2
.
22
(2)y′=(
ln
x
)′=
(ln
x)x
x ln
x
=
1 x
x
ln
x
x
x2
x2
= 1 ln x . x2
(3)y=tan x; (4)y=3xex-2x+e.
解:(3)y′=( sin x )′= (sin x)cos x sin x(cos x)
cos x
cos2 x
课堂探究 素养提升
题型一 利用导数公式求函数的导数
【例 1】 求下列函数的导数:
(1)y=x8;(2)y=
5
x2
;(3)y=4x;(4)y= log1
2
x;(5)y=sin(x+
π 2
);(6)y=sin
π 3
.
解:(1)y′=(x8)′=8x8-1=8x7.
(2)y′=(
5
x2
)′=(
2
x 5 )′=
编后语
老师上课都有一定的思路,抓住老师的思路就能取得良好的学习效果。在上一小节中已经提及听课中要跟随老师的思路,这里再进一步论述听课时如何 抓住老师的思路。
微积分应用基础第三章导数的应用

0
(0,2) 2 (2,)
— 不存在 +
0
— 不存在 +
↘
极小值 0
↗
极大值 3 16
↘
极小值 0
↗
第三章 导数的应用
例2 求函数 f (x) 3x 2 sin x 在区间 [0,2 ] 内的极
值。
解 因为 f (x) 3 2 cos x ,f (x) 2sin x 。
注意:
(1)函数的极大值和极小值是局部概念,即如果 f(x0)是f(x) 的极值,只是对极值点x0的左右近旁一个小范围来讲的。 (2)函数在一个区间上可能会有几个极大值和几个极小值,
且其中的极大值未必比极小值要大。如极大值 f(x1) 极小值f(x5)还要小。 (3)函数的极值只能在区间内部取得。
就比
z 2x2 y 2 ,点(0,0) 处,函数有极小值0。
第三章 导数的应用
二、二元函数极值的判别法 极值存在的必要条件 若函数f(x,y) 在点P0(x0,y0)
处一阶偏导数存在,且在该点函数有极值,则必有 f x′(x0,y0)= f y′(x0,y0) =0
Q(t)、Q′(t)和Q〞(t)的图形,分析上图得出如下初步结论:
(1) 该班次的产量Q随着时间t增长而增加,到一定时间 后又随着时间增长而降低; (2)Q′ >0的时间对应产品Q增加的时间,Q′<0的时 间对应产品Q减少的时间; (3) Q′=0对应产品最大的时间; (4) Q〞>0的时间对应产品增加幅度较大的时间,Q〞 <0的时间对应产品增加幅度较小及产品减少′(x)=6x(x2 - 1)2由
f′(x)=0, 得驻点x1=-1,x2=0,x3=1 。 列表考察如下:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
b=f12,c=f(3),则 A.a<b<c
B.c<b<a
()
C.c<a<b
D.b<c<a
解析 依题意得,当 x<1 时,f′(x)>0,所以函数 f(x)在
(-∞,1)上为增函数.又 f(3)=f(-1),且-1<0<12<1,因
此有 f(-1)<f(0)<f12,即有 f(3)<f(0)<f12,c<a<b,故 选 C.
第3讲 导数的应用(二)
最新考纲 1.利用导数研究函数的单调性、极(最)值,并会 解决与之有关的方程(不等式)问题;2.会利用导数解决某些 简单的实际问题.
知识梳理
1.利用导数解决生活中的优化问题的一般步骤 (1)分析实际问题中各量之间的关系,列出实际问题的数学 模型,写出实际问题中变量之间的函数关系式y=f(x),并 确定函数的定义域. (2)求函数的导数f′(x),解方程f′(x)=0. (3)比较函数在区间端点和f′(x)=0的点的函数值的大小,最 大(小)者为最大(小)值. (4)回归实际问题作答.
式共同确定.
( √)
(2)若实际问题中函数定义域是开区间,则不存在最优解.
(× )
(3)连续函数在闭区间上必有最值. (4)函数 f(x)=x2-3x+2的极小值也是最小值.
(√ ) (√ )
2.(2014·辽宁实验中学模拟)函数 f(x)在定义域 R 内可导,若 f(x)
=f(2-x),且当 x∈(-∞,1)时,(x-1)f′(x)<0,设 a=f(0),
解 (1)因为 x=5 时,y=11,所以a2+10=11,a=2. (2)由(1)知,该商品每日的销售量 y=x-2 3+10(x-6)2. 所以商场每日销售该商品所获得的利润 f(x)=(x-3)[x-2 3+10(x-6)2] =2+10(x-3)(x-6)2,3<x<6. 从而,f′(x)=10[(x-6)2+2(x-3)(x-6)] =30(x-4)(x-6).
规律方法 求实际问题中的最大值或最小值时,一般是先设 自变量、因变量,建立函数关系式,并确定其定义Байду номын сангаас,利用 求函数的最值的方法求解,注意结果应与实际情况相结 合.用导数求解实际问题中的最大(小)值时,如果函数在开 区间内只有一个极值点,那么依据实际意义,该极值点也就 是最值点.
【训练 1】 某商场销售某种商品的经验表明,该商品每日的销 售量 y(单位:千克)与销售价格 x(单位:元/千克)满足关系式 y=x-a 3+10(x-6)2,其中 3<x<6,a 为常数,已知销售价 格为 5 元/千克时,每日可售出该商品 11 千克. (1)求 a 的值; (2)若该商品的成本为 3 元 千克,试确定销售价格 x 的值, 使商场每日销售该商品所获得的利润最大.
答案 C
3.设直线x=t与函数f(x)=x2,g(x)=ln x的图象分别交于点
M,N,则当|MN|达到最小时t的值为
()
A.1
C.
5 2
B.12
D.
2 2
解析 当 x=t 时,f(t)=t2,g(t)=ln t,
∴y=|MN|=t2-ln t(t>0).
∴y′=2t-1t =2t2-t 1=2t+
5. (人教A选修11P104A5改编)如图,用铁丝弯成一个上面是 半圆,下面是矩形的图形,其面积为a m2.为使所用材料 最省,底宽应为_________m.
解析 设底宽为 x m,矩形高为 y m,铁丝总长为 l m. 则 a=π22x2+xy,∴y=ax-π8x, ∴l=π2x+x+2y=π2x+x+2xa-π4x=π4x+x+2xa, 则 l′=π4+1-2xa2 , 令 l′=0,得 x=2 π2+a4.
(2)因 V(r)=π5(300r-4r3),故 V′(r)=π5(300-12r2), 令 V′(r)=0,解得 r=5 或-5(因 r=-5 不在定义域内,舍 去). 当 r∈(0,5)时,V′(r)>0,故 V(r)在(0,5)上为增函数; 当 r∈(5,5 3)时,V′(r)<0,故 V(r)在(5,5 3)上为减函数. 由此可知,V(r)在 r=5 处取得最大值,此时 h=8. 即当 r=5,h=8 时,该蓄水池的体积最大.
答案 2
2a π+4
考点一 利用导数解决生活中的优化问题 【 例 1】 某 村 庄 拟 修 建 一 个 无 盖 的 圆 柱 形 蓄 水 池 ( 不 计 厚
度).设该蓄水池的底面半径为r米,高为h米,体积为V立 方米.假设建造成本仅与表面积有关,侧面的建造成本为 100元/平方米,底面的建造成本为160元/平方米,该蓄水池 的总建造成本为12 000π元(π为圆周率). (1)将V表示成r的函数V(r),并求该函数的定义域; (2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池 的体积最大.
解 (1)因为蓄水池侧面的总成本为 100·2πrh=200πrh 元, 底面的总成本为 160πr2 元. 所以蓄水池的总成本为(200πrh+160πr2)元. 又根据题意得 200πrh+160πr2=12 000π, 所以 h=51r(300-4r2), 从而 V(r)=πr2h=π5(300r-4r3). 因 r>0,又由 h>0 可得 r<5 3, 故函数 V(r)的定义域为(0,5 3).
22t- t
2 2 .
当 0<t< 22时,y′<0;当 t> 22时,y′>0.
∴y=|MN|=t2-ln t 在 t= 22时有最小值.
答案 D
4.若函数 f(x)=x3-3x+a有3个不同的零点,则实数a的取值 范围是_________. 解析 由于函数f(x)是连续的,故只需要两个极值异号即 可.f′(x)=3x2-3,令3x2-3=0,得x=±1,只需f(-1)·f(1) <0,即(a+2)(a-2)<0,故a∈(-2,2). 答案 (-2,2)
2.不等式问题 (1)证明不等式时,可构造函数,将问题转化为函数的极值 或最值问题. (2)求解不等式恒成立问题时,可以考虑将参数分离出来, 将参数范围问题转化为研究新函数的值域问题.
诊断自测
1.判断正误(在括号内打“√”或“×”) 精彩 PPT 展示
(1)实际问题中函数定义域要由实际问题的意义和函数解析
