(奥利康)弧齿锥齿轮几何尺寸计算资料讲解
奥利康制锥齿轮设计与加工技术

对锥齿轮,初值选取为 对硬齿面齿轮
(或参考此表)
对软齿面齿轮
对准双曲面齿轮,初值选取为
• 大轮节锥角: 对锥齿轮
对准双曲面齿轮
偏置角
u 为齿数比,E为偏置距。
公司LOGO
二、 奥利康制锥齿轮的几何设计
• 大轮大端节锥距: 对锥齿轮,初值选取为 对准双曲面齿轮,初值选取为
• 大轮齿宽: 对轻载、中载 对重载传动
公司LOGO
一、 概述
5)按齿制 格里森制:简称“格”制,主要为圆弧收缩齿,源自美国格里森公司。 奥利康制:简称“奥”制,主要为摆法线等高齿,源自瑞士奥利康公司。 克林根贝格制:简称“克”制,主要为摆线等高齿,源自克林根贝格公司。
刀盘:克林贝格刀盘为双层刀盘,内外刀不同心,可调。 奥利康刀盘为整体刀盘,内外刀同心,不可调。
连续分度原理
公司LOGO
一、 概述
2)加工优点
节锥与根锥平行,不需刀号修正,刀片规格简化。 加工原理准确,大小轮可用同一产形轮加工,理论上能加工出完全共轭的齿轮副。 连续分度、双面法加工,生产效率高,分度精度好,易于干切削。 粗精切一次完成,工序集中,工件定位精度好。 加工一个齿轮,摇台往复一次,减少了摇台往复运动冲击。 两台机床、两把刀具可加工 一对齿轮,占地面积小,劳动强度低。 在噪声、强度方面也具有一定优势,见表1。
行,当加工大轮和小轮的两个产形轮互为对偶时可以加工出具有线共轭的齿轮副,当 加工大小轮的两个产形轮只有一条相切的公共母线时,可以加工出具有点共轭的齿轮副。
线共轭与点共轭
公司LOGO
一、 概述
3、奥利康制锥齿轮加工特点及优点
1)加工特点 连续分度 粗精切一次完成 双面法加工 刀齿分组 刀盘主轴与工件轴联动 刀齿半径控制齿厚 刀倾修正接触区
弧齿锥齿轮主要参数的测绘计算

弧齿锥齿轮主要参数的测绘计作者: 日期:弧齿锥齿轮主要参数的测绘计算零部件加工部麻俊方弧齿锥齿轮具有承载能力高、运转平稳、噪音低等特点,在汽车行业中得到了广泛的应用。
通常由一对弧齿锥齿轮组成汽车驱动桥主减速器的主要传动机构。
弧齿锥齿轮的设计与测绘计算均比较复杂,下面仅介绍几种主要参数的测绘计算方法。
1.轴交角一对弧齿锥齿轮副的住从动齿轮中心轴线交于一点。
轴线间的交角刀可成任意角度,但在绝大多数汽车驱动桥上,主减速齿轮副都采用90°相交的布置。
2.齿制渐开线锥齿轮的齿制很多,多达40多种,我国常用的齿制有Gleason(格利森)制、Oerlikon(奥利康)制、Kingelnberg(克林贝格)制三种。
其中应用最广泛也是最常见到的是Gleaso n(格利森)制弧齿锥齿轮。
不同的齿制,对应不同的参数计算方法与计算公式,在测量齿轮时一定要注意区分。
3•模数弧齿锥齿轮模数是一个变值,由大端向小端与锥距成比例缩小,通常以大端面模数叫来计算。
GB12368-9C规定了锥齿轮大端端面模数,其中以》1为例,有1、1.125、1.375、1.5、1.75、2等等。
但是所测量的齿轮模数不一定为整数,也不一定符合标准模数系列。
对于模数的测绘与计算,有以下方式:1. 由测量的锥距R,可初步估算锥齿轮的大端模数 叫h(用深度尺来测量)加以复核。
对于等顶隙收缩齿(格里森制),齿顶高系数ha = 0.85,顶隙系*数C *=0.188则齿高 h=(2 ha +C *)m 。
*由此得出模数m=h(2ha +C *),进而复核模数m s 。
tm s—2.测量出锥齿轮的周节t ,根据公式 来进行计算,这种方法要求测量数据准 确无误,且被测绘齿轮无磨损现象。
3. 由齿顶圆直径反求模数。
首先测绘出齿顶圆的直径尺寸,利用齿顶圆计算公式,然 后反求模数。
所使用的反求公式为4. 由刀顶距的数值计算模数。
弧齿锥齿轮铣刀盘的刀顶距W 叫席2式中ms—大端模数的估算数值;1 0.5— L e ;R因为2 Z2 ^ 、、, ,于是便可确定锥齿轮大端模数m 2R人『云。
圆弧齿锥齿轮传动设计几何计算过程
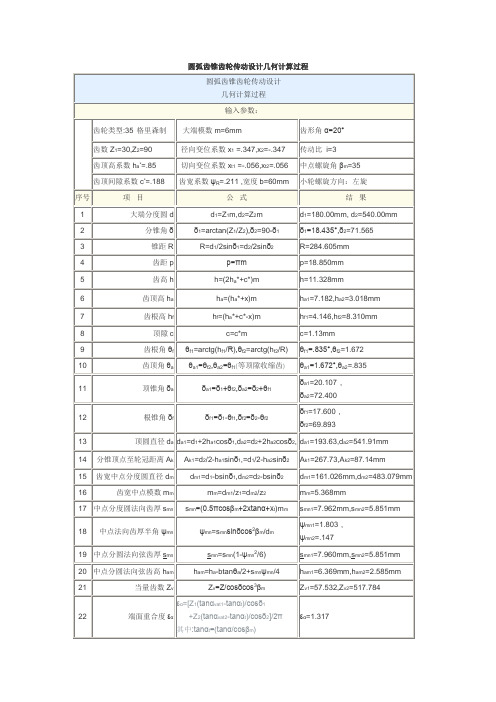
δa2=72.400°
12
根锥角δf
δf1=δ1-θf1,δf2=δ2-θf2
δf1=17.600°,
δf2=69.893°
13
顶圆直径da
da1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2,
da1=193.63,da2=541.91mm
14
分锥顶点至轮冠距离Ak
圆弧齿锥齿轮传动设计几何计算过程
圆弧齿锥齿轮传动设计
几何计算过程
输入参数:
齿轮类型:35°格里森制
大端模数m=6mm
齿形角α=20°
齿数Z1=30,Z2=90
径向变位系数x1=.347,x2=-.347
传动比i=3
齿顶高系数ha*=.85
切向变位系数xt1=-.056,xt2=.056
中点螺旋角βm=35°
+Z2(tanαvat2-tanαt)/cosδ2]/2π
其中:tanαt=(tanα/cosβm)
cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]
εα=1.317
23
齿线重合度εβ
εβ=btanβmπ/mm
εβ=2.491
24
总重合度
ε=(εα2+εβ2)1/2
ε=2.818
8
顶隙c
c=c*m
c=1.13mm
9
齿根角θf
θf1=arctg(hf1/R),θf2=arctg(hf2/R)
θf1=.835°,θf2=1.672°
10
齿顶角θa
θa1=θf2,θa2=θf1(等顶隙收缩齿)
θa1=1.672°,θa2=.835°
弧齿锥齿轮计算范文

弧齿锥齿轮计算范文1.基本概念:-弧齿锥齿轮:是一种带有锥面的圆锥形齿轮,在用于传动时,锥齿轮的啮合点在轴心线上。
-基本参数:包括齿数、模数、齿顶高系数、齿根高系数等。
-啮合角:两个齿轮齿廓线的交线与轴线间的夹角。
2.弧齿锥齿轮计算的基本公式:-模数m:弧齿锥齿轮齿数与模数的比值。
-齿距p:两个邻齿间的同心圆周弧长。
-齿厚s:齿顶与齿底之间的距离。
-齿顶高h_a:从齿顶到基圆的距离。
-齿根高h_f:从齿底到基圆的距离。
-齿顶宽b:两齿轮在法向上的接触宽度。
-(注:以上参数表示的是单齿齿轮的大小)3.弧齿锥齿轮计算的步骤:a.齿轮参数的确定:确定需求参数,如传递功率、转速比、传动效率、齿轮种类等。
b.模数的选择:应满足传递功率与转速的要求,并考虑加工性与强度。
c.齿数及啮合角的计算:使用基本公式计算齿数和啮合角。
d.齿顶高和齿根高的计算:使用基本公式计算齿顶高和齿根高,考虑强度。
e.齿轮啮合宽度的计算:使用齿顶高和齿根高计算齿轮啮合宽度,与承载能力有关。
f.齿轮等效齿数的计算:计算齿轮的等效齿数,以确定传动比。
g.法向变位系数及挤压系数的计算:根据实际情况计算法向变位系数及挤压系数,控制齿轮传动质量。
h.齿轮加工校核:计算齿轮加工校核参数。
i.绘制齿轮图样:根据以上计算结果,绘制齿轮尺寸图样。
弧齿锥齿轮计算涉及到多个参数和公式的运用,需要根据实际情况进行具体的计算和校核。
以上给出的步骤和基本公式只是一个简单的概述,实际计算中还需要考虑更多的因素,如弯曲应力、接触应力、表面质量等。
因此,在实际应用中,建议根据实际情况进行具体的计算和校核,确保齿轮传动的正常运行。
弧齿锥齿轮几何参数设计分解
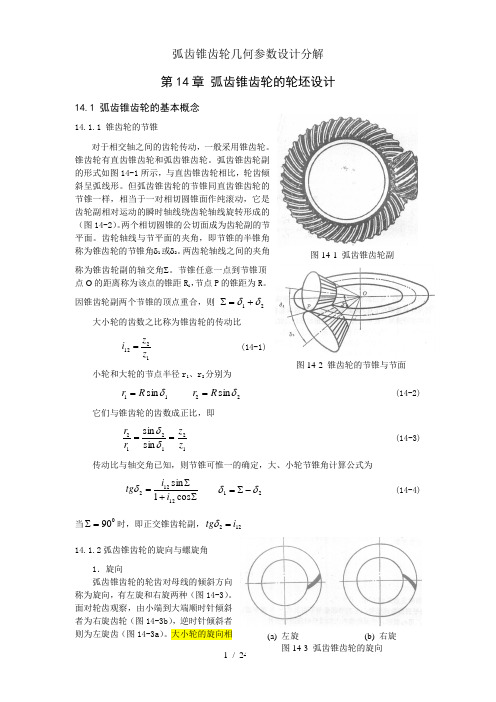
第14章 弧齿锥齿轮的轮坯设计14.1 弧齿锥齿轮的基本概念14.1.1 锥齿轮的节锥对于相交轴之间的齿轮传动,一般采用锥齿轮。
锥齿轮有直齿锥齿轮和弧齿锥齿轮。
弧齿锥齿轮副的形式如图14-1所示,与直齿锥齿轮相比,轮齿倾斜呈弧线形。
但弧齿锥齿轮的节锥同直齿锥齿轮的节锥一样,相当于一对相切圆锥面作纯滚动,它是齿轮副相对运动的瞬时轴线绕齿轮轴线旋转形成的(图14-2)。
两个相切圆锥的公切面成为齿轮副的节平面。
齿轮轴线与节平面的夹角,即节锥的半锥角称为锥齿轮的节锥角δ1或δ2。
两齿轮轴线之间的夹角称为锥齿轮副的轴交角∑。
节锥任意一点到节锥顶点O 的距离称为该点的锥距R i ,节点P 的锥距为R 。
因锥齿轮副两个节锥的顶点重合,则 21δδ+=∑大小轮的齿数之比称为锥齿轮的传动比1212z z i =(14-1) 小轮和大轮的节点半径r 1、r 2分别为11sin δR r = 22sin δR r = (14-2)它们与锥齿轮的齿数成正比,即121212sin sin z z r r ==δδ (14-3) 传动比与轴交角已知,则节锥可惟一的确定,大、小轮节锥角计算公式为∑+∑=cos 1sin 12122i i tg δ 21δδ-∑= (14-4)当090=∑时,即正交锥齿轮副,122i tg =δ 14.1.2弧齿锥齿轮的旋向与螺旋角1.旋向弧齿锥齿轮的轮齿对母线的倾斜方向称为旋向,有左旋和右旋两种(图14-3)。
面对轮齿观察,由小端到大端顺时针倾斜者为右旋齿轮(图14-3b ),逆时针倾斜者则为左旋齿(图14-3a )。
大小轮的旋向相图14-2 锥齿轮的节锥与节面(a) 左旋 (b) 右旋图14-1 弧齿锥齿轮副反时,才能啮合。
一般情况下,工作面为顺时针旋转的(从主动轮背后看,或正对被动轮观察),主动锥齿轮的螺旋方向为左旋,被动轮为右旋(图14-1);工作面为逆时针旋转的,情况相反。
这样可保证大小轮在传动时具有相互推开的轴向力,从而使主被动轮互相推开以避免齿轮承载过热而咬合。
圆弧齿锥齿轮计算公式

圆弧齿锥齿轮计算公式圆弧齿锥齿轮计算公式:1大端分度圆dd1=Z1m,d2=Z2m2分锥角δδ1=arctan(Z1/Z2),δ2=90-δ13锥距RR=d1/2sinδ1=d2/2sinδ24齿距pp=πm5齿高hh=(2ha*+c*)m6齿顶高haha=(ha*+x)m7齿根高hfhf=(ha*+c*-x)m8顶隙cc=c*m9齿根角θfθf1=arctg(hf1/R),θf2=arctg(hf2/R) 10齿顶角θaθa1=θf2,θa2=θf1(等顶隙收缩齿)顶锥角δaδa1=δ1+θf2,δa2=δ2+θf112根锥角δfδf1=δ1—θf1,δf2=δ2—θf213顶圆直径dada1=d1+2ha1cosδ1,da2=d2+2ha2cosδ2, 14分锥顶点至轮冠距离AkAk1=d2/2—ha1sinδ1,=d1/2—ha2sinδ215齿宽中点分度圆直径dmdm1=d1-bsinδ1,dm2=d2-bsinδ216齿宽中点模数mmmm=dm1/z1=dm2/z217中点分度圆法向齿厚smnsmn=(0.5πcosβm+2xtanα+xt)mm18中点法向齿厚半角ψmnψmn=smnsinδcos2βm/dm19中点分圆法向弦齿厚smnsmn=smn(1—ψmn2/6)20中点分圆法向弦齿高hamham=ha—btanθa/2+smnψmn/421当量齿数ZvZv=Z/cosδcos3βm端面重合度εαεα=[Z1(tanαvat1—tanαt)/cosδ1+Z2(tanαvat2-tanαt)/cosδ2]/2π其中:tanαt=(tanα/cosβm)cosαvat=[Zcosαt/(Z+2(ha*+x)cosδ)]εα=1.29723齿线重合度εβεβ=btanβmπ/mm24总重合度ε=(εα2+εβ2)1/2关于弧半径:求扇形弧半径扇形弧即指整个圆圈中的一部分. 通常的已知条件是由水平线除2组成的大边和以垂直线组成的小边. 如图:这类制作,在各种场合都时有所见。
弧齿锥齿轮几何参数计算

由图5-14和图5-15查得 由图5-16查得 由表5-6和图5-20查得 由表5-7查得 z2=u0z1(圆整) mt=d10/z1 mt=d20/z2
147 0 30 4.9 45
R=0.5d10/sinδ R/mm b/mm β /(0)
1
86.3787702 27 35 25.91363 49
R=0.5d20/sin(Σ -δ 1) 取0.3R和10mt中小者 b=0.25R 见表5-11,保证 ε β ≥1.25, 由图5-22查得
l
名称
弧齿锥齿轮主要参数初算 代号/单位 轴交角 Σ /(°) 齿数比初值 u0 工业用 T1/N*m T2/N*m d10/mm d20/mm z1 z2 工业用 汽车用 Σ ≤ 900 Σ > 900 工业用 汽车用 β ≠00 β =00 mt/mm δ 1/(0) 汽车用 工业用 汽车用 工业用 汽车用
序号 1 2 3 4 5 6 7 8 9 10 11 小齿轮 齿数 大端端面模数 齿宽 齿顶高系数 顶隙系数 法向压力角 工作齿高 轴交角 切向变位系数 螺旋角 螺旋方向 大端分度圆直径 分锥角 大端锥距 大端齿距 大轮齿顶高 小轮齿顶高 齿顶间隙 全齿高 齿根高 齿根角 顶锥角 根锥角 顶圆直径 冠顶距 大端理论弧齿轮
计算公式和说明 u0=i120
算例 90 1 850
大轮转矩 原始参数 小轮大端分度圆直径初值 大轮大端分度圆直径初值 小轮齿数 大轮齿数 大端端面模数 小轮分锥角 大端锥距 齿宽 螺旋角 大齿轮 30 30 4.9 27 0.85 0.188 20 8.33 90 0 0 35 r 147 147 45 45 86.37877019 15.393804 4.165 4.165 0.9212 9.2512 5.0862 5.0862 3.369829131 3.369829131 48.36982913 48.36982913 41.63017087 41.63017087 151.3759322 151.3759322 41.83265417 41.83265417 7.696902001 7.696902001
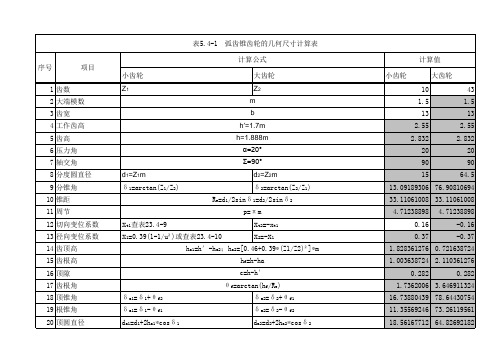
弧齿锥齿轮的几何尺寸计算表
13.09189306 76.90810694 33.11061008 33.11061008 4.71238898 0.16 0.37 4.71238898 -0.16 -0.37
xt1查表23.4-9 x1=0.39(1-1/u²)或查表23.4-10
xt2=-xt1 x2=-x1
hf=h-ha c=h-h′ θ f=arctan(பைடு நூலகம்f/Re) δ δ
s2=p/2-(ha1-ha2)tanα /cosβ m-xt1m
Smn1=(0.5πcosβm+2x1tanα+xt1)mm ψmn=Smn*cosδ*cos²βm/(mmZ) Kψ mn=1-ψ mn²/6 S′mn=SmnKψmn h′am1=ha1-0.5b*tanθf2+0.25Smn1ψmn1 查表23.4-11 N0=(θ
f1+θf2)sinβm/20
Smn2=πmmcosβm-Smn1
h′am2=ha2-0.5b*tanθf1+0.25Smn2ψmn2
1.472078944 0.525395815 9.262878463 9.262878463
设定值 传动比 4.3 齿顶高系数 顶隙系数 0.85 0.188
da1=d1+2ha1*cosδ
da2=d2+2ha2*cosδ
21 锥点至轮冠距离 22 理论弧齿厚 23 侧隙 24 中点螺旋角 25 齿宽系数 26 中点模数 27 中点法向模数 28 中点法向齿厚 29 中点法向齿厚半角 30 中点齿厚角系数 31 中点分度圆弦齿厚 32 中点分度圆弦齿高 33 刀盘直径 34 刀号
表5.4-1 序号 1 齿数 2 大端模数 3 齿宽 4 工作齿高 5 齿高 6 压力角 7 轴交角 8 分度圆直径 9 分锥角 10 锥距 11 周节 12 切向变位系数 13 径向变位系数 14 齿顶高 15 齿根高 16 顶隙 17 齿根角 18 顶锥角 19 根锥角 20 顶圆直径 δ δ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
αn
u d ′e1z 2331m e 6.331 mm 6.350 mm δ36.573 °53.427 °d e 146.05 mm
196.85 mm
Re ?R b d m 127.064 mm
171.260 mm
Zc R i 基准点锥距Rp
中点螺旋角βm
初定基准点螺旋角Z 0
5r w
2
5039.24基准点法向模数m p 基准点实际螺旋角βp 基准点法向模数m p 基准点螺旋角βp 铣刀盘名义半径
r 0刀齿组数z 0刀齿节点高度
h w0
刀号h Δax 00ha 4.34 mm 4.34 mm hf 5.34 mm
5.34 mm
x t 00d ae 153.02 mm 202.02 mm Ak 101.0118224
76.51159062
A βes e
计算结果如下:
88 mm 13119 mm
刀盘FS13-88R1 1.5-4.5 FS13-88L2 1.5-4.5
9.68 mm 略
由图16.4-8确定
r 0=70mm,β″p =39.5°,由表16.4-14选刀
盘号为EN5-70,Z 0=5
由图16.4-9查出A 点,它介于2号与3号刀片之间,由表16.4-14选3
号刀片r w 2=5039.24mm
2
4.3414 mm
39.938 °4.20 mm 40.4712 °32 mm
38.60 mm 90.56 mm 109.28 mm 35 °37.474 °
安装距大端螺旋角大端分度圆齿厚
r 0
20 °1.35145.62 mm
122.56 mm 0.26径向变位系数
齿顶高齿根高切向变位系数大端齿顶圆直径锥顶到轮冠距离
EN 刀盘或TC 刀盘
选择铣刀盘半径
选择刀片型号FS 刀盘或FSS 刀盘
齿高铣刀轴倾角外锥距齿宽系数齿宽中点分度圆直径
冠轮齿数小端锥距齿数比
估算小轮大端分度圆直径
齿数大端端面模数
分锥角大端分度圆直径
齿形角p
'。
