四年级巧求面积练习题汇编
四年级奥数巧算面积
巧算面积巧点晴——方法和技巧解答比较复杂的关于长方形、正方形的周长和面积的计算问题时,不能生搬硬套公式,需要运用移位、合并、分解、转化等解题技巧。
因此,敏锐的观察力和灵活的思维在解题中至关重要。
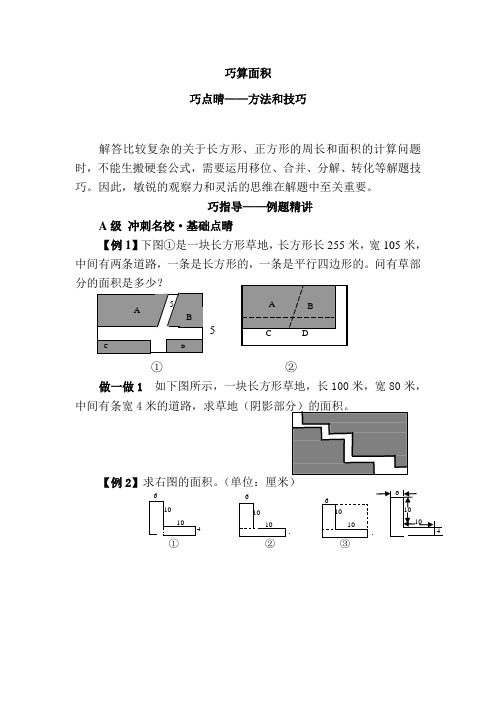
巧指导——例题精讲A级冲刺名校·基础点晴【例1】下图①是一块长方形草地,长方形长255米,宽105米,中间有两条道路,一条是长方形的,一条是平行四边形的。
问有草部分的面积是多少?5①②做一做1如下图所示,一块长方形草地,长100米,宽80米,中间有条宽4【例2】做一做2 计算下列图形的面积。
(单位:厘米)【例3】如右图,一块菜地长18米,宽10米, 菜地中间留了宽2米的路,把菜地平均分成四 小块,每一小块的面积是多少? 分析与解1 已知这块菜地的长和宽,能求出这块菜地的总面积(大长方形),再减去道路的面积,就得到四小块菜地面积之和;也可直接求出每小块菜 地的长和宽,从而求出小块菜地的面积。
每一小块菜地宽为:(10-2)÷2=4(米) 每一小块菜地长为:(18-2)÷2=8(米) 每一小块菜地的面积为:4×8=32(平方米)分析与解2 如右图,注意横道和竖道面积有一个重合部分,即虚线围成的小正方形,计算面积时,避免计算两次。
2×10+2×18-2×2=52(平方米) 或(10-2)×2+18×2=52(平方米) (18×10-52)÷4=32(平方米)分析与解3 我们还可以运用平移的办法(面积 不变)将道路平衡到菜地的边沿,如右图,先直接求 一个小长方形的面积。
(18-2)×(10-2)=128(平方米) 128÷4=32(平方米)答:每一小块的面积是32平方米。
小结 敏锐的观察力和灵活的思维在解本题时至关重要。
做一做3 如下图,一条白底的正方形手帕,它的边长是18厘米,手帕上横竖各有两道红条(图中的阴影部分),红条的宽都是2厘米。
四年级思维训练14 基本方法求面积 (试卷+解析)

四年级思维训练14 基本方法求面积1.若将一个边长为6厘米的正方形盖在一个三角形上,使两个图形重叠部分的面积占三角形面积的一半,占正方形面积的三分之二,那么这个三角形的面积是平方厘米.2.正方形一条对角线长13厘米,这个正方形的面积是平方厘米.3.一块由一个三角形和一个平行四边形组成的玉米地,其形状如下图所示(单位:米).它的面积是平方米.4.在下图中,四边形ABCD,DEFG均为正方形,C、D、E三点在同一条直线上,已知CE=14厘米,AG=2厘米,那么两个正方形的面积之和是平方厘米.5.在下图中,I3C一10厘米,EC一6厘米,直角三角形EDF的面积比直角三角形FAB的面积小5平方厘米.那么,长方形ABCD的面积是平方厘米.6.正方形ABCD与长方形BEFG如下图放置,AG=CE=2厘米,那么正方形ABCD的面积比长方形BEFG的面积大平方厘米.7.下图中甲的面积比乙的面积大平方厘米.8.如下图所示,将2006个边长为8厘米的正方形纸片,每4厘米错开排列起来,那么这2006张纸片覆盖的面积是平方厘米.9. E是正方形ABCD的边CD上的三等分点(见下图),BE把正方形分成一个梯形和一个三角形.梯形的周长比三角形的周长大8厘米.正方形ABCD的面积是平方厘米.10.下图是回字形的长方形草地(单位:厘米),阴影部分的面积为平方厘米.11.下图(单位:厘米)中大正方形中阴影部分的面积是平方厘米.12.如下图所示,四边形ABCD是梯形,上底是8厘米,下底是16厘米.点E是Bc边上任意一点,如果△AED的面积是30平方厘米,那么梯形AI3CD的面积是平方厘米13. 如下图所示,将图1中的等腰直角三角形的两端如图2那样折起,再对折后可得图3那样的图形.请问图3中的阴影部分的面积是多少平方厘米?四年级思维训练14 基本方法求面积参考答案1.若将一个边长为6厘米的正方形盖在一个三角形上,使两个图形重叠部分的面积占三角形面积的一半,占正方形面积的三分之二,那么这个三角形的面积是平方厘米.【答案】48【分析】重叠部分的面积为6×6×2﹦24(平方厘米),所以三角形的面积为324×2﹦48(平方厘米).2.正方形一条对角线长13厘米,这个正方形的面积是平方厘米.【答案】84.5【分析】正方形的面积=对角线×对角线÷2.此正方形的面积:13×13÷2﹦84.5(平方厘米)3.一块由一个三角形和一个平行四边形组成的玉米地,其形状如下图所示(单位:米).它的面积是平方米.【答案】87【分析】面积是:6×8÷2+7×9﹦87(平方米)4.在下图中,四边形ABCD,DEFG均为正方形,C、D、E三点在同一条直线上,已知CE﹦14厘米,AG﹦2厘米,那么两个正方形的面积之和是平方厘米.【答案】100【分析】由题意,两正方形的边长和是14厘米,差是2厘米,所以大正方形边长为8厘米,小正方形边长为6厘米,所以面积和是8×8+6×6﹦100(平方厘米).5.在下图中,I3C一10厘米,EC一6厘米,直角三角形EDF的面积比直角三角形FAB的面积小5平方厘米.那么,长方形ABCD的面积是平方厘米.【答案】35【分析】长方形ABCD与三角形BCE的画积差就是三角形ABF与三角形DEF的面积差,所以长方形ABCD的面积是10×6÷2+5﹦35(平方厘米).6.正方形ABCD与长方形BEFG如下图放置,AG﹦CE﹦2厘米,那么正方形ABCD的面积比长方形BEFG的面积大平方厘米.【答案】4【分析】正方形ABCD与长方形BEFG的面积差就是长方形AGHD与长方形CEFH的面积差,长方形CEFH的面积﹦CH×2,长方形AGHD的面积﹦AD×2,则长方形AGHD与长方形CEFH的面积差就是一个边长为2的正方形的面积.所以正方形ABCD的面积比长方形BEFG的面积大4平方厘米.7.下图中甲的面积比乙的面积大平方厘米.【答案】8【分析】利用差不变,S甲–S乙﹦8×6÷2﹦8×4÷2﹦8(平方厘米).8.如下图所示,将2006个边长为8厘米的正方形纸片,每4厘米错开排列起来,那么这2006张纸片覆盖的面积是平方厘米.【答案】96304【分析】由图可知除最上面一个正方形为完整图形外,其余的2005个正方形均重叠了一小部分面积,且被重叠的面积为4×4﹦16(平方厘米),则每增加一个正方形纸片,增加的面积为8×8-16﹦48(平方厘米),因此,2006个纸片的总面积为64+48×2005﹦96304(平方厘米).9. E是正方形ABCD的边CD上的三等分点(见下图),BE把正方形分成一个梯形和一个三角形.梯形的周长比三角形的周长大8厘米.正方形ABCD的面积是平方厘米.【答案】36【分析】设CE﹦a厘米,那么正方形边长等于3a厘米,- C∆BCE﹦AB+BE+ ED+ DA – BE- CE- BC﹦ 3a+3a+2a -a - 3a﹦4a,所以n 8﹦C梯形ABED﹦2,所以正方形边长为6厘米,面积为36平方厘米.10.下图是回字形的长方形草地(单位:厘米),阴影部分的面积为平方厘米.【答案】428﹦18×30-(30-8-8)×(18-5-5)﹦428(平方厘米)【分析】 S阴影11.下图(单位:厘米)中大正方形中阴影部分的面积是平方厘米.【答案】3﹦4×4-1×4÷2×2-3×3﹦3(平方厘米)【分析】S阴影12.如下图所示,四边形ABCD是梯形,上底是8厘米,下底是16厘米.点E是Bc边上任意一点,如果△AED的面积是30平方厘米,那么梯形AI3CD的面积是平方厘米【答案】90【分析】方法一:三角形ADE的高为30×2÷8﹦7.5(厘米),那么梯形面积为(8+16)×7.5÷2﹦90(平方厘米).方法二:由于BC﹦2AD,△AEB与△ECD的面积和是△AED画积的2倍,所以梯形的面积是30×(1+2)﹦90(平方厘米).13. 如下图所示,将图1中的等腰直角三角形的两端如图2那样折起,再对折后可得图3那样的图形.请问图3中的阴影部分的面积是多少平方厘米?【答案】9. 375【分析】等腰直角三角形底边上的高长度为底边的一半,原i角形面积为:10×5÷2﹦25平方厘米;现在所求的阴影部分的面积为原三角形与下图的等腰直角j角形的差的一半.则阴影部分面积为: (25-5×2.5÷2)÷2﹦9. 375(平方厘米).-----------------------------------------------学好语文的方法和技巧一、培养良好的阅读习惯良好的阅读习惯对形成阅读能力、保证阅读质量、提高阅读效率、顺利达到阅读目的有着重要作用。
人教版四年级数学思维训练第十六讲巧求面积

第十六章巧求面积知识导航同学们都知道,物体的表面或封闭图形的大小,叫作物体的面积。
我们已经学会运用公式求长方形和正方形的面积了。
但是,在平时的学习过程中,我们常常会遇到一些已知条件比较隐蔽、图形比较复杂、不能简单地用公式直接求出面积的题目。
这就需要我们切实掌握有关概念,利用“割补”“平移”“旋转”“分解”“合并”等转化方法,化难为易,化繁为简,从而正确解决问题。
图解思维训练题例1 一个长方形,如果宽不变,长增加6米,那么它的面积就增加54平方米;如果长不变,宽减少4米,那么它的面积就减少48平方米。
这个长方形的面积是多少平方米?图解思路如下图所示,这个长方形的宽用“增加的面积÷增加的长”可以求出,长用“减少的面积÷减少的宽”可以求出,然后用“长×宽”求出面积。
规范解答宽:54÷6=9(米)长:48÷4=12(米)面积:9×12=108(平方米)答:这个长方形的面积是108平方米。
例2 下图中大正方形的边长比小正方形的边长多4厘米,大正方形的面积比小正方形的面积多96平方厘米。
大正方形和小正方形的面积各是多少平方厘米?图解思路如下图所示,把大正方形比小正方形多出的96平方厘米分成了三部分。
这三部分中一部分是带阴影的小正方形,另外两个部分是没有阴影的长方形。
可以先求出带阴影的小正方形的面积,再用多出的96平方厘米减去带阴影的小正方形的面积,得到两个长方形的面积,再除以2就是一个长方形的面积。
长方形的面积知道了,再除以宽就是长。
这个长等于小正方形的边长,边长求出来了,面积就迎刃而解了。
规范解答带阴影的小正方形的面积:4×4=16(平方厘米)一个长方形的面积:(96-16)÷2=40(平方厘米)长方形的长(也就是小正方形的边长):40÷4=10(厘米)小正方形的面积:10×10=100(平方厘米)大正方形的面积:100+96=196(平方厘米)答:大正方形的面积是196平方厘米,小正方形的面积是100平方厘米。
四年级面积应用题20题 附答案

四年级面积应用题20题(附答案)知识点:长方形面积=长×宽正方形面积=边长×边长1、一张长方形课桌,长80厘米,宽60厘米,面积是多少平方分米?2、一块正方形手帕,边长为25厘米,面积为多少平方厘米?3、一块长方形菜地,面积是84平方米,长为21米,宽是多少米?4、一间教室长10米,宽8米,面积为多少平方米?如果铺上面积是5000平方厘米的方砖,需要多少块?5、一个游泳池长20米,宽12米。
要在游泳池底部铺上边长为50厘米的方砖,需要多少块?6、公园里有一块长方形的草地,长50米,宽28米。
草地中间有一个边长4米的正方形喷水池,求草地的面积。
7、张大爷用一段20米的篱笆靠墙围成一个长方形的养鸡场,(如下图)求占地面积多大。
8、如图,草坪里面修了一条19、如图,草坪里面修了两条1米宽的小路,求草地面积。
6米18米8米18米8米10、一个正方形的花坛,四周有1米宽的水泥路,如果水泥路总面积为12平方米,那么中间花坛的面积是多少平方米?11、一个周长是400米的正方形公园,它的面积是多少平方米?12、一块长方形的麦地,长300米,宽200米,共收小麦120吨,平均每平方米收小麦多少千克?13、张大伯有一块菜地,长28米,长比宽多6米,这块菜地的面积是多少平方米?14、一块长方形的地,长24米,宽12米,如果把它的宽增加5米,长不变,这块地的面积增加了多少平方米?15、一块长方形的地,长24米,宽12米,如果把它的长增加5米,宽不变,这块地的面积增加了多少平方米?16、有两个大小一样的长方形,长都是24厘米,宽都是12厘米。
⑴拼成一个正方形,正方形的周长是多少厘米?面积是多少平方厘米?⑴拼成一个长方形,长方形的周长是多少厘米?面积又是多少平方厘米?17、用一根铁丝能围成一个长48厘米,宽12厘米的长方形,如果用这跟铁丝围 成一个正方形,这个正方形的面积是多少?18、一间会议室长22米,宽15米,平均每平方米坐2人,这间会议室可以坐多少人?19、如图是学校操场的一角,请计算它的面积。
四年级思维专项训练14 基本方法求面积 (试卷+解析)

四年级思维训练14 基本方法求面积1.若将一个边长为6厘米的正方形盖在一个三角形上,使两个图形重叠部分的面积占三角形面积的一半,占正方形面积的三分之二,那么这个三角形的面积是平方厘米.2.正方形一条对角线长13厘米,这个正方形的面积是平方厘米.3.一块由一个三角形和一个平行四边形组成的玉米地,其形状如下图所示(单位:米).它的面积是平方米.4.在下图中,四边形ABCD,DEFG均为正方形,C、D、E三点在同一条直线上,已知CE=14厘米,AG=2厘米,那么两个正方形的面积之和是平方厘米.5.在下图中,I3C一10厘米,EC一6厘米,直角三角形EDF的面积比直角三角形FAB的面积小5平方厘米.那么,长方形ABCD的面积是平方厘米.6.正方形ABCD与长方形BEFG如下图放置,AG=CE=2厘米,那么正方形ABCD的面积比长方形BEFG的面积大平方厘米.7.下图中甲的面积比乙的面积大平方厘米.8.如下图所示,将2006个边长为8厘米的正方形纸片,每4厘米错开排列起来,那么这2006张纸片覆盖的面积是平方厘米.9. E是正方形ABCD的边CD上的三等分点(见下图),BE把正方形分成一个梯形和一个三角形.梯形的周长比三角形的周长大8厘米.正方形ABCD的面积是平方厘米.10.下图是回字形的长方形草地(单位:厘米),阴影部分的面积为平方厘米.11.下图(单位:厘米)中大正方形中阴影部分的面积是平方厘米.12.如下图所示,四边形ABCD是梯形,上底是8厘米,下底是16厘米.点E是Bc边上任意一点,如果△AED的面积是30平方厘米,那么梯形AI3CD的面积是平方厘米13. 如下图所示,将图1中的等腰直角三角形的两端如图2那样折起,再对折后可得图3那样的图形.请问图3中的阴影部分的面积是多少平方厘米?四年级思维训练14 基本方法求面积参考答案1.若将一个边长为6厘米的正方形盖在一个三角形上,使两个图形重叠部分的面积占三角形面积的一半,占正方形面积的三分之二,那么这个三角形的面积是平方厘米.【答案】48【分析】重叠部分的面积为6×6×2﹦24(平方厘米),所以三角形的面积为324×2﹦48(平方厘米).2.正方形一条对角线长13厘米,这个正方形的面积是平方厘米.【答案】84.5【分析】正方形的面积=对角线×对角线÷2.此正方形的面积:13×13÷2﹦84.5(平方厘米)3.一块由一个三角形和一个平行四边形组成的玉米地,其形状如下图所示(单位:米).它的面积是平方米.【答案】87【分析】面积是:6×8÷2+7×9﹦87(平方米)4.在下图中,四边形ABCD,DEFG均为正方形,C、D、E三点在同一条直线上,已知CE﹦14厘米,AG﹦2厘米,那么两个正方形的面积之和是平方厘米.【答案】100【分析】由题意,两正方形的边长和是14厘米,差是2厘米,所以大正方形边长为8厘米,小正方形边长为6厘米,所以面积和是8×8+6×6﹦100(平方厘米).5.在下图中,I3C一10厘米,EC一6厘米,直角三角形EDF的面积比直角三角形FAB的面积小5平方厘米.那么,长方形ABCD的面积是平方厘米.【答案】35【分析】长方形ABCD与三角形BCE的画积差就是三角形ABF与三角形DEF的面积差,所以长方形ABCD的面积是10×6÷2+5﹦35(平方厘米).6.正方形ABCD与长方形BEFG如下图放置,AG﹦CE﹦2厘米,那么正方形ABCD的面积比长方形BEFG的面积大平方厘米.【答案】4【分析】正方形ABCD与长方形BEFG的面积差就是长方形AGHD与长方形CEFH的面积差,长方形CEFH的面积﹦CH×2,长方形AGHD的面积﹦AD×2,则长方形AGHD与长方形CEFH的面积差就是一个边长为2的正方形的面积.所以正方形ABCD的面积比长方形BEFG的面积大4平方厘米.7.下图中甲的面积比乙的面积大平方厘米.【答案】8【分析】利用差不变,S甲–S乙﹦8×6÷2﹦8×4÷2﹦8(平方厘米).8.如下图所示,将2006个边长为8厘米的正方形纸片,每4厘米错开排列起来,那么这2006张纸片覆盖的面积是平方厘米.【答案】96304【分析】由图可知除最上面一个正方形为完整图形外,其余的2005个正方形均重叠了一小部分面积,且被重叠的面积为4×4﹦16(平方厘米),则每增加一个正方形纸片,增加的面积为8×8-16﹦48(平方厘米),因此,2006个纸片的总面积为64+48×2005﹦96304(平方厘米).9. E是正方形ABCD的边CD上的三等分点(见下图),BE把正方形分成一个梯形和一个三角形.梯形的周长比三角形的周长大8厘米.正方形ABCD的面积是平方厘米.【答案】36【分析】设CE﹦a厘米,那么正方形边长等于3a厘米,- C∆BCE﹦AB+BE+ ED+ DA – BE- CE- BC﹦ 3a+3a+2a -a - 3a﹦4a,所以n 8﹦C梯形ABED﹦2,所以正方形边长为6厘米,面积为36平方厘米.10.下图是回字形的长方形草地(单位:厘米),阴影部分的面积为平方厘米.【答案】428﹦18×30-(30-8-8)×(18-5-5)﹦428(平方厘米)【分析】 S阴影11.下图(单位:厘米)中大正方形中阴影部分的面积是平方厘米.【答案】3﹦4×4-1×4÷2×2-3×3﹦3(平方厘米)【分析】S阴影12.如下图所示,四边形ABCD是梯形,上底是8厘米,下底是16厘米.点E是Bc边上任意一点,如果△AED的面积是30平方厘米,那么梯形AI3CD的面积是平方厘米【答案】90【分析】方法一:三角形ADE的高为30×2÷8﹦7.5(厘米),那么梯形面积为(8+16)×7.5÷2﹦90(平方厘米).方法二:由于BC﹦2AD,△AEB与△ECD的面积和是△AED画积的2倍,所以梯形的面积是30×(1+2)﹦90(平方厘米).13. 如下图所示,将图1中的等腰直角三角形的两端如图2那样折起,再对折后可得图3那样的图形.请问图3中的阴影部分的面积是多少平方厘米?【答案】9. 375【分析】等腰直角三角形底边上的高长度为底边的一半,原i角形面积为:10×5÷2﹦25平方厘米;现在所求的阴影部分的面积为原三角形与下图的等腰直角j角形的差的一半.则阴影部分面积为: (25-5×2.5÷2)÷2﹦9. 375(平方厘米).。
【新版苏教版】四年级数学上册面积的计算练习题

【新版苏教版】四年级数学上册面积的计
算练习题
本文档为【新版苏教版】四年级数学上册面积的计算练题,共包括800字以上的练题。
1. 计算长方形的面积
题目:一个长方形的长为6米,宽为4米,求它的面积。
解答:长方形的面积可以通过长度乘以宽度来计算,所以这个长方形的面积为6米 × 4米 = 24平方米。
2. 计算正方形的面积
题目:一个正方形的边长是8厘米,求它的面积。
解答:正方形的面积可以通过边长的平方来计算,所以这个正方形的面积为8厘米 × 8厘米 = 64平方厘米。
3. 计算三角形的面积
题目:一个三角形的底边长是5厘米,高是3厘米,求它的面积。
解答:三角形的面积可以通过底边长乘以高再除以2来计算,所以这个三角形的面积为(5厘米 × 3厘米) ÷ 2 = 7.5平方厘米。
4. 计算梯形的面积
题目:一个梯形的上底长是6厘米,下底长是10厘米,高是4厘米,求它的面积。
解答:梯形的面积可以通过上底长、下底长和高的和再乘以高再除以2来计算,所以这个梯形的面积为((6厘米 + 10厘米) × 4厘米) ÷ 2 = 32平方厘米。
5. 计算圆的面积
题目:一个圆的半径是5厘米,求它的面积。
解答:圆的面积可以通过半径的平方再乘以π来计算,取
π=3.14,所以这个圆的面积为5厘米^2 × 3.14 ≈ 78.5平方厘米。
四年级数学下册考试必考题型图形求面积的10个方法(附例题解析)

例1:如右图,甲、乙两图形都是正方形,它们的边长分别是10厘米和12厘米.求阴影部分的面积。
一句话:阴影部分的面积等于甲、乙两个正方形面积之和减去三个“空白”三角形(△ABG、△BDE、△EFG)的面积之和。
例2:如右图,正方形ABCD的边长为6厘米,△ABE、△ADF与四边形AECF的面积彼此相等,求三角形AEF的面积。
一句话:因为△ABE、△ADF与四边形AECF的面积彼此相等,都等于正方形ABCD面积的三分之一,也就是12厘米.解:S△ABE=S△ADF=S四边形AECF=12在△ABE中,因为AB=6.所以BE=4,同理DF=4,因此CE=CF=2,∴△ECF的面积为2×2÷2=2。
所以S△AEF=S四边形AECF-S△ECF=12-2=10(平方厘米)。
例3:两块等腰直角三角形的三角板,直角边分别是10厘米和6厘米。
如右图那样重合.求重合部分(阴影部分)的面积。
一句话:阴影部分面积=S△ABG-S△BEF,S△ABG和S△BEF都是等腰三角形总结:对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合,分析整体与部分的和、差关系,问题便得到解决。
常用的基本方法有一、相加法这种方法是将不规则图形分解转化成几个基本规则图形,分别计算它们的面积,然后相加求出整个图形的面积。
例如:求下图整个图形的面积一句话:半圆的面积+正方形的面积=总面积二、相减法这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差。
例如:下图,求阴影部分的面积。
一句话:先求出正方形面积再减去里面圆的面积即可。
三、直接求法这种方法是根据已知条件,从整体出发直接求出不规则图形面积。
例如:下图,求阴影部分的面积。
一句话:通过分析发现阴影部分就是一个底是2、高是4的三角形四、重新组合法这种方法是将不规则图形拆开,根据具体情况和计算上的需要,重新组合成一个新的图形,设法求出这个新图形面积即可.例如:下图,求阴影部分的面积。
小学四年级面积应用题100道附答案(完整版)

小学四年级面积应用题100道附答案(完整版)题目1一块长方形草地,长25 米,宽18 米,这块草地的面积是多少平方米?答案:面积= 长×宽= 25×18 = 450(平方米)题目2一个正方形花坛的边长是12 米,它的面积是多少平方米?答案:面积= 边长×边长= 12×12 = 144(平方米)题目3一间教室的长是8 米,宽是 6 米,它的面积是多少平方米?答案:面积= 8×6 = 48(平方米)题目4一块长方形玻璃,长15 分米,宽8 分米,它的面积是多少平方分米?答案:15×8 = 120(平方分米)题目5正方形的周长是40 厘米,它的面积是多少平方厘米?答案:边长= 40÷4 = 10(厘米),面积= 10×10 = 100(平方厘米)题目6长方形的长是18 厘米,面积是72 平方厘米,宽是多少厘米?答案:宽= 面积÷长= 72÷18 = 4(厘米)题目7一块长方形菜地的面积是300 平方米,宽是15 米,长是多少米?答案:长= 面积÷宽= 300÷15 = 20(米)题目8一张长方形桌子的面积是48 平方分米,长是8 分米,宽是多少分米?答案:宽= 面积÷长= 48÷8 = 6(分米)题目9一个长方形果园,长50 米,宽40 米,这个果园的面积是多少平方米?答案:50×40 = 2000(平方米)题目10一块正方形手帕的边长是25 厘米,它的面积是多少平方厘米?答案:25×25 = 625(平方厘米)题目11长方形的宽是6 分米,面积是90 平方分米,长是多少分米?答案:长= 90÷6 = 15(分米)题目12一间卧室的地面是长方形,长7 米,面积是35 平方米,宽是多少米?答案:宽= 35÷7 = 5(米)题目13一块正方形稻田的周长是80 米,它的面积是多少平方米?答案:边长= 80÷4 = 20(米),面积= 20×20 = 400(平方米)题目14一个长方形的面积是180 平方厘米,长是20 厘米,宽是多少厘米?答案:宽= 180÷20 = 9(厘米)题目15正方形的面积是225 平方分米,它的边长是多少分米?答案:边长= √225 = 15(分米)题目16一块长方形菜地,长36 米,宽25 米,如果每平方米种8 棵白菜,这块地一共可以种多少棵白菜?答案:面积= 36×25 = 900(平方米),可种白菜900×8 = 7200(棵)题目17一间教室的面积是54 平方米,用边长3 分米的方砖铺地,需要多少块方砖?答案:3 分米= 0.3 米,一块方砖面积= 0.3×0.3 = 0.09(平方米),54÷0.09 = 600(块)题目18一个长方形广告牌,长16 米,宽8 米,现要给广告牌重新刷漆,每平方米用漆2 千克,一共要用多少千克漆?答案:面积= 16×8 = 128(平方米),用漆128×2 = 256(千克)题目19一块正方形土地的面积是9 公顷,它的边长是多少米?答案:1 公顷= 10000 平方米,9 公顷= 90000 平方米,边长= √90000 = 300(米)题目20长方形的长是120 米,宽是80 米,这块地的面积是多少公顷?答案:面积= 120×80 = 9600(平方米)= 0.96 公顷题目21一块长方形花园,长45 米,宽30 米,如果每5 平方米种一棵花,一共可以种多少棵花?答案:面积= 45×30 = 1350(平方米),可种花1350÷5 = 270(棵)题目22一个正方形鱼塘,边长是60 米,如果在鱼塘四周每隔 6 米种一棵柳树,一共要种多少棵柳树?答案:鱼塘周长= 60×4 = 240(米),240÷6 = 40(棵)题目23一块长方形草坪的面积是800 平方米,宽是20 米,如果宽增加到40 米,长不变,扩大后的草坪面积是多少平方米?答案:长= 800÷20 = 40(米),扩大后的面积= 40×40 = 1600(平方米)题目24正方形的边长扩大3 倍,面积扩大多少倍?答案:设原来边长为a,面积为a×a = a²。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
四年级巧求面积练习题
1、把一个长16米,宽9米的长方形的宽增加7米,可得到一个什么平面图形?面积是多少平方米?
2、一个长方形的周长是40厘米,且宽比长短2厘米,求长方形的面积是多少?
3、一个长62厘米,宽50厘米的长方形中截取一个最大的正方形,这个正方形的面积是多少?
4、如果把一个边长是10厘米的正方形的边长增加3厘米,这个正方形的面积将增加多少平方厘米?
5、有一个边长是20米的鱼塘,在它的四周有一条宽2米的道路,求道路的面积是多少平方米?
6、求下面图形的面积是多少?(单位:厘米)
7、大小两个正方形部分重合,边长分别是7厘米和5厘米,重合部分面积是10平方厘米,求两个正方形盖住的面积是多少?
8、两个相同的长方形,长是14厘米,宽是6厘米,把它们按如图叠放在一起,这个图形的面积是多少?
B组
9、一个长方形的长是30厘米,宽是20厘米,如果长和宽各增加5厘米,求面积增加多少平方厘米?
10、有两个一样的正方形,拼成一个长方形,周长比原来减少8厘米,求拼成的长方形的面积?
11、四个同样大小的长方形和一正方形拼成了一个大正方形,大正方形的面积是100平方厘米,小正方形的面积是4平方厘米,求长方形的宽是多少?
12、有一个长方形,如果它的长减少2米,或宽减少3米,它的面积就减少24平方米,求原来的长方形的面积是多少?
13、一个打谷场,长是60米,宽是45米,扩建后长增加了15米,宽增加了8米,那么打谷场的面积增加了多少平方米?
6、如图排列着两个正方形,左边一个大正方形的边长是6厘米,求阴影部分的面积?
14、如图长方形ABCD的长是12厘米,宽是6厘米,M、N分别为AB、CD的中点,求阴影部分的面积?
15、如果长方形的长是9厘米,宽是6厘米,三角形ADE和DCF的面积都是长方形面积的三分之一,求阴影部分的面积?。
