荷载结构法-举例
公路隧道明洞结构荷载计算方法(1)

最好解决上述问题的方法是通过板的空间加载求出最不利加载方式以后再使用平面梁模型进行计算根据作者的经验面板允许多辆车加载时一般把两辆车对称布于中轴线的两侧为最不利由于顶板覆土对车轮荷载起了一定的扩散作用此时车轮荷载作用在隧道顶板上的横向宽度较没有覆土时要宽得多因此此时荷载在顶板上的作用使用均布荷载表现gb5015722003地铁设计规范取10kpa均布荷载作为车辆荷载作用温度荷载隧道回填以一般较为恒定温度日差较小而隧道内由于通风等原因温度则有较大变化因此作者认为计算衬砌内外侧温差较计算衬砌整体的升温或降温更为重要通过作者的实际计算一般取1015即可同时还应注意在计算温度应力所产生的内力时应同时考虑混凝土徐变的影响tgd7022004公路隧道设计规范tb1000322001铁路隧道设计规范gb5015722003地铁设计规范gb5000722002建筑地基基础设计规范gj120299建筑基坑支护技术规范铁路工程设计技术手册隧道分册tgd6022004公路桥涵设计通用规范tgd6222004公路钢筋混凝土及预应力混凝土桥涵设计规范3072308
第6章隧道结构计算

α— 轴向力偏心影响系数。 1 1.5 e0 h
抗拉控制检算
大偏心判断准则:
e0 0.2h
此时承载能力由抗拉强度控制:
KN 1.75Rlbh
6e0 1 h
式中: Rl — 混凝土的抗拉极限强度,
其它符号意义同前。
6.5 衬砌截面强度验算
6.4 隧道洞门计算
1.洞门墙墙身抗压承载能力计算(承载能力极限状态)
2.洞门墙墙身抗裂承载能力计算(正常使用极限状态)
6.4 隧道洞门计算
3.洞门墙地基承载能力计算
4.抗倾覆计算 5.抗滑动计算
6.5 衬砌截面强度验算
6.5.1 检算内容
(1)安全系数检算 (2)偏心检算
6.5.2 适用范围
铁路隧道拼装式衬砌、复合式衬砌 双线隧道整体式衬砌 公路隧道衬砌结构
6.5.3 安全系数检算
(1) 允许安全系数 混凝土和石砌结构的强度安全系数
圬工种类及 荷载组合
破坏原因
混凝土
主 附主 要 加要 荷 荷、 载载
石砌体 主 附主 要 加要 荷 荷、 载载钢筋ຫໍສະໝຸດ 凝土主附主要
加要
荷
荷、
载
载
(钢筋)混凝土或石砌
设围岩垂直压力大于 侧向压力, 则存在拱顶 脱离区,两侧 抗力区。
6.2 结构力学方法
6.2.3 隧道衬砌荷载分类
(1) 主动荷载 主要荷载:围岩压力、支护结构自重、回填土荷载、地下 静水压力及车辆活载等。 附加荷载:冻胀压力、地震力等。 (2) 被动荷载 被动荷载是指围岩的弹性抗力,计算有共同变形理论和局 部变形理论。
直刚法计算流程
结构力学专题十六(单跨梁极限荷载计算)

P
P
A
D
B
C
l/3 l/3 l/3
共有三种可能的破坏机构
Fpu
4 l
Mu
F1
5 l
Mu
F2
4 l
Mu
2.用试算法求解
F3
9 l
Mu
作业:
16—3、 16—4。
补:求图示结构的极限荷载, 材料极限弯矩为Mu。
M
A
C
B
3m
1m
(2)平衡弯矩法
Mmax 1.5FPu M u
FPu
2 3
Mu
2F
F
2m
2m
1m
小结: 静定梁极限荷载计算特点:
静定结构无多余约束,出现一个塑性铰即成为破 坏机构。这时结构上的荷载即为极限荷载。
塑性铰出现的位置应为截面弯矩与极限弯矩之比 的绝对值最大的截面。
求出塑性铰发生的截面后,令该截面的弯矩等于 极限弯矩,利用平衡条件即可求出极限荷载。
(1)可破坏荷载 Fp
对任一破坏机构,由平衡条件求出的荷载称为可破坏 荷载;
(2)可接受荷载 Fp
同时满足屈服条件和平衡条件的荷载称为可接受荷载;
(3)极限荷载 Fpu
同时满足三个条件的荷载称为极限荷载,即极限荷载 既是可破坏荷载,又是可接受荷载。
4、一般定理
(1)基本定理(预备定理)
可破坏荷载恒不小于可接受荷载 Fp Fp
第十六章 梁和刚架的极限荷载
§16-3 单跨梁极限荷载计算
一、静定梁 例2:求图示结构的极限荷载,
材料极限弯矩为Mu。 (1)机动法
2F
F
2m
2m
1m
塑性铰出现在支座处
结构力学 位移法典型方程、计算举例
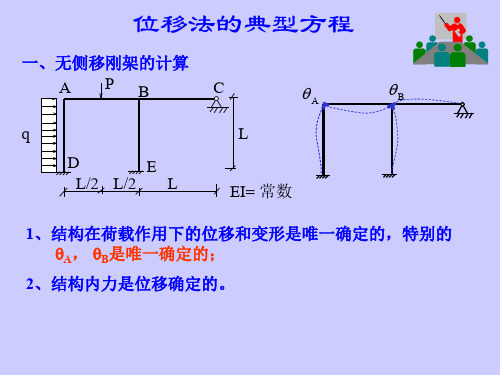
r21 B r22 CH R2
满足此方程,就消去了施加的2个约束
即,
r11 B r12 CH R1P 0 r21 B r22 CH R2 P 0
4)弯矩图的作法----消去最先附加的刚臂 P R1P R2P + MP图 R2
r
j 1
n
ij
Zj
,为消去该处的约束力,令: R iP
r
j 1
n
ij
Z j =0 即可。写成方程组的形式为:
r11 Z1 r12 Z 2 r1n Z n R1P 0 r Z r Z r Z R 0 21 1 22 2 2n n 2P rn1 Z1 rn 2 Z 2 rnn Z n RnP 0
R1P
R2P
+ +
r11 R A
1
r21R 2A
MP图 +
r12 B
r22 B
或
P
qL2/12
PL/8
4i
2i
q
R1P
R2P
+ A•
r11 8i r21 2i
2i
M 1图
MP图
4i
+
B•
4i r22 11i 2i r12 2i 3i 2i
M 2图
M M P M 1 A M 2 B
叠加右侧2个图,意味着结点B转动 及结点C侧移都发生。
叠加后B处的转角和C处的位移
分别为:B CH 则两处的约 束力必为R1,R2
r12 CH
结构力学I-第五章 虚功原理与结构位移计算(荷载位移,图乘法)

局部变形时静定结构的位移计算
⑴ 在要求的位移处,施加相应的单位荷载; ⑵ 利用力平衡条件,求出局部变形处对应的 内力M,FN,FQ; ⑶ 由虚力方程解出拟求位移: dΔ = ( Mκ + FNε + FQγ0 ) ds
Page 7
Δ A 1
B M
θ
14:32
LOGO
结构体位移计算的单位荷载法
真实荷载 弯曲 剪切
A
x
虚设荷载
B
b 截面参数 1 bh3 I=— 12 A =bh,k = 1.2
ql 4 1 2 qx dx 1.5 0 x Ebh3 2
l
变形类型
M P 0.5qx2
M x
FQP qx
F Q 1
MM P 1 ⑴ 弯曲变形引起的位移 M ds EI EI
Page 12
14:32
LOGO
荷载作用下的位移计算及举例
k F Q FQP F N FNP MM P ds ds ds EI EA GA
弯曲变形 拉伸变形 剪切变形
各类结构的位移公式
各类结构中三种变形的影响所占比重各不相同,故可简化; 例5-3 试求图示悬臂梁在A端的竖直 位移 Δ ,并比较弯曲变形和剪切变 形对位移的影响。设梁的截面为矩 形,泊松比1/3。 解:应用单位荷载法 A 1 q A x B
单位荷载法
单位荷载法求刚体体系位移
虚力原理
⑴ 虚力方程,实质为几何方程;
⑵ 虚力与实际位移状态无关,故可设 单位广义力 P = 1;单位荷载法 ⑶ 关键是找出找出虚力状态的静力平
衡关系。
Page 6
14:32
结构力学第五章-2(单位荷载法)

P
N i NPds N i NPl
EA
EA
P
MiM Pds N i NPl
EI
EA
例 2:求曲梁B点的竖向位移 By 和水 平位移 Bx。(EI、EA、GA已知) FP
解:构造虚设的力状态如图示
B
P=1
A
P =1
θ
R
M y R sin
θ
R
MP θ
R
M x R(1 cos )
~
2E 25 G
(h)2 l
E G的取值范围是什么?
G
E
2(1 )
0 0.5
2 EG 3
取:
h l
1 10
, E G 2.5 ,有:
(Ay )N
~
1, 750
(Ay )Q
~
1 500
即:
Ay
5ql 4 (1 1 1 ) 8EI 750 500
(Ay )Q 0.2% , (Ay )N 0.13%
(Ay )M
(Ay )M
因此,对受弯细长杆件,通常略去N、 V的影响。
三、几点讨论(只有荷载作用):
Ay
MiM Pds EI
N i NPds EA
V iVPds
GA
一般来说,剪切变形影响很小,通常忽略不计。
1. 对梁和刚架:
P
MiM Pds EI
2. 对桁架: 3. 对组合结构:
构;静定和超静定结构;
3. 材料性质:线性、非线性; 4. 变形类型:弯曲变形、拉(压)变形、剪切
变形;
5. 位移种类:线位移、角位移;相对线位移
和相对角位移。
试确定指定广义位移对应的单位广义力。
《荷载与结构设计方法》试题参考答案B
青岛理工大学试卷标准答案及评分标准专用纸2007 ~ _2008_学年第 1 学期荷载与结构设计方法》课程试卷标准答案及评分标准 B 卷专业:土木工程班级2005级1-14班一、选择题(2分×10=20分)1、D2、B3、B4、D5、C6、D7、C8、D9、C10、A二、判断题(1分×20=20分)1、(∨)2、(×)3、(×)4、(∨)5、(∨)6、(∨)7、(×)8、(×)9、(∨)10、(×)11、(∨)12、(×)13、(∨)14、(∨)15、(∨)16、(×)17、(×)18、(∨)19、(×)20、(∨)青岛理工大学试卷标准答案及评分标准专用纸三、 问答题(5分×8=40 分)1、举例说明:什么是可变荷载?什么是永久荷载?答:可变荷载是指在结构设计基准期内其值随时间变化,且其变化值与平均值相比不可忽略。
(2分)例如:车辆重力、风荷载、雪荷载、楼面活荷载。
(0.5分)永久荷载是指在结构设计基准期内其值不随时间变化,或其变化值与平均值相比可以忽略不计。
(2分)例如:结构自重。
(0.5分)2、为什么在计算承受梁板传递至底层墙(或柱)的荷载荷载效应时,当上部楼层较多时,楼面均布活荷载要折减?答:作用在楼面上的活荷载,不可能以标准值的大小同时布满在所有的楼面上,因此在设计梁、墙、柱和基础时,还要考虑实际荷载沿楼面分布的变异情况,也即在确定梁、墙、柱和基础的荷载标准值时,还应按楼面活荷载标准值乘以折减系数后考虑。
(5分)(注:如回答:一般情况下,考虑的楼面面积越大,实际平摊的楼面活荷载越小,故在确定梁、墙、柱和基础的荷载标准值时,还应按楼面活荷载标准值乘以折减系数后考虑。
也是正确的)3、简述青岛五四广场边一建筑平面为正方形的150m 高层的风荷载标准值的计算过程。
答:根据风荷载标准值的计算公式:0w w z s z k μμβ=,(1分)应有以下的计算过程:(1)根据青岛地区查得基本风压:20/60.0m kN w =。
结构的极限荷载和例题讲解
简化计算: 假设材料为理想弹塑性材料,其应力~应变关系下图所示。
§12-2 极限弯矩和塑性铰 破坏机构 静定梁的计算
一、弹塑性阶段工作情况
理想弹塑性材料T形截面梁处于纯弯曲状态时
弹性状态:
图b:截面处于弹性阶段,σ<σs (屈服极限) 图c:截面最外边缘处σ=σs (达到屈服极限) 屈服弯矩(弹性极限弯矩)MS = Wσs(W:弯曲截面系数) 图d:截面处于弹塑性阶段。 靠外部分形成塑性区,其应力为常数,σ=σs , 靠内部分仍为弹性区,称弹性核,其应力直线分布 图e:截面全部达到塑性——极限情形, 这时的弯矩是该截面所能承受的最大弯矩 ——极限弯矩,以Mu 表示。
等截面超静定梁(图a) (各截面Mu相同) 弹性——弹塑性阶段——极限状态过程:
(1)弹性阶段弯矩图:P≤Ps (2首)先弹在塑A性端阶形段成M并图扩:大荷,载然超后过CP截s,面塑也性形区成
塑性性铰区。。A端首先达到Mu并出现第一个塑
(3)极限状态M图:荷载再增加,A端弯矩 增量为零,当荷载增加到使跨中截面的弯矩达 到Mu时,在该截面形成第二个塑性铰,于是梁 即变为机构,而梁的承载力即达到极限值。此 时的荷载称为极限荷载Pu——极限状态(e)。
破坏机构——极限状态: 结构出现若干塑性铰而成为几何可变或瞬变体系时 ——结构丧失承载能力
三、静定梁的计算
静定梁由于没有多余联系,因此,出现一个塑性铰时,即 成为破坏机构。
对于等截面梁,在弯矩绝对值最大截面处达到极限弯矩, 该截面形成塑性铰。
由塑性铰处的弯矩等于极限弯矩和平衡条件,就可求出静 定梁的极限荷载。
结构的极限荷载和例题 讲解
§12-1 概述
结构设计方法:
1、容许应力法(弹性分析法):
荷载计算范例范文
荷载计算范例范文荷载计算是建筑工程设计中非常重要的环节之一,它是为了确保建筑物能够承受各种荷载而进行的计算和分析。
荷载计算的目的是确定建筑物的结构和基础所承受的最不利荷载,从而保证其安全性和稳定性。
以下是一个荷载计算的范例,以便更好地理解荷载计算的步骤和过程。
1.荷载的分类荷载可分为静荷载和动荷载两大类。
-静荷载是指在稳定状态下作用在结构上的荷载,包括自重、使用荷载、附加荷载等。
自重是指结构本身的重量,使用荷载是指建筑物在正常使用条件下承受的各种荷载,如人员、家具、设备等。
附加荷载是指建筑物在非正常使用条件下承受的荷载,如风荷载、地震荷载等。
-动荷载是指在运动状态下作用在结构上的荷载,包括风荷载、地震荷载等。
风荷载是指由风速引起的压力和吸力,地震荷载是指由地震引起的地震力。
2.荷载的计算方法荷载计算的方法主要有经验法和准确法两种。
-经验法是基于经验和规范的一种简单的计算方法,适用于一些简单的结构和场所。
这种方法可以根据结构的类型和用途,通过查找相关规范中的荷载系数和计算公式来进行荷载计算。
-准确法是基于结构力学和数学理论的一种准确的计算方法,适用于复杂的结构和场所。
这种方法需要进行详细的力学分析和计算,包括载荷的大小、方向、作用点等方面的细节。
3.荷载计算的步骤荷载计算的步骤一般包括以下几个方面。
-确定荷载类型和荷载作用点确定建筑物所受的静荷载和动荷载类型,以及荷载的作用点。
根据建筑物的用途和规模,确定荷载的种类和性质。
-查找相关规范和标准在进行荷载计算时,需要查找相关的建筑荷载规范和标准,获取相应的荷载系数和计算公式。
-计算荷载系数根据规范中的荷载系数和计算公式,计算建筑物所受荷载的大小。
需要注意的是,不同的荷载类型和作用点可能需要采用不同的系数和公式。
-进行结构力学分析根据荷载的大小和作用点,进行结构力学分析,确定建筑物的受力情况。
可以使用有限元分析等数学和计算工具来进行分析。
-验证荷载安全性根据荷载计算的结果,对建筑物的结构和基础进行验证。
隧道结构设计的荷载-结构法的流程
隧道结构设计的荷载-结构法的流程下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!并且,本店铺为大家提供各种各样类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,如想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by theeditor.I hope that after you download them,they can help yousolve practical problems. The document can be customized andmodified after downloading,please adjust and use it according toactual needs, thank you!In addition, our shop provides you with various types ofpractical materials,such as educational essays, diaryappreciation,sentence excerpts,ancient poems,classic articles,topic composition,work summary,word parsing,copy excerpts,other materials and so on,want to know different data formats andwriting methods,please pay attention!隧道结构设计的荷载-结构法流程解析在隧道工程的设计中,荷载-结构法是一种常用且重要的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
拱脚截面最终转角: a ap h a
(4.4.1-12)
按照变形协调条件,可以校核整个计算过程中有无错误。 s M i ds Mi a a 0 拱顶转角 EI E I (4.4.1-13) 拱顶水平 s M i yi M iyi EI ds f a E I f a 0 位移 s M i yih M iyih 最大反力 ds yah a yah a h EI E I K 点h处位移
2)弹性抗力假设 拱两侧的弹性抗 力一般假定为按二次 抛物线分布,有3个特 征点: ①上零点b,也是 脱离区的边界,其与 对称轴线间的夹角φb 一般40°~ 60°。 ②下零点a,取在 墙脚(无铰高拱 ), 该点无水平位移。
2
2015/4/21
(1)建立计算模型
2)弹性抗力假设 ③最大弹性反力点h,一般假定在衬砌最大跨度 处。 实际计算中,为了简化起见,上零点b和最大弹 性反力点最好取在结构分块的接缝上。注意点的定 位方法。 通常:
h hp h h
(4.4.1-3)
式中,δh—为h点的径向位移;δhp—为h点在主动荷载作用下h 点的径向位移;δhσ在单位被动荷载作用下h点的径向位移。 根据文克尔假定:
h K h
将其带入(4.4.1-3), h 解之即得:
hp
1 h K0
(4.4.1-4)
(4.4.1-9)
要求最大弹性反力σh,就必须先求出主动荷载和被动荷载作 用下的径向位移。求这两项位移时要考虑墙底转角的影响。按 照结构力学方法,求解位移可在原来的基本结构上进行。
h
hp
1 h K0
(4.4.1-4)
7
2015/4/21
按照结构力学力法分析原理,h点处 hp 、 h 计算公式如下
2015/4/21
荷载结构计算方法及设计模型举例
• (一)荷载—结构模型计算原理
• 以荷载-结构模型中“主动荷载+围岩弹性 约束模型”为例,介绍曲墙拱结构计算原理及 分析步骤。弹性反力分析基于局部变形理论。 (1)建立计算模型 (2)弹性抗力分布及计算 (3)截面内力计算及校核 (4)计算步骤
• • • •
曲墙拱结构的设计计算步骤(17步)
1)计算结构的几何尺寸,并绘制断面图 2)计算作用在衬砌结构上的主动荷载 3)绘制分块图 4)计算半拱轴长度 5)计算各分段截面中心的几何要素 6)计算基本结构的单位位移 ik 7)计算主动荷载在基本结构中产生的变位 1 p 2 p 8)解主动荷载作用下的力法方程 9)计算主动荷载作用下各截面的内力,并校核计算精度 10)求单位弹性反力图及相应摩擦力作用下基本结构中 产生的变位 1 2
(3)截面内力计算及校核
为便于计算,可将曲墙式的基本结构分解为在主动外荷 载和弹性抗力作用下的两个基本图式,分别计算出相应的截 面内力和位移值,然后用叠加原理求出衬砌截面的总内力。 实际上,在结构与荷载均对称的情况下,可以从拱顶切开, 以一对悬臂曲梁作为基本结构,切开处赘余力(多余未知 力):弯矩 X1、法向力X2 和 剪力X3,其中剪力X3=0。
'
' yh 为墙底外缘点至h的垂直距离。
(4.4.1-1)
yi 为拱圈上所讨论截面外缘点至h点的垂直距离。 式中,
围岩弹性反力对于衬砌的变形还会在围岩与衬砌产生相应的 摩擦力,摩擦力的分布图形与弹性反力相同,也是σh的函数。
3
2015/4/21
(2)弹性抗力分布及计算
2)最大抗力点h处的弹性抗力分析 因此,解题关键在于首先求出h点的抗力σh 。 根据文可尔假定,h点的抗力与h点的衬砌变形有关,而h 点的变形是外荷载和弹性抗力共同作用的结果:
(4.4.1-5) 式中 ik 为基本结构在单位荷载 单位位移; ip为基本结构在主动荷载 作用下,在Xi方向产生的位移。
f 矢高
ap拱脚最终转角
最终水平位移 u ap
X k 1 作用时,在 X i 方向产生的
ap
5
2015/4/21
①求主动荷载作用下衬砌 i 截面的衬砌内力 墙底拱脚的最终转角和位移计算,需要分表考虑 X 1 p , X2p 和外荷载的各自影响,再按照叠加原理相加获得,由于不考虑 拱脚的径向位移,拱脚只有转动发生,则有:
9
2015/4/21
11)解弹性反力及其摩擦力作用下的力法方程 12)求单位弹性反力图及摩擦力作用下截面的内力,并校核 其计算精度 13)计算最大弹性反力值
Xh 14)计算多余未知力X1和 2
15)计算衬砌截面总的内力并校核计算精度 16)绘制内力图 17)衬砌截面强度验算
10
(4.4.1-11)
h
( yh yi ) M i s ( yh yi ) M i ds EI E I
yh
yi
M ip
M i
8
2015/4/21
④衬砌内力计算及校核计算结果的正确性 根据叠加原理可以求出任意i截面最终的内力值。
M i M ip h M i
0 a0 M a 1
单位弹性反力作用下的基本结构
根据性反力作用下的内力计算式:
M i X 1 X 2 yi M i0
N i X 2 cos i N i0
③位移及最大弹性反力计算
hp
h
M ip M ih EI M M i ih ds yah a EI ds yah ap s M ip M ih I yab ap E s M i M ih I yab a E
(4.4.1-10)
式中各项含义见下图。1 为墙底的单位转角。
当最大弹性反力截面与竖直轴的夹角接近90°时,为简化计算, 可以将h点的位移方向视为水平。在荷载和结构均对称的情况下 拱顶没有水平位移及转角。因此,h点相对拱顶而言的水平位移, 即为h点的实际水平位移。此时,有下图计算图式。 位移计 算公式
hp
( yh yi ) M ip EI ds s ( yh yi ) M ip E I
0 ap X 1 p 1 X 2 p f1 ap
弯矩
法向力
将上式带入(4.4.1-5)式(典型方程),整理后有:
0 X 1 p (11 1 ) X 2 p (12 f1 ) 1 p ap 0
(4.4.1-6)
X 1 p ( 21 f1 ) X 2 p ( 22 f 1 ) 2 p f 0
0 M ip X 1 p X 2 p yi M ip
0 Nip X 2 p cosi Nip
(4.4.1-7)
6
2015/4/21
②被动单位荷载作用下的衬砌内力计算 计算方法同上,首先求单位弹性反力作用下的多余未 知力,公式如下:
X 1 (11 1 ) X 2 (12 f1 ) 1 a0 0
X 1 ( 21 f1 ) X 2 ( 22 f 2 1 ) 2 f a0 0
(4.4.1-8)
式中, i 以 h 1 单位弹性反力图为 荷载引起的基本结构在 X 1 方向的位移;
2 与上相同,在 X 2 方向产生的位移。
a0 为基本结构墙底的荷载转角
• (一)荷载—结构模型计算原理
• (1)建立计算模型 • 思路及过程: • 1)确定约束条件 • 2)假定弹性抗力:作用范围、抗力分布规律、最 大弹性反力点的位置。 • • 这种假定弹性抗力分布特征,用于这种地下结构 的计算方法简称为“假定抗力图形法”。在圆形衬砌、 曲墙式衬砌和直墙式衬砌的拱圈结构计算中采用。
1
2015/4/21
(1)建立计算模型 1)约束条件
墙基支承在弹性的 围岩上,视为弹性固 定端。因底部摩擦力 很大,无水平位移, 将结构视为支承在弹 性地基上的高拱。 该结构被简化为在 主动荷载(垂直荷载大 于水平荷载)及弹性抗 力共同作用下: ①支承在弹性地基 上的无铰高拱, ②无水平位移。
(1)建立计算模型
2 0 ap
式中 1 为墙底的单位转角
1
0 0 0 ap 为基本结构墙底的荷载转角 ap M ap 1
12 1 3 bd a K a K aI a
①求主动荷载作用下衬砌 i 截面的衬砌内力 根据式(4.4.1-6),可以求解出多余未知力 X 1 p
X2p
这样,主动荷载作用下的衬砌内力可以按照下式求解:
(2)弹性抗力分布及计算
按照前述方式,假定好上零点b、下零点a和最大抗力点h后, 就可以进一步讨论弹性抗力分布与计算问题。 1)弹性抗力分布假定 在上零点b和下零点a之间任意点截面的法向弹性抗力σi , 认为服从如下分布规律:
cos 2 b cos 2 i 在bh段,任意截面i处 : i h cos 2 cos 2 b h yi'2 1 (4.4.1-2) 在ah段: i '2 h yh
4
2015/4/21
(3)截面内力计算及校核
实际上,在结构与荷载均对称的情况下,可以从拱顶切 开,以一对悬臂曲梁作为基本结构,切开处赘余力(多余未 知力):弯矩 X1、法向力X2 和 剪力X3,其中剪力X3=0。
截面内力计算的具体步骤为: ①求主动荷载作用下衬砌 i 截 面的衬砌内力 ②被动单位荷载作用下的衬砌 内力计算 ③位移及最大弹性反力计算 ④衬砌内力计算及校核计算结 果的正确性
截面内力计算: ①求主动荷载作用下衬砌 i 截面的衬砌内力 多余未知力(赘余力)为 X 1 p X 2 p 拱顶截面相对转角和 相对水平位移为零,由此可以列出变形协 调方程(或叫典型方程):
