(完整word版)数字chebyshev滤波器的设计(matlab)
(完整word版)切比雪夫低通滤波器

(完整word版)切比雪夫低通滤波器课程设计题目:院(系):专业:学生姓名:学号:指导教师:2014 年01 月03 日切比雪夫低通滤波器摘要:利用ADS2008软件设计切比雪夫型低通滤波器,通过最终的图像,分析该滤波器的功能特性,并与其他滤波器对比分析,阐明此种滤波器的优点所在。
关键字:ADS2008软件切比雪夫低通滤波器功能特性目录摘要 (1)1滤波器概述 (3)1。
1滤波器分类 (3)1。
2根据滤波器的选频作用分类 (4)1.3根据“最佳逼近特性”标准分类 (4)1。
4理想滤波器 (5)2切比雪夫低通滤波器设计 (7)2.1新建滤波器工程 (7)2.2建立一个低通滤波器设计 (7)3 设计心得 (12)4 参考文献 (13)1、滤波器概述滤波器是一种选频装置,可以使信号中特定的频率成分通过,而极大地衰减其它频率成分。
在测试装置中,利用滤波器的这种选频作用,可以滤除干扰噪声或进行频谱分析。
广义地讲,任何一种信息传输的通道(媒质)都可视为是一种滤波器。
因为,任何装置的响应特性都是激励频率的函数,都可用频域函数描述其传输特性.因此,构成测试系统的任何一个环节,诸如机械系统、电气网络、仪器仪表甚至连接导线等等,都将在一定频率范围内,按其频域特性,对所通过的信号进行变换与处理.1.1 滤波器分类:滤波器特性可以用其频率响应来描述,按其特性的不同,可以分为低通滤波器,高通滤波器,带通滤波器和带阻滤波器等.低通滤波器有很多种,其中,最通用的就是巴特沃斯滤波器和切比雪夫滤波器。
巴特沃斯滤波器是滤波器的一种设计分类,其采用的是巴特沃斯传递函数,有高通、低通、带通、带阻等多种滤波器类型.巴特沃斯滤波器在通频带内外都有平稳的幅频特性,但有较长的过渡带,在过渡带上很容易造成失真。
切比雪夫滤波器同巴特沃斯滤波器相添加图片比,切比雪夫滤波器的过渡带很窄,但内部的幅频特性却很不稳定。
巴特沃斯响应能够最大化滤波器的通带平坦度.该响应非常平坦,非常接近DC信号,然后慢慢衰减至截止频率.巴特沃斯滤波器特别适用于低频应用,其对于维护增益的平坦性来说非常重要。
matlab滤波器设计

实验四 IIR 滤波器的实现(IIR 滤波器是无穷脉冲响应数字滤波器的简称)一、 讲课目的熟悉用双线性变换法设计IIR 数字滤波器和方式。
二、讲课内容(一)大体概念1、 数字滤波器是指输入、输出均为数字信号,通过必然运算关系,改变输入信号所含频率成份的相对照例或滤除某些频率成份的器件。
数字滤波器与模拟滤波器概念相同,只是信号的形式和实现滤波的方式不同。
一样数字滤波器从现实的网络结构或从单位脉冲响应分类,能够分成无穷脉冲脉冲响应(IIR)滤波器和有限脉冲响应(FIR)滤波器。
2、 IIR 滤波器设计的要紧方式是先设计低通模拟滤波器,进行频率变换,将其转换为相应的高通、带通模拟滤波器,再将模拟滤波器转换为相应的数字滤波器。
3、 N 阶模拟滤波器系统函数的一样形式为 11101110...()()...()M M M M N N N N b s b s b s b B s H s a s a s a s a A s ----++++==++++ 4、 N 阶数字模拟滤波器系统函数的一样形式为12(1)012112(1)121...()()1...()M M M M N N N N b b z b z b z b z B z H z a z a z a z a z A z ------------+++++==+++++(二)求滤波器频率响应的函数一、freqs 函数:求模拟滤波器的频率响应freqs(b,a,w)计算由向量w (rad/s )指定的频率点上(或W 直接为采样点数)频率响应,其中b 和a 别离为模拟滤波器系统函数H(s)的分子与分母。
freqs 函数将自动绘出幅频和相频曲线。
实验4-1:系统传输函数为220.20.31()0.41s s H s s s ++=++的模拟滤波器,绘出其幅频和相频谱。
a=[1,,1];b=[,,1];w=logspace(-1,1); %产生从10-1到101之间地50个等间距点,即50个频率点运行得幅频特性和相频特性如下:二、freqz函数:求数字滤波器的频率响应freqz(b,a,w)计算由向量w指定的频率点上模拟滤波器H(z)的频率响应,其中b和a别离为数字滤波器系统函数H(z)的分子与分母。
数字信号处理Matlab实验三-IIR数字滤波器的设计
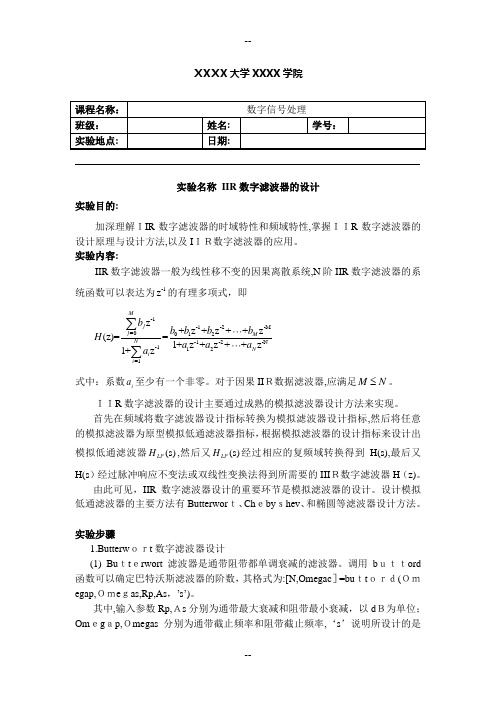
XX XX 大学XXXX 学院实验名称 IIR 数字滤波器的设计实验目的:加深理解IIR 数字滤波器的时域特性和频域特性,掌握IIR 数字滤波器的设计原理与设计方法,以及I IR数字滤波器的应用。
实验内容:IIR 数字滤波器一般为线性移不变的因果离散系统,N 阶IIR 数字滤波器的系统函数可以表达为-1z 的有理多项式,即 -1-1-2-M =0012-1-2-N -112=1z +z +z ++z (z)==1+z +z ++z 1+zM j j M N Ni i b b b b b H a a a a ∑∑ 式中:系数i a 至少有一个非零。
对于因果II R数据滤波器,应满足M N ≤。
IIR 数字滤波器的设计主要通过成熟的模拟滤波器设计方法来实现。
首先在频域将数字滤波器设计指标转换为模拟滤波器设计指标,然后将任意的模拟滤波器为原型模拟低通滤波器指标,根据模拟滤波器的设计指标来设计出模拟低通滤波器(s)LP H ,然后又(s)LP H 经过相应的复频域转换得到H(s),最后又H(s )经过脉冲响应不变法或双线性变换法得到所需要的III R数字滤波器H (z)。
由此可见,IIR 数字滤波器设计的重要环节是模拟滤波器的设计。
设计模拟低通滤波器的主要方法有Butterwor t、Ch eby shev 、和椭圆等滤波器设计方法。
实验步骤1.Butterw ort 数字滤波器设计(1) Bu tt erwort 滤波器是通带阻带都单调衰减的滤波器。
调用b uttord 函数可以确定巴特沃斯滤波器的阶数,其格式为:[N,Omegac ]=bu tt ord(Omegap,Ome gas,Rp,As ,’s ’)。
其中,输入参数Rp,As 分别为通带最大衰减和阻带最小衰减,以d B为单位;Om eg ap,Omegas 分别为通带截止频率和阻带截止频率,‘s ’说明所设计的是模拟滤波器。
输出参数为滤波器的阶数,Omegac为3dB截止频率。
数字滤波器的MATLAB设计.doc

0引言滤波器的作用是对输入信号进行滤波,它可以是软件也可以是硬件。
按照信号的成分不同,滤波器可分为数字滤波器和模拟滤波器。
数字滤波器指的是输入、输出皆为数字信号,然后通过运算改变输入信号频率成分相对比例,也有滤除一些不需要的频率成分功能的器件。
数字滤波器可以分为两种,是通过其冲击响应函数的频率特性来进行分类的,分别是无限长冲击响应(IIR)数字滤波器和有限长冲击响应(FIR)数字滤波器。
在本文屮将利用MATLAB提供的数字信号处理工具箱设计出由软件组成的IIR数字滤波器。
MATLAB信号处理工具箱能够提供多种设计方法,能把程序设计变成简单的函数调用,能够十分方便快捷的得到设计结果。
1 MATLAB的简介1.1 MATLAB的基本概念美国的MATHWORKS公司开发出来了MATLAB软件,它具有数值计算,信号显示与处理等多种功能,并且内容丰富,应用广泛。
MTALAB系统的组成部分有五个,包括MATLAB 语言体系、MATLAB工作环境、图形句相系统、MATLAB数学函数库、MATLAB 应用程序接口(API)。
MATLAB的语言体系具有很多程序语言的特性,比如能够条件控制,函数调用输入输出语言,也能够而叫对象。
我们能够利用它进行或大或小规模的编程,既能够完成基木的算法设计和算法实验,也能够开发比较S杂的应用程序。
MATLAB能够给用户提供一个工作环境,这个环境具有管理工作中数据的输山或输入方法,也具有开发、调试、管理M文件的工具。
其巾,图形句相系统是MATLAB图形系统的基础,它包括多种功能的高层MATLAB 命令,比如完成2D和3D数据图示、处理图像、生成动画、显示图形等,同时也包括一些低层命令,也包括一些开发程序的工具。
MATLAB数学函数库包括各种数学算法,比如说初等函数的算法和矩阵运算、矩阵分析这样的高等数学算法。
MATLAB应用程序接口(API) 为用户提供了一个较大的数据库,所以C程序或FORTRAN程序也能在MATLAB环境中使用,也能在MATLAB中进行动态链接,读写MAT文件。
MATLAB结合双线性变换法设计一个数字切比雪夫带阻IIR滤波器

课程设计题目Matlab课程设计——利用MATLAB 结合双线性变换法设计一个数字切比雪夫带阻IIR滤波器学院信息工程学院专业通信工程班级通信0803姓名王欢指导教师魏洪涛学号:01208103408142011 年1月月14日日武汉理工大学《Matlab课程设计》报告课程设计任务书学生姓名:王欢专业班级:通信0803指导教师:魏洪涛工作单位:信息工程学院题目: Matlab课程设计——利用MATLAB仿真软件系统结合双线性变换法设计一个数字切比雪夫带阻IIR滤波器。
初始条件:Matlab基础知识、计算机要求完成的主要任务:1.方案的理论设计2.方案的安装、调试3.设计报告的撰写时间安排:指导教师签名: 2010 年 1月日系主任(或责任教师)签名: 2010 年 1月日目录摘要 (3)ABSTRACT (4)1 数字滤波器 (5)1.1概述 (5)1.2特点 (6)1.3分类 (6)1.4设计原理 (6)2 双线性变换法 (8)2.1简介 (8)2.2对比 (11)2.2.1优点 (11)2.2.2缺点 (12)3 切比雪夫滤波器 (13)3.1概述 (13)3.2切比雪夫滤波器的种类 (13)3.2.1 I型切比雪夫滤波器 (13)3.2.2 II型切比雪夫滤波器 (13)3.3特点 (13)4 用MATLAB实现切比雪夫IIR带阻滤波器 (14)4.1程序流程图 (14)4.2MATLAB程序代码 (15)4.3仿真结果 (16)5 学习小结 (17)6 参考文献 (17)摘要随着信息时代和数字世界的到来,数字信号处理已成为当今一门极其重要的学科和技术领域。
目前数字信号处理在通信、语音、图像、自动控制、雷达、军事、航空航天、医疗和家用电器等众多领域得到了广泛的应用。
在数字信号处理中起着重要的作用并已获得广泛应用的是数字滤波器(DF,Digital Filter)。
数字滤波器是一种用来过滤时间离散信号的数字系统,通过对抽样数据进行数学处理来达到频域滤波的目的。
(完整word版)用matlab编程设计切比雪夫低通滤波器(word文档良心出品)

目录1摘要 (3)2设计原理 (4)2.1 切比雪夫滤波器介绍 (4)2.2滤波器的分类 (5)2.3 模拟滤波器的设计指标 (6)3切比雪夫I型滤波器 (7)3.1 切比雪夫滤波器的设计原理 (7)3.2切比雪夫滤波器的设计步骤 (10)3.3 用matlab编程设计切比雪夫低通滤波器 (11)4 总结 (18)5 参考文献 (18)摘要随着信息和数字时代的到来,数字信号处理已成为当今一门极其重要的学科和技术领域。
在现代通信系统中,由于信号中经常混有各种复杂成分,因此很多信号的处理都是基于滤波器而进行的。
所以,数字滤波器在数字信号处理中起着举足轻重的作用。
而数字滤波器的设计都要以模拟滤波器为基础的,这是因为模拟滤波器的理论和设计方方法都已发展的相当成熟,且有典型的模拟滤波器供我们选择。
,如巴特沃思滤波器、切比雪夫滤波器等。
本次课程设计将运用MATLAB设计一个基于切比雪夫低通滤波器,并出所设计滤波器的幅度及幅度衰减特性。
关键词:滤波切比雪夫模拟低通1切比雪夫滤波器介绍在巴特沃兹滤波器中,幅度响应在通带和阻带内都是单调的。
因此,若滤波器的技术要求是用最大通带和阻带的逼近误差来给出的话,那么,在靠近通带低频端和阻带截止频率以上的部分都会超出技术指标。
一种比较有效的途径是使逼近误差均匀地分布于通带或阻带内,或同时在通带和阻带内都均匀分布,这样往往可以降低所要求的滤波器阶次。
通过选择一种具有等波纹特性而不是单调特性的逼近方法可以实现这一点。
切比雪夫型滤波器就具有这种性质:其频率响应的幅度既可以在通带中是等波纹的,而在阻带中是单调的(称为I 型切比雪夫滤波器),也可以在通带中是单调的,而在阻带中是等波纹的(称为II 型切比雪夫滤波器),其中切比雪夫II 型滤波器又称为逆切比雪夫滤波器。
I 型切比雪夫滤波器的幅度平方函数是2|)(|Ωj H C =)/(1122c N C ΩΩ+ε (2.1) 其中ε是一个小于1的正数,它与通带波纹有关,ε越大,波纹也越大,式中为N 阶切比雪夫多项式,定义为)cos cos()(1x N x C N -= (2.2) 当N 大于或等于1时,从定义切比雪夫多项式可以直接得出由)(x C N 和)(1x C N -求)(1x C N +的递推公式。
实验6数字滤波器的matlab设计
实验6数字滤波器的matlab设计实验6:数字滤波器的matlab设计一、实验目的:1 掌握低通、高通,带通,带阻滤波器的概念2 掌握使用matlab进行进行滤波器的设计二、实验原理数字滤波器是通过一定运算关系,改变输入信号频谱的利用计算机技术实现的软或硬件。
选频数字滤波器设计过程一般可以归纳为以下三个步骤:(1)按照实际需要性能要求确定滤波器技术指标。
(2)用一个因果稳定的系统函数IIR、FIR去逼近这个要求(3)用一个有限精度的运算(软、硬件)去实现这个传递函数实验工具介绍fdatool的介绍fdatool(filter design & analysis tool)是matlab信号处理工具箱里专用的滤波器设计分析工具,matlab6.0以上的版本还专门增加了滤波器设计工具箱(filter design toolbox)。
fdatool可以设计几乎所有的基本的常规滤波器,包括fir和iir的各种设计方法。
它操作简单,方便灵活。
fdatool界面总共分两大部分,一部分是design filter,在界面的下半部,用来设置滤波器的设计参数,另一部分则是特性区,在界面的上半部分,用来显示滤波器的各种特性。
design filter部分主要分为:filter type(滤波器类型)选项,包括lowpass(低通)、highpass(高通)、bandpass (带通)、bandstop(带阻)和特殊的fir滤波器。
design method(设计方法)选项,包括iir滤波器的butterworth(巴特沃思)法、chebyshev type i(切比雪夫i型)法、chebyshev type ii(切比雪夫ii型)法、elliptic(椭圆滤波器)法和fir滤波器的equiripple法、least-squares(最小乘方)法、window (窗函数)法。
filter order(滤波器阶数)选项,定义滤波器的阶数,包括specify order(指定阶数)和minimum order(最小阶数)。
MATLAB实现数字巴特沃斯高通IIR滤波器xuejie(可编辑)
MATLAB实现数字巴特沃斯⾼通IIR滤波器xuejie(可编辑)MATLAB实现数字巴特沃斯⾼通IIR滤波器xuejie(可编辑)MATLAB实现数字巴特沃斯⾼通IIR滤波器xuejie⽬录摘要 1Abstract 21 设计项⽬要求与说明 3系统设计 3 22.1 设计思路 32.2 设计⽅法对⽐ 42.3典型模拟滤波器⽐较 5设计步骤 5 2.43 仿真程序的设计与调试 63.1 数字域指标变换成模拟域指标 6 3.2 数字域频率进⾏预畸变 6 3.3 模拟滤波器的设计 73.4 模拟滤波器变成数字滤波器 8 3.5 理论计算数字滤波器的仿真 114.程序调试中出现的问题 125. 总结与体会 13参考⽂献 14附录⼀总程序如下 15附录⼆设计数字滤波器函数总结 17摘要此报告重点介绍了⽤双线性不变法设计IIR数字滤波器的基本流程,⽐较了各种设计⽅法的优缺点,总结了模拟滤波器的性能特征。
最后以双线性不变法设计了⼀个⾼通巴特沃斯IIR数字滤波器,介绍了设计步骤,然后在Matlab环境下进⾏了仿真与调试,实现了设计⽬标。
关键词:Matlab 双线性不变法 IIR数字滤波器巴特沃斯⾼通AbstractThis report introduced with emphasis of the basic flow of designing the IIR digit filterby the bilinear political reform, compared with each kind of design method's good and bad points, summarized analog filter's performance characteristic. Finally design one by the bilinear political reform to pass Butterworth high IIR digit filter, introduced the design procedure, then has carried on the simulation and the debugging under the Matlab environment, has achieved the project objective.Key word: Matlab bilinearity political reformthe IIR digital filter pass high butterworthMatlab课程设计――设计⼀个数字巴特沃斯⾼通IIR滤波器1 设计项⽬要求与说明课题要求设计⼀个IIR数字滤波器,⾼通,采⽤双线性变换法,⽤巴特沃斯实现,⽤matlab软件对其进⾏仿真与调试。
实验五 MATLAB数字滤波器的设计
实验八 数字滤波器的设计一.实验目的和要求1.掌握双线性变换法及脉冲响应不变法设计IIR 数字滤波器的具体设计方法及其原理,熟悉用双线性变换法及脉冲响应不变法设计低通IIR 数字滤波器的计算机编程。
2.掌握用窗函数法设计FIR 滤波器的原理及方法,熟悉相应的MA TLAB 编程。
二.实验器材计算机、MA TLAB 软件三.实验内容和要求实验中有关变量的定义:实验内容:1.0.2c f kH z =,0.3f kH z τ=,1dB δ=,25t A dB =,1T m s =;(1)用脉冲响应不变法设计一巴特沃思数字低通滤波器,观察所设计数字滤波器的幅频特性曲线,记录带宽和衰减量,检查是否满足要求。
(2)用双线性变换法设计一巴特沃思数字低通滤波器,观察所设计数字滤波器的幅频特性曲线,记录带宽和衰减量,检查是否满足要求。
(3)比较这两种方法的优缺点。
wc=200*2*pi;wt=300*2*pi;[N,wn]=buttord(wc,wt,1,25,'s');[B,A]=butter(N,wn,'low','s');[num1,den1]=impinvar(B,A,1000);[h1,w]=freqz(num1,den1);wc=2*1000*tan(2*pi*200/(2*1000));wt=2*1000*tan(2*pi*300/(2*1000));[N,wn]=buttord(wc,wt,1,25,'s');[B,A]=butter(N,wn,'low','s');[num2,den2]=bilinear(B,A,1000);[h2,w]=freqz(num2,den2);f=w/pi*500;plot(f,20*log10(abs(h1)),'-.',f,20*log10(abs(h2)),'-');axis([0,500,-80,10]);grid;xlabel('频率/Hz');ylabel('幅度/dB');title('数字滤波器的设计');legend('用脉冲响应不变法','用双线性变换法');text(200,0,' \rightarrow fc=200Hz'); text(300,-25,' \rightarrow fc=300Hz');2. 15N =,带通滤波器的两个通带边界分别是10.3ωπ=20.5ωπ=。
(完整word版)用MATLAB设计滤波器
用MATLAB 设计滤波器1 IIR 滤波器的设计freqz功能:数字滤波器的频率响应。
格式:[h ,w ]=freqz (b ,a,n )[h ,f]=freqz(b ,a ,n ,Fs)[h ,w ]=freqz(b ,a,n ,’whole')[h ,f ]=freqz(b,a ,n ,'whole ’,Fs )h=freqz (b ,a ,w)h=freqz (b,a ,f ,Fs)freqz(b ,a)说明:freqz 用于计算由矢量"和b 构成的数字滤波器H (z)=A(z)B(z)= n-1--n -1 l)z a(n ....a(2)z l l)z b(n .... b(2)z b(l)++++++++ 的复频响应H (j ω).[h ,w]=freqz (b,a ,n )可得到数字滤波器的n 点的幅频响应,这n 个点均匀地分布在上半单位圆(即0~π),并将这n 点频率记录在w 中,相应的频率响应记录在h 中。
至于n值的选择没有太多的限制,只要n 〉0的整数,但最好能选取2的幂次方,这样就可采用FFT 算法进行快速计算。
如果缺省,则n=512。
[h ,f ]二freqz(b,a,n ,Fs)允许指定采样终止频率Fs (以Hz 为单位),也即在0~Fs/2频率范围内选取n 个频率点(记录在f 中),并计算相应的频率响应h 。
[h,w]=freqz(b,a,n,’whole’)表示在0~2π之间均匀选取n个点计算频率响应.[h,f]=freqz(b,a,n,'whole',Fs)则在O~Fs之间均匀选取n个点计算频率响应.h=freqz(b,a,w)计算在矢量w中指定的频率处的频率响应,但必须注意,指定的频率必须介于0和2π之间.h=freqz(b,a,f,Fs)计算在矢量f中指定的频率处的频率响应,但指定频率必须介于0和Fs之间。
butter功能:Butterworth(比特沃思)模拟和数字滤波器设计。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数字Chebyshev 滤波器的设计初始条件:1. Matlab6.5以上版本软件;2. 课程设计辅导资料:“Matlab 语言基础及使用入门”、“信号与系统”、“数字信号处理原理与实现”、“Matlab 及在电子信息课程中的应用”等;3. 先修课程:信号与系统、数字信号处理、Matlab 应用实践及信号处理类课程等。
要求完成的主要任务:(包括课程设计工作量及其技术要求,以及说明书撰写等具体要求) 1. 课程设计时间:1周;2. 课程设计内容:数字Chebyshev 滤波器的设计,具体包括:基本数字Chebyshev 滤波器的设计,数字高通、带通滤波器的设计,以及相关设计方法的应用等;3. 本课程设计统一技术要求:研读辅导资料对应章节,对选定的设计题目进行理论分析,针对具体设计部分的原理分析、建模、必要的推导和可行性分析,画出程序设计框图,编写程序代码(含注释),上机调试运行程序,记录实验结果(含计算结果和图表),并对实验结果进行分析和总结,按要求进行实验演示和答辩等;4. 课程设计说明书按学校“课程设计工作规范”中的“统一书写格式”撰写,具体包括:① 目录;② 与设计题目相关的理论分析、归纳和总结;③ 与设计内容相关的原理分析、建模、推导、可行性分析; ④ 程序设计框图、程序代码(含注释)、程序运行结果和图表、实验结果分析和总结; ⑤ 课程设计的心得体会(至少500字); ⑥ 参考文献(不少于5篇); ⑦ 其它必要内容等。
时间安排: 1周(第18周)附——具体设计内容:1. 设计一个切比雪夫Ⅱ型低通滤波器,指标如下:通带边界频率:πω2.0=P ,通带最大衰减:dB R P 1=阻带截止频率:πω4.0=S ,阻带最小衰减:dB R S 80=2. 设计一个高通Chebyshow 型数字滤波器,要求达到的指标是:wp=100Hz, ws=80Hz,Fs=300Hz,rp=1db,rs=45db.3. 设计一个带通切比雪夫数字滤波器,通带为100Hz ~200Hz ,过渡带宽均为50Hz ,通带波纹小于1dB ,阻带衰减30Hz ,采样频率1000Hz s F =。
1设计方法1.1 冲击响应不变法原理(Impulse invariance )冲击响应不变法的设计原理是使数字滤波器的单位抽样响应序列h (n ),模仿模拟滤波器的冲击响应g (t )。
设系统传递函数为G (s )的模拟滤波器的单位冲击响应g (t ),并将冲击响应g (t )进行等间隔采样,使得数字滤波器的单位抽样响应h (t )刚好等于g (t )的采样值,即: (1-1) 其中Ts 为采样周期。
因为G(s)是模拟滤波器的系统传递函数,故他是该系统冲击响应函数g (t )的拉普拉斯变换;又设H (z )是数字滤波器的系统传递函数,从而可的它是数字滤波器的单位抽样响应函数h (n )的Z 变换。
模拟信号的拉普拉斯变换与其采样序列Z 变换的关系为:(1-2)上式的物理意义为首先将模拟滤波器的系统函数G (s )作周期的延拓,再经过essT z =的映射变换,从而得到数字滤波器的系统函数H (z )。
假设s 平面上,s 在j Ω轴上取值,z 在Z 平面内的单位圆周e j ω上取值,可以得到数字滤波器的频率响应)(e j H ω=和模拟滤波器的频率响应)(ωj G 间的关系为(1-3) 其中S T Ω=ω假设模拟滤波器的系统函数G (s )只有单阶极点,且M<N ,系统传递函数可以用部分分式表示:(1-4)其拉普拉斯变换脉冲响应g (t )为:g (t )=st Nk Ke A∑=1,t ≥00 , t <0 (1-5)∑=-=Nk kK s s A s G 1)()(1)(∑∞-∞=Ω-Ω=k s j jk j G Ts H e ω)(1)(∑∞-∞==Ω-=k s S e z j s G T z H st ∑∞==-===0)()()()()(n s s stnT h nT t t g e z tg n h δ对g (t )进行等间隔采样,可以得到数字滤波器的单位取样响应函数h (n )为:当n ≥0时,h(n)=snT NK K e A ∑=1;当n <0时,h(n)=0 (1-6)然后对h(n)进行Z 变换,就可以得到数字滤波器的系统传递函数H (z ):(1-7)按照冲击响应不变法的原理,通过模拟滤波器的系统传递函数G (s ),可以直接球的数字滤波器的系统函数H (z )2切比雪夫(chebyshev )滤波器2.1切比雪夫滤波器简介切比雪夫滤波器(又译车比雪夫滤波器)是在通带或阻带上频率响应幅度等波纹波动的滤波器。
在通带波动的为“I 型切比雪夫滤波器”,在阻带波动的为“II 型切比雪夫滤波器”。
切比雪夫滤波器在过渡带比巴特沃斯滤波器的衰减快,但频率响应的幅频特性不如后者平坦。
切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小,但是在通频带内存在幅度波动。
这种滤波器来自切比雪夫多项式,因此得名,用以纪念俄罗斯数学家巴夫尼提·列波维其·切比雪夫2.2 切比雪夫滤波器原理巴特沃兹滤波器在通带内幅度特性是单调下降的,如果阶次一定,则在靠近截止 处,幅度下降很多,或者说,为了使通带内的衰减足够小,需要的阶次N 很高,为了克服这一缺点,采用切比雪夫多项式来逼近所希望的。
切比雪夫滤波器的在通带范围内是等幅起伏的,所以在同样的通常内衰减要求下,其阶数较巴特沃兹滤波器要小。
切比雪夫滤波器的振幅平方函数为∑∑∑∑=--==-∞-∞=-===Nk T s k n nT s N n N k k nn z e A z e A z n h z H k k 11011)()((2-1)式中—有效通带截止频率Ωc—与通带波纹有关的参量,大,波纹大 0<<1(x)—N阶切比雪夫多项式VN(2-2)(x)|≤1|x|≤1时,|VN|x|>1时, |x|↗, V(x)↗N切比雪夫滤波器的振幅平方特性如图所示,通带内,的变化范围为1(max) →(min)时,|x|>1,随↗,→0 (迅速趋于零)当=0时,(2-3)N为偶数,cos2()=1,得到min,,(2-4)N为奇数,cos2(,得到max,(2-5)切比雪夫滤波器的振幅平方特性如图1所示。
图1 切比雪夫滤波器的振幅平方特性2.3 Chebyshev有关参数的确定2.3.1 通带截止频率预先给定2.3.2 ε的确定与通带波纹有关的参数,通带波纹表示成(2-6)所以,,给定通带波纹值分贝数后,可求得。
2.3.3 阶数N由阻带的边界条件确定。
、A2为事先给定的边界条件,即在阻带中的频率点处,要求滤波器频响衰减到1/A2以上。
(2-7)(2-8)(2-9)(2-10)滤波器阶数N对滤波特性有极大的影响,N越大,逼近特性越好,但是相应的结构也越复杂。
一般情况下N等于通带内最大和最小个数的总和。
N的数值可根据阻带衰减来确定。
3切比雪肤低通滤波器的设计3.1 matlab函数说明1. cheb2ord.m 求切比雪夫Ⅱ型滤波器的阶次。
2.Cheb2ap.m 用来设计原型切比雪夫Ⅱ型模拟滤波器。
3.Cheby2.m 直接设计切比雪夫Ⅱ型滤波器。
此函数设计N阶切比雪夫Ⅱ型滤波器,通带波动为RpdB。
在长度为N+1的矢量b和a中返回滤波器系数。
以上3个文件的调用格式和对应的巴特沃兹滤波器的文件类似。
4.impinvar.m 用冲激响应不变法实现ω到Ω及s到z的转换。
5. zp2tf.m 将零极点模型转化成传递函数的模型。
6. zp2ss.m 表达式从零极点增益形式转换成状态方程形式。
7. lp2hp.m 实现低通到高通滤波器类型的转换。
8. Bilinear.m 采用双线性变换法,从模拟高通到数字高通。
3.2 Matlab程序及运行3.2.1 matlab程序及仿真图一、设计一个切比雪夫Ⅱ型低通滤波器wp=0.2*pi; %通带边界频率;ws=0.4*pi; %阻带截止频率;rp=1; %通带最大衰减;rs=80; %阻带最小衰减;Fs=1000 %假设抽样脉冲1000hz [N,Wn]=cheb2ord(wp,ws,rp,rs,'s'); %Chebyshev II型滤波器参数计算(模拟域);[Z,P,K]=cheby2(N,rs,Wn,'s'); %构造Chebyshev II型滤波器(零极点模型);[H,W]=zp2tf(Z,P,K); %将零极点模型转化成传递函数的模型;figure(1);freqs(H,W); %在Figure1上显示滤波器的幅频响应及相频响应;[P,Q]=freqs(H,W); %返回滤波器的冲击响应的复数形式;figure(2);plot(Q*Fs/(2*pi),abs(P));grid; %在Figure2上显示幅频特性曲线;xlabel('频率/Hz');ylabel('幅值');二、设计一个高通Chebyshow型数字滤波器wp=100;ws=80;Fs=300;rp=1;rs=45; %数字滤波器的各项指标;WP=100*2*pi; %把数字滤波器的频率特征转换成模拟滤波器的频率特征;WS=300*2*pi;[N,Wn]=cheb2ord(WP,WS,rp,rs,'s'); %Chebyshev II型滤波器参数计算(模拟域);[Z,P,K]=cheb2ap(N,rs); %创建Chebyshev滤波器原型;[A,B,C,D]=zp2ss(Z,P,K); %表达式从零极点增益形式转换成状态方程形式;[AA,BB,CC,DD]=lp2hp(A,B,C,D,Wn); %实现低通到高通滤波器类型的转换;[a,b,c,d]=bilinear(AA,BB,CC,DD,Fs); %采用双线性变换法,从模拟高通到数字高通;[P,Q]=ss2tf(a,b,c,d); %表达式从状态方程形形式转换成传输函数形式;figure(1);freqz(P,Q); %绘出频率响应;[H,W]=freqz(P,Q);figure(2);plot(W*Fs/(2*pi),abs(H));grid;xlabel('频率/Hz');ylabel('幅值');三、设计一个带通切比雪夫数字滤波器W1=100;W2=200;rp=1;rs=30;Fs=1000; %数字滤波器的各项指标;WP=[100,200];WS=[50,250];[N,Wn]=cheb1ord(WP/(Fs/2),WS/(Fs/2),rp,rs);%Chebyshev I型滤波器参数计算(数字域);[P,Q]=cheby1(N,rp,Wn,'bandpass');%创建Chebyshev带通滤波器;figure(1);freqz(P,Q); %显示产生滤波器的幅频及相频曲线;[H,W]=freqz(P,Q);figure(2);plot(W*Fs/(2*pi),abs(H));grid;xlabel('频率/Hz');ylabel('幅度');3.2.2 编程原理说明MATLAB提供了一个函数[z,p,k]=cheb2ap(N,Rp),来设计一个阶数为N,通带波动为Rp的归一化切比雪夫Ⅱ型原型滤波器,它在数组z中返回零点,数组p中返回极点,Ω的归一化的切比雪夫Ⅱ型滤波器,这可由归一化滤波并返回增益k。
