第6章 信号产生电路课堂练习
现代电子线路基础(新版教材)_第六章习题答案

第六章习题答案6.1在题图6.1所示调谐放大器中,工作频率 f o =10.7MHz,L I -3=4^ H,Q =100, N -3=20匝,N+5匝,N”5匝,晶体管3DG39在 f o =10.7MHz 时测得 g ie =2860^ S,C e =18pF, g oe =200^ S, C oe =7pF,| y fe |= 45mS, y 「e =O,试求放大器的电压增益 A 。
和通频带BW总电容 C 1/((2 f 0)2* L) 55.4pFLC 振荡回路电容 C Cp 2c °e P ;Ge 53.8pF注:由上述计算可以看出,f 。
'和f 。
相差不大,即部分接入后对谐振频率影响较小,但概念要清楚。
另外,这里给出了 y fe (即认为是g m )不要通过I EQ 来计算g m6.2题图6.2是某中放单级电路图。
已知工作频率f o =30MHz 回路电感L =1.5卩H, Q =100, N /N =4, C ~C 均为耦合电容 和旁路电容。
晶体管在工作条件下的y 参数为y ie(2.8 j3.5)mS;y 「e 0y fe (36 j27)mS y °e (0.2 j2)mS试解答下列问题: (1) 画出放大器y 参数等效电路; (2) 求回路谐振电导g 2; (3) 求回路总电容C 2;(4) 求放大器电压增益 A 。
和通频带BV y(5)当电路工作温度或电源电压变化时,A vo 和BW 是否变化?解:M~3N4~ 5NT ;5200.25 LC 振荡回路固有谐振频率f 0固有损耗电导:901— 10.85(MHz)2 . LC1 1Q 0 0 L 2 Q 0 f ° L36.7 10 6(S)222 6266G p g oe P 2 g ie g o0.25 200 100.252860 1036.7 100.228(mS)Q L1 16.32G 0LB W 邑 107656(KHz),Q L 16.3A V 00.25 0.25 45 10 0.228 1012RN2~35 20 0.25,F 2交流等效电路I C折合后的等效电路R2 2P 22C ie 18.78 10.6 o.252 18.58 7.02( pF )11rw2J1.5 106 7.02 m2491(MHz)固有损耗电导:RRdZJ 1O.25 V 362 10 328.4G0.396 10解:(1) y 参数等效电路如上图:由f o2LC 得 C1 2 2 4 Lfo42;0 621218.78( pF )P 2也丄0.25N 14 由y 参数得C ie33.5 10 3 6230 1018.58( pF),C oe3盘帝 10.6(pF)RS g oQ o o L 2 Q o f o L2 3.14 100 49.1 10*^2「6 106(S)R goe2 3P 2 gieg o 0.2 10230.252.8 1021.4 10 0.396( mS)Q L1366G 0L 0.396 102 30 101.5 108.9Q L竺 3.37( MHz )8.9AV 0C NNC 6 输入IIC 1D8上R JIA输入LN C NC 2 二 R 2V DD------- •GSL 1A C 3”2输出某场效应管调谐放大器电路如题图 6.3所示,为提高放大器稳定性,消除管子极间电容C D G 引起的部反馈,电路中分析其它各元件的作用; 画出放大器的交流等效电路; 导出放大器电压增益 A/o 表达式解:(1) L N 、C N 与C dg 组成并联谐振回路,使得漏栅之间的反馈阻抗为 ,故消除了漏栅之间的反馈,即消除了 C dg 引起得部反馈,实现了单向化。
2022《电路与信号》课程综合练习题及答案

题 81 图 82. *互感电路如题 82 图所示,求 a,b 端的等效阻抗 Zab。
题 82 图
83. *求题 83 图所示含理想变压器电路中的电压U 。
题 83 图 84. 写出题 84 图所示信号的表达式。
题 58 图
8
59. 已知 f1(t) etU (t 1), f2 (t) U (t 1) 求 f (t) f1(t) f2 (t) 60. 计算 (t 2 2) (t 3) 61. 计算 tetU (t) U (t 1) (t 1) 62. 计算U (t) eatU (t) 63. 计算U (t 1) (t 1)U(t) 64. 已知 f(t)→F(ω),求函数 (t 2) f (2t). 的频谱密度函数。 65. 已知 f(t)→F(ω),求函数(1-t) f (t-1)的频谱密度函数。 66. 求函数1 eat 的拉氏变换 F(s)
113.uC (0+)= 4.5V, uC (∞)=3V,时间常数 τ=0.5s。iC (t)=-1.5e-2tA
114.离散性 谐波性 收敛性 115. 5e j (t )
2 116. 8 (t 3)
117. 4 (t 1)
118.-1 119.2 120.3 121. (t0 )
2
122. t U (t)
103.不能,叠加定理与电流、电压的平方成正比,即是非线性关系 。
104.0.8
105.
106.uS= 1V
,R= 1
107.题 7 图电路的等效电阻 Rab =R+r
108.Rab = R 1 gR
109.Q,电压谐振
通信电子线路课后答案 第六章
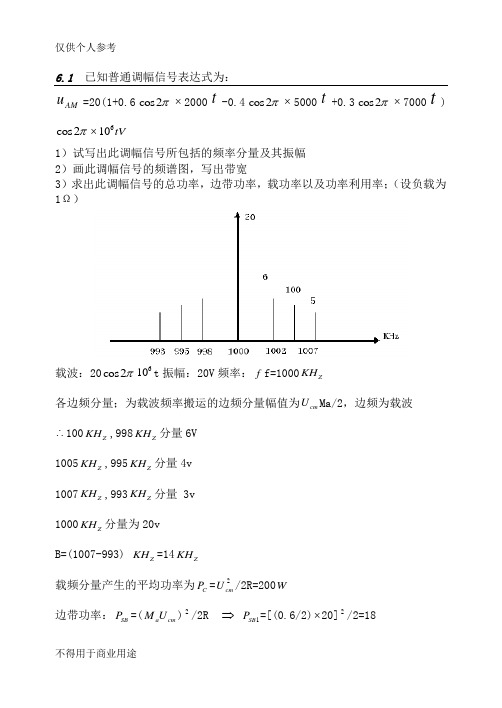
6.1 已知普通调幅信号表达式为:AMu =20(1+0.6cos2π⨯2000t-0.4cos2π⨯5000t+0.3cos2π⨯7000t )cos2π⨯610tV1)试写出此调幅信号所包括的频率分量及其振幅 2)画此调幅信号的频谱图,写出带宽3)求出此调幅信号的总功率,边带功率,载功率以及功率利用率;(设负载为1Ω)载波:20cos2π610t 振幅:20V 频率:f f=1000Z KH各边频分量;为载波频率搬运的边频分量幅值为cm U Ma/2,边频为载波∴100Z KH ,998Z KH 分量6V1005Z KH ,995Z KH 分量4v 1007Z KH ,993Z KH 分量 3v 1000Z KH 分量为20v B=(1007-993) Z KH =14Z KH载频分量产生的平均功率为C P =2cm U /2R=200W边带功率:SB P =(a cm M U )2/2R ⇒ 1SB P =[(0.6/2)⨯20]2/2=182SB P =[(0.4/2)⨯20]2=8 3SB P =[(0.3/2)⨯20]2=4.5∴ SB P =1SB P +2SB P +3SB P =30.5W两边频之和为 2⨯30.5=61W∴ av P =C P +2SB P =200+61=261W功率利用率 η=2SB P /av P =(61/261)⨯100%=23.4%6.2 已知单频普通调幅信号的最大振幅为12V ,最小振幅为4V ,试求其中载波振幅和边频振幅各是多少?调幅指数a M 又是多少?a M =(max U -min c U )/(max U +min c U )=1/2又 a M =(max U -cm U )/cm U ∴ 1/2=(12-cm U )/cm Ucm U =8V 边频振幅=cm U a M /2=1/2⨯8⨯1/2=2V6.3 左图,载波输出功率为50W ,平均调幅指数为0.4,集电极平均效率为50%,求直流电源提供的平均功率D P 、调制信号产生的交流功率P Ω和总输入平均功率av P .η=50/D P ∴ D P =50/50%=100W P Ω=2a M D P /2=1/2⨯0.16⨯100=8W电源总功率:D P +P Ω=108W ∴ av P =c j (D P +P Ω)=54Wa M CCO U 是调制信号平均振幅。
第6章习题解答

。
2〕又D触发器的特性方程 ,及其初始状态为0
3〕由此,在触发器各输入端CP和D的波形,可得 的波形
6.13维持阻塞D触发器输入端CP、A、B的波形如图P6.13所示,画出输出端Q的波形(设触发器初态为0)。
用D触发器实现T触发器:由D触发器特性方程 和JK触发器特性方程 及T触发器特性方程 可知T触发器可由J=T,K=T的JK触发器,可由JK触发器来实现,其电路见下列图
6.21用T触发器构成D和JK触发器。
解:由T触发器构成D触发器:由T触发器特性方程 和D触发器特性方程 那么可知令T触发器输入端 那么可构成D触发器,电路图如下列图所示
解:1〕又D触发器的特性方程 ,及其初始状态为0。
2〕由此,由A、B的输入波形定出D的输入信号 ,根据的波形画出 的波形如下:
6.14图P6.14所示各边沿D触发的初始状态都为0,试对应输入CP波形画出Q端的输出波形。
解:D触发器的特性方程 ,及其初始状态为0。
的波形如下:
电路如图P所示,分析电路逻辑功能,画出状态转换图。
2〕又JK触发器的特性方程为 及设触发器的初始状态为 ,当异步信号 为0时,可将触发器置为0,且它们优于时钟信号。
3〕由此,根据的波形画出 的波形如下:
6.10JK触发器组成的电路如图P0所示,试画出 、 和Y1、Y2的波形。设触发器的初始状态为Q=0。
解:1〕由传输延时型边沿JK触发器的触发时刻是CP的下降沿,输入J、K时CP下降沿前瞬的逻辑值,即触发器状态的更新发生在CP脉冲的下降沿。
并将其代入T触发器的逻辑功能表达式 整理可得该电路状态方程为 ;由该电路的状态方程可知该电路为由T触发器构成的JK触发器,其状态图如下列图所示
信号与系统第三版 第六章习题答案

2 t 2
cos
2 2
t ]u (t )
6.13 一个因果LTI系统的频率响应为:
5 jw 7 H ( jw) ( jw 4)[( jw) 2 jw 1]
(a) 求该系统的冲激响应
(b) 试确定由一阶系统和二阶系统构成的串联型结构 (c)试确定由一阶系统和二阶系统构成的串联型结构 解:(a) 5 jw 7 1 jw 2
I 2 (w) 2 jw H ( jw) E (w) 8 jw 3
(b) 对H(jw)作反傅立叶变换可得h(t)
2 jw 1 H ( jw) 8 jw 3 4
h(t ) F 1{H ( jw)}
3 32 3 jw 8 3t 1 3 8 (t ) e u (t ) 4 32
(b) 对H(jw)作反傅立叶变换可得h(t)
3 3 3( jw 3) 2 H ( jw) 2 ( jw 2)( jw 4) ( jw 2) jw 4
3 2t h(t ) F {H ( jw)} (e e 4t )u (t ) 2 (c) 3( jw 3) 3 jw 9 Y ( w) H ( jw) 2 ( jw 2)( jw 4) ( jw) 6 jw 8 X ( w)
1 X ( w) ( jw 2) 2
Y (w) H ( jw) X (w)
2 Y ( w) 3 ( jw 2) ( jw 4)
1 1 4 2 3 ( jw 2) ( jw 2) ( jw 2) ( jw 4) 1 4 1 2
1 2t 1 2t 1 2 2t 1 4t y (t ) F {Y ( w)} ( e te t e e )u (t ) 4 2 2 4 2 2 ( jw ) 2 (c) H ( jw) ( jw) 2 2 jw 1
电子电路基础第六章习题答案

第六章习题6.1 求习题图6.1所示的电路的传递函数()/o i H V V ω=gg。
习题图6.1解:1//()i o oR V V jwCjwLV -=g gg22()oi V j L RLCH R j L RLCV ωωωωω-==+-gg 6.2 对于习题图6.2所示的电路,求传递函数()o iI H I ω=gg。
习题图6.2解:2()11o iI R j CRH j CR CL I jwL R jwCωωωω===-+++gg6.3 串联RLC 网络有R=5Ω,L=10mH ,C=1F μ,求该电路的谐振角频率、特征阻抗和品质因数。
当外加电压有效值为24V 时,求谐振电流、电感和电容上的电压值。
解:电路的谐振角频率4010/rad s LCω== 特征阻抗100LCρ==Ω 品质因数020LQ Rω==谐振电流0 4.8mU I A R== 电感和电容上的电压值L 480V C m U U U Q ===6.4 设计一个串联RLC 电路,使其谐振频率050/rad s ω=,品质因数为80,且谐振时的阻抗为10Ω,并求其带宽。
解:00.625rad /B s Qω==6.5 对于习题图6.5所示的电路,求()v t 和()i t 为同相时的频率ω。
习题图6.5解:12()1Z (//)()v t jwL R L i t jwC==++ 121,1,1,1L H L H C F R ====Ω将代入2221Z ()11w w j w w w w-=+-+++谐振时虚部为零,2101w w w w -+=+ 0.7861w =得出,6.6 并联RLC 网络有R=50Ω,L 4mH =,C=160F μ,求并联电路谐振频率和品质因数。
若外接电流源有效值为2A ,求谐振时电阻、电感及电容上的电流值。
解:电路的谐振角频率30 1.2510rad /s LCω==⨯ 品质因数010LQ CR RCω=== 谐振时电阻、电感及电容上的电流值2A,20A R L C R I I I I Q ====g6.7 并联谐振电路,其品质因数为120,谐振频率是6610/rad s ⨯,计算其带宽。
通信原理(陈启兴版) 第6章作业和思考题参考答案
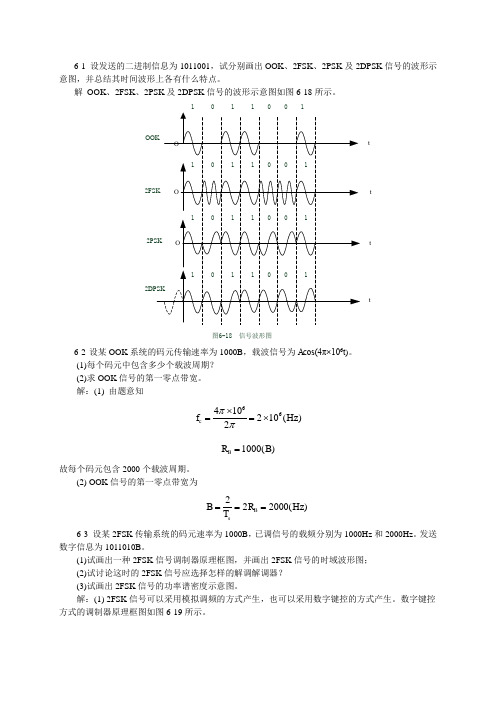
6-1 设发送的二进制信息为1011001,试分别画出OOK 、2FSK 、2PSK 及2DPSK 信号的波形示意图,并总结其时间波形上各有什么特点。
解 OOK 、2FSK 、2PSK 及2DPSK 信号的波形示意图如图6-18所示。
tttt图6-18 信号波形图6-2 设某OOK 系统的码元传输速率为1000B ,载波信号为A cos(4π×106t )。
(1)每个码元中包含多少个载波周期? (2)求OOK 信号的第一零点带宽。
解:(1) 由题意知66410210()2c f Hz ππ⨯==⨯1000()B R B =故每个码元包含2000个载波周期。
(2) OOK 信号的第一零点带宽为222000()B sB R Hz T === 6-3 设某2FSK 传输系统的码元速率为1000B ,已调信号的载频分别为1000Hz 和2000Hz 。
发送数字信息为1011010B 。
(1)试画出一种2FSK 信号调制器原理框图,并画出2FSK 信号的时域波形图; (2)试讨论这时的2FSK 信号应选择怎样的解调解调器? (3)试画出2FSK 信号的功率谱密度示意图。
解:(1) 2FSK 信号可以采用模拟调频的方式产生,也可以采用数字键控的方式产生。
数字键控方式的调制器原理框图如图6-19所示。
图6-19键控法产生2FSK 信号的原理图由题意知,码元传输速率R B =1000B ,若设“1”码对应的载波频率为f 1=1000Hz ,“0”码对应的载波频率为f 1=2000Hz ,则在2FSK 信号的时间波形中,每个“1”码元时间内共有1个周期的载波,每个“0”码元时间内有2个周期的载波。
2FSK 信号的时间波形如图6-20所示。
【注:实际中键控法的波形一般不连续。
】t2FSK图6-20 2FSK 信号的时间波形(2) 由于2FSK 信号的频谱有较大的重叠,若采用非相干解调是上下支路有较大串扰,使解调性能下降。
2012年模拟电子技术第六章-信号产生电路练习题(含答案)

第六章信号产生电路【教学要求】本章主要介绍了反馈振荡器的组成原理;正弦信号产生电路的组成原理和实际电路的分析;方波、三角波、锯齿波信号发生器的组成原理与电路分析。
教学内容、要求和重点如表6.1。
表6.1 教学内容、要求和重点【例题分析与解答】【例题6-1】试用相位平衡条件判断下图6-1所示振荡电路的交流通路中,哪些能振荡?为什么?(a)(b)(c)(d)图6-1解:对于图(a)电路,由同名端可知,变压器的相移量为0°;而放大器为共射组态,是倒相的,即相移量为180°,所以整个反馈回路的相移量为180°,不满足相位平衡条件,不能振荡。
对于图(b)电路,尽管L和C3构成的串联谐振支路可以呈容性(当振荡频率小于由L和C3构成的串联谐振频率时)或感性(当振荡频率大于由L和C3构成的串联谐振频率时),但由电路结构可知,它们与C1和C2都不能满足三点式的组成原则,所以不能振荡。
对于图(c)电路,由于场效应管放大器的极性与晶体三极管放大器完全对应一致,所以根据三点式振荡器的组成原则,只要C2和L2构成的并联谐振回路呈感性(即当振荡频率小于由C2和L2构成的并联谐振频率时),就能组成电感三点式振荡器。
对于图(d)电路,表面上看电路构成电容三点式振荡器少了一个电容,但实际上,当振荡频率较高时,晶体管的结电容就会体现,从而满足三点式的组成原则,所以能够振荡。
【例题6-2】晶体振荡电路如图6-2所示,试判断该晶体振荡器的类型。
图6-2解:当晶体串联谐振时,晶体呈短路元件,电路满足三点式组成法则,为电容三点式振荡器;而当振荡频率偏离晶体的串联谐振频率时,晶体阻抗迅速增大,并且呈容性或感性,电路不能振荡。
因此,此振荡器的振荡频率由晶体的串联谐振频率决定,它是串联型晶体振荡器。
【例题6-3】一实际振荡电路如图6-3所示,求它的振荡频率。
图6-3解:画出此振荡电路的交流通路,如图。
电路满足三点式组成法则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课堂练习
• 1、正弦波振荡电路主要 由 、 、 组成,为了保证 振荡幅值稳定且波形较好,常常还需要 环节。 • 2、正弦波振荡电路利用正反馈产生振荡的 条件是 ,其中相位平衡条件是 , 幅值平衡条件是 ,为使振荡电路起 振,幅值条件是 。
• 3、产生低频正弦波一般可用 振荡电路, 产生高频正弦波可用 振荡电路,要求频 率稳定性很高,则可用 振荡电路。
• 6、电路如下图所示,为了能产生正弦波振荡,电路应 如何连接?
• 7、为了使下图中各电Байду номын сангаас能产生正弦波振荡,请在图中 将各点正确连接起来。
• 8、电路如图所示。
(1)分别说明A1和A2各构成哪种基本电路; (2)求出uO1与uO的关系曲线uO1=f(uO); (3)求出uO与uO1的运算关系式uO=f(uO1); (4)定性画出uO1与uO的波形;
• 1、标出下图所示各电路中变压器的同铭端,使之满 足正弦波振荡的相位条件。
• 2、分别判断下图所示各电路是否满足正弦波振荡的 相位条件。
• 3、改正图2(b)(c)所示两电路中的错 误,使之有可能产生正弦波振荡。
• 4、根据振荡的相位条件判别如下图所示各电路能否 振荡?
• 5、判别如下图所示电路能否产生正弦波振荡并说明原因。
(5)说明若要提高振荡频率,可以改变哪些电路参 数,如何改变。
图6
