高联班几何测试
高联班几何测试题23

从而,∠OBF=∠ABE-∠OBA=∠A-(90°-∠C)= 90°-∠B=∠BCH.
同理∠DCF=∠CBH.
∠OBH=∠OBC-∠HBC=90°-∠A-(90°-∠C)= ∠C-∠A=∠BCF.
同理∠OCH=∠CBF.
故式○1 成立,证毕.
23-5 锐角△ABC 内接于☉O,点 E、D 分别在边 BC 的延长线上及其反向延 长线上,使得 CE=BD.作 DF⊥BC,EK⊥BC,点 F、K 与 A 直线 BC 的同侧,且∠BAF= ∠CAK.AM 为☉O 的直径.求证: ∠DFM=∠AMK.
则点 M、T 在以 BD 为直径的圆☉O1 上,点 N、L 在以 CE 为直径的圆☉O2 上.
因 B、C、N、M 四点共圆. 则 H1M·H1B=H1N·H1C, 即 H1 对圆☉O1、☉O2 的幂相等,H1 在☉O1、 ☉O2 的根轴上. 又 D、E、L、T 四点共圆. 则 H2T·H2D=H2L·H2E, 即 H2 对圆☉O1、☉O2 的幂相等,H2 在☉O1、 ☉O2 的根轴上. 因 BO1=CO2,∠O1BK=O2CK,BK=CK, 则△BO1K≌△CO2K,KO1=KO2.
证明 如图,设直线 MB 交 AF、FD 分别于 X、N, MC 与 AK 交于点 Y,点 X、A、 O、M、Y 在直线 BC 上的投影分别为 U、H、P、G、V.
因 XU∥FD∥AH,则 㐶 = ,
因 XU∥MG, Rt△BMG∽Rt△AMC,
则= = .
t
t
所以, 㐶 = t ,
同理,Biblioteka =㤲 t.
高联班几何测试题(23)
时间:150 分钟
命题人:万喜人
23-1 在△ABC 中,点 D、E 分别在 AB、AC 上,且 BD=CE,BE 与 CD 交于点 F.
高联班几何测试题

高联班几何测试题(11)时间:180分钟 命题人:万喜人11-1 在△ABC中,点D、E均在边BC上,BD=CE,点F、G,分别在AB、AC上,直线FE与GD交于点K.FD与GE交于点V,直线AK、AV分别与BC交于点L、T.求证:BL=CT.11-2 已知△ABC的外接圆⨀O,∠BAC的平分线交⨀O于点D(D≠A),过B、C两点的圆与边CA、AB的第二个交点分别为E、F,BE与CF交于点P,过A、E、F三点的圆与⨀O交于点A、K,DK与BC交于点T.求证:PT//AD.11-3 △ABC的外接圆为⨀O,点D在⨀O上,点E、F分别在AB、AC上,⨀O中的弦MN使得AD//EF//MN//BC.直线AM与EF交于点P,直线DP与⨀O的第二个交点为K.求证:E、F、N、K四点共圆.11-4 圆Γ为△ABC 的外接圆,点D 为BAC 的中点,点E 、F 在直线AD 上,使得DE=DF ,点E 、B 在线段BC 的中垂线的同侧,ET ⊥AB 于点T ,点P 是点T 关于AB 的中点的对称点,FV ⊥AC 于点V ,点K 是点V 关于AC 的中点的对称点,EK 与FP 交于点N ,直线DN 与圆Γ的第二个交点为M.求证:P 、N 、K 、M 四点共圆.11-5 △ABC内接于⨀O,点P是BC的中点,点D、E分别在射线PB、PC上,使得PD=PE,⨀O的弦MN//BC,点M、B在线段BC的中垂线的同侧,点F、G分别在直线AM、AN上,且FD⊥BC,GE⊥BC,作FL⊥AC于点L,GT⊥AB于点T,DL与ET交于点K,求证:AK⊥BC.GF高联班几何测试题(12)时间:180分钟 命题人:万喜人12-1 在△ABC中,AB+AC=2BC,P为∠BAC的角平分线上一点,PD⊥BC于点D,PE⊥AC于点 E,PF⊥AB于点 F,直线 DP与 EF交于点 K.求证:EK∙FK= 3PK3.12-2 已知△ABC ,直线d 、t 分别平分∠BAC 及其外角,点D 在直线d 上,直线DB 与t 交于点E ,直线DC 与t 交于点F ,作MN//BC 交AB 、AC 分别于点M 、N.直线EM 与FN 相交于点K ,DK 与BC 相交于点P .求证:BP=PC.t12-3 锐角△ABC 中,H 为垂心,过点B 、C 的⨀P 交CA 、AB 分别于点D 、E ,BD 与CE 交于点F ,点P 关于BC 的对称点为K.求证:FP//HK.B12-4 △ABC 内接于⨀O ,点P 是BC 的中点,点D 、E 分别在射线PB 、PC 上,使得PD=PE.⨀O 的弦MN//BC ,点M 、B 在线段BC 的中垂线的同侧,点F 、G 分别在直线AM 、AN 上,且FD ⊥BC ,GE ⊥BC.作FT ⊥AB 于点T ,GL ⊥AC 于点L ,直线DT 、EL 交于点K.求证:AK ⊥BC.G12-5 点P 、Q 是△ABC 内部的等角共轭点,延长AP 交△ABC 的外接圆圆Γ于点D ,过点P 、D 的一个圆交BC 于点E 、F ,直线DE 、DF 与圆Γ的第二个交点分别为M 、N.求证:M 、Q 、N 三点共线.。
高联班几何测试题63

高联平面几何测试(63)
时间:120分钟命题人:万喜人
63-1已知△ABC,点D、E分别在AB、AC的延长线上,且BD=BC=CE,T 为△ABC的∠A内的旁心,直线AT交△ABC的外接圆φ于点F(F≠A),交△ADE的外接圆ε于点K(K≠A).求证:TF=TK.
63-2已知△ABC,垂心H,外心O,H关于O的对称点K,直线AK与BC交于D,DE⊥AC于点E,DF⊥AB于点F.求证:AD、BE、CF三线共点或互相平行.
63-3锐角△ABC中,AB≠AC,BE⊥AC于点E,CF⊥AB于点F,BE与CF交于点H.取点B关于AC的对称点T,点C关于AB的对称点V,M、N分别为BC、TV 的中点.MN与AH交于点K.求证:AK=KH.
63-4在△ABC中,P为BC的中点,点M、N分别在射线PB、PC上,PM=PN,点E、F满足∠BAE=∠CAF,EM⊥BC,FN⊥BC,作EU⊥AB于点U,FV⊥AC于点V,直线UM与VN交于点K.求证:AK⊥BC.
63-5在△ABC中,AB≠AC,点D、E、F分别在边BC、CA、AB上,AE=AF,AD、BE、CF三线共点于P,DT⊥EF于点T,TP与BC交于点N.△ABC的外接圆φ与△AEF 的外接圆ε交于点A、K,M为BC的中点.求证:直线AM与KN的交点在圆φ上.。
高联班几何测试6图片调整打印了
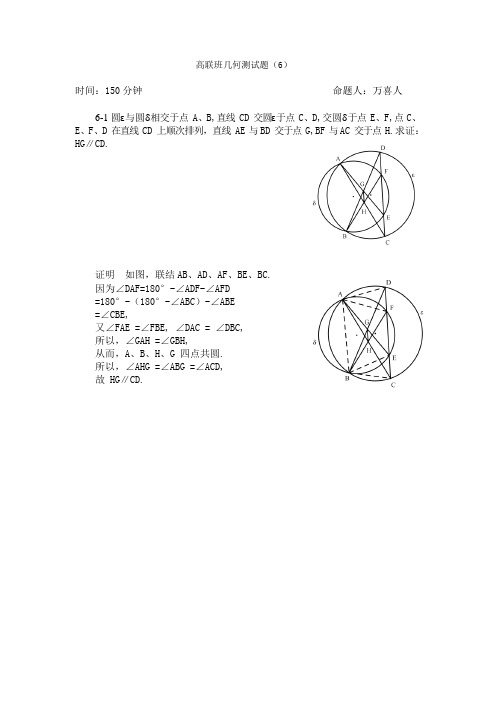
高联班几何测试题(6)时间:150 分钟命题人:万喜人6-1 圆ε与圆δ相交于点 A、B,直线 CD 交圆ε于点 C、D,交圆δ于点 E、F,点C、E、F、D 在直线 CD 上顺次排列,直线 AE 与BD 交于点 G,BF 与AC 交于点 H.求证:HG∥CD.证明如图,联结AB、AD、AF、BE、BC.因为∠DAF=180°-∠ADF-∠AFD=180°-(180°-∠ABC)-∠ABE=∠CBE,又∠FAE =∠FBE, ∠DAC = ∠DBC,所以,∠GAH =∠GBH,从而,A、B、H、G 四点共圆.所以,∠AHG =∠ABG =∠ACD,故HG∥CD.6-2. 已知△ABC,点D、E 分别在 AB、AC 上,∠AED=∠ABC,圆(BD)(表示以 BD 为直径的圆)与圆(ABC)(表示过 A、B、C 三点的圆)交于点 B、F, 圆(CE)与圆(ABC)交于点 C、T,圆(ADE)与圆(BD)交于点 D、P, 圆(ADE)与圆(CE)交于点 E、K.求证:P、K、T、F 四点共圆.证明联结线段如图所示.因∠FPK=360°-∠FPD-∠DPK= 360°-∠FBD-(180°-∠DEK)=180°-(∠FBC-∠ABC)+∠AEK-∠AED=180°-(180°-∠FTC)+180°-∠CEK(因∠AED=∠ABC)=180°-(∠CTK-∠FTC)=180°-∠FTK,即∠FPK+∠FTK=180°,所以,P、K、T、F 四点共圆.D 㠳6-3. 在△ABC 中,∠BAC 为锐角,P 为△ABC 的外接圆☉O 上一点(不与 A 、B 、C 重合),直线 AB 与 CP 交于 E,AC 与 BP 交于 F,线段 BC 的中垂线交 BC 、B ˆC (不含点 A)、EF 分别交于点 M 、D 、N.求证:D 䘐 D 㠳 =cos ²BtC .证明 设☉O 过点 B 、C 的切线交于点 N /,联结 BD 、CD.对圆内接六边形 ABBPCC,由帕斯卡定理知:E 、N /、F 三点共线,即点 N /在直线 EF 上.又 N /B=N /C,点 N /在 BC 中垂线上,所以,点 N /与 N 重合,因∠NCD=∠DBC=∠DCM,则 D 䘐= C 䘐 = cos ²㠳C 䘐 = cos ²BtCD 㠳 C 㠳 注:若∠BAC 为钝角,则D 䘐 =− cos ²BtC.6-4. 四边形 ABCD 外切于圆 I,AC 与BD 交于点 E,P 为IE 的中点,过点 I 作FK⊥AC交AB、AD 分别于点 F、K,过点 P 作GH⊥AC交AB、AD 分别于点 G、H.求证:BG·DH=FG·KH.证明设AB、BC、CD、DA 与圆I 分别切于点M、N、L、T,IB、ID 分别与GH交于点U、V.设直线MT 与BD 交点X1(可能X1是无穷远点),NL 与BD 交点X2.由梅涅劳斯定理得BX1 ·DT ·t䘐 = 1 = BX2 ·DL ·C㠳,X1D Tt 䘐 B X2D LC 㠳 B因 DT=DL,TA=AM,LC=CN,MB=NB,则BX1 = BX2 .X1D X2D从而,X1 与 X2重合,统一记为 X.因 X 在点 A 关于圆 I 的极线 MT 上,由配极原理知点 A 在点X 的极线上.同理,点 C 在点X 的极线上.所以,直线 AC 是点X 关于圆 I 的极线.故IX⊥AC.又过 I 的直线FK⊥AC,所以,F、K、X 三点共线.因AB、AC、AD、AX 是调和线束,则B、E、D、X 是调和点列,从而 IB、IE、ID、IX 是调和线束,因为GH∥IX(都与 AC 垂直)所以,PU=PV.又 PI=PE,则四边形 IUEV 是平行四边形,从而,UE∥ID,EV∥BI.故B= Bt = BE = I‴ = KѸ ,F It DE D‴DѸ所以,BG·DH=FG·KH.sin α+þ sin α+y IT· cot α+þ IT· cot α+y cos α+þ sin α+þ sin α+y cos α+y sin α+þ · sin þ sin α+y sin y sin α+y sin þ sin α+þ sin yIT· sin α cos 2α+2y sin α+þ sin y 6-5. 在△ABC 中,AB=AC,点 D 、E 不在直线 BC 上,使得 BD=AB,CE=AC, ∠DBC 和∠ECB 两角的平分线交于点 I,过点 I 作 IF⊥AD 交直线 DB 于点 F,过点 I 作 IK⊥AE 交直线 EC 于点 F.直线 BK 与 CF 交于点 P.求证:IP⊥BC.证法 1 如图,点 D 、E 和 A 均在直线 BC 的同侧(若点 D 、E 均和 A 在直线 BC 的异侧,或点 D 、E 位于直线 BC 的两侧,证明类似. )可设∠ABC=∠ACB=2α,∠ABD=2β,∠ACE=2γ.因 BD=AB,IF⊥AD,则∠BFI=β,∠BIF=∠DBI -∠BFI=α,同理,∠CKI=γ,∠CIK=α. 由正弦定理得 IC = CK , IB = BF ,IC = ,sin y sin α sin þ sin α IB 所以,CK= sin α+þ · sin þ.BF sin α+y · sin y 作 IT⊥BC 于点 T,IT 交 BK 、CF 分别于点 P 1、P 2,作 FM⊥BC 于点 M,KN⊥BC 于点 N.只要证明 P 1 与 P 2 重合即可, 这只要证明TP 1=TP 2.因 TP 1∥KN, TP 2∥FM,所以,TP 1 =BT·K 㠳 B 㠳 ,TP 2 =CT·F 䘐 . C 䘐TP =TPBT·K 㠳 = CT·F 䘐 1 2 B 㠳 C 䘐B T·K 㠳= B 㠳 ○1 CT·F 䘐C 䘐 BT·K 㠳= · CT·F 䘐= · · ·= ○2 因 CN=CK cos 2α + 2y =IC· sin α· c os 2α + 2y sin y=,则 CT+CN=IT·cos α+y sin α+y+ IT· CK· sin 2α+2y BF· sin 2α+2þsin 2α+2y sin 2α+2þ sin α cos 2α+2ysin α+y sin ycos α+þsin α+þsin α+y sin þsin α+þ sin y=IT·cos α+y sin y+sin α cos 2α+2ysin α+y sin y=IT·sin α+2y −sin α+sin 3α+2y −sin α+2y2 sin α+y sin y=IT·cos 2α+y.sin y从而,BN=BT+CT+CN=IT·+=IT·sin α+þ+y −sin α+þ−y +sin 3α+þ+y −sin α−þ+y,2 sin α+þ sin y同理,CM=IT·sin α+þ+y −sin α−þ+y +sin 3α+þ+y −sin α+þ−y2 sin α+y sin þ所以,B㠳= ○3C䘐由式○2 、○3 知式○1 成立.证毕.证法2 如图,点D、E 和A 均在直线BC 的同侧(若点D、E 均和A 在直线BC 的异侧,或点 D、E 位于直线 BC 的两侧,证明类似)可设∠ABC=∠ACB=2α,∠ABD=2β,∠ACE=2γ.因BD=AB,IF⊥AD,则∠BFI=β,∠BIF=∠DBI-∠BFI=α,同理,∠CIK=α.设直线 BD 与CE 交于点 Q(Q 可能是无穷远点).点 S 在直线 IQ 上,且在∠BIC 内部.对四边形 IBQC,由∠BIF=∠CIK(都=α)知,IP、IQ 是∠BIC 的等角共轭线,即∠BIP=∠CIS=90°-(α + β)(注意 I 为△QBC的旁心或内心)又∠IBC=α + β,所以,∠BIP=∠IBC=90°.故IP⊥BC.cos 2α+ysin y。
高联班几何测试54-5 题

高联班几何测试题(54)
时间:120分钟命题人:万喜人
54-1在四边形ABCD中,△ABC、△ADC的垂心分别为H
1、H
2
,直线BH
1
与AD
交于点M,直线DH
2与CB于点N,MN与AC交于点P.求证:H
1
、P、H
2
三点共线.
54-2I为△ABC的内心,过B、C两点的圆交AB、AC分别于点D、E.F为AD的中点,J为△ADE的内心,直线FJ与DE交于点K,KP∥AB交直线AJ于点P.求证:I、P、C、E四点共圆.
54-3锐角△ABC内接于圆φ,点D、E、F、分别在边BC、CA、AB上,满足BF=DF,CE=DE,点M在圆φ上,满足AM⊥BC,直线MD交圆φ于点M、K,求证A、F、E、K四点共圆.
54-4延长☉O的直径AB至点P,过点P作一直线交☉O于点C、D(PC<PD).作PE⊥AB于点E,PF⊥AB于点F,CF、DE与☉O的第二个交点分别于点M、N.求证:M、N、P三点共线.
54-5△ABC内接于圆Γ,P为△ABC内一点,P在边BC、CA、AB上的射影
、BAC 分别于点M、N,AM交直线EP、FP分别于T、分别为D、E、F.直线DP交BC
K.☉(ANT)与AB交于点A、U.☉(ANK)与AC交于点A、V.求证:UV∥BC。
高联班几何测试20 (2)

高联班几何测试(20)
时间:150 分钟命题人:万喜人
20-1在锐角△ABC的外接圆φ中,弦DE∥BC,直线 BD 与CE 交于点 F,BE 与CD 交于点 K.求证:∠BAK=∠CAF.
20-2定☉O的定弦 AB,动点 C 在☉O上(不与点 A、B 重合),BD⊥AC于点D,E 为BD 的中点,直线 CE 交☉O于C、F.求证:点
F 为定点.
20-3已知△ABC 中,过点 B、C 的圆与 AB、AC 还分别交于点 D、E,过 A 作直线交D⌃t、B⌃㴘分别于点 F、K,任意直线 X Y∥AC,交 CK、CF、EK、EF、BC、D E 分别于点 X、Y、U、V、M、N.求证:MX = NV.
MY NU
20-4等腰△ABC中,AB=AC,过点 B、C 的一个圆φ还与 AB、AC 相交于点 D、E.点 F 在D⌃t上,作 DN∥CF,交直线 AF、AC 分别于点 M、N.作 BV∥EF,交直线AF、AC 分别于点 U、V.DN 与BV 相交于点 P.求证:
BU·DM=PV·PN.
20-5四边形 ABCD 内接于圆φ,且AD∥BC,AC与BD 交于点 P,E 为A⌃D(不含点B、C)的中点,F 在BA 的延长线上,直线 FE 与DC 交于点 K,直线 FC 与BK 交
于点 N.求证:直线 PN 与 FK 的交点在圆φ上.。
高联班几何测试题

KE A
F
C B
M
D
2
长沙万喜教育
5. 如图,凸四边形 ABCD 内接于圆,AC 与 BD 交于点 P,作 PE∥DA,PF∥CB, PE、PF 交不含点 C 的弧������������分别于点 E、F,直线 EF 交 DA、CB 分别于点 M、N.
求证:������������ = ������������
D
lA
F
lA
F
D
E
E
B
C
B
C
1
长沙万喜教育
3. 在△ABC 中,∠BAC= 600 ,D 是△ABC 外接圆弧 AB (不含点 C)的中点. 延长 CB 至 E,使 BE=AB. 求∠BED 的度数.
A
D
E
B
C
4. 从⊙O 外一点 P 作⊙O 的两条切线,A、B 为切点,再过 P 作⊙O 的一条 割线,交⊙O 于点 C、D(PC﹤PD). K 是 AC 上一点, KB 交 AC 于点 E,作 EF ∥CD,交 KD 于点 F. 直线 AF 与 CD 交于点 M. 求证:CM=MD.
������������ ������������
.
M
A
E D
F P
N
B
C
6. 已知△ABC,内切圆☉I 与 BC 切于点 T,D 为边 BC 上一点,△ABD 和△ACD 的内切圆☉I1 和圆☉I2 不同于 BC 的外公切线 PQ 与☉I1、☉I2 分别切于点 P、Q, 直线 BP 与 CQ 交于点 K. 求证:TK、PQ、AD 三线共点.
A
K
P
Q I
I1
I2
B
TD
C
高联班几何测试题1811

高联班几何测试题(18)时间:120分钟命题人:万喜人的中点,点D关于BC的对称点为K,延18-1点D为△ABC的外接圆的弧 th长AB至E,使BE=AC,延长AC至点F,使CF=AB.求证:E、F、K三点共线.证明当AB=AC时,易知结论成立.当AB≠AC时,不妨设AB<AC.如图,作平行四边形BACP.因BP=AC=BE,∠EBP=∠A,则∠BPE=90°- ∠A.同理,∠CPF=90°- ∠A.又∠BPC=∠A,所以,∠BPE+∠BPC+∠CPF=∠180°点P在直线EF上.且∠BPE=∠CPF,EF是∠BPC的外角平分线.作△BCP的外接圆交EF于点P、K/,联结BK/、CK/、BD、CD.则∠K/BC=∠CPF=90°- ∠A=∠BPE=∠K/CB.又∠DBC=∠DCB=90°- ∠A,所以,△K/BC≌△DBC.从而,点K/、D关于BC对称.故点K/与K重合.于是,E、F、K三点共线.注:类似命题在△ABC中,AB<AC,延长AB至E,使BE=AC,在AC上取点F,(不含A)的中点,点使CF=AB,点D为△ABC的外接圆的弧 hD关于BC的对称点为K.求证:E、F、K三点共线.18-2已知△ABC,AB≠AC,∠BAC的平分线交△ABC的外接圆于D(D不同于A),点D关于BC的对称点K.点E、F分别在AB、AC上,使得BE=CF,BF与CE交于点P.求证:PK∥AD.证明如图,可设DK与BC互相垂直平分于点T,联结AT并延长至点S,使TS=TA,联结KS、PS、SC、SB.延长SB、CE使之交于点V.因TD=TK,TA=TS,则SK∥AD.因为四边形ABSC是平行四边形,则 h ㌰= 〸 ㌰=h뵸 ㌰=ht t㌰SP平分∠CSB.又因AD平分∠BAC由平行四边形ABSC的性质得SP∥AD.所以,S、P、K三点共线,且PK∥AD.18-3已知△ABC,AB≠AC,AD⊥BC于点D,作DE∥AC交AB于点E,EF∥BC交AD于点F,DK⊥BF于点K,M、N分别为BC、AD的中点.求证:D、M、K、N四点共圆.证明如图AB>AC,联结KM、KN.因M、N分别为BC、AD的中点,则2DM=BD-CD,2FN=DF-AF.因DE∥AC,EF∥BC,则 体h体= 〸t〸=体뵸t뵸 体体뵸=h体t뵸= 体㔮h体体뵸㔮t뵸=体t뵸賀又因Rt△BDK≌Rt△DFK,则体㘹뵸㘹= 体体뵸=体t뵸賀.结合∠MDK=∠NFK得△DKM∽△FKN.∠DKM=∠FKN∠MKN=∠DKF=90°=∠NDC,故D、M、K、N四点共圆.18-4在△ABC中,O为外心,点D在边B C上,过点A作直线d⊥AD,作BE ⊥BC交d于点E,作CF⊥BC交d于点F,作EP⊥AB,FP⊥AC,EP与FP相交于点P.求证:点O为线段PD的中点.证明如图,设直线AD、d与△ABC的外接圆☉O的第二个交点分别为M、N.因d⊥AD,则MN为☉O的直径.设BE、CF与☉O的第二个交点分别为T、L,则四边形BCLT为矩形,BL为☉O的直径.=賀 .所以, t作NP/⊥EF交TL于点P/,联结TN、EP/.则E、T、P/、N四点共圆.故∠P/EN=∠P/TN=∠BAM.结合EA⊥AM知EP/⊥AB.同理FP/⊥AC,所以,点P/与P重合.联结BM、CN,作MK⊥BC于点K,KV∥BC交BE于点V.因∠PEF=∠BAM=∠MCB,同理∠PFE=∠MBC,所以,△PEF∽△MCB,PN、MK是对应边上的高,从而,t賀t㘹=〸뵸 h.因MD⊥EF由MK⊥BC,BC∥FV知MK⊥FV,则∠EFV=∠DMK.所以,Rt△FVE∽Rt△MKD,从而,t体t㘹=〸뵸뵸㌰=〸뵸 h.故PN=MD,且PN∥MD.注意到O为MN的中点得P、O、D三点共线,且点O为线段PD的中点.、 th 的中点,D为直线BC一点,18-5△ABC内接于☉O,M、N分别为 hDE∥AC交AB于点E,DF∥AB交AC于点F,ND与☉O的第二个交点为K,联结EF、AK,作KP⊥AK交AM于点P.求证:PD⊥EF.证明如图,不妨设AB<AC(当AB=AC时,证明更容易).作△AKP的外接圆☉T,AB、AC的第二个交点分别为V、U,VU与BC交于点D/,AD与EF交于点X,联结线段如图所示.因∠AKP=90°,则T是AP的中点.的中点,则∠VAP=∠UAP,AV=AU.因M为 h考虑△ABC被直线VD/U所截,由梅涅劳斯定理得体 体 h·h t·t賀㌰ = ,体体 h=㌰ h .的中点,则KD平分∠BKC.因N为 th体体h=BK h㘹.因∠KVB=∠KUC,∠VBK=∠UCK,则△KVB∽△KUC.㌰ h = 㘹h㘹.故 体 体 h= 体体h D/与D重合,即V、D、U三点共线.所以,∠FDU=∠AVU=∠FUD.又四边形AEDF是平行四边形,于是,AE=DF=UF.又AT=UT,∠EAT=∠TAU=∠FUT.所以,△TAE≌△TUF TE=TF.注意X为EF的中点,得TX⊥EF.又TX为△APD的中位线,TX∥PD,所以,PD⊥EF.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
则 A⟶ E,B⟶ F,C⟶ G,D⟶ H,L⟶ T,U⟶ V. 于是 UL∥VT. 由熟知结论得点 K 关于☉O2 的极线为 UL,从而,UL⊥KO2. 故 VT⊥KO2.
高联班几何测试题(52)
时间:120 分钟
命题人:万喜人
52-1 在△ABC 中,AB≠AC,点 D、E、F 分别在边 BC、CA、AB 上,AE=AF,AD、 BE、CF 三线共点于 P,DT⊥EF 于 T,△ABC 的外接圆φ与△AEF 的外接圆ε相交于点 A、K,直线 AT 交圆φ交于点 A、V, 圆φ的过 BC 的切线相交于点 X.求证:K、V、X 三点共线.
证明 如图,作 BL⊥EF 于点 L, CJ⊥EF 于 点 J,联结线段如图所示.
对△ABC 及点 P,由塞瓦定理得 Ⰸ · tt
Ⰸt t
又 AF=EA
所以,tt tⰈ .
t
又因 BL∥DT∥CJ,
由 AE=AF 得∠BFL=∠CEJ
⟹ Rt△BFL∽Rt△CEJ.
所以, t tt tⰈ Ⰸ
t㔠Ⰸ
tt
52-3 ☉O1 与☉O2 外切于点 P,点 K 在☉O1 上,过点 K 任作一直线交☉O2 于 点 A、B,直线 AP、BP 与☉O1 的第二个交点分别为 E、F. 过点 K 作另一直线交☉ O2 于点 C、D,直线 CP、DP 与☉O1 的第二个交点分别为 G、H,直线 EH 与 FG 交于点 T, 直线 EG 与 FH 交于点 H.求证:VT⊥KO2.
证明 如图,设直线 BE、CF 分别交直线 AD 于点 T、K,设直线 FE 交 AD 于点 P,AM 交 BC 于点 N.
因 AE⊥BM,AF⊥CM,AD⊥AM. 则 A、E、M、F 四点共圆.AD 为其 切线. 因∠PET=∠MEF=∠MAF=∠K, 则 E、F、K、T 四点共圆. 于是,AP2=PE·PF=PT·PK. 因(B,C;N,D)为调和点列, 则 M(B,C;N,D)为调和线束. 从而,(T,K;A,D)为调和点列, 于是,P 为 AD 的中点,即直线 FE 平分线段 AD.
证明 (1)如图,过点 P 作☉O 的另一切线( 上一点.联结线段如图所示.
因 OK⊥PK,OA⊥PA,OE⊥PE,则 P、A、O、K、E 五点共圆. 所以,∠PEA=∠PKA=∠KBA, 又∠PAB=∠T, 则∠APE=180°-∠PAB=180°-∠T=∠AKB 从而△APE∽△AKB, 故∠EKP=∠EAP=∠BAK. 又因∠MKC=∠CAK, 所以,∠EKC=∠CAB=∠EDC.
52-5 PA 与☉O 相切于点 A,AB 是☉O 的弦,PB 交☉O 于点 B、C,PD∥AB 交 AC 的延长线于点 D,作 OE⊥PD 于点 E, ☉(CDE) (表示过 C、D、E 三点的圆)与☉ O 点 C、F,PF 交☉(CDE) 于点 F、M,点 N 为 PA 的中点.求证:(1) PF 是☉O 的 切线;(2) D、M、N 三点共线.
52-4 在△ABC 中,点 E、F 均在形内,且∠ABE=∠CBF, ∠ACF=∠BCE,点 A 在直线 BE、CE、BF、CF 上的射影分别 为 M、N、U、V,直线 MN 与 UV 交于点 P,AP 与 BC 交于点 K.求证:(1) AK⊥EF,( 2) AP=PK.
证明 (陕西省西安市铁一中杨运新解答) (1)因 AM⊥BE,AN⊥CE,则 A、M、E、N 四点共圆,此圆圆心为 AE 的中点 S, 简记☉S. 因 AU⊥BF,AN⊥CF, 则 A、F、U、V 四点共圆,此圆圆心为 AF 的中点 T,简记 ☉T. 因 E、F 为△ABC 内的等角共轭点,则可设∠BAE=∠CAF=α,∠ABE=∠CBF=β, ∠ACF=∠BCE=γ,△ABC 的三内角简记为∠A、∠B、∠C. 因 A、M、E、N,A、B、U、M 分别为四点共圆, 则∠PMU=∠NME+∠BMU=∠NAE+∠BAU=90°-∠CAE-∠ACE+90°-∠ABF = 90°-(∠A-α)-(∠C-γ)+90°-(∠B-β)=α + β + γ . 类似地,∠PUM、∠PVN、∠PNV 都等于α + β + γ .
于是,四边形 MVNU 是等腰梯形或矩形. 从而,M、V、N、U 四点共圆⟹ PM·PN =PV·PU, 即点 P 对☉S 与☉T 的幂 相等,P 在☉S 与☉T 的根轴上. 又点 A 是☉S 与☉T 的公共点,点 A 在☉S 与☉T 的根轴上. 所以,直线 AK 是☉S 与☉T 的根轴,AK⊥ST. 又因 ST 是△AEF 的中位线,ST∥EF. 故 AK⊥EF.
(2)设 AB、AC 的中点分别为 J、L. 因四边形 MVNU 是等腰梯形或矩形,则 MU 与 VN 有公共的中垂线 g,点 P 在直 线 g 上.
因 JM= AB=JU,则点 J 在直线 g 上.
同理,点 L 在直线 g 上. 从而,g 是△ABC 中平行于 BC 的中位线所在的直线. 所以,AP=PK.
t㔠
Ⰸt sin Ⰸ t t .
t sin t
因∠ABK=∠ACK, ∠AFK=∠AEK⟹∠BFK=∠CEK, 则△BFK∽△CEK
故tt tⰈ t .
t
因为 XB、XC 为圆φ的切线. 所以,K、V、X 三点共线.
52-2 在△ABC 中,AB>AC,∠BAC 的外角平分线交 BC 于点 D,点 M 在∠BAC 的平分线上,AE⊥BM 于点 E,AF⊥CM 于点 F.求证:直线 FE 平分线段 AD.
点 K 在☉(CDE)上. 于是,点 K 是☉(CDE)与☉O 除点 C 外的第 二个交点,点 K 与 F 重合. 所以,PF 是☉O 的切线. (2)因∠DPC=∠ABC=∠PAC, 则 DP2=DC· DA,即点 D 对点圆 P 与☉O 的幂相等,点 D 在点圆 P 与☉O 的根 轴上. 又∠MDC=∠MFC=∠FAC,则 DM∥AF. 因点圆 P 与☉O 的根轴是过 PA、PF 中点的直线,平行于 AF,也就是说,过点 圆 P 与☉O 根轴上一个点且平行于 AF 的直线就是根轴. 所以,D、M、N 三点共线,此直线为点圆 P 与☉O 的根轴.
