高联二试难度几何100题带图已精排适合打印预留做题空间
高联难度几何题100道(无图版)

第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
求证:PCE PCD ∠=∠。
第二题:证明四点共圆如图,AB 是⊙O 的直径,C ,D 是圆上异于A 、B ,且在AB 同侧的两点,分别过C 、D 作⊙的O 切线,它们交于点E ,线段AD 与BC 的交点为F , 线段AB 与EF 的交点为M ,求证:E 、C 、M 、D 四点共圆。
第三题:证明角的倍数关系如图,PE 、PF 是以AB 为直径圆的切线E 、F 是切点,PB 交圆于C 点,AF 、BE 交于D 点,AB 是直径。
求证:ACD DPE ∠=∠2。
第四题:证明线与圆相切已知:ABC ∆中,︒=∠90A ,AD 切⊙ABC ,AD 交BC 延长线于D ,E 是A 关于BC 的对称点,BE AY ⊥于Y ,X 是AY 中点,延长BX 交⊙ABC 于J ,求证:BD 切AJD ∆外接圆第五题:证明垂直已知四边形ABCD 内接于以BD 为直径的圆,设'A 为A 关于BD 为对称点,'B 是B 关于AC 对称点,直线AC 交'DB 于Q ,直线DB 交'CA 于P 。
求证:AC PQ ⊥。
第六题:证明线段相等已知:BC 、BD 是⊙O 切线,C 、D 是切点,BJA 是割线,A 、J 在圆上,J 离B 较近,AO DE ⊥于E ,交AB 于F ,AC 交DE 于G ,求证:FG DF =。
第七题:证明线段为比例中项已知ABC ∆中,BC AC =,M 是AB 的中点,FG 经过点M ,且CFG ∆与ABC ∆有相同的内心。
求证:GM FM AM ⨯=2。
第八题:证明垂直已知:ABC ∆为非直角三角形,AD 平分BAC ∠,D 在BC 上,AC DF ⊥于F ,AB DE ⊥于E ,CE 交BF 于P 。
求证:BC AP ⊥。
高二数学竞赛班二试平面几何讲义1

高二数学竞赛班二试平面几何讲义1梅涅劳斯定理和塞瓦定理一、知识要点:班级姓名1. 梅涅劳斯定理:若直线l不经过ABC的顶点,并且与ABC的三边BC,CA,AB或它们的延长线分别交于P,Q,R,则BPCQAR1 PCQARB证:设hA、hB、hC分别是A、B、C到直线l的垂BPCQARhBhChA线的长度,则:1PCQARBhChAhB2. 梅涅劳斯定理逆定理:设P、Q、R分别是ABC的三边BC、CA、AB上或它们的延长线上的三点,并且P、Q、R三点中,位于ABC边上的点的BPCQAR个数为0或2,若1,则P、Q、R三点共线;PCQARB证:设直线PQ与直线AB交于R',于是由定理1得:BPCQAR'__R'AR ' 1又1'=__RB由于在同一直线上的P、Q、R'三点中,位于ABC边上的点的个数也为0或2,因此R与R'或者同在AB线段上,或者同在AB的延长线上;若R与R'同在AB线段上,则R与R'必定重合,不然的话,设AR AR',ARAR'ARAR'这时AB AR AB AR,即BR BR,于是可得这与='矛盾'__R类似地可证得当R与R'同在AB的延长线上时,R与R'也重合''综上可得:P、Q、R三点共线;注:此定理常用于证明三点共线的问题,且常需要多次使用再相乘; 3. 塞瓦定理:设P、Q、R分别是ABC的BC、CA、AB边上的点,则APBP CQAR的充要条件是: 1PCQARB证:先证必要性:设AP、BQ、CR相交于点M,则:BPS ABPS BMPS ABMCQS BCMARS ACM,PCS ACPS CMPS ACMQAS ABMRBS __AR =1PCQARB1再证充分性:若BPCQAR‘1,设AP与BQ相交于M,且直线CM交AB于R,PCQARB BPCQAR’AR’AR‘ 1‘=因为R和R’都在线__BRB段AB上,所以R’必与R重合,故AP、BQ、CR相交于一点点M;二、例题精析例1:若直角ABC中,CK是斜边上的高,CE是ACK的平分线,E点在AK上,D是AC的中点,F是DE与CK的交点,证明:BF//CE。
全国高中数学竞赛二试模拟训练题(8).doc

加试模拟训练题(8)1、已知圆Q , 0,。
3,°4按顺时针的顺序内切于圆。
,设圆O i,O j(l<i< j<4)的外公切线长为,证明依次以1口」23」34」14为边长,以上」24为对角线构成的凸四边形是圆内接四边形。
2.设AABC三边长为a,b,c ,有不等式-c)2 > -c)2,试证不等式①中的系数』是最优的.33、设M={ 1, 2, 3,2m n) (m, neN*)是连续2”n个正整数组成的集合,求最小的正整数k, 使得M 的任何k元了集中都存在m+1个数,ai, a2, 满足ai|a1+i (i=l, 2, •••, m).4.已知a,eN*,旦(a,幻= 1,。
〉2,试问a +b n I a m +b m的充要条件是"Im吗?2006年山东省第二届夏令营试题)加试模拟训练题(8)1、已知圆Q ,。
2,。
3,°4按顺时针的顺序内切于圆。
,设圆O i,O j(l<i< j<4)的外公切线长为,证明依次以【提23」34」14为边长,以I。
,项为对角线构成的凸四边形是圆内接四边形。
证明设圆0,0{,02,03,04的半径分别为R,*①,乃匕,圆。
1,。
2,°3,°4与圆。
的切点分别为A,B,C,D , 00{ = a,001 = b,003 = c,004 = d , XO t OO2 = a,XO2OO3= ”,ZO3OO4 = /,Z(91(?(?4 = S ,因为R = a + f[=b + r2,所以有/p = Op; -(/] -r,)" = a2 +Z?2- 2ab cos a ~(^a-by = 2aZ?(l-cos«) = 4t?Z?sin2 -y ,即.2成屿。
同理可得"4,MM的表达式。
由托勒密定理的逆定理知,只要证始始+,23,4 = /13,24 °代入/〃的表达式,只要证sin — sin — + sin — sin — = sin —+ sin —+—,即AB CD + BC AD = AC BD o 22 2 2 2 22.设AABC^.边长为a,b,c ,有不等式- c)2 > -c)2,- 一①试证不等式①中的系数』是最优的.3证明在不等式①中,取a=b,设g = 2(a 一成一(a 一疔= (a一们2 +(》_c)2 +Q —a)? —H^±£(。
高联班几何测试6图片调整打印了
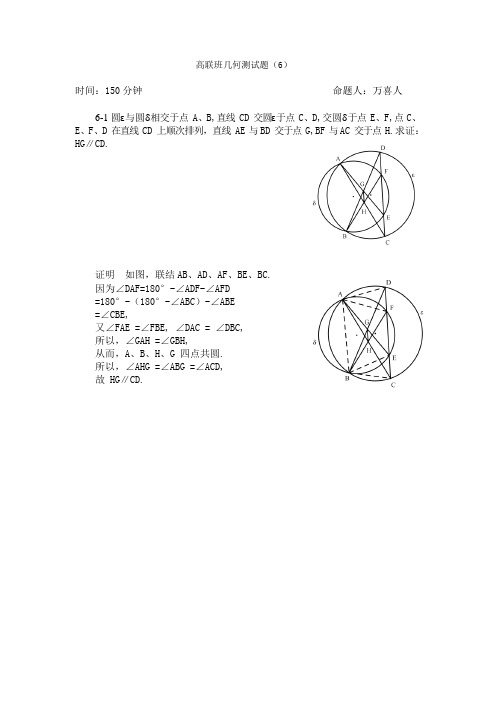
高联班几何测试题(6)时间:150 分钟命题人:万喜人6-1 圆ε与圆δ相交于点 A、B,直线 CD 交圆ε于点 C、D,交圆δ于点 E、F,点C、E、F、D 在直线 CD 上顺次排列,直线 AE 与BD 交于点 G,BF 与AC 交于点 H.求证:HG∥CD.证明如图,联结AB、AD、AF、BE、BC.因为∠DAF=180°-∠ADF-∠AFD=180°-(180°-∠ABC)-∠ABE=∠CBE,又∠FAE =∠FBE, ∠DAC = ∠DBC,所以,∠GAH =∠GBH,从而,A、B、H、G 四点共圆.所以,∠AHG =∠ABG =∠ACD,故HG∥CD.6-2. 已知△ABC,点D、E 分别在 AB、AC 上,∠AED=∠ABC,圆(BD)(表示以 BD 为直径的圆)与圆(ABC)(表示过 A、B、C 三点的圆)交于点 B、F, 圆(CE)与圆(ABC)交于点 C、T,圆(ADE)与圆(BD)交于点 D、P, 圆(ADE)与圆(CE)交于点 E、K.求证:P、K、T、F 四点共圆.证明联结线段如图所示.因∠FPK=360°-∠FPD-∠DPK= 360°-∠FBD-(180°-∠DEK)=180°-(∠FBC-∠ABC)+∠AEK-∠AED=180°-(180°-∠FTC)+180°-∠CEK(因∠AED=∠ABC)=180°-(∠CTK-∠FTC)=180°-∠FTK,即∠FPK+∠FTK=180°,所以,P、K、T、F 四点共圆.D 㠳6-3. 在△ABC 中,∠BAC 为锐角,P 为△ABC 的外接圆☉O 上一点(不与 A 、B 、C 重合),直线 AB 与 CP 交于 E,AC 与 BP 交于 F,线段 BC 的中垂线交 BC 、B ˆC (不含点 A)、EF 分别交于点 M 、D 、N.求证:D 䘐 D 㠳 =cos ²BtC .证明 设☉O 过点 B 、C 的切线交于点 N /,联结 BD 、CD.对圆内接六边形 ABBPCC,由帕斯卡定理知:E 、N /、F 三点共线,即点 N /在直线 EF 上.又 N /B=N /C,点 N /在 BC 中垂线上,所以,点 N /与 N 重合,因∠NCD=∠DBC=∠DCM,则 D 䘐= C 䘐 = cos ²㠳C 䘐 = cos ²BtCD 㠳 C 㠳 注:若∠BAC 为钝角,则D 䘐 =− cos ²BtC.6-4. 四边形 ABCD 外切于圆 I,AC 与BD 交于点 E,P 为IE 的中点,过点 I 作FK⊥AC交AB、AD 分别于点 F、K,过点 P 作GH⊥AC交AB、AD 分别于点 G、H.求证:BG·DH=FG·KH.证明设AB、BC、CD、DA 与圆I 分别切于点M、N、L、T,IB、ID 分别与GH交于点U、V.设直线MT 与BD 交点X1(可能X1是无穷远点),NL 与BD 交点X2.由梅涅劳斯定理得BX1 ·DT ·t䘐 = 1 = BX2 ·DL ·C㠳,X1D Tt 䘐 B X2D LC 㠳 B因 DT=DL,TA=AM,LC=CN,MB=NB,则BX1 = BX2 .X1D X2D从而,X1 与 X2重合,统一记为 X.因 X 在点 A 关于圆 I 的极线 MT 上,由配极原理知点 A 在点X 的极线上.同理,点 C 在点X 的极线上.所以,直线 AC 是点X 关于圆 I 的极线.故IX⊥AC.又过 I 的直线FK⊥AC,所以,F、K、X 三点共线.因AB、AC、AD、AX 是调和线束,则B、E、D、X 是调和点列,从而 IB、IE、ID、IX 是调和线束,因为GH∥IX(都与 AC 垂直)所以,PU=PV.又 PI=PE,则四边形 IUEV 是平行四边形,从而,UE∥ID,EV∥BI.故B= Bt = BE = I‴ = KѸ ,F It DE D‴DѸ所以,BG·DH=FG·KH.sin α+þ sin α+y IT· cot α+þ IT· cot α+y cos α+þ sin α+þ sin α+y cos α+y sin α+þ · sin þ sin α+y sin y sin α+y sin þ sin α+þ sin yIT· sin α cos 2α+2y sin α+þ sin y 6-5. 在△ABC 中,AB=AC,点 D 、E 不在直线 BC 上,使得 BD=AB,CE=AC, ∠DBC 和∠ECB 两角的平分线交于点 I,过点 I 作 IF⊥AD 交直线 DB 于点 F,过点 I 作 IK⊥AE 交直线 EC 于点 F.直线 BK 与 CF 交于点 P.求证:IP⊥BC.证法 1 如图,点 D 、E 和 A 均在直线 BC 的同侧(若点 D 、E 均和 A 在直线 BC 的异侧,或点 D 、E 位于直线 BC 的两侧,证明类似. )可设∠ABC=∠ACB=2α,∠ABD=2β,∠ACE=2γ.因 BD=AB,IF⊥AD,则∠BFI=β,∠BIF=∠DBI -∠BFI=α,同理,∠CKI=γ,∠CIK=α. 由正弦定理得 IC = CK , IB = BF ,IC = ,sin y sin α sin þ sin α IB 所以,CK= sin α+þ · sin þ.BF sin α+y · sin y 作 IT⊥BC 于点 T,IT 交 BK 、CF 分别于点 P 1、P 2,作 FM⊥BC 于点 M,KN⊥BC 于点 N.只要证明 P 1 与 P 2 重合即可, 这只要证明TP 1=TP 2.因 TP 1∥KN, TP 2∥FM,所以,TP 1 =BT·K 㠳 B 㠳 ,TP 2 =CT·F 䘐 . C 䘐TP =TPBT·K 㠳 = CT·F 䘐 1 2 B 㠳 C 䘐B T·K 㠳= B 㠳 ○1 CT·F 䘐C 䘐 BT·K 㠳= · CT·F 䘐= · · ·= ○2 因 CN=CK cos 2α + 2y =IC· sin α· c os 2α + 2y sin y=,则 CT+CN=IT·cos α+y sin α+y+ IT· CK· sin 2α+2y BF· sin 2α+2þsin 2α+2y sin 2α+2þ sin α cos 2α+2ysin α+y sin ycos α+þsin α+þsin α+y sin þsin α+þ sin y=IT·cos α+y sin y+sin α cos 2α+2ysin α+y sin y=IT·sin α+2y −sin α+sin 3α+2y −sin α+2y2 sin α+y sin y=IT·cos 2α+y.sin y从而,BN=BT+CT+CN=IT·+=IT·sin α+þ+y −sin α+þ−y +sin 3α+þ+y −sin α−þ+y,2 sin α+þ sin y同理,CM=IT·sin α+þ+y −sin α−þ+y +sin 3α+þ+y −sin α+þ−y2 sin α+y sin þ所以,B㠳= ○3C䘐由式○2 、○3 知式○1 成立.证毕.证法2 如图,点D、E 和A 均在直线BC 的同侧(若点D、E 均和A 在直线BC 的异侧,或点 D、E 位于直线 BC 的两侧,证明类似)可设∠ABC=∠ACB=2α,∠ABD=2β,∠ACE=2γ.因BD=AB,IF⊥AD,则∠BFI=β,∠BIF=∠DBI-∠BFI=α,同理,∠CIK=α.设直线 BD 与CE 交于点 Q(Q 可能是无穷远点).点 S 在直线 IQ 上,且在∠BIC 内部.对四边形 IBQC,由∠BIF=∠CIK(都=α)知,IP、IQ 是∠BIC 的等角共轭线,即∠BIP=∠CIS=90°-(α + β)(注意 I 为△QBC的旁心或内心)又∠IBC=α + β,所以,∠BIP=∠IBC=90°.故IP⊥BC.cos 2α+ysin y。
高联班几何测试5解答,图已调整打印了
所以, t = t
VC·ET=DT·EV.
同理,TB·DV=DT·EV. 所以,VC·ET=TB·DV,
即
=
t t
=t
=
t=
,
t
因∠PCD=∠PBE, ∠PDA=∠PEA,
则△PCD∽△PBE
=
E.
E
故
t=
E E
.
结合∠PDN=∠PEM 得△PDN∽△PEM.
所以,∠PNA=∠PMA
A、P、N、M 四点共圆.
故 GK=GM+MK= AG+ AH = GH. 即 K 是 GH 的中点.
证法 2 如图,联结线段如图所示. (1)因 AC、AD 分别为☉P、☉O 的切线, 则∠BAC=∠D,∠C=∠BAD, 所以,△BAC∽△BDA,BE、BF 为对 应边上的中线, 故∠AEB=∠DFB. 从而,A、E、B、F 四点共圆. (2)∠BAC=∠H,∠C=∠G, 则△BAC∽△BHG. 又∠BEA=∠BKA,则点 E、K 是上述 相似三角形的对应点. 因 E 为 AC 的中点,则 K 是线段 GH 的中点.
, BE= t , AD= t , CD= .
t
t
= t ,则 AE=k·AD.
由正弦定理
得 DE=AT· sin t° , AT2= DE2.
由余弦定理得
AT2= DE2 =
·
· = AD2·
,
从而,ET2=AT2-AE2= AD2 ·(2-k)2,
DT2=AT2-AD2= AD2 ·(2k-1)2.
又 A、N、F、M 四点共圆.
=90°.
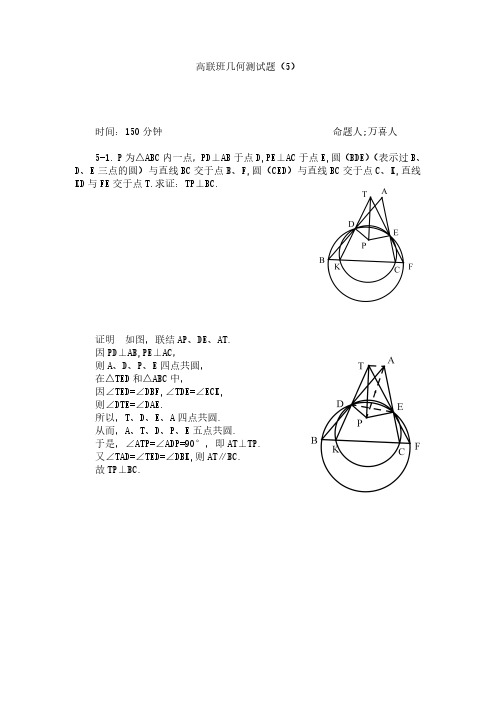
证明 如图,联结 AP、DE、AT. 因 PD⊥AB,PE⊥AC, 则 A、D、P、E 四点共圆, 在△TED 和△ABC 中, 因∠TED=∠DBF,∠TDE=∠ECK, 则∠DTE=∠DAE. 所以,T、D、E、A 四点共圆. 从而,A、T、D、P、E 五点共圆. 于是,∠ATP=∠ADP=90°,即 AT⊥TP. 又∠TAD=∠TED=∠DBK,则 AT∥BC. 故 TP⊥BC.
高联难度几何题100道

高联难度几何题100道
【实用版】
目录
1.几何题的重要性
2.高联难度几何题的特点
3.高联难度几何题的解决方法
4.高联难度几何题的训练价值
5.结语
正文
几何学作为数学的一个重要分支,其地位和作用不容忽视。
几何题在各种数学竞赛和考试中都占有重要地位,它能够锻炼学生的空间思维能力、逻辑推理能力和创新思维能力。
因此,对于学生来说,掌握几何题的解题技巧和方法是非常重要的。
高联难度几何题是几何题中难度较大的一部分,其特点是题目复杂、条件隐蔽、思路难以寻找。
这类题目的解决需要学生具有扎实的几何基础知识和丰富的解题经验,同时还需要具备敏锐的洞察力和创新思维能力。
解决高联难度几何题的方法有很多,其中最重要的方法是通过画图来帮助理解题目,找到解题思路。
此外,对于一些复杂的题目,还可以通过分割、旋转、翻转等方法来简化题目,找到解题的关键。
在解题过程中,还需要注意题目的条件和要求,避免出现低级错误。
高联难度几何题虽然难度较大,但是对于学生的数学能力和思维能力的提升具有很大的帮助。
通过解决这类题目,学生可以锻炼自己的空间思维能力和逻辑推理能力,同时也能够培养自己的创新思维和解决问题的能力。
总的来说,高联难度几何题虽然难度较大,但是对于学生的学习和发
展具有很大的帮助。
全国高中数学竞赛二试模拟训练题(52).doc
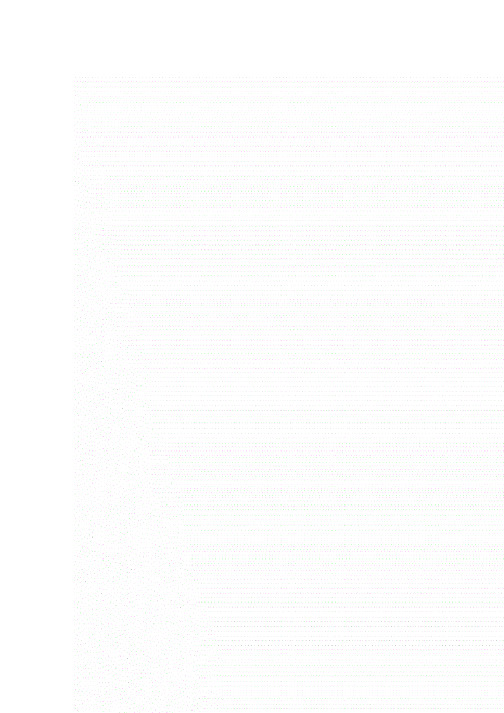
加试模拟训练题(52)1.过等腰△川%底边成'上一点夕引PM// CA交AB于阪引PN//BA交 M于也作点夕关于枷的对称点.试证:P'点在△,质外接圆上.2.设实数x、y、z满足条件yz+zx+xy=T,求x2+5y2+8z2的最小值和最大值.3.桌面上放有1989枚硬币,其中有的正面朝上,其余的正面朝下.今有1989人按下述方法依次翻转硬币,第一人翻转其中的一枚,第二人翻转其中的二枚,…,第k人翻转其中的k 枚,最后第1989人将所有硬币全部翻转.证明:1.不论硬币最初正反面的分布情况如何,他们总可采取适当步骤,使得1989人都进行过翻币手续后,恰将所有硬币朝同一方向.2.硬币最后的统一朝向与具体翻币方案无关(只依赖于初始分布).P'4. 求所有正整数m, n 满足m 2 - n 整除m + n 2,并且n~ - m 整除n + m~. 加试模拟训练题(52)1,过等腰△宛T 底边网上一点夕引PM//CA 交AB 等引PN//BA 交花于也作点夕关于洌的对称点々.试证:P'点在外接圆上.(杭州大学《中学数学竞赛习题》)分析:山已知可得妒'NP' =NP =NC,故点彤是欧的外心,点NMP AC 的外心.有A BP' ABAC,2 2ZPP' (=- APN(=- ABAC. 2 2:WBP OABP'氏ZP' PGZBAC.从而,P'点与4 B, C共圆、即月在外接圆上.由于夕,夕平分/胪,G显然还有P B-.P' OBP-.PC.2.设实数x、y、z满足条件yz+zx+xy=T,求x2+5y2+8z2的最小值和最大值.【题说】1992年英国数学奥林匹克题4.【解】由于(y-2z) 2+ (x+2y 十 2z) 2^0所以 x2+5y2+8z2^-4 (xy+yz+zx) =43 11= —* y = -—* r = +5y‘ 4-&a =4,所以+5y,-I-Sr3££ 4的最小值为4.另一方虱令M=0. B M7 x2+5y2+8z2>x2当y-0时,函数x2+5y2+8z2的值可趋于无穷大.3.桌面上放有1989枚硬币,其中有的正面朝上,其余的正面朝下.今有1989人按下述方法依次翻转硬币,第一人翻转其中的一枚,第二人翻转其中的二枚,…,第k人翻转其中的k 枚,最后第1989人将所有硬币全部翻转.证明:1.不论硬币最初正反面的分布情况如何,他们总可采取适当步骤,使得1989人都进行过翻币手续后,恰将所有硬币朝同一方向.2.硬币最后的统一朝向与具体翻币方案无关(只依赖于初始分布).【题说】1989年南昌市赛二试题3.【证】1. 1989可换成任一奇数n.对n用数学归纳法.当n=l时,结论显然成立.假设在n = 2k— 1时结论成立,当n = 2k+l时,分两种情况讨论. (1)如果这2k+l枚硬币不全同向,其中必有一枚正面朝上的(记为正)和一枚正面朝下的(记为负),将它们标上记号.让前2k—1人对其余2k—1枚硬币进行翻币手续,依假设可翻成同向,设为正.第2k人翻动2k个正向币,使得所有2k+l枚硬币都成负向.最后第2k+l人将所有硬币翻成正向.(2)如果这2k+l枚硬币方向都相同.将这2k+l枚硬币排成一圈,让第一人翻转其中一枚,第二人按顺时针方向翻转后续的二枚,第三人接着翻转后续的三枚,…,如此下去,当2k+l 人全部翻转之后,由于1 + 2 + •••+(2k+l) = (k+l) • (2k+l),所以,每枚硬币都翻动了 k + 1次,因而也同向.2.假设结论不真,则存在1989枚硬币的某种初始状态T及两种翻法A、B.由状态T开始,按方法A可翻成全正,而按方法B可翻成全反.由全正状态出发,按方法A的逆步骤翻回T状态,再按B方法翻成全反.这样每枚硬币都改变了方向,从而每枚硬币翻动了奇数次,硬币总数1989为奇数.故由全正状态到全反状态总共翻转了奇数次.另一方面,在由全正状态到全反状态的过程中,每个人均翻转了偶数枚,因此总共翻转了偶数次,矛盾.从而结论成立.4.求所有正整数m, n满足m之一〃整除m + zz?,并且〃2 一山整除n + m2.分析由对称性,我们不妨设n>m,并估计n的大体范围。
全国高中数学竞赛二试模拟训练题(7).doc

加试模拟训练题(7)1、对给定的常数P、qG(O, 1), p + q>l, p2 + q2<1> 试密刮= (l-K)♦sjq1-(l-s)a P)的最大值.2、设M是AABC内一点,D,E,F分别是^BCM,^CAM,^ABM的夕卜心,证明S'DEF AS MBC'并确定等号成立的条件。
3、平面上给定一个由有限多条线段组成的集合,线段总长为1.证明:存在一条直线/,2使得已给线段在/上的射影之和小于-.n4.设“是五位数(第一个数码不是零),加是由〃取消它的中间一个数码后所成的四位n数,试确定一切n使得上是整数。
m加试模拟训练题(7)1、对给定的常数P、qG(O, 1), p + q>l, p2 + q2<1, = Cl-r)p)的最大fi.【解】f2(X)= (1 —x)2(P2—x2) +x2[q2— (1—x)2] +2x(1-K)•w(1—x) (p —x)+x [q — (1—x) ] +X(l—x) [(p2—X2) +q2— (1—x)2] =X— (p2—q2+l)x+p2--P' 巧J + *(P + q)°-/I<^[(P*q)a-U[l-(p-q)a l其中等号成立当且仅当P2—x2 = q2— (1—x)2即当"亡尸吋,f(M)L« =存(Pp7「-(p-q)T[别解]考虑如图的直角梯形ABCD,易知f (x) =b (1—x) +ax=pqsin B cos a +pqsin a cos B= pqsin( a + B ) =pqsin 0因为c“e =亡乎仝< 彎亡I",所以2pq 2pqf («) < |7((P*A)a-D(i-(p-q)a) 界mg*- a-j:时竝.佩區=p'_f “时, f 3 晦I内首«P诃-DO・(P -小.2、设M是AABC内一点,D,E,F分别是ABCM,ACAM,AABM的夕卜心,证明S^EF >S^BC,并确定等号成立的条件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高联难度平面几何100题二〇一七年八月目录第一题:证明角平分 (5)第二题:证明四点共圆 (6)第三题:证明角的倍数关系 (7)第四题:证明线与圆相切 (8)第五题:证明垂直 (9)第六题:证明线段相等 (10)第七题:证明线段为比例中项 (11)第八题:证明垂直 (12)第九题:证明线段相等 (13)第十题:证明角平分 (14)第十一题:证明垂直 (15)第十二题:证明线段相等 (16)第十三题:证明角相等 (17)第十四题:证明中点 (18)第十五题:证明线段的二次等式 (19)第十六题:证明角平分 (20)第十七题:证明中点 (21)第十八题:证明角相等 (22)第十九题:证明中点 (23)第二十题:证明线段相等 (24)第二十一题:证明垂直 (25)第二十二题:证明角相等 (26)第二十三题:证明四点共圆 (27)第二十四题:证明两圆相切 (28)第二十五题:证明线段相等 (29)第二十六题:证明四条线段相等 (30)第二十七题:证明线段比例等式 (31)第二十八题:证明角的倍数关系 (32)第二十九题:证明三线共点 (33)第三十题:证明平行 (34)第三十一题:证明线段相等 (35)第三十二题:证明四点共圆 (36)第三十三题:证明三角形相似 (37)第三十四题:证明角相等 (38)第三十五题:证明内心 (39)第三十六题:证明角平分 (40)第三十七题:证明垂直 (41)第三十八题:证明面积等式 (42)第三十九题:证明角平分 (43)第四十题:证明角相等 (44)第四十一题:证明中点 (45)第四十二题:证明中点 (46)第四十三题:证明角相等 (47)第四十七题:证明四点共圆 (51)第四十八题:证明四点共圆 (52)第四十九题:证明四点共圆 (53)第五十题:证明角平分 (54)第五十一题:证明线段相等 (55)第五十二题:证明两圆外切 (56)第五十三题:证明垂直 (57)第五十四题:证明垂直 (58)第五十五题:证明垂直 (59)第五十六题:证明垂直 (60)第五十七题:证中点 (61)第五十八题:证明角相等 (62)第五十九题:证明角相等 (63)第六十题:证明四点共圆 (64)第六十一题:证明四点共圆 (65)第六十二题:证明四点共圆 (66)第六十三题:证明角相等 (67)第六十四题:证明角的倍数关系 (68)第六十五题:证明中点 (69)第六十六题:伪旁切圆 (70)第六十七题:证明垂直 (71)第六十八题:证明平行 (72)第六十九题:证明圆心在某线上 (73)第七十题:证明三线共点 (74)第七十一题:证明垂直 (75)第七十二题:证明垂直 (76)第七十三题:证明中点 (77)第七十四题:证明垂直 (78)第七十五题:证明垂直 (79)第七十六题:证明三线共点 (80)第七十七题:证明平行 (81)第七十八题:证明平行 (82)第七十九题:证明三线共点、证明垂直 (83)第八十题:证明三点共线(牛顿定理) (84)第八十一题:证明角平分 (85)第八十二题:证明角相等 (86)第八十三题:证明三点共线 (87)第八十四题:证明四圆共点 (88)第八十五题:证明角平分 (89)第八十六题:证明线段相等 (90)第八十七题:证明角相等 (91)第八十八题:证明线段相等 (92)第八十九题:证明线段相等 (93)第九十三题:证明西姆松定理及逆定理 (97)第九十四题:证明线段的和差关系等式 (98)第九十五题:证明角相等 (99)第九十六题:证明托勒密定理及逆定理 (100)第九十七题:证明线段的和差关系等式 (101)第九十八题:证明角相等 (102)第九十九题:证明四点共圆 (103)第一百题:证明两三角形共内心 (104)第一题:证明角平分已知PE 、PF 是⊙O 的切线,A 、B 是一组对径点,PB 交⊙O 于另一点C ,直线AF 、BE 交于D 点。
求证:PCE PCD ∠=∠。
第二题:证明四点共圆如图,AB 是⊙O 的直径,C ,D 是圆上异于A 、B ,且在AB 同侧的两点,分别过C 、D 作⊙的O 切线,它们交于点E ,线段AD 与BC 的交点为F , 线段AB 与EF 的交点为M ,求证:E 、C 、M 、D 四点共圆。
A EB第三题:证明角的倍数关系如图,PE 、PF 是以AB 为直径圆的切线E 、F 是切点,PB 交圆于C 点,AF 、BE 交于D 点,AB 是直径。
求证:ACD DPE ∠=∠2。
A PB第四题:证明线与圆相切已知:ABC ∆中,︒=∠90A ,AD 切⊙ABC ,AD 交BC 延长线于D ,E 是A 关于BC 的对称点,BE AY ⊥于Y ,X 是AY 中点,延长BX 交⊙ABC 于J ,求证:BD 切AJD ∆外接圆。
DB第五题:证明垂直已知四边形ABCD 内接于以BD 为直径的圆,设'A 为A 关于BD 为对称点,'B 是B 关于AC 对称点,直线AC 交'DB 于Q ,直线DB 交'CA 于P 。
求证:AC PQ 。
PD第六题:证明线段相等已知:BC、BD是⊙O切线,C、D是切点,BJA是割线,A、J在圆上,J离B较近,DF=。
DE⊥于E,交AB于F,AC交DE于G,求证:FGAOA第七题:证明线段为比例中项已知ABC ∆中,BC AC =,M 是AB 的中点,FG 经过点M ,且CFG ∆与ABC ∆有相同的内心。
求证:GM FM AM ⨯=2。
C第八题:证明垂直已知:ABC ∆为非直角三角形,AD 平分BAC ∠,D 在BC 上,AC DF ⊥于F ,AB DE ⊥于E ,CE 交BF 于P 。
求证:BC AP ⊥。
AB第九题:证明线段相等过圆O外一点P作圆O的两条切线PC、PD,切点分别为C、D,过劣弧CD上一点E作圆O的另一条切线分别交PC、PD于A、B,连结OE交CD于点N,连结PN交AB于点M。
MA 。
求证:MBP已知PA 、PB 是⊙O 切线,DE 是过C 的切线,D 、E 分别在AP 、PB 上,AB CF ⊥于F ,连接DF 、EF 。
求证:EFC DFC ∠=∠AC 。
设PAB是圆O的割线,PC是切线,CD是圆O的直径,DB、OP相交于E。
求证:CEP第十二题:证明线段相等设C、D是以O为圆心AB为直径的半圆上两点,过B做圆O的切线交CD于P,直线PO交直线CA、OE 。
AD分别于E、F。
求证: OF第十三题:证明角相等如图,ABC ∆中,D 、E 分别为AB 、AC 上一点,且BC DE //,BE 、CD 交于点F ,BDF ∆的外接圆⊙O ,与CEF ∆的外接圆⊙P 交于点G ,求证:CAG BAF ∠=∠。
第十四题:证明中点如图,⊙O、⊙P交于A、B两点,BO、PA延长线交于点C,CD、CE分别切⊙O、⊙P于D、E,连接DE交AB于F,求证:F为DE中点。
第十五题:证明线段的二次等式如图,半径不相等的两圆⊙O 、⊙P 交于A 、B 两点,过A 的直线CD 分别交⊙O 、⊙P 于C 、D ,CB 延长线交⊙P 于F ,DB 延长线交⊙O 于E ,过A 作CD 垂线交EF 中垂线于G ,求证:AD AC EG AG ⋅+=22C第十六题:证明角平分如图,ABC ∆内接于⊙O ,D 为BC 中点,AD 交⊙O 于E ,过E 作BC EF //,交⊙O 于F ,过C 作AC CG ⊥,交AE 于G 。
求证:FGC AGC ∠=∠。
第十七题:证明中点如图,ABC 内切圆⊙I 切BC 于D ,过I 作AD IE //交BC 于E ,过E 作⊙I 切线,分别交AB 、AC 于F 、G 。
求证:E 为FG 中点。
A第十八题:证明角相等如图,如图,⊙P、⊙Q交于A、B两点,它们的外公切线CD分别切⊙P、⊙Q于C、D,E为BA∠交FG于H。
求证:延长线上一点,EC交⊙P于F,ED交⊙Q于G,AH平分FAG∠。
=GDHFCH∠F第十九题:证明中点如图,⊙O 为ABC ∆外接圆,I 、E 分别为ABC ∆的内心和一个旁心,BAC ∠的外角平分线交BC 延长线于D ,DE IF ⊥于F ,交⊙O 于G 。
求证:G 为IF 中点。
第二十题:证明线段相等如图,在锐角ABC ∆中,C B ∠>∠,F 是BC 的中点,BE 、CD 是高。
G 、H 分别是FD 、FE 的中点,若过A 且平行于BC 的直线交GH 于I 。
求证:IF IA =B第二十一题:证明垂直如图,D 是ABC ∆边BC 上一点,ABD DAC ∠=∠,⊙O 过点B 、D 分别交AB 、AD 于E 、F ,直线BF 交DE 于G ,M 是AG 中点。
求证:AO CM ⊥。
C第二十二题:证明角相等如图,如图,CD 为⊙O 直径,PC 、PE 分别切⊙O 于C 、E ,割线PBA 交⊙O 于A 、B ,AC 、BD 交于点F ,DE 交AB 于G ,求证:ADE GFE ∠=∠。
D C如图,O 为ABC ∆外心,D 、E 分别为AB 、AC 上一点,DE OF ⊥于F ,L 、M 、N 分别为DE 、BE 、CD 中点。
求证:F 、L 、M 、N 四点共圆。
A如图,ABC ∆内切圆⊙I 切BC 于D ,BC AE ⊥于E ,F 为AE 中点,DF 交⊙I 于G ,作BCG ∆的外接圆⊙O ,求证:⊙O 、⊙I 相切于点G 。
B∆内接于⊙O,内切圆⊙I分别切AB、AC于J、K,AO交⊙O于D,连接DI,延长如图,ABCAG=。
CA到F,使得BJAF=,过F作DI的垂线交BA延长线于G,求证:CK第二十六题:证明四条线段相等如图,⊙O 为ABC ∆外接圆,AD 平分BAC ∠交⊙O 于D ,BD OE //交AB 于E ,CD OF //交AC 于F ,H 为ABC ∆垂心,AD HG //交BC 于G ,求证:CF GF GE BE ===。
第二十七题:证明线段比例等式如图,四边形ABCD 中,AC AB =,ABD ∆外接圆⊙1O 交AC 于F ,ACD ∆外接圆⊙2O 交AB 于E ,BF 、CE 交于点G ,求证:CDBDCG BG =。
第二十八题:证明角的倍数关系如图,O 为ABC ∆外心,D 为ABC ∆内一点,使得DCB DAB ∠=∠,DCB DAC ∠=∠,E 为AD 中点,过E 作AD EF ⊥交CB 延长线于F ,连接FA 、FD 、FO ,求证:OFC AFD ∠=∠2。
F第二十九题:证明三线共点的外接圆⊙P 如图,⊙O的内接四边形ABCD,AB、DC交于点E,AD、BC交于点F,EFC交⊙O于G,AG交EF于H,HC交⊙O于I,求证AI、GC、FE三线共点。
