工程结构抗震计算题大全
抗震及设计计算题答案
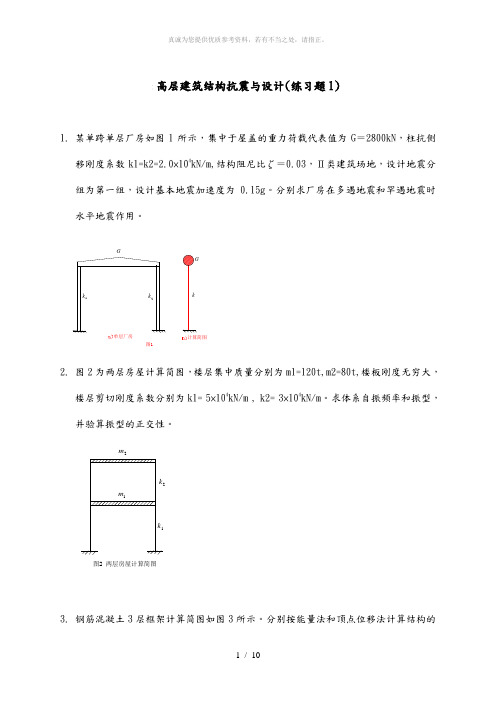
高层建筑结构抗震与设计(练习题1)1. 某单跨单层厂房如图1所示，集中于屋盖的重力荷载代表值为G ＝2800kN ，柱抗侧移刚度系数k1=k2=2.0×104kN/m,结构阻尼比ζ＝0.03，Ⅱ类建筑场地，设计地震分组为第一组，设计基本地震加速度为0.15g 。
分别求厂房在多遇地震和罕遇地震时水平地震作用。
图1单层厂房计算简图2k 1k kGG2. 图2为两层房屋计算简图，楼层集中质量分别为m1=120t,m2=80t,楼板刚度无穷大，楼层剪切刚度系数分别为k1= 5×104kN/m , k2= 3×104kN/m 。
求体系自振频率和振型，并验算振型的正交性。
图2 两层房屋计算简图1m 2m 1k 2k3. 钢筋混凝土3层框架计算简图如图3所示。
分别按能量法和顶点位移法计算结构的基本自振周期（取填充墙影响折减系数为0.6）。
图3 3层框架计算简图kgm 3310180⨯=kgm 3210270⨯=kgm 3110270⨯=mkN k /98003=mkN k /1950002=mkN k /2450001=4. 钢筋混凝土3层框架经质量集中后计算简图如图4所示。
各层高均为5米，各楼层集中质量代表值分别为：G1=G2=750kN ，G3=500kN ；经分析得结构振动频率和振型如图4所示。
结构阻尼比ζ＝0.05，Ⅰ类建筑场地，设计地震分组为第一组，设计基本地震加速度为0.10g 。
试按振型分解反应谱法确定结构在多遇地震时的地震作用效应，绘出层间地震剪力图。
s rad /22.101=ωsrad /94.272=ωsrad /37.383=ω12图4 计算简图5. 已知条件和要求同上题，试按底部剪力法计算。
1、表1为某建筑场地的钻孔资料，试确定该场地的类别。
表1解：覆盖层厚度达22m ，故取20m 深度计算，共有五个土层： s 01944.01805.3 s 01875.01603222111======s s v d t v d t s 01957.02305.4 s 02273.022********======s s v d t v d t s 01379.02904555===s v d v s 09428.0==∑i t t 平均剪切波速： m/s 2120.09428200===t d v se 由于v se 在140m/s~250m/s 之间，故该场地土为中软场地土。
最新工程结构抗震计算题大全
（二）计算题工程结构抗震计算1．已知一个水塔，可简化为单自由度体系。
10000m kg =，1kN cm k =，该结构位于Ⅱ类场地第二组，基本烈度为7度（地震加速度为0.10g ），阻尼比0.03ξ=，求该结构在多遇地震下的水平地震作用。
解：（1）计算结构的自振周期22 1.99T s === （2）计算地震影响系数查表2得，0.4g T s =，查表3得，max 0.08α=。
由于0.030.05ξ=≠应考虑阻尼比对地震影响系数形状的调整。
20.050.050.0311 1.160.08 1.60.08 1.60.03ξηξ--=+=+=++⨯0.050.050.030.90.90.940.360.360.03ξγξ--=+=+=++⨯由上图2可知，()0.94max 0.40.08 1.160.02051.99g T T γαα⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭（3）计算水平地震作用0.020*******.812011N F G α==⨯⨯=2．计算仅有两个自由度体系的自由振动频率。
假设[]11122122k k K kk ⎡⎤=⎢⎥⎣⎦ []1200m M m ⎡⎤=⎢⎥⎣⎦解：根据多自由度体系的动力特征方程[][]20K M ω-=，有[][]111212221222000k k m K M kk m ωω⎡⎤⎡⎤-=-=⎢⎥⎢⎥⎣⎦⎣⎦整理得()()4212112221112212210m m k m k m k k k k ωω-++-=解方程得2112211212k k m m ω⎛⎫=+⎪⎝⎭2112221212k k m m ω⎛⎫=++ ⎪⎝⎭3．图示钢筋混凝土框架结构的基本周期10.467T s =，抗震设防烈度为8度，Ⅱ类场地，设计地震分组为第二组（0.40g T s =）。
通过计算已经求得相应于结构基本自振周期的水平地震影响系数值10.139α=，试用底部剪力法计算多遇地震时的层间剪力。
建筑抗震设计-练习题-计算题专题
h=4m
3 地震作用与结构抗震验算 振型分解反应谱法 2.试按振型分解反应谱法确定图示钢筋混凝土框架（梁的 刚度EI=∞）的多遇水平地震作用Fij ，并绘出地震剪力图和 弯矩图。建筑场地为Ⅱ类，抗震设防烈度7度，设计地震 分组为第二组，设计基本地震加速度为0.10g，结构的阻尼 比ζ=0.05。
有一钢筋混凝土三层框架位于类场地设计基本加速度02g设计地震组别为第一组已知结构各阶周期和振0134s试用振型分解反应谱求多遇地震下框架底层地震剪力和框架顶点位移
天津城建大学
TIANJIN CHENGJIAN UNIVERSITY
建筑抗震设计
主讲人：王庆鹏
•计算题专题
1 抗震设计原则 2 场地、地基与基础 3 地震作用与结构抗震验算 4 框架、抗震墙与框架-抗震墙 5 多层砌体房屋 6 底部框架-抗震墙、多层内框架砖砌房屋 7 单层钢筋混凝土柱厂房
计算步骤：（1）计算各层柱的侧移刚度； （2）计算各柱所分配的剪力； （3）计算柱的反弯点高度； （4）确定柱端弯矩； （5）按节点弯矩平衡条件和梁的 转动刚度确定梁端弯矩。
4 框架、抗震墙与框架-抗震墙
分层法
分层法
适用范围：框架的结构与荷载沿高度比较均匀；节点的梁 柱线刚度比≥3。
计算步骤：将框架的各层梁及其上下柱所组成的框架作为 一个独立的计算单元分层用力矩分配法进行计算，分层计 算所得的梁弯矩即为梁的最后弯矩；因为每一根柱都同时 属于上下两层，所以每一个柱的柱端弯矩需由上下两层计 算所1500kg
k3=600kN/m
4m
4m
m1=2000kg
k2=1200kN/m
k1=1800kN/m
5m
3 地震作用与结构抗震验算
工程结构抗震习题及答案
一、填空题1。
构造地震为由于地壳构造运动造成地下岩层断裂或错动引起的地面振动 2、建筑的场地类别,可根据土层等效剪切波速和场地覆盖层厚度划分为四类。
3、《抗震规范》将50年内超越概率为 10％的烈度值称为基本地震烈度，超越概率为 63。
2％的烈度值称为多遇地震烈度。
4、丙类建筑房屋应根据抗震设防烈度,结构类型和房屋高度采用不同的抗震等级。
5、柱的轴压比n定义为n=N/f c A c （柱组合后的轴压力设计值与柱的全截面面积和混凝土抗压强度设计值乘积之比）6、震源在地表的投影位置称为震中，震源到地面的垂直距离称为震源深度。
7、表征地震动特性的要素有三,分别为最大加速度、频谱特征和强震持时 .8、某二层钢筋混凝土框架结构，集中于楼盖和屋盖处的重力荷载代表值相等G1=G2=1200kN,第一振型φ12/φ11=1.618/1;第二振型φ22/φ21=—0。
618/1。
则第一振型的振型参与系数= 0、724。
9、多层砌体房屋楼层地震剪力在同一层各墙体间的分配主要取决于楼盖的水平刚度（楼盖类型）和各墙体的侧移刚度及负荷面积.10、建筑平面形状复杂将加重建筑物震害的原因为扭转效应、应力集中。
11、在多层砌体房屋计算简图中，当基础埋置较深且无地下室时，结构底层层高一般取至室外地面以下500mm处。
12、某一场地土的覆盖层厚度为80米,场地土的等效剪切波速为200m/s，则该场地的场地土类别为Ⅲ类场地 (中软土).13、动力平衡方程与静力平衡方程的主要区别是，动力平衡方程多惯性力和阻尼力。
14、位于9度地震区的高层建筑的地震作用效应和其他荷载效应的基本组合为。
15、楼层屈服强度系数为为第i层根据第一阶段设计所得到的截面实际配筋和材料强度标准值计算的受剪实际承载力与第i层按罕遇地震动参数计算的弹性地震剪力的比值 .16、某一高层建筑总高为50米，丙类建筑，设防烈度为8度,结构类型为框架—抗震墙结构，则其框架的抗震等级为二级，抗震墙的抗震等级为一级。
工程结构抗震习题答案
工程结构抗震习题答案一、 填空题1、构造地震为 由于地壳构造运动造成地下岩层断裂或错动引起的地面振动 。
2、建筑的场地类别，可依据 土层等效剪切波速 和 场地覆盖层厚度 划分为四类。
3、《抗震规范》将50年内超越概率为 10% 的烈度值称为基本地震烈度，超越概率为 63.2% 的烈度值称为多遇地震烈度。
4、丙类建筑房屋应依据抗震设防烈度， 结构类型 和 房屋高度 接受不同的抗震等级。
5、柱的轴压比n 定义为 n=N/f c A c （柱组合后的轴压力设计值和柱的全截面面积和混凝土抗压强度设计值乘积之比）6、震源在地表的投影位置称为 震中 ，震源到地面的垂直距离称为 震源深度 。
7、表征地振动特性的要素有三，分别为最大加速度、 频谱特征 和 强震持时 。
8、某二层钢筋混凝土框架结构，集中于楼盖和屋盖处的重力荷载代表值相等G 1=G 2=1200kN,第一振型φ12/φ11=1.618/1;其次振型φ22/φ21=-0.618/1。
则第一振型的振型参和系数j γ= 0、724 。
9、多层砌体房屋楼层地震剪力在同一层各墙体间的支配主要取决于 楼盖的水平刚度（楼盖类型） 和 各墙体的侧移刚度及负荷面积 。
10、建筑平面形态困难将加重建筑物震害的缘由为 扭转效应、应力集中 。
11、在多层砌体房屋计算简图中，当基础埋置较深且无地下室时，结构底层层高一般取至室外地面以下500mm 处 。
12、某一场地土的覆盖层厚度为80米，场地土的等效剪切波速为200m/s,则该场地的场地土类别为 Ⅲ类场地 （中软土） 。
13、动力平衡方程和静力平衡方程的主要区分是，动力平衡方程多 惯性力和 阻尼力 。
14、位于9度地震区的高层建筑的地震作用效应和其他荷载效应的基本组合为wk w w Evk Ev Ehk Eh GE G S S S S S γϕγγγ+++=。
15、楼层屈服强度系数为)(/)()(i V i V i e y y =ξ 为第i 层依据第一阶段设计所得到的截面实际配筋和材料强度标准值计算的受剪实际承载力和第i 层按罕遇地振动参数计算的弹性地震剪力的比值 。
工程结构抗震习题及答案
一、填空题1.构造地震为由于地壳构造运动造成地下岩层断裂或错动引起的地面振动 2、建筑的场地类别，可根据土层等效剪切波速和场地《抗震规范》将50年内超越概率为 10% 覆盖层厚度划分为四类。
3、的烈度值称为基本地震烈度，超越概率为 % 的烈度值称为多遇地震烈度。
4、丙类建筑房屋应根据抗震设防烈度，结构类型和房屋高度采用不同的抗震等级。
5、柱的轴压比n定义为n=N/f c A c（柱组合后的轴压力设计值与柱的全截面面积和混凝土抗压强度设计值乘积之比）6、震源在地表的投影位置称为震中，震源到地面的垂直距离称为震源深度。
7、表征地震动特性的要素有三，分别为最大加速度、频谱特征和强震持时。
8、某二层钢筋混凝土框架结构，集中于楼盖和屋盖处的重力荷载代表值相等G1=G2=1200kN,第一振型φ12/φ11=1;第二振型φ22/φ21=1。
则第一振型的振型参与系数= 0、724。
9、多层砌体房屋楼层地震剪力在j同一层各墙体间的分配主要取决于楼盖的水平刚度（楼盖类型）和各墙体的侧移刚度及负荷面积。
10、建筑平面形状复杂将加重建筑物震害的原因为扭转效应、应力集中。
11、在多层砌体房屋计算简图中，当基础埋置较深且无地下室时，结构底层层高一般取至室外地面以下500mm处。
12、某一场地土的覆盖层厚度为80米，场地土的等效剪切波速为200m/s,则该场地的场地土类别为 Ⅲ类场地 （中软土）。
13、动力平衡方程与静力平衡方程的主要区别是，动力平衡方程多惯性力 和阻尼力。
14、位于9度地震区的高层建筑的地震作用效应和其他荷载效应的基本组合为 wk w w Evk Ev Ehk Eh GE G S S S S S γϕγγγ+++=。
15、楼层屈服强度系数为)(/)()(i V i V i e y y =ξ 为第i 层根据第一阶段设计所得到的截面实际配筋和材料强度标准值计算的受剪实际承载力与第i 层按罕遇地震动参数计算的弹性地震剪力的比值 。
建筑结构抗震计算题及例题答案
《建筑结构抗震》（清华大学出版社）计算题及例题解答1.某两层房屋计算简图如图1所示。
已知楼层集中质量为1100t m =，250t m =，每层层高均为h ，楼板平面内刚度无限大，沿某抗震主轴方向的层间剪切刚度为120000kN m k =，210000kN m k =。
求该结构体系在该抗震主轴方向的自振周期、振型和振型参与系数。
图1 动力模型计算简图【解】1m 100t =，2m 50t =，m /kN 20000k 1=，m /kN 10000k 2=（1）自振圆频率⎥⎥⎦⎤⎢⎢⎣⎡+++⎪⎪⎭⎫ ⎝⎛-±++=ω）（2212112222112212122,1m k 2m k k 2m k m k m k m k m k k 21⎥⎥⎦⎤⎢⎢⎣⎡⨯++⨯+⎪⎭⎫ ⎝⎛-±++=）（50100002100100002000021001000050100001002000050100001001000020000212）（30020030021±+==100400⎧⎨⎩ s /rad 101=ω∴，s /rad 202=ω∴（2）自振周期628.01014.322T 11=⨯=ωπ=314.02014.322T 22=⨯=ωπ=（3）振型第一主振型：210000101001000020000k m k k X X 22211211112=⨯-+=ω-+=第二主振型：110000201001000020000k m k k X X 22221212122=⨯-+=ω-+=（4）振型参与系数3225011002501100X m X m X m X m Xm Xm 222122211112211121i 21ji21i 1ii1=⨯+⨯⨯+⨯=++==γ∑∑== 3115011001501100X m X m X m X m Xm X m 222222221122221121i 22ii21i 2ii2=-⨯+⨯-⨯+⨯=++==γ∑∑==）（）（2. 某三层钢筋混凝土框架，如图2和图3所示。
工程结构抗震计算题
1某两层钢筋混凝土框架，集中于楼盖和屋盖处的重力荷载代表值相等，每层层高皆为4.0m ，框架的自振周期；Ⅱ类场地，7度第二组（，结构的阻尼比为，试用底部剪力法计算各层水平地震作用Fi 及各层层剪力Vi 。
（1）求结构总水平地震作用：033.008.0028.140.09.0max 9.011=⨯⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=ααTT g（3分）kN 2040)12001200(85.0eq =+=∑=G C G （3分）kN 32.672040033.0eq 1Ek =⨯==G F α （3分） （2）求作用在各质点上的水平地震作用s T s T g 56.04.04.14.1028.11=⨯=>=092.001.0028.108.001.008.01=+⨯=+=T n δ（2分）kN 2.632.67092.0Ek n n =⨯==∆F F δ（1分） )1(n Ek 1111δ-=∑=F HG H G F nj jjkN 37.20)092.01(32.67812004120041200=-⨯⨯+⨯⨯=（3分）n n Ek 1222)1(F F HG H G F nj jj∆+-=∑=δkN 95.462.6)092.01(32.67812004120081200=+-⨯⨯+⨯⨯=（4分）（3）求层间剪力 kN 32.6795.4637.20211=+=+=F F V （1分）kN 95.4622==F V （1分）2某两层钢筋混凝土框架，集中于楼盖和屋盖处的重力荷载代表值相等kN 120021==G G ，每层层高皆为4.0m ，框架的自振周期s 393.0 s,028.121==T T ；第一主振型000.111=φ，618.112=φ；第二主振型000.121=φ，618.022-=φ；Ⅱ类场地，7度第二组（)08.0 s,40.0max ==αg T ，结构的阻尼比为05.0=ζ，试按振型分解反应谱法计算框架的楼层地震剪力。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
（二）计算题工程结构抗震计算1．已知一个水塔，可简化为单自由度体系。
10000m kg =，1kN cm k =，该结构位于Ⅱ类场地第二组，基本烈度为7度（地震加速度为0.10g ），阻尼比0.03ξ=，求该结构在多遇地震下的水平地震作用。
解：（1）计算结构的自振周期22 1.99T s === （2）计算地震影响系数查表2得，0.4g T s =，查表3得，max 0.08α=。
由于0.030.05ξ=≠应考虑阻尼比对地震影响系数形状的调整。
20.050.050.0311 1.160.08 1.60.08 1.60.03ξηξ--=+=+=++⨯0.050.050.030.90.90.940.360.360.03ξγξ--=+=+=++⨯由上图2可知，()0.94max 0.40.08 1.160.02051.99g T T γαα⎛⎫⎛⎫==⨯⨯= ⎪ ⎪⎝⎭⎝⎭（3）计算水平地震作用0.020*******.812011N F G α==⨯⨯=2．计算仅有两个自由度体系的自由振动频率。
假设[]11122122k k K kk ⎡⎤=⎢⎥⎣⎦ []1200m M m ⎡⎤=⎢⎥⎣⎦解：根据多自由度体系的动力特征方程[][]20K M ω-=，有[][]111212221222000k k m K M kk m ωω⎡⎤⎡⎤-=-=⎢⎥⎢⎥⎣⎦⎣⎦整理得()()4212112221112212210m m k m k m k k k k ωω-++-=解方程得2112211212k k m m ω⎛⎫=+⎪⎝⎭2112221212k k m m ω⎛⎫=++ ⎪⎝⎭3．图示钢筋混凝土框架结构的基本周期10.467T s =，抗震设防烈度为8度，Ⅱ类场地，设计地震分组为第二组（0.40g T s =）。
通过计算已经求得相应于结构基本自振周期的水平地震影响系数值10.139α=，试用底部剪力法计算多遇地震时的层间剪力。
3.5m3.5m3.5m3K=2K=1K=解：（1）计算结构等效总重力荷载代表值()1230.850.85eqG G G G G==⨯++∑()0.852*********.8=⨯++⨯5997.6kN=（2）计算结构总水平地震作用10.1395997.6833.7kNEK eqF Gα==⨯=（3）计算顶部附加水平地震作用11.4 1.40.40 5.6s0.467sgT T=⨯=>=故，不需考虑顶部附加水平地震作用，即0nδ=。
（4）计算各楼层水平地震作用（如下图所示）根据公式()11i ii n EKnj jjG HF FG Hδ==-∑分别计算各楼层水平地震作用，如下：12709.8 3.5833.7166.7kN2709.8 3.52709.871809.810.5F⨯⨯=⨯=⨯⨯+⨯⨯+⨯⨯22709.87.0833.7333.5kN2709.8 3.52709.871809.810.5F⨯⨯=⨯=⨯⨯+⨯⨯+⨯⨯32709.810.5833.7333.5kN 2709.8 3.52709.871809.810.5F ⨯⨯=⨯=⨯⨯+⨯⨯+⨯⨯（5）计算各楼层的层间地震剪力（如下图所示）1123833.7kN V F F F =++= 223667.0kN V F F =+=33333.5kN V F ==3333.5kNV =2667.0kNV =1833.7kNV =4．某多层砌体接结构承重墙段A ，如下图所示，两端均设构造柱，墙厚240mm ，长度4000mm ，采用烧结普通砖砌筑。
砌体抗剪强度设计值v 0.14MPa f =时，对应于重力荷载代表值的砌体截面平均压应力00.3MPa σ=。
求，该墙段截面抗震受剪承载力（kN ）2402404000240解：两端均有构造柱约束的承重墙体RE 0.9γ=。
该墙体的v0.32.140.14f σ==，查表得正应力影响系数N 1.138ξ=。
代入式子vE N v f f ξ=中，得到砌体沿阶梯型截面破坏的抗震抗剪强度设计值为：vE N v 1.1380.140.159MPa f f ξ==⨯=代入式子vE REf AV γ=中，则得该墙段截面抗震受剪承载力为：vE RE0.1594000240169.6kN 0.9f AV γ⨯⨯===三 计算题（38分）1.某二层钢筋混凝土框架，层高 H1=H2=4m ，跨度为8m ，集中于楼盖和屋盖处的重力荷载代表值相等G1=G2=1176KN,相应质量m1=m2=120000kg,柱的截面尺寸400mmx 400mm ，层间刚度K1=K2=20000KN/m 要求计算结构自振周期和相应振型，并验算振型刚度矩阵的正交性（10分）解：（1）G 2[]()m N K K K K K K K K K K /10.20.20.20.4022211211222216⨯⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--+= []()kg g G gG m m M 5102.1002.1/200/12001⨯⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡= 由2222112111200122211211222=--=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡ωωωm K K K m K m m K K K K 可得()()()12112221122211141222111212221m /K K K K m /K m /K /m /K m /K /,--++=μω = 66.6321=ω s /98.71=ω S T 79.0/211==ωπ339.43622=ωs /89.202=ωS T 301.0/222==ωπ5分相应的振型为：1618011112211121.m K K X X =--=ω 1618111112221222.m K K X X -=--=ω 验算振型正交性：{}{}010003.0101618.1202020401,618.022122221121121,1166≈⨯=⨯⎭⎬⎫⎩⎨⎧-⎥⎦⎤⎢⎣⎡--=⎭⎬⎫⎩⎨⎧⎥⎦⎤⎢⎣⎡X X K K K K X X 2二质点体系如图所示，各质点的重力荷载代表值分别为G 1=600KN ， G 2=500KN ，层高如图所示。
该结构建造在设防烈度为8度、场地土特征周期T g =0.25s 的场地上，其水平地震影响系数最大值分别为αmax =0.16（多遇地震）。
已知结构的阻尼比为0.05，主振型和自振周期分别为⎭⎬⎫⎩⎨⎧=⎭⎬⎫⎩⎨⎧000.1488.01211X X ⎭⎬⎫⎩⎨⎧-=⎭⎬⎫⎩⎨⎧000.1710.12221X X =1T 0.358s =2T 0.156s要求：用振型分解反应谱法计算结构在多遇地震作用下各层的层间地震剪力i V (10分)解：由已知条件得s T g 25.016.0max ==α，116.016.00.1358.025.09.0m ax 11=⨯⨯⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=ηααγT T g16.0max 2==ηαα{}[]{}{}[]{}233.11111==X M X R M X T T γ{}[]{}{}[]{}233.02222-==X M X R M X T TγKN X G F 88.411111111==γα KN X G F 514.712112121==γα3分KN X G F 25.381221212==γα KN X G F 64.182222222-==γα3分最后求层间剪力。
第二层层间剪力：()KN F F V 90.732222221=+=2分第一层层间剪力： ()()()KN F F F F V 075.11512221222111=+++=3．如图所示体系，各层重力荷载代表值G 1＝2700KN 、G 2 ＝2700KN 、G 3＝1800KN ，刚度K 1＝245000KN/m 、 K 2 ＝195000KN/m 、 K 3＝98000KN/m ，层高H 1=3.5m 、H 2=3.5m 、 H 3=3.5m ，建筑场地为二类，抗震设防烈度为8度，设计地震分组为第二组，试求结构的基本自振周期并用底部剪力法求结构在多遇地震作用下各层的水平地震作用(结构阻尼比为0.05)。
（15分）G 3解：求结构基本自振周期将各质点重力荷载代表值作为水平力分别作用在各质点处，1，2，3质点水平位移为：()()mK G u u m K G G u u mK G G G u 0709.03/3230525.02/32120294.01/3211=+==++==++=采用能量法，结构基本自振周期为：s u G u G u G u G u G u G T 465.033221133221121222=++++= 7分由已知条件查表得s T g 4.016.0max ==α，14.016.00.1465.04.09.0m ax 1=⨯⨯⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛=ηααγTT gs T T g 35.04.11=≤，()KN G F eq EK 8.85618002700270085.014.0=++⨯⨯==α各质点水平地震作用标准值为： KN F H G H G H G H G F EK 36.171332211111=++=KN F H G H G H G H G F EK 72.342332211222=++=KN F H G H G H G H G F EK 72.342332211333=++=其中11h H = 212h h H += 3213h h h H ++=五、计算题（本大题共2个小题，共30分）。
1．根据下表计算场地的等效剪切波速。
（10分）土层厚度 2.2 5.8 8.2 4.5 4.3 )/(smvs180 200 260 420 530 2．试用底部剪力法计算下图体系在多遇地震下的各层地震剪力。
已知设防烈度为8度，设计基本加速度为0.2g，Ⅲ类场地一区，m1=116.62t, m2=110.85t, m3=59.45t,T1=0.716s,δn=0.0673,ξ=0.05.（20分）m axamax245.0aηmax)(aTTa gγ=max21)]5(2.0[aTTag--=ηηγaT(s)00.1Tg5Tg 6.0当ξ=0.05时，η2=1.0 η1=0.02 γ=0.9地震影响系数曲线水平地震影响系数最大值kN Geq F EK 95.250105.08.9)45.5985.11062.116(85.01=⨯⨯++⨯==α kN F F EK n n 89.1695.2500673.0=⨯==∆δ[]31208.903.31848.9)5.60.60.5(45.595.1285.1105.662.116=⨯=⨯++⨯+⨯+⨯=∑jjHG 作用在结构各楼层上的水平地震作用为：kN F n H G H G F EK jj 72.5595.250)0673.01(03.31845.662.116)1(111=⨯-⨯⨯=-=∑δkN F n H G H G F EK jj 86.10195.250)0673.01(03.31845.1285.110)1(222=⨯-⨯⨯=-=∑δkN F n H G H G F EK jj 48.7695.250)0673.01(03.31845.1745.59)1(333=⨯-⨯⨯=-=∑δ 各楼层的地震剪力为：kN F F F F V n 95.2503211=∆+++=kN F F F V n 23.195322=∆++= kN F F V n 37.9333=∆+=1、某两层钢筋混凝土框架，集中于楼盖和屋盖处的重力荷载代表值相等kN 120021==G G ，每层层高皆为4.0m ，各层的层间刚度相同m /kN 863021=∑=∑D D ；Ⅱ类场地，设防烈度为7度，设计基本地震加速度为0.10g ，设计分组为第二组，结构的阻尼比为05.0=ζ。