传热学分章作业
传热学9-10

t0
dx
H
0
具有内热源的平板导热微分方程
8
内热源强度的确定
为单位时间肋片单位体积
l
Φc
h t∞
的对流散热量 如图,在距肋基x处取一长度 为dx的微元段,该段的对流换 热量为:
根据牛顿冷却定律
δ
0
Φx
Φx+dx
x
t0
dx
H
肋片表面温度 流体温度
s = h (pdx)(t – t∞)
因此该微元段的内热源强度为:
于是肋端温度:tH = H + tf = 71.98 + 20 = 91.98 ℃ 肋片散热量:
Ac o m th m H
2 6 8 .5 W
=120×0.8×0.006×5.796×(95-20)×0.282
=70.62 W
29
本次作业
2-51;2-52;2-55; 2-58; 2-59
27
【例】一矩形肋厚6mm, 高度H=50mm, 宽800mm, 材料的 导热系数=120W/(m℃)。肋基处温度T0= 95℃, 肋片周围 流体为Tf=20 ℃, 如果取表面传热系数h= 12W/(m2℃)。 试求肋端的温度与肋片的散热量。
解: 依题意H=0.05m, = 0.006m
m hP
在温度均与的流体中 两侧流体特性相同
l
t
t0 h t∞ h t∞
温度分布对称 R = /2
24
x
2. 肋片如何选用?
Bi
1 h
=
h
≤0.25
(1)肋片应该选用大的材料还是小的材料? (2)加薄肋好还是加厚肋好? (3)如果管子两侧的h相差很大,肋片应该加在h大 的一侧还是加在h小的一侧?
数值传热学作业-第二章
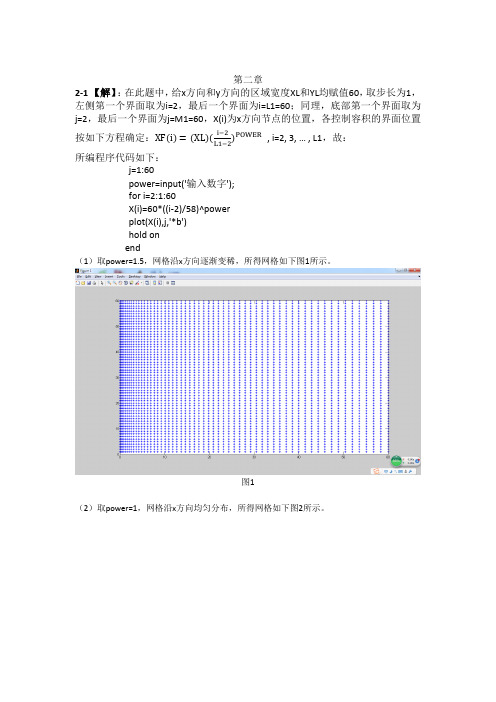
第二章2-1 【解】:在此题中,给x方向和y方向的区域宽度XL和YL均赋值60,取步长为1,左侧第一个界面取为i=2,最后一个界面为i=L1=60;同理,底部第一个界面取为j=2,最后一个界面为j=M1=60,X(i)为x方向节点的位置,各控制容积的界面位置)POWER, i=2, 3, … , L1,故:按如下方程确定:XF(i)=(XL)(i−2L1−2所编程序代码如下:j=1:60power=input('输入数字');for i=2:1:60X(i)=60*((i-2)/58)^powerplot(X(i),j,'*b')hold onend(1)取power=1.5,网格沿x方向逐渐变稀,所得网格如下图1所示。
图1(2)取power=1,网格沿x方向均匀分布,所得网格如下图2所示。
图2(3)取power=0.5,网格沿x方向逐渐变密,所得网格如下图3所示。
图32-2、2-3 【解】守恒形式如下:u ðuðx=12ð(u2)ðx=ηð2uðy2方程两端积分如下:∫∫∫12ð(u2)ðxsn dtdxdywe =∫∫∫ηð2uðy2sndtdxdywet+Δttt+Δtt所以∫∫12(u w2−u e2)dtdy we =∫∫η[(ðuðy)n−(ðuðy)s]dtdxwet+Δttt+Δtt对流项:取为阶梯式,则:∫∫12(u w2−u e2)dtdywe =12[(u2)e t−(u2)w t]∆t∆yt+Δt t扩散项: 取为阶梯式,则∫∫η[(ðu ðy )n −(ðu ðy )s ]dtdx wet+Δtt=η[(ðu ðy )n t −(ðu ðy )s t]∆t∆xu 随x,y 分段线性变化,则u e2=u E 2−u P 22, u e 2=u W 2−u P22(ðu ðy )n t =u N 2−u P 2(δy )n ,(ðu ðy )n t =u P 2−u S 2(δy )n因为 (δy )n=(δy )n =∆y所以:u E 2−u W24η∆x=u N t −2u P 2+u St (∆y )22-7【解】将2,i T 、3,i T 及4,i T 对点()1,i 作Taylor 展开,有:()()()()Λ+∆∂∂+∆∂∂+∆∂∂+∆∂∂+=!4!3!24443332221,2,y yT y y T y y T y y T T T i i (2-7-1)()()()()Λ+∆∂∂+∆∂∂+∆∂∂+∆∂∂+=!42!32!2224443332221,3,y yT y y T y y T y y T T T i i (2-7-2)()()()()Λ+∆∂∂+∆∂∂+∆∂∂+∆∂∂+=!43!33!2334443332221,4,y yT y y T y y T y y T T T i i (2-7-3)(2-7-1)×18 +(2-7-2)×(-9)+(2-7-3)×2 得:i,1i,2i,3i,4y 011T 18T 9T 2T Ty6y=-+-∂=-∂∆ (2-7-4)由0=∂∂-=y B yT q λ,将式(2-7-4)代入得;B i,1i,2i,3i,46yq 1T 18T 9T 2T 11λ∆⎛⎫=-++ ⎪⎝⎭(2-7-5)2-9解:另点2对点1做泰勒展开,有p(2,n)=p(1,n)+ðpðx |1,n∆x+ð2pðx2|1,n∆x22!….另点3对点1做泰勒展开,有p(3,n)=p(1,n)+ðpðx |1,n2∆x+ð2pðx2|1,n(2∆x)22!….将第一式乘4减去第二式,则存在下式ðp ðx |1,n=4p2−p3−3p12∆x,O(∆x2)则此式为二阶精度的边界节点1上的压力梯度表示式.。
传热学作业——精选推荐

传热学作业第一章绪论能量平衡分析1-8.有两个外形相同的保温杯A与B,注入同样温度、同样体积的热水后不久,A杯的外表面就可以感觉到热,而B杯的外表面则感觉不到温度的变化,试问哪个保温杯的质量较好?答:B:杯子的保温质量好。
因为保温好的杯子热量从杯子内部传出的热量少,经外部散热以后,温度变化很小,因此几乎感觉不到热。
导热1-10 一炉子的炉墙厚13cm,总面积为20m2,平均导热系数为1.04w/m.k,内外壁温分别是520℃及50℃。
试计算通过炉墙的热损失。
如果所燃用的煤的发热量是2.09×104kJ/kg,问每天因热损失要用掉多少千克煤?解:根据傅利叶公式每天用煤Q??A?t1.04?20?(520?50)??75.2KW?0.1324?3600?75.2?310.9Kg/d4 2.09?10 1-12 在一次测定空气横向流过单根圆管的对流换热实验中,得到下列数据:管壁平均温度tw=69℃,空气温度tf=20℃,管子外径d=14mm,加热段长80mm,输入加热段的功率8.5w,如果全部热量通过对流换热传给空气,试问此时的对流换热表面传热系数多大?解:根据牛顿冷却公式q?2?rlh?tw?tf? qh??dtw?tf=49.33W/(m2.k) 所以热阻分析1-21 有一台气体冷却器,气侧表面传热系数h1=95W/(m2.K),壁面厚?=2.5mm,??46.5W/(m.K)水侧表面传热系数h2?5800W/(m2.K)。
设传热壁可以看成平壁,试计算各个环节单位面积的热阻及从气到水的总传热系数。
你能否指出,为了强化这一传热过程,应首先从哪一环节着手?解:R1?111?0.010526;R20.0025?5.376?10?5;R31.724?10?4;h1h25800?46. 5K?则111h1h2?=94.7W/(m2.K),应强化气体侧表面传热。
第二章稳态热传导平板导热2-2 一冷藏室的墙由钢皮矿渣棉及石棉板三层叠合构成,各层的厚度依次为0.794mm.,152mm及9.5mm,导热系数分别为45W/(m.K),0.07W/(m.K)及0.1W/(m.K)。
传热学第五第1-4章习题解答

《传热学》(第五版)第0章-第3 章习题解答第0章 绪论0-4、解答题略。
0-6 答:对流换热和对流不是同一现象.热对流是指:若流体有宏观运动,且内部存在温差,则由于流体各部分之间发生相对位移,冷热流体相互掺混而产生的热量传递现象,简称对流.如热空气往上升时,把热量传给上部空间的冷空气的流动属于对流.对流换热是指流体在与它温度不同的壁面上流动时,二者之间(流体与壁面之间)产生的热量交换现象。
它是导热与热对流同时存在的复杂热传递过程。
如暖气片周围的空气受热后,沿着教室墙壁的流动;热水在热力管道内的流动等属于对流换热.0-6 答:首先,冬季和夏季的最大区别在于室外温度的不同.夏季室外温度比室内温度高,因此通过墙壁的热量传递是由室外传向室内.而冬季室外气温比较比室内低, 通过墙壁的热量传递是由室内传向室外.因此冬季和夏季墙壁内表面的温度不同,夏季高而冬季低.因此人体在冬季通过辐射而与墙壁的散热比夏季高很多.人对冷暖感觉的衡量指标是散热量的大小而不是温度的高低,即当人体散热量少时感到热, 人体散热量多时感到冷.拉上窗帘后顿觉暖和,是因为窗帘起到了保温层的作用,减少了通过窗户向外散失的热量,故顿觉暖和!0-9 答:真空玻璃夹层:阻止热传导和对流换热;夹层内镀银:反射辐射热;热量如何通过瓶胆传到外界: 略瓶胆的玻璃尖嘴打破变得很差,因为空气进入夹层后,会由于空气与瓶胆壁面之间的对流换热而引起热量散失. 0-13:解: 61.0124161.036.08711121=++=++=h h R k λδ(m 2·K)/W 64.1610.011===k R k W/(m 2·K) 92.45)1018(64.1)(21=+=-=f f t t k q W/m 2 ∵)(111w f t t h q -= ∴47.178792.4518111=-=-=h q t t f w ℃ 又∵)(222f w t t h q -= ∴63.912492.4510222-=+-=+=h q t t f w ℃38.292.45⨯⨯==ΦqA =385.73 W0-14:解:4104.723452.0-⨯=⨯⨯==A R A λδ K/W (面积为A 2的平板表面上的热阻) 3104.4452.0-⨯===λδR (m 2·K)/W (单位面积热阻)431007.3104.4150285⨯=⨯-=∆=-R t q W/m 2 541084.161007.3⨯≈⨯⨯==ΦqA W0-15:解: ∵)(f w t t h q -= ∴15573511085=+=+=h q t t f w ℃ W7.20065.214.31050511023=⨯⨯⨯⨯=⋅⋅==Φ-lR q qA π0-17:解: (1)012.0851500011121=+=+=h h R (m 2·K)/W 3.83012.011===R k W/(m 2·K) 90963624)45500(3.83=⨯-⨯=∆=ΦtA k W(2)92820024)45500(85'=⨯-⨯=∆=ΦtA k W误差%2909636909636928200%100'≈-=⨯ΦΦ-Φ=ε (3)可以忽略,因为厚度很小,金属的导热系数较大,则导热热阻λδ很小。
数值传热学作业-第四章

4-1解:采用区域离散方法A 时;内点采用中心差分123278.87769.9T T T ===22d T T=0dx - 有 i+1i 122+T 0i i T T T x---=∆ 将2点,3点带入 321222+T 0T T T x --=∆ 即321209T T -+= 432322+T 0T T T x --=∆4321322+T 0T T T x --=∆ 即4321209T T T -+-= 边界点4(1)一阶截差 由x=1 1dT dx =,得 4313T T -=(2)二阶截差 11B M M q x x xT T S δδλλ-=++V所以 434111. 1.36311T T T =++即 43122293T T -=采用区域离散方法B22d TT=0dx - 由控制容积法 0w edT dT T x dT dT ⎛⎫⎛⎫--∆= ⎪ ⎪⎝⎭⎝⎭ 所以代入2点4点有322121011336T T T T T ----= 即 239028T T -=544431011363T T T T T ----= 即3459902828T T T -+= 对3点采用中心差分有432322+T 013T T T --=⎛⎫⎪⎝⎭即2349901919T T T -+= 对于点5 由x=11dT dx =,得 5416T T -= (1)精确解求左端点的热流密度由 ()21x x eT e e e -=-+所以有 ()2220.64806911x xx x dT e e q e e dxe e λ-====-+=-=++ (2)由A 的一阶截差公式210.247730.743113x T T dT q dxλ=-=-==⨯= (3)由B 的一阶截差公式0.216400.649213x dTq dxλ=-=-== (4)由区域离散方法B 中的一阶截差公式:210.108460.6504()B BT T dT dx x δ-⎛⎫==⨯= ⎪⎝⎭ 通过对上述计算结果进行比较可得:区域离散B 有控制容积平衡法建立的离散方程与区域离散方程A 中具有二阶精度的格式精确度相当!4-3解: 对平板最如下处理:1 2 3 4由左向右点分别表述为1、2、3、4点,x 的正方向为由左向右; 控制方程为λd 2tdx +S =0 (1)边界条件为X=0,T=75℃;X=0.1,λdTdx +ℎ(T −T f )=0;则2、3点采用二阶截差格式,有 则有以下两式:λT3−2T2+T1∆x+S=0(2)λT4−2T3+T2∆x2+S=0(3)一阶截差公式可由λdTdx+ℎ(T−T f)=0变形得到λ(T4−T3∆x)=h(T4−T f)再变形得到T4=[T3+h×∆xλT f]/(1+h×∆xλ)(4)二阶截差公式可以联立λT5−2T4+T3∆x2+S=0和λ(T5−T32∆x)=h(T4−T f),可得以下公式T4=[T3+∆x2S2λ+h×∆xλ]/(1+h×∆xλ)(5)分别联立2、3、4式与2、3、5式,把S=50×103W/m3,λ=10W/m∙℃,h=50 W/m∙℃,T f=25℃,T1=75℃,∆x= 1/30带入到式子中,则有联立2、3、4式的解为:T2=78.58℃,T3=76.59℃,T4=69.03℃联立3、4、5式的解为:T2=80.42℃,T3=80.28℃,T4=74.58℃对控制方程进行积分,并将边界条件带入,则有关于T的方程T=−2500x2+250x+75(6)把x2=130,x3=230,x3=0.1代入上述6式则有:T2=80.56℃,T3=80.56℃,T4=75.1℃相比之下,对右端点采用二阶截差的离散更接近真实值4-4解:对平板作如下分析:1 2 3 4 5 由左向右分别对点编号为1、2、3、4、5 控制方程与4-3相同,为λd 2tdx +S =0 (1)边界条件为X=0,T=75℃;X=0.1,λdTdx +ℎ(T −T f )=0;设1点和2点的距离为∆x ,另1点对2点进行泰勒展开,有d 2t dx =(T 1−T 2+dT dx ∆x )2∆x其中dT dx=T 3−T 22∆x,则有λ2T 1−3T 2+T 3∆x 2+S =0 (2)对3点进行离散有λT 4−2T 3+T 2∆x 2+S =0 (3)对右端点有: [a p +A 1ℎ+(δx )5λ]T 4=a w T 3+[S/∆x +AT f 1ℎ+(δx )5λ]代入数据有T 3−3T 2+155.56=0 T 4−2T 3+T 2=−5.56342.85T4-300T3=1681解得:T2=78.1℃,T3=78.7℃,T4=73.8℃由导热定律有T4−T3∆x =2T5−T4∆x则有T5=71.35℃4—12编写程序:M=rand(10,3)A=M(:,1);B=M(:,2);C=M(:,3);B(10)=0;C(1)=0;T=12:21;D(1)=A(1)*T(1)-B(1)*T(2)for i=2:9;D(i)= A(i)*T(i)-B(i)*T(i+1)-C(i)*T(i-1)endD(10)= A(10)*T(10)-C(10)*T(9);P(1)=B(1)/A(1);Q(1)= D(1)/A(1);for i=2:10;P(i)=B(i)/(A(i)-C(i)*P(i-1));Q(i)=(D(i)+C(i)*Q(i-1))/(A(i)-C(i)*P(i-1)); endfor i=10:-1:2;t(10)=Q(10);t(i-1)=P(i-1)*t(i)+Q(i-1);enddisp(D(1:10))disp(T(1:10))disp(t(1:10))运行结果:由运行结果可知:无论系数怎样变化,T与t都是一致的。
(完整版)第四版传热学第一、二章习题解答

传热学习题集第一章思考题1. 试用简练的语言说明导热、对流换热及辐射换热三种热传递方式之间的联系和区别。
答:导热和对流的区别在于:物体内部依靠微观粒子的热运动而产生的热量传递现象,称为导热;对流则是流体各部分之间发生宏观相对位移及冷热流体的相互掺混。
联系是:在发生对流换热的同时必然伴生有导热。
导热、对流这两种热量传递方式,只有在物质存在的条件下才能实现,而辐射可以在真空中传播,辐射换热时不仅有能 量的转移还伴有能量形式的转换。
2. 以热流密度表示的傅立叶定律、牛顿冷却公式及斯忒藩-玻耳兹曼定律是应当熟记的传热学公式。
试写出这三个公式并说明其中每一个符号及其意义。
答:① 傅立叶定律:dx dt q λ-=,其中,q -热流密度;λ-导热系数;dx dt-沿x 方向的温度变化率,“-”表示热量传递的方向是沿着温度降低的方向。
② 牛顿冷却公式:)(f w t t h q -=,其中,q -热流密度;h -表面传热系数;wt -固体表面温度;ft -流体的温度。
③ 斯忒藩-玻耳兹曼定律:4T q σ=,其中,q -热流密度;σ-斯忒藩-玻耳兹曼常数;T -辐射物体的热力学温度。
3. 导热系数、表面传热系数及传热系数的单位各是什么?哪些是物性参数,哪些与过程有关?答:① 导热系数的单位是:W/(m.K);② 表面传热系数的单位是:W/(m 2.K);③ 传热系数的单位是:W/(m 2.K)。
这三个参数中,只有导热系数是物性参数,其它均与过程有关。
4. 当热量从壁面一侧的流体穿过壁面传给另一侧的流体时,冷、热流体之间的换热量可以通过其中任何一个环节来计算(过程是稳态的),但本章中又引入了传热方程式,并说它是“换热器热工计算的基本公式”。
试分析引入传热方程式的工程实用意义。
答:因为在许多工业换热设备中,进行热量交换的冷、热流体也常处于固体壁面的两侧,是工程技术中经常遇到的一种典型热量传递过程。
5. 用铝制的水壶烧开水时,尽管炉火很旺,但水壶仍然安然无恙。
传热学作业学-作业

[4-1]:两块不同材料的平板组成如图4-73所示的大平板。
两板的面积分别为A 1和A 2,热导率分别为λ1和λ2。
如果该大平板的两个表面分别维持在均匀温度t 1及t 2,试导出通过该大平板的导热热量计算式。
t 2t 1A 1A 2λ1λ2解:取板A 为研究对象,取如下图所示的坐标,在距其侧面x 处,取一层厚dx 的微元体,列傅利叶定律的表达式,即111dt A dxφλ=- 分离变量后积分,并注意到热流量1φ与x 无关,得2211111x tx tdxdt A φλ=-⎰⎰。
即2121112111211()t t x x dt t t A x x dx A λλφ---==-⎰⎰,若设板厚为δ,则12111()t t A λφδ--=。
同理,板A2的导热量22122()t t A λφδ--=故大于板的导热量21121122()()t t A A φφφλλδ--=+=+[4-2]:有一厚度为20mm 的平面墙,热导率为1.3W/(m.K )。
为使每平方米墙的热损失不超过1500W ,在外面上覆盖了一层热导率为0.1 W/(m.K )的保温材料。
已知复合璧两侧的温度分别为750℃及55℃,试确定此时保温层的厚度。
解:通过平璧和保温层的热流密度 122121()t t q δδλλ-=+,即3311(75055)90.352010210 1.31.30.1q δδ---==⨯⨯++ 已知热量损失即导热量1500qA Φ=≤,A =1m 3固有3190.351500210 1.3δ-≤⨯+,解得10.0448m δ≥,因此,保温层厚度至少为45mm 。
t w1t w2t w3t w4[2-21]: 一钢制热风管,内径为160mm ,外径为170mm ,热导率λ1=58.2W/(m.K )。
热风管外包有两层保温材料,内层厚2=30mm δ,热导率λ2=0.135W/(m.K );外层厚2=80mm δ,热导率λ3=0.0932W/(m.K )。
传热学第五版章熙民_答案第一二三章

2T x 2
x
x
T dx c f dx b U dx T 4
整理得棒温度分布的导热微分方程式:
2T x 2
x
U 4 c T b T (T 取热力学温标) f
从微分方程的形式看,应该需要一个初始条件、两个边界条 件才能获得特解。 边界条件为:1) x 0 时
q q z q I r rdrddzd r r z q r t t t ; q ; q z ; r r z
2t 1 2t 2t I 2 2 2 rdrddzd 2 r r z
q x dt 2 b x dx
q x 0 0 ,无热流量
q x 2 ( 2000 ) 45 0.05 9000 ( W / m 2 )
(2) 将二阶导数代入式(a)
qv d 2t dx
2
2 b 2 ( 2000 ) 45 180000 ( W / m 3 )
整理得:
1-10 从宇宙飞船伸出一根细长散热棒, 以辐射换热将热量散 发到外部空间去,已知棒的发射率(黑度)为 ,导热系数 为 ,棒的长度为 l ,横截面面积为 f ,截面周长为 U ,棒根 部温度为 T0 ,外部空间是绝对零度的黑体,试写出描写棒温 度分布的导热微分方程式和相应的边界条件。 解: 导热微分方程,就是将付立叶定律结合能量守恒定 律(没有功交换时,就是热平衡原理)推出的数学关系式。 如图所示,取一个微元体长度为 dx ,从左边导入的热量
t x 600 K ; t x 400 K ;
解:这是一维的、无内热源的、常物性的、稳态导热问题。 平板内沿厚度方向温度分布呈线性。则 温度梯度: grad t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-10一长圆管被置于方形通道的正中间,如附图 所示,试确定每一对边的角系数、两邻边的角系数 及任一边对管子的角系数。
θ α
8-18一管状电加热器内表面温度为900k,ε=1,试 计算从加热表面投入到圆盘上的总辐射能。
解:作虚拟表面3、4
8-24 两块无限大平板的表面温度分别为t1和t2,发 射率分别为ε1及ε2,其间遮热板的发射率为ε3,试 画出稳态时三板之间辐射换热的网络图。
7-19暖房的升温作用可以从玻璃的光谱的穿透比变 化特性得到解释。有一块厚为3mm的玻璃,经测 定,其对波长为0.3-2.5μm的辐射能的穿透比为 0.9,而对其它波长的辐射能可以认为完全不穿透。 试据此计算温度为5800K的黑体辐射及温度为 300K的黑体投射到该玻璃上时各自的总穿透比。
7-23一直径为20mm的热流计探头,用以测定一 微小表面积A1的辐射热流,该表面的温度 T1=1000K。环境温度很低,因而对探头的影响 可以忽略不计。因某些原因,探头只能安置在与 A1表面法线成45°处,距离l=0.5m(见附图)。 探头测得的热量是1.815×10-3w。表面A1是漫射 的,而探头表面的吸收比可近似的取为1。试确定 A1的发射率。A1的表面积为4×10-4m2。
3.写出对流换热过程中的无量纲准则Re数、Pr数、 Pe数和Gr数的物理量组成,指出它们各自表示的 物理意义?并指出Nu数与导热过程中产生的Bi数 的差别?
Re
u L
; Pr
a; Pe
Pr• Re;Gr
gTL3
2
Re――表征给定流场的流体惯性力与其黏性力的对比 关系;Pe――表征给定流场的流体热对流能力与其热 传导(扩散)能力的对比关系; Pr――反映物质的动量扩散特性与其热量扩散特性的 对比关系; Gr――主要表征给定流场在浮升力作用下产生的流体 惯性力与其黏性力的对比关系。
热系数λ=17.5w/m•K,试问在稳态工况下表面3的
tw3温度为多少?
δ
解:
表面1到表面2的辐射换热量=表面2到表面3的导热
0 (T24
T14 )
t w3
tw2
ε=1.0
t w3
tw2
0 (T24 T14 )
127
5.67 (44 34 ) 0.1 17.5
a 15.2 4.23 10 6 (m2 / s) c 7820 460
1 15.2 2.45 Bi h 125 0.05
F0
a 2
4.23 10 6 360 0.05 2
0.61
由图3-6查得θm/θ0=0.85
tm=t∞-0.85(t∞- t0)=5+0.85(200-20)=47℃
面传热系数为h,物体的体积V,参与换热的面积
A,比热容和密度分别为c和ρ,物体的内热阻可
忽略不计,试列出物体温度随时间变化的微分方
程式。
解:
cV
dt
d
hA(t
t ) A (T 4
T4 )
0
t(0) t0
3-9一热电偶的ρcV/A之值为2.094kJ/m2·K,初始温 度为20℃,后将其置于320℃的气流中。试计算在气 流与热电偶之间的表面传热系数为58 w/m2·K及116 w/m2·K的两种情形下,热电偶的时间常数。
作为一维导热问题处理,试决定所需保温材料的厚度
环境温度tf2=25℃,外表面总表面传热系数h2=9.5
w/m2•K。
δA δB
解:按热平衡关系,有:
t f1 tw
1 A B
2 (tw t f 2 )
h1 tf1
h2 tf2
tw
A B
400 50 9.5(50 25)
132 .7
tw3
tw1=27℃
tw2=127℃
2-4一烘箱的炉门由两种保温材料A和B做成,且
δA=2δB(见附图)。已知λA=0.1 w/m•K,λB=0.06 w/m•K。烘箱内空气温度tf1=400℃,内壁面的总表 面传热系数h1=50 w/m2•K。为安全起见,希望烘箱 炉门的外表面温度不得高于50℃。设可把炉门导热
A1
8-2 设有如附图所示的两个微小面积A1、A2, A1=2×10-4m2,A2=3×10-4m2,A1为漫射表面, 辐射力E1=5×104W /m2,试计算由A1发出而落到 A2上的辐射能。
8-6试用简捷方法确定本题附图中的角系数X1,2。
解:(1)A1X1,2=A2X2,1,X2,1=1, X 1, 2
解:不考虑空气隙时侧得的导热系数记为λ0,则
At
d 2
4
150
0.02915
0
58.2
已知空气隙的平均厚度Δ1、Δ2均为0.1mm,并设导热系数分别为λ1、
λ2,则试件实际的导热系数应满足: 1 1 At
所以 1 1
0 1 2
分章作业
1-1对于附图所示的两种水平夹层,试分析冷、 热表面间热量交换的方式有何不同?
(a)中热量交换的方式主要有热传导和热辐 射。
(b)热量交换的方式主要有热传导,自然对 流和热辐射。
1-7一炉子的炉墙厚13cm,总面积为20m2,平均导 热系数为1.04w/m·k,内外壁温分别是520℃及50℃ 试计算通过炉墙的热损失。如果所燃用的煤的发热量 是2.09×104kJ/kg,问每天因热损失要用掉多少千克 煤?
3-48 一初始温度为25℃的正方形人造木块被置 于425℃的环境中,设木块的6个表面均可受到加 热,表面传热系数h=6.5W/m2.K,经过4小时50 分24秒后,木块局部地区开始着火。试推算此种 材料的着火温度。已知木块的边长0.1m,材料试 各向同性的,λ=0.65 W/m.K,ρ=810kg/m3, c=2550J/kg.K。 解:木块温度最高处位于角顶,这是三块无限大 平板相交处。
解:根据牛顿冷却公式
Q
8.5
49.3w / m2 • c
At 3.14 0.014 0.08 (69 20)
1-14宇宙空间可近似的看作0K的真空空间。一 航天器在太空中飞行,其外表面平均温度为 250K,表面发射率为0.7,试计算航天器单位 表面上的换热量?
解:航天器单位表面上的换热量
0 1 2
即
0
1 1 1 2
0.0001 0.00378
0.0001 0.00267
0.02646
0.03745
21.92
0.02915
0.02915
ቤተ መጻሕፍቲ ባይዱ
%
0
2-11一根直径为3mm的铜导线,每米长的电阻为 2.22×10-3Ω。导线外包有1mm、导热系数 0.15w/m.k的绝缘层。限定绝缘层的最高温度为65℃ 最低温度0℃,试确定这种条件下导线中允许通过的最 大电流。
解:最大允许通过电流发生在绝缘层表面温度为65℃, 最低温度0℃的情形。此时每米导线的导热量
Q 2 t 3.14 0.15 65 119.9W / m
l
ln d2 d1
ln
5 3
最大允许通过电流满足 Im2R 119.9
所以 I m 232 .4A
3-6一初始温度为t0的固体,被置于室温为t∞的房 间中。物体表面的发射率为ε,表面与空气间的表
Bi 6.5 0.05 0.5 1 0.65
由图3-7查得θs/θm=0.8
F0
a
r2
0.65 17424 810 2550 0.052
2.19
由图3-6查得θm/θ0=0.41 θs/θ0=(θm/θ0)( θs/θm)=0.8×0.41=0.328 角顶处无量纲温度:(θs/θ0)3=0.0353 所以角顶温度等于411℃。
8-28一平板表面接受到的太阳辐射为1262W/m2, 该表面对太阳能的吸收比为α,自身辐射的发射率为 ε。平板的另一侧绝热。平板的向阳面对环境的散热 相当于对-50℃的表面进行辐射换热。试对ε=0.5、 α=0.9;ε=0.1、α=0.15两种情况,确定平板表面 处于稳定工况下的温度。
8-37两个相距1m、直径为2m的平行放置的圆盘, 相对表面的温度分别为t1=500℃,t2=200℃,发射 率分别为ε1=0.3及ε2=0.6,圆盘的另外两个表面的 换热略而不计。试确定下列两种情况下每个圆盘的净 辐射换热量: 1.两圆盘被置于t3=20℃的大房间中; 2.两圆盘被置于一绝热空腔中。
1 2 B B
50 0.1 0.06
由此得,δ =0.0396m
2-8在如图所示的平板导热系数测定装置中,试件 厚度δ远小于直径d。由于安装制造不好,试件与冷 热表面之间存在着一厚度为Δ=0.1mm的空气隙。 设热表面温度t1=180℃,冷表面温度t2=30℃,空 气隙的导热系数可分别按t1、t2查取。试计算空气 隙的存在给导热系数的测定带来的误差。通过空气 隙的辐射换热可以忽略不计。(Φ=58.2w d=120mm)
1. 非周期性的加热或冷却过程可以分为哪两个阶 段,它们各自有什么特征?
答:非周期性的加热或冷却过程可以分为初始状况阶段和正 规状况阶段.前者的温度分布依然受着初始温度分布的影响, 也就是说热扰动还没有扩散到整个系统,系统中仍然存在着
初始状态,此时的温度场必须用无穷级数加以描述;而后者
却是热扰动已经扩散到了整个系统,系统中各个地方的温度
解:时间常数 cV
hA
对h=58 w/m2·K,有 2.094 103 36.1s
