结构力学 朱慈勉 第6章课后答案全解
最新完整的结构力学答案-同济大学朱慈勉
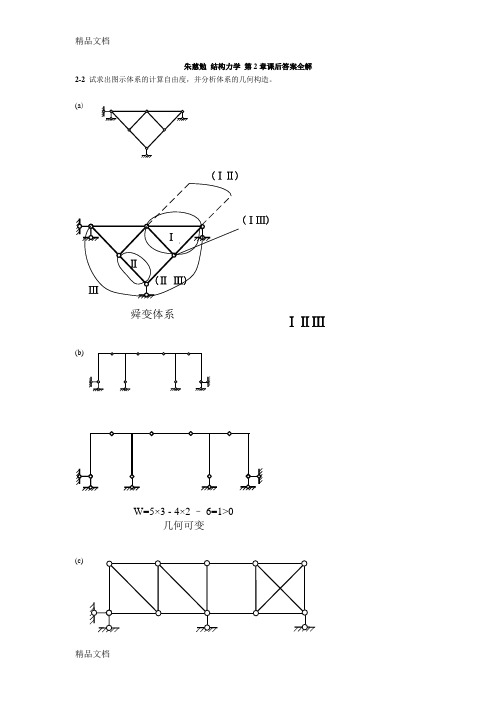
C 10kN
D
A
40kN·m
6m
精品文档
3m
精品文档
M 30
30 30
Q 10
210
(c)
2kN/m 4kN
B
C
6kN
A
D
6m
M 6
6
3m
3m
10 110
Q
5
4
7
2
2m 2m
(d)
4kN·m 2kN
C
D
E 2kN
A
B
6m
精品文档
精品文档
M 4
4 N
0
Q
4 4 4 4/3
0
0
(e)
C
1kN/m 4m
2
qa 2
q
G
H
qa2 IJ
B
C
a
a
3qa 2 2
qa 2
a
3qa 2 2
qa 2 2
a
对H点求矩:
qa 2
qa 2 2
HC
a
HC
1.5qa()
对F点求矩:
qa 1.5a H A a 0 H A 1.5qa() H D 0, MGF qa2, MGH 1.5qa2
qa 2
qa 2 2
xB
1 EI
M ( )M ( )ds
1
2
qR2(1 cos )R sin Rd
1
qR 4 ()
EI 0
2EI
5-7 试用图乘法计算图示梁和刚架的位移:(a) ΔyC ;(b) ΔyD ;(c) ΔxC ;(d) ΔxE ;(e) D ;(f) ΔyE 。 (a)
朱慈勉结构力学力法

6.46 EA
kN
(
)
2 5 m 1 15
2 5 m 1 15
C2E 4.A 23kNm
θD
6.46kN EA
1 m 1 1 m 1 35 35
例6-12 求图示组合结构C点的竖向位移ΔC和AD与BD杆间的相对转角
ΔθD。忽略受弯杆的轴向变形。 已知AD和BD杆:EA EI m2
2次超静定
9
选取基本结构为切断竖杆:
X 1h
t0
1 EA
1 kl
§6-7超静定结构的位移计算
F E N F N d A s k 0 F G Q F Q d A s M E M d I s F R c
1)载作用下的位移计算
F N F Nd P s EA
k 0F G Q F Qd P A s
M M P ds EI
求超静定结构因温度改变、支座移动产生的位移时, 若选原结构建立虚拟力状态,计算将会更简单。
EI, l,t0 ,Δt
①
M、Q、N
EMIht、ENAt0、G kQA
P=1
②
T 2 1 1 R *c W 21
c M * E M I h t d s N * E N A t0 d s Q * G kd Q
2次超静定
9
解:⑴ 确定超静定次数;
⑵ 用力法求解, 并作M图和FN图; ⑶ 选取基本结构为铰结体系求位移;
⑷ 求AD杆与BD间的相对转角:
⑸ 施加单位荷载并求各杆轴力:
D
FN1FN l EA
1 m 1
35m 25m 1 1 .8 9 k N 1 .3 4 k N 3 5
E A 1 5
1 m 1 35
b h
结构力学第06章

荷载作用;
温度变化和材料胀缩; 支座沉降和制造误差。
AB
绝对位移
截面A角位移 A A点线位移 A 包含: 水平线位移 AH 竖向线位移 AV
相对位移
CD两点的水平相对线位移:
( CD ) H C D
AB两截面的相对转角:
AB A B
M M dx A y A y
i k 1 1 2
2
A3 y3
二.几种常见图形的面积和形心位置
【例6.5】求图示矩形截面悬臂梁在A端的竖向位移。
解:
先求实际荷载作用下结构的内力图,再求虚设单位荷 载作用下结构的内力图。 q FP 1
L
A
B
1 2 ql 2
A
B
L
实际荷载作用下的内力图
轴力 FNP 、F N —— 以拉力为正; 剪力 FQP 、F Q —— 使微段顺时针转动者为正;
弯矩 M P 、 —— 只规定乘积 M P M 的正负号。当M M 与 M P 使杆件同侧纤维受拉时,其乘积取正值。
二.各类结构的位移计算公式
Байду номын сангаас和刚架 在梁和刚架中,位移主要是弯矩引起的,轴力和剪力的影 响较小,因此位移公式可简化为
(a x l )
虚设单位荷载作用下的内力为 M 1
相对转角
(0 x l )
MMP ds EI
a
0
FP b xdx EIl
FP a x FP ab 1 dx a EI l 2 EI
l
刚架的位移
【例6.3】求图示刚架C端的角位移。已知抗弯刚度为EI。
1
结构力学课后习题答案(朱慈勉)

取虚线所示的两个隔离体有:
M B 0,
2 2
FN
2
a
FN 1
a
Fx 0, FN1
2 2
FN
2
4 3
a
2a
联立方程解得:FN1
a 3
,
FN 2
2a 3
杆3的内力可以通过D节点求得
a
a
a
a
FN 3 P
(c)
先去除结构中的零力杆
2
再求出支座反力
1
在A, B点用节点法可求得
43
FN1
13 2
1.5qa
FP
)
FP
FP
FP
FP
、
3-12 试求图示桁架各指定杆件的内力。 (b)
3m
3 ×3m
D
1
1
B
3
2KN
4m
7.5KN
4m
2kN
E
2 3kN
1
A F3
10.5KN
4m
然后再依次隔离A, B, D点不难求得 F2 7.5KN (), FBD 3KN , F1 4KN ()
先求出支座反力,如图所示。零杆亦示于图中。 取1-1截面以上部分分析
$
2-3 试分析图示体系的几何构造。 (a)
(ⅠⅢ) (ⅠⅡ)
Ⅰ
Ⅱ
Ⅲ
几何不变
(Ⅱ Ⅲ)
,
(b)
(ⅠⅡ) Ⅰ
(ⅡⅢ) Ⅱ
(ⅠⅢ)
Ⅲ
几何不变
<
2-4 试分析图示体系的几何构造。
(a)
(ⅠⅢ)
·
(b)
Ⅰ
Ⅱ
(ⅠⅡ)
Ⅲ
结构力学课后习题答案(朱慈勉)
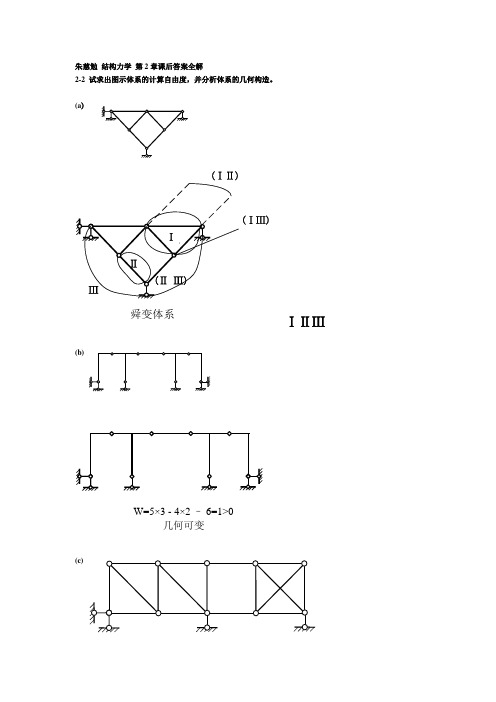
朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F两铰的位lx l lx置。
结构力学课后习题答案(朱慈勉)

朱慈勉 结构力学 第2章课后答案全解2-2 试求出图示体系的计算自由度,并分析体系的几何构造。
(a(ⅠⅡ)(ⅠⅢ)舜变体系ⅠⅡⅢ(b)W=5×3 - 4×2 – 6=1>0几何可变(c)有一个多余约束的几何不变体系(d)W=3×3 - 2×2 – 4=1>0可变体系2-3 试分析图示体系的几何构造。
(a)(ⅡⅢ)Ⅲ几何不变2-4 试分析图示体系的几何构造。
(a)几何不变(b)W=4×3 -3×2 -5=1>0几何可变体系(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体(ⅠⅢ)(ⅡⅢ)(ⅠⅡ)舜变体系(f)(ⅠⅢ)(ⅡⅢ)无多余约束内部几何不变(h)二元体W=3×8 - 9×2 – 7= -1, 有1个多余约束2-5 试从两种不同的角度分析图示体系的几何构造。
(a)(ⅠⅢ)ⅠⅡⅢ(ⅠⅡ)(ⅡⅢ)舜变体系(b)Ⅲ(ⅡⅢ)(ⅠⅢ)同济大学朱慈勉 结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·m ABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
同济大学朱慈勉结构力学课后习题答案
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
完整的结构力学答案-同济大学朱慈勉
完整的结构力学答案-同济大学朱慈勉结构力学朱慈勉版本答案朱慈勉结构力学第2章课后答案全解2-2试求出图示体系的计算自由度,并分析体系的几何构造。
(a) (ⅠⅡ)(ⅠⅢ)舜变体系(b)ⅠⅡⅢW=5某3-4某2–6=1>0几何可变(c)结构力学朱慈勉版本答案有一个多余约束的几何不变体系(d)W=3某3-2某2–4=1>0可变体系2-3试分析图示体系的几何构造。
(a)(ⅡⅢ)结构力学朱慈勉版本答案(b)Ⅲ几何不变2-4试分析图示体系的几何构造。
(a)几何不变(b)W=4某3-3某2-5=1>0几何可变体系结构力学朱慈勉版本答案(ⅠⅢ)(ⅡⅢ)几何不变(d)Ⅲ(ⅠⅢ)有一个多余约束的几何不变体结构力学朱慈勉版本答案(ⅠⅢ)(ⅠⅡ)(ⅡⅢ)舜变体系(f)(ⅠⅢ)无多余约束内部几何不变(ⅡⅢ)结构力学朱慈勉版本答案(h)W=3某8-9某2–7=-1,有1个多余约束二元体结构力学朱慈勉版本答案2-5试从两种不同的角度分析图示体系的几何构造。
(a)ⅡⅠ(ⅠⅡ)Ⅲ(ⅠⅢ)舜变体系(ⅡⅢ)(ⅡⅢ)Ⅲ(ⅠⅢ)结构力学朱慈勉版本答案同济大学朱慈勉结构力学第3章习题答案3-2试作图示多跨静定梁的弯矩图和剪力图。
(a) FPaFPa2QFPFP23FP4(b)结构力学朱慈勉版本答案2020Q10/31026/3(c)60(d)3m结构力学朱慈勉版本答案M7.54484Q2.5523-3试作图示刚架的内力图。
(a)1kN/mC4kN·mA3m6mM181824Q20616(b)40kN·B10kNm3m结构力学朱慈勉版本答案M303030210(c)m3m36mM(d)mm26mQ10110Q54结构力学朱慈勉版本答案M4444N(e)484(f)Q244/3``结构力学朱慈勉版本答案M22203-4试找出下列各弯矩图形的错误之处,并加以改正。
(a)FP(b)(c)结构力学朱慈勉版本答案(d)(e)(f)F3-5试按图示梁的BC跨跨中截面的弯矩与截面B和C的弯矩绝对值都相等的条件,确定E、F两铰的位置。
同济大学朱慈勉 结构力学 第6章习题答案
同济大学朱慈勉 结构力学 第6章习题答案6-1 试确定图示结构的超静定次数。
(a)(b)(d)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4次超静定(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M+=11l F p 61l F p 612l 3l 3 题目有错误,为可变体系。
+ p lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解:基本结构为:l 1Ml l 2Ml F p 21p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδp M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)l2l 2 l2l l 2Q 图12解:基本结构为:1Mp M 01111=∆+p X δ p M X M M +=11(b)解:基本结构为:4a 2a4a4a3m6m 6m810 810计算1M,由对称性知,可考虑半结构。
同济大学 结构力学课后习题及答案解析(完整版)
R=2m
4m
A O
M ( ) 1 (R sin )2 1 2 R(1 cos ) 2
M ( ) 1
B
1 EI
2 1 [1 (R sin )2 1 2 R(1 cos )]Rd 02
= (8-3 ) -1.42 (逆时针)
EI
EI
(d) A q
R EI=常数
O
B
5-7 试用图乘法计算图示梁和刚架的位移:(a) ΔyC ;(b) ΔyD ;(c) ΔxC ;(d) ΔxE ;(e) D ;(f) ΔyE 。 (a)
5-5 已知桁架各杆的 EA 相同,求 AB、BC 两杆之间的相对转角 ΔB 。 5-6 试用积分法计算图示结构的位移:(a) ΔyB ;(b) ΔyC ;(c) B ;(d) ΔxB 。
(a)
q2 q1
A
EI
B
l
以B点为原点,向左为正方向建立坐标。
q( x)
q2
l
q1
x
q1
M
p(x)
1 2
52.17
M
248.49
104.37 52.14
6-6 试用力法求解图示超静定桁架,并计算 1、2 杆的内力。设各杆的 EA 均相同。
(a)
(b)
1
1
2
FP
FP
a
a
a
2m
题 6-6 图
6-7 试用力法计算图示组合结构,求出链杆轴力并绘出 M 图。
2
30kN 2m
(a)
a 1.5m
l
A
kθ=
12EI l
2 3
2 3
6 1 20 62 8
3 2
1 6180 3 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
结构力学 第6章 习题答案6-1 试确定图示结构的超静定次数。
(a)(b)(d)(f)(g) 所有结点均为全铰结点2次超静定6次超静定4次超静定3次超静定去掉复铰,可减去2(4-1)=6个约束,沿I-I截面断开,减去三个约束,故为9次超静定沿图示各截面断开,为21次超静定刚片I 与大地组成静定结构,刚片II 只需通过一根链杆和一个铰与I 连接即可,故为4次超静定(h)6-2 试回答:结构的超静定次数与力法基本结构的选择是否有关?力法方程有何物理意义? 6-3 试用力法计算图示超静定梁,并绘出M 、F Q 图。
(a) 解:上图=l1M p M01111=∆+p X δ其中:EIl l l l l l l EI l l l l EI 8114232332623232333211311=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δEIl F l lF l lF EI l pp p p817332322263231-=⎪⎭⎫ ⎝⎛⨯-⨯⨯-⨯=∆0817*******=-EIl F X EI l p p F X 211=p M X M M +=11l F p 61l F p 61 2l 3l3题目有错误,为可变体系。
+lF 2 1=1M 图p Q X Q Q +=11p F 21p F 2(b) 解:基本结构为:l1Mll 2Ml F p 21 p Ml F p 31⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ p M X M X M M ++=2211p Q X Q X Q Q ++=22116-4 试用力法计算图示结构,并绘其内力图。
(a)l2l 2l2ll2Q 图12解:基本结构为:1Mp M 01111=∆+p X δ p M X M M +=11(b)解:基本结构为:4a2a4a4a3m6m6m810810计算1M,由对称性知,可考虑半结构。
1M 计算pM:荷载分为对称和反对称。
对称荷载时:aq22q26qa26qa26qa反对称荷载时:aq22q14qa2pM01111=∆+p X δ p M X M M +=116-5 试用力法计算图示结构,并绘出M 图。
解:基本结构为:1M2Mp M用图乘法求出p p 21221211,,,,∆∆δδδ⎪⎩⎪⎨⎧=∆++=∆++0022221211212111p p X X X X δδδδ (b)6m 6m3m3mX 233解:基本结构为:1MMp M M()EI EI 1086623323326611=⨯⨯+⨯⨯+⨯⨯=δ ()03323326612=⨯⨯-⨯⨯=EI δ()EIEI 1086623323326622=⨯⨯+⨯⨯+⨯⨯=δEI EI p 27003231806212362081632323180621121=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⨯⨯⨯=∆EI EI p 5403231806212362081632323180621122=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯-⨯⎪⎭⎫ ⎝⎛⨯⨯⨯⨯+⨯⨯⨯⨯=∆ 6m6m3180150⎩⎨⎧-=-=⇒⎪⎪⎩⎪⎪⎨⎧=+=+5250540108027001082111X X EI X EIEIX EI m KN M CA ⋅=⨯-⨯-=9035253180 m KN M CB ⋅=⨯+⨯-=12035253180 ()m KN M CD ⋅-=-⨯=3056(c)解:基本结构为:1N 1Mp M()EI I E EI 5558293299233256633263111=⨯⎥⎦⎤⎢⎣⎡⨯⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯=δ ()EI I E p 1442103109109231025661-=⨯⎥⎦⎤⎢⎣⎡⨯+⨯+⨯⨯+⨯⨯⨯-=∆ 01111=∆+p X δ29.11=⇒Xm KN M AC ⋅=-⨯=61.11029.196m3m199m KN M DA ⋅-=-⨯=13.61029.13m KN M DC ⋅=⨯=87.329.13M(d)解:基本结构为:1M2Mp M()()EII E EI 6.111293299233256623326311=⨯⨯⨯+⨯⨯+⨯⨯⨯+⨯⨯⨯=δ6m3m10k N /mX296()EI I E 2.256396256612-=⨯+⨯⨯⨯-=δ()()EII E I E 4.5066226666256622=⨯⨯⨯+⨯⨯⨯=δ()EI EI I E EIp 25.17216456325194540534059245325664334533111=⎪⎭⎫ ⎝⎛⨯⨯⨯-⨯+⨯+⨯⨯+⨯⨯⨯+⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=∆02=∆p⎩⎨⎧-=-=⇒⎪⎪⎩⎪⎪⎨⎧=+-=+-69.839.1704.502.25025.17212.256.111212121X X X EI X EIEIX EI X EI m KN M AD ⋅=⨯-=49.24839.179405()m KN M BF ⋅=⨯--⨯=37.10439.17969.86 ()m KN M FE ⋅-=-⨯=17.5239.173()m KN M CG ⋅-=-⨯=14.5269.86M49.248 37.104 14.526-6 试用力法求解图示超静定桁架,并计算1、2杆的内力。
设各杆的EA 均相同。
(a) (b)题6-6图6-7 试用力法计算图示组合结构,求出链杆轴力并绘出M 图。
(a)aaa2解:基本结构为:l 21M p M()EIl l k l l l EI l EA l 272222262311=+⨯⨯+=θδ ()EI l F l k l F l l F l l F EI lp p p p p 2222631=+⨯+⨯⨯=∆θ01111=∆+p X δp F X 721-=⇒l F l F l F M p p p A 73272=⨯-=73M (b)llaa16-8 试利用对称性计算图示结构,并绘出M 图。
(a)解: 原结构① ② ①中无弯矩。
②取半结构:基本结构为:1Mp MEI EI22433299921211⨯=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯=δp p p F EIF EI 22433292992111=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯⨯=∆p p F X X 41011111-=⇒=∆+δ6m6m9mpFpFpFpFp Fp FpFp F 2M 图 整体结构M 图(b)(c)解:根据对称性,考虑1/4结构:基本结构为: q1 2l qEIl l EI=⎪⎭⎫ ⎝⎛⨯⨯⨯=2121111δEIql ql l ql l EI p 121821823112221=⎪⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯⨯=∆llAB CDEI=常数 q q 3m4m5m4m60kNABCDEI=常数p 49p 4p F 49p 201111=∆+pX δ1221ql X -=⇒p M X M M +=112ql 242ql 242ql242ql 242ql M(d)解:取1/4结构:q基本结构为:11 2M p MlllDEAB EI=常数qq C F122ql 122ql22l qEIl l l EI 332213211=⎪⎪⎭⎫ ⎝⎛⨯⨯=δ EI l l EI212112212-=⎪⎭⎫⎝⎛⨯⨯-=δEIll l EI 2311112122=⎪⎭⎫ ⎝⎛⨯⨯+⨯⨯=δ EI ql l ql l EI p 8432311421-=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⨯-=∆ EI ql ql l EI p612311322=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯=∆ ⎪⎪⎩⎪⎪⎨⎧==⇒⎪⎪⎩⎪⎪⎨⎧=++-=--221321242213361125062320823ql X ql X EI ql X EI l X EIl EI ql X EI l X EI l362ql 362ql 362ql 362ql M(e)92ql92ql 92ql(f)( BEH 杆弯曲刚度为2EI ,其余各杆为EI )取① ② ②中弯矩为0。
考虑①:反对称荷载作用下,取半结构如下:③ ④ ④中无弯矩。
考虑③:弯矩图如下:2a 2apFF F F F 2p F p F 2p F 2F F 2F paF p 2(g)解:原结构① ②①弯矩为0。
反对称荷载下:基本结构为:1M p MEIa a a a EI 3832222211311=⎪⎭⎫ ⎝⎛⨯⨯⨯⨯=δaaa a2p F 2p F2p F 2p F2p F 2p F F p 2EI a F a F a a F a EI a p p p p 1252222631-=⎪⎪⎭⎫⎝⎛⨯-⨯⨯-=∆p p pF X X EI a a EI F X EI a k X X 485341253811331311111=⇒-=-⇒-=∆+δM 图如下:(h) 6-9 试回答:用力法求解超静定结构时应如何恰当地选取基本结构? 6-10 试绘出图示结构因支座移动产生的弯矩图。
设各杆EI 相同。
(a)(b)题6-10图6-11 试绘出图示结构因温度变化产生的M 图。
已知各杆截面为矩形,EI=常数,截面高度h=l/10,材料线膨胀系数为α。
(a) (b)lll+5℃4a4a4a3aAB D B ′EI=常数CDlD2l 2 l 2llhl llla p a F p 247p 24题6-11图6-12 图示平面链杆系各杆l 及EA 均相同,杆AB 的制作长度短了D ,现将其拉伸(在弹性范围内)拼装就位,试求该杆轴力和长度。
题6-12图 题6-13图6-13 刚架各杆正交于结点,荷载垂直于结构平面,各杆为相同圆形截面,G = E ,试作弯矩图和扭矩图。
6-14 试求题6-11a 所示结构铰B 处两截面间的相对转角B Δ 。
6-15 试判断下列超静定结构的弯矩图形是否正确,并说明理由。
(a) (b) (c)(d)题6-15图6-16 试求图示等截面半圆形两铰拱的支座水平推力,并画出M 图。
设EI=常数,并只考虑弯曲变形对位移的影响。
题6-16图PqRRR。
