福大结构力学课后习题详细答案
结构力学课后习题答案
习题7-1 试确定图示结构的位移法基本未知量数目，并绘出基本结构。
(a) (b) (c)EIEI EI 2EI2EI1个角位移 3个角位移，1个线位移 4个角位移，3个线位移(d) (e) (f)EI 1=∞EAEIEI 1=∞3个角位移，1个线位移 2个线位移 3个角位移，2个线位移(g) (h) (i)k一个角位移，一个线位移一个角位移，一个线位移三个角位移，一个线位移7-2 试回答：位移法基本未知量选取的原则是什么？为何将这些基本未知位移称为关键位移？是否可以将静定部分的结点位移也选作位移法未知量？7-3 试说出位移法方程的物理意义，并说明位移法中是如何运用变形协调条件的。
7-4 试回答：若考虑刚架杆件的轴向变形，位移法基本未知量的数目有无变化？如何变化？7-5 试用位移法计算图示结构，并绘出其内力图。
(a)lACD i iiq解：（1）确定基本未知量和基本结构有一个角位移未知量，基本结构见图。
11r 11Z 3i 4i2i ii1M 图1pR 213ql216qlp M 图（2）位移法典型方程11110p r Z R （3）确定系数并解方程iql Z ql iZ ql R i r p24031831,821212111（4）画M 图2724ql 2524qlM 图218ql 216ql (b)4m ADB 10kNEI 2EI2.5kN/m EI解：（1）确定基本未知量1个角位移未知量，各弯矩图如下11r 11Z 1M 图32EI EI12EI 590p M 图（2）位移法典型方程11110pr Z R （3）确定系数并解方程1115,352pr EI R 153502EIZ 114Z EI（4）画M 图()KNm M 图2640147(c) F P解：（1）确定基本未知量一个线位移未知量，各种M 图如下11r 1M 图11Z 27EI 227EI 27EI 1243EI2243EI1243EI p M 图pF 1pR （2）位移法典型方程11110pr Z R （3）确定系数并解方程1114,243p pr EI R F 140243p EIZ F 12434Z EI（4）画M 图94pF 94pF 92p F M 图(d)解：（1）确定基本未知量一个线位移未知量，各种M 图如下11Z2/25EA a4/25EA a11r 1M 图25EA11r 1M 图2/25EA a 2/25EA a 简化图1p R pF pF 45a35a15a pM（2）位移法典型方程11110pr Z R （3）确定系数并解方程11126/,55p p r EA a R F 126055pEA Z F a13a Z EA（4）画M 图a 2a a 2aaEAEAABCDEFF PF PEI 1=∞图M 0.6p F ap F a1.2p F 0.6pF (e)解：（1）确定基本未知量两个线位移未知量，各种M 图如下图11Z 11r 21r 112121424EA r lEA r l1M 2EA lEA l图21Z 12r 22r 22214EA r l2M 2EA lEA lllEAABCDEAEAF P图120p p pR F R p M 1pR pF 0（2）位移法典型方程1111221211222200p pr Z r Z R r Z r Z R （3）确定系数并解方程1112212212221,44214,0pp p EA EA r r r l lEA r lR F R 代入，解得121222121212ppl Z F EA lZ F EA（4）画M 图图M 122212pF 2212pF 1212pF 7-6 试用位移法计算图示结构，并绘出M 图。
结构力学课后习题答案
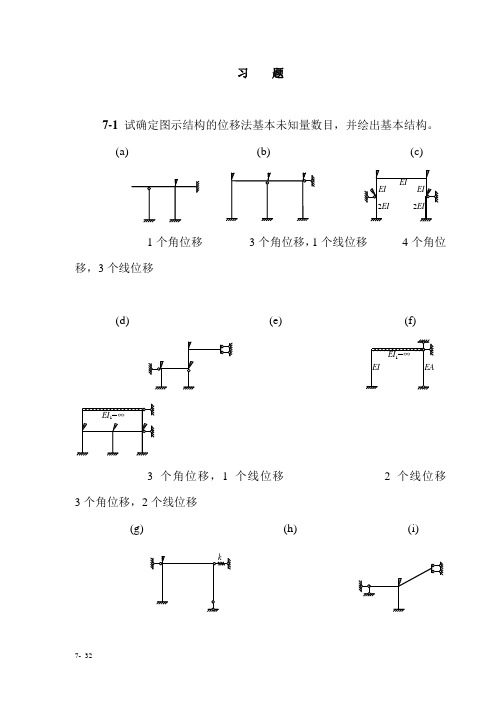
习题7-1 试确定图示结构的位移法基本未知量数目，并绘出基本结构。
(a) (b) (c)1个角位移3个角位移，1个线位移4个角位移，3个线位移(d) (e) (f)3个角位移，1个线位移2个线位移3个角位移，2个线位移(g) (h)(i)7- 327- 33一个角位移，一个线位移 一个角位移，一个线位移 三个角位移，一个线位移7-2 试回答：位移法基本未知量选取的原则是什么？为何将这些基本未知位移称为关键位移？是否可以将静定部分的结点位移也选作位移法未知量？7-3 试说出位移法方程的物理意义，并说明位移法中是如何运用变形协调条件的。
7-4 试回答：若考虑刚架杆件的轴向变形，位移法基本未知量的数目有无变化？如何变化？7-5 试用位移法计算图示结构，并绘出其内力图。
(a)解：（1）确定基本未知量和基本结构有一个角位移未知量，基本结构见图。
lll7- 34Z 1M 图（2）位移法典型方程11110pr Z R +=（3）确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==（4）画M 图M 图(b)4m4m 4m7- 35解：（1）确定基本未知量1个角位移未知量，各弯矩图如下1Z =1M 图32EIp M 图（2）位移法典型方程11110pr Z R +=（3）确定系数并解方程 1115,352p r EI R ==- 153502EIZ -=114Z EI=（4）画M 图()KNm M ⋅图(c)6m6m9m7- 36解：（1）确定基本未知量一个线位移未知量，各种M 图如下1M 图243EI 243EI 1243EI p M 图F R（2）位移法典型方程11110pr Z R +=（3）确定系数并解方程 1114,243p pr EI R F ==- 140243p EIZ F -=12434Z EI=（4）画M 图7- 3794M 图(d)解：（1）确定基本未知量一个线位移未知量，各种M 图如下11Z1111r 252/25EA a 简化a2a a2aa F P7- 38图1pR pp M（2）位移法典型方程11110pr Z R +=（3）确定系数并解方程 11126/,55p pr EA a R F ==-126055p EA Z F a -=13a Z EA=（4）画M 图图M(e)l7- 39解：（1）确定基本未知量两个线位移未知量，各种M 图如下图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M p（2）位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++=（3）确定系数并解方程7- 4011122122121,1,0p p p EA r r r l EA r l R F R ⎛=== ⎝⎭⎛=+ ⎝⎭=-=代入，解得12p p lZ F EAlZ F EA=⋅=⋅（4）画M 图图M p7-6 试用位移法计算图示结构，并绘出M 图。
《结构力学习题》(含答案解析)
《结构力学习题》(含答案解析)本页仅作为文档封面，使用时可以删除This document is for reference only-rar21year.March20 第三章 静定结构的位移计算一、判断题：1、虚位移原理等价于变形谐调条件，可用于求体系的位移。
2、按虚力原理所建立的虚功方程等价于几何方程。
3、在非荷载因素(支座移动、温度变化、材料收缩等)作用下，静定结构不产生内力，但会有位移且位移只与杆件相对刚度有关。
4、求图示梁铰C 左侧截面的转角时，其虚拟状态应取：A.;; B.D.M C.=1=1=15、功的互等、位移互等、反力互等和位移反力互等的四个定理仅适用于线性变形体系。
6、已知M p 、M k 图，用图乘法求位移的结果为：()/()ωω1122y y EI +。
M kM p 21y 1y 2**ωω( a )M =17、图a 、b 两种状态中，粱的转角ϕ与竖向位移δ间的关系为：δ=ϕ 。
8、图示桁架各杆E A 相同，结点A 和结点B 的竖向位移均为零。
Aa a9、图示桁架各杆EA =常数，由于荷载P是反对称性质的，故结点B的竖向位移等于零。
2121二、计算题：10、求图示结构铰A 两侧截面的相对转角ϕA ，EI = 常数。
q l l l /211、求图示静定梁D 端的竖向位移 ∆DV 。
EI = 常数 ，a = 2m 。
a a a 10kN/m12、求图示结构E 点的竖向位移。
EI = 常数 。
l l l /3 2 /3/3q13、图示结构，EI=常数 ，M =⋅90kN m , P = 30kN 。
求D 点的竖向位移。
P 3m 3m 3m14、求图示刚架B 端的竖向位移。
q15、求图示刚架结点C 的转角和水平位移，EI = 常数 。
q16、求图示刚架中Ｄ点的竖向位移。
EI ＝常数。
l ll/217、求图示刚架横梁中Ｄ点的竖向位移。
EI＝常数。
18、求图示刚架中D点的竖向位移。
结构力学课后习题答案
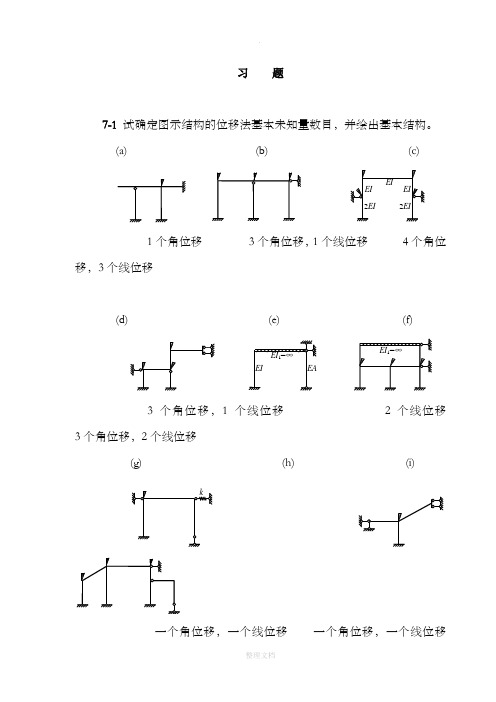
习题7-1 试确定图示结构的位移法基本未知量数目，并绘出基本结构。
(a) (b) (c)1个角位移3个角位移，1个线位移4个角位移，3个线位移(d) (e) (f)3个角位移，1个线位移2个线位移3个角位移，2个线位移(g) (h)(i)一个角位移，一个线位移一个角位移，一个线位移三个角位移，一个线位移7-2 试回答：位移法基本未知量选取的原则是什么？为何将这些基本未知位移称为关键位移？是否可以将静定部分的结点位移也选作位移法未知量？7-3 试说出位移法方程的物理意义，并说明位移法中是如何运用变形协调条件的。
7-4 试回答：若考虑刚架杆件的轴向变形，位移法基本未知量的数目有无变化？如何变化？7-5 试用位移法计算图示结构，并绘出其内力图。
(a)解：（1）确定基本未知量和基本结构有一个角位移未知量，基本结构见图。
lllZ 1M 图（2）位移法典型方程 11110pr Z R +=（3）确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==（4）画M 图M 图(b)4m4m 4m解：（1）确定基本未知量1个角位移未知量，各弯矩图如下1Z =1M 图32EIp M 图（2）位移法典型方程 11110pr Z R +=（3）确定系数并解方程1115,352p r EI R ==-153502EIZ -=114Z EI=（4）画M 图()KN m M ⋅图(c) 9m解：（1）确定基本未知量一个线位移未知量，各种M 图如下1M 图243EI 243EI 1243EI p M 图F R（2）位移法典型方程 11110pr Z R +=（3）确定系数并解方程1114,243p p r EI R F ==-140243p EIZ F -=12434Z EI=（4）画M 图94M 图(d)解：（1）确定基本未知量一个线位移未知量，各种M 图如下11Z1111r 252/25EA a 简化a 2aa2a aF P图1pR pp M（2）位移法典型方程 11110pr Z R +=（3）确定系数并解方程11126/,55p p r EA a R F ==-126055p EA Z F a -=13a Z EA=（4）画M 图图M(e)l解：（1）确定基本未知量两个线位移未知量，各种M 图如下图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M pF（2）位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++=（3）确定系数并解方程11122122121,4414,0p p p EA r r r l l EA r l R F R ⎛⎫=+== ⎪⎝⎭⎛=+ ⎝⎭=-=代入，解得12p p lZ F EAlZ F EA=⋅=⋅（4）画M 图图M p7-6 试用位移法计算图示结构，并绘出M 图。
福大结构力学课后习题详细答案[祁皑].._副本
![福大结构力学课后习题详细答案[祁皑].._副本](https://img.taocdn.com/s3/m/772b5cbb0975f46526d3e113.png)
结构力学（祁皑）课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)解 原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。
因此，原体系为几何不变体系，且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (c)（c-1）（a ）（a-1）（b ）（b-1）（b-2）（c-2） （c-3）解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (d)（d-1） （d-2） （d-3）解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。
因此，原体系为几何不变体系，且无多余约束。
注意：这个题的二元体中有的是变了形的，分析要注意确认。
1-1 (e)解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。
在该体系中，阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。
在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。
因此，原体系为几何可变体系，缺少一个必要约束。
1-1 (f)解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉只分析其余部分。
很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。
因此，原体系为几何不变体系，且无多余约束。
1-1 (g)（d ）（e ）（e-1）ABCAB （e-2）（f ）（f-1）解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉，只分析其余部分。
余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。
因此，原体系为几何不变体系，且无多余约束。
结构力学习题及答案
构造力学习题第2章平面体系的几何组成分析2-1～2-6 试确定图示体系的计算自由度。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图2-7～2-15 试对图示体系进展几何组成分析。
假设是具有多余约束的几何不变体系，那么需指明多余约束的数目。
题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图题2-13图题2-14图题2-15图题2-16图题2-17图题2-18图题2-19图题2-20图题2-21图2-11=W2-1 9-W=2-3 3-W=2-4 2-W=2-5 1-W=2-6 4-W=2-7、2-8、2-12、2-16、2-17无多余约束的几何不变体系2-9、2-10、2-15具有一个多余约束的几何不变体系2-11具有六个多余约束的几何不变体系2-13、2-14几何可变体系为2-18、2-19 瞬变体系2-20、2-21具有三个多余约束的几何不变体系第3章静定梁和静定平面刚架的内力分析3-1 试作图示静定梁的内力图。
〔a〕〔b〕(c) (d)习题3-1图3-2 试作图示多跨静定梁的内力图。
〔a〕〔b〕(c)习题3-2图3-3～3-9 试作图示静定刚架的内力图。
习题3-3图习题3-4图习题3-5图习题3-6图习题3-7图习题3-8图习题3-9图3-10 试判断图示静定构造的弯矩图是否正确。
(a)(b)(c)(d)局部习题答案3-1〔a 〕m kN M B ⋅=80〔上侧受拉〕，kN F RQB 60=，kN F L QB 60-=〔b 〕m kN M A ⋅=20〔上侧受拉〕，m kN M B ⋅=40〔上侧受拉〕，kN F RQA 5.32=，kN F L QA 20-=，kN F LQB 5.47-=，kN F R QB 20=(c)4Fl M C =〔下侧受拉〕，θcos 2F F L QC =3-2 (a)0=E M ，m kN M F ⋅-=40〔上侧受拉〕，m kN M B ⋅-=120〔上侧受拉〕〔b 〕m kN M RH ⋅-=15(上侧受拉)，m kN M E ⋅=25.11〔下侧受拉〕〔c 〕m kN M G ⋅=29(下侧受拉)，m kN M D ⋅-=5.8(上侧受拉)，m kN M H ⋅=15(下侧受拉) 3-3 m kN M CB ⋅=10〔左侧受拉〕，m kN M DF ⋅=8〔上侧受拉〕，m kN M DE ⋅=20〔右侧受拉〕 3-4 m kN M BA ⋅=120〔左侧受拉〕3-5 m kN M F ⋅=40〔左侧受拉〕，m kN M DC ⋅=160〔上侧受拉〕，m kN M EB ⋅=80(右侧受拉) 3-6 m kN M BA ⋅=60〔右侧受拉〕，m kN M BD ⋅=45〔上侧受拉〕，kN F QBD 46.28=3-7 m kN M C ⋅=70下〔左侧受拉〕，m kN M DE ⋅=150〔上侧受拉〕，m kN M EB ⋅=70(右侧受拉) 3-8 m kN M CB ⋅=36.0〔上侧受拉〕，m kN M BA ⋅=36.0〔右侧受拉〕 3-9 m kN M AB ⋅=10〔左侧受拉〕，m kN M BC ⋅=10〔上侧受拉〕 3-10 〔a 〕错误 〔b 〕错误 〔c 〕错误 〔d 〕正确第4章 静定平面桁架和组合构造的内力分析4-1 试判别习题4-1图所示桁架中的零杆。
结构力学_福州大学中国大学mooc课后章节答案期末考试题库2023年
结构力学_福州大学中国大学mooc课后章节答案期末考试题库2023年1.用矩阵位移法求解图示刚架时，其结构的综合结点荷载列阵为：{F}={40.5kN·m 31.5kN·m 72kN }T。
（）【图片】答案:正确2.该体系为几何（）体系，有（）个多余约束，缺（）必要约束。
备注：第1个空格填“不变、瞬变、可变”字样，第2个、第3个空格填数字。
三个答案之间用“，”号分隔，每空2分。
【图片】答案:不变，0，03.图示连续梁,用力矩分配法求得杆端弯矩MBC= -M/2。
（）【图片】答案:错误4.用力矩分配法计算图示结构时，BC杆的分配系数是：（）；【图片】答案:16/25，5.在力矩分配法的计算中,当放松某个结点时,其余结点所处状态为：（）答案:相邻结点锁紧6.在力矩分配法中反复进行力矩分配及传递，结点不平衡力矩愈来愈小，主要是因为分配系数及传递系数< 1。
（）答案:正确7.用力矩分配法计算结构时,汇交于每一结点各杆端力矩分配系数总和为1,则表明力矩分配系数的计算绝对无错误。
（）答案:错误8.结构体系的计算自由度。
答案:一定小于等于实际自由度。
9.瞬变体系不能做为常规工程结构的原因是。
答案:约束的位置不对；10.图示结构中B结点的不平衡力矩（约束力矩）为：（）【图片】答案:-1kNm11.图示结构中,当结点B作用外力偶M时,用力矩分配法计算得MBA等于：（）【图片】答案:2M/512.真实的结构是。
答案:可能是没有多余约束的几何不变体系，或者是有多余约束的几何不变体系。
13.图示连续梁用力矩分配法求得AB杆B端的弯矩是：（）【图片】答案:6kNm14.二元体的含义是。
答案:从一个单铰出发的两个不共线的刚片，只在远端与其它体系相连。
15.该体系为几何（）体系，有（）个多余约束，缺（）必要约束。
备注：第1个空格填“不变、瞬变、可变”字样，第2个、第3个空格填数字。
三个答案之间用“，”号分隔，每空2分。
结构力学课后习题答案[1]
![结构力学课后习题答案[1]](https://img.taocdn.com/s3/m/8c0493dc80eb6294dd886c23.png)
)e( 移位线个 1�移位角个 3 移位角个 1
)d(
)c(
。构结本基出绘并�目数量知未本基法移位的构结示图定确试 1-7
)b(
) a(
题
习
33 -7
下如图矩弯各�量知未移位角个 1 m4 m4
量知未本基定确�1� �解 C IE
m4
D Nk01
IE
B
IE2 m/Nk5.2
A )b(
图M
42 lq 2 5
图矩弯终最画�4� 得解�入代
61.53
IE
3
0 � p 2 R , 0 3 � p 1R 6 � 2 2r IE � 1 2r � 2 1r , I E 2 � 1 1r
程方解并数系定确�3�
p2
11
1
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
N K 0 3 � � p 2 R , N K 0 3 � p 1R 4 � � 2 2r 0 � 1 2r � 2 1r , i1 1 � 1 1r
p2
得解�入代
i3
程方解并数系定确�3�
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
程方型典法移位�2�
程方型典法移位�2�
0�
p1
图p M
03 � p 1R � 0 � p 1R
03
04 -7
m2
m2 数常=IE F
B E
m2
m2
D
A
m2
Nk03
C )c(
90.92 55.43
图M
81.8 19.02 54.57 02
《结构力学》习题解答(内含解答图)
解：将固定铰支座换为单铰，如图（b），由于与基础的约束多余三个，故基础作为刚片Ⅰ。铰结BF为刚片Ⅱ，铰结△CDE为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆AB和支撑杆F相连，虚铰在无穷远处，刚片Ⅰ与刚片Ⅲ是由杆AC和支撑杆E相连，虚铰在两杆的延长线的交点处，而刚片Ⅱ与刚片Ⅲ是由杆BC和杆FD相连，虚铰在两杆的延长线的交点处。此时，三铰不共线，该体系为几何不变体，且无多余约束。
所以，体系是几何不变得，且无多余约束。
习题2-2试对图示体系进行几何组成分析。
解：从图2-15（b）可知，杆件CD和链杆3及铰D构成二元体，可以去掉；取杆件CB为刚片Ⅰ，基础作为刚片Ⅱ，根据规则一，两刚片是通过杆AB、链杆1、2组成几何不变体。所以，整个体系为几何不变体系，且无多余约束。
习题2-2图习题2-2解答图
习题2-10试对图示体系进行几何组成分析。
习题2-10图习题2-10解答图
解：由于与基础的约束多余三个，故基础作为刚片Ⅰ。铰结△ABF为刚片Ⅱ，铰结△BCD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由杆EA和支撑杆F相连，虚铰在两杆的延长线的交点处，刚片Ⅰ与刚片Ⅲ是由杆EC和支撑杆D相连，虚铰在两杆的延长线的交点处，而刚片Ⅱ与刚片Ⅲ是铰B相连。此时，三铰不共线，该体系为几何不变体，且无多余约束。
习题2-26图习题2-26解答图
解：将链杆截断，截断一处，去掉一个约束，共去掉四个约束；再将刚性联结杆截断，截断一处，去掉三个约束，共去掉十二个约束，如图（b）。此时，体系变成与基础独立相连的三个单一杆件，见图（b）。所以，该体系具有十六个多余约束的几何不变体。
2.3.2提高题
提高题2-1 试对图示体系作几何组成分析。
所以，由规则一知，体系是几何不变体，且无多余约束。
福大结构力学课后习题详细答案(祁皑)
结构力学（祁皑）课后习题详细答案答案仅供参考第1章1-1分析图示体系的几何组成。
1-1(a)解 原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。
因此，原体系为几何不变体系，且有一个多余约束。
1-1 (b)解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (c)（c-1）（a ）（a-1）（b ）（b-1）（b-2）（c-2） （c-3）解 原体系依次去掉二元体后，得到一个三角形。
因此，原体系为几何不变体系，且无多余约束。
1-1 (d)（d-1） （d-2） （d-3）解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。
因此，原体系为几何不变体系，且无多余约束。
注意：这个题的二元体中有的是变了形的，分析要注意确认。
1-1 (e)解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。
在该体系中，阴影所示的刚片与支链杆C 组成了一个以C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。
在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。
因此，原体系为几何可变体系，缺少一个必要约束。
1-1 (f)解 原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉只分析其余部分。
很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。
因此，原体系为几何不变体系，且无多余约束。
1-1 (g)（d ） （e ）（e-1）ABCAB （e-2）（f ）（f-1） （g ） （g-1） （g-2）解 原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。
因此，可以将该刚片和相应的约束去掉，只分析其余部分。
余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。
结构力学章节习题及参考答案
习题7.2填空题
（1）习题5.2(1)图(a)所示超静定梁的支座A发生转角，若选图(b)所示力法基本结构，则力法方程为_____________，代表的位移条件是______________，其中1c=_________；若选图(c)所示力法基本结构时，力法方程为____________，代表的位移条件是______________，其中1c=_________。
(a)
习题3.7改正习题3.7图所示刚架的弯矩图中的错误部分。
(a)(b)(c)
(d)(e)(f)
习题3.7图
习题3.8作习题3.8图所示刚架的内力图。
(a)
(b)
习题3.8图
第4章 静定拱习题解答
习题4.1是非判断题
(1) 三铰拱的水平推力不仅与三个铰的位置有关，还与拱轴线的形状有关。（ ）
(2) 所谓合理拱轴线，是指在任意荷载作用下都能使拱处于无弯矩状态的轴线。 （ ）
习题3.2(2)图
习题3.3作习题3.3图所示单跨静定梁的M图和 图。
(a) (b)
(c) (d)
(e) (f)
习题3.3图
习题3.4作习题3.4图所示单跨静定梁的内力图。
(c)
习题3.4图
习题3.5作习题3.5图所示斜梁的内力图。
习题3.5图
习题3.6作习题3.6图所示多跨梁的内力图。
(a)
习题3.6图
(4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。( )
(5) 习题2.1(5) 图所示体系去掉二元体CEF后，剩余部分为简支刚架，所以原体系为无多余约束的几何不变体系。( )
习题 2.1(5)图
结构力学课后习题答案
习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】「习题11】【习题12】【习题13】【习题14】【参考答衆】习题22-1〜2-14试对图示体系进行儿何组成分析，如果是只有多余联系的儿何不变体系，则应指出多余联系的数目。
d5∑° X 厂^τ"βH题2-2图ΓΛ题2-3图题2-5图题2-6图题2-1图H 2-9 图题2-10图题2-11图题2-12图题2-13图习题3试作图示多跨挣定梁的M及Q图。
(a) (b)题3-1图3-2试不计算反力而绘出梁的M图。
题3-2图习题44-1作图示刚架的M、Q、N图。
40fcN 40kN20kNm4-2作图示刚架的M图。
2OkN m SkN mSkXm 40fcN题4-1图4-3作图示三狡刚架的M图。
4-4作图示刚架的M图。
AEmJnIAr lD1题4-2图4-5己知结构的M图•试绘出荷载。
题4-4图3IOkNnlJ^1.5mC(a)题4-3日6erIB9 9题5-1图5-2带拉杆拱，拱轴线方程y= il(l-χ)χ,求截面K 的弯矩。
题5-2图5-3试求图示带拉杆的半圆三狡拱截面K 的内力・4-6检査F 列刚架的M 图，并予以改正。
题4-5图ω∙I ∣ULL∏ ∏ ⅛)题4-6图习题5图示抛物纟戈三铁拱轴线方程y = ff(l-x)x ，试求D 截面的内力。
IkNm15m [ 5m [ ICm 1=3OmC题5-3图习题6 6-1判定图示桁架中的零杆。
题6-1图6-2用结点法计算图示桁架中各杆内力。
(a) FGH月Λ4x4m=16m题6-2图6-3用截面法计算图示桁架中指定各杆的内力。
40kN题6-3图6-4试求图示组介结构中齐链杆的轴力并作受弯杆件的Q图。
2m ] 2m ]lm]lπ⅝] 2m [题6-4图6-5用适宜方法求桁架中指定杆内力。
题6-6图习题88-1试作图示悬臂梁的反力V B 、MB 及内力Q C 、MC 的影响线。
结构力学课后习题答案
结构力学课后习题答案结构力学是一门研究结构在外力作用下的内力、变形和稳定性的学科。
课后习题是帮助学生巩固理论知识和提高解题技巧的重要环节。
以下是一些结构力学课后习题的参考答案，供学习者参考：第一章：结构力学基础1. 静定结构与超静定结构的区别：静定结构是指在已知外力作用下，其内力和位移可以通过静力平衡方程和几何关系唯一确定的结构。
超静定结构则是指静力平衡方程和几何关系不足以唯一确定其内力和位移的结构。
2. 弯矩图的绘制方法：绘制弯矩图首先需要确定结构的支反力，然后通过截面平衡条件，逐步求出各截面的弯矩值，并将其绘制成图形。
第二章：静定梁的内力分析1. 简支梁的内力计算：对于简支梁，可以通过静力平衡条件和截面平衡条件来计算梁的内力，包括剪力和弯矩。
2. 悬臂梁的内力计算：悬臂梁的内力计算需要考虑梁端的外力和力矩，通过静力平衡条件求解。
第三章：静定桁架的内力分析1. 节点法的应用：节点法是通过在桁架的节点上施加平衡条件来求解节点的反力，进而求得杆件的内力。
2. 截面法的应用：截面法是通过选取桁架的某一截面，对该截面进行平衡分析，求得截面两侧杆件的内力。
第四章：静定拱的内力分析1. 三铰拱的内力计算：三铰拱的内力计算通常需要利用静力平衡条件和几何关系，计算出拱的反力和弯矩。
2. 双铰拱和无铰拱的内力特点：双铰拱和无铰拱的内力计算更为复杂，需要考虑更多的平衡条件和几何关系。
第五章：超静定结构的内力分析1. 力法的应用：力法是通过建立力的平衡方程来求解超静定结构的内力，通常需要引入多余未知力。
2. 位移法的应用：位移法是通过建立位移的平衡方程来求解超静定结构的内力，通常需要引入位移未知数。
第六章：结构的稳定性分析1. 欧拉临界载荷的计算：欧拉临界载荷是指细长杆件在轴向压力作用下失稳的临界载荷，可以通过欧拉公式计算。
2. 非线性稳定性分析：对于非线性问题，稳定性分析需要考虑材料的非线性特性和几何非线性，通常需要采用数值方法求解。
结构力学课后习题答案
习题7-1 试确定图示结构的位移法基本未知量数目，并绘出基本结构。
(a) (b) (c)1个角位移3个角位移，1个线位移4个角位移，3个线位移(d) (e) (f)3个角位移，1个线位移2个线位移3个角位移，2个线位移(g) (h)(i).7- 33一个角位移，一个线位移 一个角位移，一个线位移 三个角位移，一个线位移7-2 试回答：位移法基本未知量选取的原则是什么？为何将这些基本未知位移称为关键位移？是否可以将静定部分的结点位移也选作位移法未知量？7-3 试说出位移法方程的物理意义，并说明位移法中是如何运用变形协调条件的。
7-4 试回答：若考虑刚架杆件的轴向变形，位移法基本未知量的数目有无变化？如何变化？7-5 试用位移法计算图示结构，并绘出其力图。
(a)解：（1）确定基本未知量和基本结构有一个角位移未知量，基本结构见图。
lll.Z 1M 图（2）位移法典型方程11110pr Z R +=（3）确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==（4）画M 图M 图(b)4m 4m 4m7- 35解：（1）确定基本未知量1个角位移未知量，各弯矩图如下1Z =1M 图32EIp M 图（2）位移法典型方程11110pr Z R +=（3）确定系数并解方程 1115,352p r EI R ==- 153502EIZ -=114Z EI=（4）画M 图()KNm M ⋅图(c)6m6m9m.解：（1）确定基本未知量一个线位移未知量，各种M 图如下1M 图243EI 243EI 1243EI p M 图F R（2）位移法典型方程11110pr Z R +=（3）确定系数并解方程 1114,243p pr EI R F ==- 140243p EIZ F -=12434Z EI=（4）画M 图7- 3794M 图(d)解：（1）确定基本未知量一个线位移未知量，各种M 图如下11Z1111r 252/25EA a 简化a 2aa2a aF P.图1pR pp M（2）位移法典型方程11110pr Z R +=（3）确定系数并解方程 11126/,55p pr EA a R F ==-126055p EA Z F a -=13a Z EA=（4）画M 图图M(e)l7- 39解：（1）确定基本未知量两个线位移未知量，各种M 图如下图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M p（2）位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++=（3）确定系数并解方程.11122122121,4414,0p p p EA r r r l l EA r l R F R ⎛⎫=+== ⎪⎝⎭⎛=+ ⎝⎭=-=代入，解得12p p lZ F EAlZ F EA=⋅=⋅（4）画M 图图M p7-6 试用位移法计算图示结构，并绘出M 图。
福州大学-考研《结构力学考试样题库》2-静定结构内力
第二章 静定结构内力计算一、是非题1、 静定结构的全部内力及反力，只根据平衡条件求得，且解答是唯一的。
2、静定结构受外界因素影响均产生内力，内力大小与杆件截面尺寸无关。
3、静定结构的几何特征是几何不变且无多余约束。
4、图示结构||M C =0。
aa5、图示结构支座A 转动ϕ角，M AB = 0， R C = 0。
BCaaAϕ2a26、荷载作用在静定多跨梁的附属部分时，基本部分一般内力不为零。
7、图示静定结构，在竖向荷载作用下， AB 是基本部分，BC 是附属部分。
ABC8、图示结构B 支座反力等于P /2()↑。
9、图示结构中，当改变B 点链杆的方向（不通过A 铰）时，对该梁的影响是轴力有变化。
ＡＢ10、在相同跨度及竖向荷载下，拱脚等高的三铰拱，水平推力随矢高减小而减小。
11、图示桁架有9根零杆。
12、图示桁架有：N 1=N 2=N 3= 0。
aaaa13、图示桁架DE 杆的内力为零。
a a14、图示对称桁架在对称荷载作用下，其零杆共有三根。
15、图示桁架共有三根零杆。
16、图示结构的零杆有7根。
17、图示结构中，CD 杆的内力 N 1=－P 。
a 418、图示桁架中，杆1的轴力为0。
4a19、图示为一杆段的M 、Q 图，若Q 图是正确的，则M 图一定是错误的。
图M Q 图二、选择题1、对图示的AB 段，采用叠加法作弯矩图是：A. 可以；B. 在一定条件下可以；C. 不可以；D. 在一定条件下不可以。
2、图示两结构及其受载状态，它们的内力符合：A. 弯矩相同，剪力不同；B. 弯矩相同，轴力不同；C. 弯矩不同，剪力相同；D. 弯矩不同，轴力不同。
PPP2 l ll l3、图示结构M K（设下面受拉为正）为：A. qa22；B. －qa2；C. 3qa22；D. 2qa2。
2a4、图示结构M DC（设下侧受拉为正）为：A. －Pa；B.Pa；C. －Pa；D. Pa。
a a5、在径向均布荷载作用下，三铰拱的合理轴线为：A．圆弧线；B．抛物线；C．悬链线；D．正弦曲线。
结构力学课后习题答案
习题7-1 试确定图示结构的位移法基本未知量数目，并绘出基本结构。
(a) (b) (c)1个角位移 3个角位移，1个线位移 4个角位移，3个线位移(d) (e) (f)3个角位移，1个线位移 2个线位移3个角位移，2个线位移(g) (h) (i)一个角位移，一个线位移一个角位移，一个线位移三个角位移，一个线位移7-2 试回答：位移法基本未知量选取的原则是什么为何将这些基本未知位移称为关键位移是否可以将静定部分的结点位移也选作位移法未知量7-3 试说出位移法方程的物理意义，并说明位移法中是如何运用变形协调条件的。
7-4 试回答：若考虑刚架杆件的轴向变形，位移法基本未知量的数目有无变化如何变化7-5 试用位移法计算图示结构，并绘出其内力图。
(a)lBl l解：（1）确定基本未知量和基本结构有一个角位移未知量，基本结构见图。
Z 1M 图（2）位移法典型方程 11110pr Z R +=（3）确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==（4）画M 图M 图(b)4m 4m4mC解：（1）确定基本未知量1个角位移未知量，各弯矩图如下1Z =1M 图32EIp M 图（2）位移法典型方程 11110pr Z R +=（3）确定系数并解方程 1115,352p r EI R ==- 153502EIZ -=114Z EI=（4）画M 图()KN mM ⋅图(c)6m6m9m解：（1）确定基本未知量 一个线位移未知量，各种M 图如下1M 图243EI 243EI 1243EI p M 图F R（2）位移法典型方程 11110pr Z R +=（3）确定系数并解方程 1114,243p pr EI R F ==- 140243p EIZ F -=12434Z EI=（4）画M 图94M 图(d)解：（1）确定基本未知量 一个线位移未知量，各种M 图如下11Z1111r 252/25EA a 简化a2aa2aaF F P图1pR pp M（2）位移法典型方程 11110pr Z R +=（3）确定系数并解方程 11126/,55p pr EA a R F ==-126055p EA Z F a -=13a Z EA=（4）画M 图图M(e)l解：（1）确定基本未知量 两个线位移未知量，各种M 图如下图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M pF（2）位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++=（3）确定系数并解方程11122122121,4414,0p p p EA r r r l l EA r l R F R ⎛⎫=+== ⎪⎝⎭⎛=+ ⎝⎭=-=代入，解得12p p lZ F EAlZ F EA=⋅=⋅（4）画M 图图M p7-6 试用位移法计算图示结构，并绘出M 图。
结构力学课后习题解答：5力法习题解答
第5章力法习题解答习题5.1是非判断题（1）习题5.1(1)图所示结构，当支座A发生转动时，各杆均产生内力。
（）习题5.1(1)图习题5.1(2)图（2）习题5.1(2)图所示结构，当内外侧均升高t1℃时，两杆均只产生轴力。
（）（3）习题5.1(3)图(a)和(b)所示两结构的内力相同。
（）q q(a)(b)习题5.1(3)图（4）习题5.1(3)图(a)和(b)所示两结构的变形相同。
（）【解】（1）错误。
BC部分是静定的附属部分，发生刚体位移，而无内力。
（2）错误。
刚结点会沿左上方发生线位移，进而引起所连梁柱的弯曲。
（3）正确。
两结构中梁两跨的抗弯刚度比值均为1:1，因此两结构内力相同。
（4）错误。
两结构内力相同，但图(b)结构的刚度是图(a)的一倍，所以变形只有图(a)的一半。
习题5.2 填空题（1）习题5.2(1) 图(a)所示超静定梁的支座A发生转角θ，若选图(b)所示力法基本结构，则力法方程为_____________，代表的位移条件是______________，其中∆1c =_________；若选图(c)所示力法基本结构时，力法方程为____________，代表的位移条件是______________，其中∆1c=_________。
(a)(b)(c)习题5.2(1)图（2）习题 5.2(2)图(a)所示超静定结构，当基本体系为图(b)时，力法方程为____________________，∆1P=________；当基本体系为图(c)时，力法方程为____________________，∆1P=________。
q(a)(b)(c)习题5.2(2)图（3）习题5.2(3)图(a)所示结构各杆刚度相同且为常数，AB杆中点弯矩为________，____侧受拉；图(b)所示结构M BC=________，____侧受拉。
(a)(b)习题5.2(3)图（4）连续梁受荷载作用时，其弯矩图如习题5.2(4)图所示，则D点的挠度为________，位移方向为____。
结构力学课后习题答案
结构力学课后习题答案(总23页)--本页仅作为文档封面，使用时请直接删除即可----内页可以根据需求调整合适字体及大小--习题及参考答案【习题2】【习题3】【习题4】【习题5】【习题6】【习题8】【习题9】【习题10】【习题11】【习题12】【习题13】【习题14】【参考答案】习题22-1～2-14试对图示体系进行几何组成分析，如果是具有多余联系的几何不变体系，则应指出多余联系的数目。
题2-1图题2-2图题2-3图题2-4图题2-5图题2-6图题2-7图题2-8图题2-9图题2-10图题2-11图题2-12图 题2-13图 题2-14图习题33-1 试作图示多跨静定梁的M 及Q 图。
(b)(a)20kN10kN40kN20kN/m40kN题3-1图3-2 试不计算反力而绘出梁的M 图。
(b)5kN/m40kN(a)题3-2图习题44-1 作图示刚架的M 、Q 、N 图。
(c)(b)(a)/20kN /m2kN /m题4-1图4-2 作图示刚架的M 图。
P(e)(d)(a)(b)(c)20k N /m4kN题4-2图4-3 作图示三铰刚架的M 图。
(b)(a)题4-3图4-4 作图示刚架的M 图。
(a)题4-4图4-5 已知结构的M 图，试绘出荷载。
(b)(a)题4-5图4-6 检查下列刚架的M 图，并予以改正。
(e)(g)(h)P(d)(c)(a)(b)(f)题4-6图习题55-1 图示抛物线三铰拱轴线方程x x l lfy )(42-=，试求D 截面的内力。
题5-1图5-2 带拉杆拱，拱轴线方程x x l lf y )(42-=，求截面K 的弯矩。
C题5-2图 题5-3图5-3 试求图示带拉杆的半圆三铰拱截面K 的内力。
习题66-1 判定图示桁架中的零杆。
(c)(b)题6-1图6-2 用结点法计算图示桁架中各杆内力。
(b)题6-2 图6-3 用截面法计算图示桁架中指定各杆的内力。
(b)题6-3图6-4 试求图示组合结构中各链杆的轴力并作受弯杆件的M 、Q 图。
结构力学课后练习题+答案
2cm
A CB 2cm 2cm
42、求图示结构 A 点竖向位移（向上为正） AV 。
M EI
EI A
a
EI
EI = ∞ 1
3 EI
K = a3
a
a
43、求图示结构 C 点水平位移 CH ，EI = 常数。
M B
2l
C 6 EI k=
l3
A l
44、求图示结构 D 点水平位移 DH 。EI= 常数。
a/ 2 D
a
A
c1
A'
a
B B'
aห้องสมุดไป่ตู้
c2
35、图示结构 B 支座沉陷 = 0.01m ，求 C 点的水平位移。
C l
A
B
l/2 l/2
—— 25 ——
《结构力学》习题集
36、结构的支座 A 发生了转角 和竖向位移 如图所示，计算 D 点的竖向位移。
A
D
l
l l/ 2
37、图示刚架 A 支座下沉 0.01l ，又顺时针转动 0.015 rad ，求 D 截面的角位移。
P
P
l
l
l
l
18、用力法计算图示结构并作弯矩图。
—— 31 ——
100 kN C EI
《结构力学》习题集
100 kN D
2 EI A
2 EI
4m
B
1m
6m
1m
19、已知 EI = 常数，用力法计算并作图示对称结构的 M 图。
q
q
EA=
l
l
l
20、用力法计算并作图示结构的 M 图。EI =常数。
a
P q
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
大刚片。这时，原体系中的其余两个链杆（图（j-5）中的虚线所示）都是在两端用铰
与这个大刚片相连，各有一个多余约束。因此，原体系为几何不变体系，有两个多余 约束。
1-2分析图示体系的几何组成。
1-2 （a）
I
(a-1)
解本例中共有11根杆件，且没有二元体，也没有附属部分可以去掉。如果将两
此，原体系为几何不变体系，且无多余约束。
1-1 (g)
(g-2)
解原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变 体系的组成规律。因此，可以将该刚片和相应的约束去掉，只分析其余部分。余下的 部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。因此，原体
系为几何不变体系，且无多余约束。
1-1 （h）
解原体系与基础用一个铰和一个支链杆相连，符合几何不变体系的组成规律。 因此，可以只分析余下部分的内部可变性。这部分（图（h-1））可视为阴影所示的两
个刚片用一个杆和一个铰相连，是一个无多余约束几何不变体系。因此，原体系为几 何不变体系，且无多余约束。
解 这是一个分析内部可变性的题目。上部结构中，阴影所示的两个刚片用一个
结构力学（祁皑）课后习题详细答案
解 原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。因此，原体系为几
何不变体系，且有一个多余约束。
1- 1 (b)
解 原体系依次去掉二元体后，得到一个三角形。因此ห้องสมุดไป่ตู้原体系为几何不变体系,
且无多余约束。
1-1 （c）
(c-3)
解 原体系依次去掉二元体后，得到一个三角形。因此，原体系为几何不变体系,
个三角形看成刚片，选择两个三角形和另一个不与这两个三角形相连的链杆作为刚片
（图（a-1））。则连接三个刚片的三铰（二虚、一实）共线，故体系为几何瞬变体系。
1-2 (b)
(b-1)
且无多余约束。
1-1 （d）
解 原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。因
此，原体系为几何不变体系，且无多余约束。注意：这个题的二元体中有的是变了形 的，分析要注意确认。
解 原体系去掉最右边一个二元体后，得到（e-1）所示体系。在该体系中，阴影
所示的刚片与支链杆C组成了一个以C为顶点的二元体，也可以去掉，得到（e-2）
所示体系。在图（e-2）中阴影所示的刚片与基础只用两个链杆连接，很明显，这是一 个几何可变体系，缺少一个必要约束。因此，原体系为几何可变体系，缺少一个必要 约束。
1-1 （f）
解原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相 连，符合几何不变体系的组成规律。因此，可以将该刚片和相应的约束去掉只分析其 余部分。很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。因
铰和一个链杆相连（图（i-1））。因此，原体系为几何不变体系，且无多余约束。
解 去掉原体系中左右两个二元体后，余下的部分可只分析内部可变性（图
（j-1））。本题中杆件比较多，这时可考虑由基本刚片通过逐步添加杆件的方法来分析。 首先将两个曲杆部分看成两个基本刚片（图（j-2））。然后，增加一个二元体（图（j-3））。