2017年高考数学真题三角函数
2017年高考三角函数真题集
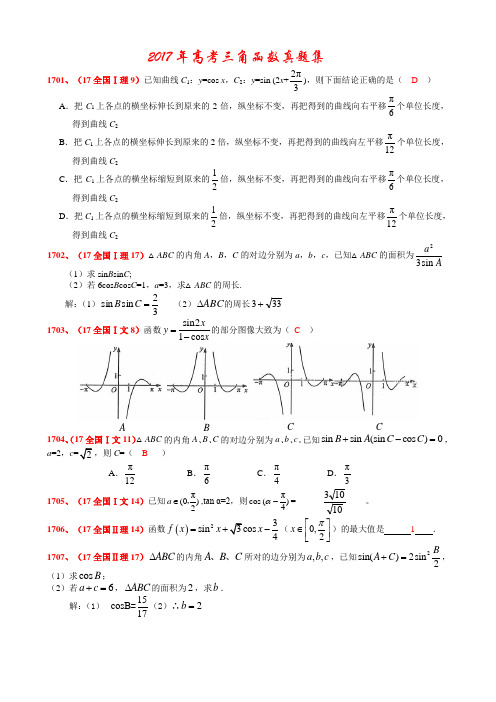
2017年高考三角函数真题集1701、（17全国Ⅰ理9）已知曲线C 1：y =cos x ，C 2：y =sin (2x +2π3)，则下面结论正确的是（ D ） A ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2B ．把C 1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 2C ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C 2D ．把C 1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C 21702、（17全国Ⅰ理17）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin B sin C ;（2）若6cos B cos C =1，a =3，求△ABC 的周长.解：（1）32sin sin =C B （2）ABC ∆的周长333+ 1703、（17全国Ⅰ文8）函数sin21cos xy x=-的部分图像大致为（ C ）A B C C1704、（17全国Ⅰ文11）△ABC 的内角A 、B 、C 的对边分别为a 、b 、c 。
已知sin sin (sin cos )0B A C C +-=，a =2，c 2，则C =（ B ）A ．π12B ．π6C ．π4D ．π31705、（17全国Ⅰ文14）已知π(0)2a ∈，,tan α=2，则πcos ()4α-=______10103____。
1706、（17全国Ⅱ理14）函数()23sin 34f x x x =+-（0,2x π⎡⎤∈⎢⎥⎣⎦）的最大值是 1 ． 1707、（17全国Ⅱ理17）ABC ∆的内角A B C 、、所对的边分别为,,a b c ，已知2sin()2sin 2BA C +=，（1）求cos B ；（2）若6a c +=，ABC ∆的面积为2，求b ．解：（1）15cosB=cosB 171（舍去），=（2）∴2=b1708、（17全国Ⅱ文3）函数()fx =πsin （2x+）3的最小正周期为（ C ）A.4πB.2πC. πD.2π 1709、（17全国Ⅱ文13）函数()cos sin =2+fx x x 的最大值为5 .1710、（17全国Ⅱ文16）△ABC 的内角A,B,C 的对边分别为a,b,c,若2b cosB=a cosC+c cosA,则B= 3π 1711、（17全国Ⅲ理6）．设函数f (x )=cos(x +3π)，则下列结论错误的是（ D ） A ．f (x )的一个周期为−2πB ．y =f (x )的图像关于直线x =83π对称C ．f (x +π)的一个零点为x =6π D ．f (x )在(2π,π)单调递减1712、（17全国Ⅲ理17）ABC ∆的内角A ，B ，C 的对边分别为a ，b ，c ，已知sin A +3cos A =0，a =27,b =2．（1）求c ；（2）设D 为BC 边上一点，且AD ⊥ AC,求ABD ∆的面积．解： （1）4=c （2）⨯⨯∠=∆142sin 23，所以的面积为 3.2BAC ABD 1713、（17全国Ⅲ文4）已知4sin cos 3αα-=，则sin 2α=（ A ）A ．79-B ．29-C ． 29D ．791714、（17全国Ⅲ文6）函数f (x )=15sin(x +3π)+cos(x −6π)的最大值为（ A ） A ．65 B ．1 C ．35 D ．151715、（17全国Ⅲ文7）函数y =1+x +2sin xx的部分图像大致为（ D ）A B C D ． 1716、（17北京理12）在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若1sin 3α=，cos()αβ-=______79-_____. 1717、（17北京理15）在△ABC 中，A ∠ =60°，c =37a . （Ⅰ）求sin C 的值；（Ⅱ）若a =7，求△ABC 的面积.答案（1）1433 （2）1139S =sin =733322144△=⨯⨯⨯⨯ABC ac B 1718、（17北京文9）在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若sin α=13，则sin β=____31_____．1719、（17北京文16）已知函数()3cos(2)2sin cos 3f x x -x x π=-.（I ）求f (x )的最小正周期；（II ）求证：当[,]44x ππ∈-时，()12f x ≥-． 解：（Ⅰ）2ππ2T ==. （Ⅱ）1()2f x ≥-.1720、（17山东理9）在C ∆AB 中，角A ，B ，C 的对边分别为a ，b ，c ．若C ∆AB 为锐角三角形，且满足()sin 12cosC 2sin cosC cos sinC B +=A +A ，则下列等式成立的是（ A ）（A ）2a b = （B ）2b a = （C ）2A =B （D ）2B =A1721、（17山东理10）已知当[]0,1x ∈时，函数()21y mx =-的图象与y x m =+的图象有且只有一个交点，则正实数m 的取值范围是（ B ）（A ）(])0,123,⎡+∞⎣U （B ）(][)0,13,+∞U（C ）()0,223,⎤⎡+∞⎦⎣U （D ）([)0,23,⎤+∞⎦U1722、（17山东理16）设函数()sin()sin()62f x x x ππωω=-+-，其中03ω<<.已知()06f π=.（Ⅰ）求ω；（Ⅱ）将函数()y f x =的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移4π个单位，得到函数()y g x =的图象，求()g x 在3[,]44ππ-上的最小值. 解：2=ω 最小值23-1723、（17山东文4）已知cosx=，则cos2x=（ D ）A ．﹣B ．C ．﹣D ．1724、（17山东文17）在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，已知b=3，6-=•AC AB ，3=∆ABC S ，求A 和a ．解：A=135°， a=1725、（17天津理4）设θ∈R ，则“ππ||1212θ-<”是“1sin 2θ<”的( A ) （A ）充分而不必要条件（B ）必要而不充分条件（C ）充要条件（D ）既不充分也不必要条件1726、（17天津理7）设函数()2sin()f x x ωϕ=+，x ∈R ，其中0ω>，||ϕ<π.若5()28f π=，()08f 11π=，且()f x 的最小正周期大于2π，则( A )（A ）23ω=，12ϕπ= （B ）23ω=，12ϕ11π=-（C ）13ω=，24ϕ11π=- （D ）13ω=，24ϕ7π=1727、（17天津理15）在ABC △中，内角,,A B C 所对的边分别为,,a b c .已知a b >，5,6a c ==，3sin 5B =. （Ⅰ）求b 和sin A 的值；（Ⅱ）求πsin(2)4A +的值. 解：b 的值为13，sin A 的值为31313. πππ72sin(2)sin 2cos cos 2sin 44426A A +=+=πππ72sin(2)sin 2cos cos 2sin 44426A A A +=+= 1728、（17天津文7）设函数()2sin(),f x x x ωϕ=+∈R ，其中0,||πωϕ><.若5π11π()2,()0,88f f ==且()f x 的最小正周期大于2π，则( A )（A ）2π,312ωϕ== （B ）211π,312ωϕ==-（C ）111π,324ωϕ==- （D ）17π,324ωϕ==1729、（17天津文15）在ABC △中，内角,,A B C 所对的边分别为,,a b c .已知sin 4sin a A B =，2225()ac a b c =--.（I ）求cos A 的值；（II ）求sin(2)B A -的值.解：(1)55-(2)255-1730、（17江苏5）若61)4tan(=-πα，则tanα= 57． 1731、（17江苏12）如图，在同一个平面内，向量OA ，OB ，OC 的模分别为1，1，，OA 与OC 的夹角为α，且tanα=7，OB 与OC 的夹角为45°．若OB n OA m OC +=),(R n m ∈，则=+n m 31732、（17江苏16）已知向量)sin ,(cos x x a =ϖ，)3,3(-=b ϖ，],0[π∈x 。
2017年浙江省高考数学试卷(真题详细解析)
2017年浙江省高考数学试卷(真题详细解析)1.已知集合P={x|-1<x<1}，Q={x|1<x<2}，则P∪Q=(-1,2)。
2.椭圆+1的离心率是1/2.3.几何体的三视图无法确定，无法计算体积。
4.若x、y满足约束条件z=x+2y，则z的取值范围是[4.+∞)。
5.函数f(x)=x^2+ax+b在区间[0,1]上的最大值是M，最小值是m，则M-m与a有关，但与b无关。
6.已知等差数列{an}的公差为d，前n项和为Sn，则d>0是S4+S6>2S5的必要不充分条件。
7.函数y=f(x)的图象可能是B。
8.已知随机变量ξi满足P(ξi=1)=pi，P(ξi=0)=1-pi，i=1，2.若0<p1<p2<1，则E(ξ1)<E(ξ2)，D(ξ1)<D(ξ2)。
9.正四面体D-ABC，P、Q、R分别为AB、BC、CA上的点，AP=PB=√2，记二面角D-PR-Q，D-PQ-R，D-QR-P的平面角为α、β、γ，则α<β<γ。
10.平面四边形ABCD，AB⊥BC，AB=BC=AD=2，CD=3，AC与BD交于点O，记I1=OI2/OC，I2=OI3/OD，I3=OI1/OA，则I3<I1<I2.二、填空题：11．XXX创立的“割圆术”可以估算圆周率π，理论上能把π的值计算到任意精度，祖冲之继承并发展了“割圆术”，将π的值精确到小数点后七位。
割圆术的第一步是计算单位圆内接正六边形的面积S6，S6=3√3/2.12．已知a、b∈R，（a+bi）2=3+4i（i是虚数单位），则a2+b2=5，ab=2.13．已知多项式（x+1）（x+2）=x2+3x+2，则a4=34，a5=123.14．已知△ABC，AB=AC=4，BC=2，点D为AB延长线上一点，BD=2，连结CD，则△BDC的面积是2√3，cos∠BDC=1/2.15．已知向量a、b满足||a||=1，||b||=2，则|a+b|+|a-b|-|a|-|b|的最小值是0，最大值是4.16．从6男2女共8名学生中选出队长1人，副队长1人，普通队员2人组成4人服务队，要求服务队中至少有1名女生，共有56种不同的选法。
2017年三角函数高考真题
8【. 2017年新课标Ⅲ卷，17】ABC 的内角A，B，C的对边分别为a，b，c，已知 sin A a 2 7 ，b2．
（1）求c； （2）设 D 为 BC 边上一点，且 AD AC ，求 △ABD 的面积．
3 cos A 0 ，
A． f (x) 的一个周期为 2π
B． y f (x) 的图像关于直线 x 8π 对称 3
C．
f
(x
)
的一个零点为
x
π 6
D．
f
(x)
在
(π 2
,
π)
单调递减
3.【2017 年新课标Ⅱ卷，14】函数 f x sin2 x
3
cos
x
3 4
（
x
0,
2
）的最大值
是
．
4. 【2017 年新课标Ⅱ卷，文 13】函数 f (x) 2 cos x sin x 的最大值为
.
5. （【 2017 年 新 课 标 Ⅱ 卷 ， 文 16 】 △ABC 的 内 角 A, B, C 的 对 边 分 别 为 a, b, c ， 若 2bcosB=acosC+ccosA，则 B= 6.【2017 年新课标Ⅰ卷，17】△ABC 的内角 A，B，C 的对边分别为 a，b，c，已知△ABC
2017 年 高考真题（三角）
2π
1.【2017 年新课标Ⅰ卷，9】已知曲线 C1：y=cos x，C2：y=sin (2x+ )，则下面结正确的
3
是（ ）
π A．把 C1 上各点的横坐标伸长到原来的 2 倍，纵坐标不变，再把得到的曲线向右平移 6
2017年上海高考数学真题试卷(word解析版)
绝密★启用前2017年普通高等学校招生全国统一考试（上海卷）数学试卷（满分150分，考试时间120分钟）1、考生注意2、1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页.3、2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置.4、3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分.5、4.用2B 铅笔作答选择题目，用黑色字迹钢笔、水笔或圆珠笔作答非选择题目.一.填空题目（本大题共12题，满分54分，第1~6题每题4分，第7~12题每题5分）1.已知集合{1,2,3,4}A ，集合{3,4,5}B ，则A B ∩2.若排列数6654m P ，则m3.不等式11x x 的解集为4.已知球的体积为36 ，则该球主视图的面积等于5.已知复数z 满足30z z，则||z6.设双曲线22219x y b(0)b 的焦点为1F 、2F ，P 为该双曲线上的一点，若1||5PF ，则2||PF7.如图，以长方体1111ABCD A B C D 的顶点D 为坐标原点，过D 的三条棱所在的直线为坐标轴，建立空间直角坐标系，若1DB 的坐标为(4,3,2)，则1AC的坐标为8.定义在(0,) 上的函数()y f x 的反函数为1()y f x ，若31,0()(),0x x g x f x x为奇函数，则1()2f x 的解为9.已知四个函数：①y x ；②1y x；③3y x ；④12y x .从中任选2个，则事件“所选2个函数的图像有且仅有一个公共点”的概率为10.已知数列{}n a 和{}n b ，其中2n a n ，*n N ，{}n b的项是互不相等的正整数，若对于任意*n N ，{}n b 的第na 项等于{}n a 的第nb 项，则149161234lg()lg()b b b b b b b b11.设1a 、2a R ，且121122sin 2sin(2) ，则12|10| 的最小值等于12.如图，用35个单位正方形拼成一个矩形，点1P、2P 、3P 、4P 以及四个标记为“”的点在正方形的顶点处，设集合1234{,,,}P P P P ，点P ，过P 作直线P l ，使得不在P l 上的“”的点分布在P l 的两侧.用1()P D l 和2()P D l 分别表示P l 一侧和另一侧的“”的点到P l 的距离之和.若过P 的直线P l 中有且只有一条满足12()()P P D l D l ，则 中所有这样的P 为二.选择题目（本大题共4题，每题5分，共20分）13.关于x 、y 的二元一次方程组50234x y x y的系数行列式D 为（）A.0543 B.1024 C.1523 D.605414.在数列{}n a 中，1(2nn a ，*n N ，则lim n n a （）A.等于12B.等于0C.等于12D.不存在15.已知a 、b 、c 为实常数，数列{}n x 的通项2n x an bn c ，*n N ，则“存在*k N ，使得100kx 、200kx 、300kx 成等差数列”的一个必要条件是（）A.0aB.0b C.0c D.20a b c 16.在平面直角坐标系xOy 中，已知椭圆221:1364x y C 和222:19y C x .P 为1C 上的动点，Q 为2C 上的动点，w 是OP OQ的最大值.记{(,)|P Q P 在1C 上，Q 在2C 上，且}OP OQ w，则 中元素个数为（）A.2个B.4个C.8个D.无穷个三.解答题（本大题共5题，共14+14+14+16+18=76分）17.如图，直三棱柱111ABC A B C 的底面为直角三角形，两直角边AB 和AC 的长分别为4和2，侧棱1AA 的长为5.（1）求三棱柱111ABC A B C 的体积；（2）设M 是BC 中点，求直线1A M 与平面ABC 所成角的大小.18.已知函数221()cos sin 2f x x x，(0,)x .（1）求()f x 的单调递增区间；（2）设△ABC 为锐角三角形，角A所对边a ，角B 所对边5b ，若()0f A ，求△ABC 的面积.19.根据预测，某地第n *()n N 个月共享单车的投放量和损失量分别为n a 和n b （单位：辆），其中4515,1310470,4n n n a n n，5n b n ，第n 个月底的共享单车的保有量是前n 个月的累计投放量与累计损失量的差.（1）求该地区第4个月底的共享单车的保有量；（2）已知该地共享单车停放点第n 个月底的单车容纳量24(46)8800n S n （单位：辆）.设在某月底，共享单车保有量达到最大，问该保有量是否超出了此时停放点的单车容纳量？20.在平面直角坐标系xOy 中，已知椭圆22:14x y ，A 为 的上顶点，P 为 上异于上、下顶点的动点，M 为x 正半轴上的动点.（1）若P在第一象限，且||OP ，求P的坐标；（2）设83(,)55P ，若以A 、P 、M 为顶点的三角形是直角三角形，求M 的横坐标；（3）若||||MA MP ，直线AQ 与 交于另一点C ，且2AQ AC ，4PQ PM ，求直线AQ 的方程.21.设定义在R 上的函数()f x 满足：对于任意的1x 、2x R ，当12x x 时，都有12()()f x f x .（1）若3()1f x ax ，求a 的取值范围；（2）若()f x 为周期函数，证明：()f x 是常值函数；（3）设()f x 恒大于零，()g x 是定义在R 上、恒大于零的周期函数，M 是()g x 的最大值.函数()()()h x f x g x .证明：“()h x 是周期函数”的充要条件是“()f x 是常值函数”.2017年普通高等学校招生全国统一考试上海--数学试卷考生注意1.本场考试时间120分钟，试卷共4页，满分150分，答题纸共2页.2.作答前，在答题纸正面填写姓名、准考证号，反面填写姓名，将核对后的条形码贴在答题纸指定位置.3.所有作答务必填涂或书写在答题纸上与试卷题号对应的区域，不得错位.在试卷上作答一律不得分.4.用2B 铅笔作答选择题目，用黑色字迹钢笔、水笔或圆珠笔作答非选择题目.一、填空题目（本大题共有12题，满分54分，第1-6题每题4分，第7-12题每题5分）考生应在答题纸的相应位置直接填写结果.1.已知集合1,2,3,4,3,4,5A B ,则A B ∩.【解析】本题考查集合的运算，交集，属于基础题【答案】3,42.若排列数6P 654m ,则m .【解析】本题考查排列的计算，属于基础题【答案】33.不等式11x x 的解集为.【解析】本题考查分式不等式的解法，属于基础题【答案】,0 4.已知球的体积为36 ，则该球主视图的面积等于.【解析】本题考查球的体积公式和三视图的概念，343633R R ,所以29S R ，属于基础题【答案】95.已知复数z 满足30z z，则z .【解析】本题考查复数的四则运算和复数的模，2303z z z设z a bi ，则22230,a b abi a b,z【答案】6.设双曲线 222109x y b b 的焦点为12F F 、,P为该双曲线上的一点.若15PF ,则2PF.【解析】本题考查双曲线的定义和性质，1226PF PF a （舍），2122611PF PF a PF 【答案】117.如图，以长方体1111ABCD A B C D 的顶点D 为坐标原点，过D 的三条棱所在的直线为坐标轴，建立空间直角坐标系.若1DB 的坐标为(4,3,2),则1AC的坐标是.【解析】本题考查空间向量，可得11(400)(03,2)(432)A C AC，，，，，，,属于基础题【答案】(432) ，，8.定义在(0,) 上的函数()y f x 的反函数-1()y f x .若31,0,()(),0x x g x f x x 为奇函数，则-1()=2f x 的解为.【解析】本题考查函数基本性质和互为反函数的两个函数之间的关系，属于中档题10,0,()31()()13x x x x g x g x g x,所以1()13x f x,当2x 时，8()9f x,所以18(29f【答案】9x9.已知四个函数：①y x ；②1y x；③3y x ；④12y x .从中任选2个，则事件“所选2个函数的图像有且仅有一个公共点”的概率为.【解析】本题考查事件的概率，幂函数的图像画法和特征，属于基础题总的情况有：42C 6种，符合题意的就两种：①和③，①和④【答案】1310.已知数列na 和 nb ,其中2,N na n n ， nb 的项是互不相等的正整数.若对于任意N n n b ，中的第n a 项等于 n a 中的第n b 项，则149161234lg lg b b b b b b b b.【解析】本题考查数列概念的理解，对数的运算，属于中档题由题意可得：222222114293164(),,,n n a b n n b a b b b b b b b b b b ，所以214916123412341234lg lg =2lg lg b b b b b b b b b b b b b b b b 【答案】211.设12R ，,且121122sin 2sin(2) ，则1210 的最小值等于.【解析】考查三角函数的性质和值域，121111,1,12sin 32sin(2)3，，要使121122sin 2sin(2) ，则111122221=122sin 2,,1=12sin(2)4k k k Z k1212min min31010(2)44k k,当122=11k k 时成立【答案】412.如图，用35个单位正方形拼成一个矩形，点1234,,,P P P P 以及四个标记为“▲”的点在正方形的顶点处.设集合1234=,,,P P P P ，点P .过P 作直线P l ，使得不在P l 上的“▲”的点分布在P l 的两侧.用1()P D l 和2()P D l 分别表示P l 一侧和另一侧的“▲”的点到P l 的距离之和.若过P 的直线P l 中有且只有一条满足12()=()P P D l D l ，则 中所有这样的P 为.【解析】本题考查有向距离，以左下角的顶点为原点建立直角坐标系。
2017年高考全国名校试题数学分项汇编 专题04 三角函数与解三角形(原卷版) Word版无答案
一、填空题1. 【2016高考冲刺卷（9）【江苏卷】】已知()23tantan 1,sin 3sin 222ααβαβ+==+，则()tan αβ+=2. 【2016高考冲刺卷（7）【江苏卷】】直线3=y 与曲线)0(sin 2>=ωωx y 相距最近的两个交点间距离为6π，则x y ωsin 2=的最小正周期为 ． 3. 【2016高考冲刺卷（6）【江苏卷】】已知θ是第三象限角，且52cos 2sin -=-θθ，则=+θθcos sin4. 【2016高考冲刺卷（5）【江苏卷】】已知312sin =α，则⎪⎭⎫ ⎝⎛-4cos 2πα=_____▲____．5. 【2016高考冲刺卷（3）【江苏卷】】将函数()sin(),(0,)22f x x ππωϕωϕ=+>-<<图象上每一点的横坐标缩短为原来的一半，纵坐标不变，再向右平移4π个单位长度得到sin y x =的图象，则()6f π= ．6. 【2016高考冲刺卷（1）【江苏卷】】若α、β均为锐角，且1cos 17α=，47cos()51αβ+=-，则cos β= ．7. 【江苏省苏中三市（南通、扬州、泰州）2016届高三第二次调研测试数学试题】若将函数)4sin(πω+=x y 的图象向左平移6π个单位长度后，与函数)4cos(πω+=x y 的图象重合，则正数ω的最小值为_____________.8. 【江苏省南京市2016届高三年级第三次学情调研适应性测试数学】将函数f (x )＝sin(2x ＋θ)()22ππθ-<<的图象向右平移φ(0＜φ＜π)个单位长度后得到函数g (x )的图象，若f (x )，g (x )的图象都经过点P ，则φ的值为 ▲ ．9. 【2016高考冲刺卷（2）【江苏卷】】已知函数f (x )＝|sin |x －kx (x ≥0，k ∈R )有且只有三个零点，设此三个零点中的最大值为0x ，则200(1)sin 2x x x +＝ ▲ ． 10. 【2016高考押题卷（3）【江苏卷】】已知函数b a x b x a x f ,(cos sin )(+=为常数，且R x a ∈≠,0），若函数)4(π+=x f y 是偶函数，则)4(π-f 的值为 ．11. 【2016高考押题卷（3）【江苏卷】】设α为锐角，若31)6sin(=-πα，则αcos 的值为 ． 12. 【2016高考押题卷（3）【江苏卷】】如图，在平面四边形ABCD 中，若090,2,2,1=∠===ACD DC AD BC AB ，则对角线BD 的最大值为 ．13. 【2016高考押题卷（1）【江苏卷】】将函数3cos sin y x x x的图像向左平移0m m个单位长度后，所得的图像关于y 轴对称，则m 的最小值是_______.14. 【2016年第四次全国大联考【江苏卷】】已知sin 2cos αα+=，那么tan2α的值为_______.15. 【2016年第三次全国大联考【江苏卷】】已知]4,4[ππθ-∈，且314cos -=θ，则=--+)4(sin )4(sin 44πθπθ ．16. 【 2016年第二次全国大联考（江苏卷）】已知1sin tan(),(,)72ααβαπ=+=∈π，那么tan β的值为_______.二、解答题1. 【 2016年第二次全国大联考（江苏卷）】（本小题满分14分）在ABC △中，角CB A 、、分别是边c b a 、、的对角，且b a 23=， （Ⅰ）若 60=B ，求C sin 的值； （Ⅱ）若2cos 3C=，求sin()A B -的值． 2. 【 2016年第二次全国大联考（江苏卷）】（本小题满分16分）如图，290,,3OC km AOB OCD πθ=∠=∠=,点O 处为一雷达站，测控范围为一个圆形区域（含边界），雷达开机时测控半径r 随时间t 变化函数为3r =，且半径增大到81km 时不再变化．一架无人侦察机从C 点处开始沿CD 方向飞行,其飞行速度为15/min km ．(Ⅰ) 当无人侦察机在CD 上飞行t 分钟至点E 时，试用t 和θ表示无人侦察机到O 点的距离OE ；（Ⅱ）若无人侦察机在C 点处雷达就开始开机，且4πθ=，则雷达是否能测控到无人侦察机？请说明理由.3. 【2016年第三次全国大联考【江苏卷】】（本小题满分14分）在平面直角坐标系xOy 中，设锐角α的始边与x 轴的非负半轴重合，终边与单位圆交于点11(,)P x y ，将射线OP 绕坐标原点O 按逆时针方向旋转2π后与单位圆交于点22(,)Q x y . 记12()f y y α=+.(Ⅰ)求函数()f α的值域；(Ⅱ)设ABC ∆的角,,A B C 所对的边分别为,,a b c，若()f C =a =1c =，求b的值.4. 【2016年第四次全国大联考【江苏卷】】（本小题满分14分）在ABC ∆中，角C B A 、、分别是边c b a 、、的对角，且(cos ,sin ),(cos ,sin ),cos2,sin sin 3sin sin A A B B C A B A B =-=⋅=+=m n m n ，（Ⅰ）求角C 的值；（Ⅱ）若3c =，求ABC ∆的面积．5. 【2016年第四次全国大联考【江苏卷】】（本小题满分14分）如图，等边三角形OAB 的边O C DEAB长为4km.现在线段OB 上取一点D （不含线段OB 端点）建发电站向,A B 两点供电．如果线段DB 上每公里建设费用为a 万元（a 为正常数），线段AD 上每公里建设费用为3a 万元，设ADO θ∠=，建设总费用为S 万元.(Ⅰ) 写出S 关于θ的函数关系式，并指出θ的取值范围； （Ⅱ）AD 等于多少时，可使建设总费用S 最少？6. 【2016年第一次全国大联考【江苏卷】】（本小题满分14分）已知角α终边逆时针旋转6π与单位圆交于点 且2tan()5αβ+=. （1）求sin(2)6πα+的值，（2）求tan(2)3πβ-的值.7. 【2016高考押题卷（1）【江苏卷】】（本小题满分14分）如图，两座建筑物AB ，CD 的底部都在同一个水平面上，且均与水平面垂直，它们的高度分别是9m 和15m ，从建筑物AB 的顶部A 看建筑物CD 的张角45CAD ∠=． （1）求BC 的长度；（2）在线段BC 上取一点P (点P 与点B ，C 不重合)，从点P 看这两座建筑物的张角分别为APB α∠=，DPC β∠=，问点P 在何处时，tan()αβ+最小？8. 【2016高考押题卷（3）【江苏卷】】（本小题满分14分）已知ABC ∆的面积是30，内角C B A ,,所对边长分别是c b a ,,，且144-=⋅AC AB ． （1）求A cos 的值；（2）若4=-b c ，求a 的值．9. 【2016高考押题卷（2）【江苏卷】】（本小题满分14分） 已知函数2()sin(2)cos 6f x x x π=+-．(1)求()f x 的最小正周期及2[,]123x ππ∈时()f x 的值域；(2)在△ABC 中，角A 、B 、C 所对的边为c b a ,,，其中角C 满足423)4(-=+πC f ，若ABC S ∆，2=c ，，求)(,b a b a >的值．10. 【江苏省扬州中学2015—2016学年第二学期质量检测】（本小题满分14分）设ABC ∆的内角,,A B C 的对边分别为,,,tan a b c a b A =，且B 为钝角.（1）证明：2B A π-=； （2）求sin sin A C +的取值范围.11. 【2016高考冲刺卷（4）【江苏卷】】（本小题满分14分）已知函数()2sin cos()3f x x x ωωπ=+（0ω>）的最小正周期为π. （Ⅰ）求ω的值；（Ⅱ）求()f x 在区间[,]62ππ-上的最大值和最小值.12. 【南京市2016届高三年级第三次模拟考试】（本小题满分14分）在△ABC 中，已知a ，b ，c 分别为角A ，B ，C 的对边．若向量m ＝(a ，cos A )，向量n ＝(cos C ，c )，且m ·n ＝3b cos B ． （1）求cos B 的值；（2）若a ，b ，c 成等比数列，求11tan tanCA +的值． 13. 【2016高考冲刺卷（1）【江苏卷】】(本小题满分14分)已知ABC ∆中，角A 、B 、C 所对的边分别为a 、b 、c ，满足sin sin sin sin b a B Cc B A--=+． ⑴求角A 的值；⑵若a ，c ，b 成等差数列，试判断ABC ∆的形状．14. 【2016高考冲刺卷（3）【江苏卷】】（本小题满分14分）若A B C 、、为ABC ∆的三内角，且其对边分别为a b c 、、．若向量2(cos ,cos 1)22A A m =-，向量(1,cos 1)2An =+，且21m n ⋅=-．（1）求A 的值；（2）若a =S =b c +的值．15. 【2016高考冲刺卷（5）【江苏卷】】(本题满分14分)已知函数2()2sin cos f x x x x =+．（1）求函数()f x 的最小正周期和单调减区间；（2）已知ABC ∆的三个内角A ，B ，C 的对边分别为a ，b ，c ，其中7a =，若锐角A 满足()26A f π-=sin sin B C +=，求bc 的值． 16. 【2016高考冲刺卷（6）【江苏卷】】在△ABC 中，角A 、B 、C 的对边分别为c b a ,,，已知A C B cos 1)cos(-=-，且c a b ,,成等比数列.（1）求C B sin sin ⋅之值； （2）求角A 的大小； （3）求C B tan tan +的值。
2017年高考真题——数学(浙江卷)解析
2017年高考真题——数学(浙江卷)解析2 绝密★启用前2017年普通高等学校招生全国统一考试（浙江卷）数学【试卷点评】选择题部分（共40分）一、选择题：本大题共10小题，每小题4分，共40分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．已知集合{|11}P x x =-<<，{02}Q x =<<，那么P Q =UA ．(1,2)-B ．(0,1)C ．(1,0)-D ．(1,2)【答案】A【考点】集合运算【名师点睛】对于集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图处理．2．椭圆22194xy+=的离心率是 A 13B ．5C ．23D ．59【答案】B【解析】 试题分析：945e -==B ．【考点】 椭圆的简单几何性质3【名师点睛】解决椭圆和双曲线的离心率的求值及范围问题，其关键就是确立一个关于,,a b c 的方程或不等式，再根据,,a b c 的关系消掉b 得到,a c 的关系式，建立关于,,a b c 的方程或不等式，要充分利用椭圆和双曲线的几何性质、点的坐标的范围等．3．某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：cm 3）是（第3题图）A ．12π+ B ．32π+ C ．312π+ D ．332π+ 【答案】A【考点】 三视图【名师点睛】思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，4其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽．由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整．4．若x ，y 满足约束条件03020x x y x y ≥⎧⎪+-≥⎨⎪-≤⎩，则2z x y =+的取值范围是A ．[0，6]B ．[0，4]C ．[6，)+∞D ．[4，)+∞【答案】D【解析】试题分析：如图，可行域为一开放区域，所以直线过点(2,1)时取最小值4，无最大值，选D ．【考点】 简单线性规划【名师点睛】本题主要考查线性规划问题，首先由不等式组作出相应的可行域，作图时，可将不等式++≥转化为y kx bAx By C≥+），“≤”取下方，“≥”≤+（或y kx b取上方，并明确可行域对应的是封闭区域还是开放区域、分界线是实线还是虚线，其次确定目标函数的几何意义，是求直线的截距、两点间距离的平方、直线的斜率、还是点到直线的距离等等，最后结合图形确定目标函数最值取法、值域范围．5．若函数f(x)=x2+ ax+b在区间[0，1]上的最大值是M，最小值是m，则M–mA．与a有关，且与b有关B．与a有关，但与b无关C．与a无关，且与b无关D．与a无关，但与b有关B【答案】【考点】二次函数的最值【名师点睛】对于二次函数的最值或值域问题，通常先判断函数图象对称轴与所给自变量闭区间的关系，结合图象，当函数图象开口向上时，若对称轴在区间的左边，则函数在所给区间内单调递增；若对称轴在56区间的右边，则函数在所给区间内单调递减；若对称轴在区间内，则函数图象顶点的纵坐标为最小值，区间端点距离对称轴较远的一端取得函数的最大值．6．已知等差数列{a n }的公差为d ，前n 项和为S n ，则“d >0”是“S 4 + S 6>2S 5”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C【解析】试题分析：由46511210212(510)SS S a d a d d +-=+-+=，可知当0d >时，有46520S S S +->，即4652S S S +>，反之，若4652S S S +>，则0d >，所以“d >0”是“S 4 + S 6>2S 5”的充要条件，选C ．【考点】 等差数列、充分必要性【名师点睛】本题考查等差数列的前n 项和公式，通过套入公式与简单运算，可知4652S S S d +-=， 结合充分必要性的判断，若p q ⇒，则p 是q 的充分条件，若p q ⇐，则p 是q 的必要条件，该题“0d >”⇔“46520S S S +->”，故互为充要条件．7．函数y=f (x )的导函数()y f x '=的图象如图所示，则函数y=f(x)的图象可能是（第7题图）【答案】D【考点】导函数的图象【名师点睛】本题主要考查导数图象与原函数图象的关系：若导函数图象与x轴的交点为x，且图象在0x两侧附近连续分布于x轴上下方，则x为原函数单调性的拐点，运用导数知识来讨论函数单调性时，由导函数f'x的正负，得出原函数()f x的单调区间．()8．已知随机变量iξ满足P（iξ=1）=p i，P（iξ=0）=1–p i，，则i=1，2．若0<p1<p2<12A．1()Eξ，1()Dξ>2()Eξ<2()DξEξ<2()Eξ，1()Dξ<2()DξB．1()C．1()Eξ，1()Eξ>2()Dξ>2()DξDξ<2()DξD．1()Eξ>2()Eξ，1()【答案】A78【解析】试题分析：∵1122(),()E p E p ξξ==，∴12()()E E ξξ<， ∵111222()(1),()(1)D p p D p p ξξ=-=-，∴121212()()()(1)0D D p p p p ξξ-=---<，故选A ．【考点】 两点分布【名师点睛】求离散型随机变量的分布列，首先要根据具体情况确定X 的取值情况，然后利用排列，组合与概率知识求出X 取各个值时的概率．对于服从某些特殊分布的随机变量，其分布列可以直接应用公式给出，其中超几何分布描述的是不放回抽样问题，随机变量为抽到的某类个体的个数．由已知本题随机变量iξ服从两点分布，由两点分布数学期望与方差的公式可得A 正确． 9．如图，已知正四面体D –ABC （所有棱长均相等的三棱锥），P ，Q ，R 分别为AB ，BC ，CA 上的点，AP=PB ，2BQCR QC RA ==，分别记二面角D –PR –Q ，D –PQ –R ，D –QR –P的平面角为α，β，γ，则9（第9题图）A ．γ<α<βB ．α<γ<βC ．α<β<γD ．β<γ<α【答案】B【考点】 空间角（二面角）【名师点睛】立体几何是高中数学中的重要内容，也是高考重点考查的考点与热点．这类问题的设置一般有线面位置关系的证明与角度距离的计算等两类问题．解答第一类问题时一般要借助线面平行与垂直的判定定理进行；解答第二类问题时先建立空间直角坐标系，运用空间向量的坐标形式及数量积公式进行求解．10．如图，已知平面四边形ABCD ，AB ⊥BC ，AB ＝BC＝AD ＝2，CD ＝3，AC 与BD 交于点O ，记1·I OA OB u u u r u u u r ＝，2·I OB OC u u u r u u u r ＝，3·I OC OD u u u r u u u r ＝，则（第10题图）A．123<<C．312I I I<<I I II I I<<B．132D．213<<I I IC【答案】【考点】平面向量的数量积运算【名师点睛】平面向量的计算问题，往往有两种形式，一是利用数量积的定义式，二是利用数量积的坐标运算公式，涉及几何图形的问题，先建立适当的平面直角坐标系，可起到化繁为简的妙用．利用向量夹角公式、模公式及向量垂直的充要条件，可将有关角度问题、线段长问题及垂直问题转化为向量的数量积来解决．列出方程组求解未知数．本题通过所给条件结合数量积运算，易得90∠=∠>o，AOB COD由AB＝BC＝AD＝2，CD＝3，可求得OA OC<，<，OB OD1011进而得到312I I I <<．非选择题部分（共110分）二、填空题：本大题共7小题，多空题每题6分，单空题每题4分，共36分。
备战2017高考黄金100题解读与扩展系列之三角函数：1 三角函数定义的应用 含解析
I ．题源探究·黄金母题 【例1】已知角α的终边经过点()3,4P --，求角α的正弦、余弦和正切值． 【解析】由已知可得：()()220345OP x =-+-=．如图，设角α的终边与单位圆交于点(),P x y ．分别过点0,P P 作x 轴的垂线00,,MP M P 则0004,,3,M P MP y OM ==-= ,OM x OMP =-∆∽00OM P ∆，于是， 0004sin 15MP M P y y OP OP α-====-=-； 003cos 15OM OM x x OP OP α-====-=-；sin 4tan cos 3y x ααα===．精彩解读【试题来源】人教版A 版必修4第12页例2．【母题评析】本题考查任意角终边上任意一点三角函数的定义．【思路方法】一般地，设角α的终边上任意一点P 的坐标为(),x y ，它与原点的距离为r，则()sin ,cos ,tan 0y x yx r r xααα===≠．【变式】已知角α的终边上有一点P 的坐标是()3,4a a ，其中0a ≠，求sin ,cos ,tan ααα的值．（人教版A 版必修4第20页习题A 组第2题）II ．考场精彩·真题回放【例2】【2013新课标全国II 卷】设θ为第二象限角，若1tan 42πθ⎛⎫+=⎪⎝⎭，则sin cos θθ+= ．【解析】11tan 11tan ,,tan ,421tan 23πθθθθθ+⎛⎫+=∴=∴=- ⎪-⎝⎭Q Q 为第二象限角，设角θ的终边上有一点()()3,0,10,P k k k r k ->∴【命题意图】本题主要考查三角函数的定义的应用，考查考生基本计算能力．【考试方向】这类试题在考查题型上，通常以选择题或填空题的形式出现，难度中等偏易，考查基础知识的识记与理解．【难点中心】解答此类问题的关键是正确运用三角函数的定义，注意角所在的象限．10sin ,cos ,sin cos 51010y x r r θθθθ∴====-∴+=-．III ．理论基础·解题原理 任意角αα−−−−→唯一对应的终边的位置−−−−→唯一对应终边与单位圆的交点坐标，即任意角α−−−−→唯一对应终边与单位圆的交点坐标．一、三角函数的单位圆定义法设α是一个任意角，它的终边与单位圆交于点(),P x y ，那么：正弦sin y α=；余弦cos x α=；正切tan (0)yx xα=≠． 即：正弦、余弦、正切都是以角（实数）为自变量，以单位圆上点的坐标或坐标的比值为函数值的函数，我们称它们为三角函数．（单位圆定义法） 二、三角函数的终边定义法设α是一个任意角，α的终边上任意一点P 的坐标是(),x y ，它与原点的距离是()220r r x y =+>，则()sin ,cos ,tan 0y x yx r r xααα===≠． 三、三角函数线如图（I ）～（IV ），设任意角α的顶点在原点，始边与x 轴的正半轴重合且与单位圆交于点A ，终边与单位圆交于点(),P x y ，过点P 作PM 垂直x 轴于点M ，过点A 作x 轴垂线与角α的终边或其延长线交于点T ，则有向线段,,MP OM AT 分别称为角α的正弦线、余弦线、正切线，即正弦线：sin MP y α==；余弦线：cos OM x α==；正切线：tan (0)yAT x xα==≠．正弦线、余弦线、正切线统称为三角函数线． IV ．题型攻略·深度挖掘 【考试方向】这类试题在考查题型上，通常以选择题或填空题的形式出现，一般难度较小，考查对基础知识的识记与理解，考查考生基本计算能力． 【技能方法】（1）已知角α的终边上一点P 的坐标求角α的三角函数值，可先求出点P 到原点的距离r ，然后利用三角函数的终边定义法求解；（2）已知角α的终边所在的直线方程求角α的三角函数值，则可先设出终边上一点的坐标，求出点到原点的距离，然后利用三角函数的终边定义法求解相关的问题．若直线的倾斜角为特殊角，也可以直接写出角α的三角函数值；（3）各象限三角函数值符号规律的口诀：一全正、二正弦、三正切、四余弦． 【易错指导】当角的终边所在的位置不是唯一确定的时候要注意分情况讨论，机械地使用三角函数的定义会出现错误．V ．举一反三·触类旁通【例3】【2016新课标Ⅱ学易大联考三】已知函数()sin 2()f x x ＝＋ϕ（0ϕ<<π），若角ϕ的终边经过点(3,3)，则()4f π的值为（ ）A ．3B ．3C ．2D ．23 【命题意图】本题考查诱导公式、三角函数的定义等基础知识，意在考查数形结合思想和基本运算能力． 【答案】A【例4】【2016年湖北龙泉中学高三月考】已知角θ的顶点与原点重合，始边与x 轴非负半轴重合，终边在直线2y x =上，则sin 24πθ⎛⎫+⎪⎝⎭的值为（ ） A ．7210-B ．210C ．210-D ．210【答案】D【解析】由题意可知2tan =θ，))2sin 2sin 2cos 2sin cos cos 422πθθθθθθ⎛⎫+=+=+- ⎪⎝⎭102221tan )1(tan 222)1(tan cos 222=-++=-+=θθθθ，所以本题的正确选项为D ． 【例5】【2016届湖南省四大名校高三3月联考数学（理）试卷】在直角坐标系中，P 点的坐标为34,,55Q ⎛⎫⎪⎝⎭是第三象限内一点，1OQ =， 且34POQ π∠=，则Q 点的横坐标为 （ ）A ．B ．． D ．【答案】A【解析】由题设可设)sin ,(cos ),sin ,(cos ααθθP Q ，则Z k k ∈+=-==,245,54sin ,53cos ππαθαα，所以Z k k ∈++=,245παπθ，所以cos(cos =θ102754225322)45-=⨯-⨯-=+απ，故应选A ． 【例6】【2015-2016福建师大附中高一下期中考数学】若点(sin cos ,2cos )P θθθ位于第三象限，那么角θ终边落在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 【答案】B【解析】由题设0sin ,0cos ><θθ，故角θ的终边在第二象限．故应选B ．【例7】【2015-2016学年湖南衡阳一中高一下期末数学试卷】已知角α的终边过点(8,3)P m ，且4cos 5α=-，则m 的值为（ ）A ．12-B ．12C ．2-D ． 2【答案】A【解析】由题设549648cos 2-=+=m mα可得21±=m ，经检验21-=m 成立，应选A ．【例8】【2015-2016学年西藏山南二中高一下期末数学试卷】若角600o的终边上有一点(4,)a -，则a的值是（ ）A ．．-．±．0 【答案】B【解析】由题意得tan 6004tan 604aa =-⇒=-=-oo B ． 【方法点睛】利用三角函数的定义，求一个角的三角函数值，需确定三个量：角的终边上任意一个异于原点的点的横坐标x ，纵坐标y ，该点到原点的距离r ．若题目中已知角的终边在一条直线上，此时注意在终边上任取一点有两种情况（点所在象限不同）．【例9】【2015-2016学年黑龙江鹤岗一中高二下期末理科数学试卷】已知角α的终边过点()m m P 34，-()0m <，则ααcos sin 2+的值是（ ）A ．1B ．52C ．52- D ．－1 【答案】C【解析】因m m m r 591622-=+=，故54cos ,53sin =-=αα，所以52cos sin 2-=+αα，故选C ．【例10】【2015-2016学年西藏日喀则一中高二下期末文科数学试卷】已知角α终边与单位圆221x y +=的交点为1,2y ⎛⎫P ⎪⎝⎭，则sin 22πα⎛⎫+= ⎪⎝⎭（ ）A ．12-B ．12C ．-．1【答案】A 【解析】因21cos =α，故sin 22πα⎛⎫+= ⎪⎝⎭211cos 22cos 2-=-=αα，故应选A ． 【例11】【2016届吉林四平一中高三五模文科数学试卷】已知锐角α的终边上一点(1cos 40,sin 40)P +o o ，则锐角α=（ ）A ．80oB ．70oC ．20oD ．10o【答案】C【解析】sin 4040tan tan tan 20,201cos 402αα====+o o o oo．【例12】【2015-2016学年海南省国兴中学高一下第一次月考数学试卷】已知()P y 为角β的终边上的一点，且sin β=，则y的值为（ ） A ．12±B ．12C ．12- D ．2± 【答案】B 【解析】13133sin 2=+=y y β，解得21=y ，故选B ． 【例13】【2015-2016学年湖北省黄冈市蕲春县高一下期中数学试卷】已知α为锐角，且α5的终边上有一点)130cos ),50(sin(00-P ，则α的值为（ ）A ．08 B ．044 C ．026 D ．040 【答案】B【解析】利用诱导公式，可以将点P 化简为P （cos220°，sin220°），因为0°＜α＜45°， 所以5α=220°，所以α=44°．故选B【例14】【2015-2016学年湖南省株洲市十八中高一下期中理科数学试卷】若,54cos ,53sin -==αα则在角α终边上的点是（ ）A ． )3,4(-B ． )4,3(-C ． )3,4(-D ． )4,3(- 【答案】A【解析】由三角函数定义可知，角终边上的点(),x y满足3445y r xrr ⎧=⎪⎪⎪=-⎨⎪⎪=⎪⎩，所以43x y =-⎧⎨=⎩，点为)3,4(-．【例15】【2015-2016学年湖南省株洲市十八中高一下期中理科数学试卷】已知点P （ααcos ,tan ）在第三象限，则角α在（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 【答案】B【解析】因为点P （tan α，cos α）在第三象限，所以，tan α＜0，cos α＜0，则角α的终边在第二象限．【例16】【2015-2016学年湖南省醴陵二中、四中高一下期中数学试卷】若点(sin cos ,tan )P ααα-在第一象限，则在[0,2)π内α的取值范围是（ ）A ．5(,)(,)424ππππU B ．35(,)(,)244ππππU C ．)23,45()2,4(ππππY D ．33(,)(,)244ππππU 【答案】A 【解析】由题意得sin cos 0tan 0ααα->⎧⎨>⎩，由[0,2)απ∈可得α的取值范围是5(,)(,)424ππππU 【例17】【2015-2016学年福建省晋江市季延中学高一下期中数学试卷】已知正角α的终边上一点的坐标为（32cos ,32sinππ），则角α的最小值为（ ） A ．65π B ．32π C ．35π D ．611π【答案】D【解析】由题点坐标为；（32cos ,32sinππ），1)2-， 则：111sin ,26y r παα==-= 【例18】【2016届湖北省襄阳五中高三5月高考模拟一文科数学试卷】在平面直角坐标系中，角α的顶点与原点重合，始边与x 轴的非负半轴重合，终边过点(3,1)P --，则sin(2)2πα-=（ ） A ．3 B ．3- C ．12 D ．12- 【答案】D 【解析】因33tan =α，则67πα=，故sin(2)2πα-21-=，选D ． 【例19】【2015-2016学年吉林省松原市扶余一中高一下期中数学试卷】若角α的终边过点P （2cos120°，sin225°），则cosα=（ ） A ．B ．C ．D ．【答案】【例20】【2016届河北省衡水中学高三下学期猜题理科数学试卷】若点55(sin,cos )66ππ在角α的终边上，则sin α的值为（ ） A ．3．12- C ．12 D 3【答案】A ．【解析】根据任意角的三角函数的定义，5cos 36sin 12πα==-，故选A ． 【例21】【2015-2016学年贵州花溪清华中学高一5．28周练】若角α和β的终边关于直线0x y +=对称， 且3πα=-，则β角的集合是 ．【答案】|2,6k k Z πββπ⎧⎫=-∈⎨⎬⎩⎭【解析】根据象限角可得3-πα=关于0=+y x 对称的一个角是6πβ-=，那么根据终边相同的角的集合的表示为|2,6k k Z πββπ⎧⎫=-∈⎨⎬⎩⎭． 【例22】【2015-2016学年江苏省连云港东海县房山高中高一下期中数学试卷】已知角的终边过点(1,2)P -，则sin α的值为 ．【答案】5【解析】由题角的终边过点(1,2)P -： 因为：sin yrα=，r ==则；sin 5α= 【例23】【2015-2016学年北京市怀柔区高一上期末数学试卷】已知角α的终边经过点1(2P ，则tan α的值为____________． 【答案】3 【解析】3tan ==xyα 【例24】【2015-2016学年福建师大附中高二下期末文科数学试卷】设0<a ，角α的终边经过点(3,4)P a a -，则αsin =__________． 【答案】45-【解析】44sin 55a a α===--． 【例25】【2015-2016学年广东仲元中学高二上期末数学试卷】在平面直角坐标系xoy 中，以x 的非负半轴为始边作两个锐角βα,，它们的终边分别与单位圆交于点A ，B ，已知A 的横坐标为55，B 的纵坐标为102，则=+βα2______． 【答案】43π【解析】由三角函数的定义可知：cos 5α=，sin 10β=，sin5α∴=，cos 10β=， 4sin25α∴=，23cos 212(55α=-⨯=-，472322sin(2)()55αβ∴+=⨯+-⨯=，324παβ∴+=． 【例26】【2015-2016学年内蒙古赤峰二中高一上第二次月考文数学卷】已知角α的终边上一点()3,,0P y y -≠，且2sin 4y α=，求cos ,tan αα的值． 【答案】6155.cos ,tan ,43y αα==-=-或6155,cos ,tan 43y αα=-=-=．【例27】【2015-2016学年甘肃省金昌市永昌一中高一上学期期末考】已知角α的终边在直线y=x 上，求sinα，cosα，tanα的值．【答案】sinα=﹣，cosα=﹣，ta nα=【解析】试题分析：分类讨论，取特殊点的坐标，由三角函数定义可得． 试题解析：直线y=x ，当角α的终边在第一象限时，在α的终边上取点（1，），则sinα=，cosα=，tanα=；当角α的终边在第三象限时，在α的终边上取点（﹣1，﹣），则sinα=﹣，cosα=﹣，tanα=．【例28】【2015-2016学年福建省清流县一中高一上学期期中考试数学试卷】 （1）已知角α的终边经过一点)0)(3,4(>-a a a P ，求ααcos sin 2+的值； （2）已知角α的终边在一条直线x y 3=上，求αsin ，αtan 的值．【答案】（1）25-；（2）3tan=α，当0>a时，23sin=α；当0<a时，23sin-=α．。
2017年高考数学—三角函数(解答+答案)
2017年高考数学—三角函数（解答+答案）1.（17全国1理17．（12分））△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A（1）求sin sin B C ;（2）若6cos cos 1,3B C a ==，求△ABC 的周长.2.（17全国2理17.（12分））ABC ∆的内角A B C 、、所对的边分别为,,a b c ，已知2sin()8sin 2B AC +=， （1）求cos B ；（2）若6a c +=，ABC ∆的面积为2，求b ．3.（17全国3理17．（12分））ABC ∆的内角,,A B C 的对边分别为,,a b c ，已知sin 0,2A A a b +===（1）求c ；（2）设D 为BC 边上一点，且AD AC ⊥，求ABD △的面积．4.（17北京理（15）（本小题13分））在ABC ∆中，360,7A c a ∠==o（Ⅰ）求sin C 的值；（Ⅱ）若7a =，求ABC ∆的面积.已知函数())2sin cos 3f x x x x π=--（Ⅰ）求()f x 的最小正周期； （Ⅱ）求证：当[,]44x ππ∈-时，1()2f x ≥-6.（17山东理16）设函数()sin()sin()62f x x x ππωω=-+-，其中03ω<<.已知()06f π=. （Ⅰ）求ω；（Ⅱ）将函数()y f x =的图象上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图象向左平移4π个单位，得到函数()y g x =的图象，求()g x 在3[,]44ππ-上的最小值.7.（17山东文（17）（本小题满分12分））在△ABC 中，角A,B,C 的对边分别为a,b,c,已知b=3，6AB AC =-u u r u u u rg ,3ABC S ∆=，求A 和a 。
8.（17天津理15.（本小题满分13分））在ABC △中，内角,,A B C 所对的边分别为,,a b c .已知a b >，5,6a c ==，3sin 5B =. （Ⅰ）求b 和sin A 的值； （Ⅱ）求πsin(2)4A +的值.在ABC △中，内角,,A B C 所对的边分别为,,a b c .已知sin 4sin a A b B =，2225()ac a b c =--.（I ）求cos A 的值； （II ）求sin(2)B A -的值.10.（17浙江18．（本题满分14分））已知函数22()sin cos 23sin cos ()f x x x x x x R =--∈（Ⅰ）求2()3f π的值. （Ⅱ）求()f x 的最小正周期及单调递增区间.11.（17江苏16. （本小题满分14分））已知向量(cos ,sin ),(3,3),[0,]a x x b x π==-∈. （1）若//a b ，求x 的值； （2）记,求()f x 的最大值和最小值以及对应x 的值参考答案：1.解：（1）由题设得21sin 23sin a ac B A =，即1sin 23sin ac B A=由正弦定理得1sin sin sin 23sin AC B A =故2sin sin 3B C =。
高考数学真题09 三角函数的图象与性质问题(教师版)
C．把C1上各点的横坐标缩短到原来的 倍，纵坐标不变，再把得到的曲线向右平移 个单位长度，得到曲线C2
D．把C1上各点的横坐标缩短到原来的 倍，纵坐标不变，再把得到的曲线向左平移 个单位长度，得到曲线C2
8．答案1解析依题意，f(x)＝sin2x＋ cosx－ ＝－cos2x＋ cosx＋ ＝－ 2＋1，因为x
∈ ，所以cosx∈[0,1]，因此当cosx＝ 时，f(x)max＝1．
9．(2013·全国Ⅰ)设当x＝θ时，函数f(x)＝sinx－2cosx取得最大值，则cosθ＝________.
9．答案－ 解析f(x)＝sinx－2cosx＝ ＝ sin (x－φ)，其中sinφ＝ ，
则 ＜ωπ＋ ≤3π，解得 ＜ω≤ ，即ω∈( ， ]．故选C．
【知识总结】
1．三种三角函数的图象和性质
正弦函数y＝sinx
余弦函数y＝cosx
正切函数y＝tanx
图象
定义域
R
R
{x|x≠ ＋kπ，k∈Z}
值域
[－1,1] (有界性)
[－1,1] (有界性)
R
零点
{x|x＝kπ，k∈Z}
{x|x＝ ＋kπ，k∈Z}
专题09三角函数的图象与性质问题
【高考真题】
1．(2022·北京)已知函数f(x)＝cos2x－sin2x，则()
A．f(x)在(－ ，－ )上单调递减B．f(x)在(－ ， )上单调递增
C．f(x)在(0， )上单调递减D．f(x)在( ， )上单调递增
1．答案C解析因为f(x)＝cos2x－sin2x＝cos2x．对于A选项，当－ ＜x＜－ 时，－π＜2x＜－ ，则
2017高考数学一轮复习第三章三角函数、三角恒等变换、解三角形第2讲同角三角函数的基本关系及诱导公式习题
2017高考数学一轮复习 第三章 三角函数、三角恒等变换、解三角形第2讲 同角三角函数的基本关系及诱导公式习题A 组 基础巩固一、选择题1．sin210°cos120°的值为导学号 25400726( ) A ．14 B ．－34C ．－32D ．34[答案] A[解析] sin210°cos120°＝－sin30°(－cos60°)＝12³12＝14.故选A ．2．已知sin(5π2＋α)＝15，那么cos α＝导学号 25400727( )A ．－25B ．－15C ．15D ．25 [答案] C[解析] sin(5π2＋α)＝sin[2π＋(π2＋α)]＝sin(π2＋α)cos α＝15.3．若sin(π6－α)＝13，则cos(2π3＋2α)等于导学号 25400728( )A ．－79B ．－13C ．13D ．79 [答案] A[解析] ∵(π3＋α)＋(π6－α)＝π2，∴sin(π6－α)＝sin[π2－(π3＋α)]＝cos(π3＋α)＝13.则cos(2π3＋2α)＝2cos 2(π3＋α)－1＝－79.4．已知sin(π－α)＝－2sin(π2＋α)，则sin α²cos α等于导学号 25400729( )A ．25B ．－25C ．25或－25D ．－15[答案] B[解析] 由sin(π－α)＝－2sin(π2＋α)得sin α＝－2cos α，所以tan α＝－2，∴sin α²cos α＝sin α²cos αsin 2α＋cos 2α＝tan α1＋tan 2α＝－25，故选B ． 5．已知f (α)＝sin π－α ²cos 2π－α cos －π－α ²tan π－α ，则f (－25π3)的值为导学号 25400730( )A ．12B ．－12C ．32D ．－32[答案] A [解析] ∵f (α)＝sin αcos α－cos α² －tan α＝cos α，∴f (－25π3)＝cos(－25π3)＝cos 25π3＝cos(8π＋π3)＝cos π3＝12.6．若sin θ，cos θ是方程4x 2＋2mx ＋m ＝0的两个根，则m 的值为导学号 25400731( )A ．1＋ 5B ．1－ 5C ．1± 5D ．－1－ 5[答案] B[解析] 由题意得sin θ＋cos θ＝－m 2，sin θ²cos θ＝m4，又(sin θ＋cos θ)2＝1＋2sin θ²cos θ，所以m 24＝1＋m2，解得m ＝1±5，又Δ＝4m 2－16m ≥0，解得m ≤0或m ≥4，所以m ＝1－5，故选B ．二、填空题7．已知α∈(π2，π)，sin α＝45，则tan α＝________.导学号 25400732[答案] －43[解析] ∵α∈(π2，π)，∴cos α＝－1－sin 2α＝－35，∴tan α＝sin αcos α＝－43.8．化简：sin π2＋α ²cos π2－α cos π＋α ＋sin π－α ²cos π2＋αsin π＋α ＝________.导学号 25400733[答案] 0[解析] 原式＝cos α²sin α－cos α＋sin α －sin α－sin α＝－sin α＋sin α＝0.9．(2015²绍兴二模)若f (cos x )＝cos2x ，则f (sin15°)＝________.导学号 25400734 [答案] －32[解析] f (sin15°)＝f (cos75°)＝cos150°＝cos(180°－30°)＝－cos30°＝－32. 10．(2015²浙江嘉兴联考)已知α为钝角，sin(π4＋α)＝34，则sin(π4－α)＝________，cos(α－π4)＝________.导学号 25400735[答案] －74，34[解析] sin(π4－α)＝cos[π2－(π4－α)]＝cos(π4＋α)，∵α为钝角，∴34π＜π4＋α＜54π.∴cos(π4＋α)＜0.∴cos(π4＋α)＝－1－ 34 2＝－74.cos(α－π4)＝sin[π2＋(α－π4)]＝sin(π4＋α)＝34.三、解答题11．已知sin(3π＋α)＝2sin(3π2＋α)，求下列各式的值：导学号 25400736(1)sin α－4cos α5sin α＋2cos α； (2)sin 2α＋sin2α. [答案] (1)－16 (2)85[解析] 由已知得sin α＝2cos α. (1)原式＝2cos α－4cos α5³2cos α＋2cos α＝－16.(2)原式＝sin 2α＋2sin αcos αsin 2α＋cos 2α＝sin 2α＋sin 2αsin 2α＋14sin 2α＝85. 12．已知0＜α＜π2，若cos α－sin α＝－55，试求2sin αcos α－cos α＋11－tan α的值.导学号 25400737[答案]55－95[解析] ∵cos α－sin α＝－55，∴1－2sin αcos α＝15. ∴2sin αcos α＝45.∴(sin α＋cos α)2＝1＋2sin αcos α＝1＋45＝95.∵0＜α＜π2，∴sin α＋cos α＝35 5.与cos α－sin α＝－55联立，解得 cos α＝55，sin α＝255.∴tan α＝2. ∴2sin αcos α－cos α＋11－tan α＝45－55＋11－2＝55－95.B 组 能力提升1．(2015²福建福州一模)设α是第二象限角，P (x,4)为其终边上的一点，且cos α＝15x ，则tan α＝导学号 25400738( )A ．43B ．34C ．－34D ．－43[答案] D[解析] 因为α是第二象限角，所以cos α＝15x ＜0，即x ＜0.又cos α＝15x ＝xx 2＋16.解得x ＝－3，所以tan α＝4x ＝－43，故选D ．2．(2015²河南郑州一模)已知θ为第二象限角，sin θ，cos θ是关于x 的方程2x 2＋(3－1)x ＋m ＝0(m ∈R )的两根，则sin θ－cos θ等于导学号 25400739( )A ．1－32B ．1＋32C ． 3D ．－ 3[答案] B[解析] ∵sin θ，cos θ是方程2x 2＋(3－1)x ＋m ＝0(m ∈R )的两根， ∴sin θ＋cos θ＝1－32，sin θcos θ＝m2.可得(sin θ＋cos θ)2＝1＋2sin θcos θ，即2－32＝1＋m ，∴m ＝－32. ∵θ为第二象限角，∴sin θ＞0，cos θ＜0，即sin θ－cos θ＞0. ∵(sin θ－cos θ)2＝(sin θ＋cos θ)2－4sin θ²cos θ＝4－234－2m ＝1－32＋3＝2＋32， ∴sin θ－cos θ＝2＋32＝1＋32. [点拨] 利用根与系数的关系表示出sin θ＋cos θ＝1－32，sin θcos θ＝m2，利用完全平方公式及同角三角函数间基本关系整理求出m 的值，再利用完全平方公式求出sin θ－cos θ的值即可．3．(2015²河北石家庄一模)已知α为第二象限角，则cos α²1＋tan 2α＋sin α1＋1tan 2α＝________.导学号 25400740 [答案] 0[解析] 原式＝cos αsin 2α＋cos 2αcos 2α＋sin α²sin 2α＋cos 2αsin 2α＝cos α1|cos α|＋sin α1|sin α|，因为α是第二象限，所以sin α＞0，cos α＜0，所以cos α1|cos α|＋sin α1|sin α|＝cos α－cos α＋sin αsin α＝－1＋1＝0.4．已知：f (α)＝sin －α cos π＋α cos π2－αcos π－α sin 2π＋α tan π＋α .导学号 25400741(1)化简f (α)；(2)若角α的终边在第二象限，且sin α＝35，求f (α)．[答案] (1)f (x )＝－cos α (2)45[解析] (1)f (α)＝sin －α cos π＋α cos π2－αcos π－α sin 2π＋α tan π＋α＝－sin α －cos α sin α－cos αsin αtan α＝－cos α.(2)由题意，知cos α＝－1－sin 2α＝－45，所以f (α)＝－cos α＝45.5．已知－π2＜α＜0，且函数f (α)＝cos(3π2＋α)－sin α²1＋cos α1－cos α－1.导学号 25400742(1)化简f (α)；(2)若f (α)＝15，求sin α²c os α和sin α－cos α的值．[答案] (1)f (α)＝sin α＋cos α (2)－1225，－75[解析] (1)f (α)＝sin α－sin α² 1＋cos α 21－cos 2α－1＝sin α＋sin α²1＋cos αsin α－1＝sin α＋cos α.(2)方法一：由f (α)＝sin α＋cos α＝15，平方可得sin 2α＋2sin α²cos α＋cos 2α＝125，即2sin α²cos α＝－2425. ∴sin α²cos α＝－1225.∵(sin α－cos α)2＝1－2sin α²cos α＝4925，又－π2＜α＜0，∴sin α＜0，cos α＞0，∴sin α－cos α＜0，∴sin α－cos α＝－75.方法二：联立方程⎩⎪⎨⎪⎧sin α＋cos α＝15，sin 2α＋cos 2α＝1，解得⎩⎪⎨⎪⎧sin α＝－35，cos α＝45或⎩⎪⎨⎪⎧sin α＝45，cos α＝－35.∵－π2＜α＜0，∴⎩⎪⎨⎪⎧sin α＝－35，cos α＝45.∴sin α²cos α＝－1225，sin α－cos α＝－75.。
2017年高考真题全国2卷文科数学(附答案解析)
uuur uuur uuur BA= λ AC ⇔ OA=
1
uuur OB +
1+ λ
λ
uuur OC .
1+ λ
(2)向量垂直： a ⊥ b ⇔ a ⋅ b = 0 ⇔ x1x2 + y1 y2 = 0 .
(3)向量运算： a ± b = (x1 ± x2 , y1 ± y2 ), a2 = | a |2 , a ⋅ b = | a | ⋅ | b | cos a, b .
y=lnt 为增函数，
故函数 f(x)=ln( x2 − 2x − 8 )的单调递增区间是(4,+∞)，
故选 D.
点睛：形如 y = f ( g ( x)) 的函数为 y = g ( x) , y = f ( x) 的复合函数， y = g ( x) 为内层函
数, y = f ( x) 为外层函数.
简称为“同增异减”. 9．A 【解析】 【分析】 根据甲的所说的话，可知乙、丙的成绩中一位优秀、一位良好，再结合简单的合情推理逐一 分析可得出结果. 【详解】 因为甲、乙、丙、丁四位同学中有两位优秀、两位良好， 又甲看了乙、丙的成绩且还不知道自己的成立，即可推出乙、丙的成绩中一位优秀、一位良 好， 又乙看了丙的成绩，则乙由丙的成绩可以推出自己的成绩， 又甲、丁的成绩中一位优秀、一位良好，则丁由甲的成绩可以推出自己的成绩. 因此，乙、丁知道自己的成绩，故选：A. 【点睛】 本题考查简单的合情推理，解题时要根据已知的情况逐一分析，必要时可采用分类讨论的思 想进行推理，考查逻辑推理能力，属于中等题. 10．B 【解析】 【详解】
2 （1）证明：直线 BC / / 平面 PAD ; （2）若△ PCD 面积为 2 7 ，求四棱锥 P − ABCD 的体积.
高考数学专题：三角函数的图象与性质
y t 2 3t 1 4
当t
3 2
时，ymax
1
上一页
返回导 航
下一页
第二部分 专题一 三角函数与解三角形
11
［明考情—备考如何学］ 高考对此部分内容主要以选择、填空题的形式考查，难度为中等偏下，大多出现在 第 6～12 题或第 14、15 题位置上，命题的热点主要集中在三角函数的定义、图象与性 质，主要考查图象的变换，函数的单调性、奇偶性、周期性、对称性及最值，并常与三 角恒等变换交汇命题．
上一页
返回导 航
下一页
第二部分 专题一 三角函数与解三角形
18
2.(2019·湖南省五市十校联考)函数 f(x)＝Asin(ωx＋φ)(A>0，ω>0，0≤φ<2π)的部分图象 如图所示，则 f(2 019)的值为___-_1____．
上一页
返回导 航
下一页
第二部分 专题一 三角函数与解三角形
19
B．在π4，51π2上单调递减
C．1π2，0是 g(x)图象的一个对称中心
D．直线 x＝－π6是 g(x)图象的一条对称轴
上一页
返回导 航
下一页
第二部分 专题一 三角函数与解三角形
26
2. (2019·洛阳尖子生第二次联考)已知函数 f(x)＝sinωx＋π6(ω>0)在区间－π4，23π上单调
(3)基本关系：
sin2x＋cos2x＝1，
tan
x＝csions
x x.
上一页
返回导 航
下一页
第二部分 专题一 三角函数与解三角形
13
［研考点考向·破重点难点］
考点1 三角函数的定义、诱导公式及基本关系
2017年全国统一高考真题数学试卷(理科)(新课标ⅲ)(含答案及解析)
2017年全国统一高考数学试卷（理科）（新课标Ⅲ）一、选择题：本题共12小题，每小题5分，共60分。
在每小题给出的四个选项中，只有一项是符合题目要求的。
1．（5分）已知集合A={（x，y）|x2+y2=1}，B={（x，y）|y=x}，则A∩B中元素的个数为（）A．3B．2C．1D．02．（5分）设复数z满足（1+i）z=2i，则|z|=（）A．B．C．D．23．（5分）某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2014年1月至2016年12月期间月接待游客量（单位：万人）的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）A．月接待游客量逐月增加B．年接待游客量逐年增加C．各年的月接待游客量高峰期大致在7，8月D．各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳4．（5分）（x+y）（2x﹣y）5的展开式中的x3y3系数为（）A．﹣80B．﹣40C．40D．805．（5分）已知双曲线C：﹣=1 （a＞0，b＞0）的一条渐近线方程为y=x，且与椭圆+=1有公共焦点，则C的方程为（）A．﹣=1B．﹣=1C．﹣=1D．﹣=1 6．（5分）设函数f（x）=cos（x+），则下列结论错误的是（）A．f（x）的一个周期为﹣2πB．y=f（x）的图象关于直线x=对称C．f（x+π）的一个零点为x=D．f（x）在（，π）单调递减7．（5分）执行如图的程序框图，为使输出S的值小于91，则输入的正整数N 的最小值为（）A．5B．4C．3D．28．（5分）已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A．πB．C．D．9．（5分）等差数列{a n}的首项为1，公差不为0．若a2，a3，a6成等比数列，则{a n}前6项的和为（）A．﹣24B．﹣3C．3D．810．（5分）已知椭圆C：=1（a＞b＞0）的左、右顶点分别为A1，A2，且以线段A1A2为直径的圆与直线bx﹣ay+2ab=0相切，则C的离心率为（）A．B．C．D．11．（5分）已知函数f（x）=x2﹣2x+a（e x﹣1+e﹣x+1）有唯一零点，则a=（）A．﹣B．C．D．112．（5分）在矩形ABCD中，AB=1，AD=2，动点P在以点C为圆心且与BD相切的圆上．若=λ+μ，则λ+μ的最大值为（）A．3B．2C．D．2二、填空题:本题共4小题，每小题5分，共20分。
2017年高考真题(全国Ⅰ卷)数学理科含答解析
2017年普通高等学校招生统一考试全国I 卷理科数学一、选择题：本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知集合A ={x |x <1}，B ={x |31x <}，则 A ．{|0}A B x x =< B ．A B =R C ．{|1}A B x x =>D ．A B =∅【答案】A 【解析】试题分析：由31x <可得033x <，则0x <，即{|0}B x x =<，所以{|1}{|0}A B x x x x =<<{|0}x x =<，{|1}{|0}{|1}A B x x x x x x =<<=< ，故选A.【考点】集合的运算，指数运算性质【名师点睛】集合的交、并、补运算问题，应先把集合化简再计算，常常借助数轴或韦恩图进行处理. 2．如图，正方形ABCD 内的图形来自中国古代的太极图.正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称.在正方形内随机取一点，则此点取自黑色部分的概率是A ．14 B ．π8 C ．12D ．π4【答案】B 【解析】试题分析：设正方形边长为a ，则圆的半径为2a ，正方形的面积为2a ，圆的面积为2π4a .由图形的对称性可知，太极图中黑白部分面积相等，即各占圆面积的一半.由几何概型概率的计算公式得，此点取自黑色部分的概率是221ππ248a a ⋅=，选B.秒杀解析：由题意可知，此点取自黑色部分的概率即为黑色部分面积占整个面积的比例，由图可知其概率p 满足1142p <<，故选B. 【考点】几何概型【名师点睛】对于几何概型的计算，首先确定事件类型为几何概型并确定其几何区域（长度、面积、体积或时间），其次计算基本事件区域的几何度量和事件A 区域的几何度量，最后计算()P A . 3．设有下面四个命题1p ：若复数z 满足1z∈R ，则z ∈R ；2p ：若复数z 满足2z ∈R ，则z ∈R ；3p ：若复数12,z z 满足12z z ∈R ，则12z z =； 4p ：若复数z ∈R ，则z ∈R .其中的真命题为 A ．13,p pB ．14,p pC ．23,p pD ．24,p p【答案】B【考点】复数的运算与性质【名师点睛】分式形式的复数，分子、分母同乘以分母的共轭复数，化简成i(,)z a b a b =+∈R 的形式进行判断，共轭复数只需实部不变，虚部变为原来的相反数即可.4．记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为 A ．1B ．2C ．4D ．8【答案】C 【解析】【考点】等差数列的基本量求解【名师点睛】求解等差数列基本量问题时，要多多使用等差数列的性质，如{}n a 为等差数列，若m n p q +=+，则m n p q a a a a +=+.5．函数()f x 在(,)-∞+∞单调递减，且为奇函数．若(11)f =-，则满足21()1x f --≤≤的x 的取值范围是 A ．[2,2]-B ．[1,1]-C ．[0,4]D ．[1,3]【答案】D 【解析】试题分析：因为()f x 为奇函数且在(,)-∞+∞单调递减，要使1()1f x -≤≤成立，则x 满足11x -≤≤，从而由121x -≤-≤得13x ≤≤，即满足1(2)1f x -≤-≤成立的x 的取值范围为[1,3]，选D. 【考点】函数的奇偶性、单调性【名师点睛】奇偶性与单调性的综合问题，要充分利用奇、偶函数的性质与单调性解决不等式和比较大小问题，若()f x 在R 上为单调递增的奇函数，且12()()0f x f x +>，则120x x +>，反之亦成立. 6．621(1)(1)x x++展开式中2x 的系数为 A ．15B ．20C ．30D ．35【答案】C 【解析】试题分析：因为6662211(1)(1)1(1)(1)x x x x x ++=⋅++⋅+，则6(1)x +展开式中含2x 的项为22261C 15x x ⋅=，621(1)x x ⋅+展开式中含2x 的项为442621C 15x x x⋅=，故2x 的系数为151530+=，选C.【考点】二项式定理【名师点睛】对于两个二项式乘积的问题，用第一个二项式中的每项乘以第二个二项式的每项，分析含2x 的项共有几项，进行相加即可.这类问题的易错点主要是未能分析清楚构成这一项的具体情况，尤其是两个二项展开式中的r不同.7．某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12 C．14 D．16【答案】B【解析】试题分析：由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为12(24)2122⨯+⨯⨯=，故选B.【考点】简单几何体的三视图【名师点睛】三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合，解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图. 8．下面程序框图是为了求出满足3n−2n>1000的最小偶数n，那么在和两个空白框中，可以分别填入A．A>1 000和n=n+1 B．A>1 000和n=n+2C．A≤1 000和n=n+1 D．A≤1 000和n=n+2【答案】D【考点】程序框图【名师点睛】解决此类问题的关键是读懂程序框图，明确顺序结构、条件结构、循环结构的真正含义.本题巧妙地设置了两个空格需要填写，所以需要抓住循环的重点，偶数该如何增量，判断框内如何进行判断可以根据选项排除.9．已知曲线C1：y=cos x，C2：y=sin (2x+2π3)，则下面结论正确的是A．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2B．把C1上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2C．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线C2D．把C1上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线C2 【答案】D 【解析】试题分析：因为12,C C 函数名不同，所以先将2C 利用诱导公式转化成与1C 相同的函数名，则22π2πππ:sin(2)cos(2)cos(2)3326C y x x x =+=+-=+，则由1C 上各点的横坐标缩短到原来的12倍变为cos 2y x =，再将曲线向左平移π12个单位长度得到2C ，故选D.【考点】三角函数图象变换【名师点睛】对于三角函数图象变换问题，首先要将不同名函数转换成同名函数，利用诱导公式，需要重点记住ππsin cos(),cos sin()22αααα=-=+；另外，在进行图象变换时，提倡先平移后伸缩，而先伸缩后平移在考试中也经常出现，无论哪种变换，记住每一个变换总是对变量x 而言.10．已知F 为抛物线C ：y 2=4x 的焦点，过F 作两条互相垂直的直线l 1，l 2，直线l 1与C 交于A 、B 两点，直线l 2与C 交于D 、E 两点，则|AB |+|DE |的最小值为 A ．16B ．14C ．12D ．10【答案】A【考点】抛物线的简单几何性质【名师点睛】对于抛物线弦长问题，要重点抓住抛物线定义，到定点的距离要想到转化到准线上，另外，直线与抛物线联立，求判别式，利用根与系数的关系是通法，需要重点掌握.考查最值问题时要能想到用函数方法和基本不等式进行解决.此题还可以利用弦长的倾斜角表示，设直线的倾斜角为α，则22||sin pAB α=，则2222||πcos sin (+)2p pDE αα==，所以222221||||4(cos sin cos p p AB DE ααα+=+=+ 222222222111sin cos )4()(cos sin )4(2)4(22)16sin cos sin cos sin ααααααααα=++=++≥⨯+=. 11．设x 、y 、z 为正数，且235x y z==，则A ．2x <3y <5zB ．5z <2x <3yC ．3y <5z <2xD ．3y <2x <5z【答案】D【考点】指、对数运算性质【名师点睛】对于连等问题，常规的方法是令该连等为同一个常数，再用这个常数表示出对应的,,x y z ，通过作差或作商进行比较大小.对数运算要记住对数运算中常见的运算法则，尤其是换底公式以及0与1的对数表示.12．几位大学生响应国家的创业号召，开发了一款应用软件.为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列1，1，2，1，2，4，1，2，4，8，1，2，4，8，16，…，其中第一项是20，接下来的两项是20，21，再接下来的三项是20，21，22，依此类推.求满足如下条件的最小整数N ：N >100且该数列的前N 项和为2的整数幂.那么该款软件的激活码是 A ．440B ．330C ．220D ．110【答案】A 【解析】试题分析：由题意得，数列如下：11,1,2,1,2,4,1,2,4,,2k -则该数列的前(1)122k k k ++++=项和为 11(1)1(12)(122)222k k k k S k -++⎛⎫=+++++++=-- ⎪⎝⎭，要使(1)1002k k +>，有14k ≥，此时122k k ++<，所以2k +是第1k +组等比数列1,2,,2k 的部分和，设1212221t t k -+=+++=- ，所以2314t k =-≥，则5t ≥，此时52329k =-=， 所以对应满足条件的最小整数293054402N ⨯=+=，故选A. 【考点】等差数列、等比数列【名师点睛】本题非常巧妙地将实际问题和数列融合在一起，首先需要读懂题目所表达的具体含义，以及观察所给定数列的特征，进而判断出该数列的通项和求和.另外，本题的难点在于数列里面套数列，第一个数列的和又作为下一个数列的通项，而且最后几项并不能放在一个数列中，需要进行判断. 二、填空题：本题共4小题，每小题5分，共20分.13．已知向量a ，b 的夹角为60°，|a |=2，|b |=1，则| a +2b |= .【答案】23 【解析】试题分析：222|2|||44||4421cos60412+=+⋅+=+⨯⨯⨯+= a b a a b b ，所以|2|1223+==a b . 秒杀解析：利用如下图形，可以判断出2+a b 的模长是以2为边长，一夹角为60°的菱形的对角线的长度，则为23.【考点】平面向量的运算【名师点睛】平面向量中涉及有关模长的问题时，常用到的通法是将模长进行平方，利用向量数量积的知识进行解答，很快就能得出答案；另外，向量是一个工具型的知识，具备代数和几何特征，在做这类问题时可以使用数形结合的思想，会加快解题速度.14．设x ，y 满足约束条件21210x y x y x y +≤⎧⎪+≥-⎨⎪-≤⎩，，，则32z x y =-的最小值为 .【答案】5- 【解析】试题分析：不等式组表示的可行域如图所示，易求得1111(1,1),(,),(,)3333A B C ---，由32z x y =-得322zy x =-在y 轴上的截距越大，z 就越小，所以，当直线32z x y =-过点A 时，z 取得最小值， 所以z 的最小值为3(1)215⨯--⨯=-. 【考点】线性规划【名师点睛】本题是常规的线性规划问题，线性规划问题常出现的形式有：①直线型，转化成斜截式比较截距，要注意z 前面的系数为负时，截距越大，z 值越小；②分式型，其几何意义是已知点与未知点的斜率；③平方型，其几何意义是距离，尤其要注意的是最终结果应该是距离的平方；④绝对值型，转化后其几何意义是点到直线的距离.15．已知双曲线C ：22221x y a b-=（a >0，b >0）的右顶点为A ，以A 为圆心，b 为半径作圆A ，圆A 与双曲线C 的一条渐近线交于M ，N 两点.若∠MAN =60°，则C 的离心率为 .【答案】233【解析】试题分析：如图所示，作AP MN ⊥，因为圆A 与双曲线C 的一条渐近线交于M 、N 两点，则MN 为双曲线的渐近线by x a=上的点，且(,0)A a ，||||AM AN b ==， 而AP MN ⊥，所以30PAN ∠= ， 点(,0)A a 到直线by x a=的距离22||||1b AP b a =+，在Rt PAN △中，||cos ||PA PAN NA ∠=，代入计算得223a b =，即3a b =， 由222c a b =+得2c b =， 所以22333c b e a b ===.【考点】双曲线的简单几何性质【名师点睛】双曲线渐近线是其独有的性质，所以有关渐近线问题备受出题者的青睐.做好这一类问题要抓住以下重点：①求解渐近线，直接把双曲线后面的1换成0即可；②双曲线的焦点到渐近线的距离是b ；③双曲线的顶点到渐近线的距离是abc. 16．如图，圆形纸片的圆心为O ，半径为5 cm ，该纸片上的等边三角形ABC 的中心为O .D ，E ，F 为圆O上的点，△DBC ，△ECA ，△F AB 分别是以BC ，CA ，AB 为底边的等腰三角形.沿虚线剪开后，分别以BC ，CA ，AB 为折痕折起△DBC ，△ECA ，△F AB ，使得D ，E ，F 重合，得到三棱锥.当△ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为.【答案】415 【解析】试题分析：如下图，连接DO 交BC 于点G ，设D ，E ，F 重合于S 点，正三角形的边长为x (x >0)，则1332OG x =⨯36x =.∴356FG SG x ==-， 222233566SO h SG GO x x ⎛⎫⎛⎫==-=-- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭3553x ⎛⎫=- ⎪ ⎪⎝⎭， ∴三棱锥的体积21133553343ABC V S h x x ⎛⎫=⋅=⨯⨯- ⎪ ⎪⎝⎭△451535123x x =-. 设()45353n x x x =-，x >0，则()3453203n x x x '=-， 令()0n x '=，即43403x x -=，得43x =，易知()n x 在43x =处取得最大值.∴max 15485441512V =⨯⨯-=.【考点】简单几何体的体积【名师点睛】对于三棱锥最值问题，需要用到函数思想进行解决，本题解决的关键是设好未知量，利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决，当变量是高次时需要用到求导的方式进行解决.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. （一）必考题：共60分. 17．（12分）△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，已知△ABC 的面积为23sin a A.（1）求sin B sin C ;（2）若6cos B cos C =1，a =3，求△ABC 的周长. 【解析】试题分析：（1）由三角形面积公式建立等式21sin 23sin a ac B A=，再利用正弦定理将边化成角，从而得出sin sin B C 的值；（2）由1cos cos 6B C =和2sin sin 3B C =计算出1cos()2B C +=-，从而求出角A ，根据题设和余弦定理可以求出bc 和b c +的值，从而求出ABC △的周长为333+.【考点】三角函数及其变换【名师点睛】在处理解三角形问题时，要注意抓住题目所给的条件，当题设中给定三角形的面积，可以使用面积公式建立等式，再将所有边的关系转化为角的关系，有时需将角的关系转化为边的关系；解三角形问题常见的一种考题是“已知一条边的长度和它所对的角，求面积或周长的取值范围”或者“已知一条边的长度和它所对的角，再有另外一个条件，求面积或周长的值”，这类问题的通法思路是：全部转化为角的关系，建立函数关系式，如sin()y A x b ωϕ=++，从而求出范围，或利用余弦定理以及基本不等式求范围；求具体的值直接利用余弦定理和给定条件即可. 18．（12分）如图，在四棱锥P−ABCD 中，AB//CD ，且90BAP CDP ∠=∠= .（1）证明：平面P AB ⊥平面P AD ；（2）若P A =PD =AB =DC ，90APD ∠= ，求二面角A −PB −C 的余弦值. 【解析】试题解析：（1）由已知90BAP CDP ∠=∠=︒，得AB ⊥AP ，CD ⊥PD . 由于AB//CD ，故AB ⊥PD ，从而AB ⊥平面P AD . 又AB ⊂平面P AB ，所以平面P AB ⊥平面P AD . （2）在平面PAD 内作PF AD ⊥，垂足为F ，由（1）可知，AB ⊥平面PAD ，故AB PF ⊥，可得PF ⊥平面ABCD .以F 为坐标原点，FA 的方向为x 轴正方向，||AB 为单位长，建立如图所示的空间直角坐标系F xyz -.由（1）及已知可得2(,0,0)2A ，2(0,0,)2P ，2(,1,0)2B ，2(,1,0)2C -. 所以22(,1,)22PC =-- ，(2,0,0)CB = ，22(,0,)22PA =- ，(0,1,0)AB = .设(,,)x y z =n 是平面PCB 的法向量，则0,0,PC CB ⎧⋅=⎪⎨⋅=⎪⎩ n n 即220,2220,x y z x ⎧-+-=⎪⎨⎪=⎩可取(0,1,2)=--n .设(,,)x y z =m 是平面PAB 的法向量，则0,0,PA AB ⎧⋅=⎪⎨⋅=⎪⎩ m m 即220,220.x z y ⎧-=⎪⎨⎪=⎩可取(1,0,1)=m . 则3cos ,||||3⋅==-<>n m n m n m ， 所以二面角A PB C --的余弦值为33-. 【考点】面面垂直的证明，二面角平面角的求解【名师点睛】高考对空间向量与立体几何的考查主要体现在以下几个方面：①求异面直线所成的角，关键是转化为两直线的方向向量的夹角；②求直线与平面所成的角，关键是转化为直线的方向向量和平面的法向量的夹角；③求二面角，关键是转化为两平面的法向量的夹角.建立空间直角坐标系和表示出所需点的坐标是解题的关键. 19．（12分）为了监控某种零件的一条生产线的生产过程，检验员每天从该生产线上随机抽取16个零件，并测量其尺寸（单位：cm ）．根据长期生产经验，可以认为这条生产线正常状态下生产的零件的尺寸服从正态分布2(,)N μσ．（1）假设生产状态正常，记X 表示一天内抽取的16个零件中其尺寸在(3,3)μσμσ-+之外的零件数，求(1)P X ≥及X 的数学期望；（2）一天内抽检零件中，如果出现了尺寸在(3,3)μσμσ-+之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查． （ⅰ）试说明上述监控生产过程方法的合理性； （ⅱ）下面是检验员在一天内抽取的16个零件的尺寸：9.95 10.12 9.96 9.96 10.01 9.92 9.98 10.04 10.26 9.91 10.13 10.02 9.22 10.04 10.05 9.95经计算得16119.9716i i x x ===∑，16162221111()(16)0.2121616i i i i s x x x x ===-=-≈∑∑，其中i x 为抽取的第i 个零件的尺寸，1,2,,16i =⋅⋅⋅．用样本平均数x 作为μ的估计值ˆμ，用样本标准差s 作为σ的估计值ˆσ，利用估计值判断是否需对当天的生产过程进行检查？剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据，用剩下的数据估计μ和σ（精确到0.01）．附：若随机变量Z 服从正态分布2(,)N μσ，则(33)0.997 4P Z μσμσ-<<+=，160.997 40.959 2≈，0.0080.09≈．【解析】试题解析：（1）抽取的一个零件的尺寸在(3,3)μσμσ-+之内的概率为0.9974，从而零件的尺寸在(3,3)μσμσ-+之外的概率为0.0026，故~(16,0.0026)X B .因此16(1)1(0)10.99740.0408P X P X ≥=-==-≈.X 的数学期望为160.00260.0416EX =⨯=.（2）（i ）如果生产状态正常，一个零件尺寸在(3,3)μσμσ-+之外的概率只有0.0026，一天内抽取的16个零件中，出现尺寸在(3,3)μσμσ-+之外的零件的概率只有0.0408，发生的概率很小.因此一旦发生这种情况，就有理由认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查，可见上述监控生产过程的方法是合理的.（ii ）由9.97,0.212x s =≈，得μ的估计值为ˆ9.97μ=，σ的估计值为ˆ0.212σ=，由样本数据可以看出有一个零件的尺寸在ˆˆˆˆ(3,3)μσμσ-+之外，因此需对当天的生产过程进行检查.剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据9.22，剩下数据的平均数为1(169.979.22)10.0215⨯-=，因此μ的估计值为10.02.162221160.212169.971591.134ii x==⨯+⨯≈∑，剔除ˆˆˆˆ(3,3)μσμσ-+之外的数据9.22，剩下数据的样本方差为221(1591.1349.221510.02)0.00815--⨯≈， 因此σ的估计值为0.0080.09≈. 【考点】正态分布，随机变量的期望和方差【名师点睛】数学期望是离散型随机变量中重要的数学概念，反映随机变量取值的平均水平.求解离散型随机变量的分布列、数学期望时，首先要分清事件的构成与性质，确定离散型随机变量的所有取值，然后根据概率类型选择公式，计算每个变量取每个值的概率，列出对应的分布列，最后求出数学期望.正态分布是一种重要的分布，之前考过一次，尤其是正态分布的3σ原则. 20．（12分）已知椭圆C ：2222=1x y a b +（a >b >0），四点P 1（1,1），P 2（0,1），P 3（–1，32），P 4（1，32）中恰有三点在椭圆C 上. （1）求C 的方程；（2）设直线l 不经过P 2点且与C 相交于A ，B 两点.若直线P 2A 与直线P 2B 的斜率的和为–1，证明：l 过定点. 【解析】试题分析：（1）根据3P ，4P 两点关于y 轴对称，由椭圆的对称性可知C 经过3P ，4P 两点.另外由222211134a b a b +>+知，C 不经过点P 1，所以点P 2在C 上.因此234,,P P P 在椭圆上，代入其标准方程，即可求出C 的方程；（2）先设直线P 2A 与直线P 2B 的斜率分别为k 1，k 2，再设直线l 的方程，当l 与x轴垂直时，通过计算，不满足题意，再设l ：y kx m =+（1m ≠），将y kx m =+代入2214x y +=，写出判别式，利用根与系数的关系表示出x 1+x 2，x 1x 2，进而表示出12k k +，根据121k k +=-列出等式表示出k 和m 的关系，从而判断出直线恒过定点.试题解析：（1）由于3P ，4P 两点关于y 轴对称，故由题设知C 经过3P ，4P 两点. 又由222211134a b a b +>+知，C 不经过点P 1，所以点P 2在C 上.因此22211,131,4b ab ⎧=⎪⎪⎨⎪+=⎪⎩解得224,1.a b ⎧=⎪⎨=⎪⎩故C 的方程为2214x y +=.（2）设直线P 2A 与直线P 2B 的斜率分别为k 1，k 2，如果l 与x 轴垂直，设l ：x =t ，由题设知0t ≠，且||2t <，可得A ，B 的坐标分别为（t ，242t -），（t ，242t --）.则22124242122t t k k t t---++=-=-，得2t =，不符合题设. 从而可设l ：y kx m =+（1m ≠）.将y kx m =+代入2214x y +=得222(41)8440k x kmx m +++-=. 由题设可知22=16(41)0k m ∆-+>.设A （x 1，y 1），B （x 2，y 2），则x 1+x 2=2841kmk -+，x 1x 2=224441m k -+.而12121211y y k k x x --+=+ 121211kx m kx m x x +-+-=+ 1212122(1)()kx x m x x x x +-+=.由题设121k k +=-，故1212(21)(1)()0k x x m x x ++-+=.即222448(21)(1)04141m kmk m k k --+⋅+-⋅=++.解得12m k +=-.当且仅当1m >-时，0∆>，于是l ：12m y x m +=-+，即11(2)2m y x ++=--， 所以l 过定点（2，1-）.【考点】椭圆的标准方程，直线与圆锥曲线的位置关系【名师点睛】椭圆的对称性是椭圆的一个重要性质，判断点是否在椭圆上，可以通过这一方法进行判断；证明直线过定点的关键是设出直线方程，通过一定关系转化，找出两个参数之间的关系式，从而可以判断过定点情况.另外，在设直线方程之前，若题设中未告知，则一定要讨论直线斜率不存在和存在两种情况，其通法是联立方程，求判别式，利用根与系数的关系，再根据题设关系进行化简. 21．（12分）已知函数2()e (2)e x x f x a a x =+--. （1）讨论()f x 的单调性；（2）若()f x 有两个零点，求a 的取值范围. 【解析】试题分析：（1）讨论()f x 单调性，首先进行求导，发现式子特点后要及时进行因式分解，再对a 按0a ≤，0a >进行讨论，写出单调区间；（2）根据第（1）问，若0a ≤，()f x 至多有一个零点.若0a >，当ln x a =-时，()f x 取得最小值，求出最小值1(ln )1ln f a a a-=-+，根据1a =，(1,)a ∈+∞，(0,1)a ∈进行讨论，可知当(0,1)a ∈时有2个零点.易知()f x 在(,ln )a -∞-有一个零点；设正整数0n 满足03ln(1)n a>-，则0000()e (e2)e 20n n n n f n a a n n n =+-->->->.由于3ln(1)ln a a->-，因此()f x 在(ln ,)a -+∞有一个零点.从而可得a 的取值范围为(0,1).试题解析：（1）()f x 的定义域为(,)-∞+∞，2()2e (2)e 1(e 1)(2e 1)x x x x f x a a a '=+--=-+， （ⅰ）若0a ≤，则()0f x '<，所以()f x 在(,)-∞+∞单调递减. （ⅱ）若0a >，则由()0f x '=得ln x a =-.当(,ln )x a ∈-∞-时，()0f x '<；当(ln ,)x a ∈-+∞时，()0f x '>，所以()f x 在(,ln )a -∞-单调递减，在(ln ,)a -+∞单调递增.（2）（ⅰ）若0a ≤，由（1）知，()f x 至多有一个零点.（ⅱ）若0a >，由（1）知，当ln x a =-时，()f x 取得最小值，最小值为1(ln )1ln f a a a-=-+. ①当1a =时，由于(ln )0f a -=，故()f x 只有一个零点； ②当(1,)a ∈+∞时，由于11ln 0a a-+>，即(ln )0f a ->，故()f x 没有零点； ③当(0,1)a ∈时，11ln 0a a-+<，即(ln )0f a -<. 又422(2)e (2)e 22e 20f a a ----=+-+>-+>，故()f x 在(,ln )a -∞-有一个零点.设正整数0n 满足03ln(1)n a>-，则00000000()e (e 2)e 20n n n n f n a a n n n =+-->->->. 由于3ln(1)ln a a->-，因此()f x 在(ln ,)a -+∞有一个零点. 综上，a 的取值范围为(0,1).【考点】含参函数的单调性，利用函数零点求参数取值范围【名师点睛】研究函数零点问题常常与研究对应方程的实根问题相互转化.已知函数()f x 有2个零点求参数a 的取值范围，第一种方法是分离参数，构造不含参数的函数，研究其单调性、极值、最值，判断y a =与其交点的个数，从而求出a 的取值范围；第二种方法是直接对含参函数进行研究，研究其单调性、极值、最值，注意点是若()f x 有2个零点，且函数先减后增，则只需其最小值小于0，且后面还需验证最小值两边存在大于0的点.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做，则按所做的第一题计分. 22．[选修4−4：坐标系与参数方程]（10分）在直角坐标系xOy 中，曲线C 的参数方程为3cos ,sin ,x y θθ=⎧⎨=⎩（θ为参数），直线l 的参数方程为4,1,x a t t y t =+⎧⎨=-⎩（为参数）. （1）若a =−1，求C 与l 的交点坐标；（2）若C 上的点到l 距离的最大值为17，求a . 【解析】试题分析：（1）先将曲线C 和直线l 的参数方程化成普通方程，然后联立两方程即可求出交点坐标；（2）由直线l 的普通方程为440x y a +--=，设C 上的点为(3cos ,sin )θθ，易求得该点到l 的距离为|3cos 4sin 4|17a d θθ+--=.对a 再进行讨论，即当4a ≥-和4a <-时，求出a 的值.试题解析：（1）曲线C 的普通方程为2219x y +=. 当1a =-时，直线l 的普通方程为430x y +-=.由22430,19x y x y +-=⎧⎪⎨+=⎪⎩解得3,0x y =⎧⎨=⎩或21,2524.25x y ⎧=-⎪⎪⎨⎪=⎪⎩从而C 与l 的交点坐标为(3,0)，2124(,)2525-. （2）直线l 的普通方程为440x y a +--=，故C 上的点(3cos ,sin )θθ到l 的距离为|3cos 4sin 4|17a d θθ+--=.当4a ≥-时，d 的最大值为917a +.由题设得91717a +=，所以8a =； 当4a <-时，d 的最大值为117a -+.由题设得11717a -+=，所以16a =-. 综上，8a =或16a =-. 【考点】坐标系与参数方程【名师点睛】化参数方程为普通方程的关键是消参，可以利用加减消元、平方消元、代入法等等；在极坐标方程与参数方程的条件下求解直线与圆的位置关系问题时，通常将极坐标方程化为直角坐标方程，参数方程化为普通方程来解决. 23．[选修4−5：不等式选讲]（10分）已知函数2–4()x ax f x =++，11()x x g x =++-||||.（1）当a =1时，求不等式()()f x g x ≥的解集；（2）若不等式()()f x g x ≥的解集包含[–1，1]，求a 的取值范围. 【解析】试题分析：（1）将1a =代入，不等式()()f x g x ≥等价于2|1||1|40x x x x -+++--≤，对x 按1x <-，11x -≤≤，1x >讨论，得出不等式的解集；（2）当[1,1]x ∈-时，()2g x =.若()()f xg x ≥的解集包含[1,1]-，等价于当[1,1]x ∈-时()2f x ≥.则()f x 在[1,1]-的最小值必为(1)f -与(1)f 之一，所以(1)2f -≥且(1)2f ≥，从而得11a -≤≤.试题解析：（1）当1a =时，不等式()()f x g x ≥等价于2|1||1|40x x x x -+++--≤.① 当1x <-时，①式化为2340x x --≤，无解；当11x -≤≤时，①式化为220x x --≤，从而11x -≤≤；当1x >时，①式化为240x x +-≤，从而11712x -+<≤.- 21 - 所以()()f x g x ≥的解集为117{|1}2x x -+-≤≤.【考点】绝对值不等式的解法，恒成立问题【名师点睛】零点分段法是解答绝对值不等式问题常用的方法，也可以将绝对值函数转化为分段函数，借助图象解题.。
高考数学专题《三角函数的图象与性质》习题含答案解析
专题5.3 三角函数的图象与性质1．（2021·北京市大兴区精华培训学校高三三模）下列函数中，既是奇函数又以π为最小正周期的函数是（）A ．cos 2y x =B ．sin2y x=C ．sin cos y x x=+D ．tan 2y x=【答案】B 【解析】由三角函数的奇偶性和周期性判断即可得出答案.【详解】解：A 选项：cos 2y x =是周期为π的偶函数，故A 不正确；B 选项：sin2y x =是周期为π的奇函数，故B 正确；C选项：sin cos 4y x x x π⎛⎫=+=+ ⎪⎝⎭，周期为2π且非奇非偶函数，故C 不正确；D 选项：tan 2y x =是周期为2π的奇函数，故D 不正确.故选：B.2．（2021·海南高三其他模拟）下列函数中，既是偶函数又存在零点的是（ ）A ．ln y x =B ．21y x =+C ．sin y x=D ．cos y x=【答案】D 【解析】根据题意，依次分析选项中函数的奇偶性以及是否存在零点，综合即可得答案．【详解】解：根据题意，依次分析选项：对于A ，y lnx =，为对数函数，不是奇函数，不符合题意，对于B ，21y x =+，为二次函数，是偶函数，但不存在零点，不符合题意，对于C ，sin y x =，为正弦函数，是奇函数，不符合题意，对于D ，cos y x =，为余弦函数，既是偶函数又存在零点，符合题意，故选：D ．练基础3．（2021·浙江高三其他模拟）函数y =sin tan x e xx在[-2，2]上的图像可能是（ ）A ．B ．C ．D ．【答案】B 【解析】利用同角三角函数的商数关系并注意利用正切函数的性质求得函数的定义域，可以化简得到()cos ,2x k f x e x x k Z π⎛⎫=≠∈ ⎪⎝⎭，考察当x 趋近于0时，函数的变化趋势，可以排除A,考察端点值的正负可以评出CD.【详解】()sin cos ,tan 2x x e x k f x e x x k Z x π⎛⎫==≠∈ ⎪⎝⎭,当x 趋近于0时，函数值趋近于0cos 01e =,故排除A;()22cos 20f e =<,故排除CD,故选：B4．（2021·全国高三其他模拟（理））函数y =tan(3x +6π)的一个对称中心是（ ）A ．(0，0)B ．(6π，0)C ．(49π，0)D ．以上选项都不对【答案】C 【解析】根据正切函数y =tan x 图象的对称中心是(2k π，0)求出函数y =tan(3x +6π)图象的对称中心，即可得到选项.【详解】解：因为正切函数y =tan x 图象的对称中心是(2k π，0)，k ∈Z ；令3x +6π=2k π，解得618k x ππ=-，k ∈Z ；所以函数y =tan(3x +6π)的图象的对称中心为(618k ππ-，0)，k ∈Z ；当k =3时,C 正确，故选：C.5．（2019年高考全国Ⅱ卷文）若x 1=，x 2=是函数f (x )=(>0)两个相邻的极值点，则=（ ）A ．2B ．C ．1D ．【答案】A【解析】由题意知，的周期，解得．故选A ．6．（2021·临川一中实验学校高三其他模拟（文））若函数cos (0)y x ωω=>的图象在区间,24ππ⎛⎫- ⎪⎝⎭上只有一个对称中心，则ω的取范围为（ ）A ．12ω<≤B ．ω1≤<2C ．13ω<≤D ．13ω≤<【答案】A 【解析】根据题意可得422πππω≤<，即可求出.【详解】4π43πsin x ωωω3212()sin f x x ω=232()44T ωπππ==-=π2ω=由题可知，cos (0)y x ωω=>在,42ππ⎡⎫⎪⎢⎣⎭上只有一个零点，又2x πω=，2x πω=，所以422πππω≤<，即12ω<≤.故选：A.7.(2019年高考北京卷文)设函数f （x ）=cos x +b sin x （b 为常数），则“b =0”是“f （x ）为偶函数”的（ ） A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】C【解析】时，，为偶函数；为偶函数时，对任意的恒成立，即，，得对任意的恒成立，从而.从而“”是“为偶函数”的充分必要条件，故选C.8．（2021·青海西宁市·高三二模（文））函数()cos 218f x x π⎛⎫=-- ⎪⎝⎭图象的一个对称中心为（ ）A ．,14π⎛⎫-- ⎪⎝⎭B ．,14π⎛⎫-⎪⎝⎭C ．,116π⎛⎫-- ⎪⎝⎭D ．3,116π⎛⎫-- ⎪⎝⎭【答案】D 【解析】根据余弦函数的对称中心整体代换求解即可.【详解】令2()82x k k πππ-=+∈Z ，可得5()216k x k ππ=+∈Z ．所以当1k =-时，316x π=-，故3,116π⎛⎫-- ⎪⎝⎭满足条件，当0k =时，516x π=，故5,116π⎛⎫-⎪⎝⎭满足条件；故选：D0b =()cos sin cos f x x b x x =+=()f x ()f x ()=()f x f x -x ()cos()sin()cos sin f x x b x x b x -=-+-=-cos sin cos sin x b x x b x +=-sin 0b x =x 0b =0b =()f x9．（2021·全国高一专题练习）设函数()cos 3f x x π⎛⎫=+ ⎪⎝⎭，则下列结论错误的是（ ）A ．()f x 的最小正周期为2πB ．()f x 的图象关于直线23x π=对称C ．()f x 在,2ππ⎛⎫⎪⎝⎭单调递减D ．()f x 的一个零点为6x π=【答案】C 【解析】根据解析式结合余弦函数的性质依次判断每个选项的正误即可.【详解】函数()cos 3f x x π⎛⎫=+ ⎪⎝⎭，()f x ∴的最小正周期为2π，故A 正确；22(cos 1333f πππ⎛⎫=+=- ⎪⎝⎭，∴()f x 的图象关于直线23x π=对称，故B 正确；当x ∈,2ππ⎛⎫⎪⎝⎭时，54,363πππx ⎛⎫+∈ ⎪⎝⎭，()f x 没有单调性，故C 错误；()cos 0663f πππ⎛⎫=+= ⎪⎝⎭，∴()f x 的一个零点为6x π=，故D 正确.综上，错误的选项为C.故选：C.10．（2017·全国高考真题（理））函数f (x )=s in 2x +3cosx ―34（x ∈0,__________．【答案】1【解析】化简三角函数的解析式，则f (x )=1―cos 2x+3cos x ―34=―cos 2x +3cos x +14= ―(cos x ―32)2+1，由x ∈[0,π2]可得cos x ∈[0,1]，当cos x =32时，函数f (x )取得最大值1．练提升1．（2021·河南高二月考（文））已知函数()()sin 0,02f x x πωϕωϕ⎛⎫=+ ⎪⎝⎭＞＜＜的相邻的两个零点之间的距离是6π，且直线18x π=是()f x 图象的一条对称轴，则12f π⎛⎫=⎪⎝⎭（ ）A．B ．12-C ．12D【答案】D 【解析】由相邻两个零点的距离确定周期求出6ω=，再由对称轴确定6π=ϕ，代入12x π=可求出结果.【详解】解：因为相邻的两个零点之间的距离是6π，所以26T π=，23T ππω==，所以6ω=，又sin 6sin 118183f πππϕϕ⎛⎫⎛⎫⎛⎫=⨯+=+=±⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，且02πϕ＜＜，则6π=ϕ，所以()sin 66f x x π⎛⎫=+ ⎪⎝⎭，则sin 612126f πππ⎛⎫⎛⎫=⨯+= ⎪ ⎪⎝⎭⎝⎭.故选：D.2.（2020·山东潍坊�高一期末）若函数的最小正周期为，则（ ）A ．B ．C ．D ．【答案】C 【解析】由题意，函数的最小正周期为，可得，解得，即，()tan (0)4f x x πωω⎛⎫=+> ⎪⎝⎭π(2)(0)5f f f π⎛⎫>>-⎪⎝⎭(0)(2)5f f f π⎛⎫>>-⎪⎝⎭(0)(2)5f f f π⎛⎫>-> ⎪⎝⎭(0)(2)5f f f π⎛⎫->> ⎪⎝⎭()tan (0)4f x x πωω⎛⎫=+> ⎪⎝⎭πwππ=1w =()tan()4f x x π=+令，即，当时，，即函数在上单调递增，又由，又由，所以.故选：C.3．（2021·广东佛山市·高三二模）设()0,θπ∈，则“6πθ<”是“1sin 2θ<”的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A 【解析】由条件即06πθ<<，由06πθ<<，得1sin 2θ<；反之不成立，可举反例．再由充分必要条件的判定得答案．【详解】由()0,θπ∈，则6πθ<，即06πθ<<所以当06πθ<<时，由正弦函数sin y x =的单调性可得1sin sin62πθ<=，即由6πθ<可以得到1sin 2θ<.反之不成立，例如当56πθπ<<时，也有1sin 2θ<成立，但6πθ<不成立.故“6πθ<”是“1sin 2θ<”的充分不必要条件故选：A4．（2021·四川省华蓥中学高三其他模拟（理））已知函数()sin()0,0,||2f x A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭的最,242k x k k Z πππππ-+<+<+∈3,44k x k k Z ππππ-+<<+∈1k =544x ππ<<()f x 5(,)44ππ4(0)(),()()()555f f f f f πππππ=-=-+=425ππ>>(0)(2)5f f f π⎛⎫>-> ⎪⎝⎭大值为2，其图象相邻两条对称轴之间的距离为2π且()f x 的图象关于点,06π⎛⎫-⎪⎝⎭对称，则下列判断不正确的是（）A ．要得到函数()f x 的图象，只需将2cos 2y x =的图象向右平移12π个单位B ．函数()f x 的图象关于直线712x π=对称C ．,126x ππ⎡⎤∈-⎢⎥⎣⎦时，函数()f x D ．函数()f x 在5,612ππ⎡⎤⎢⎥⎣⎦上单调递减【答案】C 【解析】根据最大值为2，可得A ，根据正弦型函数的周期性，可求得ω，根据对称性，可求得ϕ，即可得()f x 解析式，根据正弦型函数的单调性、值域的求法，逐一分析选项，即可得答案.【详解】由题意得A =2，因为其图象相邻两条对称轴之间的距离为2π，所以22Tπ=，可得2T ππω==，所以2ω=，所以()2sin(2)f x x ϕ=+，因为,06π⎛⎫-⎪⎝⎭为对称中心，所以2,6k k Z πϕπ⎛⎫⨯-+=∈ ⎪⎝⎭，因为||2ϕπ<，令k =0，可得3πϕ=，所以2n 2)3(si f x x π⎛⎫=+⎪⎝⎭.对于A ：将2cos 2y x =的图象向右平移12π个单位，可得2cos 22cos 22cos 22sin 22sin 21266263y x x x x x ππππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=-=-=-=--=+ ⎪ ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦，故A 正确；对于B ：令2,32x k k Z πππ+=+∈，解得,212k x k Z ππ=+∈，令k =1，可得712x π=，所以函数()f x 的图象关于直线712x π=对称，故B 正确；对于C ：因为,126x ππ⎡⎤∈-⎢⎥⎣⎦，所以22,363x πππ⎡⎤+∈⎢⎥⎣⎦，所以当236x ππ+=时，min ()2sin16f x π==，故C 错误；对于D ：令3222,232k x k k Z πππππ+≤+≤+∈，解得7,1212k x k k Z ππππ+≤≤+∈，令k =0，可得一个单调减区间为7,1212ππ⎡⎤⎢⎥⎣⎦，因为57,,6121212ππππ⎡⎤⎡⎤⊂⎢⎥⎢⎥⎣⎦⎣⎦，所以函数()f x 在5,612ππ⎡⎤⎢⎥⎣⎦上单调递减，故D 正确.故选：C5．（2021·玉林市第十一中学高三其他模拟（文））已知函数()sin (0)f x x ωω=>的图象向右平移4π个单位长度得y =g (x )的图象，若函数g (x )的图象与直线y =在,22ππ⎡⎤-⎢⎥⎣⎦上恰有两个交点，则a 的取值范围是（ ）A ．[416,)39B ．1620,[)99C ．[208,93D ．[8,4)3【答案】B 【解析】由函数的平移可得()sin 4g x x πωω⎛⎫=- ⎪⎝⎭，结合三角函数的图象与性质可得ω满足的不等式，即可得解.【详解】由题意，()sin sin 44g x x x ππωωω⎡⎤⎛⎫⎛⎫=-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，当,22x ππ⎡⎤∈-⎢⎥⎣⎦时，3,444x πωπωπωω⎡⎤-∈-⎢⎥⎣⎦，因为函数g (x )的图象与直线y =在,22ππ⎡⎤-⎢⎥⎣⎦上恰有两个交点，则3542,2433122,2433k k k k πωπππππωππππ⎧⎛⎤-∈-+-+ ⎪⎥⎪⎝⎦⎨⎡⎫⎪∈++⎪⎢⎪⎣⎭⎩或3412,2433272,2433k k k k πωπππππωππππ⎧⎛⎤-∈-++ ⎪⎥⎪⎝⎦⎨⎡⎫⎪∈++⎪⎢⎪⎣⎭⎩，k Z ∈，又0>ω，所以1620,99ω⎡∈⎫⎪⎢⎣⎭.故选：B.6．（2020·北京四中高三其他模拟）函数tan 42y x ππ⎛⎫=- ⎪⎝⎭ 的部分图象如图所示，则 ()OA OB AB +⋅=（ ）A ．6B ．5C ．4D ．3【答案】A 【解析】根据正切函数的图象求出A 、B 两点的坐标，再求出向量的坐标，根据向量数量积的坐标运算求出结果．【详解】由图象得,令tan 42y x ππ⎛⎫=- ⎪⎝⎭=0,即42x ππ-=kπ，k Z∈k =0时解得x =2，令tan 42y x ππ⎛⎫=-⎪⎝⎭=1,即424x πππ-=，解得x =3，∴A (2,0),B (3,1)，∴()()()2,0,3,1,1,1OA OB AB ===，∴()()()5,11,1516OA OB AB +⋅=⋅=+=.故选：A .7．（2020·全国高三其他模拟（文））若函数()(0)xf x n nπ=>图象上的相邻一个最高点和一个最低点恰好都在圆222:O x y n +=上，则()1f =（ ）A B ．C ．-D ．【答案】A 【解析】首先由题意判断该正弦型函数的大概图象及相邻最高点和最低点与圆的交点情况.从而解得n 的取值，再代入1x =求解.【详解】解：设两交点坐标分别为()11,x y ，()22,x y ，则1y =，2y =-又函数()(0)xf x n nπ=>为奇函数，∴12x x =-，当22xnx n ππ=⇒=时，函数取得最大值，∴12n x =-，22nx =，由题，函数()(0)xf x n nπ=>图象上的相邻一个最高点和一个最低点恰好都在圆22: O x y n +=上，∴22242n n n ⎛⎫+=⇒= ⎪⎝⎭，则(1)4f π==.故选：A.8．【多选题】（2021·全国高三其他模拟）已知函数()2sin(),(0,0)f x x ωϕωϕπ=+><<图象的一条对称轴为23x π=，4⎛⎫= ⎪⎝⎭f π，且()f x 在2,43ππ⎛⎫ ⎪⎝⎭内单调递减，则以下说法正确的是（ ）A ．7,012π⎛⎫-⎪⎝⎭是其中一个对称中心B ．145ω=C ．()f x 在5,012π⎛⎫- ⎪⎝⎭单増D ．16f π⎛⎫-=- ⎪⎝⎭【答案】AD 【解析】先根据条件求解函数的解析式，然后根据选项验证可得答案.【详解】∵f (x )关23x π=对称，4⎛⎫= ⎪⎝⎭f π，f (x )在2,43ππ⎛⎫ ⎪⎝⎭单调递减，232232,22643k k ωπωϕπππππϕωϕπ⎧=+=+⎧⎪⎪⎪∴∴⎨⎨=⎪⎪+=+⎩⎪⎩，B 错误；()2sin 2,6f x x π⎛⎫=+ ⎪⎝⎭令2,6x k k ππ+=∈Z ，可得,,122k x k ππ=-+∈Z 当1k =-时，7,12x π=-即()f x 关于7,012π⎛⎫- ⎪⎝⎭对称，A 正确；令222,262k x k πππππ-+<+<+得,312k x k ππππ-+<<+∴()f x 在,312ππ⎡⎤-⎢⎥⎣⎦单调递増，即C 错误；2sin 2sin 16366f ππππ⎛⎫⎛⎫⎛⎫-=-+=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，D 正确，故选：AD.9．【多选题】（2021·重庆市蜀都中学校高三月考）已知函数()f x 满足x R ∀∈，有()(6)f x f x =-，且(2)(2)f x f x +=-，当[1,1]x ∈-时，)()lnf x x =-，则下列说法正确的是（ ）A ．(2021)0f =B ．(2020,2022)x ∈时，()f x 单调递增C ．()f x 关于点(1010,0)对称D ．(1,11)x ∈-时，方程()sin 2f x x π⎛⎫=⎪⎝⎭的所有根的和为30【答案】CD 【解析】利用已知条件可知()f x 在[1,1]x ∈-上为奇函数且单调递减，关于21x k =+、(2,0)k ，k Z ∈对称，且周期为4，即可判断各选项的正误.【详解】由题设知：()))()f x x x f x -===-=-，故()f x 在[1,1]x ∈-上为奇函数且单调递减，又(2)(4)(2)f x f x f x +=-=-，即关于21x k =+、(2,0)k ，k Z ∈对称，且最小周期为4，A ：(2021)(50541)(1)1)0f f f =⨯+==-≠，错误；B ：(2020,2022)x ∈等价于(0,2)x ∈，由上易知：(0,1)上递减，(1,2)上递增，故()f x 不单调，错误；C ：由上知：()f x 关于(2,0)k 对称且k Z ∈，所以()f x 关于(1010,0)对称，正确；D ：由题意，只需确定()f x 与sin 2xy π=在(1,11)x ∈-的交点，判断交点横坐标的对称情况即可求和，如下图示，∴共有6个交点且关于5x =对称，则16253410x x x x x x +=+=+=，∴所有根的和为30，正确.故选：CD10.（2021·浙江杭州市·杭州高级中学高三其他模拟）设函数sin 3xy π=在[,1]t t +上的最大值为()M t ，最小值为()N t ，则()()M t N t -在3722t ≤≤上最大值为________．【答案】1【解析】依题意可得函数在39,22⎡⎤⎢⎥⎣⎦上单调递减，则39[,1],22t t ⎡⎤+⊆⎢⎥⎣⎦，所以()()cos 36t M t N t ππ⎛⎫-=-+⎪⎝⎭，即可求出函数的最大值；【详解】解：函数sin3xy π=的周期为6，函数sin3xy π=在39,22⎡⎤⎢⎥⎣⎦上单调递减，当3722t ≤≤时，39[,1],22t t ⎡⎤+⊆⎢⎥⎣⎦(1)()()sinsin2cos sin cos 3336636tt t t M t N t πππππππ+⎛⎫⎛⎫⎛⎫-=-=+-=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭因为3722t ≤≤，所以243363t ππππ≤+≤，所以11cos 362t ππ⎛⎫-≤+≤-⎪⎝⎭所以1()()12M t N t ≤-≤当52t =时取最大值1故答案为：11．（2021·全国高考真题（理））已知命题:,sin 1p x x ∃∈<R ﹔命题:q x ∀∈R ﹐||e 1x ≥，则下列命题中为真命题的是（ ）A ．p q ∧B ．p q⌝∧C ．p q∧⌝D ．()p q ⌝∨【答案】A 【解析】由正弦函数的有界性确定命题p 的真假性，由指数函数的知识确定命题q 的真假性，由此确定正确选项.【详解】由于1sin 1x -≤≤，所以命题p 为真命题；由于0x ≥，所以||e 1x ≥，所以命题q 为真命题；所以p q ∧为真命题，p q ⌝∧、p q ∧⌝、()p q ⌝∨为假命题.故选：A ．2.（2021·全国高考真题）下列区间中，函数()7sin 6f x x π⎛⎫=-⎪⎝⎭单调递增的区间是（ ）练真题A ．0,2π⎛⎫⎪⎝⎭B ．,2ππ⎛⎫⎪⎝⎭C ．3,2ππ⎛⎫ ⎪⎝⎭D ．3,22ππ⎛⎫ ⎪⎝⎭【答案】A 【解析】解不等式()22262k x k k Z πππππ-<-<+∈，利用赋值法可得出结论.【详解】因为函数sin y x =的单调递增区间为()22,22k k k Z ππππ⎛⎫-+∈ ⎪⎝⎭，对于函数()7sin 6f x x π⎛⎫=- ⎪⎝⎭，由()22262k x k k Z πππππ-<-<+∈，解得()22233k x k k Z ππππ-<<+∈，取0k =，可得函数()f x 的一个单调递增区间为2,33ππ⎛⎫-⎪⎝⎭，则20,,233πππ⎛⎫⎛⎫⊆- ⎪ ⎪⎝⎭⎝⎭，2,,233ππππ⎛⎫⎛⎫⊄- ⎪ ⎪⎝⎭⎝⎭，A 选项满足条件，B 不满足条件；取1k =，可得函数()f x 的一个单调递增区间为58,33ππ⎛⎫⎪⎝⎭，32,,233ππππ⎛⎫⎛⎫⊄- ⎪ ⎪⎝⎭⎝⎭且358,,233ππππ⎛⎫⎛⎫⊄ ⎪ ⎪⎝⎭⎝⎭，358,2,233ππππ⎛⎫⎛⎫⊄ ⎪⎪⎝⎭⎝⎭，CD 选项均不满足条件.故选：A.3.（2019年高考全国Ⅰ卷文）函数f (x )=在的图象大致为（ ）A ．B ．C ．D ．【答案】D2sin cos ++x xx x[,]-ππ【解析】由，得是奇函数，其图象关于原点对称，排除A ．又，排除B ，C ，故选D ．4．（2020·全国高考真题（理））设函数()cos π(6f x x ω=+在[π,π]-的图像大致如下图，则f (x )的最小正周期为（ ）A ．10π9B ．7π6C ．4π3D ．3π2【答案】C 【解析】由图可得：函数图象过点4,09π⎛⎫-⎪⎝⎭，将它代入函数()f x 可得：4cos 096ππω⎛⎫-⋅+= ⎪⎝⎭又4,09π⎛⎫-⎪⎝⎭是函数()f x 图象与x 轴负半轴的第一个交点，所以4962πππω-⋅+=-，解得：32ω=所以函数()f x 的最小正周期为224332T πππω===故选：C22sin()()sin ()()cos()()cos x x x xf x f x x x x x -+----===--+-+()f x 22π1π42π2(1,π2π()2f ++==>2π(π)01πf =>-+5．（2020·全国高考真题（理））关于函数f （x ）=1sin sin x x+有如下四个命题：①f （x ）的图像关于y 轴对称．②f （x ）的图像关于原点对称．③f （x ）的图像关于直线x =2π对称．④f （x ）的最小值为2．其中所有真命题的序号是__________．【答案】②③【解析】对于命题①，152622f π⎛⎫=+=⎪⎝⎭，152622f π⎛⎫-=--=- ⎪⎝⎭，则66f f ππ⎛⎫⎛⎫-≠ ⎪ ⎪⎝⎭⎝⎭，所以，函数()f x 的图象不关于y 轴对称，命题①错误；对于命题②，函数()f x 的定义域为{},x x k k Z π≠∈，定义域关于原点对称，()()()()111sin sin sin sin sin sin f x x x x f x x x x ⎛⎫-=-+=--=-+=- ⎪-⎝⎭，所以，函数()f x 的图象关于原点对称，命题②正确；对于命题③，11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫-=-+=+⎪ ⎪⎛⎫⎝⎭⎝⎭- ⎪⎝⎭ ，11sin cos 22cos sin 2f x x x x x πππ⎛⎫⎛⎫+=++=+⎪ ⎪⎛⎫⎝⎭⎝⎭+ ⎪⎝⎭，则22f x f x ππ⎛⎫⎛⎫-=+ ⎪ ⎪⎝⎭⎝⎭，所以，函数()f x 的图象关于直线2x π=对称，命题③正确；对于命题④，当0x π-<<时，sin 0x <，则()1sin 02sin f x x x=+<<，命题④错误.故答案为：②③.6．（2018·北京高考真题（理））设函数f （x ）=cos(ωx ―π6)(ω>0)，若f (x )≤f (π4)对任意的实数x 都成立，则ω的最小值为__________．【答案】23【解析】因为f (x )≤f (π4)对任意的实数x 都成立，所以f (π4)取最大值，所以π4ω―π6=2k π(k ∈Z )，∴ω=8k +23(k∈Z )，因为ω>0，所以当k =0时，ω取最小值为23.。
2017年高考真题全国2卷理科数学(附答案解析)
说不知道自已的成绩，假定丙是优，则乙是良，乙就知道自己成绩．给丁看甲成绩，因
为甲不知道自己成绩，乙丙是一优一良，则甲丁也是一优一良，丁看到甲成绩，假定甲
是优，则丁是良，丁肯定知道自已的成绩了
故选：D．
【点睛】
本题考查了合情推理的问题，关键掌握四人所知只有自己看到，老师所说及最后甲说话，
属于中档题． 8．B
2x + 3y − 3 ≤ 0 作出 2x − 3y + 3 ≥ 0 表示的可行域，如图，
y + 3 ≥ 0
2x + 3y − 3 =0 x = −6
由
可得
，
2x − 3y + 3 =0 y = −3
将=z 2x + y 变形为 y =−2x + z ， 平移直线 y =−2x + z ，
由图可知当直 y =−2x + z 经过点 (−6, −3) 时，
4 − 2i
＝2－i.
2
参考答案
故选 D. 【点睛】 这个题目考查了复数的除法运算，复数常考的还有几何意义，z＝a＋bi(a，b∈R)与复平面上
uuur 的点 Z(a，b)、平面向量 OZ 都可建立一一对应的关系(其中 O 是坐标原点)；复平面内，实
轴上的点都表示实数；虚轴上的点除原点外都表示纯虚数．涉及到共轭复数的概念，一般地， 当两个复数的实部相等，虚部互为相反数时，这两个复数叫做互为共轭复数，复数 z 的共轭
a2 b2
截
得的弦长为 2，则 C 的离心率为
（）
A．2
B． 3
C． 2
D． 2 3 3
10．已知直三棱柱 ΑΒC − Α1Β1C1 中， ∠ΑΒC = 120o， ΑΒ = 2 ， ΒC= CC=1 1，则
全国卷历年高考三角函数及解三角形真题归类分析2019(含答案)
全国卷历年高考三角函数及解三角形真题归类分析（2015年-2019年共14套） 三角函数（共20小题）一、三角恒等变换（6题）1.（2015年1卷2）o o o o sin 20cos10cos160sin10- =（ ）（A ）32-（B ）32（C ）12- （D ）12【解析】原式=o o o o sin 20cos10cos 20sin10+ =o sin 30=12，故选D.2.（2018年3卷4）若，则A. B. C. D.【解析】,故答案为B.3.（2016年3卷7）若3tan 4α=，则2cos 2sin 2αα+=（ ） (A)6425 (B) 4825 (C) 1 (D)1625【解析】由3tan 4α=，得34sin ,cos 55αα==或34sin ,cos 55αα=-=-，所以2161264cos 2sin 24252525αα+=+⨯=，故选A ．4.（2016年2卷9）若π3cos 45α⎛⎫-= ⎪⎝⎭，则sin 2α=（ ）（A ）725 （B ）15 （C ）15- （D ）725-【解析】∵3cos 45πα⎛⎫-= ⎪⎝⎭，2ππ7sin 2cos 22cos 12425ααα⎛⎫⎛⎫=-=--= ⎪ ⎪⎝⎭⎝⎭，故选D ．5.（2018年2卷15）已知，，则__________．【解析】：因为，，所以，因此6.（2019年2卷10）已知a ∈（0，π2），2sin2α=cos2α+1，则sinα=（ ） A.15B.5C.33D.255【解析】2sin 2cos 21α=α+，24sin cos 2cos .0,,cos 02π⎛⎫∴α⋅α=αα∈∴α> ⎪⎝⎭．sin 0,2sin cos α>∴α=α，又22sin cos 1αα+=，2215sin 1,sin 5∴α=α=，又sin 0α>，55B ． 【点评】这类题主要考查三角函数中二倍角公式（几乎必考）、两角和与差公式、诱导公式、同角三角函数基本关系式等三角函数公式，难度以容易、中等为主。
【高考真题汇编】2017年高考数学理科真题汇编解析：第04章三角函数
第四章 三角函数第一节 三角函数概念、同角三角函数关系式和诱导公式题型42 终边相同的角的集合的表示与识别——暂无 题型43 倍角、等分角的象限问题——暂无 题型44 弧长与扇形面积公式的计算——暂无 题型45 三角函数定义题——暂无 题型46 三角函数线及其应用——暂无题型47 象限符号与坐标轴角的三角函数值——暂无 题型48 诱导求值与变形——暂无题型49 同角求值——已知角与目标角相同——暂无第二节 三角函数的图像与性质题型50 已知解析式确定函数性质1.（2017全国3理6）设函数()πcos 3f x x ⎛⎫=+⎪⎝⎭，则下列结论错误的是（ ）. A ．()f x 的一个周期为2-πB ．()y f x =的图像关于直线83x π=对称 C ．()f x +π的一个零点为6x π=D ．()f x 在上π,2⎛⎫π⎪⎝⎭单调递减 解析 函数()πcos 3f x x ⎛⎫=+ ⎪⎝⎭的图像可由cos y x =向左平移π3个单位长度得到，由图可知，()f x 在π,π2⎛⎫⎪⎝⎭上先递减后递增，所以D 选项错误.故选D.π题型51 根据条件确定解析式1.（2017天津理7）设函数()2sin()f x x ωϕ=+，x ∈R ，其中0ω>，||ϕ<π.若528f π⎛⎫= ⎪⎝⎭，08f 11π⎛⎫= ⎪⎝⎭，且()f x 的最小正周期大于2π，则（ ）.A.23ω=，12ϕπ= B.23ω=，12ϕ11π=- C.13ω=，24ϕ11π=- D.13ω=，24ϕ7π= 解析 解法一：由题意125π282118k k ωϕωϕπ⎧+=π+⎪⎪⎨π⎪+=π⎪⎩，其中12,k k ∈Z ，所以()2142233k k ω=--.又22T ωπ=>π，所以01ω<<，从而23ω=.由11212k ϕ=π+π，由ϕ<π，得π12ϕ=.故选A ．解法二：由528f π⎛⎫= ⎪⎝⎭，08f 11π⎛⎫= ⎪⎝⎭，易知58x π=为()()2sin f x x ωϕ=+的一条对称轴，点11,08π⎛⎫⎪⎝⎭为()f x 的一个零点，则()11521884T k ππ-=+⨯，又因为2T ωπ= ，即()221=3k ω+.又0ω>，且()f x 的最小正周期大于2π，所以2=3ω，从而52+2832k ϕππ⨯=π+，又ϕ<π，所以=12ϕπ.故选A. 2.(2017浙江理18)已知函数()()22sin cos cos f x x x x x x =--∈R .（1）求23f π⎛⎫⎪⎝⎭的值； （2）求()f x 的最小正周期及单调递增区间. 解析 （1）由2sin 3π=21cos 32π=-，得222112322f π⎛⎫⎛⎫⎛⎫=----= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. （2）由22cos2cos sin x x x=-，sin22sin cos x x x=，得()cos 222sin 26f x x x x π⎛⎫=-=-+ ⎪⎝⎭，所以()f x 的最小正周期是2π2T ==π. 由正弦函数的性质得3222,262k x k k πππ+π++π∈Z 剟，解得2,63k x k k ππ+π+π∈Z 剟. 所以()f x 的单调递增区间是2,63k k k ππ⎡⎤+π+π∈⎢⎥⎣⎦Z ，.题型52 三角函数的值域（最值)——暂无 题型53 三角函数图像变换1.（2017全国1理9）已知曲线1cos C y x =：，22πsin 23C y x ⎛⎫=+ ⎪⎝⎭：， 则下面结论正确的是（ ）.A.把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CB.把1C 上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2CC.把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向右平移π6个单位长度，得到曲线2CD.把1C 上各点的横坐标缩短到原来的12倍，纵坐标不变，再把得到的曲线向左平移π12个单位长度，得到曲线2C解析 1:cos C y x =，22π:sin 23⎛⎫=+⎪⎝⎭C y x . 首先曲线1C ，2C 统一为一三角函数名，可将1:cos C y x =用诱导公式处理．πππcos cos sin 222⎛⎫⎛⎫==+-=+ ⎪ ⎪⎝⎭⎝⎭y x x x ．横坐标变换需将1=ω变成2=ω，即112πππsin sin 2sin 2224C y x y x x ⎛⎫⎛⎫⎛⎫=+−−−−−−−−−−→=+=+→⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭上各坐短到原的倍点横标缩来2ππsin 2sin 233y x x ⎛⎫⎛⎫=+=+ ⎪ ⎪⎝⎭⎝⎭．注意ω的系数，左右平移需将2=ω提到括号外面，这时π4+x 平移至π3+x ， 根据“左加右减”原则，“π4+x ”到“π3+x ”需加上π12，即再向左平移π12．故选D. 2.（2017山东理1）设函数()sin sin 62f x x x ωωππ⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭，其中03ω<<.已知06f π⎛⎫= ⎪⎝⎭. （1）求ω；（2）将函数()y f x =的图像上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图像向左平移4π个单位，得到函数()y g x =的图像，求()g x 在3,44ππ⎡⎤-⎢⎥⎣⎦上的最小值. 解析 （1）因为()sin sin 62f x x x ωωππ⎛⎫⎛⎫=-+- ⎪ ⎪⎝⎭⎝⎭， 所以()1cos cos 2f x x x x ωωω=--3cos 2x x ωω=-1sin 2x x ωω⎫==⎪⎪⎭sin 3x ωπ⎫-⎪⎭.由题设知06f π⎛⎫=⎪⎝⎭，所以63k ωππ-=π，k ∈Z . 故62k ω=+，k ∈Z ，又03ω<<，所以2ω=.（2）由（1）得()23f x xπ⎛⎫=- ⎪⎝⎭，所以()4312g x x x πππ⎛⎫⎛⎫=+-=- ⎪ ⎪⎝⎭⎝⎭.因为3,44x ππ⎡⎤∈-⎢⎥⎣⎦，所以2,1233x πππ⎡⎤-∈-⎢⎥⎣⎦，当123x ππ-=-，即4x π=-时，()g x 取得最小值32-.第三节 三角恒等变换题型54 化简求值1.（17江苏05）若π1tan 46α⎛⎫-= ⎪⎝⎭，则tan α= ． 解析 解法一（角的关系）：tan tan 44ααππ⎛⎫=-+ ⎪⎝⎭7tan 1746551tan 64ααπ⎛⎫-+ ⎪⎝⎭===π⎛⎫-- ⎪⎝⎭．故填75．解法二（直接化简）：πtan 11tan 41tan 6ααα-⎛⎫-== ⎪+⎝⎭，所以7tan 5α=．故填75． 2.(2017北京理12)在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若1sin 3α=，()cos αβ-=___________. 解析 由题作出图形，如图所示，1sin 3α=，则cos 3α=，由于α与β关于y 轴对称， 则()1sin sin 3βα=π-=，cos 3β=-，故()117cos 33339αβ⎛-=⨯-+⨯=- ⎝⎭.3.（2017全国2理14）函数()23s i n c o s 0,42f x x x x ⎛π⎫⎡⎤=-∈ ⎪⎢⎥⎣⎦⎝⎭的最大值是 ．解析 ()2233πsin 1cos 0442f x x x x x x ⎛⎫⎡⎤=+-=-+-∈ ⎪⎢⎥⎣⎦⎝⎭，，令c o sx t =且[]01t ∈，，214y t =-+21t ⎛=-+ ⎝⎭，当t ，即6x π=时，()f x 取最大值为1．4.(2017浙江理18)已知函数()()22sin cos cos f x x x x x x =--∈R . （1）求23f π⎛⎫⎪⎝⎭的值； （2）求()f x 的最小正周期及单调递增区间.解析 （1）由2sin 3π=21cos 32π=-，得222112322f π⎛⎫⎛⎫⎛⎫=----= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. （2）由22cos2cos sin x x x=-，sin22sin cos x x x=，得()co 23s i n 22si n 26fx x x x π⎛⎫=-=-+ ⎪⎝⎭， 所以()f x 的最小正周期是2π2T ==π. 由正弦函数的性质得3222,262k x k k πππ+π++π∈Z 剟，解得2,63k x k k ππ+π+π∈Z 剟. 所以()f x 的单调递增区间是2,63k k k ππ⎡⎤+π+π∈⎢⎥⎣⎦Z ，.第四节 解三角形题型55 正弦定理的应用1.（2017天津理15）在ABC △中，内角,,A B C 所对的边分别为,,a b c .已知a b >，5,6a c ==，3sin 5B =. （1）求b 和sin A 的值； （2）求πsin 24A ⎛⎫+⎪⎝⎭的值. 解析 （1）在ABC △中，因为a b >，故由3sin 5B =，可得4cos 5B =.由已知及余弦定理，得2222cos 13b a c ac B =+-=，所以b =由正弦定理sin sin a bA B=，得sin sin a B A b ==.（2）由（Ⅰ）及a c <，得cos A =，所以12sin 22sin cos 13A A A ==，25cos 212sin 13A A =-=-，故πππsin 2sin 2cos cos 2sin 44426A A A ⎛⎫+=+= ⎪⎝⎭. 2.（2017山东理9）在ABC △中，角A ，B ，C 的对边分别为a ，b ，c ．若ABC △为锐角三角形，且满足()sin 12cos 2sin cos cos sin B C A C A C +=+，则下列等式成立的是（ ）.A.2a b =B.2b a =C.2A B =D.2B A = 解析因为s i n ()2s i n c o s 2s i A C B C A C A C++=+，所以2sin cos sin cos B C A C =，又02C π<<，得2sin sin B A =，即2b a =.故选A.题型56 余弦定理的应用题型57 判断三角形的形状——暂无 题型58 解三角形的综合应用1.（2017江苏18）如图所示，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm ，容器Ⅰ的底面对角线AC 的长为cm ，容器Ⅱ的两底面对角线EG ，11E G 的长分别为14cm 和62cm ． 分别在容器Ⅰ和容器Ⅱ中注入水，水深均为12cm ． 现有一根玻璃棒l ，其长度为40cm （容器厚度、玻璃棒粗细均忽略不计）.（1）将l 放在容器Ⅰ中，l 的一端置于点A 处，另一端置于侧棱1CC 上，求l 没入水中部分的长度；（2）将l 放在容器Ⅱ中，l 的一端置于点E 处，另一端置于侧棱1GG 上，求l 没入水中部分的长度．ACA 11容器ⅠE G 1H 1容器Ⅱ解析 （1）由正棱柱的定义，1CC ⊥平面ABCD ，所以平面11A ACC ⊥平面ABCD ，1CC AC ⊥．记玻璃棒的另一端落在1CC 上点M 处，如图所示为截面11A ACC的平面图形．因为AC =40AM =，所以30MC ==，从而3sin 4MAC ∠=.记AM 与水面的交点为1P ， 过点1P 作11PQ AC ⊥，1Q 为垂足，则11PQ ⊥平面ABCD ，故1112PQ =，从而11116sin PQ AP MAC==∠．答：玻璃棒l 没入水中部分的长度为16cm ．问(1)AC 1A 1CMP 1Q 1（2）如图所示为截面11E EGG 的平面图形，O ，1O 是正棱台两底面的中心．由正棱台的定义，1OO ⊥平面EFGH ， 所以平面11E EGG ⊥平面EFGH ，1O O EG ⊥． 同理，平面11E EGG ⊥平面1111E F G H ，111O O E G ⊥． 记玻璃棒的另一端落在1GG 上点N 处．过G 作11GK E G ⊥，K 为垂足，则132GK OO ==． 因为 14EG =，1162E G =，所以16214242KG -==，从而1GG =40==．设1EGG α∠=，ENG β∠=，则114sin sin cos 25KGG KGG απ⎛⎫=+==⎪⎝⎭∠∠． 因为2απ<<π，所以3cos 5α=-． 在ENG △中，由正弦定理可得4014sin sin αβ=，解得7sin 25β=． 因为02βπ<<，所以24cos 25β=， 于是()()sin sin sin =NEG αβαβ=π--=+∠sin cos cos sin αβαβ+4243735255255⎛⎫=⨯+-⨯= ⎪⎝⎭． 记EN 与水面的交点为2P ，过2P 作22P Q EG ⊥，2Q 为垂足，则22P Q ⊥平面EFGH ， 故2212P Q =，从而22220sin PQ EP NEG==∠．答：玻璃棒l 没入水中部分的长度为20cm ．问(2)G O E Q 2P 2NG 1KE 1O 1评注 此题本质上考查解三角形的知识，但在这样的大背景下构造的应用题让学生有畏惧之感，且该应用题的实际应用性也不强．也有学生第（1）问采用相似法解决，解法如下：AC =40AM =，所以30CM ==，1112PQ =，所以由11AP A Q CM △△∽，111PQ AP CM AM =，即1123040AP =，解得116AP =． 答：玻璃棒l 没入水中部分的长度为16cm ． 2.(2017北京理15)在ABC △中，60A ∠=，37c a =. （1）求sin C 的值；（2）若7a =，求ABC △的面积.解析 （1）在ABC △中，因为60A ∠=，37c a =，所以由正弦定理得sin 3sin 7c A C a ===. （2）因为7a =，所以3737c =⨯=.由余弦定理2222cos a b c bc A =+-，得222173232b b =+-⨯⨯，解得8b =或5b =-（舍）.所以ABC △的面积11sin 8322S bc A ==⨯⨯=3.（2017全国1理17）ABC △的内角A ，B ，C 的对边分别为a ，b ，c ，已知ABC△的面积为23sin a A.（1）求sin sin B C 的值；（2）若6cos cos 1B C =，3a =，求ABC △的周长.分析 本题主要考查三角函数及其变换，正弦定理，余弦定理等基础知识的综合应用.解析 （1）因为ABC △的面积23sin a S A =且1sin 2S bc A =，所以21sin 3sin 2a bc A A =，即223sin 2a bc A =.由正弦定理得223sin sin sin sin 2A B C A =，由sin 0A ≠，得2sin sin 3B C =. （2）由（1）得2sin sin 3B C =，又1cos cos 6B C =，因为πA B C ++=， 所以()()1cos cos πcos sin sinC cos cos 2A B C B C B B C =--=-+=-=.又因为()0πA ∈，，所以60A =，sin A =，1cos 2A =. 由余弦定理得2229a b c bc =+-= ① 由正弦定理得sin sin a b B A =⋅，sin sin a c C A =⋅，所以22sin sin 8sin a bc B C A=⋅= ②由①，②，得b c +=3a b c ++=ABC △周长为34.（2017全国2理17）ABC △的内角,,A B C 的对边分别为,,a b c ，已知()2sin 8sin 2B AC +=． (1)求cos B ; (2)若6a c +=，ABC △的面积为2，求.b解析 （1）依题得21cos sin 8sin 84(1cos )22B B B B -==⋅=-． 因为22sin cos 1B B +=，所以2216(1cos )cos 1B B -+=，所以(17cos 15)(cos 1)0B B --=，得c o s 1B =（舍去）或15cos 17B =. （2）由⑴可知8sin 17B =，因为2ABC S =△，所以1sin 22ac B ⋅=，即182217ac ⋅=，得172ac =.因为15cos 17B =，所以22215217a cb ac +-=，即22215a c b +-=，从而22()215a c ac b +--=， 即2361715b --=，解得2b =．5.（2017全国3理17）ABC △的内角,,A B C 的对边分别为,,a b c ，已知s i n c o s 0A A =，a =2b =．（1）求c ；（2）设D 为BC 边上一点，且 AD AC ⊥，求ABD △的面积．解析 （1）由sin 0A A =，得π2sin 03A ⎛⎫+= ⎪⎝⎭，即()ππ3A k k +=∈Z ， 又()0,πA ∈，所以ππ3A +=，得2π3A =.由余弦定理得2222cos a b c bc A =+-⋅.又因为12,cos 2a b A ===-代入并整理得()2125c +=，解得4c =.（2）因为2,4AC BC AB ===，由余弦定理得222cos 2a b c C ab +-==因为AC AD ⊥，即ACD △为直角三角形，则cos AC CD C =⋅，得CD从而点D 为BC的中点，111sin 222ABD ABC S S AB AC A ==⨯⨯⨯⨯=△6.(2017浙江理14)已知ABC △，4AB AC ==，2BC =. 点D 为AB 延长线上的一点，2BD =，联结CD ，则BDC △的面积是___________，cos BDC ∠=__________. 解析 如图所示，取BC 的中点为O ，在等腰ABC △中，AO OB ⊥，所以AO =sin sin 4CBD OBA ??， 所以BDC △的面积为1sin 2BC BD OBA 创葱=．因为2BC BD ==，所以BDC△是等腰三角形，所以2πC B D B D C ??，21cos cos(π2)12cos 4CBDBDC BDC ?-?-?-，解得cos BDC ?OD C B A。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第四章 三角函数
第一节 三角函数概念、同角三角函数关系式和诱导公式
题型42 终边相同的角的集合的表示与识别——暂无
题型43 倍角、等分角的象限问题——暂无
题型44 弧长与扇形面积公式的计算——暂无
题型45 三角函数定义题——暂无
题型46 三角函数线及其应用——暂无
题型47 象限符号与坐标轴角的三角函数值——暂无
题型48 诱导求值与变形——暂无
题型49 同角求值——已知角与目标角相同——暂无
第二节 三角函数的图像与性质
题型50 已知解析式确定函数性质
1.（2017全国3理6）设函数，则下列结论错误的是（ ）.
A ．的一个周期为
B ．的图像关于直线对称
C ．的一个零点为
D ．在上单调递减
解析 函数的图像可由向左平移个单位长度得到，由图可知，在上先递减后递增，所以D 选项错误.故选D.
题型51 根据条件确定解析式
1.（2017天津理7）设函数，，其中，.若，，且的最小正周期大于，则（ ）.
A.，
B.，
C.，
D.，
解析 解法一：由题意，其中，所以.又，所以，从而.由，由，得.故选A ．
解法二：由，，易知为的一条对称轴，点为的一个零点，则，又因为 ，即.又，且的最小正周期大于，所以，从而，又，所以.故选A.
2.(2017浙江理18)已知函数()()22sin cos cos f x x x x x x =--∈R .
（1）求23f π⎛⎫ ⎪⎝⎭
的值； （2）求()f x 的最小正周期及单调递增区间.
解析 （1）由2
sin 3π=21cos 32π=-，得2
22112322f π⎛⎫⎛⎫⎛⎫=----= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.
（2）由22cos2cos sin x x x =-，sin22sin cos x x x =，得()cos 222sin 26f x x x x π⎛⎫=-=-+ ⎪⎝⎭
，
所以()f x 的最小正周期是2π2T
==π. 由正弦函数的性质得3222,262k x k k π
ππ+π+
+π∈Z 剟，解得2,63k x k k ππ+π+π∈Z 剟. 所以()f x 的单调递增区间是2,63
k k k π
π⎡⎤+π+π∈⎢⎥⎣⎦Z ，. 题型52 三角函数的值域（最值)——暂无
题型53 三角函数图像变换
1.（2017全国1理9）已知曲线，，
则下面结论正确的是（ ）.
A.把上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线
B.把上各点的横坐标伸长到原来的2倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线
C.把上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向右平移个单位长度，得到曲线
D.把上各点的横坐标缩短到原来的倍，纵坐标不变，再把得到的曲线向左平移个单位长度，得到曲线
解析 ，.
首先曲线，统一为一三角函数名，可将用诱导公式处理．
．横坐标变换需将变成，
即．
注意的系数，左右平移需将提到括号外面，这时平移至，
根据“左加右减”原则，“”到“”需加上，即再向左平移．故选D.
2.（2017山东理1）设函数，其中.已知.
（1）求；
（2）将函数的图像上各点的横坐标伸长为原来的2倍（纵坐标不变），再将得到的图像向左平移个单位，得到函数的图像，求在上的最小值.
解析 （1）因为，
所以
.
由题设知，所以，.
故，，又，所以.
（2）由（1）得，所以.
因为，所以，当，即时，取得最小值.
第三节 三角恒等变换
题型54 化简求值
1.（17江苏05）若，则 ．
解析 解法一（角的关系）：．故填．
解法二（直接化简）：，所以．故填．
2.(2017北京理12)在平面直角坐标系中，角与角均以为始边，它们的终边关于轴对称.若，=___________.
解析 由题作出图形，如图所示，，则，由于与关于轴对称，
则，，故.
3.（2017全国2理14）函数的最大值是 ．
解析 ()2233πsin 1cos 0442f x x x x x x ⎛⎫⎡⎤=+-=--∈ ⎪⎢⎥⎣
⎦⎝⎭，，令且，，当，即时，取最大值为1．
4.(2017浙江理18)已知函数()()22sin cos cos f x x x x x x =--∈R .
（1）求23f π⎛⎫ ⎪⎝⎭
的值； （2）求()f x 的最小正周期及单调递增区间.
解析 （1）由2
sin 3π=21cos 32π=-，得2
22112322f π⎛⎫⎛⎫⎛⎫=----= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.
（2）由22
cos2cos sin x x x =-，sin22sin cos x x x =，得()cos 222sin 26f x x x x π⎛⎫=-=-+ ⎪⎝⎭， 所以()f x 的最小正周期是2π2T
==π. 由正弦函数的性质得3222,262k x k k π
ππ+π+
+π∈Z 剟，解得2,63k x k k ππ+π+π∈Z 剟. 所以()f x 的单调递增区间是2,63
k k k π
π⎡⎤+π+π∈⎢⎥⎣⎦Z ，. 第四节 解三角形
题型55 正弦定理的应用
1.（2017天津理15）在中，内角所对的边分别为.已知，，.
（1）求和的值；
（2）求的值.
解析 （1）在中，因为，故由，可得.由已知及余弦定理，得，所以.
由正弦定理，得.
（2）由（Ⅰ）及，得，所以，
，故.
2.（2017山东理9）在中，角，，的对边分别为，，．若为锐角三角形，且满足，则下列等式成立的是（）.
A. B. C. D.
解析因为，所以，又，得，即.故选A.
题型56 余弦定理的应用
题型57 判断三角形的形状——暂无
题型58 解三角形的综合应用
1.（2017江苏18）如图所示，水平放置的正四棱柱形玻璃容器和正四棱台形玻璃容器的高均为，容器的底面对角线的长为，容器的两底面对角线，的长分别为和．分别在容器和容器中注入水，水深均为．现有一根玻璃棒，其长度为（容器厚度、玻璃棒粗细均忽略不计）.
（1）将放在容器中，的一端置于点处，另一端置于侧棱上，求没入水中部分的长度；
（2）将放在容器中，的一端置于点处，另一端置于侧棱上，求没入水中部分的长度．
解析（1）由正棱柱的定义，平面，所以平面平面，．
记玻璃棒的另一端落在上点处，如图所示为截面的平面图形．因为，，所以，从而.记与水面的交点为，过点作，为垂足，则平面，故，从而．
答：玻璃棒没入水中部分的长度为．
（2）如图所示为截面的平面图形，，是正棱台两底面的中心．
由正棱台的定义，平面，所以平面平面，．
同理，平面平面，．
记玻璃棒的另一端落在上点处．
过作，为垂足，则．
因为，，所以，
从而．
设，，则．
因为，所以．
在中，由正弦定理可得，解得．
因为，所以，
于是
．
记与水面的交点为，过作，为垂足，则平面，
故，从而．
答：玻璃棒没入水中部分的长度为．
评注此题本质上考查解三角形的知识，但在这样的大背景下构造的应用题让学生有畏惧之感，且该应用题的实际应用性也不强．
也有学生第（1）问采用相似法解决，解法如下：
，，所以，，
所以由，，即，解得．
答：玻璃棒没入水中部分的长度为．
2.(2017北京理15)在中，，.
（1）求的值；
（2）若，求的面积.
解析（1）在中，因为，，
所以由正弦定理得.
（2）因为，所以.由余弦定理，得，
解得或（舍）.所以的面积.
3.（2017全国1理17）ABC
△的内角，，的对边分别为，，，已知的面积为.
（1）求的值；
（2）若，，求的周长.
分析本题主要考查三角函数及其变换，正弦定理，余弦定理等基础知识的综合应用.
解析（1）因为的面积且，所以，即.
由正弦定理得，由，得.
（2）由（1）得，又，因为，
所以.
又因为，所以，，.
由余弦定理得①
由正弦定理得，，所以②
由①，②，得，所以，即周长为.
4.（2017全国2理17）的内角的对边分别为，已知．
(1)求;
(2)若，的面积为2，求
解析（1）依题得．
因为，所以，所以，得（舍去）或.
（2）由⑴可知，因为，所以，即，得.因为，所以，即，从而， 即，解得．
5.（2017全国3理17）的内角的对边分别为 ，已知，，．
（1）求；
（2）设为边上一点，且，求的面积．
解析 （1）由，得，即，
又，所以，得.由余弦定理得.
又因为代入并整理得，解得.
（2）因为，由余弦定理得.
因为，即为直角三角形，则，得.
从而点为的中点，.
6.(2017浙江理14)已知ABC △，4AB AC ==，2BC =.?点D 为AB 延长线上的一点，2BD =，联结CD ，则BDC △的面积是___________，cos BDC ∠=__________.
解析 如图所示，取BC 的中点为O ，在等腰ABC △中，AO OB ⊥，所以
AO =
sin sin CBD OBA ??，
所以BDC △的面积为1sin 2
2BC BD OBA 创葱=．因为2BC BD ==，所以BDC △是等腰三角形，所以2πCBD BDC
??，21cos cos(π2)12cos 4CBD BDC BDC ?-?-?-，解得
cos BDC ?。