解题技巧专题:平面直角坐标系中的图形面积
2020年中考数学压轴题-专题10 动点产生的面积关系(解析版)
专题10 动点产生的面积关系教学重难点1.体会点的运动过程,能从点的运动过程中抓住一些不变的量;2.能从点的运动过程中建立自变量与面积的关系式;3.让学生学会求一些基本图形的面积;4.体会压轴题的解题方法和思路。
【备注】:1.此部分知识点梳理,根据第1个图先让学生初步体会到压轴题中求图形面积的种类,可以看看每一类图形学生都是怎么求解的;2再根据第2个图引导学生总结求三角形面积的一般方法。
时间5分钟左右完成。
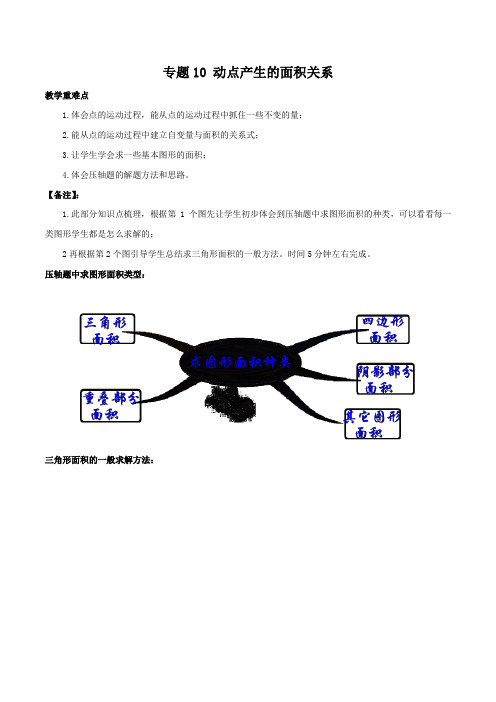
压轴题中求图形面积类型:三角形面积的一般求解方法:【备注】:1.以下每题教法建议,请老师根据学生实际情况参考;2.在讲解时:不宜采用灌输的方法,应采用启发、诱导的策略,并在读题时引导学生发现一些题目中的条件(相等的量、不变的量、隐藏的量等等),使学生在复杂的背景下自己发现、领悟题目的意思;3.可以根据各题的“参考教法”引导学生逐步解题,并采用讲练结合;注意边讲解边让学生计算,加强师生之间的互动性,让学生参与到例题的分析中来;4.例题讲解,可以根据“参考教法”中的问题引导学生分析题目,边讲边让学生书写,每个问题后面有答案提示;5.引导的技巧:直接提醒,问题式引导,类比式引导等等;6.部分例题可以先让学生自己试一试,之后再结合学生做的情况讲评;7.每个题目的讲解时间根据实际情况处理,建议每题7分钟,选讲例题在时间足够的情况下讲解。
例1(2020静安区建承中学一模)在平面直角坐标系xOy 中(如图),已知二次函数2y ax bx c =++(其中a 、b 、c 是常数,且a ≠0)的图像经过点A (0,-3)、B (1,0)、C (3,0),联结AB 、AC .(1)求这个二次函数的解析式;(2)点D 是线段AC 上的一点,联结BD ,如果:3:2ABD BCD S S ∆∆=,求tan∠DBC 的值; (3)如果点E 在该二次函数图像的对称轴上,当AC 平分∠BAE 时,求点E 的坐标.【整体分析】(1)直接利用待定系数法,把A 、B 、C 三点代入解析式,即可得到答案; (2)过点D 作DH ∠BC 于H ,在∠ABC 中,设AC 边上的高为h ,利用面积的比得到32AD DC =,然后求出DH 和BH ,即可得到答案;(3)延长AE 至x 轴,与x 轴交于点F ,先证明△OAB∠∠OFA ,求出点F 的坐标,然后求出直线AF 的方程,即可求出点E 的坐标. 【详解】解:(1)将A (0,-3)、B (1,0)、C (3,0)代入20y ax bx c a =++≠()得,03,0934,300a b a b c =+-⎧⎪=+-⎨⎪-=++⎩解得143a b c =-⎧⎪=⎨⎪=-⎩,∴此抛物线的表达式是:243y x x =-+-.(2)过点D 作DH ⊥BC 于H ,在∠ABC中,设AC边上的高为h,则11:():():3:222ABD BCDS S AD h DC h AD DC∆∆=⋅⋅==,又∠DH//y轴,∴25 CH DC DHOC AC OA===.∵OA=OC=3,则∠ACO=45°,∴△CDH为等腰直角三角形,∴26355 CH DH==⨯=.∴64255 BH BC CH=-=-=.∴tan∠DBC=32 DHBH=.(3)延长AE至x轴,与x轴交于点F,∠OA=OC=3,∴∠OAC=∠OCA=45°,∠∠OAB=∠OAC-∠BAC=45°-∠BAC,∠OFA=∠OCA-∠FAC=45°-∠FAC,∠∠BAC=∠FAC,∴∠OAB=∠OFA . ∴△OAB∠∠OFA , ∴13OB OA OA OF ==. ∴OF=9,即F (9,0);设直线AF 的解析式为y=kx+b (k≠0),可得093k b b =+⎧⎨-=⎩ ,解得133k b ⎧=⎪⎨⎪=-⎩,∴直线AF 的解析式为:133y x =-, 将x=2代入直线AF 的解析式得:73y =-,∴E (2,73-). 【点睛】本题考查了相似三角形的判定和性质,二次函数的性质,求二次函数的解析式,等腰直角三角形的判定和性质,求一次函数的解析式,解题的关键是掌握二次函数的图像和性质,以及正确作出辅助线构造相似三角形.例2..已知9023ABC AB BC AD BC P ∠===°,,,∥,为线段BD 上的动点,点Q 在射线AB 上,且满足PQ AD PC AB =(如图所示)。
平面面积的求法

线等所溯成的区域面积。谯这里不一一介绍。
综上所述,我们看到由特殊曲线湖成的图形面积可由
积分求姆。并且同一图形的瓣积问题逐可以有多攀争不同酶
积分方浚,逶避总络鞍整瑾,我秘迸一步瑾释黎受积分鹃实
质及内涵,为了计算这类区域的面积,我们可归绪为计算特
定结构的和式的极限。同时.我们还可以借助黎曼积分进
一步总络夔线弧妖熬求法、ll|l蘸蠢积憋求法及支体体积的
[收稿日期3zoos-11—16 [作者简介]孛宏(1980--),女。辽宁庄河人,黑龙江幼儿师范i蠹i葶专科学校助理讲师,主要研究穷向为数学与应用数学。 · 132 ·
万方数据
一。疗旧m…m—a曲霄sinz tdt;-2abfT‘c·
一cos2 f)凌;2ab(1一百1 sin2#)|亏=垃兢
1.3 檄坐标系申的面积 若包围平面图形的曲线由极坐标方糨:r;r(口),(a≤口 ≤黟绘窭,篡ee r(鳓褒[a,羽连续,筘一a≤2嚣,麦基线冬巍条 射线疗=a、o=fl所围成的平面翻形s通常称为扇形(如图
1.用定积分求解平面面积 1.1 直角坐标系中的面积
一般情况下,由两条连续的藏线Y一五(z)程Y一 兵(茗)及直线z=a,x—b(a<酗鳜嚣憨乎覆匿影,其嚣积
谛舞公式A=|。阪(工)一苁(烹>鼯。(鞠踅1)
佩一
一l,\LLu x
y。f,∞
j,4
y-)d
‰ 拶j t l
l y_i / l。
O
j
露l
霉2
1帕
4)。则扇形的面积A一÷I‘r2(口)棚.
铡4求双纽线 rz 5 a2 cos2。(Ⅱ>O) 嗣成区域(如图5)的
八胁口。 Y
聋
哆r
\\ 衫 \./f
第七章平面直角坐标系常考题型

平面直角坐标系常考题型一选择题1.若点P(x,y)在第三象限,且点P到x轴的距离为3,到y轴的距离为2,则点P的坐标是( )A.(-2,-3)B.(-2,3)C.(2,-3)D.(2,3)2.若点A(2,m)在x轴上,则点B(m﹣1,m+1)在( )A.第一象限B.第二象限C.第三象限D.第四象限3.一个长方形在平面直角坐标系中,三个顶点的坐标分别是(-1,-1)、(-1,2)、(3,-1),则第四个顶点的坐标是( )A.(2,2)B.(3,2)C.(3,3)D.(2,3)4.若点A(m,n)在第二象限,那么点B(-m,│n│)在( )A.第一象限B.第二象限;C.第三象限D.第四象限5.已知点P(x,y),且,则点P在( )A.第一象限B.第二象限C.第三象限D.第四象限7.如图,在5×4的方格纸中,每个小正方形边长为1,点O,A,B在方格纸的交点(格点)上,在第四象限内的格点上找点C,使三角形ABC的面积为3,则这样的点C共有( )A.2个B.3个C.4个D.5个填空题1.已知点A(0,1),B(0 ,2),点C在x轴上,且S三角形ABC=2,则点C的坐2.在平面直角坐标系中,点C(3,5),先向右平移了5个单位,再向下平移了33.若A(a,b)在第二、四象限的角平分线上,a与b的关系是_________.解题技巧专题:平面直角坐标系中的图形面积——代几结合,突破面积及点的存在性问题◆类型一直接利用面积公式求图形的面积1.如图,在平面直角坐标系中,三角形ABC的面积是( )A.2 B.4 C.8 D.6第1题图第2题图2.如图,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),C(-4,3),则三角形ABC的面积为________.◆类型二利用分割法求图形的面积3.如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2),则四边形ABCO的面积为________.4.观察下图,图中每个小正方形的边长均为1,回答以下问题:【方法14】(1)写出多边形ABCDEF各个顶点的坐标;(2)线段BC,CE的位置各有什么特点?(3)求多边形ABCDEF的面积.◆类型三利用补形法求图形的面积5.在如图所示的正方形网格中,每个小正方形的边长均为1,三角形ABC 的三个顶点恰好是正方形网格的格点.【方法14】(1)写出三角形ABC各顶点的坐标;(2)求出此三角形的面积.◆类型四与图形面积相关的点的存在性问题6.(2017·定州市期中)如图,A(-1,0),C(1,4),点B在x轴上,且AB =3.(1)求点B的坐标;(2)求三角形ABC的面积;(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.难点探究专题:平面直角坐标系中动点问题——掌握不同规律,以不变应万变◆类型一沿坐标轴方向运动的点的坐标规律探究1.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2016次运动后,动点P的坐标是________.2.(2017·阿坝州中考)如图,在平面直角坐标系中,一动点从原点O出发,沿着箭头所示方向,每次移动1个单位,依次得到点P1(0,1),P2(1,1),P3(1,0),P4(1,-1),P5(2,-1),P6(2,0),…,则点P2017的坐标是________.3.如图,在直角坐标系中,第一次将三角形OAB变换成三角形OA1B1,第二次将三角形OA1B1变换成三角形OA2B2,第三次将三角形OA2B2变换成三角形OA3B3……已知A(1,3),A1(2,3),A2(3,3),A3(4,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)仔细观察每次变换前后的三角形有何变化,找出规律,按此变换规律将三角形OA3B3变换成三角形OA4B4,则A4的坐标是_________,B4的坐标是_________ ;(2)若按第(1)题的规律将三角形OAB进行了n次变换,得到三角形OAn Bn,比较每次变换中三角形顶点坐标有何变化,找出规律,请推测:An的坐标是_________,Bn的坐标是_________.◆类型二绕原点呈“回”字形运动的点的坐标规律探究1.如图,一个质点在第一象限及x轴、y轴上运动,在第一秒时,它从原点(0,0)运动到(0,1),然后接着按图中箭头所示方向运动,即(0,0)→(0,1)→(1,1)→(1,0)•••,且每秒移动一个单位,那么第80秒时质点所在位置的坐标是( )A.(0,9)B.(9,0)C.(0,8)D.(8,0)2.将自然数按以下规律排列:第一列第二列第三列第四列第五列表中数2在第二行,第一列,与有序数对(2,1)对应;数5与(1,3)对应;数14与(3,4)对应;根据这一规律,数2014对应的有序数对为.。
人教版七年级数学下册解题技巧专题

人教版七年级数学下册解题技巧专题目录:目录:【专题一】平行线中作辅助线的方法【专题一】平行线中作辅助线的方法【专题二】相交线与平行线中的思想方法【专题三】开方运算及无理数判断中的易错题【专题四】平面直角坐标系中的图形面积【专题五】平面直角坐标系中的变化规律【专题六】解二元一次方程组【专题六】解二元一次方程组【专题七】一元一次不等式(组)与学科内知识的综合【专题八】一元一次不等式(组)中含字母系数的问题【专题一】平行线中作辅助线的方法——形成思维定式,快速解题◆类型一类型一 含一个拐点的平行线问题含一个拐点的平行线问题 1.(2017·南充中考)如图,直线a ∥b ,将一个直角三角尺按如图所示的位置摆放.若∠1=58°,则∠2的度数为( ) A .30°B .32°C .42°D .58°第1题图 第2题图题图2.(2017·潍坊中考)如图,∠BCD =90°,AB ∥DE ,则∠α与∠β满足( ) A .∠α+∠β=180°B .∠β-∠α=90°C .∠β=3∠αD .∠α+∠β=90° 3.阅读下列解题过程,然后解答后面的问题.如图①,已知AB ∥CD ,∠B =35°,∠D =32°,求∠BED 的度数.的度数. 解:过E 作EF ∥AB .∵AB ∥CD ,∴CD ∥EF .∵AB ∥EF ,∴∠1=∠B =35°35°..又∵CD ∥EF ,∴∠2=∠D =32°,∴∠BED =∠1+∠2=35°+32°=67°67°. . 如图②、如图②、图③,图③,图③,是明明设计的智力拼图玩具的一部分,是明明设计的智力拼图玩具的一部分,是明明设计的智力拼图玩具的一部分,现在明明遇到两个问现在明明遇到两个问题,请你帮他解决.题,请你帮他解决.(1)如图②,已知∠D =30°,∠ACD =65°,为了保证AB ∥DE ,∠A 应多大?应多大? (2)如图③,要使GP ∥HQ ,则∠G ,∠GFH ,∠H 之间有什么关系?之间有什么关系?◆类型二类型二 含多个拐点的平行线问题含多个拐点的平行线问题4.如图,已知AB ∥DE ,∠ABC =70°,∠CDE =140°,则∠BCD 的大小为( ) A .20°B .30°C .40°D .70°第4题图 第5题图题图5.如图,直线l 1∥l 2,∠α=∠β,∠1=40°,则∠2的度数为________. 6.如图,给出下列三个论断:①∠B +∠D =180°;②AB ∥CD ;③BC ∥DE .请你以其中两个论断作为已知条件,请你以其中两个论断作为已知条件,填入“已知”栏中,填入“已知”栏中,以剩余一个论断作为结论,填入“结论”栏中,使之成为一道由已知可得到结论的题目,并解答该题.已知:______________,结论:______________. 解:解:7.如图①,AB ∥CD ,EOF 是直线AB ,CD 间的一条折线.间的一条折线. (1)试说明:∠EOF =∠BEO +∠DFO ;(2)如果将折一次改为折两次,如图②,则∠BEO ,∠EOP ,∠OPF ,∠PFC 之间会满足怎样的数量关系?并说明理由.【专题二】相交线与平行线中的思想方法——明确解题思想,体会便捷渠道◆类型一方程思想类型一 方程思想1.如图,直线AB,CD相交于点O,∠AOC=60°,OE把∠BOD分成两部分,且∠BOE∶∠EOD=1∶2,则∠AOE的度数为() A.180°B.160°C.140°D.120°题图第1题图第2题图2.(2017·无棣县期末)如图,直线AB,CD相交于点O,OE平分∠BOD,OF平分∠COB,∠AOD∶∠EOD=4∶1,则∠AOF的度数为________.3.如图,已知FC∥AB∥DE,∠α∶∠D∶∠B=2∶3∶4.求∠α,∠D,∠B 的度数.的度数.4.(2017·启东市期末)如图,AD∥BC,BE平分∠ABC交AD于点E,BD平分∠EBC. (1)若∠DBC=30°,求∠A的度数;的度数;(2)若点F在线段AE上,且7∠DBC-2∠ABF=180°,请问图中是否存在与∠DFB相等的角?若存在,请写出这个角,并说明理由;若不存在,请说明理由.由.◆类型二分类讨论思想类型二 分类讨论思想5.若∠α与∠β的两边分别平行,∠α比∠β的3倍少36°,则∠α的度数是() A.18°B.126°C.18°或126°D.以上都不对.以上都不对6.(2017·玄武区期末)在直线MN上取一点P,过点P作射线P A、PB.若P A⊥PB,MPA A=40°,则∠NPB的度数是________________.当∠MP7.(2017·江干区一模)一副直角三角尺按如图①所示方式叠放,现将含45°角的三角尺ADE固定不动,将含30°角的三角尺ABC绕顶点A顺时针转动,使两块三角尺至少有一组边互相平行.如图②,当∠BAD=15°时,BC∥DE,则180°))其他所有可能符合条件的度数为________________.∠BAD(0°<∠BAD<180°8.如图,已知直线l1∥l2,直线l3交l1于C点,交l2于D点,P是线段CD 上的一个动点.当P在直线CD上运动时,请你探究∠1,∠2,∠3之间的关系.之间的关系.第9题图题图第10题图。
专题03 平面直角坐标系(专题详解)(解析版)

专题03 平面直角坐标系专题03 平面直角坐标系 (1)7.1 平面直角坐标系 (2)知识框架 (2)一、基础知识点 (2)知识点1 有序数对 (2)知识点2 平面直角坐标系 (2)知识点3 点的坐标特点 (3)二、典型题型 (6)题型1 有序数对 (6)题型2 平面直角坐标系的概念 (6)题型3 点的坐标的特征 (6)一、点的位置与坐标 (7)二、点的坐标与距离 (8)三、点的坐标与平行于坐标轴的直线(数形结合思想) (8)四、点的坐标与图形的面积 (9)(1)知坐标,求面积 (9)(2)知面积,求坐标(方程思想) (10)(3)分类讨论 (12)三、难点题型 (14)题型1 确定点所在的象限 (14)题型2 点到坐标轴的距离 (14)题型3 探究平面直角坐标系坐标的变化规律 (15)7.2 坐标系的简单运用 (17)知识框架 (17)一、基础知识点 (17)知识点1 用坐标表示地理位置 (17)知识点2 用坐标表示平移 (18)二、典型题型 (20)题型1 用坐标表示地理位置 (20)题型2 用坐标表示平移 (21)一、点的平移 (21)(1)已知点和平移方式,求对应点 (21)(2)已知点和对应点,求平移方式 (21)二、图形的平移 (22)三、难点题型 (23)题型1 动点问题 (23)7.1 平面直角坐标系知识框架{基础知识点{有序数对平面直角坐标系点的坐标的特点典型题型{ 有序数对平面直角坐标系的概念点的坐标的特征{ 点的位置与坐标点的坐标与距离点的坐标与平行于坐标轴的直线(数形结合思想)点的坐标与图形的面积{知坐标,求面积知面积,求坐标(方程思想)分类讨论难点题型{确定点所在的象限点到坐标轴的距离探究平面直角坐标系坐标的变化规律 一、基础知识点知识点1 有序数对1)我们把有顺序的两个数a 与b 组成的数对,用于表示平面中某一确定位置的,叫作有序数对,记作(a ,b )注:①(a ,b )与(b ,a )表达的含义不同,注意有序数对的顺序②在表达有序数对时,一般行在前,列在后。
沪科版八年级上册数学解题技巧精炼专题

沪科版数学解题技巧精炼专题八年级上册目录沪科版八年级上册数学解题技巧精炼专题 (3)解题技巧专题一:平面直角坐标系中的图形面积 (3)◆类型一直接利用面积公式求图形的面积 (3)◆类型二利用分割法求图形的面积 (3)◆类型三利用补形法求图形的面积 (3)◆类型四探究平面直角坐标系中与面积相关的点的存在性 (4)难点探究专题二:平面直角坐标系中点的坐标的变化规律(选做) (5)◆类型一沿坐标轴运动的点的坐标的探究 (5)◆类型二绕原点呈“回”字形运动的点的坐标的探究 (5)◆类型三图形变化的点的坐标的探究 (6)解题技巧专题三:一次函数的图象信息题 (6)◆类型一根据实际问题判断函数图象 (6)◆类型二根据函数图象进行判断 (7)◆类型三一次函数图象与字母系数的关系 (7)难点探究专题四:一次函数与几何的综合问题(选做) (8)◆类型一一次函数与面积问题 (8)◆类型二一次函数与几何图形综合的探究性问题 (9)类比归纳专题五:三角形中内、外角的有关计算 (10)◆类型一直接利用内角和或结合方程思想求角的度数 (10)◆类型二利用外角的性质求角的度数 (11)◆类型三综合内外角求角的度数 (11)◆类型四在三角板或直尺中求角的度数 (11)◆类型五与平行线相结合求角的度数 (12)◆类型六与截取或折叠相关求角的度数 (12)解题技巧专题六:利用全等解决问题的模型与技巧 (13)◆类型一全等三角形的基本模型 (13)◆类型二证明线段间的等量关系 (14)难点探究专题七:动态变化中的三角形全等(选做) (15)◆类型一动点变化与全等三角形 (15)◆类型二图形变换与三角形全等 (15)易错专题八:等腰三角形中易漏解或多解的问题 (16)◆类型一求边长(或周长)时忽略三边关系 (16)◆类型二当腰或底不明时求角度时没有分类讨论 (17)◆类型三三角形的形状不明时与高结合没有分类讨论 (17)难点探究专题九:等腰三角形中辅助线的作法(选做) (17)◆类型一利用“三线合一”作辅助线【方法18】 (17)◆类型二巧用等腰三角形构造全等 (19)◆类型三截长补短构造等腰三角形 (19)模型构建专题十:共顶点的等腰三角形 (20)◆类型一共直角顶点的等腰直角三角形 (20)◆类型二共顶点的等边三角形 (20)类比归纳专题十一:证明线段相等的基本思路 (21)◆类型一已知边的关系或边角关系用全等三角形的性质 (21)◆类型二已知角度、平行关系在同一三角形中用“等角对等边” (21)◆类型三已知线段的垂直平分线或角的平分线+垂直用相应性质 (22)◆类型一求同一顶点的角平分线与高线的夹角的度数 (22)◆类型二求两内角平分线的夹角的度数 (23)◆类型三求一内角平分线与一外角平分线的夹角的度数 (23)◆类型四求两外角平分线的夹角的度数【方法5】 (24)解题技巧专题一:平面直角坐标系中的图形面积参考答案与解析 (25)难点探究专题二:平面直角坐标系中点的坐标的变化规律(选做)参考答案与解析 (26)解题技巧专题三:一次函数的图象信息题参考答案与解析 (27)难点探究专题四:一次函数与几何的综合问题(选做)参考答案与解析 (27)类比归纳专题五:三角形中内、外角的有关计算参考答案与解析 (28)解题技巧专题六:利用全等解决问题的模型与技巧参考答案与解析 (30)难点探究专题七:动态变化中的三角形全等(选做)参考答案与解析 (30)易错专题八:等腰三角形中易漏解或多解的问题参考答案与解析 (32)难点探究专题九:等腰三角形中辅助线的作法(选做)参考答案与解析 (33)模型构建专题十:共顶点的等腰三角形参考答案与解析 (36)类比归纳专题十一:证明线段相等的基本思路参考答案与解析 (37)类比归纳专题十二:与三角形的高、角平分线有关的计算模型参考答案与解析 (38)沪科版八年级上册数学解题技巧精炼专题解题技巧专题1:平面直角坐标系中的图形面积——代几结合,突破面积及点的存在性问题◆类型一直接利用面积公式求图形的面积1.如图,在平面直角坐标系中,△ABC的面积是()A.2 B.4 C.8 D.6第1题图第2题图2.如图,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),C(-4,3),则△ABC 的面积为________.◆类型二利用分割法求图形的面积3.如图,在平面直角坐标系中,A(4,0),B(3,2),C(-2,3),D(-3,0).求四边形ABCD的面积.◆类型三利用补形法求图形的面积4.如图,已知△ABC,点A(-2,1),B(1,-3),C(3,4),求△ABC的面积.◆类型四 探究平面直角坐标系中与面积相关的点的存在性5.如图,在平面直角坐标系中,点A (4,0),B (3,4),C (0,2).(1)求S 四边形ABCO ;(2)连接AC ,求S △ABC ;(3)在x 轴上是否存在一点P ,使S △P AB =10?若存在,请求点P 的坐标.6.如图,在平面直角坐标系中,已知A (0,a ),B (b ,0),C (b ,c )三点,其中a 、b 、c满足关系式|a -2|+(b -3)2=0和(c -4)2≤0.(1)求a 、b 、c 的值;(2)如果在第二象限内有一点P ⎝⎛⎭⎫m ,12,请用含m 的式子表示四边形ABOP 的面积; (3)在(2)的条件下,是否存在点P ,使得四边形ABOP 的面积与△ABC 的面积相等?若存在,求出点P 的坐标;若不存在,请说明理由.难点探究专题二:平面直角坐标系中点的坐标的变化规律(选做)——掌握不同规律,以不变应万变◆类型一沿坐标轴运动的点的坐标的探究1.如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2)……按这样的运动规律,经过第2016次运动后,动点P的坐标是________.2.如图,平面直角坐标系上的点A(1,0)第1次跳至点A1(-1,1),第2次跳至点A2(2,1),第3次跳至点A3(-2,2),第4次跳至点A4(3,2)……依此规律跳下去,点A第100次跳至的点A100的坐标是________.第2题图第3题图3.★如图,一个动点在第一象限内及x轴、y轴上运动,第1分钟从原点运动到(1,0),第2分钟内从(1,0)运动到(1,1),然后它接着按图中箭头所示的方向来回运动(在第一象限内运动时,运动方向与x轴或y轴平行),且每分钟移动1个单位长度.(1)当动点所在位置是(2,2)时,所经过的时间是________;(2)在第2016分钟时,这个动点所在位置的坐标是________.◆类型二绕原点呈“回”字形运动的点的坐标的探究4.(甘孜州中考)如图,正方形A1A2A 3A4,A5A6A7A8,A9A10A11A12,…(每个正方形从第三象限的顶点开始,按顺时针方向顺序,依次记为A1,A2,A3,A4;A5,A6,A7,A8;A9,A10,A11,A12;…)的中心均在坐标原点O,各边均与x轴或y轴平行,若它们的边长依次是2,4,6,…则顶点A20的坐标为________.第4题图第5题图5.★如图,一甲虫从原点出发按图示方向作折线运动,第1次从原点到A1(1,0),第2次运动到A2(1,1),第3次运动到A3(-1,1),第4次运动到A4(-1,-1),第5次运动到A5(2,-1)……则第2015次运动到的点A2015的坐标是________.◆类型三图形变化的点的坐标的探究6.如图,长方形ABCD的两边BC、CD分别在x轴、y轴上,点C与原点重合,点A(-1,2),将长方形ABCD沿x轴向右翻滚,经过1次翻滚点A对应点记为A1,经过2次翻滚点A对应点记为A2……依此类推,经过5次翻滚后点A对应点A5的坐标为() A.(5,2) B.(6,0) C.(8,0) D.(8,1)7.如图,在直角坐标系中,第1次将△OAB变换成△OA1B1,第2次将△OA1B1变换成△OA2B2,第3次将△OA2B2变换成△OA3B3.已知A(1,3),A1(2,3),A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),B3(16,0).(1)观察每次变换后的三角形有何变化,找出规律,按此变换规律再将△OA3B3变换成△OA4B4,则A4的坐标是________,B4的坐标是________;(2)若按第(1)题找到的规律将△OAB进行了n次变换,得到△OA n B n,比较每次变换中三角形顶点坐标有何变化,找出规律,推测A n的坐标是________,B n的坐标是__________.解题技巧专题三:一次函数的图象信息题——数形结合,快准解题◆类型一根据实际问题判断函数图象1.小明所在学校离家距离为2千米,某天他放学后骑自行车回家,行驶了5分钟后,因故停留10分钟,继续骑了5分钟到家.下面哪一个图象能大致描述他回家过程中离家的距离s(千米)与所用时间t(分钟)之间的关系()◆类型二根据函数图象进行判断2.小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程s(km)与北京时间t(时)的函数图象如图所示.根据图象得到下列结论,其中错误的是() A.小亮骑自行车的平均速度是12km/hB.妈妈比小亮提前0.5小时到达姥姥家C.妈妈在距家12km处追上小亮D.9:30妈妈追上小亮第2题图第3题图3.某复印店复印收费y(元)与复印面数x(面)的函数图象如图所示,从图象中可以看出,复印超过100面的部分,每面收费()A.0.2元B.0.4元C.0.45元D.0.5元◆类型三一次函数图象与字母系数的关系4.如图为一次函数y=kx+b(k≠0)的图象,则下列正确的是()A.k>0,b>0 B.k>0,b<0 C.k<0,b>0 D.k<0,b<05.直线y=ax+b经过第一、二、四象限,则直线y=bx-a的图象只能是图中的()6.下列表示一次函数y=mx+n与正比例函数y=mnx(m,n为常数,且mn≠0)的图象正确的是()7.若函数y=(a-2)x+b-3在直角坐标系中的图象如图所示.化简:|b-a|-|3-b|-|2-a|=________.8.如图,一次函数y=(m-3)x-m+1的图象分别与x轴正半轴、y轴负半轴相交于A、B.(1)求m的取值范围;(2)若该一次函数的图象向上平移4个单位长度后可得某正比例函数的图象.试求这个正比例函数的解析式.难点探究专题四:一次函数与几何的综合问题(选做)◆类型一一次函数与面积问题一、由一次函数图象求面积1.直线y=2x-4与两坐标轴所围成的三角形面积等于()A.8 B.6 C.4 D.162.已知直线l1:y1=2x+3与直线l2:y2=kx-1交于A点,A点横坐标为-1,且直线l1与x轴交于B点,与y轴交于D点,直线l2与y轴交于C点.(1)求出A点的坐标及直线l2的解析式;(2)连接BC,求出S△ABC.二、由面积求一次函数关系式3.若直线y =-2x +b (b >0)与两坐标轴围成的三角形的面积是1,则该直线的解析式为__________.4.在平面直角坐标系中,点O 是坐标原点,过点A (1,2)的直线y =kx +b 与x 轴交于点B ,且S △AOB =4.则该直线的解析式为____________________.三、一次函数上的动点与面积问题5.(盐城中考)如图,在边长为2的正方形ABCD 中剪去一个边长为1的小正方形CEFG ,动点P 从点A 出发,沿A →D →E →F →G →B 的路线绕多边形的边匀速运动到点B 时停止(不含点A 和点B ),则△ABP 的面积S 随着时间t 变化的函数图象大致是( )6.如图所示,直线y =kx -1与x 轴、y 轴分别交于B 、C 两点,OB OC =12. (1)求B 点坐标和k 的值;(2)若点A (x ,y )是直线y =kx -1在第一象限内的部分上的一个动点,试写出在点A 运动过程中,三角形AOB 的面积S 与x 的函数表达式;(3)探索:当动点A (x ,y )可在直线y =kx -1上任意移动时,若S △AOB =14,试确定点A 的位置.【易错4】◆类型二 一次函数与几何图形综合的探究性问题7.如图所示,直线y =x +1与y 轴交于点A 1,以OA 1为边作正方形OA 1B 1C 1,然后延长C 1B 1与直线y =x +1交于点A 2,得到第1个梯形A 1OC 1A 2;再以C 1A 2为边作正方形C 1A 2B 2C 2,同样延长C 2B 2与直线y =x +1交于点A 3得到第2个梯形A 2C 1C 2A 3;再以C 2A 3为边作正方形C 2A 3B 3C 3,延长C 3B 3,得到第3个梯形……则第2个梯形A 2C 1C 2A 3的面积是________;第n (n 是正整数)个梯形的面积是____________(用含n 的式子表示).第7题图 第8题图8.★如图,直角坐标系中,点P (t ,0)是x 轴上的一个动点,过点P 作y 轴的平行线,分别与直线y =12x ,直线y =-x 交于A 、B 两点,以AB 为边向右侧作正方形ABCD .(1)当t =2时,正方形ABCD 的周长是________;(2)当点(2,0)在正方形ABCD 内部时,t 的取值范围是__________________.类比归纳专题五:三角形中内、外角的有关计算◆类型一 直接利用内角和或结合方程思想求角的度数1.△ABC 中,∠A =60°,∠C =70°,则∠B 的度数是( ) A .50° B .60° C .70° D .90°2.(太和县期末)在△ABC 中,已知∠A =2∠B =3∠C ,则△ABC 是( ) A .锐角三角形 B .直角三角形 C .钝角三角形 D .形状无法确定 3.如图,在△ABC 中,∠C =∠ABC =2∠A ,BD 是AC 边上的高,则∠DBC =________度.4.如图,在△ABC 中,AD ⊥BC ,AE 平分∠BAC ,∠B =70°,∠C =30°. (1)∠BAE 的度数为________; (2)∠DAE 的度数为________;(3)探究:小明认为如果只知道∠B -∠C =40°,也能得出∠DAE 的度数?你认为可以吗?若能,请你写出求解过程;若不能,请说明理由.【方法10】◆类型二利用外角的性质求角的度数5.(柳州中考)如图,图中∠1的大小等于()A.40°B.50°C.60°D.70°第5题图第6题图6.如图,BD 、CD分别平分∠ABC和∠ACE,∠A=60°,则∠D的度数是【方法10】()A.20°B.30°C.40°D.60°◆类型三综合内外角求角的度数7.如图,∠B=20°,∠A=∠C=40°,则∠CDE的度数为________.第7题图第8题图8.(和县期末)如图,在△ABC中,D是AB上一点,E是AC上一点,BE,CD相交于F,∠A=70°,∠ACD=20°,∠ABE=28°,则∠CFE的度数为()A.62°B.68°C.78°D.90°9.★如图,△ABC的∠ABC、∠ACB的外角的平分线交于点P.(1)若∠ABC=50°,∠A=70°,求∠P的度数;(2)若∠A=68°,求∠P的度数;(3)根据以上计算,试写出∠P与∠A的数量关系.◆类型四在三角板或直尺中求角的度数10.如图所示,将三角形的直角顶点放在直尺的一边上,∠1=30°,∠3=20°,则∠2=________.第10题图第11题图11.将一副三角板按如图所示摆放,图中∠α的度数是()A.120°B.105°C.90°D.75°12.一副三角板如图所示叠放在一起,则图中∠α的度数是________.◆类型五与平行线相结合求角的度数13.如图,AB∥CD,直线PQ分别交AB、CD于点F、E,EG是∠DEF的平分线,交AB于点G.若∠PF A=40°,那么∠EGB 的度数为()A.80°B.100°C.110°D.120°第13题图第14题图14.如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=45°,∠BDC=60°,则∠BDE=________度.15.如图,A点在B点的北偏东40°方向,C点在B点的北偏东75°方向,A点在C点的北偏西50°方向.(1)试证明△ABC为直角三角形;(2)求∠ACB的度数.◆类型六与截取或折叠相关求角的度数16.如图,Rt△ABC中,∠ACB=90°,∠A=52°,将其折叠,使点A落在边CB上A′处,折痕为CD,则∠A′DB=________.第16题图第17题图17.在△ABC中,∠B=70°,若沿图中虚线剪去∠B,则∠1+∠2等于________.18.如图.(1)将△ABC纸片沿DE折叠成图①,此时点A落在四边形BCDE内部,则∠A与∠1、∠2之间有一种数量关系保持不变,请找出这种数量关系并说明理由;(2)若折成图②或图③,即点A落在BE或CD上时,分别写出图②中∠DAE与∠2、图③中∠DAE与∠1之间的关系式(不必证明);(3)若折成图④,写出∠A与∠1、∠2之间的关系式(不必证明).解题技巧专题六:利用全等解决问题的模型与技巧——明模型,先观察,再猜想,后证明◆类型一全等三角形的基本模型1.如图,AC=AD,BC=BD,∠A=50°,∠B=90°,则∠C=________.【方法12】第1题图第2题图第3题图2.如图,锐角△ABC的高AD、BE相交于F,若BF=AC,BC=7,CD=2,则AF的长为________.3.如图,点A、D、C、E在同一条直线上,AB∥EF,AB=EF,∠B=∠F,AE=10,AC=6,则CD的长为()A.2 B.4 C.4.5 D.34.如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD交AC于点F.(1)求证:△BAD≌△CAE;(2)猜想BD、CE有何特殊位置关系,并说明理由.◆类型二证明线段间的等量关系一、等线段代换5.如图,Rt△ABC中,AB=AC,∠BAC=90°,直线l为经过点A的任一直线,BD⊥l 于D,CE⊥l于E,若BD>CE,试问:(1)AD与CE的大小关系如何?请说明理由;(2)线段BD,DE,CE之间的数量关系如何?并说明理由.【方法13】二、截长补短法6.★如图,在四边形ABDE中,C是BD边的中点,若AC平分∠BAE,∠ACE=90°,猜想线段AE、AB、DE的长度满足的数量关系,并证明.【方法12】三、倍长中线法7.★在△ABC中,AB=8,AC=6,则BC边上的中线AD的取值范围是()A.6<AD<8 B.2<AD<14 C.1<AD<7 D.无法确定难点探究专题七:动态变化中的三角形全等(选做)◆类型一动点变化与全等三角形1.如图,CA⊥AB,垂足为点A,AB=8厘米,AC=4厘米,射线BM⊥AB,垂足为点B,一动点E从A点出发以2厘米/秒的速度沿射线AN运动,点D为射线BM上一动点,随着E点运动而运动,且始终保持ED=CB,当点E运动______________秒时,△DEB与△BCA 全等.2.★如图,点A的坐标为(-2,0),P为y轴负半轴上一个动点,当点P向y轴负半轴下方运动时,以P为顶点作△APD,并使P A=PD,∠APD=90°,过点D作DE⊥x轴于E点,求OP-DE的值.【方法13】◆类型二图形变换与三角形全等3.如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.(1)求证:△BCD≌△FCE;(2)若EF∥CD,求∠BDC的度数.4.如图甲,已知A 、E 、F 、C 在一条直线上,AE =CF ,过E 、F 分别作DE ⊥AC ,BF ⊥AC ,且AB =CD .(1)试问OE =OF 吗?请说明理由;(2)若△DEC 沿AC 方向平移到如图乙的位置,其余条件不变,上述结论是否仍成立?请说明理由.5.★如图,将Rt △ABC 沿斜边翻折得到△ADC ,点E ,F 分别为DC ,BC 边上的点,且∠EAF =12∠DAB .试猜想DE ,BF ,EF 之间有何数量关系,并证明你的猜想.【方法12】易错专题八:等腰三角形中易漏解或多解的问题——易错归纳,各个击破◆类型一 求边长(或周长)时忽略三边关系1.(盐城中考)若一个等腰三角形的两边长分别是2和5,则它的周长为( ) A .12 B .9C .12或9D .9或72.学习了三角形的有关问题后,王老师请同学们交流这样一个问题:“已知一个等腰三角形的周长是12,其中一条边长为3,求另外两条边的长.”同学们经过片刻思考和交流后,小明同学举手讲:“另两条边长为3,6或4.5,4.5”.你认为小明回答是否正确:________,理由是______________________.3.已知一个等腰三角形的两边长a 、b 满足方程组⎩⎪⎨⎪⎧4a -3b =11,2a +b =13.(1)求a 、b 的值;(2)求这个等腰三角形的周长.4.已知等腰三角形ABC中,一腰AC上的中线BD将三角形的周长分成9cm和15cm 两部分,求这个三角形的腰长和底边的长.【易错8】◆类型二当腰或底不明时求角度时没有分类讨论5.已知等腰三角形的一个内角为50°,则这个等腰三角形的顶角为()A.50°B.80°C.50°或80°D.40°或65°6.等腰三角形的一个外角是60°,则它的顶角的度数是________.7.★若一个大的等腰三角形能被分割为两个小等腰三角形,试求该大等腰三角形顶角的度数(要求画出相应图形,写出求解过程).◆类型三三角形的形状不明时与高结合没有分类讨论8.等腰三角形的一内角为80°,则它的一腰上的高与底边的夹角的度数是________.【易错8】9.等腰三角形一腰上的高与另一腰的夹角的度数是20°,试求这个等腰三角形各内角的度数.【易错8】难点探究专题九:等腰三角形中辅助线的作法(选做)——形成精准解题思维◆类型一利用“三线合一”作辅助线【方法18】一、已知等腰作垂线(或中线、角平分线)1.如图,在△ABC 中,AB =AC ,AE ⊥BE 于点E ,且BE =12BC ,若∠EAB =20°,则∠BAC =________.2.(庐江县期末)如图,△ABC 是等边三角形,D 是AC 的中点,E 是BC 延长线上的一点,CE =CD ,DM ⊥BC ,垂足为M .求证:M 是BE 的中点.3.如图,在△ABC 中,AB =AC ,点E 在CA 的延长线上,∠E =∠AFE .求证:EF ⊥BC .二、构造等腰三角形4.如图,△ABC 的面积为1cm 2,AP 垂直∠ABC 的平分线BP 于P ,则△PBC 的面积为( )A .0.4cm 2B .0.5cm 2C .0.6cm 2D .0.7cm 25.★如图,在△ABC 中,AB =AC ,点P 从点B 出发沿线段BA 移动,同时,点Q 从点C 出发沿线段AC 的延长线移动,已知点P 、Q 移动的速度相同,PQ 与直线BC 相交于点D .(1)如图①,当点P 为AB 的中点时,求证:PD =QD ;(2)如图②,过点P 作直线BC 的垂线,垂足为E ,当点P 、Q 在移动的过程中,线段BE 、DE 、CD 中是否存在长度保持不变的线段?请说明理由.◆类型二巧用等腰三角形构造全等6.★如图,△ABC是等边三角形,△BDC是等腰三角形,BD=CD,∠BDC=120°,以点D为顶点作一个60°的角,角的两边分别交AB、AC于M、N两点,连接MN.求证:MN=BM+NC.◆类型三截长补短构造等腰三角形7.★如图,△ABC中,∠C=2∠A,BD平分∠ABC交AC于D.求证:AB=BC+CD.8.★如图,CE、CB分别是△ABC、△ADC的中线,且AB=AC.求证:CD=2CE.模型构建专题十:共顶点的等腰三角形——明模型,记结论◆类型一共直角顶点的等腰直角三角形1.如图,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE =90°,点A、D、E 在同一直线上,CM为△DCE中DE边上的高,连接BE.(1)求∠AEB的度数;(2)探究线段CM、AE、BE之间的数量关系,并说明理由.◆类型二共顶点的等边三角形2.如图,在四边形ABCD中,AB∥CD,AB=CD,AD∥BC,AD=BC,分别延长DC,BC到点E,F,使得△BCE和△CDF都是等边三角形.(1)求证:AE=AF;(2)求∠EAF的度数.类比归纳专题十一:证明线段相等的基本思路——分类型、理条件、定思路◆类型一已知边的关系或边角关系用全等三角形的性质1.如图,在四边形ABCD中,∠B+∠ADC=180°,BC=DC,延长AD到E点,使DE=AB,连接AC,CE.求证:AC=CE.2.★如图,点D在等边三角形ABC的边AB上,点F在边AC上,连接DF并延长交BC的延长线于点E,EF=FD,求证:AD=CE.【方法19】◆类型二已知角度、平行关系在同一三角形中用“等角对等边”3.如图,在△ABC中,CD与CF分别是△ABC的内角、外角平分线,DF∥BC交AC 于点E.求证:DE=EF.4.如图,在△ABC中,∠ACB=2∠B,∠BAC的平分线AD交BC于D,过C作CN⊥AD 交AD于H,交AB于N.(1)求证:AN=AC;(2)试判断BN与CD的数量关系,并说明理由.◆类型三已知线段的垂直平分线或角的平分线+垂直用相应性质5.如图,△ABC中,∠CAB的平分线与BC的垂直平分线DG相交于D,过点D作DE⊥AB,DF⊥AC,求证:BE=CF.6.★如图,∠AOB=90°,OM是∠AOB的平分线,将三角板的直角顶点P在射线OM 上滑动,两直角边分别与OA、OB交于C、D,PC和PD有怎样的数量关系?请说明理由.类比归纳专题十二:与三角形的高、角平分线有关的计算模◆类型一求同一顶点的角平分线与高线的夹角的度数1.如图,AD,AE分别是△ABC的高和角平分线.(1)已知∠B=40°,∠C=60°,求∠DAE的度数;(2)设∠B=α,∠C=β(α<β),请用含α,β的代数式表示∠DAE,并证明.◆类型二 求两内角平分线的夹角的度数2.如图,△ABC 中,∠ABC 和∠ACB 的平分线交于点O .若∠BOC =120°,则∠A =_____.3.如图,△ABC 中,点P 是∠ABC ,∠ACB 的平分线的交点. (1)若∠A =80°,求∠BPC 的度数.(2)有位同学在解答(1)后得出∠BPC =90°+12∠A 的规律,你认为正确吗?请给出理由.◆类型三 求一内角平分线与一外角平分线的夹角的度数4.如图,在△ABC 中,BA 1平分∠ABC ,CA 1平分∠ACD ,BA 1,CA 1相交于点A 1. (1)求证:∠A 1=12∠A ;(2)如图,继续作∠A 1BC 和∠A 1CD 的平分线交于点A 2,得∠A 2;作∠A 2BC 和∠A 2CD 的平分线交于点A 3,得∠A 3……依此得到∠A 2017,若∠A =α,则∠A 2017=_____________.◆类型四求两外角平分线的夹角的度数【方法5】5.(1)如图,BO平分△ABC的外角∠CBD,CO平分△ABC的外角∠BCE,则∠BOC 与∠A的关系为____________;(2)请就(1)中的结论进行证明.解题技巧专题1:平面直角坐标系中的图形面积参考答案与解析1.B 2.7.53.解:分别过C 作CE ⊥x 轴于E ,过B 作BF ⊥x 轴于F .由题意,得DE =1,CE =3,BF =2,AF =1,EF =5.S四边形ABCD =S △CDE +S梯形CEFB +S △ABF =12×1×3+12×(3+2)×5+12×1×2=15.4.解:过点A 作x 轴的垂线,过点B 作y 轴的垂线,过点C 分别作x 轴、y 轴的垂线,交于点D ,E ,F 三点,如图所示.由题意,得CD =EF =5,DE =CF =7,AD =3,CD =5,AE =4,BE =3,BF =2.方法一:S △ABC =S长方形CDEF -S △ACD -S △ABE -S △BCF =CD ·DE -12AD ·CD -12AE ·BE -12BF ·CF =5×7-12×3×5-12×4×3-12×2×7=292.方法二:S △ABC =S梯形BCDE -S △ACD -S △ABE =12(BE +CD )·DE -12AD ·CD -12AE ·BE =12×(3+5)×7-12×3×5-12×4×3=292.方法三:S △ABC =S 梯形CAEF -S △ABE -S △BCF =12(AE +CF )·EF -12AE ·BE -12BF ·CF =12×(4+7)×5-12×4×3-12×2×7=292.方法点拨:本题运用了补形法,对于平面直角坐标系中的三角形,可以通过作垂线,运用补形法将三角形补形,将它转化为便于计算面积的图形,通过这些图形面积的和差关系来求原三角形的面积.5.解:(1)过点B 作BD ⊥OA 于点D .由题意,得OC =2,OD =3,AD =1,BD =4.S 四边形ABCO=S 梯形BCOD +S △ABD =12×(2+4)×3+12×1×4=11;(2)S △ABC =S 四边形ABCO -S △AOC =11-12×2×4=7;(3)存在.设点P 的坐标为(x ,0),则AP =|4-x |,由题意,得12×4×|4-x |=10,∴|4-x |=5,∴x =9或x =-1,∴点P 的坐标为(9,0)或(-1,0).6.解:(1)∵|a -2|+(b -3)2=0,(c -4)2≤0,∴a =2,b =3,c =4;(2)∵P ⎝⎛⎭⎫m ,12在第二象限,∴m <0.S 四边形ABOP =S △ABO +S △AOP =12OA ·OB +12OA ·|m |=12×2×3+12×2×(-m )=3-m ;(3)存在.由B (3,0),C (3,4),A (0,2),得S △ABC =12×3×4=6.由(2)可知S 四边形ABOP =3-m ,∴3-m =6,∴m =-3,∴点P 的坐标为⎝⎛⎭⎫-3,12. 难点探究专题二:平面直角坐标系中点的坐标的变化规律(选做)参考答案与解析1.(2016,0) 解析:结合图象可知,当运动次数为偶数次时,P 点运动到x 轴上,且横坐标与运动次数相等.∵2016为偶数,∴运动2016次后,动点P 的坐标是(2016,0).2.(51,50) 解析:由题意,得A 100在第一象限,纵坐标为1002=50,横坐标比纵坐标大1.∴点A 100的坐标为(51,50).3.(1)6分钟(2)(44,8) 解析:观察图形得第12分钟坐标为(1,0),第22分钟坐标为(0,2),第32分钟坐标为(3,0),第42分钟坐标为(0,4)……∵2016<452=2025,第2025分钟坐标为(45,0),第2024分钟坐标为(44,0),2024-2016=8,∴在第2016分钟时,这个动点所在位置的坐标是(44,8).4.(5,-5) 解析:∵20÷4=5,∴点A 20在第四象限.∵点A 4所在正方形的边长为2,∴点A 4的坐标为(1,-1),同理可得点A 8的坐标为(2,-2),点A 12的坐标为(3,-3),∴点A 20的坐标为(5,-5).5.(-504,504) 解析:观察图形序号(大于4),被4除余数为1的点在第四象限,被4除余数为2的点在第一象限,余数为3的点在第二象限,能被4整除的点在第三象限.2015被4除商为503,余数为3.由A 3(-1,1),A 7(-2,2),可得A 2015(-504,504).6.D 解析:由题意可得下图,经过5次翻滚后点A 对应点A 5的位置如图所示,故A 5的坐标为(8,1).故选D.7.(1)(16,3) (32,0) (2)(2n ,3) (2n +1,0)解析:(1)∵A 1(2,3),A 2(4,3),A 3(8,3),∴A 4的横坐标为24=16,纵坐标为3.故A 4的坐标为(16,3).∵B 1(4,0),B 2(8,0),B 3(16,0),∴B 4的横坐标为25=32,纵坐标为0.故点B 4的坐标为(32,0);(2)由A 1(2,3),A 2(4,3),A 3(8,3),可以发现它们各点坐标的关系为横坐标是2n ,纵坐标都是3.故A n 的坐标为(2n ,3).由B 1(4,0),B 2(8,0),B 3(16,0),可以发现它们各点坐标的关系为横坐标是2n +1,纵坐标都是0.故B n 的坐标为(2n +1,0).解题技巧专题三:一次函数的图象信息题参考答案与解析1.D2.D 解析:根据图象知9:00妈妈追上小亮,故D 选项错误. 3.B 4.C5.B 解析:由直线y =ax +b 经过第一、二、四象限,得a <0,b >0,∴-a >0.∴y =bx -a 的图象经过第一、二、三象限.故选B.6.A 解析:当mn >0时,直线y =mnx 经过第一、三象限,m ,n 同号.m ,n 同正时,直线y =mx +n 经过第一、二、三象限;m ,n 同负时,直线y =mx +n 经过第二、三、四象限,故B 、D 错;当mn <0时,直线y =mnx 经过第二、四象限,mn 异号.m >0,n <0时,直线y =mx +n 经过第一、三、四象限;m <0,n >0时,直线y =mx +n 经过第一、二、四象限,故A 正确,C 错误.故选A.7.1 解析:由图可知y =(a -2)x +b -3的图象经过第一、二、四象限,∴a -2<0,b -3>0,∴a <2,b >3.∴|b -a |-|3-b |-|2-a |=b -a -(b -3)-(2-a )=1.8.解:(1)由图可知y =(m -3)x -m +1经过第一、三、四象限,∴⎩⎪⎨⎪⎧m -3>0,-m +1<0,∴m >3;(2)将y =(m -3)x -m +1的图象向上平移4个单位得y =(m -3)x -m +5,由题意,得-m +5=0,∴m =5,∴这个正比例函数的解析式为y =2x .难点探究专题四:一次函数与几何的综合问题(选做)参考答案与解析1.C2.解:(1)当x =-1时,y 1=-2+3=1,∴A 点的坐标为(-1,1).∵直线l 2:y 2=kx -1经过点A (-1,1),∴1=-k -1,∴k =-2,∴y 2=-2x -1;(2)∵直线y 1=2x +3与y 轴交于D (0,3),直线y 2=-2x -1与y 轴交于C (0,-1),∴CD =4,∴S △ADC =12×4×1=2.∵直线y 1=2x +3与x 轴交于B ⎝⎛⎭⎫-32,0,∴S △BCD =12×4×32=3,∴S △ABC =S △BCD -S △ACD =3-2=1.3.y =-2x +24.y =-23x +83或y =25x +85 解析:设B 点坐标为(m ,0),则S △AOB =12·|m |·2=|m |.又∵S △AOB=4,∴|m |=4,∴m =±4.当m =4时,由直线y =kx +b 过点A (1,2),B (4,0),得⎩⎪⎨⎪⎧2=k +b ,0=4k +b ,。
平面直角坐标系中三角形面积的求法(例题及对应练习)

例析平面直角坐标系中面积的求法我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.一、有一边在坐标轴上例1 如图1,平面直角坐标系中,△ABC的顶点坐标分别为(-3,0),(0,3),(0,-1),你能求出三角形ABC的面积吗?分析:根据三个顶点的坐标特征可以看出,△ABC的边BC在y轴上,由图形可得BC=4,点A到BC边的距离就是A点到y轴的距离,也就是A点横坐标的绝对值3,然后根据三角形的面积公式求解.解:因为B(0,3),C(0,-1),所以BC=3-(-1)=4.因为A(-3,0),所以A点到y轴的距离,即BC边上的高为3,二、有一边与坐标轴平行例2 如图2,三角形ABC三个顶点的坐标分别为A(4,1),B(4,5),C(-1,2),求三角形ABC的面积.分析:由A(4,1),B(4,5)两点的横坐标相同,可知边AB与y 轴平行,因而AB的长度易求.作AB边上的高CD,则D点的横坐标与A点的横坐标相同,也是4,这样就可求得线段CD的长,进而可求得三角形ABC的面积.解:因为A,B两点的横坐标相同,所以边AB∥y轴,所以AB=5-1=4. 作AB边上的高CD,则D点的横坐标为4,所以CD=4-(-1)=5,所以=.三、三边均不与坐标轴平行例3 如图2,平面直角坐标系中,已知点A(-3,-1),B(1,3),C(2,-3),你能求出三角形ABC的面积吗?分析:由于三边均不平行于坐标轴,所以我们无法直接求边长,也无法求高,因此得另想办法.根据平面直角坐标系的特点,可以将三角形围在一个梯形或长方形中,这个梯形(长方形)的上下底(长)与其中一坐标轴平行,高(宽)与另一坐标轴平行.这样,梯形(长方形)的面积容易求出,再减去围在梯形(长方形)内边缘部分的直角三角形的面积,即可求得原三角形的面积.解:如图,过点A、C分别作平行于y轴的直线,与过点B平行于x 轴的直线交于点D、E,则四边形ADEC为梯形.因为A(-3,-1),B(1,3),C(2,-3),所以AD=4,CE=6,DB=4,BE=1,DE=5.所以=(AD+CE)×DE-AD×DB-CE×BE=×(4+6)×5-×4×4-×6×1=14.平面直角坐标系中的面积问题(提高篇)“割补法”的应用一、已知点的坐标,求图形的面积。
人教版七年级数学下册巧用坐标求涉图形的面积问题的五种方法

5.如图,四边形 OABC 各个顶点的坐标分别是 O(0,0),A(2, 0),B(4,2),C(2,3),过点 C 与 x 轴平行的直线 EF 与 过点 B 与 y 轴平行的直线 EH 交于点 E.
4.如图,已知 A(-2,0),B(4,0),C(2,4), (1)求△ABC 的面积;
解:过 C 作 CD⊥AB 于 D,则 CD=4. 又易知 AB=4-(-2)=6, ∴S(2)设 P 为 x 轴上一点,若 S△APC=12S△PBC,求 P 的坐标.
3.在如图所示的平面直角坐标系中,四边形 OABC 各顶点分别 是 O(0,0),A(-4,10),B(-12,8),C(-14,0).求四边 形 OABC 的面积.
【点拨】本题的解题技巧在于把不规则的四边形 OABC 分割为 几个规则图形,实际上分割的方法是不唯一的,并且不仅可以用 分割法,还可以用补形法.
人教版 七年级下
第七章 平面直角坐标系
阶段核心方法专训 巧用坐标求涉图形的面积问题的五种
方法
1.如图,已知 A(-2,0),B(4,0),C(-4,4),求三角形 ABC 的面积.
解:因为 C 点的坐标为(-4,4), 所以△ABC 的 AB 边上的高为 4. 因为点 A,B 的坐标分别为(-2,0),(4,0),所以 AB=6. 所以 S△ABC=12×6×4=12.
(2)在线段 EH 上是否存在点 P,使得四边形 OAPC 的面积为 7?若不存在,说明理由;若存在,求点 P 的坐标.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解题技巧专题:平面直角坐标系中的图形面积
——代几结合,突破面积及点的存在性问题
◆类型一直接利用面积公式求图形的面积
1.如图,在平面直角坐标系中,三角形ABC的面积是()
A.2 B.4 C.8 D.6
第1题图
第2题图
2.如图,在平面直角坐标系xOy中,已知A(-1,5),B(-1,0),C(
-4,3),则三角形ABC的面积为________.
◆类型二利用分割法求图形的面积
3.如图,在平面直角坐标系中,点A(4,0),B(3,4),C(0,2),则四边形ABCO的面积为________.
4.观察下图,图中每个小正方形的边长均为1,回答以下问题:【方法14】
(1)写出多边形ABCDEF各个顶点的坐标;
(2)线段BC,CE的位置各有什么特点?
(3)求多边形ABCDEF的面积.
◆类型三利用补形法求图形的面积
5.在如图所示的正方形网格中,每个小正方形的边长均为1,三角形ABC的三个顶点恰好是正方形网格的格点.【方法14】
(1)写出三角形ABC各顶点的坐标;
(2)求出此三角形的面积.
◆
类型四与图形面积相关的点的存在性问题
6.(2017·定州市期中)如图,A(-1,0),C(1,4),点B在x轴上,且AB=3.
(1)求点B的坐标;
(2)求三角形ABC的面积;
(3)在y轴上是否存在点P,使以A,B,P三点为顶点的三角形的面积为10?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案与解析
1.B 2.
15
2
3.11解析:过点B作BD⊥x轴于D.∵A(4,0),B(3,4),C(0,2),∴OC=2,BD =4,OD=3,OA=4,∴AD=OA-OD=1,则S四边形ABCO=S梯形OCBD+S三角形ABD=
1
2×(4+2)×3+
1
2×1×4=9+2=11.
4.解:(1)A(-2,0),B(0,-3),C(3,-3),D(4,0),E(3,3),F(0,3).
(2)线段BC平行于x轴(或线段BC垂直于y轴),线段CE垂直于x轴(或线段CE平行于y轴).
(3)S多边形ABCDEF=S三角形ABF+S长方形BCEF+S三角形CDE=
1
2×(3+3)×2+3×(3+3)+
1
2×(3+3)×1=6+18+3=27.
5.解:(1)A(3,3),B(-2,-2),C(4,-3).
(2)如图,分别过点A,B,C作坐标轴的平行线,交点分别为D,E,F.S三角形ABC=S正方形DECF
-S三角形BEC-S三角形ADB-S三角形AFC=6×6-
1
2×6×1-
1
2×5×5-
1
2×6×1=
35
2.
6.解:(1)点B在点A的右边时,-1+3=2,点B在点A的左边时,-1-3=-4,所以点B的坐标为(2,0)或(-4,0).
(2)S三角形ABC=
1
2×3×4=6.
(3)存在这样的点P.设点P到x轴的距离为h,则
1
2×3h=10,解得h=
20
3.点P在y轴正半轴时,P⎝⎛⎭⎫
0,
20
3,点P在y轴负半轴时,P⎝
⎛
⎭
⎫
0,-
20
3,综上所述,点P的坐标为⎝
⎛
⎭
⎫
0,
20
3或⎝
⎛
⎭
⎫
0,-
20
3.。
