万有引力定律讲解(附答案)
万有引力定律课件

有关,与是否存在其他物体无关,故选项 C 正确。物体间的万有引力
是一对同性质的力,选项 D 错误。
答案:C
二、 万有引力和重力的关系
知识精要
1.万有引力和重力的关系
如图所示,设地球的质量为 M,半径为 R,A 处物体的质量为 m,则
(1)当物体在赤道上时,F、mg、F'三力同向。此时满足 F'+mg=F,
物体的重力最小,方向指向地心。
(2)当物体在两极点时,F'=0,F=mg=G
2
。
(3)当物体在地球的其他位置时,三力方向不同,F>mg,重力略小
于万有引力,重力的方向不指向地心。
(4)当忽略地球自转时,重力等于万有引力,即 mg=
7
F=F1-F2=
2
。
36
7
答案:
362
思悟升华
运用“填补法”解题的关键是紧扣规律适用的条件,先填补,后运
算。而在运用“填补法”解题的过程中,本题也运用了“等效法”的思想。
“等效法”是高中物理中常用的一种思维方法,是在保证效果相
同的情况下,将陌生、复杂的问题变换成熟悉、简单的模型并进行分
间的引力可直接用公式计算,但式中的 r 是指两球心间的距离,或者
说是行星的轨道半径。
典题例解
【例 1】 对于质量为 m1 和质量为 m2 的两个物体间的万有引力
的表达式 F=G 12 2,下列说法正确的是(
)
A.两物体所受引力总是大小相等,方向相反,是一对平衡力
B.当两物体间的距离 r 趋于 0 时,万有引力无穷大
万有引力定律在天体运动问题中的应用模型 (含答案)(5)

万有引力定律在天体运动问题中的应用模型大连市物理名师工作室 门贵宝1、一个简化模型: 一颗 环绕天体 绕一颗 中心天体 做近似的匀速圆周运动。
如图所示:中心天体的质量为M ,半径为R ,表面重力加速度为g ;环绕天体的质量为m ,环绕速度(线速度)为v ,角速度为ω,环绕周期为T ,轨道半径为r ,环绕天体可看成质点。
2、一个核心方程:环绕天体做匀速圆周运动所需的向心力由中心天体对它的万有引力提供。
r v mrMm G 22= 或 22ωmr rMm G = 3、两组常用推论:第一组:环绕速度与轨道半径的关系rGMv = 3r GM =ω第二组:轨道半径和环绕周期的关系2234πGM T r =2324GT r M π=4、两个常用近似:当研究中心天体表面问题或近天体表面环绕问题时,有以下两个近似关系:r R =mg R MmG =2mRT )M ( g )5、综合“金三角”关系圈:6、“人造地球同步卫星”问题:地球同步卫星的特点是它绕地轴运转的角速度与地球自转的角速度相同,同步卫星轨道是 (“椭圆”、“圆 ” ),为 (赤道轨道、极地轨道、顺行轨道、逆行轨道 );其高度一定,约为36000Km ,环绕速度一定,约为 3100m ∕s 。
同步卫星的发射,通常都采用变轨发射的方法。
要实现全球通信,至少需发射三颗地球同步卫星且对称分布在同一轨道上。
7、 “嫦娥1号”奔月问题:一般环绕问题天体表面问题近天体表面环绕问题rGM v =2234πGM T r =2RGM g =mggRv =)(22ωmr rv m 2rMmG8、“神舟八号”与“天宫一号”的对接问题: 9、“双星”问题: 针对训练1.人造地球卫星的轨道半径越大,则( B ) A .速度越小,周期越小 B .速度越小,周期越大 C .速度越大,周期越小 D .速度越大,周期越大2.两颗人造地球卫星,都在圆形轨道上运行,它们的质量相等,轨道半径之比r 1/r 2=2,则它们动能之比E 1/E 2等于( C ) A . 2 B .1 C . 1/2 D . 43.已知引力常量G 、月球中心到地球中心的距离R 和月球绕地球运行的周期T 。
人教版高一物理必修二 6.3 万有引力定律(含解析)

人教版高一物理必修二 6.3万有引力定律(含解析)人教版高一物理必修二第六章第三节6.3万有引力定律(含解析)一、单选题1.有关物理学史,以下说法正确的是( )A.伽利略首创了将实验和逻辑推理相结合的物理学研究方法B.卡文迪许通过库仑扭秤实验总结出点电荷相互作用规律C.法拉第不仅发现电磁感应现象,而且还总结出了电磁感应定律D.开普勒在天文观测数据的基础上,总结出行星运动的规律并发现了万有引力定律【答案】A【解析】伽利略首创了将实验和逻辑推理相结合的物理学研究方法,选项A正确;库伦通过库仑扭秤实验总结出点电荷相互作用规律,选项B错误;法拉第发现了电磁感应现象,但没有总结出了电磁感应定律,是韦伯和纽曼发现了电磁感应定律,故C错误;开普勒在天文观测数据的基础上,总结出行星运动的规律,牛顿发现了万有引力定律,选项D错误;故选A.2.2018年9月7日将发生海王星冲日现象,海王星冲日是指海王星、地球和太阳几乎排列成一线,地球位于太阳与海王星之间。
此时海王星被太阳照亮的一面完全朝向地球,所以明亮而易于观察。
地球和海王星绕太阳公转的方向相同,轨迹都可近似为圆,地球一年绕太阳一周,海王星约164.8年绕太阳一周。
则A.地球的公转轨道半径比海王星的公转轨道半径大B.地球的运行速度比海王星的运行速度小C.2019年不会出现海王星冲日现象D.2017年出现过海王星冲日现象【答案】D【解析】地球的公转周期比海王星的公转周期小,根据万有引力提供向心力1 / 122224Mm G m r r T π=,可得:2T =可知地球的公转轨道半径比海王星的公转轨道半径小,故A 错误;根据万有引力提供向心力,有22Mm v G m r r=,解得:v =可知海王星的运行速度比地球的小,故B 错误; T 地=1年,则T 木=164.8年,由(ω地-ω木)·t =2π,可得距下一次海王星冲日所需时间为: 2 1.01-t πωω=≈地火年,故C 错误、D 正确。
备战2020年高考物理计算题专题复习:《万有引力定律》(解析版)

《万有引力定律》一、计算题1.2019年1月3日,嫦娥四号探测器成功着陆在月球背面,并通过“鹊桥”中继卫星传回了第一张近距离拍摄月球背面的图片。
此次任务实现了人类探测器首次在月球背面软着陆、首次在月球背面通过中继卫星与地球通讯,因而开启了人类探索月球的新篇章。
探测器在月球背面着陆的难度要比在月球正面着陆大很多。
其主要原因在于:由于月球的遮挡,着陆前探测器将无法和地球之间实现通讯。
2018年5月,我国发射了一颗名为“鹊桥”的中继卫星,在地球和月球背面的探测器之间搭了一个“桥”,从而有效地解决了通讯问题。
为了实现通讯和节约能量,“鹊桥”的理想位置就是围绕“地—月”系统的一个拉格朗日点运动,如图1所示。
所谓“地—月”拉格朗日点是指空间中的某个点,在该点放置一个质量很小的天体,该天体仅在地球和月球的万有引力作用下保持与地球和月球的相对位置不变。
设地球质量为M,月球质量为m,地球中心和月球中心间的距离为L,月球绕地心运动,图1中所示的拉格朗日点到月球球心的距离为r。
推导并写出r与M、m和L之间的关系式。
地球和太阳组成的“日—地”系统同样存在拉格朗日点,图2为“日—地”系统示意图,请在图中太阳和地球所在直线上用符号“”标记出几个可能拉格朗日点的大概位置。
2.利用万有引力定律可以测量天体的质量.英国物理学家卡文迪许,在实验室里巧妙地利用扭秤装置,比较精确地测量出了引力常量的数值,他把自己的实验说成是“称量地球的质量”.已知地球表面重力加速度为g,地球半径为R,引力常量为若忽略地球自转的影响,求地球的质量.测“双星系统”的总质量所谓“双星系统”,是指在相互间引力的作用下,绕连线上某点O做匀速圆周运动的两个星球A和B,如图所示.已知A、B间距离为L,A、B绕O点运动的周期均为T,引力常量为G,求A、B的总质量.测月球的质量若忽略其它星球的影响,可以将月球和地球看成“双星系统”已知月球的公转周期为,月球、地球球心间的距离为你还可以利用、中提供的信息,求月球的质量.3.如图所示是“月亮女神”、“嫦娥1号”绕月做圆周运行时某时刻的图片,用、、、、分别表示“月亮女神”和“嫦娥1号”的轨道半径及周期,用R表示月亮的半径.请用万有引力知识证明:它们遵循其中k是只与月球质量有关而与卫星无关的常量经多少时间两卫星第一次相距最远;请用所给“嫦娥1号”的已知量.估测月球的平均密度.4.2014年10月8日,月全食带来的“红月亮”亮相天空,引起人们对月球的关注。
高中物理必修二72万有引力定律(解析版)

7.2 万有引力定律【学习目标】1. 了解万有引力定律得出的思维过程,知道地球上物体下落与天体运动的统一性..2.理解万有引力定律的含义,知道万有引力定律的适用范围和适用条件,会用万有引力定律解决相关引力计算问题. 3.了解引力常量G. 【知识要点】 一、万有引力定律1.万有引力定律的表达式:F =G m 1m 2r 2.2.万有引力的特性(1)普遍性:万有引力存在于宇宙中任何两个有质量的物体之间(天体间、地面物体间、微观粒子间). (2)相互性:两个物体间相互作用的引力是一对作用力和反作用力,符合牛顿第三定律.(3)宏观性:天体间万有引力很大,它是支配天体运动的原因.地面物体间、微观粒子间的万有引力很小,不足以影响物体的运动,故常忽略不计. 3.万有引力公式的适用条件 (1)两个质点间.(2)两个质量分布均匀的球体间,其中r 为两个球心间的距离.(3)一个质量分布均匀的球体与球外一个质点间,r 为球心到质点的距离. 4.引力常量G =6.67×10-11N·m 2/kg 2(1)物理意义:引力常量在数值上等于两个质量都是1 kg 的质点相距1 m 时的相互吸引力. (2)引力常量测定的意义卡文迪许利用扭秤装置通过改变小球的质量和距离,得到了G 的数值及验证了万有引力定律的正确性.引力常量的确定使万有引力定律能够进行定量的计算,显示出真正的实用价值. 二、万有引力和重力的关系1.万有引力和重力的关系:如图所示,设地球的质量为M ,半径为R ,A 处物体的质量为m ,则物体受到地球的吸引力为F ,方向指向地心O ,由万有引力公式得F =G Mm r2.引力F 可分解为F1、F2两个分力,其中F1为物体随地球自转做圆周运动的向心力F 向,F2就是物体的重力mg.2.近似关系:如果忽略地球自转,则万有引力和重力的关系:mg =GMmR 2,g 为地球表面的重力加速度.3.重力与高度的关系:若距离地面的高度为h ,则mg ′=G Mm(R +h )2(R 为地球半径,g′为离地面h 高度处的重力加速度).所以距地面越高,物体的重力加速度越小,则物体所受的重力也越小. 【题型分类】题型一、对万有引力定律的理解例1 对于质量为m 1和质量为m 2的两个物体间的万有引力的表达式F =G m 1m 2r 2,下列说法正确的是( )A .公式中的G 是引力常量,它是由实验得出的,而不是人为规定的B .当两物体间的距离r 趋于零时,万有引力趋于无穷大C .m 1和m 2所受引力大小总是相等的,而与m 1、m 2是否相等无关D .两个物体间的引力总是大小相等、方向相反,是一对平衡力解析 引力常量G 值是由英国物理学家卡文迪许运用构思巧妙的扭秤实验测定出来的,而不是像牛顿第二定律表达式中的k 那样是人为规定的,所以选项A 正确.当两物体间的距离r 趋近于零时,物体就不能再视为质点,万有引力定律就不再适用,所以不能得出此时万有引力趋于无穷大的结论,选项B 错误.两个物体之间的万有引力是一对作用力与反作用力,它们总是大小相等、方向相反,分别作用在两个物体上,所以选项C 正确,D 错误. 答案 AC 【同类练习】1.下面关于行星与太阳间的引力的说法中,正确的是( ) A .行星对太阳的引力与太阳对行星的引力是同一性质的力 B .行星对太阳的引力与太阳的质量成正比,与行星的质量无关 C .太阳对行星的引力大于行星对太阳的引力D .行星对太阳的引力大小与太阳的质量成正比,与行星和太阳的距离成反比 答案 A解析 行星对太阳的引力和太阳对行星的引力是一对作用力和反作用力,它们的关系是等值、反向、同性质,故选项A 正确,选项C 错误;行星对太阳的引力F =G Mmr2,故选项B 、D 错误. 2.对于万有引力定律的表达式122m m F Gr ,下列说法正确的是( ) A .公式中G 为引力常量,它是由牛顿通过实验测得的 B .当r 趋于零时,万有引力趋于无穷大C .质量为m 1、m 2的物体之间的引力是一对平衡力D .质量为m 1、m 2的物体之间的引力总是大小相等的 【答案】D 【解析】卡文迪许通过扭秤实验测出万有引力常量,故A 错误;当物体之间的距离r 趋于零时,物体不能简化为质点,万有引力公式不再适用,引力不会趋于无穷大,故B 错;质量为m 1、m 2的物体之间的引力是一对作用力与反作用力,大小总是相等,故C 错,D 对。
万有引力定律(附带答案)

万有引力定律姓名:_______________班级:_______________考号:_______________一、计算题1、(15分) 要使一颗人造地球通讯卫星(同步卫星)能覆盖赤道上东经75.0°到东经135.0°之间的区域,则卫星应定位在哪个经度范围内的上空?地球半径R0= 6.37×106m.地球表面处的重力加速度g = 9. 80m/s2.2、(2011·武汉市四月调研)人们通过对月相的观测发现,当月球恰好是上弦月时,如图甲所示,人们的视线方向与太阳光照射月球的方向正好是垂直的,测出地球与太阳的连线和地球与月球的连线之间的夹角为θ.当月球正好是满月时,如图乙所示,太阳、地球、月球大致在一条直线上且地球在太阳和月球之间,这时人们看到的月球和在白天看到的太阳一样大(从物体两端引出的光线在人眼光心处所成的夹角叫做视角,物体在视网膜上所成像的大小决定于视角).已知嫦娥飞船贴近月球表面做匀速圆周运动的周期为T,月球表面的重力加速度为g0,试估算太阳的半径.3、假设某次天文现象中,地球和某行星在同一轨道平面内同向绕太阳做匀速圆周运动,如图所示,地球的轨道半径为R,运转周期为T。
地球和太阳中心的连线与地球和行星的连线所夹的角叫做地球对该行星的观察视角(简称视角)。
已知该行星的最大视角为θ,当行星处于最大视角处时,是地球上的天文爱好者观察该行星的最佳时期。
若某时刻该行星正处于最佳观察期,行星、地球的绕太阳的运行方向相同,如图所示,求:(1)该行星绕太阳的运转周期T 1(2)问该行星下一次处于最佳观察期至少需要经历多长的时间Δt4、西昌卫星发射中心用长征三号丙运载火箭,成功将“天链一号02星”送入太空.火箭飞行约26分钟后,西安卫星测控中心传来的数据表明,星箭分离,卫星成功进入地球同步转移轨道.“天链一号02星”是我国第二颗地球同步轨道数据中继卫星,又称跟踪和数据中继卫星,由中国航天科技集团公司所属中国空间技术研究院为主研制.中继卫星被誉为“卫星的卫星”,是航天器太空运行的数据“中转站”,用于转发地球站对中低轨道航天器的跟踪测控信号和中继航天器发回地面的信息的地球静止通信卫星.(1)已知地球半径R,地球表面的重力加速度g,地球自转周期T,万有引力常量为G,请你求出地球的密度和“天链一号02星”距地面的高度?(2)某次有一个赤道地面基站发送一个无线电波信号,需要位于赤道地面基站正上方的“天链一号02星”把该信号转发到同轨道的—个航天器,如果航天器与“天链一号02星”处于同轨道最远可通信距离的情况下,航天器接收到赤道地面基站的无线电波信号的时间是多少?(已知地球半径为R,地球同步卫星轨道半径为r,无线电波的传播速度为光速c.)5、如图所示,在半径为R,质量分布均匀的某星球表面,有一倾角为θ的斜坡。
专题 万有引力定律(解析版)

万有引力定律一、重力加速度:某星球表面处(即距球心R ):mg =GMm R 2二、距离该星球表面h 处(即距球心R +h 处):mg ′=G Mm(R +h )2(R 为地球半径,g ′为离地面h 高度处的重力加速度)三、黄金代换:GM =gR 2(R 为地球半径)1.2022年11月29日“神舟十五号”飞船顺利发射,六名中国宇航员完成首次太空交接班。
已知核心舱绕地球运行近似为匀速圆周运动,离地面距离为400km ,做圆周运动的周期为90min ,向心加速度大小为a 1,地球赤道上物体随地球自转的向心加速度大小为a 2,已知地球半径为6400km ,地球表面的重力加速度为g ,下列关系正确的是()A.a 1=1617gB.a 2=gC.a 1=272a 2D.a 1=1716 2a2【解答】解:A .对地球表面物体有GMmR 2=mg 对核心舱有GMm(R +h )2=ma 1联立两式,代入数据解得a 1=16172g故A 错误;B .对地球表面物体有GMmR 2=mg 地球赤道上物体随地球自转,有G MmR2=ma 2+mg 赤对比两式,可知a 2<g ,故B 错误;CD .对核心舱有a 1=(R +h )2πT 12其中T 1=90min =1.5h对地球赤道上随地球自转的物体有a 2=R 2πT 22其中T 2=24h联立两式,代入数据解得a 1=272a 2故C 正确,D 错误。
故选:C 。
2.某星球的质量是地球的p 倍,半径是地球的q 倍。
一运动员在地球上能够跳起的最大高度为h ,假定运动员在地球上和该星球上起跳的最大初速度相同,则运动员在该星球上能够跳起的最大高度为()A.q phB.pqhC.q 2phD.p 2qh【解答】解:设地球质量为M ,半径为R ,表面的重力加速度为g ;球形星体的质量为M ',半径为R ',表面的重力加速度为g ',万有引力大小等于重力大小,则有G MmR 2=mg GM 'mR '2=mg '联立解得g 'g =R 2M 'R '2M =p q 2运动员起跳上升过程中有0-v 20=-2gh 0-v 20=-2g 'h '联立解得h '=q 2p h ,故C 正确,ABD 错误。
(完整word)万有引力定律知识点(含答案),推荐文档
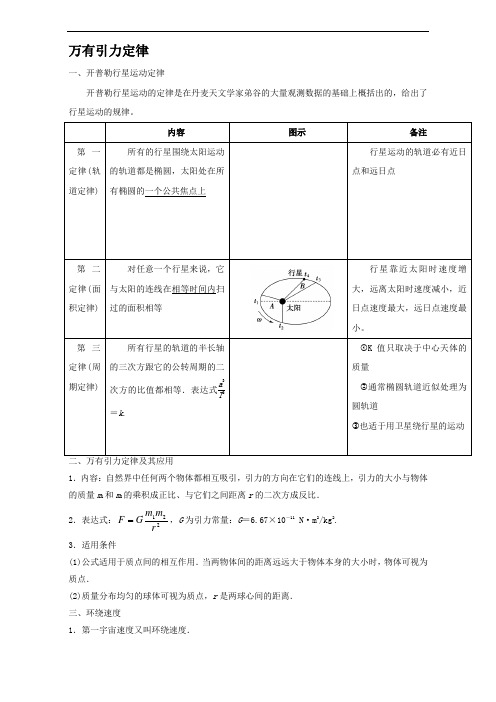
万有引力定律一、开普勒行星运动定律开普勒行星运动的定律是在丹麦天文学家弟谷的大量观测数据的基础上概括出的,给出了行星运动的规律。
内容图示备注第一定律(轨道定律) 所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个公共焦点上行星运动的轨道必有近日点和远日点第二定律(面积定律) 对任意一个行星来说,它与太阳的连线在相等时间内扫过的面积相等行星靠近太阳时速度增大,远离太阳时速度减小,近日点速度最大,远日点速度最小。
第三定律(周期定律) 所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等.表达式a 3T2=k .①K 值只取决于中心天体的质量②通常椭圆轨道近似处理为圆轨道③也适于用卫星绕行星的运动1.内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m 1和m 2的乘积成正比、与它们之间距离r 的二次方成反比. 2.表达式:221rm m G F ,G 为引力常量:G =6.67×10-11 N·m 2/kg 2. 3.适用条件(1)公式适用于质点间的相互作用.当两物体间的距离远远大于物体本身的大小时,物体可视为质点.(2)质量分布均匀的球体可视为质点,r 是两球心间的距离. 三、环绕速度1.第一宇宙速度又叫环绕速度.r mv rMm G mg 212== 得:gR rGMv ==1=7.9 km/s. 第一宇宙速度是人造卫星的最大环绕速度,也是人造地球卫星的最小发射速度. 第二宇宙速度(脱离速度):v 2=11.2 km/s ,使物体挣脱地球引力束缚的最小发射速度. 第三宇宙速度(逃逸速度):v 3=16.7 km/s ,使物体挣脱太阳引力束缚的最小发射速度. 特别提醒:(1) 两种周期——自转周期和公转周期的不同(2)两种速度——环绕速度与发射速度的不同,最大环绕速度等于最小发射速度 (3)两个半径——天体半径R 和卫星轨道半径r 的不同 四、近地卫星、赤道上物体及同步卫星的运行问题 1.近地卫星、同步卫星、赤道上的物体的比较比较内容赤道表面的物体 近地卫星 同步卫星向心力来源 万有引力的分力 万有引力向心力方向指向地心重力与万有引力的关系 重力略小于万有引力重力等于万有引力线速度v1=ω1Rv2=GM Rv3=ω3(R +h)=GMR +hv 1<v 3<v 2(v 2为第一宇宙速度)角速度ω1=ω自ω2=GM R3ω3=ω自=GMR +h 3ω1=ω3<ω2向心加速度a 1=ω21Ra 2=ω2R =GM R2a 3=ω23(R +h) =GMR +h 2a 1<a 3<a 2五、天体的追及相遇问题两颗卫星在同一轨道平面内同向绕地球做匀速圆周运动,a 卫星的角速度为ωa ,b 卫星的角速度为ωb ,若某时刻两卫星正好同时通过地面同一点正上方,相距最近(如图甲所示)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.3 万有引力定律班级: 组别: 姓名:【课前预习】1.万有引力定律:(1)内容:自然界中任何两个物体都相互吸引,引力的方向在它们的连线上,引力的大小与物体的质量m 1和m 2的乘积成正比,与它们之间距离r 的二次方成反比。
(2)表达式: F =G m 1m 2r 2 。
2.引力常量(1)引力常量通常取G = 6.67×10-11 N·m 2/kg 2,它是由英国物理学家卡文迪许在实验室里测得的。
(2)意义:引力常量在数值上等于两个质量都是1kg 的质点,相距1m 时的相互吸引力。
【新课教学】一、牛顿的“月——地”检验 1.检验的目的:地球对月亮的力,地球对地面上物体的力,太阳对行星的力,是否是同一种力。
2.基本思路 (理论计算):如果是同一种力,则地面上物体的重力G ∝21R ,月球受到地球的力21r f ∝。
又因为地面上物体的重力mg G =产生的加速度为g ,地球对月球的力提供月球作圆周运动的向心力,产生的向心加速度,有向ma F =。
所以可得到:22Rr F G a g ==向 又知月心到地心的距离是地球半径的60倍,即r=60R ,则有:322107.23600-⨯==⋅=g g r R a 向m/s 2。
3.检验的过程(观测计算):牛顿时代已测得月球到地球的距离r月地 = 3.8×108 m ,月球的公转周期T = 27.3天,地球表面的重力加速度g = 9.8 m /s 2,则月球绕地球运动的向心加速度:=向a (2πT )2r 月地 (字母表达式) =向a (2π27.3×24×3600)2×3.8×108 (数字表达式) =向a 2.7×10-3m/s 2 (结果)。
4.检验的结果:理论计算与观测计算相吻合。
表明:地球上物体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从相同的规律。
二、万有引力定律1.内容:自然界中任何两个物体都相互吸引,引力的大小与物体的质量m 1和m 2的乘积成正比,与它们之间的距离r 的二次方成反比,引力的方向在它们的连线上。
2.表达式: 221r m m G F = 描述式中质量的单位用kg ;距离的单位用m ;G 叫引力常量,最早由英国物理学家卡文迪许在实验室中通过对几个铅球之间万有引力的测量,比较准确的得出了G 的数值,通常取 G =6.67×10-11N·m 2/kg 2,其意义是引力常量在数值上等于两个质量都是1kg 的质点,相距1m 时的相互吸引力。
(测定引力常量的意义:A.卡文迪许利用扭秤装置通过改变小球的质量和距离,证实了万有引力的存在及万有引力定律的正确性。
B.引力常量的测定使得万有引力能够进行定量计算,使万有引力定律有了真正的使用价值。
)3.万有引力的普遍性:万有引力不但存在于行星和太阳之间,也存在于宇宙中的任何天体之间。
但地球上的物体,由于物体间的万有引力远小于物体的重力,所以人们很难感受或观察到,往往忽略物体间的万有引力。
4.适用条件:(1)万有引力公式适用于质点之间的引力大小的计算。
(2)对于实际物体间的相互作用,当两个物体间的距离远远大于物体本身的大小时,物体可视为质点。
(3)两个质量分布均匀的球体间可用万有引力公式求解,式中r 即两球心之间的距离;一个质量分布均匀的球体与球外一质点之间的万有引力亦可用公式求解,r 即质点到球心的距离。
【例题精讲】知识点1万有引力公式的理解【例1】对于质量为1m 、2m 的两个物体间的万有引力的表达式221r m m GF =,下列说法正确的是( AC )A .公式中的G 是恒量,是实验测定的,而不是人为规定的B .当r 趋于零时,万有引力趋于无穷大C .1m 与2m 受到的引力总是大小相等、方向相反,是一对作用力和反作用力D .1m 与2m 受到的引力大小相等、方向相反,是一对平衡力[思路分析]由基本概念、万有引力定律及其应用条件判断。
引力常量G 值是由英国物理学家卡文迪许运用扭秤实验测量出来的,所以A 正确;当r 趋于零时,此公式不能直接应用,所以直接应用公式得到的万有引力趋于无穷大是错误的,所以B 错;两个物体之间的万有引力是一对作用力和反作用力,它们总是大小相等、方向相反,分别作用在两个物体上.所以C 正确。
答案:AC知识点2 万有引力公式的应用【例2】火星半径是地球半径的一半,火星质量约为地球质量的1/9。
那么地球表面质量为50 kg 的人受到地球的吸引力约为火星表面同质量物体受到火星引力的多少倍?[思路分析]设火星质量为M 1,地球质量为M 2,火星半径为r 1,地球半径为r 2,则有万有引力定律221r m m G F =得:4922211212=⋅=r r M M F F 即人所受地球的吸引力约为火星表面同质量物体所受火星吸引力的2.25倍。
知识点3太阳与行星间引力的应用【例3】已知太阳的质量为M ,地球的质量为m 1,月亮的质量为m 2,当发生日全食时,太阳、月亮、地球几乎在同一直线上,且月亮位于太阳与地球中间,如图所示.设月亮到太阳的距离为a ,地球到月亮的距离为b ,则太阳对地球的引力F 1和对月亮的引力F 2的大小之比为多少?答案:m 1a 2m 2(a +b )2【例4】地球的质量是月球质量的81倍,若地球吸引月球的力的大小为F ,则月球吸引地球的力的大小为( B )A .F/81B .FC .9FD .81F【方法技巧练】一、用割补法求解万有引力的技巧6.有一质量为M 、半径为R 的密度均匀的球体,在距离球心O 为2R 的地方有一质量为m 的质点,现在从M中挖去一半径为R 2的球体,如图1所示,求剩下部分对m 的万有引力F 为多大? 答案:7GMm 36R 2解析:一个质量均匀分布的球体与球外的一个质点间的万有引力可以用公式F =G mM r2直接进行计算,但当球体被挖去一部分后,由于质量分布不均匀,万有引力定律就不再适用.此时我们可以用“割补法”进行求解.设想将被挖部分重新补回,则完整球体对质点m 的万有引力为F 1,可以看做是剩余部分对质点的万有引力F 与被挖小球对质点的万有引力F 2的合力,即F 1=F +F 2.设被挖小球的质量为M ′,其球心到质点间的距离为r ′由题意知M ′=M 8,r ′=3R 2; 由万有引力定律得F 1=G Mm (2R )2=GMm 4R 2F 2=G M ′m r ′2=G M 8m (32R )2=GMm 18R 2 故F =F 1-F 2=7GMm 36R 2. 方法总结:本题易错之处为求F 时将球体与质点之间的距离d 当做两物体间的距离,直接用公式求解.求解时要注意,挖去球形空穴后的剩余部分已不是一个均匀球体,不能直接运用万有引力定律公式进行计算,只能用割补法.【教材补充】卡文迪许实验在牛顿发现万有引力定律100年后,英国物理学家卡文迪许(H.Cavendish)于1789年巧妙地利用扭秤测出了引力常量。
卡文迪许的实验装置如图所示。
在一根金属丝下倒挂着一个T形架,架的水平横梁两端各装一个质量为m的小球,T形架的竖直部分装有一面小平面镜,两个小球由于受到质量均为M的两个大球的吸引而转动,使金属丝发生扭转.当吸引力的力矩跟金属丝的扭转力矩平衡时,T形架停止不动.根据平面镜反射的光点在标尺上移动的距离可算出金属丝的扭转角度,结合事先测定的金属丝扭转角度跟扭转力矩的关系,就可以算出扭转力矩,从而算出引力F和引力常量。
卡文迪许测定的引力常量G=6.754×10-11 N·m2/kg2。
在以后的八九十年间,竟无人超过他的测量精度。
引力常量的测定是验证万有引力定律的一个重要实验,它使万有引力定律有了真正的实用价值。
卡文迪许把他的这个实验说成是“称地球的重量”(应该是“称地球的质量”)。
有了G值后,我们还可以“称”出太阳或其他星球的质量。
1、实验原理:力矩平衡,即引力矩=扭转力矩2、巧妙处:两次放大及等效的思想:扭秤装置把微小力转变成力矩来反映(一次放大),扭转角度(微小形变)通过光标的移动来反映(二次放大),从而确定物体间的万有引力。
3、卡文迪许扭秤实验的伟大之处:A、证明了万有引力的存在B、开创了测量弱力的新时代C、使得万有引力定律有了真正的实用价值4、G值为6.67×10-11 Nm2/kg2物理含义:两个质量为1kg的物体相距1m时,它们之间万有引力为6.67×10-11 N测定引力常量的意义:A.卡文迪许利用扭秤装置通过改变小球的质量和距离,证实了万有引力的存在及万有引力定律的正确性。
B.引力常量的测定使得万有引力能够进行定量计算,使万有引力定律有了真正的使用价值。
【随堂练习】1.月—地检验的结果说明(AD )A.地面物体所受地球的引力与月球所受地球的引力是同一种性质力B.地面物体所受地球的引力与月球所受地球的引力不是同一种类型的力C.地面物体所受地球的引力只与物体质量有关,与地球质量无关D.月球所受地球的引力除与月球质量有关外,还与地球质量有关2.下列说法中正确的是(D )A.万有引力定律是卡文迪许发现的B.卡文迪许扭秤是用来验证万有引力定律是否正确的C .被人们称为“能称出地球质量的人”是牛顿D .万有引力常量是一个有单位的常量3.两大小相同的实心小铁球紧靠在一起,它们之间的万有引力为F ,若两个半径是小铁球2倍的实心大铁球紧靠在一起,则它们之间的万有引力为( D )A .2FB .4FC .8FD .16F4.已知地球半径为R ,将一物体从地面移到离地面高h 处时,物体所受万有引力减少到原来的一半,则h 为 ( D )A .RB .2RC .2RD .(2-1)R5.两个质量均为M 的星体.其连线的垂直平分线为AB ,0为两星体连线的中点,如图所示,一质量为M 的物体从0沿OA 方向运动,则它受到的两星体万有引力的合力大小变化情况是( D )A .一直增大B .一直减小C .先减小,后增大D .先增大,后减小【课后作业】1.下列关于万有引力定律的说法正确的是 ( ABCD )A.万有引力定律是牛顿发现的B. 中的G 是一个比例常数,是有单位的 C.万有引力定律适用于质点间的相互作用 D.两个质量分布均匀的分离的球体之间的相互作用力也可以用来计算,r 是两球体球心的距离 2.设想人类开发月球,不断把月球上的矿藏搬运到地球上,假定经过长时间开采后,地球仍可看作是均匀的球体,月球仍沿开采前的圆周轨道运动,则与开采前比( B )A .地球与月球间的万有引力将变大B .地球与月球间的万有引力将变小C .地球与月球间的万有引力将不变D .无法确定3.据报道,最近在太阳系外发现了首颗“宜居”行星,其质量约为地球质量的6.4倍,一个在地球表面质量为600N 的人在这个行星表面的质量将变为960N 。
