三角函数单调性
三角函数的单调区间与不等式

三角函数的单调区间与不等式三角函数是高中数学中重要的概念之一,它在数学和物理等领域有广泛的应用。
而了解三角函数的单调性及其与不等式的关系,对于解题和理解数学概念都极为重要。
本文将详细讨论三角函数的单调区间与不等式的相关内容。
一、正弦函数的单调性与不等式正弦函数是最常见的三角函数之一,其定义域为实数集合R,值域在[-1, 1]之间。
首先我们来研究正弦函数的单调性。
我们知道,正弦函数的一个周期是2π,那么我们可以利用周期性来研究其单调性。
在每个周期内,正弦函数在[0, π/2]、[π/2, π]、[π, 3π/2]、[3π/2, 2π]上的单调性是相同的。
首先来看在[0, π/2]区间内的单调性。
在这个区间内,正弦函数的值是递增的,即sin(x1) < sin(x2)当且仅当0 ≤ x1 < x2 ≤ π/2。
接下来是在[π/2, π]区间内的单调性。
在这个区间内,正弦函数的值是递减的,即sin(x1) > sin(x2)当且仅当π/2 ≤ x1 < x2 ≤ π。
同理,在[π, 3π/2]和[3π/2, 2π]区间内的正弦函数分别是递增和递减的。
根据上述的单调性分析,我们可以利用单调性来解不等式。
比如对于sin(x) > a这样的不等式,我们可以通过分析sin(x)和a的关系,得出x的取值范围。
二、余弦函数的单调性与不等式余弦函数也是一种常见的三角函数,其定义域和值域与正弦函数相同。
我们将讨论余弦函数的单调性及其与不等式的关系。
与正弦函数类似,余弦函数也具有周期性。
在每个周期内,余弦函数在[0, π]、[π, 2π]区间上的单调性是相同的。
在[0, π]区间内,余弦函数的值是递减的,即cos(x1) > cos(x2)当且仅当0 ≤ x1 < x2 ≤ π。
在[π, 2π]区间内,余弦函数的值是递减的,即cos(x1) < cos(x2)当且仅当π ≤ x1 < x2 ≤ 2π。
三角函数的性质(单调性)

4、函数值外的符号要相同。
另外注意首先大致地判断一下有没有符号不同的 情况,以便快速解题。
1 π 例3. 函数y sin( x ), x [-2π, 2π]的单调递增区间. 2 3 1 令 解: Z x , 函数y sin Z的单调递增区间是 2 π 3 [ 2k , 2k ], k Z 2 2 1 5 由 2k x 2k , 得 4k x 4k 2 2 3 2 3 3 5 2 3 4k 1 5 于是- k 由x [总结:在解决这类问题时要“牢记五点作图、 2 , 2 ]可知, , 12 12 4k 2 谨记整体换元、挂靠三角函数”
例2.在锐角△ABC中,试比较sin A与cosB的大小。
π π 解: 由△ABC为锐角三角形, A+B , 故A > - B 有 2 2 π π π 又0 < A < , 0 < B < 2 2 2
π 故sinA > sin( B) cosB,即sinA > cosB 2
)
练习2:下列关系式中正确的是(
总结:在解决这类问题时要“牢记五点作图、 谨记整体换元、挂靠三角函数”
-2π
5π 3
2π
π 3
练习3.
π 求函数的 y 2cos( 2 x), x [0, 2π]单调区间 3
课堂小结
3
k Z, k 0
5π π x , 而[ 5π ,π ] [-2π, ] 2π 3 3 3 3 1 π 5π π 函数y sin( x ), x [2π, 2π]的单调递增区间是[ , ]. 2 3 3 3
三角函数单调递增区间公式

三角函数单调递增区间公式
如果你想知道三角函数单调递增区间公式是什么,那么你来对地方。
三角函数单调递增区间公式可以帮助我们确定一个函数是单调递增的。
下面就让我们来了解一下它是怎样工作的:
1. 三角函数单调递增区间的基本公式
三角函数单调递增区间的基本公式由两个端点表示,相邻的两组端点
定义一个单调递增的区间。
每一个单调递增的区间的定义如下:
- 如果函数是奇函数,则端点为:(n-1/2)π -- (n+1/2)π;
- 如果函数是偶函数,则端点为:nπ -- (n+1)π。
其中n 为任意整数。
2. 三角函数单调递增区间的更进一步实现
在确定三角函数单调递增区间的时候,如果需要更进一步实现,可以
将相邻两个端点间的值分别记为x1,x2。
然后根据以下公式计算x1、x2:
x1 = nπ + (-1)^n * (1/2)π
x2 = (n+1)π + (-1)^n * (1/2)π
其中n 为任意整数,(-1)^n 是以指数的形式表达的一元二次函数。
3. 三角函数单调递增图象的描绘
通过以上公式,我们可以将三角函数从数学角度上表达出来,然后在图上更加直观的描绘出三角函数的单调递增区间。
在描绘的时候,可以使用两个不同颜色的典型实例线性绘制对应区间。
最后,三角函数单调递增区间公式通过解决关于三角函数诸多函数概念的数学现象,使人们能够更加真实的解答问题。
总之,三角函数单调递增区间的计算主要使用上述的基本公式,此公式可以帮助我们确定一个函数是单调递增的,并且基于此可以更进一步实现更多的概念,从而更加准确地描绘出三角函数单调递增图象。
高考数学专题讲解:三角函数的单调性

8
8
计算三角函数单调性
例题:求函数f (x) 3tan( 1 x ) 1的单调性。
26
解法设计:A 3 0 1 0 三角函数单调性发生改变
2
k 1 x k
2
2 62
原始单调递增,单调性改变,现在单调递减
k 1 x k
6
6
x [ 7 2k, 2k] f (x)单调递增
6
6
计算三角函数单调性
例题:求函数 f (x) cos(2x )的单调性。
4
解法设计:A 1 0 2 0 三角函数单调性不发生改变
2k 2x 2 2k
4
3
原创解法设计中心
2
3
训练三:求函数 f (x) 3tan( x ) 2 的单调性。
4
训练四:求函数 f (x) 2sin( 3x )的单调性。
4
训练五:求函数 f (x) 4cos(x ) 3 的单调性。
6
训练六:求函数 f (x) 2tan(x ) 的单调性。
5
2
2
当x [ 2k,2 2k]时:
函数 f (x) cos x单调递增
知识点储备
y
0
2
2
f (x) tan x的单调性
3
x
当x
(
2
k,
2
k )
时:
2
函数 f (x) tan x单调递增
计算三角函数单调性
A 振幅A 0 三角函数的单调性不发生改变 振幅A 0 三角函数的单调性发生改变 A0
三角函数的单调性

假期专题辅导系列三-------三角函数的单调性江苏省海安高级中学------罗湘军三角函数的单调性是三角函数的重要性质,在三角函数的各种问题中都能见到单调性的独特应用之处,特别是在比较大小、求三角函数的单调区间,解不等式等方面有着不可替代的作用,下面我们借助于几个例子来进行分析. 一. 典例分析1. 利用三角函数的单调性比较大小 例1 比较下列各组数的大小 (1)33sin(sin),sin(cos)88ππ; (2)13tan4π与17tan5π解析: (1) ∵3cossin 88ππ=,∴330cossin188ππ<<<.而sin y x =在(0,1)内递增,∴33sin(sin )sin(cos)88ππ<.(2) 13tantan 4π= 4π,172tan tan55ππ=, ⎪⎭⎫⎝⎛=<<2,0tan ,5240πππ在x y 内单调递增, 2tantan.45ππ∴<。
点评:比较两个三角函数值的大小常常先将它们化为同名函数,然后将角化为在该函数的同一单调区间内的角.最后利用函数的单调性来比较函数值的大小.2. 利用三角函数的单调性求单调区间 例2 求函数⎪⎭⎫ ⎝⎛-=324sin 21x y π的单调区间.解析:原函数变形为⎪⎭⎫⎝⎛--=432sin 21πx y 令432π-=x u ,则只需求u y sin =的单调区间即可. 2243222sin πππππ+≤-=≤-=k x u k u y 在 (Z k ∈)上单调递增即893833ππππ+≤≤-k x k ,(Z k ∈)上单调递增,u y sin =在2322()2342x k u k k Z πππππ+≤=-≤+∈上单调递减即在)(,8213893Z k k x k ∈+≤≤+ππππ上单调递减故⎪⎭⎫ ⎝⎛-=324sin 21x y π的递减区间为:,893,833⎥⎦⎤⎢⎣⎡+-ππππk k ()k Z ∈ 故原函数递增区间为:)(,8213,893Z k k k ∈⎥⎦⎤⎢⎣⎡++πππ. 点评:研究三角函数的性质时常用整体思想.本题将函数⎪⎭⎫ ⎝⎛-=324sin 21x y π作整体代换,转化为对函数sin y x =的性质的研究.另外,本题也可以画出函数⎪⎭⎫ ⎝⎛-=324sin 21x y π的图象,通过图象来研究性质. 3. 利用三角函数的单调性求值域例3设G 、H 分别为非等边三角形ABC 的重心与外心,A(0,2),B (0,-2),且AB GM λ=(λ∈R).(Ⅰ)求点C(x ,y )的轨迹E 的方程;(Ⅱ)过点(2,0)作直线L 与曲线E 交于点M 、N 两点,设ON OM OP +=,是否存在这样的直线L ,使四边形OMPN 是矩形?若存在,求出直线的方程;若不存在,试说明理由.例3.求函数)3cos(2π-=x y 在6π≤x ≤32π范围内的值域。
三角函数的单调性
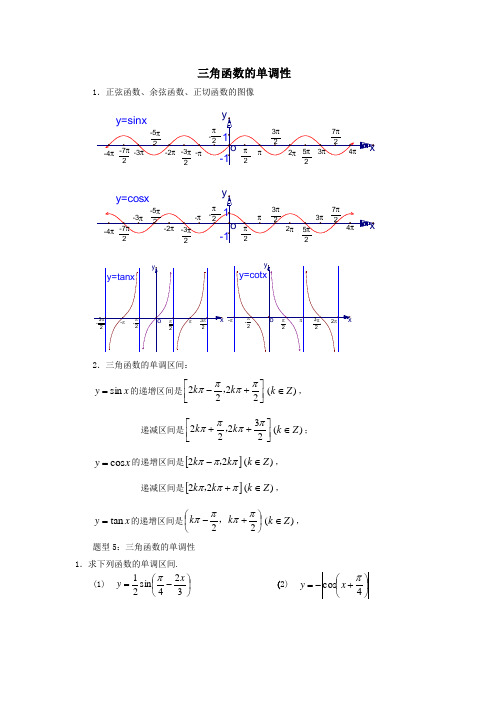
三角函数的单调性1.正弦函数、余弦函数、正切函数的图像2.三角函数的单调区间:x y sin =的递增区间是⎥⎦⎤⎢⎣⎡+-2222ππππk k ,)(Z k ∈,递减区间是⎥⎦⎤⎢⎣⎡++23222ππππk k ,)(Z k ∈; x y cos =的递增区间是[]πππk k 22,-)(Z k ∈,递减区间是[]πππ+k k 22,)(Z k ∈,x y tan =的递增区间是⎪⎭⎫ ⎝⎛+-22ππππk k ,)(Z k ∈,题型5:三角函数的单调性 1.求下列函数的单调区间.(1) ⎪⎭⎫ ⎝⎛-=324sin 21x y π (2) ⎪⎭⎫ ⎝⎛+-=4cos πx y解:(1).原函数变形为⎪⎭⎫⎝⎛--=432sin 21πx y 令432π-=x u ,则只需求u y sin =的单调区间即可.2243222sin πππππ+≤-=≤-=k x u k u y 在 ,(Z k ∈)上 即893833ππππ+≤≤-k x k ,(Z k ∈)上单调递增, u y sin =在)(,23243222Z k k x u k ∈+≤-=≤+πππππ,上 即)(,8213893Z k k x k ∈+≤≤+ππππ,上单调递减 故⎪⎭⎫ ⎝⎛-=324sin 21x y π的递减区间为:,893,833⎥⎦⎤⎢⎣⎡+-ππππk k ()k Z ∈ 递增区间为:)(,8213,893Z k k k ∈⎥⎦⎤⎢⎣⎡++πππ.(2)原函数的增减区间即是函数⎪⎭⎫ ⎝⎛+=4cos πx y 的减增区间,令4π+=x u由函数u y cos =的图象可知:周期π=T 且 u y cos =在,42ππππk x u k ≤+=≤-上,即Z k k x k ∈-≤≤-,443ππππ上递增, 在24ππππ+≤+=≤k x u k 即在Z k k x k ∈+≤≤-,44ππππ上递减故所求的递减区间为⎥⎦⎤⎢⎣⎡--4,43ππππk k ,递增区间为,44k k ππππ⎡⎤-+⎢⎥⎣⎦(Z k ∈) 2.函数y =2sin x的单调增区间是( ) A .[2k π-2π,2k π+2π](k ∈Z )B .[2k π+2π,2k π+23π](k ∈Z ) C .[2k π-π,2k π](k ∈Z ) D .[2k π,2k π+π](k ∈Z )解析:A ;函数y =2x为增函数,因此求函数y =2sin x的单调增区间即求函数y =sin x 的单调增区间。
三角函数的性质对称性与单调性

03
三角函数的基本图像
正弦函数图像
1
正弦函数图像是周期函数,其周期为$2pi$。
2
正弦函数图像在$[0, pi]$区间内是单调递增的, 而在$[pi, 2pi]$区间内是单调递减的。
3
正弦函数图像关于直线$y = 0$对称,也即关于 原点对称。
余弦函数图像
余弦函数图像也是周期函数, 其周期为$2pi$。
在统计学中,三角函数用于描述数据的分布和变化规 律,如正态分布、泊松分布等。
计量经济学
在计量经济学中,三角函数用于建立经济模型和进行 预测分析,如时间序列分析、回归分析等。
THANKS FOR WATCHING
感谢您的观看
三角函数的有界性
正弦函数y=sinx和余弦函数y=cosx都是有界函数, 其值域分别为[-1,1]。
有界性的应用
有界性是三角函数的一个重要性质,在解决 三角函数的值域、最值等问题中有着重要的 应用。
02
三角函数的对称性
轴对称
总结词
三角函数的图像关于y轴对称,这是由于三角函数的定义和性 质决定的。
振动与波动
三角函数在描述简谐振动和波动 问题时也经常用到,例如振幅、 相位、频率等参数都可以用三角 函数来表示。
电磁波
在研究电磁波的传播和辐射时, 三角函数也扮演着重要的角色, 如电磁波的极化、偏振等现象都 可以用三角函数来描述。
在工程中的应用
01
机械振动
在机械工程中,三角函数被广泛 应用于描述各种振动现象,如弹 簧振荡、阻尼振荡等。
详细描述
三角函数在数学中有着广泛的应用,它们的图像具有特定的 对称性。例如,正弦函数和余弦函数的图像都是关于y轴对称 的。这种对称性是由三角函数的定义和性质决定的,对于理 解三角函数的性质和行为非常重要。
三角函数的单调性、奇偶性、周期性

(A)f(x+2)是奇函数
(C)f(x-2)是奇函数
(B)f(x+2)是偶函数
(D)f(x-2)是偶函数
3 .已知 函 数 f(x)=asin(πx+α)+bcos(πx+β)+4, 当 f(2001)=5 时 , f(2002)=( )B (A)1 (B)3 (C)5 (D)7
4.函数y=2sin2x+sin2x是( D ) (A)以2π为周期的奇函数 (B)以2π为周期的非奇非偶函数 (C)以π为周期的奇函数 (D)以π为周期的非奇非偶函数 5.下列命题中正确的是( D ) (A)若α,β是第一象限角,且α>β,则sinα>sinβ (B)函数y=sinx· cotx的单调递增区间是(2kπ-π/2,2kπ+ π/2),k∈Z (C)函数y=(1-cos2x)/sin2x的最小正周期是2π (D) 函 数 y=sinxcos2φ-cosxsin2φ 的 图 象 关 于 y 轴 对 称 , 则 φ=kπ/2+π/4,k∈Z
2.判断下列函数是否为周期函数;若是,判断其是否存 在最小正周期,若存在,求出它的最小正周期:
1 ①y sin 4 x 1 ②y sin x 3 3 x ③y tan 4 6 ④y 2
【 解 题 回 顾 】 若 三 角 函 数 y=f(x)的 最 小 正 周 期 为 T, 则 f(ωx+φ)的最小正周期就是T|ω|;另外,周期函数的图像必 然呈现一种“周而复始”的规律特征,反之亦然,所以判 断函数的周期性的一个有效方法是作图
5 3.已知函数 f x 5 sin x cos x 5 3 cos x 3 x R 2
2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:Q
y=sinx单调递增区间为
2
2k
,
2
2k
,k
Z
减区间为
2
2k ,
3
2
2k
,
k
Z
y=1+2sinx单调递增区间为
2
2k
,
2
2k
,
k
Z
减区间为
2
2k , 3
2
2k
,
k
Z
例1:求下列函数的单调区间。
(2).y 1 2sin x
解:Q
y=sinx单调递增区间为
2
2k
,
2
2k
,k
Z
减区间为
(2)cos( 23 )与cos(17 ).
5
(求增找减)
余弦函数也有类似规律
练习(1).求y -1 1 sin x的单调增区间 2
解:Q y=sinx单调递增区间
为
2
2k
,
2
2k
,k
Z
y=-1+
1 2
sinx单调递增区间
为
2
2k ,
2
2k
,
k
Z
练习(2).求y 1 2cos x的单调减区间
解:Q y=cosx单调递增区间
为 2k , 2k ,k Z
7
12
k,- k
12
,k z
,
例(. 2)求y sin( -2x)的单调减区间
3
分析:y sin( -2x)
3
=sin[-(2x- )]
3
=-sin(2x- )
3
例(. 2)求y
sin(
3
-
1 2
x)的单调减区间
解Q y sin( - 1 x)= sin[(1 x )]= sin(1 x )
32
23
23
例.利用三角函数的单调性,比较大小.
(1)sin( )与sin( );
18
10
(2)cos( 23 )与cos( 17 ).
5
4
解:(1)Q 0,
2 10 18
且y
sin
x在
2
,
2
递增
sin( ) sin( )
10
18
例.利用三角函数的单调性,比较大小.
3
8
k, k
8
,k z
,
例(. 2)求y sin( -2x)的单调减区间
3
解:Q
y
sin
x的单调减区间为2
2k,3
2
2k ,k
Z
错 2k 2x 3 2k , (k z)
2
3
2
得 7 k x k ,(k z)
的 12
12
函数y=sin(2x+
4
)的单调递减区间为:
1
-3 5 -2 3
2
2
-
o 2
-1
2
3
2
2
5 2
x
3
7 2
4
x -
…
2
…
0… 2
…
cosx -1
0
1
0
-1
y=cosx (xR)
增区间为 [ +2k, 2k],kZ 其值从-1增至1
减区间为 [2k, 2k,+ ], kZ 其值从 1减至-1
例1:求下列函数的单调区间。
(1).y 1 2sin x
2
2 32
得 5 4k x 4k ,(k z)
3
3
函数y=sin(12
x+
3
)的单调递增区间为:
5
3
4k,
3
4k
,k z
,
练习1.求y sin 2x的单调增区间
解:Q
y
sin
x的单调增区间为
2
2k,
2
2k
,k
Z
2k 2x 2k , (k z)
2
2
得 k x k ,(k z)
增区间。用增求增
当<0时,先将y sin(x )的化为正,然后用增求减
如:y sin( 1 x)= sin[(1 x )]= sin(1 x )
32
23
23
(2)当>0时,求y cos(x )增区间,用增求增 当<0时,先将y cos(x )的化为大于0,然后
用增求增
如:y co(s 1 x)= cos[(1 x )]= co(s 1 x )
2
2k ,
3
2
2k
,
k
Z
y=1-2sinx单调递减区间为
2
2k
,
2
2k
,
k
Z
递增区间为 2
2k
,
3
2
2k
,k
Z
总结:
(1)当A>0时,y B Asin x与y sin x对应区间单调性相同 如:求y 1 2sin x的增区间,就找y sin x的增区间
(求增找增)
(2)当A<0时,y B Asin x与y sin x对应区间单调性相反 如:求y 1 2sin x的增区间,就找y sin x的减区间;
单调性
y=cosx
y
1
0
2
3 2 5 x
2
2
-1
xR
y [1,1]
x 2k 时, ymax 1 x 2k 时,ymin 1
对称轴: x k , k Z
对称中心:(2 k , 0) k Z
偶函数
T 2 2
新授课:正弦、余弦函数的单调性
1,正弦函数的单调性 y
1
-3 5 -2 3
y=1-2cosx单调递减区间
为 2k , 2k , k Z
例题2:求下列函数的单调增区间。
(1).y sin(1 x )
23
(2).y sin( 1 x)
32
(1).y sin(1 x )
23
解:Q
y
sin
x的单调增区间为
2
2k,
2
2k
,k
Z
2k 1 x+ 2k , (k z)
2
2
-
o
2
-1
2
3
2
2
5 2
x
3
7 2
4
x
2
…
0
…
2
sinx -1
0
1
… 0
…
3 2
-1
y=sinx (xR)
增区间为
[[
2+22k,,
π 22
+2]k],kZ
其值从-1增至1
减区间为
[[
2
+22k,, 332 +2]k],kZ
其值从 1减至-1
新授课:正弦、余弦函数的单调性
2,余弦函数的单调性y
§1.4.2正弦余弦函数的性质
---------单调性
高一级备课组
函数 图形
y
1
2
0
-1
y=sinx
2
3 2 5 x
2
2
定义域 值域
最值
xR
y [1,1]
x
2
2k 时, ymax
1
x
2
2k 时,ymin
1
对称性
对称轴: x
2
k
,k
Z
对称中心: (k , 0) k Z
奇偶性
奇函数
周期T 2 2ຫໍສະໝຸດ 322323
而y
sin
x的单调增区间为2
2k,3
2
2k ,k Z
2k x 3 2k , (k z)
2
23 2
得 5 4k x 11 4k ,(k z)
3
3
函数y=sin(3
-
1 2
x)的单调递减区间为:
5
3
4k,11
3
4k
,k z
,
总结:
(1)当>0时,用y sin x的单调增区间求y sin(x )的
4
4
函数y=sin2x的单调递增区间为:
4
k,
4
k
,k z
,
练习2.求y sin(2x )的单调减区间
4
解:Q
y
sin
x的单调减区间为2
2k,3
2
2k
,k
Z
2k 2x+ 2k , (k z)
2
42
得 3 k x k ,(k z)
8
8
函数y=sin(2x+
4
)的单调递减区间为:
