正弦交流电路例题
(完整版)正弦交流电章节习题1

正弦交流电章节习题一、选择题1、已知正弦电压u (t)=2Usin(ωt+φu ),其相量表达式为( )A 、u m U U ϕ∠=2B 、u m U U ϕ∠=•2C 、u U U ϕ∠=2D 、u U U ϕ∠=•22、已知正弦量u1=2202sin314tV 和u2=1102sin(314t-60°)V ,则两个电压间的相位差φ1- φ2为( )A 、314t-60°B 、60°C 、-60°D 、0°3、已知某电路的正弦电压u 和正弦电流i 的相位差为30°,电路呈容性,则电压u 和电流i 的相位关系是( )A 、u 滞后i 相位30°B 、u 超前i 相位30°C 、u 和i 同相D 、u 和 i 反相4、已知某二端网络N 的等效阻抗是z=20+j20Ω,则二端网络N 呈( )A 、纯电容性B 、容性C 、纯电感性D 、感性5、在RLC 串联电路中,各元件上的电压分别为U R ,U L ,U C ,则ab 两端的总电压U 为( )A 、C L R U U U U ++=B 、C L R U U U U -+=C 、222C L R U U U U -+=D 、22)(C L R U U U U -+=6、在RLC 并联电路中,三条支路上的电流分别为I1、I2、I3,则总电流I 是( )A 、321I I I I ++=B 、321I I I I -+=C 、23221)(I I I I -+=D 、232221I I I I -+=7、如图所示电路中,R=XL=XC ,则电压表的读数为( ) A 、0V B 、1V C 、2V D 、4V8、如图所示正弦交流电路中,已知Z=40+j40Ω,X C =40Ω,U=400V,则电压源U S 有效值为( )A 、283VB 、200VC 、400VD 、600V9、如图所示正弦交流电路中,已知R=4Ω,L=2mH,ω=2000rad/s ,则电流i1和i2的角度关系为( )A 、i1与i2同相B 、i1超前i2 135°C 、i1超前i2 90°D 、i1超前i2 45°10、在RLC 并联电路中,总电流•I 等于( )A 、C L R I I I I ••••-+=B 、C L R I I I I ••••++= C 、C L R I I I I -+=•D 、C L R I I I I ++=•11、供电线路采取提高功率因数措施的目的在于( )A 、减少用电设备的有功功率B 、减少用电设备的无功功率C 、减少用电设备的视在功率D 、减少电源向用电设备提供的视在功率12、在R 、L 串联的正弦交流电路中,R=4Ω,X L =3Ω,电路的无功功率Q=30var,则有功功率为( )A 、120WB 、80WC 、60WD 、40W13、12、在R 、L 并联的正弦交流电路中,R=4Ω,X L =3Ω,电路的无功功率Q=30var,则有功功率为( )A 、22.5WB 、40WC 、60WD 、80W14、正弦交流电路的视在功率S ,有功功率P 和无功功率Q 的关系为( )A 、222)(C L Q Q P S ++=B 、2222C L Q Q P S ++=C 、C L Q Q P S ++=D 、C L Q Q P S -+=15、当R 、L 、C 并联电路处于谐振状态时,若增大电感L 的值,则电路将呈现( )A 、阻性B 、感性C 、容性D 、性质不确定16、RLC 串联电路的谐振角频率ω0,设电路中的电源信号的角频率为ω,当ω=ω0时电路呈现( )当ω<ω0时电路呈现( )当ω>ω0时电路呈现( )A 、阻性、容性、感性B 、阻性、感性、容性C 、容性、阻性、感性D 、容性、感性、阻性17、当R 、L 、C 串联谐振时,若电感L 变为原来的21,则电容应变为原来的( ),才能保证在原频率下保持串联谐振。
(完整版)正弦交流电试题

一、选择题(每小题2分,共40分)1、产生串联谐振的条件是( )A. XL >XcB. XL <XcC. XL =XcD. XL≥Xc /2、交流电的三要素是指最大值、频率、( )。
A. 相位B. 角度C. 初相角D. 电压3、串联谐振是指电路呈纯( )性。
A .电阻 B. 电容 C. 电感 D. 电抗4、正弦交流电的幅值就是( )。
A.正弦交流电最大值的2倍B.正弦交流电最大值C.正弦交流电波形正负之和D.正弦交流电最大值的1.414倍5、一电感线圈接到f=50Hz 的交流电路中,感抗XL=50Ω,若改接到f=150Hz 的电源时,则感抗XL 为( )ΩA .150 B.250 C. ,10 D.606、一电容接到f=50Hz 的交流电路中, 容抗Xc=240Ω, 若改接到f=25Hz 的电源时,则容抗Xc 为( )Ω。
A. 80B.120C. 160D. 4807、纯电容电路的电压与电流频率相同, 电流的相位超前于外加电压为8.纯电容电路的电压与电流频率相同, 电流的相位超前于外加电压为( )A. 60°B. 30°C. 90°D. 180°8、已知工频正弦电压有效值和初始值均为380V ,则该电压的瞬时值表达式为( )A 、t u 314sin 380=V ;B 、)45314sin(537︒+=t u V ;C 、)90314sin(380︒+=t u VD 、537sin(31490)u t =+︒V/9、一个电热器,接在10V 的直流电源上,产生的功率为P 。
把它改接在正弦交流电源上,使其产生的功率为P /2,则正弦交流电源电压的最大值为( )A 、7.07V ;B 、5V ;C 、14V ;D 、10V 。
10、提高供电线路的功率因数,下列说法正确的是( )A 、减少了用电设备中无用的无功功率;B 、可以节省电能;C 、减少了用电设备的有功功率,提高了电源设备的容量;D 、可提高电源设备的利用率并减小输电线路中的功率损耗11、已知)90314sin(101︒+=t i A ,︒+=30628sin(102t i )A ,则( )A 、i 1超前i 260°;B 、i 1滞后i 260°;C 、相位差无法判断。
正弦交流电路习题

第2章 正弦交流电路一、选择题1.在负载为纯电容元件的正弦交流电路中,电压u 与电流i 的相位关系是( A ) A.u 滞后i 90º B.u 超前i 90º C.反相D.同相2.已知正弦电流的有效值相量为 则此电流的瞬时值表达式是下列式中的( C )A .10sin(ωt-45º)AB .10sin(ωt+45º)AC .102sin(ωt-45º)AD .102 sin(ωt+45º)A3.通过电感L 的电流为i L =62sin(200t+30º)A ,此电感的端电压U L =2.4V ,则电感L 为( B )A.2mHB.2mHC.8mHD.400Mh4.某电路元件中,按关联方向电流)90314sin(210︒-=t i A ,两端电压t u 314sin 2220=V ,则此元件的无功功率Q 为( c )A.-4400WB.-2200varC.2200varD.4400W5.纯电感元件的正弦交流电路如图示,已知电源的角频率为ω,其U与I 的正确关系是( b )A.L I j U ω-=B.L I j U ω=C.L1Ij Uω-= D. L1Ij Uω=6.图示电路中,u 为正弦交流电压,其角频率为ω,则此电路中的阻抗模|Z|为( a ) A.2221)C1L ()R R (ω-ω++ B.2221)C1L ()R R (ω+ω++C. C1L )R R (21ω-ω++ D.C1L R R 21ω+ω++U••R 2Cu7.R 、L 串联的正弦交流电路中,若u R =52sin(ωt+10°)V ,u L =52sin(ωt+100°)V ,则总电压u 为( b )A . 5sin(ωt+45°)VB . 10sin(ωt+55°)VC . 52sin(ωt+110°)VD . 102sin(ωt+70°)V8.在正弦交流电路中,某负载的有功功率P=1000W ,无功功率Q=577var ,则该负载的功率因数为( d ) A. 0.5B. 0.577C. 0.707D. 0.8669.图示正弦交流电路中U=220V ,R=ωL=1ωC=100Ω,此电路消耗的有功功率是( b )A . 2.2×100WB . 2.22×100WC . 2.2×300WD . 2.22×300WC•U10.电路如图所示,已知I 1=3A ,I 2=8A ,I 3=4A 则电流I 等于( b ) A .1A B .5A C .7A D .15AI 3••11.为了提高感性负载电路的功率因数,通常采用的方法有( d ) A .串联电感 B .串联电容C .并联电感D .并联电容12.图示正弦交流电路中,若C I 超前U角︒45,则R 应等于( c ) A.32Ω B. 1Ω C.1.5Ω D. 2Ω13.在图示的正弦电路中,5,C AB BC R X U U ==Ω=,且电路处于谐振状态,则复阻抗Z 为( a )-jX C•A.(2.5 2.5)j +ΩB.(2.5 2.5)j -ΩC.545∠ΩD.0∠Ω14.有一RLC 串联电路,已知5L C R X X ===Ω,端电压U=10V ,则I =( c )A A.23B.12C. 2D. 115.已知某感性负载的阻抗模7.07,5Z R =Ω=Ω,则其功率因数是( c ) A. 0.5 B. 0.6 C. 0.707 D.0.8二、填空题1.在正弦交流电路中,电源的频率越高,电感元件的感抗越 大 。
电工基础练习题(正弦交流电路)

电工技术练习题(正弦交流电路)一、填空题:1、正弦交流电路中,_______元件上电压与电流同相位;_______元件上电压在相位上超前电流900;________元件上电压滞后电流900。
2、已知一正弦交流电流i=102sin (314t+4π)安培,则该交流电的最大值为______安培,有效值为______安培,频率为_____赫兹,周期为______秒,初相为______。
3、三相四线制供电线路可以提供二种电压。
火线与零线之间的电压叫做________,火线与火线之间的电压叫做_______。
4、对称三相负载星形联接在三相四线制电路中,线电流是相电流_______倍,线电压是相电压_______倍,中线电流为______安培。
5、5个“10伏,30微法”的电容器串联,等效电容是____微法,耐压是___伏.6、在我国提供给日光灯使用的交流电的频率是 Hz ,其周期是 s 。
7、电容器有隔直流通交流的作用,这是由于电容具有 的特性;它在过程中电流逐渐减小,电压Uc 也逐渐减小。
8、已知一电感线圈通过50Hz 的电流时,其感抗为10Ω,当频率升高至5000Hz 时,其感抗为 。
9、正弦交流电的三要素是 、 和 。
10、在纯电容电路中由于电容不消耗电能,所以 功率为零.二、选择题:1、线圈电感的单位是——-----—。
(A)亨利 (B)法拉 (C )韦伯 (D)特斯拉2、在纯电感电路中,下列各式正确的是——----(A )I= L U (B )I= LU ω (C )I=ωLU (D )I=L X u 3、同一个三相对称负载接在同一电源中,作三角形联接时三相电路的总有功功率是作星形联接时的_______(A )3倍 (B )3倍 (C )31倍 (D )31倍 4、若两个正弦交流电为u 1=102sin(314t+2π)伏特,u 2=10sin (128t+2π)伏特,则_______ (A )u 1比u 2超前 (B )u 1比u 2滞后(C)在相位上同相 (D)不能比较5、交流电的功率因数等于_______(A)有功功率/无功功率(B)有功功率/视在功率(C)无功功率/有功功率(D)视在功率/有功功率6、下列说法正确的是( )A.RL串联电路中总电压超前电流π/2B.RC串联电路中电容两端电压滞后电流π/2C.无功功率即是无用的功率D.无功功率与视在功率的比值叫做功率因数7、在RLC串联电路中,总电压与电流的相位关系如图所示,这个电路呈( )A。
第6章 正弦交流电路的分析练习题及答案

第6章 正弦交流电路的分析习题答案6-1 在RL 串联的交流电路中,R 上端电压为16V ,L 上端电压为12V ,则总电压为多少?解:V 2012162222=+=+=L R U U U6-2 RL 串联电路接到220V 的直流电源时功率为1.2kW ,接在220V 、50Hz 的电源时功率为0.6kW ,试求它的R 、L 值。
解:接直流电源时,电感元件相当于短路,只有电阻作用,因此Ω===3.40k 2.122022P U R ,接交流电源时,A 86.33.40k6.0===R P I , 由此得707.086.3220k 6.0cos =⨯==UI P φ,所以阻抗角︒=45φ, 感抗Ω=︒⨯=⋅=3.4045tan 3.40tan φR X L ,H 13.05014.323.402=⨯⨯==∴f X L L π6-3 已知交流接触器的线圈电阻为200Ω,电感量为7H ,接到工频220V 的交流电源上,求线圈中的电流I 。
如果误将此接触器接到220V 的直流电源上,线圈中的电流又为多少?如果此线圈允许通过的电流为0.2A ,将产生什么后果?解:线圈接工频交流电时,Ω=⨯+=+=+=2207)7314(200)(222222L R X R Z L ω,由此得线圈中电流A 1.02207220≈==Z U I 。
如果将该线圈接到直流电源上,A 1.1200220≈==R U I 如果此线圈允许通过的电流为0.2A ,在直流电中线圈将烧毁,在工频交流电中可以正常使用。
6-4 在RLC 串联电路中,已知R =10Ω,L =1H ,C =0.005F ,电源电压V 20sin 2100t u =,计算:(1)X C 、X L 、Z ;(2)I &、R U &、LU &、C U &,并画出相量图; (3)写出i 、u R 、u L 、u C 的表达式。
解:(1)X C =1/(ωC )=1/(20×0.005)=10Ω,X L =ωL =20×1=20Ω,Z=R+j(X L -X C )=10+ j10=102∠45°。
(完整版)正弦交流电试题

C、减少了用电设备的有功功率,提高了电源设备的容量; D、可提高电源设备的利用率并减小输电线路中的功率损耗
11、已知 i1 10 sin(314t 90) A, i2 10 sin(628t 30 )A,则( )
A、i1 超前 i260°; B、i1 滞后 i260°; C、相位差无法判断。 12、纯电容正弦交流电路中,电压有效值不变,当频率增大时,电路中电流将( )
题5图
4
/9、一个电热器,接在 10V 的直流电源上,产生的功率为 P。把它改接在正弦交流电源上,
使其产生的功率为 P/2,则正弦交流电源电压的最大值为( )
A、7.07V;
B、5V;
C、14V;
D、10V。
10、提高供电线路的功率因数,下列说法正确的是( )
A、减少了用电设备中无用的无功功率;
B、可以节省电能;
1
The shortest way to do many things is
15、已知非正弦周期电流 i(t) 4 2.5cos wt 1.5cos(2wt 900 ) 0.8cos3wtA ,则它
的有效值I =( )。
A. 42 2.52 1.52 0.82 A
B. 42 2.52 1.52 0.82 A 222
The shortest way to do many things is
一、选择题(每小题 2 分,共 40 分)
1、产生串联谐振的条件是( )
A. XL>Xc B. XL<Xc C. XL=Xc D. XL≥Xc /
2、交流电的三要素是指最大值、频率、( )。
A. 相位 B. 角度 C. 初相角 D. 电压
1
C.
42 2.52 1.52 0.82 A
第三章:正弦交流电路

& =U & = − jI & X = − j 2 × 50∠45 o = 50 2∠ − 45 o V U ao C C C & =U & = jI & X = j 2 × 50∠ − 45o = 50 2∠45o V U bo L L L & & & U = U − U = 50 2∠ − 45o − 50 2∠45o =
2
& 与U & 之间的相位差 I R
ϕ = arctan
XC 1 = arctan R Rω C
第三章
正弦交流电路
31
& 与U & 之间的相位差 U θ = 2ϕ ab 由上式可知,当改变电阻 R 时,输出电压 Uab 是一个不变恒定的值,即有 U U ab = 2 20 本题中 U ab = = 10V 2 当电阻 R 由零变到无穷大时, ϕ 角由 90o 变到零, θ 角由 180o 变到零。当电阻 R & 的相位从 180o 减小到: 由零变到 1.5kΩ 时, U
& = jI &X = j4.4 × 40∠73o = 176∠163o V U L L & & U C = − jIX C = − j4.4 × 80∠73o = 352∠ − 17 o V 【例题 3.2】 图 3.2(a)为 RC 移相电路。已知电阻 R = 100 Ω ,输入电压 u1 的频率为
Z = R + j( X L − X C ) = 30 + j(40 − 80) = 30 − j40 = 50∠ − 53o Ω
28
电工学试题精选与答题技巧
o & & = U = 220∠20 = 4.4∠73o Α I Z 50∠ − 53o & =I &R = 4.4 × 30∠73o = 132∠73o V U R
正弦交流电路_典型例题(全)
a
Zeq
2.5 2.5
Zeq
Po I 2 Ro Po最大则I最大
I
Zeq
Uoc Ro
1 j
C 0
.+ Uoc − Zeq
b . I
1 R0 C0
第二章 正弦交流电路
2.4 正弦交流电路中的功率与功率因素的提高
代入可得:
I
U oc
3 j(1- 1 )
C0
I
Uoc
22
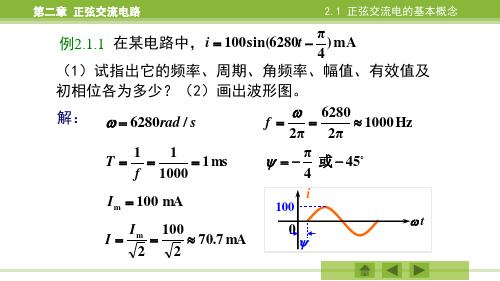
f 6280 1000 Hz
2π 2π
π 或 45
4
i
100
0
t
第二章 正弦交流电路
2.1 正弦交流电的基本概念
例2.1.2若 i1 10 2 sin(t 30 ),A 分别用相量和相量图表示。
i2 6 2 sin(t 60 ) A
有效值相量: I1 1030A
I2 6 60A 最大值相量:I1m 10 230A
解:
cos1=0.6 1=53.13 + cos=0.9 =25.84 U
C
P
U
2
(tgφ1
tgφ
)
_
P=20kW C
cos1=0.6
20103 (tg53.13 tg25.84) 375 F
314 3802
第二章 正弦交流电路
例2.5.1 串联谐振应用
2.5 交流电路的频率特性
L1
C
L2
L3
RL2 20C1 150pF
解:I0
Us1 RL2
0.5 A
解: u 220 2 sint V
11
XC C 2π fC 135.5
U 220
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
-jXC
Z AB = ( R1 || jX L ) + ( R2 || − jX C ) = 150 − j50(Ω)
可见: 可见:
求:I 和X
A ZAB
& I
Z
& & E = U ABO
(1) 当X=50Ω 时电 Ω 流的有效值达到最 大。 (2)Imax=1.1A
& E
例1
下图中已知:I1=10A、UAB =100V, 求: A 、UO 的读数
•
(P150 )4.5.1
− j10 Ω
•
I1
A
A
C2
•
B
C1 I
I2
5Ω j5Ω UO
解题方法有两种: 1.利用复数进行相量运算 2.利用相量图求结果
解法1: 利用复数进行相量运算
•
− j10 Ω
•
I1
A
A
UO
•
C2
5Ω
−6
& I
-jXC
设参考节点如图所示。 设参考节点如图所示。 两点把待求支路断开, 从 A、B两点把待求支路断开,分别求 、B两 两点把待求支路断开 分别求A 两 点的开路电压
(交流习题课-10)
& 端的入端阻抗 UABO 和AB端的入端阻抗ZAB。
R1
R2 B -jXC
& U
A jXL
求:AB端开路电压 jX L & = & V AO U R1 + jX L
欲使Z中流过的电流的有效值最大 求:欲使 中流过的电流的有效值最大, 欲使 中流过的电流的有效值最大, X=? Imax=?
(交流习题课-9)
解:用戴维南定理求解。 用戴维南定理求解。
R1 R2 Z
& U
A
jXL
B
& U = 220∠ − 45o V X L = 1000× 0.1 = 100Ω X C = 1 /(1000× 5 ×10 ) = 200Ω
B
CI1
I2
已知: I1=10A、 UAB =100V, 求:A、UO的读数
j5 Ω
& 设: U AB 为参考相量,
则:
& 即:U AB = 100 ∠ 0 o V
o
& I 2 = 100
5 + j5
= 10 2 ∠ − 45
A
& = 10 ∠ 90 o = j10 A I1 & = I + I = 10∠0o A ∴ I &1 &2
B
o & E 220∠45 & I= = A Z + Z AB 200 + j ( X − 50)
(交流习题课-12)
例4: 移相电路 :
R1 R 2
& 已知: 已知 R1=R2 , U i = 2U ∠ 0 o
证明: 证明 当R由 0→∞ 变化时 由 →∞ 变化时, & 的有效值不变, & U 的有效值不变 U
代入 ω 、L、C1 得: 、
C2 = 75.1 µF
(交流习题课-20)
& & UR 与 UC 的相位差总等 & 于90°。如果以 U 为直径 ° i
作一个半圆 ,当 R由 0→∞ 当 由 →∞
& UR
ϕ
& UO
& 变化时, 变化时, & R 与 UC 构成的 U
直角顶点总在这个半圆上。 直角顶点总在这个半圆上。
& U R1
& UC & Ui & UR2
(2) UO=0.5Ui=U 即UO的有效值恒定不变。 的有效值恒定不变。 (3) 当 R=0 时,UR=0V ,ϕ =180° ° ° 当 R=∞ 时,UC=0V, ϕ =0° ∞
& Ui
1
R1
R
& UR
2
(2)用相量图表示各相量的关系。 用相量图表示各相量的关系。 用相量图表示各相量的关系
& UR2
& UO
R2 C
& UR
& UC
& U R1
ϕ
& UO
& UC & Ui & UR2
& & & & & UO =UR2 −UC = UR2 +( −UC )
(交流习题课-16)
由相量图可见: 由相量图可见 (1)
C1 C2 解:
ui
已知: 已知:
L
R
uo
被滤掉
ui = 2U1 sin ωt + 2U 2 sin 3ωt (1)若使 u O = 2U 1 sin ω t ,L 、C1 应在 3ω 下 )
产生并联谐振, 的信号才能被滤掉。 产生并联谐振,3ω 的信号才能被滤掉。
∴X
(交流习题课-19)
C1
= X
一般正弦交流电路的解题步骤
在正弦交流电路中,若正弦量用相量表示,电路参 数用复数阻抗表示,则直流电路中介绍的基本定律、 公式、分析方法都能用。具体步骤如下: 1、据原电路图画出相量模型图(电路结构不变)
R →R、L → jXL、 C →− jXC & & & u →U、 i →I、 e →E
2、根据相量模型列出相量方程式或画相量图 3、用复数符号法或相量图求解 4、将结果变换成要求的形式
UC1=I XC1=100V uC1落后于 i 90°
& I1
& & & I = I1 + I 2
& U AB
45°
& I
I&2
C1
& UO
由图得: I=5.3 图中, 图中 I1=10A, I2=10 2 A, U= 200V, R=5Ω, Ω XL=R2; 试求 XC, XL, R2 试求I,
(交流习题课-7)
相位角交待 不清楚!
& = U ∠0o 解 : 设U AB & AB
& I
R A
& I1 & I
2
- jXC B jXL
& I1 = 10∠90o A & I = 10 2∠ − 45o A
2
& U
R2
& = 10∠0o A I & = 50∠0o V U
R
I=10A , XC=15Ω , Ω R2=7.5Ω , XL=7.5Ω Ω Ω
& I
R A
& I1 & I
2
- jXC B jXL
& U
R2
(交流习题课-6)
& I
解:
R A
& I1 & I
2
- jXC B jXL
& I1 = 10∠90 A & = 10 2∠ − 45o A I
o 2
& U
R2
& = 10∠0o A I U R = 50V U AB = 150V
I=10A, XC=15Ω, R2=7.5Ω, XL=7.5Ω Ω Ω Ω
1
& & & U O= V1 −V2
(交流习题课-14)
1 & = 1U − & & UO Ui i 1 + j ω RC 2 & U i − 1 + j ω RC = 2 1 + j ω RC & Ui = 2 1 + (ω RC ) ∠ (180 − tg ω RC )
2 o −1
1 + (ω RC ) ∠ tg ω RC
(交流习题课-17)
因此,相位差在 因此, 0→180o间变化 →
例四: 例四:选频电路
C1 C2
ui
已知: 已知:
L
R
uo
ui = 2U1 sin ωt + 2U 2 sin 3ωt L = 0.12 H
ω = 314 rad/s
若使
uO =
2U 1 sin ω t
(交流习题课-18)
C1 = ? C 2 = ?
A读数为 10安
•
− j10 Ω
•
I1
C1
I
A
A
•
I2
C2
5Ω
B
已知: I1=10A、 UAB =100V, 求:A、UO的读数
j5 Ω
UO
& = I + I = 10∠0o A I &1 &2
& & U C 1 = I( − j10 ) = − j100 V
& & & U o = U C 1 + U AB = 100 − j100 = 100 2 ∠ − 45
j100 o = 220 ∠ − 45 100 + j100 = 110 2 ∠ 0
o
V
& V BO =
& U ABO
(交流习题课-11)
− jX C & = 110 2 ∠ − 90 o V U R 2 − jX C & − V = 220 ∠ 45 o V & = V AO BO
求: AB端入端阻阻抗 ZAB
L
1 ⇒ = 3ω L 3ω C 1
值得: 代入 ω 和 L 值得:
C 1 = 9 .4 µ F
