二进制下的康托展开
二进制相移键控基本原理

二进制相移键控基本原理今天来聊聊二进制相移键控的原理。
我最开始接触这个概念是在研究通信技术的时候。
咱们就从生活中的一个小场景说起吧。
你想啊,假如你和朋友玩一种特别的游戏,你们只能通过闪手电筒来传递信息,而且只有两种状态,亮亮闪闪的方式就类似于二进制里的0和1。
这就有点像二进制相移键控的雏形啦。
二进制相移键控呢,简单来说,就是通过改变信号相位来表示不同的二进制信息。
这里的相位是什么呢?打个比方,就像咱们看时钟,时针指向不同的刻度就好像是不同的相位。
在二进制相移键控里,0和1就对应着不同的相位状态。
比如说,0可能对应的是0度相位,1可能对应的是180度相位。
有意思的是,传输信号为啥要用这种改变相位的方式呢?其实是为了更有效地利用通信资源。
就好比我们在有限的道路上(通信信道),想要运送更多种类的货物(信息),那就得通过巧妙的方式去标记这些货物,改变信号相位就像是给货物贴上特殊的标签。
说到这里,你可能会问,那接收端是怎么识别这些相位所代表的二进制数呢?接收端就像一个很聪明的小助手,它能够根据接收到的信号相位的变化,准确判断是0还是1。
这其实依赖于一些特定的算法和线路设计。
在实际应用方面,二进制相移键控在早期的数字通信里应用非常广泛。
举个例子,以前的一些无线电台和最早期的数字调制解调器就用这种技术。
不过,它也有注意事项哦。
因为在实际传输中可能会受到噪声或者干扰,就像咱们传递闪手电筒信息的时候突然有别的强光晃眼睛了,这就可能导致接收端识别错误。
我一开始也不明白为啥不能直接用高低电平这种简单方式,非要采用这么复杂的相移键控呢?后来才知道这是为了适应越来越复杂的通信需求。
在学习这个原理的过程中,我逐渐明白每一个技术都是逐步发展来的。
这里还有延伸的思考,随着技术越来越发达,二进制相移键控是否会逐渐被新的技术完全替代呢?现在的通信技术发展飞快,像更复杂的正交相移键控等技术不断出现,但二进制相移键控作为基础,依然在某些简单设备中有着不可或缺的地位。
十进制二进制八进制十六进制关系新
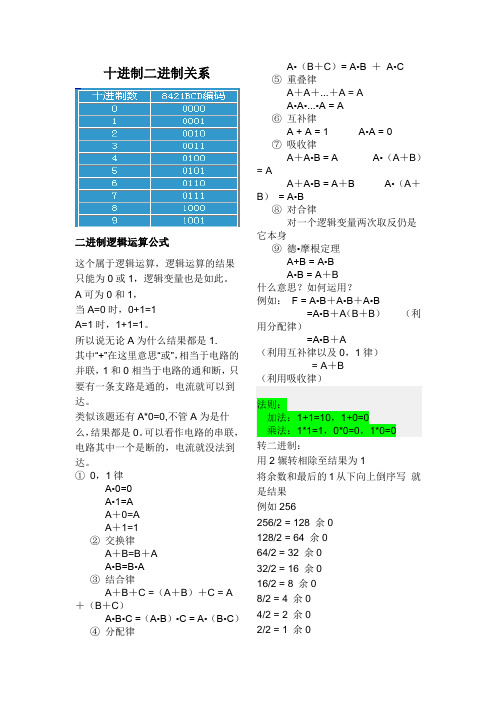
十进制二进制关系二进制逻辑运算公式这个属于逻辑运算,逻辑运算的结果只能为0或1,逻辑变量也是如此。
A可为0和1,当A=0时,0+1=1A=1时,1+1=1。
所以说无论A为什么结果都是1.其中“+”在这里意思“或”,相当于电路的并联,1和0相当于电路的通和断,只要有一条支路是通的,电流就可以到达。
类似该题还有A*0=0,不管A为是什么,结果都是0。
可以看作电路的串联,电路其中一个是断的,电流就没法到达。
①0,1律A•0=0A•1=AA+0=AA+1=1②交换律A+B=B+AA•B=B•A③结合律A+B+C =(A+B)+C = A+(B+C)A•B•C =(A•B)•C = A•(B•C)④分配律A•(B+C)= A•B +A•C⑤重叠律A+A+...+A = AA•A•...•A = A⑥互补律A + A = 1 A•A = 0⑦吸收律A+A•B = A A•(A+B)= AA+A•B = A+B A•(A+B)= A•B⑧对合律对一个逻辑变量两次取反仍是它本身⑨德•摩根定理A+B = A•BA•B = A+B什么意思?如何运用?例如: F = A•B+A•B+A•B=A•B+A(B+B)(利用分配律)=A•B+A(利用互补律以及0,1律)= A+B(利用吸收律)法则:加法:1+1=10,1+0=0乘法:1*1=1,0*0=0,1*0=0转二进制:用2辗转相除至结果为1将余数和最后的1从下向上倒序写就是结果例如256256/2 = 128 余0128/2 = 64 余064/2 = 32 余032/2 = 16 余016/2 = 8 余08/2 = 4 余04/2 = 2 余02/2 = 1 余0故二进制为100000000二进制的加减例如:1、100100000+10010000+100100 =110110000+100100=1110101002、如果人工计算,应该按照减法进行,即:0000 1100 - 1111 0111 = 0001 0101。
康托三分集几个性质的一种证明方法

康托三分集几个性质的一种证明方法白秀琴(1) 杨宝玉(2)((1).平顶山工业职业技术学院,河南平顶山467001;(2).平顶山工业职业技术学院,河南 平顶山467001)摘要:通过釆用三进制表示法,将康托三分集中的数用三进制表示,通过建立一一对应从而证明了康托三分集是完备的、列紧的、不可数的。
关键词:度量空间;康托三分集;不可数集;证明方法中图分类号: O141 文献标示码:A康托三分集的有关性质,在不少文献中(如文中[1]~ [4] 中)都有表述,但其证明不够简洁,难懂。
文章通过引入度量空间,建立一一对应关系从而比较简洁的证明了康托三分集的性质。
1 预备知识定义 1 在集合X 上的一个函数d:+ℜ→X ⨯X , 若满足以下性质:∀X z y x ∈,, (1)d (x,y)≥0, d (x,y)=0当且仅当x=y; (2) d (x,y)=d (y,x); (3) d (x,y)≤d (x,x)+d (y,y); 则称d (x,y) 为x 与y 之间的距离,(X,d )称为一个度量空间. 定义 2 在度量空间X 中,若x X x ,∈∀都是一个极限点,则称X 是完备的. 定义 3 在度量空间X 中,若{}0,x x X x k n n →∃⊂∀,则称X 列紧的.定义 4 在度量空间X 中,若0,, M X y x ∃∈∀,使得d (x,y) <M, 则称X 是有界的. 2 康托三分集3 定义 6将区间[]1,00=s 三等分,挖去中间的开区间⎪⎭⎫⎝⎛32,31,剩下的为⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=1,3231,01 S ,将剩下的两个闭区间⎥⎦⎤⎢⎣⎡31,0再分别三等分,挖去各自中间的开区间⎪⎭⎫ ⎝⎛92,91与⎪⎭⎫ ⎝⎛98,97,记剩下的⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=1,9897,3231,9291,02 s . 再将剩下的四个闭区间分别三等分,再挖去各自中间的开区间, ……这样继续不断进行下去,由区间中剩下的点所构成的集合称为康托三分集,简称为康托集,记作K ,如下图所示 _________________________________0s____________01s ____________2____002s ____02____20_____22_0003s_002 _020_022_200_202_220_222∞==1n nsK定理 康托三分集是完备的、列紧的、有界的、不可数集.3 用三进制表示康托三分集K用三进制表示一个数有有限制和无限制两种表示形式. 我们常选择无限制表示形式. ,除非末位是2 时才用有限制形式表示. 例如31有两种三进制形式:.1和 . 2_0,然而我们选择无限制形式表示形式.2_0 。
日记(菜的连比赛都参加不了)

⽇记(菜的连⽐赛都参加不了)(差评,去年就在我家门⼝),4.5~4.7,4.5~4.7今年R1在河海⼤学常州分校(差评,去年就在我家门⼝)今年R1在河海⼤学常州分校,连⾮正式都没有了我没有正式名额qwqwq我没有正式名额qwqwq,连⾮正式都没有了(赛(JSOI2019/APIO2019)后再补吧(怕是永久咕咕咕了))懒着写题解就写⽇记,咕咕咕?懒着写题解就写⽇记,咕咕咕?(赛(JSOI2019/3.19 准备⽉考,颓废了⼀晚上但愿⽂化课不要倒数3.20 ⽉考爆炸然后sb错误调了⼀晚上晚上⽆聊写,实际我考场上当时已经接近正解了,但还是⾃⼰太菜,没想起来相似的题,然后sb错误调了⼀晚上晚上⽆聊写,实际我考场上当时已经接近正解了,但还是⾃⼰太菜,没想起来相似的题,3.21 ⼜做了⼀道ynoi,莫队+bitset被卡了,最后写了⼀个很妙的树状数组3.22 下午停了⼀⼩会课,做了两道fft的经典题晚上学了⼀下linux系统qwqwq3.23 凌晨才睡,⽐我⼩还⽐我强的lxr问我cf题的做法,然后我不会凌晨才睡,⽐我⼩还⽐我强的lxr问我cf题的做法,然后我不会3.23⼀⼤早上数学课,学换底公式,差点把我整晕然后下午晚上都在做题第⼀次忘开ll,觉得后⾯题不太可做就去做⾃⼰的题了,觉得后⾯题不太可做就去做⾃⼰的题了先闲着没事写了咕咕⽉赛的T1,先闲着没事写了咕咕⽉赛的T1,第⼀次忘开llP3966 [TJOI2013]单词 :以前⽤ac⾃动机写过,但我现在不会写ac⾃动机了,写了个后缀数组P5268 [SNOI2017]⼀个简单的询问 :莫队+推公式P2485 [SDOI2011]计算器 :bsgs基础题UVA1223 Editor :后缀数组裸题,输出height的最⼤值,先⽤后缀数组找出两个⼦串的lcs,剩下暴⼒找就⾏了UVA760 DNA Sequencing :因输出格式整错了很久,先⽤后缀数组找出两个⼦串的lcs,剩下暴⼒找就⾏了UVA760 DNA Sequencing :因输出格式整错了很久P4474 王者之剑 :推导⼀下发现就变成了P2774 ⽅格取数问题 ,写个跑⼀下最⼩割就⾏了,两道题代码⼀模⼀样,双倍经验,两道题代码⼀模⼀样,双倍经验,P4474 王者之剑 :推导⼀下发现就变成了P2774 ⽅格取数问题 ,写个跑⼀下最⼩割就⾏了,双倍快乐P4462 [CQOI2018]异或序列 :做⼀个异或前缀和,跑莫队开桶统计就⾏了好困啊qwqwq3.24噩耗来临:连⾮正式名额都没有了,⼀切初中⽣禁⽌参加省选qwqwqAPIO有可能变成NOI春令营我是不是该在APIO/NOI春令营之后退役?还是先好好做题吧qwqwqCF547E Mike and Friends :后缀数组+线段树⼤⼒瞎搞CF427D Match & Catch :后缀数组求两个字符串最短的且在每个串中仅出现过⼀次公共⼦串长度P3355 骑⼠共存问题 :⿊⽩染⾊,求最⼩割P5030 长脖⼦⿅放置 :还是⿊⽩染⾊(染⾊⽅法略有不同),求最⼩割SP32577 ADAPHOTO - Ada and Terramorphing :后缀数组求最长公共⼦串P4542 [ZJOI2011]营救⽪卡丘 :神奇建模,跑最⼩费⽤最⼤流3.25思考了⼀天是否该退役,决定还是作为爱好吧,但停课还是算了UVA1303 Wall :有点像信⽤卡凸包,就是凸包周长+整圆的周长P5108 仰望半⽉的夜空 :后缀数组+⼆分答案3.26⽩天在学校学计⼏?P3763 [TJOI2017]DNA :建出sa后暴⼒就⾏了(P1452 Beauty Contest :旋转卡壳模板题,但要注意特判不能形成凸包的情况P4662 [BalticOI 2008]⿊⼿党 :⼗分套路的拆点跑最⼩割,最后搜索⼀下,寻找割边3.27我apio⾮正式也没有,想好好退役也得到NOIP2019啊qwqwq颓废的⼀天,⽂竞两开花,就写了⼀下你的名字,sa被卡常了3.28⼏乎肛了⼀整天⽂化课qwqwq,晚上只做了两道sb⽹络流(数据有坑)UVA1194 Machine Schedule :最⼩点覆盖=最⼤匹配,上⽹络流就⾏了(数据有坑)UVA1194 Machine Schedule :最⼩点覆盖=最⼤匹配,上⽹络流就⾏了P4304 [TJOI2013]攻击装置 :骑⼠共存原题?真·良⼼。
二进制与数制转换课件-高中信息技术人教版必修1

2.(77)8
=( 63 )10
5.(132)10=( 204 )8
3.(11E)16
=( 286 )10
6.(321)10=( 141 )16
7 .( 11 00110 1101 ) 2 = (
3155
8.(110011100110) 2 =(
CE6
)8
) 16
信息技术
课堂例题
9.(77)8=( 111111 )2
110
100
010
二进制十六进制
信息技术
四缩一,一放四
把二进制数由低位到高位,每四位分割(不满四位用0填
充),分割后的每四位二进制转化为相应的10进制,最后
用16进制表示。
0111 1010
2进制
7
10
10进制
7
A
16进制
【牛刀小试】二进制数(11011001)2转换成十六进制数是( A)
(A)D9H
1.2 位权:
一个与数字位置有关的常数,位权=−
2. 常见数制之间的转换
2.1 十进制转二进制、八进制和十六进制:
除R取余法
2.2 二进制、八进制和十六进制转十进制:
位权法
2.3 二进制与八进制的相互转换:
二进制数的三位相当于八进制数的一位
2.4 二进制与十六进制的相互转换:
二进制数的四位相当于十六进制数的一位
在实际应用中,还尝过哪些计数制?
在实际应用中,还使用其他的计数制,如三双鞋(两只鞋为一双)、两周实
习(七天为一周)、4打信封(十二个信封为一打)、半斤八两(一斤十六
两)、三天(72小时)、一刻钟(15分)、二小时(120分)等等。
这种逢几进一的计数法,称为进位计数制。简称“数制”或“进制”。
二进制魔术原理

二进制魔术原理嘿,你有没有想过,在我们这个看起来如此复杂、充满各种信息的数字世界里,其实有一种超级神奇的“魔法”在背后默默支撑着一切?这魔法呀,就是二进制。
我有个朋友,叫小李,他以前对计算机啥的一窍不通。
有一次我们聊天,我就跟他说:“小李啊,你知道吗?你每天用的手机、电脑,它们内部都在玩一种超级有趣的魔术,这个魔术的秘诀就是二进制。
”小李瞪大了眼睛,就像听到了天方夜谭一样,说:“二进制?那是什么玩意儿?听起来就很神秘。
”我就开始给他解释。
我说:“你看啊,我们生活中的数字是十进制的,就像我们有十个手指头,所以很自然地就用0到9这十个数字来表示数。
但是在计算机的世界里,就像一个奇怪的小王国,这里的居民只认识0和1,这就是二进制。
你可以把0想象成一个小矮人在睡觉,1呢,就是这个小矮人醒着,在做事情。
”小李听了哈哈大笑,说:“你这比喻可真逗。
”那二进制怎么就成了魔术呢?我接着说:“想象一下,你有一个装满宝藏的盒子,这个盒子里的宝藏其实就是各种信息,像你手机里的照片、音乐、你打的字发的消息。
计算机就像一个超级魔术师,它要把这些宝藏用0和1来表示。
比如说一个字母A,在计算机里可不是像我们手写的那样,它是被转化成了一串由0和1组成的代码。
这就好比把一个美丽的花朵,拆成了一个个小小的零件,每个零件就是0或者1。
”这时候小李有点疑惑了,他问:“那怎么把这些0和1又变回我们能看懂的东西呢?这不是把好好的东西拆得乱七八糟了吗?”我笑了笑说:“这就是这个魔术的神奇之处啊。
你看,计算机有一套规则,就像魔术师有自己的魔法咒语一样。
当它要把这些0和1组合展示给我们看的时候,它就按照这个规则,把0和1重新组合成我们能认识的字母、数字或者图像。
这就好像那个超级魔术师又把那些小小的零件重新组装成了原来美丽的花朵。
”我又给他举了个例子。
我说:“你知道电灯开关吧?它只有开和关两种状态,开就相当于1,关就相当于0。
如果我们用一组这样的开关来表示信息,比如说三个开关,那就有000、001、010、011、100、101、110、111这八种状态。
八数码(双向搜索)解题报告

a)广搜的优化:用布尔数组、哈希表、二叉排序树等提高判重效率,用双向搜索、滚动数组改善空间效率,用二进制改进产生式、存储空间以及判重效率例题:【问题描述】:在3 * 3 的棋盘上,摆有八个棋子,每个棋子上标有1 至8 的某一数字。
棋盘中留有一个空格。
空格周围的棋子可以移到空格中。
要求解的问题是,给出一种初始布局[ 初始状态] 和目标布局[ 目标状态] ,输出从初始布局到目标布局的转变至少需要的步数。
【输入格式】输入由两行组成,每行8个数,分别表示初始状态和目标状态:【输出格式】输出步数,若无解输出“No solution!”。
【输入输出样例】输入文件名:8num.in283164705123804765输出文件名:8num.out5时限:前两组数据不超过1秒,第三组数据不超过10秒program shuangguang8; {Made By P.D.B (AYLA)}{此程序可全部AC,用时0 ms}const ji:array[1..8]of longint=(40320,5040,720,120,24,6,2,1);{康托展开时用到的常数,分别为为9-1的阶乘}var d1,d2:array[0..10000]of string[10];{两个队,分别存放双向广搜的一支} k1,k2:array[0..370000]of boolean;{Hash表,康托展开的数组,判重用}kb1,kb2:array[0..370000]of integer;{Hash表,康托展开的数组,存放每种情况的步数}fu1,fu2:array[0..10000]of integer;{两个队,存放当前步数}w1,w2,h1,t1,h2,t2,i,j,tol,lei,b:longint;m,n,z:string[10];l,c:char;{辅助变量} procedure print;{输出}beginwriteln(kb1[lei]+kb2[lei]);{从起始到当前情况与从目标到当前情况的步数和} halt;end;function PDhash1(x:string):boolean;{判断当前情况在队列1中是否重复}beginlei:=0;for i:=8 downto 1 do {康托展开,i表示当前位数}begintol:=0;for j:=i to 9 do {将当前位数前比当前位数大的数的个数与当前位数的阶乘相乘,并累加到l变量lei中}if x[i]>x[j] then inc(tol);lei:=lei+ji[i]*tol;end;PDhash1:=k1[lei];end;function PDhash2(x:string):boolean;{判断当前情况在队列2中是否重复}beginlei:=0;for i:=8 downto 1 dobegintol:=0;for j:=i to 9 doif x[i]>x[j] then inc(tol);lei:=lei+ji[i]*tol;end;PDhash2:=k2[lei];end;procedure hash1(x:string[10]);{将当前情况加入到队列1的Hash表中,可与PDhash1过程合并,为便于理解将其分开}beginlei:=0;for i:=8 downto 1 dobegintol:=0;for j:=i to 9 doif x[i]>x[j] then inc(tol);lei:=lei+ji[i]*tol;end;k1[lei]:=true;kb1[lei]:=fu1[t1]; {将当前步数存入康托展开后的数组中}if k2[lei] then print; {如果反向搜索状态中由此情况,则输出,并结束程序} end;procedure hash2(x:string[10]);{将当前情况加入到队列2的Hash表中,可与PDhash2过程合并,为便于理解将其分开}beginlei:=0;for i:=8 downto 1 dobegintol:=0;for j:=i to 9 doif x[i]>x[j] then inc(tol);lei:=lei+ji[i]*tol;end;k2[lei]:=true;kb2[lei]:=fu2[t2]; {将当前步数存入康托展开后的数组中}if k1[lei] then print; {如果正向搜索状态中由此情况,则输出,并结束程序} end;procedure init;{读入}beginfillchar(k1,sizeof(k1),false);fillchar(k2,sizeof(k2),false);{for i:=1 to 3 dobeginfor j:=1 to 3 dobeginread(c); m:=m+c; read(c);end;readln;end;}m:='123456780';for i:=1 to 3 dobeginfor j:=1 to 3 dobeginread(c); n:=n+c; read(c);end;readln;end;end;procedure WFS;{双向广搜}begint1:=1;t2:=1;h1:=0;h2:=0;repeatinc(h1); {正向搜索}w1:=pos('0',d1[h1]);if w1-3>0 then {查找'0'的位置,判断'0'可移动的方向}beginz:=d1[h1];l:=z[w1];z[w1]:=z[w1-3];z[w1-3]:=l;{移动'0'}if not PDhash1(z) then {判断是否重复}begininc(t1); d1[t1]:=z;fu1[t1]:=fu1[h1]+1; {当前情况步数等于其父节点的步数加1}hash1(z); {加入Hash表}end;end;if w1+3<10 thenbeginz:=d1[h1];l:=z[w1];z[w1]:=z[w1+3];z[w1+3]:=l;if not PDhash1(z) thenbegininc(t1); d1[t1]:=z;fu1[t1]:=fu1[h1]+1;hash1(z);end;end;case w1 mod 3 of {判断'0'可移动的方向}0: beginz:=d1[h1];l:=z[w1];z[w1]:=z[w1-1];z[w1-1]:=l;if not PDhash1(z) thenbegininc(t1); d1[t1]:=z;fu1[t1]:=fu1[h1]+1;hash1(z);end;end;1: beginz:=d1[h1];l:=z[w1];z[w1]:=z[w1+1];z[w1+1]:=l;if not PDhash1(z) thenbegininc(t1); d1[t1]:=z;fu1[t1]:=fu1[h1]+1;hash1(z);end;end;2:beginz:=d1[h1];l:=z[w1];z[w1]:=z[w1-1];z[w1-1]:=l;if not PDhash1(z) thenbegininc(t1); d1[t1]:=z;fu1[t1]:=fu1[h1]+1;hash1(z);end;z:=d1[h1];l:=z[w1];z[w1]:=z[w1+1];z[w1+1]:=l;if not PDhash1(z) thenbegininc(t1);d1[t1]:=z;fu1[t1]:=fu1[h1]+1;hash1(z);end;end;end;inc(h2);{反向搜索,过程与正向搜索基本相同}w1:=pos('0',d2[h2]);if w1-3>0 thenbeginz:=d2[h2];l:=z[w1];z[w1]:=z[w1-3];z[w1-3]:=l;if not PDhash2(z) thenbegininc(t2);d2[t2]:=z;fu2[t2]:=fu2[h2]+1;hash2(z);end;end;if w1+3<10 thenbeginz:=d2[h2];l:=z[w1];z[w1]:=z[w1+3];z[w1+3]:=l;if not PDhash2(z) thenbegininc(t2);d2[t2]:=z;fu2[t2]:=fu2[h2]+1;hash2(z);end;end;case w1 mod 3 of0: beginz:=d2[h2];l:=z[w1];z[w1]:=z[w1-1];z[w1-1]:=l;if not PDhash2(z) thenbegininc(t2);d2[t2]:=z;fu2[t2]:=fu2[h2]+1;hash2(z);end;end;1: beginz:=d2[h2];l:=z[w1];z[w1]:=z[w1+1];z[w1+1]:=l;if not PDhash2(z) thenbegininc(t2); d2[t2]:=z;fu2[t2]:=fu2[h2]+1;hash2(z);end;end;2:beginz:=d2[h2];l:=z[w1];z[w1]:=z[w1-1];z[w1-1]:=l;if not PDhash2(z) thenbegininc(t2); d2[t2]:=z;fu2[t2]:=fu2[h2]+1;hash2(z);end;z:=d2[h2];l:=z[w1];z[w1]:=z[w1+1];z[w1+1]:=l;if not PDhash2(z) thenbegininc(t2); d2[t2]:=z;fu2[t2]:=fu2[h2]+1;hash2(z);end;end;end;until (h2>=t2)or(h1>=t1);end;begin {主程序,十分简洁}init;d1[1]:=m; {初始化,队中存入起始状态}d2[1]:=n; {初始化,队中存入目标状态}hash1(m);hash2(n);WFS;writeln('Impossible'); {无解则输出Impossible} end.。
康托展开(编码方式)

program cantor;
var
a:array[1..10] of integer;
n,i,j,t,ans:longint;
begin
readln(n);
for i:=1 to n do
read(a[i]);
ans:=0;
for i:=1 to n-1 do
begin
t:=0;
for j:=i+1 to n do
if a[j]<a[i] then
inc(t);
ans:=ans*(n+1-i)+t;
end;
inc(ans);
writeln(ans);
第三位是4,比4小的有1,2,3;3在前面出现了,还有2个比4小的数,2*2!;
第四位是1,没有比1小的数,所以是0*1!;
最后一位无论是几,比它小的数在前面肯定都出现了,所以有0*0!;
所以,比35412小的排列数共有:2*4!+3*3!+2*2!+0*1!+0*0!=70,35412是第71小的数。
康托展开2009-03-25 19:08 这篇文章主要是给像我,3,4,...,n}表示1,2,3,...,n的排列,如 {1,2,3} 按从小到大排列一共6个:123 132 213 231 312 321,代表数字 1 2 3 4 5 6,也就是把10进制数与一个排列对应起来,他们间的对应关系可由康托展开来找到。简单的说就是求一个排列数在所有排列中是第几小的。当然,要实现这个功能,途径有很多,比如我们把所有的排列都找出来,然后排个序,二分查找……
end.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
构造法——二进制下的康托展开
KEY: 康托展开
情景:
对于一个有n 位的二进制们数来说,题目中给出其中1的个数的上限,求一个第k小的数。
应用康托展开,是特殊的二进制情况下。
对于二维矩阵cantor[m][n],代表长度为m,至多有n个1 的数的个数。
由组合数递推公式:
Cantor[m][n] = cantor[m-1][n] + cantor[m-1][n-1];
初始化:cantor[0][i] = cantor[i][0] = 1;
Cantor是一个康托展开的常量表,规模为cantor[32][32],所以数据是32位的整数,用double实现。
读入之后,主函数用递归的形式进行构造,即构造一个有k-1个数比他小的数。
Work(int bits,int nOnes,int k)中,
如果bits = 0,就是说到了最后一位。
到达递归终点,直接返回。
调出cantor[bits-1][n],就是所有比他小的数的数目。
如果比k小或等于k,则该位是1,否则是0.因为该位如果是0,那么比它低的位中,一共有cantor[m-1][n],个数,如果数目比k 小,那么不能符合要求,要把该位定为1。
下面是一个康托常量表
j \ i 0 1 2 3 4 5 6 7 8 9 10
double can[32][32] = {0};
int nOnes,nbits;
double index;
int init(){
int i,j;
for( i = 0 ; i <= 31 ; i++ ){
can[0][i] = 1;
can[i][0] = 1;
}
for( i = 1 ; i <= 31 ; i++ )
for( j = 0 ; j <= 31 ; j++ )
if( j != 0 )
can[i][j] = can[i-1][j] + can[i-1][j-1];
fscanf(fp1,"%d%d%lf",&nbits,&nOnes,&index);
}
int work(int nbits,int nOnes,double index){
if( nbits == 0 )
return 0;
double s;
s = can[nbits-1][nOnes];
if( s <= index ){
fprintf(fp2,"1");
work(nbits-1,nOnes-1,index-s);
}
else{
fprintf(fp2,"0");
work(nbits-1,nOnes,index);
}
}。
