第4章 生产论---选修
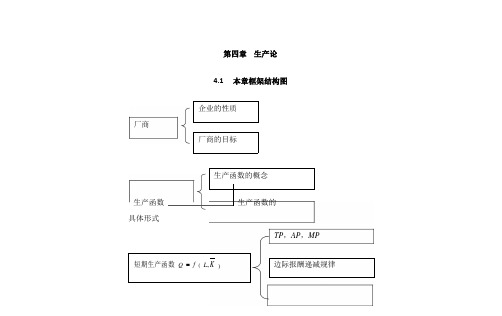
合集下载
微观经济学生产论课件

西方经济学中的生产四要素:
劳动 L
(Labor)
资本 K
(Capital)
土地 N
(Natural)
企业家才能 E (Entrepreneurship)
为了简化分析,假定两种生产要素的生产函数:
Q f (L, K )
(二)生产的短期和长期划分
短期指生产者来不及调整全部生产要素的数量, 至少有一种生产要素的数量是固定不变的时间周期 长期是指生产者可以调整全部生产要素的数量的 时间周期。 短期和长期的划分是以生产者能否变动全部要素 投入的数量作为标准的。
第一阶段:MP>AP,AP递 增,TP递增(生产力尚 未充分发挥的阶段)
第二阶段:AP>MP>0,AP 递减,总产量增加一直 达到最大(生产的合理 阶段)
第三阶段:MP<0,TP递 减(生产不经济阶段)
Q
L不足
合
理
B
区 域
G K不足 TP
Ⅰ
ⅡⅢ
A
E F AP
O
L1 L2 L3
MP L
• 总之,一种生产要素的合理投入区域应在第II区域 。但应在II区域的哪一点上呢?这就还要考虑到其 他因素。先要考虑厂商的目标,如果厂商的目标
三、一种可变生产要素的生产函数(短期分析) (一)短期生产函数(short-term)
在资本投入量固定时,由劳动投入量变化所带 来的最大产量的变化。
Q f L, K
(二)总产量、平均产量和边际产量
总产量TP(total product) :与一定量的可变要素劳动相 对应的最大产量。
TPL f (L, K )
注意:边际报酬递减规律是短期生产的一条基本 规律。它的存在需要满足以下条件:
[经济学]第四章 生产论
![[经济学]第四章 生产论](https://img.taocdn.com/s3/m/c745eb4b25c52cc58bd6be5f.png)
可变技术系数:要素的配合
比例可变,要素之间可以相互 替代。
固定技术系数:只存在唯一
一种要素配合比例,必须按同 一比例增减,要素之间不可替 代。
2018/11/20 湖北经济学院经贸学院
同样产量,可采用 劳动密集型(多用 劳动少用资本), 也可采用资本密集 型(多用资本少用 劳动)。
一人一台缝纫机 一个萝卜一个坑
今后讨论中始终坚持的一个基本假设:实现 利润最大化是一个企业竞争生存的基本准则 。
2018/11/20
湖北经济学院经贸学院
7
第二节 生产函数
生产要素:劳动、土地、资本、企业家才能 生产函数
在一定的时期内,在技术水平不变的情况下, 生产中所使用的各种生产要素的数量与所能 生产的最大产量之间的关系。 Q = f (x1,x2,∙∙∙,xn) Q = f (L,K)
也称为厂商或者企业,它是指能够作出统一 的生产决策的单个经济单位。或者把投入转 化为产出的生产经营性组织。
1.企业的形式
业主制 合伙制 公司制
3
2018/11/20
湖北经济学院经贸学院
2.厂商(企业)的本质
•分工、专业化生产带来高效率 •规模经济 •交易活动内部化,降低交易成 本
不确定性 不完全 信息 导致 信息不对称 市场 与企 业的 并存
之一数量不变,单独增加另一要素量,则产量不变。
2018/11/20
湖北经济学院经贸学院
9
2.柯布-道格拉斯生产函数
(C-D生产函数)由美国数学家柯布和经济学
家道格拉斯于1982年根据历史统计资料提出
Q AL K
A为规模参数,A>0, a表示劳动贡献在总产中所占份额
西方经济学第四章 生产论

•2.函数表达式:假定X1,X2,X3,顺次表示某产品生产过程中所使用的n种 生产要素的投入数量,Q表示所能生产的最大产量,则生产函数可以写成以下形 式:
•Q = f ( X 1,X2, ···,Xn)
• 该生产函数表示在既定的生产技术水平下生产要素组合( X 1,X2, ···,Xn) 在每一时期所能生产的最大产量为Q。生产要素一般被划分为劳动、土地、资本和企
效用递减规律是从消费者心理感受中得来的,边际效用是不可计量的。
西方经济学第四章 生产论
•五、总产量、平均产量和边际产量相互之间的关系
•Q
• 总产量、平均产量和边际产量之
•Ⅰ
•Ⅱ •C •Ⅲ
间的关系有这样几个特点: • 第一,在资本量不变的情况下,
随着劳动量的增加,最初总产量、平
•B
•TPL
均产量和边际产量都是递增的,但各 自增加到一定程度以后就分别递减。
所以总产量曲线,平均产量曲线和边
•A
际产量曲线都是先上升而后下降。
•A * •B*
• 第二,边际产量曲线与平均产量 曲线相交于平均产量曲线的最高点。 在相交前平均产量是递增的,边际产
•0
•L1•L2
•C * •APL
•L3 •MP
量大于平均产量,即MPL>APL;在相
•L 交后,平均产量是递减的,边际产量
•劳动的平均产量APL是指总产量与所使用的可变要素劳动的投入量之比。 •公式为:
•TPL ( L , K )
• •=
APL
•L
•劳动的边际产量MPL是增加一单位可变要素劳动投入量所增加的产量。
•公式为:
•∆•TPL ( L , K )
•MP •=
L
•∆•L
•Q = f ( X 1,X2, ···,Xn)
• 该生产函数表示在既定的生产技术水平下生产要素组合( X 1,X2, ···,Xn) 在每一时期所能生产的最大产量为Q。生产要素一般被划分为劳动、土地、资本和企
效用递减规律是从消费者心理感受中得来的,边际效用是不可计量的。
西方经济学第四章 生产论
•五、总产量、平均产量和边际产量相互之间的关系
•Q
• 总产量、平均产量和边际产量之
•Ⅰ
•Ⅱ •C •Ⅲ
间的关系有这样几个特点: • 第一,在资本量不变的情况下,
随着劳动量的增加,最初总产量、平
•B
•TPL
均产量和边际产量都是递增的,但各 自增加到一定程度以后就分别递减。
所以总产量曲线,平均产量曲线和边
•A
际产量曲线都是先上升而后下降。
•A * •B*
• 第二,边际产量曲线与平均产量 曲线相交于平均产量曲线的最高点。 在相交前平均产量是递增的,边际产
•0
•L1•L2
•C * •APL
•L3 •MP
量大于平均产量,即MPL>APL;在相
•L 交后,平均产量是递减的,边际产量
•劳动的平均产量APL是指总产量与所使用的可变要素劳动的投入量之比。 •公式为:
•TPL ( L , K )
• •=
APL
•L
•劳动的边际产量MPL是增加一单位可变要素劳动投入量所增加的产量。
•公式为:
•∆•TPL ( L , K )
•MP •=
L
•∆•L
经济学课件第四章生产理论

2.几种常见的生产函数
美国经济学家柯布-道格拉斯提出的线性齐次生产函数公式:Q = AK L1- = 1.01L0.75 K0.25 劳动贡献为3/4,资本贡献为1/4(当时的情况)。 技术系数---生产一定量某种产品所需要的各种生产要素的配合比例。技术系数作为生产一定产量的产品所需要的投入物的比例,可以是可变的,也可以是固定的,通常情况下是可变的。 劳动密集型、资本密集型
TP
O
L
TP
APL
P1
P2
L1 L2 L3
P3
L1 L2 L3
Ⅰ
Ⅱ
Ⅲ
MPL
O
L
TP
第二节一种可变要素的生产函数
第三节两种可变生产要素的生产函数
两种可变生产要素的生产函数Q=f(L,K)
KL
1
2
3
4
5
1 2 3 4 5
5 14 21 26 32
11 20 26 31 34
14 24 29 34 36
16 26 31 36 37
17 27 32 37 38
二、等产量线 1含义:生产同一产量的两种生产要素投入的各种不同组合点的轨迹。 2类型:按要素之间的替代程度分为完全可替代、完全不可替代和不完全替代 3特点:离原点越远的等产量线所代表的产量水平越高;任意两条等产量线不能相交; 边际技术替土地——劳动比率
总产量
平均产量
边际产量
1
0
0
1
1
1
100
100
1
2
0.5
240
120
140
1
3
0.33
390
130
150
1
4
美国经济学家柯布-道格拉斯提出的线性齐次生产函数公式:Q = AK L1- = 1.01L0.75 K0.25 劳动贡献为3/4,资本贡献为1/4(当时的情况)。 技术系数---生产一定量某种产品所需要的各种生产要素的配合比例。技术系数作为生产一定产量的产品所需要的投入物的比例,可以是可变的,也可以是固定的,通常情况下是可变的。 劳动密集型、资本密集型
TP
O
L
TP
APL
P1
P2
L1 L2 L3
P3
L1 L2 L3
Ⅰ
Ⅱ
Ⅲ
MPL
O
L
TP
第二节一种可变要素的生产函数
第三节两种可变生产要素的生产函数
两种可变生产要素的生产函数Q=f(L,K)
KL
1
2
3
4
5
1 2 3 4 5
5 14 21 26 32
11 20 26 31 34
14 24 29 34 36
16 26 31 36 37
17 27 32 37 38
二、等产量线 1含义:生产同一产量的两种生产要素投入的各种不同组合点的轨迹。 2类型:按要素之间的替代程度分为完全可替代、完全不可替代和不完全替代 3特点:离原点越远的等产量线所代表的产量水平越高;任意两条等产量线不能相交; 边际技术替土地——劳动比率
总产量
平均产量
边际产量
1
0
0
1
1
1
100
100
1
2
0.5
240
120
140
1
3
0.33
390
130
150
1
4
第4章生产论

第一节 厂商
一、厂商:或企业。它是指能够作出统一的生产决策的单个 经济单位。组织形式:个人业主制,合伙制企业和股份制 企业。
二、厂商的性质 1、分工合作、专业化生产的高效率 2、规模经济(有效利用资源) 3、可降低交易成本 三、厂商的目标:利润最大化
第二节 生产函数
❖ 一、生产函数的概念 ❖ 1、生产要素 ❖ 2、生产函数:在一定时期,在技术水平不变的情况下,各
种生产要素的投入量与产出量间的关系。Q=f(L .K. N. E)
❖ Q=f(L .K)
❖ 二、两种典型的生产函数
❖ 1、固定比例的生产函数(里昂惕夫生产函数):在每一个 产量水平上,任何一对要素投入量之间的比例都是固定的一
种的生产系数。Q=Minimum(L/u.k/v)(u﹥0 v﹥0)
❖ 2、柯布-道格拉斯生产函数: Q=ALa K1-a (0﹤a﹤1)或
❖
= ALa Kb (0﹤a﹤1 , 0﹤b﹤1 )( a+b=1)
1、生产要素
❖ 生产要素:生产中投入的经济资源,包括劳动、资本、土地、企业家才 能。
❖ (1)劳动:人类在生产过程中提供的体力和智力的总和。 ❖ (2)资本:实物形态和资本形态的资本。 ❖ (3)土地:土地本身及地上和地下的一切自然资源,森林、江河、湖
K 规模报酬递增
G
K3
K2 K1
J I H
Q3=300 Q2=200
Q1=100
O
L1 L2 L3
L
0L1/OK1=OL2/OK2=OL3/OK3 OL1﹥L1L2﹥L2L3
OK1 ﹥ K1K2 ﹥ K2K3
OH﹥HI﹥IJ
当100 →200时, OL2﹤2OL1 OK2﹤2OK1
一、厂商:或企业。它是指能够作出统一的生产决策的单个 经济单位。组织形式:个人业主制,合伙制企业和股份制 企业。
二、厂商的性质 1、分工合作、专业化生产的高效率 2、规模经济(有效利用资源) 3、可降低交易成本 三、厂商的目标:利润最大化
第二节 生产函数
❖ 一、生产函数的概念 ❖ 1、生产要素 ❖ 2、生产函数:在一定时期,在技术水平不变的情况下,各
种生产要素的投入量与产出量间的关系。Q=f(L .K. N. E)
❖ Q=f(L .K)
❖ 二、两种典型的生产函数
❖ 1、固定比例的生产函数(里昂惕夫生产函数):在每一个 产量水平上,任何一对要素投入量之间的比例都是固定的一
种的生产系数。Q=Minimum(L/u.k/v)(u﹥0 v﹥0)
❖ 2、柯布-道格拉斯生产函数: Q=ALa K1-a (0﹤a﹤1)或
❖
= ALa Kb (0﹤a﹤1 , 0﹤b﹤1 )( a+b=1)
1、生产要素
❖ 生产要素:生产中投入的经济资源,包括劳动、资本、土地、企业家才 能。
❖ (1)劳动:人类在生产过程中提供的体力和智力的总和。 ❖ (2)资本:实物形态和资本形态的资本。 ❖ (3)土地:土地本身及地上和地下的一切自然资源,森林、江河、湖
K 规模报酬递增
G
K3
K2 K1
J I H
Q3=300 Q2=200
Q1=100
O
L1 L2 L3
L
0L1/OK1=OL2/OK2=OL3/OK3 OL1﹥L1L2﹥L2L3
OK1 ﹥ K1K2 ﹥ K2K3
OH﹥HI﹥IJ
当100 →200时, OL2﹤2OL1 OK2﹤2OK1
4第四章 生产论 微观经济学
四、长期生产函数:两种可变生产要素的生产函 数1.长期生产函数的形式 在生产理论中,为了简化分析,通常以两种可变生产要素的生产函数来考察长期生产问题。假定生产者使用劳 动和资本两种可变生产要素来生产一种产品,则两种可变生产要素的长期生产函数可以写为:
Q f L,K 2.等产量曲线 等产量曲线(Equal-Product Curves)是在技术水平不变的条件下生产同一产量的两种生产要素投入量的所有不 同组合的轨迹,每一条等产量曲线对应的是特定的产出水平。等产量曲线如图4-2所示。
点的线段的斜率,就是相应的 APL 值。(3)边际产量和平均产量之间 的关系
就平均产量 APL 和边际产量 MPL来说,当 MPL APL 时, APL 曲线是上升的;当MPL APL 时,APL曲
线是下降的;当 MPL APL 时,APL 曲线达极大值。数学证明如下:
dTPL L −TP
d APL d TPL dL
二、生产函数 1.生产函数的概念
劳动、土地、资本和企业家才能
生产函数表示在一定时期内,在技术水平不变的情况下,生产中所使用的各种生产要素的数量与所能生产的最
大产量之间的关系(The production function specifies the maximum output that can be produced with a given quantity of
劳动的平均产量 APL 指平均每一单位可变要素劳动的投入量所生产的产量,即 APL = TPL L,K 。
L
劳动的边际产量 MPL 指增加一单位可变要素劳动投入量所增加的产量,即:
TPL L,K
MP
lim
TP dTPL L,K
L
L
第四章 生产论 西方经济学 教学课件

(3)长期雇佣专业人员比从市场上购买相应的服务 更有利。
4.企业内部特有的交易成本 企业的内部交易会消除和降低一部分市场交易成本。
但同时也能带来企业内部特有的交易成本:原因是信 息不完全性。
具体:P100
(1)企业内部的契约、监督和激励。其运行需要成本。 (2)企业隶属层次的增多会导致信息传导过程中的缺损,企业
K
点上: Q= L/u= K/v
Q2
OR:所有产量水平下最小
Q1
要素投入组合
O
L
3.柯布-道格拉斯生产函数 (C-D生产函数),由美国数学家柯布和经济学家道
格拉斯于20世纪30年代根据历史统计资料提出的。
Q ALK
QALK1
A为规模参数,A>0, a表示劳动贡献在总产出中所占份额
(0<a<1), 1-a表示资本贡献在总产中所占份额
K
2
L与K,以2:1比例替代
1
L
2
4
2.固定投入比例的生产函数(里昂惕夫生产函数)
在每一产量水平上任何一对要素投入量之间的比例 都是固定的
Q=Min(L/u,K/v) (u,v>0) u:固定的劳动生产系数(单位产量配备的劳动数)
v:固定的资本生产系数(单位产量配备的资本数) 最小要素投入组合在直角
效率的损失。 (3)下级向上级隐瞒信息、制造虚假和传递错误信息,会导致
企业效率的损失。 企业的扩张是有限的。企业扩张的界限: 多增加一次内部交易的成本=通过市场交易的成本
三、厂商的目标:利润最大化(TR-TC)
(符合理性人假定)
但在现实生活中,厂商有可能选择销售收入最大化 或市场销售份额最大化。
原因:信息是不完全的,厂商面临的需求可能是不确定的。 厂商可能对产量变化引起生产成本变化情况缺乏了解。
微观经济学课件第四章:生产论

最优组合
企业需要找到各种生产要素的最佳组 合,以实现产量最大化和成本最小化。 这需要考虑不同要素之间的替代和互 补关系。
长期决策
企业需要制定长期的生产计划,以应 对市场变化和不确定性。在制定长期 决策时,企业需要考虑生产要素的价 格变化趋势、技术进步和市场需求等 因素。
THANKS.
所带来的产量减少。
规模经济
在一定时期内,随着生 产规模的扩大,长期平
均成本下降。
生产要素最优组合的实现方式
1 2
等产量曲线与等成本线的切点
在等产量曲线与等成本线的切点上,既定成本下 可以实现最大产量或者最大产量下可以实现成本 最小化。
利润最大化原则
企业追求利润最大化,在利润最大的点上实现生 产要素的最优组合。
原因
此时的生产要素组合能够使生产者获得最大的利润或最小的成本。
生产扩展线
定义
01
生产扩展线是指在生产要素价格和生产技术水平不变的条件下,
生产者扩大生产的路径。
特点
02
生产扩展线是一条从原点出发的射线,其斜率等于等产量线的
斜率。
原因
03
随着生产的扩大,为了保持相同的产量,一种Байду номын сангаас产要素的投入
量会逐渐增加,而另一种生产要素的投入量保持不变。
一种常见的生产函数形式,假设劳动 和资本的替代弹性为常数,且资本的 贡献率为正值,劳动的贡献率为负值。
变动替代比例生产函数
在一定的技术条件下,对于不同的投 入品,其替代比例是变化的。
短期生产理论
02
短期生产函数
01
02
03
定义
短期生产函数描述了在短 期内,一定数量的资本和 劳动的组合所能生产的最 大产量。
企业需要找到各种生产要素的最佳组 合,以实现产量最大化和成本最小化。 这需要考虑不同要素之间的替代和互 补关系。
长期决策
企业需要制定长期的生产计划,以应 对市场变化和不确定性。在制定长期 决策时,企业需要考虑生产要素的价 格变化趋势、技术进步和市场需求等 因素。
THANKS.
所带来的产量减少。
规模经济
在一定时期内,随着生 产规模的扩大,长期平
均成本下降。
生产要素最优组合的实现方式
1 2
等产量曲线与等成本线的切点
在等产量曲线与等成本线的切点上,既定成本下 可以实现最大产量或者最大产量下可以实现成本 最小化。
利润最大化原则
企业追求利润最大化,在利润最大的点上实现生 产要素的最优组合。
原因
此时的生产要素组合能够使生产者获得最大的利润或最小的成本。
生产扩展线
定义
01
生产扩展线是指在生产要素价格和生产技术水平不变的条件下,
生产者扩大生产的路径。
特点
02
生产扩展线是一条从原点出发的射线,其斜率等于等产量线的
斜率。
原因
03
随着生产的扩大,为了保持相同的产量,一种Байду номын сангаас产要素的投入
量会逐渐增加,而另一种生产要素的投入量保持不变。
一种常见的生产函数形式,假设劳动 和资本的替代弹性为常数,且资本的 贡献率为正值,劳动的贡献率为负值。
变动替代比例生产函数
在一定的技术条件下,对于不同的投 入品,其替代比例是变化的。
短期生产理论
02
短期生产函数
01
02
03
定义
短期生产函数描述了在短 期内,一定数量的资本和 劳动的组合所能生产的最 大产量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2、厂商的组织形式: --个人企业 --合伙制企业 --公司制企业(有限责任公司、股份有限公司)
2、厂商的组织形式
企业类型 个人企业 特 点
资金有限,规模较小,容易建立, 决策自由,易于管理,发展受限制。
资金较多,规模较大,易于管理,决策 多样化,但不利于协调和统一,合伙人 之间的关系不稳定。
合伙制企业
第4章 生产论
本章主要内容: 一、厂商和生产函数 二、短期生产理论(一种可变要素) 三、长期生产理论(两种可变要素)
◆等产量线 ◆等成本线
◆生产者的最优生产规模
◆规模报酬
第1节 厂商
一、厂商(企业)及其组织形式
1、厂商或企业:生产者,能够做出统一生产决策的 单个经济单位。即组织生产要素进行生产、销售产 品和服务的经营性组织。
第2节 生产函数
一、生产函数 生产是对各种生产要素进行组合以制成产品的行为, 在生产中要投入各种生产资源以生产出产品,即生 产是把投入转化为产出的过程。因此生产过程一头 通过要素需求与要素市场相连,另一头通过产品供 给与产品市场相连。 1、生产要素:生产过程中投入的各种经济资源。 劳动、土地、资本、企业家才能。
要素投入量之间的比例是固定的。
u为固定的劳动的生产技术系数
v为固定的资本的生产技术系数
L K 则Q Min( , ) u v
有时候也表示为Q Min(aL, bK)
2、固定投入比例生产函数
K
g K2 K1 a h L1 L2
Q2
b Q1
K K1 K 2 L L1 L 2
O
L
3、柯布-道格拉斯生产函数
第3节 短期生产理论
(一种可变生产要素的生产函数)
生产中的短期和长期 ◆短期:生产者来不及调整所有生产要素的数量,即 至少有一种生产要素的数量保持不变的时间周期。 ◆长期:生产者可以调整所有生产要素的数量的时间 周期。
短期和长期的划分是以生产者能否变动所有生产要素的数 量为标准的。
第3节 短期生产理论
生产要素
◆劳动:劳动不是指劳动者本身,而是指劳动者提
供的体力和智力的总和。劳动的价格是工资。 ◆土地:西方经济学所讲的土地是一个广义的概念, 不仅包括土地,还包括河山、森林、能源、矿藏、 原料等一切自然资源。土地的价格是地租。 ◆资本:实物资本和货币资本。实物资本指生产过 程中的设备,如机器、厂房等。资本的价格是利息。 ◆马歇尔在其《经济学原理》一书中,增加了新的 生产要素:企业家才能,即组织建立和经营管理企 业的才能。
(一种可变生产要素的生产函数)
不变要素投入:短期内数量固定不变的那部分生产 要素;如机械设备、厂房等。 ●可变要素投入:短期内数量可变化的那部分生产要 素;如劳动、原材料等。 ●在长期由于所有的生产要素数量都可以调整,也就 不存在可变要素投入和不变要素投入之分。
●
一、一种可变生产要素的生产函数 (短期生产函数)
三、边际报酬递减规律-3
3、几点说明: ◆生产技术不变的条件下; ◆它强调一种趋势,而不是说一种要素的边际产 量一开始就递减。
四、总产量、平均产量和边际产量的关系
Q
极大值点,递增 与递减的转折点
Qmax
S
dQ 0 dL
TPL
R
TP切线斜率 = MP,如点M TP连线斜率 = AP,如点N 点R切线、连线斜率 相等 MP&AP
Q AL K
3、柯布-道格拉斯生产函数
Q AL K
◆
L—劳动, K—资本; ◆ A—技术水平(参数), 、—参数。 A>0, 0<<1 , 0<<1。 ◆ 、 分别代表劳动所得和资本所得在总产量中
所占份额。 ◆若+>1,规模报酬递增; 若+=1,规模报酬不变; 若+<1,规模报酬递减。
生产三阶段(生产要素的合理投入区域)
□ Ⅲ(第三阶段): ◆ MPL<0 ◆ APL↓:Q/L↓(L/Q↑)可变投入劳动效率降低 ◆ TPL↓:Q↓(K/Q↑)固定投入资本效率降低
∴增加可变投入将降低所有投入的效率,或者说这时 可变投入太多。减少可变要素的投入量是有利的。
生产三阶段(生产要素的合理投入区域)
◆
Ⅱ
Ⅲ
O
L1 L2
S’ L3 MPL L
APL
生产三阶段(生产要素的合理投入区域)
□Ⅰ(第一阶段): ◆ MPL>0 ◆ APL↑:Q/L↑(L/Q↓)可变投入劳动效率提高 ◆ TPL↑:Q↑(K/Q↓)固定投入资本效率提高
∴增加可变投入可提高所有投入的效率,或者说这时 可变投入太少。增加可变要素的投入量是有利的。
拐点,凸弧与 凹弧的转折点
N M
d 2Q 0 2 dL
L
O
L0 L1 L2
L3
TP曲线先以递增速度上升,再以递减速度上升,到达最高点后下降
四、总产量、平均产量和边际产量的关系
TP、MP、AP曲线:
◆TP曲线先以递增速度上升,再以递减速度上升,到达最高
点后下降。N点为拐点,S点为最大值。
◆ MP曲线是TP曲线切线的斜率。
◆在技术水平不变的条件下,在连续等量地把某一
种可变生产要素增加到其他一种或几种数量不变的 生产要素上去的过程中,当这种可变要素的投入量 小于某一特定值时,增加该要素投入所带来的边际 产量是递增的;当这种可变要素的投入量连续增加 并超过这个特定值时,增加该要素投入所带来的边 际产量是递减的。
三、边际报酬递减规律-2
Q=aK+bL(a、b>0) K
2
1
Q2 Q1
O
2
4
L
2、固定投入比例生产函数
◆技术系数:为生产一定数量的产品所需要的各种
生产要素的配合比例。 --固定技术系数(两种要素不能相互替代) --可变技术系数(两种要素之间可以相互替代)
2、固定投入比例生产函数
◆固定投入比例生产函数在每一产量水平上任何一对
生产三阶段(生产要素的合理投入区域)
•生产三阶段的划分: 第Ⅰ阶段:0~APmax
TPmax
R Q S TPL
第Ⅱ阶段:APmax~TPmax
第Ⅲ阶段:TPmax ~
M
N
O AP MP
MPmax APmax
L1 L2
L3
L
Ⅰ
N’ R’
生产要素的合理投入区 域:第Ⅱ阶段,即经济区 域。第Ⅰ、Ⅲ阶段为不经 济区域
TP递增; TP递减; TP达到最大值。
M N
2、总产量与平均产量 3、平均产量与边际产量
O AP MP
MPmax APmax
L1 L2 N’ R’
L3
L
若MP>AP,则AP↑;
若MP<AP,则AP↓; 若MP=AP,则APmax。 MP的变动快于AP。
O
L1 L2
S’ L3 MPL L
APL
四、总产量、平均产量与边际产量的关系
TPL MPL L dTPL TPL ' f '( L,K) dL
例题:
已知生产函数 Q f ( L) 27 L 12 L L
2 3
TPL f (L) 27L 12L L
2
3
f (L) APL 27 12 L L2 L
df (L) MPL f'(L) 27 24 L 3L2 dL
2、解释:
□生产过程中,可变生产要素与不变生产要素之间
在数量上存在一个最佳数量组合比例。
◆开始时,由于可变要素投入量小于最佳组合比例
所需数量,随着可变要素投入量的逐渐增加,越来 越接近最佳组合比例,边际产量是呈递增的趋势。 ◆当达到最佳组合比例后,再增加可变要素的投入, 就会越来越偏离生产要素的最佳数量组合比例,可 变生产要素的边际产量就呈递减趋势。
◆平均产量与边际产量(数学证明)
证明:
dQ dL L Q d d Q dL APL ( ) dL dL dL L L2 1 dQ Q 1 ( ) ( MPL APL ) L dL L L
于是,当MPL>APL,则dAPL/dL>0,APL递增;
当MPL<APL,则dAPL/dL<0,APL递减; 当MPL=APL,则dAPL/dL=0,APL极大。
MP 先递增后递减。在N点
MP最大值,在S点时MP=0。
◆ AP曲线是TP曲线上的点和原点连线的斜率。
AP 先递增后 递减。R点为最大值,R点:连线和切线重合,即MP=AP。
四、总产量、平均产量与边际产量的关系
1、总产量与边际产量 •MP>0 , •MP<0 , •MP=0 ,
Qmax
R Q S TPL
在经济学中,一般只分析劳动和资本这两种生产要素,则: Q f ( L, K )
二、常见的生产函数具体形式
1、固定替代比例的生产函数
2、固定投入比例生产函数 3、柯布-道格拉斯生产函数
1、固定替代比例的生产函数(线性生产函数)
◆固定替代比例的生产函数:又称线性生产函数,
表示在每一个产量水平上任何两种生产要素之间的 替代比例都是固定的。可以表示为:
2、生产函数(production function)
◆生产函数定义:
一定时期内,在技术水平不变的情况下,生产中所使 用的各种生产要素的数量与所能生产的最大产量之间 的关系。
▼假定:
-企业经营管理得好,一切投入要素的使用都 是非常有效的—最大产量。 -技术水平给定。
2、生产函数
假设X 1 , X 2 ,..., X n为生长过程中使用的n种生产要素的数量, Q表示所能生产的最大产量,则生产函数可表示为: Q f ( X 1 , X 2 ,..., X n )
2、厂商的组织形式
企业类型 个人企业 特 点
资金有限,规模较小,容易建立, 决策自由,易于管理,发展受限制。
资金较多,规模较大,易于管理,决策 多样化,但不利于协调和统一,合伙人 之间的关系不稳定。
合伙制企业
第4章 生产论
本章主要内容: 一、厂商和生产函数 二、短期生产理论(一种可变要素) 三、长期生产理论(两种可变要素)
◆等产量线 ◆等成本线
◆生产者的最优生产规模
◆规模报酬
第1节 厂商
一、厂商(企业)及其组织形式
1、厂商或企业:生产者,能够做出统一生产决策的 单个经济单位。即组织生产要素进行生产、销售产 品和服务的经营性组织。
第2节 生产函数
一、生产函数 生产是对各种生产要素进行组合以制成产品的行为, 在生产中要投入各种生产资源以生产出产品,即生 产是把投入转化为产出的过程。因此生产过程一头 通过要素需求与要素市场相连,另一头通过产品供 给与产品市场相连。 1、生产要素:生产过程中投入的各种经济资源。 劳动、土地、资本、企业家才能。
要素投入量之间的比例是固定的。
u为固定的劳动的生产技术系数
v为固定的资本的生产技术系数
L K 则Q Min( , ) u v
有时候也表示为Q Min(aL, bK)
2、固定投入比例生产函数
K
g K2 K1 a h L1 L2
Q2
b Q1
K K1 K 2 L L1 L 2
O
L
3、柯布-道格拉斯生产函数
第3节 短期生产理论
(一种可变生产要素的生产函数)
生产中的短期和长期 ◆短期:生产者来不及调整所有生产要素的数量,即 至少有一种生产要素的数量保持不变的时间周期。 ◆长期:生产者可以调整所有生产要素的数量的时间 周期。
短期和长期的划分是以生产者能否变动所有生产要素的数 量为标准的。
第3节 短期生产理论
生产要素
◆劳动:劳动不是指劳动者本身,而是指劳动者提
供的体力和智力的总和。劳动的价格是工资。 ◆土地:西方经济学所讲的土地是一个广义的概念, 不仅包括土地,还包括河山、森林、能源、矿藏、 原料等一切自然资源。土地的价格是地租。 ◆资本:实物资本和货币资本。实物资本指生产过 程中的设备,如机器、厂房等。资本的价格是利息。 ◆马歇尔在其《经济学原理》一书中,增加了新的 生产要素:企业家才能,即组织建立和经营管理企 业的才能。
(一种可变生产要素的生产函数)
不变要素投入:短期内数量固定不变的那部分生产 要素;如机械设备、厂房等。 ●可变要素投入:短期内数量可变化的那部分生产要 素;如劳动、原材料等。 ●在长期由于所有的生产要素数量都可以调整,也就 不存在可变要素投入和不变要素投入之分。
●
一、一种可变生产要素的生产函数 (短期生产函数)
三、边际报酬递减规律-3
3、几点说明: ◆生产技术不变的条件下; ◆它强调一种趋势,而不是说一种要素的边际产 量一开始就递减。
四、总产量、平均产量和边际产量的关系
Q
极大值点,递增 与递减的转折点
Qmax
S
dQ 0 dL
TPL
R
TP切线斜率 = MP,如点M TP连线斜率 = AP,如点N 点R切线、连线斜率 相等 MP&AP
Q AL K
3、柯布-道格拉斯生产函数
Q AL K
◆
L—劳动, K—资本; ◆ A—技术水平(参数), 、—参数。 A>0, 0<<1 , 0<<1。 ◆ 、 分别代表劳动所得和资本所得在总产量中
所占份额。 ◆若+>1,规模报酬递增; 若+=1,规模报酬不变; 若+<1,规模报酬递减。
生产三阶段(生产要素的合理投入区域)
□ Ⅲ(第三阶段): ◆ MPL<0 ◆ APL↓:Q/L↓(L/Q↑)可变投入劳动效率降低 ◆ TPL↓:Q↓(K/Q↑)固定投入资本效率降低
∴增加可变投入将降低所有投入的效率,或者说这时 可变投入太多。减少可变要素的投入量是有利的。
生产三阶段(生产要素的合理投入区域)
◆
Ⅱ
Ⅲ
O
L1 L2
S’ L3 MPL L
APL
生产三阶段(生产要素的合理投入区域)
□Ⅰ(第一阶段): ◆ MPL>0 ◆ APL↑:Q/L↑(L/Q↓)可变投入劳动效率提高 ◆ TPL↑:Q↑(K/Q↓)固定投入资本效率提高
∴增加可变投入可提高所有投入的效率,或者说这时 可变投入太少。增加可变要素的投入量是有利的。
拐点,凸弧与 凹弧的转折点
N M
d 2Q 0 2 dL
L
O
L0 L1 L2
L3
TP曲线先以递增速度上升,再以递减速度上升,到达最高点后下降
四、总产量、平均产量和边际产量的关系
TP、MP、AP曲线:
◆TP曲线先以递增速度上升,再以递减速度上升,到达最高
点后下降。N点为拐点,S点为最大值。
◆ MP曲线是TP曲线切线的斜率。
◆在技术水平不变的条件下,在连续等量地把某一
种可变生产要素增加到其他一种或几种数量不变的 生产要素上去的过程中,当这种可变要素的投入量 小于某一特定值时,增加该要素投入所带来的边际 产量是递增的;当这种可变要素的投入量连续增加 并超过这个特定值时,增加该要素投入所带来的边 际产量是递减的。
三、边际报酬递减规律-2
Q=aK+bL(a、b>0) K
2
1
Q2 Q1
O
2
4
L
2、固定投入比例生产函数
◆技术系数:为生产一定数量的产品所需要的各种
生产要素的配合比例。 --固定技术系数(两种要素不能相互替代) --可变技术系数(两种要素之间可以相互替代)
2、固定投入比例生产函数
◆固定投入比例生产函数在每一产量水平上任何一对
生产三阶段(生产要素的合理投入区域)
•生产三阶段的划分: 第Ⅰ阶段:0~APmax
TPmax
R Q S TPL
第Ⅱ阶段:APmax~TPmax
第Ⅲ阶段:TPmax ~
M
N
O AP MP
MPmax APmax
L1 L2
L3
L
Ⅰ
N’ R’
生产要素的合理投入区 域:第Ⅱ阶段,即经济区 域。第Ⅰ、Ⅲ阶段为不经 济区域
TP递增; TP递减; TP达到最大值。
M N
2、总产量与平均产量 3、平均产量与边际产量
O AP MP
MPmax APmax
L1 L2 N’ R’
L3
L
若MP>AP,则AP↑;
若MP<AP,则AP↓; 若MP=AP,则APmax。 MP的变动快于AP。
O
L1 L2
S’ L3 MPL L
APL
四、总产量、平均产量与边际产量的关系
TPL MPL L dTPL TPL ' f '( L,K) dL
例题:
已知生产函数 Q f ( L) 27 L 12 L L
2 3
TPL f (L) 27L 12L L
2
3
f (L) APL 27 12 L L2 L
df (L) MPL f'(L) 27 24 L 3L2 dL
2、解释:
□生产过程中,可变生产要素与不变生产要素之间
在数量上存在一个最佳数量组合比例。
◆开始时,由于可变要素投入量小于最佳组合比例
所需数量,随着可变要素投入量的逐渐增加,越来 越接近最佳组合比例,边际产量是呈递增的趋势。 ◆当达到最佳组合比例后,再增加可变要素的投入, 就会越来越偏离生产要素的最佳数量组合比例,可 变生产要素的边际产量就呈递减趋势。
◆平均产量与边际产量(数学证明)
证明:
dQ dL L Q d d Q dL APL ( ) dL dL dL L L2 1 dQ Q 1 ( ) ( MPL APL ) L dL L L
于是,当MPL>APL,则dAPL/dL>0,APL递增;
当MPL<APL,则dAPL/dL<0,APL递减; 当MPL=APL,则dAPL/dL=0,APL极大。
MP 先递增后递减。在N点
MP最大值,在S点时MP=0。
◆ AP曲线是TP曲线上的点和原点连线的斜率。
AP 先递增后 递减。R点为最大值,R点:连线和切线重合,即MP=AP。
四、总产量、平均产量与边际产量的关系
1、总产量与边际产量 •MP>0 , •MP<0 , •MP=0 ,
Qmax
R Q S TPL
在经济学中,一般只分析劳动和资本这两种生产要素,则: Q f ( L, K )
二、常见的生产函数具体形式
1、固定替代比例的生产函数
2、固定投入比例生产函数 3、柯布-道格拉斯生产函数
1、固定替代比例的生产函数(线性生产函数)
◆固定替代比例的生产函数:又称线性生产函数,
表示在每一个产量水平上任何两种生产要素之间的 替代比例都是固定的。可以表示为:
2、生产函数(production function)
◆生产函数定义:
一定时期内,在技术水平不变的情况下,生产中所使 用的各种生产要素的数量与所能生产的最大产量之间 的关系。
▼假定:
-企业经营管理得好,一切投入要素的使用都 是非常有效的—最大产量。 -技术水平给定。
2、生产函数
假设X 1 , X 2 ,..., X n为生长过程中使用的n种生产要素的数量, Q表示所能生产的最大产量,则生产函数可表示为: Q f ( X 1 , X 2 ,..., X n )
