微观经济学答案解析第四章生产论
(完整版)微观经济学第4章生产论习题与答案

第4章生产论【练习及思考】参考答案要点1.填空题(1)总产量曲线、平均产量曲线和边际产量曲线都呈现出先上升,而后达到最大值以后,再呈现出下降的趋势。
其中,边际产量最先达到最大值,而后开始下降并与平均产量的最大值相交。
(2)边际产量的变化随着可变要素投入的增加一般经历两个阶段,即递增和递减两个阶段。
(3)按照生产过程中使用的生产要素的搭配情况可将那生产函数分为两种类型固定比例生产函数和可变比例生产函数。
2.判断题(下列判断正确的在括号内打√,不正确的打×)1)(√)在一种可变投入生产函数中,可变要素合理投入区域应在AP>MP>0的阶段。
2)(×)在一种可变投入生产函数中,可变要素合理投入区域应在MP>AP的第一阶段。
3)(√)生产理论中的短期是指未能调整全部生产要素的时期。
4)(×)AP曲线与MP曲线交于MP曲线的最高点。
5)(×)能提供相同效用的不同商品数量组合的点的连线即为等产量曲线。
6)(×)等产量曲线表示的是用同样数量劳动和资本生产不同的产量。
7)(√)当劳动的边际产量小于其平均产量时,平均产量肯定是下降的。
8)(×)边际产量递减,平均产量也递减。
9)(√)在生产的第Ⅱ阶段,AP是递减的。
3.选择题1)理性的生产者选择的生产区域应是(CD)。
A.MP>AP阶段B.MP下降阶段C.AP>MP>0阶段D.MP与AP相交之点起至MP与横轴交点止2)下列说法中正确的是(AC)。
A.只要总产量减少,边际产量一定为负B.只要MP减少,总产量一定减少C.MP曲线必定交于AP曲线的最高点D.只要MP减少,AP 也一定减少3)最优生产要素组合点上应该有(ABD)。
A.等产量曲线和等成本线相切B.MRTS LK=w/rC.dk/dl=w/rD.MP L/MP k=w/r4)等产量曲线上任意两点的产量肯定是(A )。
A.相等B.不等C.无关D.以上情况都存在5)若横轴代表劳动,纵轴表示资本,且劳动的价格为w,资本的价格为r,则等成本线的斜率为(C )。
微观经济学第四章习题答案完整版

微观经济学第四章习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】第四章生产论1. 下面(表4—1)是一张一种可变生产要素的短期生产函数的产量表:可变要素的数量可变要素的总产量可变要素的平均产量可变要素的边际产量122103244125606677080963(2)该生产函数是否表现出边际报酬递减如果是,是从第几单位的可变要素投入量开始的解答:(1)利用短期生产的总产量(TP)、平均产量(AP)和边际产量(MP)之间的关系,可以完成对该表的填空,其结果如表4—2所示:可变要素的数量可变要素的总产量可变要素的平均产量可变要素的边际产量1222212610324812448122456012126661167701048708\f(34)09637-7高点以后开始逐步下降的这样一种普遍的生产现象。
本题的生产函数表现出边际报酬递减的现象,具体地说,由表4—2可见,当可变要素的投入量从第4单位增加到第5单位时,该要素的边际产量由原来的24下降为12。
2. 用图说明短期生产函数Q=f(L,eq \o(K,\s\up6(-)))的TPL曲线、APL 曲线和MPL曲线的特征及其相互之间的关系。
解答:短期生产函数的TPL曲线、APL曲线和MPL曲线的综合图如图4—1所示。
图4—1由图4—1可见,在短期生产的边际报酬递减规律的作用下,MPL曲线呈现出先上升达到最高点A以后又下降的趋势。
从边际报酬递减规律决定的MPL曲线出发,可以方便地推导出TPL 曲线和APL曲线,并掌握它们各自的特征及相互之间的关系。
关于TPL 曲线。
由于MPL=eq \f(d TP L,d L),所以,当MP L>0时,TP L曲线是上升的;当MPL <0时,TPL曲线是下降的;而当MPL=0时,TPL曲线达最高点。
换言之,在L=L3时,MPL曲线达到零值的B点与TPL曲线达到最大值的B′点是相互对应的。
微观经济学第四章答案
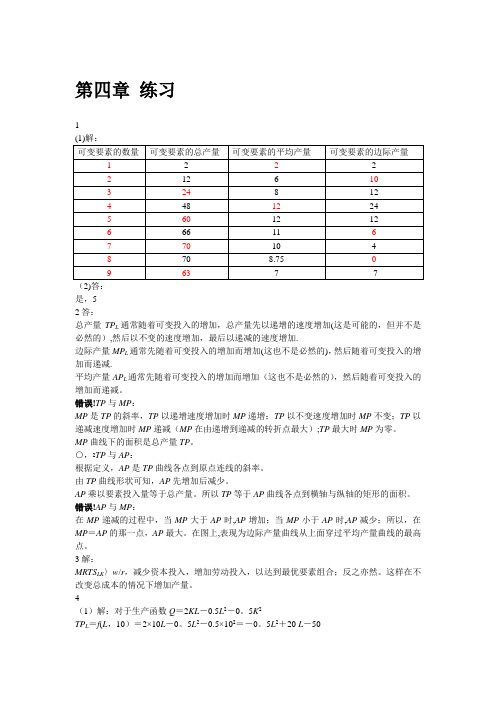
第四章练习1(2)答:是,52答:总产量TP L通常随着可变投入的增加,总产量先以递增的速度增加(这是可能的,但并不是必然的),然后以不变的速度增加,最后以递减的速度增加.边际产量MP L通常先随着可变投入的增加而增加(这也不是必然的),然后随着可变投入的增加而递减.平均产量AP L通常先随着可变投入的增加而增加(这也不是必然的),然后随着可变投入的增加而递减。
错误!TP与MP:MP是TP的斜率,TP以递增速度增加时MP递增;TP以不变速度增加时MP不变;TP以递减速度增加时MP递减(MP在由递增到递减的转折点最大);TP最大时MP为零。
MP曲线下的面积是总产量TP。
○,2TP与AP:根据定义,AP是TP曲线各点到原点连线的斜率。
由TP曲线形状可知,AP先增加后减少。
AP乘以要素投入量等于总产量。
所以TP等于AP曲线各点到横轴与纵轴的矩形的面积。
错误!AP与MP:在MP递减的过程中,当MP大于AP时,AP增加;当MP小于AP时,AP减少;所以,在MP=AP的那一点,AP最大。
在图上,表现为边际产量曲线从上面穿过平均产量曲线的最高点。
3解:MRTS LK〉w/r,减少资本投入,增加劳动投入,以达到最优要素组合;反之亦然。
这样在不改变总成本的情况下增加产量。
4(1)解:对于生产函数Q=2KL-0.5L2-0。
5K2TP L=f(L,10)=2×10L-0。
5L2-0.5×102=-0。
5L2+20 L-50AP L=TP L/L=-0。
5L+20-50/LMP L=d(TP L)/dL=-L+20(2)解:对于总产量函数Q=-0.5L2+20L-50,要求其极大值,只要取其MP L=-L+20=0,就可求得L=20。
又d2Q/dL2=-1<0,故L=20为极大点。
对于平均产量函数AP L=-0.5L+20-50/L,要求其极大值,只要取其导数d(AP L)/ dL=-0。
5+50/L2=0,L2=100,L=10,又d2 (AP L)/ dL2=-100/L3<0,故L=10时,平均产量达到极大.对于边际产量函数MP L=-L+20,为负斜率的直线,而且L≥0,故L=0时,MP L最大,等于20.(3)解:当AP L=MP L,即-0。
习题--《微观经济学》第四章 生产函数--高鸿业,人教版

第四章生产论一、选择题1.当劳动(L)的总产量下降时()。
A.APL 是递增的 B.APL为零 C.MPL为零 D.MPL为负2.如果连续地增加某种生产要素,在总产量达到最大时边际产量曲线()。
A.与纵轴相交 B.经过原点C.与平均产量曲线相交 D.与横轴相交3.在生产者均衡点上()。
A.MRTSLK =PL/PKB.MPL/PL=MPK/PKC.等产量曲线与等成本曲线相切 D.以上说法均正确4.规模报酬递减是在下述情况下发生的()A.按比例连续增加各种生产要素B.不按比例连续增加各种生产要素C.连续地投入某种生产要素而保持其他生产要素不变D.上述都正确5.如果规模报酬不变,单位时间里增加了10%的劳动使用量;但保持资本量不变,则产出将()A.增加10% B.减少10% C.增加大于10% D.增加小于10%6.经济学中,短期是指()。
A.一年或一年以内的时期B.在这时期内所有投入量都是可变的C.在这时期内所有投入量都是不可变的D.在这时期内,至少有一种投入量是固定的,也至少有一种投入量是可变的7.当雇佣第7个工人,每周产量从100单位增加到110单位;当雇佣第8个工人时,每周产量从110单位增加到118单位,这种情况()。
A.规模收益递减B.边际成本递减C.边际收益递减D.资本密集型生产8.某企业的生产函数为F(K,L)=2.2K1/3L1/2,则()A.生产规模报酬递增 B.生产规模报酬递减C.生产规模报酬不变 D.无法判断9.边际产量递减规律所研究的问题是()A.各种生产要素同时变动对产量的影响。
B.两种生产要素同时变动对产量的影响。
C.其他生产要素不变,一种生产要素变动时对产量的影响。
D.一种生产要素不变,其他生产要素变动是对产量的影响。
10.当生产函数Q=f ( L,K ) 的APL 为递减时,则MPL()。
A.递减且为正 B.递减且为负 C.为零 D.上述情况都可能11.当边际产量大于平均产量时()A.产量递增B.平均产量递减C.平均产量不变D.边际产量递增12.等产量曲线是指在这条曲线上的各点代表()A.生产同等产量投入要素的各种组合比例是相同的。
微观经济学第4章生产论习题讲解学习

微观经济学第4章生产论习题第4章生产论一、名词解释1.生产函数2.边际报酬递减规律3.等产量曲线4.边际技术替代率5.等成本线6.规模报酬二、判断正误并解释原因1.在生产函数中,如果有一种投入是固定不变的,应是短期生产函数。
( )2.只要边际产量减少,总产量也一定减少。
( )3.当平均产量最大时,总产量最大。
( )4.只要边际产量上升,平均产量就上升;反过来说,只要平均产量上升,边际产量就上升。
() 5.边际报酬递减规律成立的原因是:可变要素和固定要素间有一个最佳比例关系。
( )6.等产量线一定是凸向原点的。
( )7.假定生产X产品使用A、B两种要素,则A的价格下降必导致B的使用量增加。
( )8.在要素A和B的当前使用水平上,A的边际产量是3,B的边际产量是2,每单位要素A的价格是5,B的价格是4,由于B是较便宜的要素,厂商若减少A的使用量而增加B的使用量,社会会以更低的成本生产出同样多产品。
( )9.在生产的经济区域以外的区域,资本或劳动的边际产量必有一个为负。
( )10.等成本线的斜率是两种生产要素的价格之比,因此,当要素价格发生变化时,等成本的率一定发生变化。
( )11.生产扩展线上的要素组合最优。
( )12.只有长期生产函数才有规模报酬问题。
( )13.考虑到规模报酬问题,企业的规模越大越好。
( )14.若生产函数K=,且L,K价格相同,则为实现利润最大化,企业4⋅Lq9应投入较多的劳动和较少的资本。
( )15.规模报酬递增的厂商不可能也会面临要素报酬递减的现象。
( ) 16* 拥有范围经济的企业,必定存在规模经济。
( )三、判断题1.等产量线是指在一定技术水平下,为生产一定数量的产品所使用的两种生产要素的不同组合方式的坐标点的轨迹。
()2.边际产量达到最大时,平均产量也达到最大。
()3.边际产量为零时,总产量达到最大。
()4.边际产量与平均产量不可能相等。
()5.理性的生产者将在生产过程的第二阶段进行生产。
微观经济学习题及解析

《微观经济学》习题第一章引论一、选择正确答案1.经济学可定义为()。
A.企业赚取利润的活动B.研究人们如何依靠收入生活的问题C.研究稀缺资源如何有效配置的问题D.政府对市场制度的干预2.“资源是稀缺”指的是()。
A.世界上的资源最终将被消耗尽B.资源是不可再生的C.资源必须留给下一代D.相对于需求而言,资源总是不足的3.一个经济体系必须回答的基本问题是()。
A.生产什么,生产多少B. 如何生产C.为谁生产D.以上都包括4.下列属于规范分析表述的是()。
A.鼓励私人购买汽车有利于促进我国汽车工业的发展B.随着收入水平的提高,拥有汽车的人会越来越多C.由于我国居民收入水平低,大多数人还买不起汽车D.个人汽车拥有量的增多,给我国居民的出行带来交通隐患5.下列属于实证分析表述的是()。
A.治理通货膨胀比减少失业更重要B.通货膨胀对经济发展有利C.通货膨胀对经济发展不利D.只有控制货币量才能抑制通货膨胀答案:1.C; 2.D; 3.D; 4.B; 5.A。
二、分析讨论1.如何理解西方经济学是一门考察稀缺的资源合理配置的科学。
答:西方经济学认为,人类的欲望和由此引起的对物品和劳务的需要是无限多样的,可是用来满足这些无限需要的手段即用来提供这些物品和劳务的生产资源是稀缺的。
这样,就产生了如何分配使用这些有限的资源来满足无限需要的问题,这就是“选择”,也就是“配置”资源的问题。
人类社会面临的经济问题就是如何把有限的资源合理地和有效率地分配使用于各种途径以满足人类无限多样的需要。
在市场经济中,资源的配置是通过市场价格机制来实现的。
生产什么、生产多少、如何生产、为谁生产,都是由市场价格决定的。
假若人类能无限量地生产出各种物品,或者人类的欲望能够完全得到满足,即在这样一个丰裕的伊甸园里,不存在稀缺物品,所有的物品都是免费的,像沙漠中的沙和海岸边的海水,价格和市场互不相关,那么经济学就无须存在了。
正是由于人类欲望的无限性和生产资源的有限性之间的矛盾才引起了人类的经济活动,西方经济学也就成为一门考察稀缺资源的配置的科学。
微观经济学-----第四章{生产者理论}-习题-(上海商学院)

第四章生产函数分析一、名词解释生产者生产函数生产要素固定投入比例生产函数一种可变要素的生产函数短期生产长期生产柯布一道格拉斯生产函数总产量平均产量边际产量边际报酬递减规律等产量线边际技术替代率边际技术替代率递减规律等成本线等斜线生产要素最优组合扩展线规模报酬规模报酬递增规模报酬不变规模报酬递减二、选择题知识点:生产函数1.生产要素(投入)和产出水平的关系称为()。
A.生产函数B.生产可能性曲线C.总成本曲线D.平均成本曲线2.生产函数表示( )。
A.一定数量的投入,至少能生产多少产品B.生产一定数量的产品,最多要投入多少生产要素C.投入与产出的关系D.以上都对观察图4。
1,回答第3—6题.3.如图4.1的生产函数,不变劳动投入的是( )。
A.L0B.L1 C L2D.L34.如图4.1的生产函数,下面关于劳动的边际生产率和平均生产率的说法中不正确的是( )。
A.边际生产率是生产函数的斜率B.在L3平均生产率等于边际生产率C.平均生产率开始先上升,然后下降D.边际生产在L3处达到最大5.如图4.1的生产函数,下列关于边际产量和平均产量的说法中,不正确的一项是( )。
A.在L2和L4处平均生产率相等B.边际生产率在L2处达到最大C.在L2处,平均生产率等于边际生产率D.平均生产率在L3处达到最大6.如图4.1的生产函数,则下列关于边际产量和平均产量的说法中,正确的一项是()。
A.C和D之间的平均生产率下降B.A和C之间的边际产量上升C.C点的平均生产率最小D.B和D之间的平均生产率上升7.如果生产函数为Q = min (3L,K),w = 5,r = 10,则劳动与资本的最优比例为()。
A.3 :1 B.1 :2 C.1 : 3 D.2 : 18.下面情形表示生产仍有潜力可挖的是()。
A.生产可能性边界上的任意一点B.生产可能性边界外的任意一点C.生产可能性边界内的任意一点D.以上都有可能知识点:总产出、平均产出、边际产出的概念及三者之间的关系9.当生产函数Q = f(L,K)的AP L为正且递减时,MP L可以是( ).A.递减且为正B.为0 C.递减且为负D.上述任何一种情况都有可能10.在总产量、平均产量和边际产量的变化过程中,下列说法中正确的是().A.总产量最先开始下降D.平均产量首先开始下降C.边际产量首先开始下降D.平均产量下降速度最快11.下列各项中,正确的是()。
4第四章 生产论 微观经济学
四、长期生产函数:两种可变生产要素的生产函 数1.长期生产函数的形式 在生产理论中,为了简化分析,通常以两种可变生产要素的生产函数来考察长期生产问题。假定生产者使用劳 动和资本两种可变生产要素来生产一种产品,则两种可变生产要素的长期生产函数可以写为:
Q f L,K 2.等产量曲线 等产量曲线(Equal-Product Curves)是在技术水平不变的条件下生产同一产量的两种生产要素投入量的所有不 同组合的轨迹,每一条等产量曲线对应的是特定的产出水平。等产量曲线如图4-2所示。
点的线段的斜率,就是相应的 APL 值。(3)边际产量和平均产量之间 的关系
就平均产量 APL 和边际产量 MPL来说,当 MPL APL 时, APL 曲线是上升的;当MPL APL 时,APL曲
线是下降的;当 MPL APL 时,APL 曲线达极大值。数学证明如下:
dTPL L −TP
d APL d TPL dL
二、生产函数 1.生产函数的概念
劳动、土地、资本和企业家才能
生产函数表示在一定时期内,在技术水平不变的情况下,生产中所使用的各种生产要素的数量与所能生产的最
大产量之间的关系(The production function specifies the maximum output that can be produced with a given quantity of
劳动的平均产量 APL 指平均每一单位可变要素劳动的投入量所生产的产量,即 APL = TPL L,K 。
L
劳动的边际产量 MPL 指增加一单位可变要素劳动投入量所增加的产量,即:
TPL L,K
MP
lim
TP dTPL L,K
L
L
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四章生产论1. 下面(表4—1)是一张一种可变生产要素的短期生产函数的产量表:(2)该生产函数是否表现出边际报酬递减?如果是,是从第几单位的可变要素投入量开始的?解答:(1)利用短期生产的总产量(TP)、平均产量(AP)和边际产量(MP)之间的关系,可以完成对该表的填空,其结果如表4—2所示:开始逐步下降的这样一种普遍的生产现象。
本题的生产函数表现出边际报酬递减的现象,具体地说,由表4—2可见,当可变要素的投入量从第4单位增加到第5单位时,该要素的边际产量由原来的24下降为12。
2. 用图说明短期生产函数Q=f(L,K-)的TP L曲线、AP L曲线和MP L曲线的特征及其相互之间的关系。
解答:短期生产函数的TP L 曲线、AP L 曲线和MP L 曲线的综合图如图4—1所示。
图4—1由图4—1可见,在短期生产的边际报酬递减规律的作用下,MP L 曲线呈现出先上升达到最高点A 以后又下降的趋势。
从边际报酬递减规律决定的MP L 曲线出发,可以方便地推导出TP L 曲线和AP L 曲线,并掌握它们各自的特征及相互之间的关系。
关于TP L 曲线。
由于MP L =d TP L d L,所以,当MP L >0时,TP L 曲线是上升的;当MP L<0时,TP L 曲线是下降的;而当MP L =0时,TP L 曲线达最高点。
换言之,在L =L 3时,MP L 曲线达到零值的B 点与TP L 曲线达到最大值的B ′点是相互对应的。
此外,在L <L 3即MP L >0的范围内,当MP ′L >0时,TP L 曲线的斜率递增,即TP L 曲线以递增的速率上升;当MP ′L <0时,TP L 曲线的斜率递减,即TP L 曲线以递减的速率上升;而当MP ′=0时,TP L 曲线存在一个拐点,换言之,在L =L 1时,MP L 曲线斜率为零的A 点与TP L 曲线的拐点A ′是相互对应的。
关于AP L 曲线。
由于AP L =TP LL ,所以,在L =L 2时,TP L 曲线有一条由原点出发的切线,其切点为C 。
该切线是由原点出发与TP L 曲线上所有的点的连线中斜率最大的一条连线,故该切点对应的是AP L 的最大值点。
再考虑到AP L 曲线和MP L 曲线一定会相交在AP L 曲线的最高点。
因此,在图4—1中,在L =L 2时,AP L 曲线与MP L 曲线相交于AP L 曲线的最高点C ′,而且与C ′点相对应的是TP L 曲线上的切点C 。
3. 已知生产函数Q =f(L , K)=2KL -0.5L 2-0.5K 2, 假定厂商目前处于短期生产,且K =10。
(1)写出在短期生产中该厂商关于劳动的总产量TP L 函数、劳动的平均产量AP L 函数和劳动的边际产量MP L 函数。
(2)分别计算当劳动的总产量TP L 、劳动的平均产量AP L 和劳动的边际产量MP L 各自达到最大值时的厂商的劳动投入量。
(3)什么时候AP L =MP L ?它的值又是多少?解:(1)由生产函数Q =2KL -0.5L 2-0.5K 2,且K =10,可得短期生产函数为 Q =20L -0.5L 2-0.5×102=20L -0.5L 2-50于是,根据总产量、平均产量和边际产量的定义,有以下函数 劳动的总产量函数:TP L =20L -0.5L 2-50劳动的平均产量函数:AP L =TP LL =20-0.5L -50L劳动的边际产量函数:MP L =d TP L d L=20-L(2)关于总产量的最大值: 令d TP L d L=0,即d TP L d L=20-L =0解得 L =20 且d 2TP L d L 2=-1<0所以,当劳动投入量L =20时,劳动的总产量TPL 达到极大值。
关于平均产量的最大值: 令d AP L d L=0,即d AP L d L=-0.5+50L -2=0解得 L =10(已舍去负值) 且d 2AP L d L 2=-100L -3<0所以,当劳动投入量L =10时,劳动的平均产量AP L 达到极大值。
关于边际产量的最大值:由劳动的边际产量函数MP L =20-L 可知,边际产量曲线是一条斜率为负的直线。
考虑到劳动投入量总是非负的,所以,当劳动投入量L =0时,劳动的边际产量MP L 达到极大值。
(3)当劳动的平均产量AP L 达到最大值时,一定有AP L =MP L 。
由(2)已知,当L =10时,劳动的平均产量AP L 达到最大值,即相应的最大值为AP L 的最大值=20-0.5×10-5010=10将L =10代入劳动的边际产量函数MP L =20-L ,得MP L =20-10=10。
很显然,当AP L =MP L =10时,AP L 一定达到其自身的极大值,此时劳动投入量为L =10。
4.区分边际报酬递增、不变和递减的情况与规模报酬递增、不变和递减的情况。
解答:边际报酬变化是指在生产过程中一种可变要素投入量每增加一个单位时所引起的总产量的变化量,即边际产量的变化,而其他生产要素均为固定生产要素,固定要素的投入数量是保持不变的。
边际报酬变化具有包括边际报酬递增、不变和递减的情况。
很显然,边际报酬分析可视为短期生产的分析视角。
规模报酬分析方法是描述在生产过程中全部生产要素的投入数量均同比例变化时所引起的产量变化特征,当产量的变化比例分别大于、等于、小于全部生产要素投入量变化比例时,则分别为规模报酬递增、不变、递减。
很显然,规模报酬分析可视为长期生产的分析视角。
5. 已知生产函数为Q =min {2L , 3K}。
求:(1)当产量Q =36时,L 与K 值分别是多少?(2)如果生产要素的价格分别为P L =2,P K =5,则生产480单位产量时的最小成本是多少?解答:(1)生产函数Q =min {2L , 3K}表示该函数是一个固定投入比例的生产函数,所以,厂商进行生产时,总有Q =2L =3K 。
因为已知产量Q =36,所以,相应地有L =18,K =12。
(2)由Q =2L =3K ,且Q =480,可得 L =240,K =160 又因为P L =2,P K =5,所以有 C =P L ·L +P K ·K =2×240+5×160=1 280即生产480单位产量的最小成本为1 280。
6.假设某厂商的短期生产函数为 Q =35L +8L 2-L 3。
求:(1)该企业的平均产量函数和边际产量函数。
(2)如果企业使用的生产要素的数量为L =6,是否处理短期生产的合理区间?为什么? 解答:(1)平均产量函数:AP(L)=Q(L)L =35+8L -L 2边际产量函数:MP(L)=d Q(L)d L=35+16L -3L 2(2)首先需要确定生产要素L 投入量的合理区间。
在生产要素L 投入量的合理区间的左端,有AP =MP ,于是,有35+8L -L 2=35+16L -3L 2。
解得L =0和L =4。
L =0不合理,舍去,故取L =4。
在生产要素L 投入量的合理区间的右端,有MP =0,于是,有35+16L -3L 2=0。
解得L =-53和L =7。
L =--53不合理,舍去,故取L =7。
由此可得,生产要素L 投入量的合理区间为[4,7]。
因此,企业对生产要素L 的使用量为6是处于短期生产的合理区间的。
7.假设生产函数Q =3L 0.8K 0.2。
试问: (1)该生产函数是否为齐次生产函数?(2)如果根据欧拉分配定理,生产要素L 和K 都按其边际产量领取实物报酬,那么,分配后产品还会有剩余吗?解答:(1)因为f(λL ,λK)=3(λL)0.8(λK)0.2=λ0.8+0.23L 0.8K 0.2 =λ·3L 0.8K 0.2=λ·f(L ,K)所以,该生产函数为齐次生产函数,且为规模报酬不变的一次齐次生产函数。
(2)因为MP L =d Q d L=2.4L -0.2K 0.2 MP K =d Q d K=0.6L 0.8K -0.8所以,根据欧拉分配定理,被分配掉的实物总量为MP L ·L +MP K ·K =2.4L -0.2K 0.2·L +0.6L 0.8K -0.8·K =2.4L 0.8K 0.2+0.6L 0.8K 0.2=3L 0.8K 0.2可见,对于一次齐次的该生产函数来说,若按欧拉分配定理分配实物报酬,则所生产的产品刚好分完,不会有剩余。
8.假设生产函数Q = min {5L,2K}。
(1)作出Q =50时的等产量曲线。
(2)推导该生产函数的边际技术替代率函数。
(3)分析该生产函数的规模报酬情况。
解答:(1)生产函数Q =min{5L,2K }是固定投入比例生产函数,其等产量曲线如图4—2所示为直角形状,且在直角点两要素的固定投入比例为K L =52。
图4—2当产量Q =50时,有5L =2K =50,即L =10,K =25。
相应的Q =50的等产量曲线如图4—2所示。
(2)由于该生产函数为固定投入比例,即L 与K 之间没有替代关系,所以,边际技术替代率MRTS LK =0。
(3) 因为Q =f(L ,K)=min {5L,2K}f(λL ,λK)=min {5λL,2λK}=λmin {5L,2K}所以该生产函数为一次齐次生产函数,呈现出规模报酬不变的特征。
9.已知柯布道格拉斯生产函数为Q =AL αK β。
请讨论该生产函数的规模报酬情况。
解答:因为 Q =f(L ,K)=AL αK βf(λL ,λK)=A(λL)α(λK)β=λα+βAL αK β所以当α+β>1时,该生产函数为规模报酬递增;当α+β=1时,该生产函数为规模报酬不变;当α+β<1时,该生产函数为规模报酬递减。
10. 已知生产函数为 (a )Q =5L 13K 23;(b )Q =KLK +L ;(c )Q =KL 2;(d )Q =min {3L , K}。
求:(1)厂商长期生产的扩展线方程。
(2)当P L =1,P K =1,Q =1 000时,厂商实现最小成本的要素投入组合。
解答:(1)(a )关于生产函数Q =5L 13K 23。
MP L =53L -23K 23MP K =103 L 13K -13由最优要素组合的均衡条件MP LMP K =P LP K ,可得53L -23K 23103 L 13K -13=P LP K整理得 K2L =P LP K即厂商长期生产的扩展线方程为K =⎝ ⎛⎭⎪⎫2P L P K L (b )关于生产函数Q =Q =KLK +L 。
