初三数学九下锐角三角函数所有知识点总结和常考题型练习题
苏教版九年级下册数学[锐角三角函数—知识点整理及重点题型梳理]
![苏教版九年级下册数学[锐角三角函数—知识点整理及重点题型梳理]](https://img.taocdn.com/s3/m/4dd5d51a0722192e4436f605.png)
苏教版九年级下册数学重难点突破知识点梳理及重点题型巩固练习锐角三角函数—知识讲解【学习目标】1.结合图形理解记忆锐角三角函数定义;2.会推算30°、45°、60°角的三角函数值,并熟练准确的记住特殊角的三角函数值; 3.理解并能熟练运用“同角三角函数的关系”及“锐角三角函数值随角度变化的规律”.【要点梳理】要点一、锐角三角函数的概念如图所示,在Rt △ABC 中,∠C =90°,∠A 所对的边BC 记为a ,叫做∠A 的对边,也叫做∠B 的邻边,∠B 所对的边AC 记为b ,叫做∠B 的对边,也是∠A 的邻边,直角C 所对的边AB 记为c ,叫做斜边.锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即sin A aA c ∠==的对边斜边;锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即cos A bA c ∠==的邻边斜边;锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即tan A aA A b∠==∠的对边的邻边.同理sin B b B c ∠==的对边斜边;cos B aB c∠==的邻边斜边;tan B b B B a ∠==∠的对边的邻边.要点诠释:(1)正弦、余弦、正切函数是在直角三角形中定义的,反映了直角三角形边与角的关系,是两条线段的比值.角的度数确定时,其比值不变,角的度数变化时,比值也随之变化. (2)sinA ,cosA ,tanA 分别是一个完整的数学符号,是一个整体,不能写成,,,不能理解成sin 与∠A ,cos 与∠A ,tan 与∠A 的乘积.书写时习惯上省略∠A 的角的Ca b记号“∠”,但对三个大写字母表示成的角(如∠AEF),其正切应写成“tan∠AEF”,不能写成“tanAEF”;另外,、、常写成、、.(3)任何一个锐角都有相应的锐角三角函数值,不因这个角不在某个三角形中而不存在.(4)由锐角三角函数的定义知:当角度在0°<∠A<90°间变化时,,,tanA>0.要点二、特殊角的三角函数值(1)通过该表可以方便地知道30°、45°、60°角的各三角函数值,它的另一个应用就是:如果知道了一个锐角的三角函数值,就可以求出这个锐角的度数,例如:若,则锐角.(2)仔细研究表中数值的规律会发现:、、的值依次为、、,而、、的值的顺序正好相反,、、的值依次增大,其变化规律可以总结为:①正弦、正切值随锐角度数的增大(或减小)而增大(或减小);②余弦值随锐角度数的增大(或减小)而减小(或增大).要点三、锐角三角函数之间的关系如图所示,在Rt△ABC中,∠C=90°.(1)互余关系:,;(2)平方关系:;(3)倒数关系:或;(4)商数关系:.要点诠释:锐角三角函数之间的关系式可由锐角三角函数的意义推导得出,常应用在三角函数的计算中,计算时巧用这些关系式可使运算简便.【典型例题】类型一、锐角三角函数值的求解策略1.(2016•安顺)如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC 的正切值是()A.2 B.C.D.【思路点拨】根据勾股定理,可得AC、AB的长,根据正切函数的定义,可得答案.【答案】D.【解析】解:如图:,由勾股定理,得AC=,AB=2,BC=,∴△ABC为直角三角形,∴tan∠B==,故选:D.【总结升华】本题考查了锐角三角函数的定义,先求出AC、AB的长,再求正切函数.举一反三:【课程名称:锐角三角函数395948:例1(1)-(2)】【变式】在RtΔABC中,∠C=90°,若a=3,b=4,则c=,sinA=,cosA=,sinB=,cosB=.a【答案】c = 5 ,sinA = 35 , cosA =45,sinB =45, cosB =35.类型二、特殊角的三角函数值的计算2.求下列各式的值:(1)(2015•茂名校级一模) 6tan 230°﹣sin60°﹣2sin45°;(2)(2015•乐陵市模拟) sin60°﹣4cos 230°+sin45°•tan60°;(3)(2015•宝山区一模) +tan60°﹣.【答案与解析】 解:(1)原式==12(2) 原式=×﹣4×()2+×=﹣3+3;(3) 原式=+﹣=2+﹣=3﹣2+2【总结升华】熟记特殊角的三角函数值或借助两个三角板推算三角函数值,先代入特殊角的三角函数值,再进行化简.举一反三:【课程名称: 锐角三角函数 395948 :例1(3)-(4)】 【变式】在Rt ΔABC 中,∠C =90°,若∠A=45°,则∠B = ,sinA=,cosA=,sinB=,cosB=.【答案】∠B=45°,sinA=,cosA=,sinB=cosB=.类型三、锐角三角函数之间的关系3.(2015•河北模拟)已知△ABC中的∠A与∠B满足(1﹣tanA)2+|sinB﹣|=0(1)试判断△ABC的形状.(2)求(1+sinA)2﹣2﹣(3+tanC)0的值.【答案与解析】解:(1)∵|1﹣tanA)2+|sinB﹣|=0,∴tanA=1,sinB=,∴∠A=45°,∠B=60°,∠C=180°﹣45°﹣60°=75°,∴△ABC是锐角三角形;(2)∵∠A=45°,∠B=60°,∠C=180°﹣45°﹣60°=75°,∴原式=(1+)2﹣2﹣1=.【总结升华】本题考查的是特殊角的三角函数值,熟记各特殊角度的三角函数值是解答此题的关键.类型四、锐角三角函数的拓展探究与应用4.如图所示,AB是⊙O的直径,且AB=10,CD是⊙O的弦,AD与BC相交于点P,若弦CD=6,试求cos∠APC的值.【答案与解析】连结AC,∵ AB是⊙O的直径,∴∠ACP=90°,又∵∠B=∠D,∠PAB=∠PCD,∴△PCD∽△PAB,∴PC CDPA AB=. 又∵ CD =6,AB =10, ∴ 在Rt △PAC 中,63cos 105PC CD APC PA AB ∠====.【总结升华】直角三角形中,锐角的三角函数等于两边的比值,当这个比值无法直接求解,可结合相似三角形的性质,利用对应线段成比例转换,间接地求出这个比值.锐角的三角函数是针对直角三角形而言的,故可连结AC ,由AB 是⊙O 的直径得∠ACB =90°,cos PC APC PA ∠=,PC 、PA 均为未知,而已知CD =6,AB =10,可考虑利用△PCD ∽△PAB 得PC CDPA AB=.5.通过学习三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.类似的,可以在等腰三角形中建立边角之间的联系.我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图1①,在△ABC 中,AB =AC ,顶角A 的正对记作sadA ,这时sadA BCAB==底边腰.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.根据上述角的正对定义,解下列问题:(1)sad60°=________.(2)对于0<A <180°,∠A 的正对值sadA 的取值范围是_______.(3)如图1②,已知sinA =35,其中∠A 为锐角,试求sadA 的值.【答案与解析】(1)1; (2)0<sadA <2;(3)如图2所示,延长AC 到D ,使AD =AB ,连接BD .设AD =AB =5a ,由3sin 5BC A AB ==得BC =3a ,∴ 4AC a ==,∴ CD =5a-4a =a ,BD ==,∴ sadA BD AD == 【总结升华】(1)将60°角放在等腰三角形中,底边和腰相等,故sadA =1;(2)在图①中设想AB =AC的长固定,并固定AB 让AC 绕点A 旋转,当∠A 接近0°时,BC 接近0,则sadA 接近0但永远不会等于0,故sadA >0,当∠A 接近180°时,BC 接近2AB ,则sadA 接近2但小于2,故sadA <2;(3)将∠A 放到等腰三角形中,如图2所示,根据定义可求解.。
最新初三锐角三角函数知识点总结、典型例题、练习(精选)
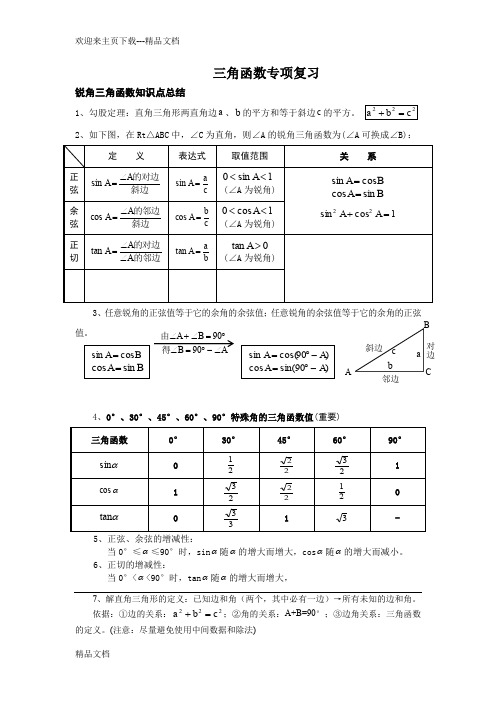
三角函数专项复习锐角三角函数知识点总结1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
222c b a =+2、如下图,在Rt △ABC 中,∠C 为直角,则∠A 的锐角三角函数为(∠A 可换成∠B):定 义表达式取值范围关 系正弦 斜边的对边A A ∠=sin c aA =sin 1sin 0<<A (∠A 为锐角)B A cos sin =B A sin cos =1cos sin 22=+A A余弦 斜边的邻边A A ∠=cos c bA =cos 1cos 0<<A (∠A 为锐角) 正切 的邻边的对边A tan ∠∠=A A b aA =tan 0tan >A (∠A 为锐角)3、任意锐角的正弦值等于它的余角的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、0°、30°、45°、60°、90°特殊角的三角函数值(重要) 三角函数 0° 30°45°60°90° αsin 0 21 22 23 1 αcos1 23 2221 0 αtan33 1 3-5、正弦、余弦的增减性:当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:当0°<α<90°时,tan α随α的增大而增大,7、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:222c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
(注意:尽量避免使用中间数据和除法) )90cos(sin A A -︒=)90sin(cos A A -︒=BA cos sin =BA sin cos =A90B 90∠-︒=∠︒=∠+∠得由B A对边邻边斜边 ACBba c8、应用举例:(1)仰角:视线在水平线上方的角;俯角:视线在水平线下方的角。
初三锐角三角函数知识点与典型例题

3 5 3 4
,那么 tanA 的值等于( D.
4 3
).
B.
4 5
C.
类型二 . 利用角度转化求值: 1.已知:如图, Rt △ ABC 中,∠ C = 90°. D 是 AC 边上一点, DE ⊥ AB 于 E 点. DE ∶ AE = 1 ∶ 2. 求: sin B、 cosB 、 tanB.
F
90 , AC
C
6 , D 为 AC 上一点,若
7. 如图 6 ,在等腰直角三角形
ABC 中,
C
tan DBA
1 5
,则
AD 的长为 ( )
A. C. 1
2
B D
.
2
.2 2
8. 如图 6 ,在 Rt △ ABC 中,∠ C=90 °, AC =8,∠ A 度数及边 BC 、 AB 的长 .
A
AD =
的顶点为 O ,它的一边在 x 轴的正半轴上,另一边 .
OA 上有
sin
4.( 2009 ・ 庆阳中考)如图,菱形 的面积 = cm .
2
ABCD 的边长为 10cm, DE ⊥ AB , sin A
3 5
,则这个菱形
5.( 2009 ・ 齐齐哈尔中考)如图, 径为
⊙ O 是 △ ABC 的外接圆, AD 是 ⊙O 的直径,若 ⊙ O 的半
(昌平) 1) . 计算: 2 cos 30
2 sin 45
tan 60 .
(朝阳) 2)计算: tan 60
sin 45
2
2 cos 30 .
( 2009 ・ 黄石中考)计算:
3 +(2 π - 1) -
-1
0
初三数学九下锐角三角函数所有知识点总结和常考题型练习题
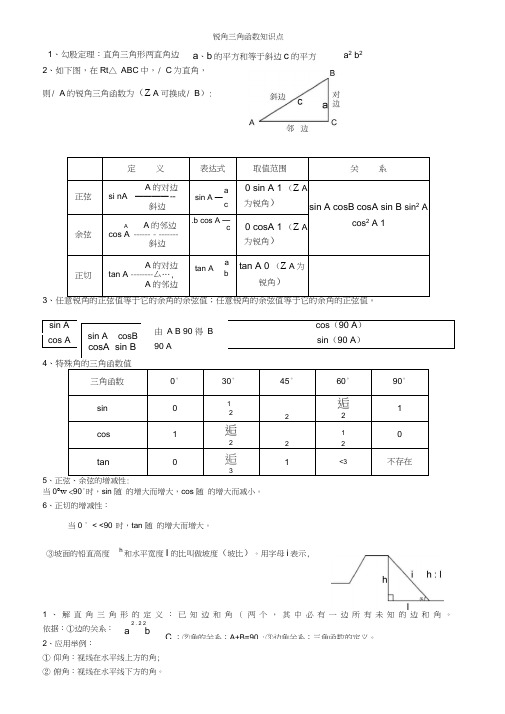
锐角三角函数知识点③坡面的铅直高度h和水平宽度I 的比叫做坡度(坡比)。
用字母i 表示,2、如下图,在Rt △ ABC 中,/ C 为直角, 则/ A 的锐角三角函数为(Z A 可换成/ B ):定义 表达式取值范围 关 系正弦A 的对边si nA ———— --斜边 asin A —c 0 sin A 1 (Z A为锐角)sin A cosB cosA sin B sin 2 Acos 2 A 1余弦AA 的邻边cos A ------ - -------斜边 .b cos A —c0 cosA 1 (Z A为锐角)正切A 的对边tan A -------- 厶…,A 的邻边atan Abtan A 0 (Z A 为锐角)3 cos (90 A ) sin A sin (90 A )cos A4三角函数 0° 30°45° 60° 90° sin 0 122逅21 cos1 逅2212 0 tan逅31<3不存在5当0°w <90°时,sin 随 的增大而增大,cos 随 的增大而减小。
6、正切的增减性:当0 ° < <90°时,tan 随 的增大而增大。
1、解直角三角形的定义:已知边和角(两个,其中必有一边所有未知的边和角。
依据:①边的关系: 2 . 2 2a bC ;②角的关系:A+B=90°;③边角关系:三角函数的定义。
2、应用举例:① 仰角:视线在水平线上方的角; ② 俯角:视线在水平线下方的角。
1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方a 2b 2sin A cosBcosA sin B由 A B 90 得 B 90 A6、计算 tan60o 「2 sin45o 2cos30o 的结果是)i ——即 l 。
坡度一般写成1:m 的形式,女口 i 1:5等。
初三锐角三角函数知识点与典型例题

锐角三角函数:知识点一:锐角三角函数的定义:一、锐角三角函数定义:在Rt△ ABC 中,/ C=90°, / A、/ B、/ C 的对边分别为a、b、c, 则/ A的正弦可表示为:sinA= __________ ,/ A的余弦可表示为cosA= ___________/ A的正切:tanA= ________ ,它们弦称为/ A的锐角三角函数【特别提醒:1、sinA、/ cosA、tanA表示的是一个整体,是两条线段的比,没值只与_________ 有关,与直角三角形的_________ 无关2、取值范围___ vsinA _______ c osA< ______ tanA> ________】例1.如图所示,在Rt△ ABC中,/ C = 90°.例2.锐角三角函数求值:在Rt△ ABC 中,/ C= 90°,若a= 9,sinA= ______ , cosA= ______sinB = _____ , cosB = ______例3.已知:如图,Rt△ TNM 中,/ TMN = 90°, MR丄TN 于R点,TN= 4, 求: sin/TMR、cos/TMR、tan/ TMR.典型例题:类型一:直角三角形求值有,这些比① sin A 一()斜边② cosA -)斜边③ tan A _ ()Z A的邻边sin B 一()斜边;cos^ =—)斜边.B的对边tan B ------------- =.()b= 12,贝U c=_______tanA = ______ ,tanB = ______ .MN = 3. 第1题图3431 已知 Rt △ ABC 中, C =90,ta nA, BC =12,求 AC 、AB 和 cosB . 432. 已知:如图,O O 的半径 OA = 16cm , OC 丄AB 于C 点,sin. AOC 二—-4求:AB 及OC 的长.33. 已知:O O 中,OC 丄 AB 于 C 点,AB = 16cm , sin . AOC 二—5 (1)求O O 的半径OA 的长及弦心距 OC ; ⑵求 cos / AOC 及 tan / AOC .84.已知• A 是锐角,si nA,求cosA , ta nA 的值 17对应训练:C = 90° 若 BC = 1,AB=J 5,贝U tanA 的值为B.-5类型二.利用角度转化求值:1. 已知:如图, Rt △ ABC 中,/ C = 90°. D 是AC 边上一点,DE 丄AB 于E 点.DE : AE = 1 : 2.求: sinB 、cosB 、tanB .(房山)5.在△ ABC 中,/ C=90° sinA= 3,那么tanA 的值等于(5(西城北)3.在Rt △ ABC 中,/ C. D.-32. 如图,直径为10的O A 经过点C (0,5)和点0(0,0),与x 轴的正半轴交于点 D , B 是y的面积= _______ cm 2.3半径为3 , AC =2,则sin B 的值是()2轴右侧圆弧上一点,则 cos / OBC 的值为(C . 3:-的顶点为0,它的一边在x 轴的正半轴上,另OA 上有ABCD 的边长为10cm , DE 丄AB ,则这个菱形5. (2009齐齐哈尔中考)如图,O O 是厶ABC 的外接圆, AD 是O O 的直径, 若O O 的D .3. (2009孝感中考)如图,角4. (2009庆阳中考)如图,菱形3度数及边BC 、AB 的长.类型三.化斜三角形为直角三角形例 1 ( 2012?安徽)如图,在△ ABC 中,/ A=30°,/ B=45 , AC=2 .3,求 AB 的长.1 例 2.已知:如图,△ ABC 中,AC = 12cm , AB = 16cm , sinA= — (1)求AB 边上的高CD ; ⑵求△ ABC 的面积S ; ⑶求tanB .6.如图4,沿AE 折叠矩形纸片 ABCD ,使点 BC =10, AB=8,则 tan / EFC 的值为(F 处•已知AB =8,A. 3 4B. 4 3C. 3 5在等腰直角三角形:ABC 中,.C =90 , AC =6 ,1tan 一匕 DBA57.如图6,则AD 的长为()A. C..2.28.如图 6,在 Rt △ ABC 中,/ C=90° , AC=8,/ A 的平分线D 为AC 上一点,若AD = ^ 求3D 落在BC 边的点 D.图6例 3.已知:如图,在△ ABC 中,/ BAC = 120°, AB = 10 , AC = 5. 求:sin / ABC 的值.对应训练1. ( 2012?重庆)如图,在 Rt △ ABC 中,/ BAC=90°,点D 在BC 边上,且△ ABD 是等边 三角形.若AB=2,求△ ABC 的周长.(结果保留根号)2. 已知:如图,△ ABC 中,AB = 9, BC = 6,A ABC 的面积等于 9,求sinB .3. ABC 中,/ A=60°, AB=6 cm , AC=4 cm ,则△ ABC 的面积是A.2 ■■ 3 cm 2 C.6 一 3 cm 2类型四:利用网格构造直角三角形例1 (2012?内江)如图所示,△ ABC 的顶点是正方形网格的格点, 则sinA 的值为()A 丄B 国C 巫D M2510 5l' i1 i ■ ■1 -…右…[4L… t 7Zu /:c1■ 1 8对应练习:1.如图,△ ABC 的顶点都在方格纸的格点上,贝Usin A = ______B.4 - 3 cm 2 D.12 cm 2A B特殊角的三角函数值锐角G 30°45°60°si n otcosotta n a当________ 时,正弦和正切值随着角度的增大而 ___________ 余弦值随着角度的增大而例1求下列各式的值.(昌平)1).计算:2cos30 = .2sin45 ‘—tan 60 .(朝阳)2)计算:ta n60°+si n245 °- 2cos30°.(2009黄石中考)计算:3一1+(2 n-1)0-号tan30—tan45°△AC'B',则tanB'的值为1 1 1A. —B. —C.—D. 14 3 2J7_A」———aB. 2 ,'55tan / AOB的值是(C.2D. 22 .如图,A、B、C三点在正方形网络线的交点处,若将ABC绕着点A逆时针旋转得到3•正方形网格中, / AOB如图放置,则(石景山)4 •计算:+ T2cos60 * + si n4 5°-"¥ta n30 =(5)已知:•为锐角,且tan(鼻亠30°) =3,求tan 〉的值例3.三角函数的增减性11. 已知/ A 为锐角,且sin A < ,那么/ A 的取值范围是2A. 0 <A < 30° B. 30<A v 60° C. 60 <A < 90° D. 30 <A < 902. 已知A 为锐角,且cos A < sin 300,贝U ()A. 0 <A < 60° B. 30 <A < 60° C. 60 <A < 90 ° D. 30 <A < 90例4.三角函数在几何中的应用(通县)5 •计算:tan 45 sin 30 ;1 -cos60例2.求适合下列条件的锐角:-•1(1) COS _:i⑵ tan 二=(3) si n2:=、22(4) 6cos(: - 16 )=3.3(■')在=ABC 中,若cosA-丄 2(sinB --2)2 = 0,2.A, . B 都是锐角,求■ C 的度求此菱形的周长.2. 已知:如图,Rt△ ABC 中,/ C= 90°, AC =BC =$3,作/ DAC=30 ° , AD交CB于D点,求:(1) / BAD;(2) sin / BAD、cos/ BAD 和tan / BAD .13. 已知:如图△ABC中,D为BC中点,且/BAD =90°,tan^B ,求:sin/CAD、cos 3/ CAD、tan/ CAD .34. 如图,在Rt△ ABC 中,/ C=90° , sin B ,点D在BC 边上,DC= AC = 6,求tan / BAD 5的值.1已知:如图,在菱形ABCD 中,DE 丄AB 于E, BE= 16cm,sinA,13BDC5. (本小题5分)如图,△ ABC中,/ A=30 AC = 4、、3 .求AB 的长.,tanB 二,2C解直角二角形:1在解直角三角形的过程中,一般要用的主要关系如下(如图所示):在 Rt △ ABC 中,/ C = 90°, AC = b , BC = a , AB = c , ① 三边之间的等量关系: ___________________________________ ② 两锐角之间的关系: _____________________________________ ③ 边与角之间的关系:sinA=cosB= ______ ; cosA = sinB =④ 直角三角形中成比例的线段(如图所示)• 在 Rt △ ABC 中,/ C = 90°, CD 丄 AB 于 D • CD 2= _________ ; AC 2= ________ ; BC 2= _________ ; AC • BC = ________ •类型一例 1.在 Rt A ABC 中,/ C = 90°.(1)已知:a = 35, c=35.2,求/ A 、/ B , b ;⑵已知:a = 2. 3 , b=2,求/ A 、/ B , c ;⑶已知:2sin A, c = 6,求 a 、b ;3⑷已知:3tan B , b = 9,求 a 、c ;2⑸已知:/ A = 60°,A ABC 的面积 S =12、. 3,求 a 、b 、c 及/ B .tan A =1 tan Btan B =tan A例2.已知:如图,△ ABC 中,/ A = 30°,/ B= 60°,AC = 10cm .求AB 及BC 的长.类型二:解直角三角形的实际应用仰角与俯角: 例1.(2012?福州)如图,从热气球C处测得地面A、B两点的俯角分别是30° 45°如果此时热气球C处的高度CD为100米,点A、D、B在同一直线上,则AB两点的距离是()例2•已知:如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知/ BAC = 60°,/ DAE =45° .点D到地面的垂直距离DE =3、2m,求点B到地面的垂直距离BC.例3 (昌平)19.如图,一风力发电装置竖立在小山顶上,小山的高BD=30m从水平面上一点C测得风力发电装置的顶端A的仰角/ DCA=60°,测得山顶B的仰角/ DCB=30°,求风力发电装置的高AB的长.例3.已知:如图,Rt△ ABC中,/ D =90 =10cm .求AD的长.,/ B = 45,/ ACD = 60 ° .BC例4.已知:如图,△ ABC中,/ A = 30°,/C. 220 二米D. 100 (V)米高,已知小聪和树都与地面垂直,且相距为1.7米,求这棵树的高度•例5.已知:如图,河旁有一座小山,从山顶 A 处测得河对岸点 C 的俯角为30 °,测得岸 边点D 的俯角为45°,又知河宽CD 为50m .现需从山顶 A 到河对岸点C 拉一条笔直的缆 绳AC ,求山的高度及缆绳 AC 的长(答案可带根号).例5. (2012?泰安)如图,为测量某物体 AB 的高度,在D 点测得A 点的仰角为30°,朝物 体AB 方向前进20米,到达点C ,再次测得点A 的仰角为60°,则物体AB 的高度为( )DCBA . 10血米B .10米C . 20近米D 竽米例6. (2012?益阳)超速行驶是引发交通事故的主要原因之一•上周末,小明和三位同学尝 试用自己所学的知识检测车速•如图,观测点设在 A 处,离益阳大道的距离(AC )为30米.这时,一辆小轿车由西向东匀速行驶,测得此车从 B 处行驶到C 处所用的时间为8秒,/ BAC=75 .(1 )求B 、C 两点的距离;(2)请判断此车是否超过了益阳大道 60千米/小时的限制速度? (计算时距离精确到1 米,参考数据:sin75 °~ 0.9659cos75°~ 0.2588 tan75 °~ 3.732亦 ~ 1.732 60 千米 /小时 ~ 16.7米/秒)3.3米,小聪身高 ABA BE类型四.坡度与坡角类型五.方位角继续向北航行时,与灯塔 M 之间的最短距离是多少 ?(精确到0.1海里,.3 1.732)2. (2012?恩施州)新闻链接,据[侨报网讯]外国炮艇在南海追袭中国渔船被中国渔政逼退 2012年5月18日,某国3艘炮艇追袭5条中国渔船.刚刚完成黄岩岛护渔任务的 中国渔政310”船人船未歇立即追往北纬 11度22分、东经110度45分附近海域护渔,保护 100多 名中国渔民免受财产损失和人身伤害. 某国炮艇发现中国目前最先进的渔政船正在疾速驰救图1 图2例.(2012?广安)如图,某水库堤坝横断面迎水坡 则应水坡面AB 的长度是( )A . 100mB . 100.3 mC . 150mAB 的坡比是1:3,堤坝高BC=50m ,D . 50 3m 1•已知:如图,一艘货轮向正北方向航行,在点每小时20海里的速度航行,1小时后到达 A 处测得灯塔M 在北偏西30°,货轮以 B处,测得灯塔 M 在北偏西45°,问该货轮0 A解决问题如图2,已知中国渔政310”船(A )接到陆地指挥中心(B)命令时,渔船(C)位于陆地指挥中心正南方向,位于中国渔政310”船西南方向,中国渔政310”船位于陆地指挥中心南偏东60°方向,AB「::海里,中国渔政310”船最大航速20海里/时.根据以上信息,3请你求出中国渔政310”船赶往出事地点需要多少时间.综合题:三角函数与四边形:tan/ BDC=(1)求BD的长;⑵求AD的长.(2011东一)18.如图,在平行四边形ABCD中,过点A分别作AE丄BC于点E, AF丄CD于点F .(1)求证: / BAE= / DAF ;24 3(2)若AE=4, AF= , sin. BAE ,求CF 的长.5 5三角函数与圆:1.如图,直径为10的O A经过点C(0,5)和点0(0,0),与x轴的正半轴交于点D, B是y轴右侧圆弧上一点,则cos/ OBC的值为()A.-B.C.34 D.2255 y\A;O1B第8题图(西城二模)1 .如图,四边形ABCD中, / BAD= 135°,(延庆)19.已知:在O O 中,AB 是直径,CB 是O O 的切线,连接 AC 与O O 交于点D, (1)求证:/ AOD=2/ C4⑵ 若AD=8 tanC=—,求O O 的半径。
人教版九年级数学下册锐角三角函数知识点及例题整理

28. 锐角三角函数知识点一: 正弦的定义及其表示方法1. 在直角三角形中,一个锐角的对边与斜边的比叫做这个锐角的正弦,如:∠A 的正弦记作sinA ,即sinA = ∠A 的对边斜边 = a c.2. 求锐角的正弦值,要以正弦的概念为依据,在直角三角形中求解。
若题目中给出的角不是在直角三角形中,应先构造直角三角形再求解。
3. 画出符合题意的图形,弄清所求角的对边与斜边。
4. 没有直接给出对边与斜边的题目,一般先根据勾股定理,求出所需的边长再求解。
例1:判断:在Rt△ABC 中,∠A 的正弦,记作cosA.______(填”对”或“错”) 例2:判断:在Rt△ABC 中,∠A 的正弦都等于∠A 的邻边与对边的比.______(填”对”或“错”)例3:Rt△ABC 中,∠C=90°,a 、b 、c 分别是∠A、∠B、∠C 的对边,下列式子中,正确的是( )A. a=b ⋅sinA ;B. a=c ⋅sinA ;C. b=a ⋅sinA ;D. c=b ⋅sinA ; 例4:下列说法中,不正确的有______个.①直角三角形中,锐角的正弦为对边比斜边②直角三角形中,锐角的正弦为斜边比对边③直角三角形中,锐角的正弦为一条直角边比另一条直角边④直角三角形中,锐角的正弦为任意一条直角边比斜边例5:下列说法中,正确的有______个.①一个锐角的正弦值是一个无单位的量②某一锐角的正弦值与这个锐角所在的三角形的大小无关③sinA 既是一个完整的符号,同时也可以表示为sin×A 的乘积关系④在所有的ΔABC中,都可以计算出sinA= BC AB【答案】1.错; 2.错; 3.B; 4. 3; 5. 2;知识点二:余弦的定义及其表示方法1.如图,在直角三角形中,∠C=90°,我们把锐角A的邻边b与斜边c的比叫做∠A的余弦,记作cos A,即cos A =∠A的邻边斜边=bc.2.注意:(1)余弦也是建立在直角三角形中的,当锐角度数一定时,不论直角三角形的大小,它的邻边与斜边的比是一个固定值,换句话说,余弦值只与锐角的大小有关。
人教版九年级数学下册《锐角三角函数》知识小结与练习

知识点总结一、锐角三角函数的概念: 在Rt △ABC 中,∠C 为直角,∠A 、∠B 、∠C 对的边分别是a 、b 、c ,则锐角A 的各三角函数的定义如下:1、角A 的正弦:锐角A 的对边与斜边的比叫做∠A 的正弦,记作sinA ,即sinA =ac; 2、角A 的余弦:锐角A 的邻边与斜边的比叫做∠A 的余弦,记作cosA ,即cosA = bc ; 3、角A 的正切:锐角A 的对边与邻边的比叫做∠A 的正切,记作tanA ,即tanA = ab.二、特殊角的三角函数值:三、解直角三角形:1、直角三角的边角关系:如图,在Rt △ABC 中,∠A 、∠B 为锐角,∠C=90º,它们所对的边分别为a,b,c ,其中除直角∠C 外,其余的5个元素之间有以下关系:(1)三边之间的关系:a 2+b 2=c 2(勾股定理); (2)锐角之间的关系:∠A+∠B=90º; (3)边角之间的关系:sinA=cosB=a c ,cosA=sinA=b c,tanA=a b ,tanB=ba. 2、解直角三角型的类型与解法:三角函数 三角 值函数300450600a sin21 22 23 a cos23 22 21 a tan33 13角四、解直角三角形的简单应用:1、与仰角俯角有关的实际问题2、与方向角有关的实际问题3、与坡度坡角有关的实际问题4、与生活有关的实际问题易错点知识分析一、对锐角三角函数的定义理解错误:例1 如图所示,在△ABC中,AB=AC=3,BC=4,求sinB的值.∴sinB=53AD AB =【点评】锐角三角函数是在直角三角形中定义的,而△ABC 不是直角三角形,必须构建直角三角形解决问题.二、混淆特殊角的三角函数值例2、计算:tan45°-cos60°sin60°·tan30°三、对仰角、俯角、坡角、坡度方向角等概念理解错误例3、如图,某飞机于空中A 处探测到目标C ,此时飞行高度AC=h 米,从飞机上看地面控制点B 的俯角为α,则BC 的距离约为( ). A. h ·tan α米 B. tan hα米 C.sin hα米 D. h ·sin α米课堂学习检测一、填空题二、解答题2.求下列各式的值.(1)o 45cos 230sin 2-︒(2)tan30°-sin60°·sin30°(3)cos45°+3tan30°+cos30°+2sin60°-2tan45°(4)︒+︒+︒+︒-︒45sin 30cos 30tan 130sin 145cos 2223.求适合下列条件的锐角α .(1)21cos =α(2)33tan =α(3)222sin =α (4)33)16cos(6=-οα4.用计算器求三角函数值(精确到0.001).(1)sin23°=______; (2)tan54°53′40″=______. 5.用计算器求锐角α (精确到1″).(1)若cos α =0.6536,则α =______;(2)若tan(2α +10°31′7″)=1.7515,则α =______.综合、运用、诊断6.已知:如图,在菱形ABCD 中,DE ⊥AB 于E ,BE =16cm ,⋅=1312sin A 求此菱形的周长.7.已知:如图,在△ABC 中,∠BAC =120°,AB =10,AC =5.求:sin ∠ACB 的值.8.已知:如图,Rt △ABC 中,∠C =90°,∠BAC =30°,延长CA 至D 点,使AD =AB .求:(1)∠D 及∠DBC ;(2)tan D 及tan ∠DBC ;(3)请用类似的方法,求tan22.5°.9.已知:如图,Rt △ABC 中,∠C =90°,3==BC AC ,作∠DAC =30°,AD 交CB 于D 点,求:(1)∠BAD ;(2)sin ∠BAD 、cos ∠BAD 和tan ∠BAD .10.已知:如图△ABC 中,D 为BC 中点,且∠BAD =90°,31tan =∠B ,求:sin ∠CAD 、cos ∠CAD 、tan ∠CAD .拓展、探究、思考11.已知:如图,∠AOB =90°,AO =OB ,C 、D 是上的两点,∠AOD >∠AOC ,求证:(1)0<sin ∠AOC <sin ∠AOD <1;(2)1>cos ∠AOC >cos ∠AOD >0;(3)锐角的正弦函数值随角度的增大而______; (4)锐角的余弦函数值随角度的增大而______.12.已知:如图,CA ⊥AO ,E 、F 是AC 上的两点,∠AOF >∠AOE .(1)求证:tan ∠AOF >tan ∠AOE ;(2)锐角的21世纪教育网值随角度的增大而______.13.已知:如图,Rt △ABC 中,∠C =90°,求证:(1)sin 2A +cos 2A =1; (2)⋅=AAA cos sin tan。
(完整)锐角三角函数知识点总结及单元测试题,推荐文档
角。
仰仰仰
仰仰
仰仰 仰仰仰 仰仰
仰仰
h
i h:l
α
l
.
.
(2)坡面的铅直高度 h 和水平宽度l 的比叫做坡度(坡比)。用字母 i 表示,即 i h 。坡度一般写成1: m 的形式,如 i 1: 5 等。
l
把坡面与水平面的夹角记作 (叫做坡角),那么 i h tan 。
D.c=a·cotA
5.已知△ABC 中,∠C=90°,设 sinA=m,当∠A 是最小的内角时,m 的取值范围是( )
1 A.0<m<2
B.0<m<
C.0<m<
D.0<m<
6.小明沿着坡角为 30°的坡面向下走了 2 米,那么他下降( )
A.1 米 B. 3 米
C.2 3 米 D. 米 4
7.已知 Rt△ABC 中,∠C=90°,tanA=3,BC=8,则 AC 等于( ) 32
(附加)小阳发现电线杆 AB 的影子落在土坡的坡面 CD 和地面 BC 上,量得 CD=8 米,
BC=20 米,CD 与地面成 30º 角,且此时测得 1 米杆的影长为 2 米,则电线杆的高度为
() A.9 米 B.28 米 C.(7+ 3)米 D.(14+2 3)米 A
二、填空题:(每题 3 分,共 30 分)
A.6
B. 3
C.10
D.12
8.sin2 +sin2(90°- ) (0°< <90°)等于( )
B N
A0
B1
C2
D 2sin2
C
D
A
M
9.如图,在△ABC 中,∠C=90°,AC=8cm,AB 的垂直平分线 MN 交
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1文档来源为:从网络收集整理.word 版本可编辑.
锐角三角函数知识点
1、勾股定理:直角三角形两直角边a 、b 的平方和等于斜边c 的平方。
2
则∠A 3、任意锐角的正弦值等于它的余角
的余弦值;任意锐角的余弦值等于它的余角的正弦值。
4、特殊角的三角函数值
5、正弦、余弦的增减性:
当0°≤α≤90°时,sin α随α的增大而增大,cos α随α的增大而减小。
6、正切的增减性:
当0°<α<90°时,tan α随α的增大而增大。
1、解直角三角形的定义:已知边和角(两个,其中必有一边)→所有未知的边和角。
依据:①边的关系:2
22c b a =+;②角的关系:A+B=90°;③边角关系:三角函数的定义。
2、应用举例:
①仰角:视线在水平线上方的角; ②俯角:视线在水平线下方的角。
③坡面的铅直高度h 和水平宽度l 的比叫做坡度(坡比)。
用字母i 表示,
即
h i l =。
坡度一般写成1:m 的形式,如1:5i =等。
把坡面与水平面的夹角记作α(叫做坡角),那么
tan h
i l α=
=。
:i h l
=h
l
α
1文档来源为:从网络收集整理.word 版本可编辑. ④从某点的指北方向按顺时针转到目标方向的水平角,叫做方位角。
如图3,OA 、OB 、OC 、OD 的方向角分别是:45°、135°、225°。
⑤指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角。
如图4:OA 、OB 、OC 、OD 的方向角分别是:北偏东30°(东北方向),南偏东45°(东南方向),南偏西60°(西南方向),北偏西60°(西北方向)。
锐角三角函数练习
一、选择题
1、把Rt △ABC 各边的长度都扩大2倍得Rt △A ′B ′C ′,那么锐角A 、A ′的正弦值的关系为( ). A .sinA =sinA ′ B . sinA =2sinA ′ C .2sinA =sinA ′ D .不能确定
2、在Rt △ABC 中,∠C =90°,若AB =5,AC =4,则sinA 的值是( )
A . 35
B . 45
C . 34
D . 43
3、如图,△ABC 的顶点都是正方形网格中的格点,则sin ∠BAC 等于( )
A . 2
3 B .55
C . 105
D .13
4、如果∠α是等腰直角三角形的一个锐角,则COS α的
值是( )
A.12 B.22
C.1
D.2
5、如图,在△ABC 中,∠ACB=90°,CD ⊥AB 于D ,若56AC =,65AB =,则tan ∠ACD 的值为( )
A.5
B.5
5 C.30
6 D.6
6、计算tan 602sin 452cos30+-的结果是( )
A .2
B .2
C .1
D .
23
13-
.
7、如图,已知等腰梯形ABCD 中,AB ∥CD ,∠A=60°,AB=10,CD=3,则此梯形的周长为( ) A . 25 B . 26 C . 27 D . 28. 8、如图,小明利用一个含60°角的直角三角板测量一栋楼的高度,已知他与楼之间的水平距离BD 为10m ,眼高AB 为1.6m (即小明的眼睛距地面的距离),那么这栋楼的高是( )
A .(81035+
)m B .21.6m C . 103m D .103835⎛⎫
+ ⎪ ⎪⎝
⎭
m
9、如图,已知AB 是半圆O 的直径,弦AD 、BC 相交于点P ,若∠DPB=α,那么CD
AB 等于( )
A .sin α
B .COS α
C .tan α
D .1
tan α
二、填空题
D C
B
A E
C A α
P
D
C
文档收集于互联网,已重新整理排版.word 版本可编辑.欢迎下载支持.
1文档来源为:从网络收集整理.word 版本可编辑.
10. 在Rt △ABC 中,∠C=90°,a 、b 、c 分别是∠A 、∠B 、∠C 的对边,若b=3a ,则tanA= . 11. 在△ABC 中,∠C =90°,cosA =3
4,c =4,则a =_______.
12. 如图,P 是∠α的边OA 上一点,且P 点坐标为(2,3),则sin α=______ . 13.已知:α是锐角,tan α=
7
24
,则cos α=_______. 14.在Rt △ABC 中,两边的长分别为3和4,求最小角的正弦值为 15.tan 230°+2sin60°-tan45°·sin90°-tan60°+cos 230°=____________.
16.如图,已知Rt △ABC 中,AC=3,BC= 4,过直角顶点C 作CA 1⊥A B ,垂足为A 1,再过A 1作A 1C 1⊥BC ,垂足为C 1,过C 1作C 1A 2⊥AB ,垂足为A 2,再过A 2作A 2C 2⊥BC ,垂足为C 2,…,这样一直做下去,得到了一组线段CA 1,A 1C 1,12C A ,…,则CA 1= ,=5
55
4C A A C 三、解答题
17、如图,在△ABC 中,∠ABC=90°,BD ⊥AC 于D ,∠CBD=α,AB=3,•BC=4,•求tan α的值. 18、先化简,再求值:
+1,其中,tan 60x = .
19、如图,在Rt △ABC 中,CD 、CE 分别为斜边AB 上的高和中线,BC=a ,AC=b
(b >a ),若tan ∠DCE=1
2,求
a
b 的值.
20、如图,Rt △ABC 中,∠C=90°,D 为CA 上一点,∠DBC=30°,DA=3,AB=19,求tanA 的值.
21、已知:如图,在山脚的C 处测得山顶A 的仰角为︒45,沿着坡
度为︒30 的斜坡前进400米到D 处(即︒=∠30DCB ,
400=CD 米)
,测得A 的仰角为︒60,求山的高度AB 。
22、 如图,台风中心位于点P ,并沿东北方向PQ 移动,已知台风移动的速度为30千米/时,受影响区域的半径为200千米,B 市位于点P 的北偏东75°方向上,距离点P 320千米处.
(1) 说明本次台风会影响B 市; (2)求这次台风影响B 市的时间.
b
a
E D C
B
A
B A
D P
北
B
Q
D
C
B
A
()
2
22
1x x x x +-÷。
