指派问题例题
整数规划-案例1-指派问题

3
4
4
故模型为: min z
ci Βιβλιοθήκη 1 j 144ij
xij
4 xij 1, i 1,2,3,4 j 1 4 xij 1, j 1,2,34 i 1 xij 0 or 1(i, j 1,2,3,4)
设ijx表示第i个人去完成第j项任务则????项任务时个人不去完成第当第项任务时个人去完成第当第jijixij01?项任务时个人不去完成第当第ji0每个人去完成一项任务的约束为????????????1112423222114131211xxxxxxxx每一项任务必有一人完成的约束
3.指派问题:现在不妨设有4个人,各有能力
记 系 数 矩 阵 为
2 15 11 4 10 4 14 15 cij 9 14 16 13 7 8 11 9
称其为效益(价值)矩阵.
cij 表示第 i 个人去完成 第 j 项任务时有关的效
益 (时间、 费用、 价值等) 。 则目标函数可表示为
min z cij xij
4
用lingo求解后,可知让甲去完成任 务D,乙完成任务B,丙完成任务A, 丁完成任务C,所用时间最少为28.
5
x11 x 21 x31 x 41 1 x x x x 1 12 22 32 42 x13 x 23 x33 x 43 1 x14 x 24 x34 x 44 1
2
目标函数:
min z 2 x11 15x12 13x13 4 x14 10x21 4 x22 14x23 15x24 9 x31 14x32 16x33 13x34 7 x41 8 x42 11x43 9 x44
运筹学指派问题作业
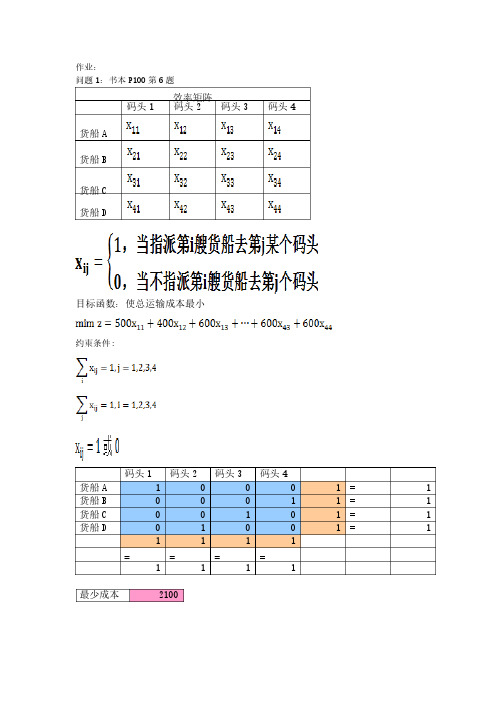
作业:作业:问题1:书本P100第6题效率矩阵效率矩阵码头1 码头2 码头3 码头4货船A货船B货船C货船D目标函数:使总运输成本最小目标函数:使总运输成本最小约束条件约束条件: :码头1 码头2 码头3 码头4货船A 1 0 0 0 1 = 1 货船B 0 0 0 1 1 = 1 货船C 0 0 1 0 1 = 1 货船D 0 1 0 0 1= 11 1 1 1 ====1 1 1 1最少成本最少成本2100问题问题 2: 2: 2: 书本书本书本P101P101P101第第7题效率矩阵效率矩阵A B C D E甲乙丙丁目标函数:使总花费时间最小目标函数:使总花费时间最小约束条件约束条件: :方案矩阵方案矩阵AB C D E甲 2.22E-16 1 0 0 0 1 <= 1 <= 2 乙 0 0 1 1 2.22E-16 1 <=2 <= 2 丙 0 1.11E-16 0 0 1 1 <=1 <=2 丁 1 0 0 4.44E-16 0 1 <=1 <=2 1 11 1 1= == ==11 1 1 1时间最少时间最少131问题3:五人翻译五种外文的速度(印刷符号:五人翻译五种外文的速度(印刷符号//小时)如下表所示:小时)如下表所示: 语种语种语种 人 英 俄俄 日日 德德 法法 甲甲乙 丙 丁 戊900 400 600 800 500 800 500 900 1000 600 900 700 300 500 800400 800 600 900 5001000 500 300 600 800若规定每人专门负责一个语种的翻译工作,那么,试解答下列问题:若规定每人专门负责一个语种的翻译工作,那么,试解答下列问题: (1)应如何指派,使总的翻译效率最高?应如何指派,使总的翻译效率最高?效率矩阵效率矩阵英俄 日 德 法 甲 乙 丙 丁目标函数:使翻译效率最高目标函数:使翻译效率最高约束条件约束条件: :方案矩阵方案矩阵英俄 日 德 法甲0 011 =1乙0 1 0 0 0 1 = 1 丙0 0 0 1 0 1 = 1丁 1 0 0 0 0 1 = 1 戊0 0 1 0 0 1 = 11 1 1 1 1= = = = =1 1 1 1 1效率最高 2200效率最高若甲不懂德文,乙不懂日文,其他数字不变,则应如何指派?(2)若甲不懂德文,乙不懂日文,其他数字不变,则应如何指派?方案矩阵方案矩阵英俄日德法甲0 1 0 0 0 1 = 1 乙0 0 0 0 1 1 = 1 丙0 0 0 1 0 1 = 1 丁 1 0 0 0 0 1 = 1 戊0 0 1 0 0 1 = 11 1 1 1 1= = = = =1 1 1 1 1。
指派问题

数学模型为:
max Z 85x11 92x12 73x13 90x14 95x21 87x22
78x23 95x24 82x31 83x32 79x33 90x34
86x41 90x42 80x43 88x44 甲
A
x11 x12 x13 x14 1
xx3211
6 4
9 8 0 0
4
0 6 3 6 5
经行运算即可得每行每列都有 0 元素的系数矩阵,
再按上述步骤运算,得到:
5 0 2 0 2
2 3 0 0
0
0 10 5 7 2
9 8 0 0
4
0 6 3 6 5
所画 0元素少于n,未得到最优解。
5 0 2 0 2 2 3 0 0 0 0 10 5 7 2 9 8 0 0 4 0 6 3 6 5
将前面的例题连续作进行下
任务 人
A
B
C
D
E
甲
12 7
9
7
9
乙
8
9
6
6
6
丙
7 17 12 14 9
丁
15 14 6
6 10
戊
4 10 7 10 9
12 7 9 7
8
9 66
9
6
7 6
5 0 2 0 2
2 3 0 0
【精品】指派问题——匈牙利法

最优解:x13=1,x21=1,x32=1,x44=1
若◎元素的数目m=n,则该指派问题的最优 解已经得到,否则转入Step 3;
13
指派问题的匈牙利解法——步骤(续)
Step 3. 设有 m<n 个◎, 找最少覆盖所有0的直线
1) 对没有◎的行打√
2) 对已打√行中含所在列打√ 3) 对已打√列中含◎所在行打√ 4) 重复2)~3), 直至没有要打√的行和列为止 5) 对没有打√的行划横线, 对打√的列划竖线 得到最少覆盖所有0的直线数l。
i 1 j1 ik n n j1 n j1
n
n
n
cijx ij c kjx kj (s)
i 1 j1 ik j1
z (s)
指派问题的匈牙利解法
• 根据此定理,可以对 做如下改变,目的是 找出C 中的 n个不同行不同列的0元素: • 将 C的每一行减去该行中的最小元素,得 到C’矩阵 ,则C’ 的每行中均至少出现一个 0元素,且所有cij0 。同样,对C 的列亦进 行如此计算,由此,我们完全可以从原效 率矩阵 出发,得到一个新的效率矩阵 ,使 C的每行每列中均至少存在一个0元素,而 不改变问题的最优解。
Z=15
独立练习 • P161第6.4题
6.5.4 非标准形式的指派问题 • 非标准型指派问题求解的总原则是化非标准 形式为标准形式,然后用匈牙利解法求解。 (1) 最大化指派问题 设效率矩阵为 C (cij )nn ,其中最大元素
5.5 指派问题

cij 为第 i 个人为完成第 j 项任务时的工时消
3. 指派问题数学模型—标准形式 如果一个指派模型满足以下三个条件:
1)目标要求为min
2)效率矩阵(cij)为m阶方阵
3)效率矩阵中所有元素cij≥0,且为常数
则称上面的数学模型为指派问题的标准形.
4. 指派模型的标准形的特点: 含有m×m个决策变量,均为0-1变量 m+m=2m个约束方程 给定一个指派问题时,必须给出效率矩阵(系数矩阵) C=(cij)mxm,且cij0,因此必有最优解 。
0 1 0 0
0 0 0 1
指派问题的解矩阵应具有如下特点: (1)解矩阵(xij)中各行各列的元素之和都是1; (2)可行解(最优解)中恰含有4个非零元,即4个1; (3)可行解(最优解)矩阵中的1恰取于不同行不同列。
人 工作 译成英文 译成日文 译成德文 译成俄文 任务
甲 2 15 13 4 1
定理1 如果从指派问题效率矩阵[cij]的每一行元素中分别 减去(或加上)一个常数ui(被称为该行的位势), 从每一列分别减去(或加上)一个常数vj(称为该列的位势) 得到一个新的效率矩阵[bij], 若其中bij=cij-ui-vj, 则[bij]的最优解的结构等价于[cij]的最优解的结构.
证明:将从[bij]中得到的解 代入分配问题模型的目标函数式,有
从只有一个0元素的行(或列)开始,
给这个0元素加圈,记, 这表示对这行所 代表的人,只有一种任务可指派。 然后划去所在的列(或行)的其他0元素,记作Ø。 这表示这列所代表的任务已指派完,不必再考虑别人
0
6
13
7 6 3 0
0 9 2 0
5 1
0
给只有一个0元素的列(或行)中的0元素加圈, 记, 然后划去所在的行(或列)的其他0元素,记作Ø。 这表示这行所代表的人已指派完, 不必再考虑他做别的任务了。 反复进行上述两步,直到所有的0元素都被圈出和 划掉为止。
运输问题和指派问题

4、运输问题和指派问题案例1:P&T公司的配送问题家族经营的小公司,加工蔬菜罐头并分销到各地:–三个食品厂,四个分销仓库面临的问题:运输成本不断攀升目前的运输策略:–首先考虑最偏远的厂,先将其产品充分满足距它最近的仓库,再运至次之的仓库;–再考虑最偏远的仓库,优先从距其最近的工厂进货;–距离居中的工厂用于补充不足的部分。
问题:如何改进运输策略以降低成本?CANNERY 1BellinghamCANNERY 2EugeneWAREHOUSE 1 Sacramento WAREHOUSE 2Salt Lake CityWAREHOUSE 3Rapid CityWAREHOUSE 4AlbuquerqueCANNERY 3Albert Lea最偏远的厂最偏远的仓库300合计100Albert Lea 125Eugene 75Bellingham 产量(车)工厂Albert Lea5Eugene 75Bellingham 工厂SacramentoFrom\To运费995Albert Lea352Eugene $464Bellingham 工厂Sacramento From\To 总运费:Total shipping cost = 75($464) + 5($352) + 65($416) + 55($690)运输问题的基本术语P&T 公司问题罐头罐头厂仓库罐头厂的产量各仓库的需求量每车运费Ì运输问题是物流中的一个重要问题,即如何以尽可能小的成本把货物从一系列出发地(如工厂、仓库)运输到一系列目的地(如仓库、顾客)。
需求假设:–每个出发地都有一个固定的供应量,且所有供应量均须配送到目的地;–每个目的地都有一个固定的需求量,且所有需求量均须被满足可行解特征:–运输问题有可行解,当且仅当供应量总和等于需求量总和(供求平衡) 成本假设:–从任一出发地到任一目的地的配送成本与所配送的货物量成正比,即配送成本等于单位配送成本乘以配送量供应量、需求量和单位成本提供了运输问题所需的一切数据整数解:–运输问题通常以运送的车数作为计量单位,因此其解一般为整数整数解性质:只要运输问题的供应量和需求量都是整数,任何有可行解的运输问题必然有使所有决策变量都是整数的最优解。
指派问题考前复习

指派问题
例3、某工厂有4个工人甲、乙、丙、丁,他们都可以从事4种不同的工作A,B,C,D,但每个人在不同的岗位创造的产出是不同的,见下表。
现给每个工人分配一个岗位,求如何安排才能使产出最
大?
解:
这是一个求最大值的问题,因此首先对系数矩阵
进行变换,表中的系数矩阵最大值是10,因此
bij=M-cij=10-cij,然后就可以按照匈牙利法德步
骤进行求解,具体过程如下:
注意:设分配问题中人数为m,任务数为n,当m>n时虚拟m-n项任务,对应的效率为零;当m<n 时,虚拟n-m个人,对应的效率为零,转化为人数与任务数相等的平衡问题后再求解。
如有5个人分配做3项工作,效率矩阵变化如下,。
指派问题例题

• 第四步 划线——无行、打列划线
• 第五步 造0——直线未覆盖旳元素,减
去其最小值,交叉点上加最小元素,产
生新旳0元素,Go to 2
0 6 2 1 -1 5 1 0 0 4 0
Cij= 0 5 3 1 -1 0 4 2 0 3 1 0
0001
1 0 1
2 0 2
1320
2 3 2 2 2 1
数模: minZ=ΣΣcijxij Σxij=1 i=1,…,n Σxij=1 j=1,…,n Xij=0或1
任务 人 时间
甲 乙 丙 丁
ABC D 4 10 7 5 2763 3344 4663
指派问题解法—匈牙利法
• 解:类似运送问题旳最小元素法
• 第一步 造0——各行各列减其最小元素
4 10 7 5 -4 0 6 3 1 6 2 1
+1
• 最优2 7 6 3 -2 0 5 4 1 0 5 3 1
3 3 4 4 -3 0 0 1 1 0 0 1
4 6 6 3 -3 1 3 3 0 1 3 2
-1
• 第二步 圈0——寻找不同行不同列旳0元素,
圈之。 所在行和列其他0元素划掉
• 第三步 打——无旳行打,打行上0列打
,打列上行打,打行上0列打 …
指派问题
任务 人 时间
甲 乙 丙 丁
ABC D 4 10 7 5 2763 3344 4663
最大流问题
v1
5,2
5,5 5,5
vs 6,4 v2
4,2
v4 6,6
v3
2,2
4,2 vt
5,3
指派问题——匈牙利法
• 练习例题:甲乙丙丁四个人,A、B、C、D 四项任务,不同旳人做不同旳工作效率不同, 表中数据为时耗,怎样指派不同旳人去做不 同旳工作使效率最高?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
