优化算法在船体型线参数化设计中的应用
参数化方法的中型豪华游船特殊球艏线型优化

参数化方法的中型豪华游船特殊球艏线型优化王杉;王艳霞;赵强;魏锦芳;陈京普【摘要】以一艘中型豪华游船为例,在分析豪华游船船型特点的基础上,对其球鼻艏线型进行了优化.优化过程中采用参数方法生成了一系列球鼻艏线型,通过CFD方法对其兴波阻力和总阻力进行评估分析,并通过灵敏度分析得到对阻力影响最为显著的参数,获得了阻力性能较好的球鼻艏线型方案.最后通过模型试验对优化线型进行了模型试验验证,试验结果表明文中优化的线型具有良好阻力性能,为进一步开展豪华游船线型设计提供良好的技术参考.%According to the study on the lines characteristic of luxury cruises, the bulbous bow of a medium-sized luxury cruise ship is optimized in this paper.Parametric design method is utilized to generate a series of bow lines,and the resistance is evaluated by CFD.Sensitivity analysis is also carried out to identify the most suitable and relevant parameters,and an optimized lines is obtained.Then the model test for the optimized lines is carried out in towing tank at CSSRC,and the model test results show the optimized lines is of good resistance performance.【期刊名称】《江苏科技大学学报(自然科学版)》【年(卷),期】2017(031)005【总页数】4页(P646-649)【关键词】豪华游船;参数化建模;球艏优化;CFD;模型试验【作者】王杉;王艳霞;赵强;魏锦芳;陈京普【作者单位】中国船舶科学研究中心上海分部,上海200011;中国船舶科学研究中心上海分部,上海200011;中国船舶科学研究中心上海分部,上海200011;中国船舶科学研究中心上海分部,上海200011;中国船舶科学研究中心上海分部,上海200011【正文语种】中文【中图分类】U661.32+2;O35豪华游船是当今船舶工业最具代表性的高技术船型之一,能够设计和建造豪华游船代表了一个国家的综合造船实力和水平.目前,国内对这种船型的研究还处于起步阶段,仍未完全掌握豪华游船的设计、建造技术.鉴于豪华游船的重要性和技术复杂性,中国船舶科学研究中心对豪华游船水动力性能开展了追踪研究.船体线型水动力性能设计的技术含量通常集中在船体的首部和尾部,近代豪华游船广泛采用能显著降低船体兴波阻力的鹅颈型球艏和鸭型尾线型设计[1].鹅颈型球艏可以产生不同于船体主波相位的子波,利用这种相位差削弱船体主波,从而减小船体的兴波阻力.文中在总结豪华游船线型特点的基础上,完成了一艘5万吨级豪华游船特殊球艏线型的设计优化.采用参数化建模手段,通过选取相应的特征参数,完成了球艏线型的全参数化模型;并基于建立的参数化模型,通过修改特征参数,生成了一系列球鼻艏线型方案,通过集成CFD方法对其兴波和总阻力进行评估分析,实现了豪华游船特殊球艏线型的自动优化;并通过灵敏度分析得到对阻力影响最为显著的参数,获得了阻力性能较好的球鼻艏线型方案.采用快速的阻力性能评估方法进行多方案的比较,根据流动特点将船体分为两部分求解:第一部分采用非线性兴波数值计算方法,计算兴波阻力和自由面波形;第二部分采用粘性流数值方法获得船尾流场.非线性兴波数值计算方法首先假设受约束的船舶以航速V沿x轴的正向运动,o-xyz为固定在船上的直角坐标系,xy平面与静水面重合,z轴垂直向上.在o-xyz坐标系中流动为定常势流,忽略表面张力的影响,水域为无限深,这样船舶绕流存在速度势φ,且满足以下方程和边界条件:在流场中满足Laplace方程:在自由面上满足运动学边界条件:φxζx+φyζy-φz=0 z=ζ(x,y)此外,在自由面上还要满足动力学边界条件:ζ=(V2-φ·φ) z=ζ(x,y)在船体湿表面上满足不可穿透条件:在无穷远前方满足辐射条件:式中:ζ为自由面波高,下标“x,y,z”表示在该方向上的偏导数;φn为速度势在法向方向上的偏导数;g为重力加速度.船舶兴波问题就是求解定解问题,其中一个难点就是自由边界条件的非线性,自由面边界条件是非线性的,且自由面初始位置不可知方程组[2].求解这个非线性问题的通常方法是[3-4]:在一个已知的基本解的基础上对自由面边界条件线性化处理,然后采用迭代的方式求解这个问题.粘性流数值求解方法主要是基于求解Navier-Stokes方程和连续方程组.粘流数值求解时使用显式代数应力模型(EASM),控制方程使用有限体积法离散,其中对流项使用二阶迎风格式,扩散项采用中心差分格式;离散得到的差分方程组具有耦合性,使用交替隐式迭代法(ADI)方法求解线性方程组[4].文中选择5万吨级豪华游船作为母型船,保持19站之后的线型不变,只针对19站之前的线型进行优化.在优化过程中,采用参数化方法生成了一系列球鼻艏线型,通过CFD计算对其设计航速下的兴波阻力和总阻力进行评估分析,并通过灵敏度分析得到对阻力影响最为显著的参数,最终得到了阻力性能较好的球鼻艏线型方案.基于FRIENDSHIP软件建立豪华游船球艏区域的全参数化模型[5].首先截掉船型球鼻艏以及19站之后的线型区域(图1),参数化生成球鼻艏以后用光顺曲面连接新球艏和船体.球鼻艏生成所用的控制线如图2,图中的xt为球鼻艏生成区间控制线,up和down两条控制线控制球鼻艏的上下轮廓线,beam为球鼻艏最宽处的宽度控制线,elevation为球鼻艏最宽处的高度控制线.利用Friendship的Feature功能,通过这些控制线生成球鼻艏的Curve Engine,最后生成球鼻艏的MetaSurface.球鼻艏生成以后,使用Feature定义的fillet曲面光顺连接球鼻艏和船体部分(图3),图中A部分为原船体曲面,D部分为生成的球鼻艏曲面,B和C两部分为fillet曲面,其中C的控制线连接A和D,并且在端点处二阶连续可导,B的控制线连接A和C,并且在端点处二阶连续可导,从而保证了船体曲面的光顺性.对建立的新球艏,在设计吃水、设计航速Vs=21 kn(傅汝德数约为0.246)下,以兴波阻力作为目标函数,采用试验设计方法进行优化.首先采用SOBOL方法进行全局搜索,对建立球艏时所用的设计变量进行优化,在大范围内搜索兴波阻力较低的球艏形状,其次对试验设计的结果进行参数灵敏度分析,分析对兴波阻力影响最大的参数.选择控制球艏长度、高度和宽度的3个参数作为设计变量,并在保证船体曲面光顺的前提下确定各设计变量的取值范围,设计变量的名称、取值范围以及变量说明如表1,bulbx,bulby,bulbz为设计参数名.通过改变上述设计变量的取值,就可以得到相应的球艏线型,图4为当球艏长度、高度和宽度分别改变时所得到的线型与初始方案的对比.采用SOBOL算法共生成200个方案[6],以设计航速Vs=21 kn时的兴波阻力系数作为目标函数,对设计空间进行初步探索.图5为优化过程中设计变量bulbz在其设计空间内的分布,由图可知,设计变量在设计空间内的分布很均匀.因此采用SOBOL算法进行试验设计能够对整个设计空间进行比较准确的探索评估,为参数灵敏度分析提供良好的数值支持.对兴波阻力进行参数灵敏度分析,各参数对目标函数的影响如图6,图中bulbx,bulby表示负效应,bulbz表示正效应.由参数灵敏度分析可得:① 控制球艏宽度的参数bulby对设计航速下兴波阻力的影响远大于另外两个参数,且球艏越瘦,兴波阻力越小;② 控制球艏长度的参数bulbx对设计航速下兴波阻力的影响较小,且球艏越短,兴波阻力越小;③ 控制球艏高度的参数bulbz对设计航速下兴波阻力的影响最小,且球艏越高,兴波阻力越小.根据参数化方法确定了球艏优化的方向,继续从球艏宽度、长度方向深入优化,最终得到了优化方案.优化方案与原型的球艏区域的线型比较如图7.对上述原型和改型在Vs=21 kn时的兴波阻力和静水总阻力分别进行计算,改型在Vs=21 kn时的兴波阻力系数比原型降低约9.80 %,总阻力系数降低了2.61%,舷侧波形对比如图8,改型较原型在船艏和船舯附近的波形也较原型有所改善.图中:h 为波高;Lpp为垂直线间长;x/Lpp表示沿x方向上的位置.根据文中优化的线型方案加工船模,并在中国船舶科学研究中心深水拖曳水池开展了阻力模型实验,其中图9为设计航速Vs=21 kn的波面照片.此外,为了验证中高速船的阻力计算精度,数值计算和模型试验得到阻力曲线(图10),Ct为静水总阻力系数.从图中结果来看,文中采用的数值模拟方法和模型试验结果的误差在3%左右,也反映了该方法具有较强的工程实用价值.(1) 综合运用参数化方法和CFD技术优化船型,采用非线性兴波和粘流数值模拟方法进行分析评估.(2) 完成了中型豪华游船特殊球艏的线型优化工作,并针对优化方案加工模型开展了阻力模型试验,数值计算的总阻力和模型试验结果的误差在3%左右.【相关文献】[ 1 ] Raimo Hämäläinen. The high comfort class appendage design for cruise liners, ferries and ropax vess els [C]∥First International Symposium on Marine Propulsors, Trondheim, Norway:[s.n.], 2009.[ 2 ] 陈京普, 朱德祥, 何术龙, 等. 一种快速评估方法在船舶线型优化中的应用[J]. 中国造船, 2009,50(4): 7-12. DOI:10.3969/j.issn.1000-4882.2009.04.002.CHEN Jingpu, ZHU Dexiang, HE Shulong, et al. Application of a fast computing approachin hull lines optimization[J]. Shipbuilding of China, 2009, 50(4): 7-12.DOI:10.3969/j.issn.1000-4882.2009.04.002.(in Chinese)[ 3 ] RAVEN H C. Inviscid calculations of ship wave making-capabilities, limitations, andpr ospects[C]∥Poceedings of Symposium on Ship Hydrodynamics,Bethesda,MD,USA:[s.n],1998.[ 4 ] BRENNER M. Integration of CAD and CFD for the hydrodynamics design of appendages in viscous flow[D]. Berlin:Technical University of Berlin, 2008.[ 5 ] HARRIES S, TILLIG F, WILKEN M, et al. An integrated approach for simulation in the early ship design of a tanker[C]∥International Conference on Computer and It Applications,Berlin:[s.n.],2011.[ 6 ] HARRIES S. Investigating multi-dimensional design spaces using first principle methods[C]∥7th Int Conf High-Performance Marine Vehicles (HIPER),Melbourne,Australia:[s.n.],2010.。
优化算法在船体型线参数化设计中的应用

优化算法在船体型线参数化设计中的应用船体型线参数化设计是指通过建立数学模型和设定一系列参数,对船体的外形进行设计和优化。
优化算法在船体型线参数化设计中的应用,可以帮助设计师快速有效地寻找到最优的设计方案,提高设计效率和减少设计成本。
本文将探讨优化算法在船体型线参数化设计中的具体应用,并对其优势和未来发展进行讨论。
首先,优化算法在船体型线参数化设计中的应用主要体现在以下几个方面:1.参数空间:通过对船体外形的各种参数进行设定,建立参数化模型,并利用优化算法对参数空间进行,找到最优的设计方案。
常用的优化算法包括遗传算法、粒子群算法、模拟退火算法等,这些算法可以有效地参数空间,找到全局最优解或局部最优解。
2.多目标优化:船体设计通常涉及到多个目标函数,如减少阻力、提高航速、增加载货量等。
利用多目标优化算法,可以在不同的目标函数之间进行权衡,找到一组平衡的设计方案,满足各种需求。
3.约束条件优化:在船体设计中,通常存在各种约束条件,如船体结构强度、稳性、操纵性等。
优化算法可以在满足这些约束条件的前提下,找到最优的设计方案,提高设计的安全性和可靠性。
4.设计空间探索:参数化设计和优化算法可以帮助设计师在设计空间中进行探索,快速提取并处理大量的设计数据,挖掘潜在的设计方案,为创新设计提供更多可能性。
5.自动化设计:结合参数化建模和优化算法,可以实现船体设计的自动化,减少人工干预,提高设计效率和质量。
1.提高设计效率:优化算法可以快速有效地参数空间,找到最优的设计方案,减少设计时间和成本。
2.提高设计质量:优化算法可以在大量设计方案中找到最优解,提高设计的精度和质量。
3.提高创新性:优化算法可以帮助设计师在设计空间中进行探索,挖掘潜在的设计方案,推动创新设计的发展。
4.降低风险:优化算法可以在满足约束条件的前提下,找到最优的设计方案,降低设计的风险和错误率。
未来,随着船舶设计的需求越来越复杂和多样化,优化算法在船体型线参数化设计中的应用将会越来越重要。
船舶型线信息化设计方法

05
船舶型线信息化设计流程与规 范制定
设计流程梳理与优化建议
梳理现有设计流程
对现有船舶型线设计流程进行全 面梳理,包括设计准备、初步设 计、详细设计等阶段。
02
加强多学科协同设计研究,实现 多专业之间的无缝对接。
拓展该系统的应用范围,将其应 用于更多类型的船舶设计中。
03
加强与国内外相关研究机构的合 作与交流,共同推动船舶型线信
息化设计技术的发展。
04
THANKS
谢谢您的观看
实施方案
02
03
持续改进
制定具体的实施方案,包括规范 宣传、培训、监督检查等环节, 确保规范的有效实施。
根据实施情况,对规范进行持续 改进和优化,不断提高设计质量 和效率。
持续改进措施与未来发展方向
持续改进措施
建立持续改进机制,定期对设计流程和规范进行评估和改进,确保设计工作的不断完善和提高。
未来发展方向
02
船舶型线信息化设计概述
船舶型线定义与分类
船舶型线定义
船舶型线是描述船舶外形和浮力性能的重要参数,包括船体基线、横剖线、纵剖 线等。
船舶型线分类
根据船舶类型和用途,船舶型线可分为民用船舶型线、军用舰船型线、工程船型 线等。
信息化设计概念及特点
信息化设计概念
信息化设计是指利用计算机技术、网络技术等信息技术手段 ,对产品进行设计、分析、优化和管理的过程。
参数化设计
通过参数化设计方法,实现船舶型线的快速修改和优 化。
一种快速评估方法在船舶线型优化中的应用

50卷第4期(总第188期)中国造船V ol.50 No.4 (Serial No. 188) 2009年12月 SHIPBUILDING OF CHINA Dec. 2009文章编号:1000-4882 (2009) 04-0007-06一种快速评估方法在船舶线型优化中的应用陈京普,朱德祥,何术龙,黄少锋,杨奕(中国船舶科学研究中心,江苏无锡 214082)摘要采用一种势流兴波数值优化方法与RANS求解器的优化结合的方法对某中速船的首部进行线型优化,以便使其速度达到设计要求。
经过多轮数值优化试验,取得一个优化方案。
最终的优化方案经模型试验验证,总阻力下降约2.7%,预报航速提高约0.4kn。
关键词:船舶、舰船工程;非线性兴波;RANS;线型优化;CFD中图分类号:U662.9 文献标识码:A0 引言用于船舶阻力预报及船型优化的CFD方法主要有两类:基于势流的兴波数值预报的优化方法和基于粘性流场RANS求解的优化方法。
已经有不少成功应用势流兴波数值方法进行船型优化的先例[1~3]。
近些年来我国部分研究院所及船厂[4~7]也在船舶势流兴波数值方法的研究与应用上,取得了不少进展。
随着计算机能力的进一步发展,考虑自由面效应的粘流求解(RANS)已经较广泛地应用于船舶研究与设计,粘流CFD计算结果数据信息量丰富,不仅可以进行船体阻力、自由面以及伴流计算,还可以考虑船、桨、舵以及附体相互干扰[8,9]。
近年来的研究资料表明,考虑自由面效应的RANS求解器预报精度有很大提高,应用范围在逐步扩大,而且某些研究机构已经将RANS求解器应用于实际船舶的线型优化[10],不过这种运算对计算机的要求很高,文献[10]提及的船型优化系统依赖于64个CPU的并行机。
近些年来,国内通过对商业软件的开发应用,也将考虑自由面效应粘流CFD计算在水动力学问题的某些范围得到有效应用[11,12]。
某中速船在给定功率条件下,原始线型的预报航速低于设计航速0.3kn,为此须进行线型优化。
基于数学模型与优化算法的船舶航线规划技术研究

基于数学模型与优化算法的船舶航线规划技术研究随着全球海运业的发展,航线规划技术越来越成为船舶航行中不可缺少的一项技术。
船舶航线规划技术是指根据船舶运行的需求和航道环境,设计出一条最优船舶航线,使得船只可以高效稳定地航行。
为了实现最优航线的设计,数学模型与优化算法已经成为了航线规划技术的主要研究手段。
数学模型是指建立起数学模型来描述船舶在不同的航线上运行时的运行特性和相互作用,以求得最优的航线。
最常用的数学模型是高斯-马尔可夫(Gauss-Markov)模型和蒙特卡罗(Monte-Carlo)模型。
高斯-马尔可夫模型是一种线性模型,它可以描述船舶在运行过程中的确定性因素,包括船速、船长等因素。
蒙特卡罗模型则是一种基于随机模拟的模型,可以描述船舶在未知状态下的运行情况,例如海况变化、船舶故障等因素。
基于以上数学模型,航线规划技术还需要应用优化算法,以求得最优航线。
优化算法是指利用现代优化理论和方法来确定最优的航线方案,最常用的优化算法包括遗传算法、蚁群算法、神经网络算法等。
这些方法可以在多个航线之间进行评估和选择,以求得最优的航线方案。
例如,遗传算法可以模拟自然进化算法,通过不断的遗传变异和选择,最终找到最优的航线方案。
蚁群算法则是模拟蚂蚁自发聚集形成路径的行为,通过相互合作和信息交流,找到最优航线方案。
神经网络算法则是模拟人脑神经元的思维方式,通过不断的学习和演化,找到最优的航线方案。
除了数学模型和优化算法,航线规划技术还需要考虑实际航行情况和船舶的特殊需求。
例如,航行期间需要考虑风向、海流等因素对船舶的影响,以避免出现不必要的风险。
此外,船舶在规划航线时还需要考虑非标准条件下的海域和漩涡、暗礁等地形结构,以确保船只安全运行。
同时,如果需要进行海洋调查、数据采集等工作,可能需要单独计算航线,以保证航行期间数据的准确性。
总的来说,船舶航线规划技术是一项复杂的技术体系,需要综合考虑多种因素,才能达到最优航线的设计。
基于BP-GA算法实现船体结构多目标优化

基于BP-GA算法实现船体结构多目标优化随着人们对船舶性能和安全性的要求不断提高,船体结构的多目标优化成为了船舶设计中重要的任务之一。
为了实现船体结构多目标优化,人们提出了多种算法,其中基于BP-GA算法的优化方法由于其高效性和可行性逐渐受到了广泛关注。
BP-GA算法是将BP神经网络和遗传算法相结合的一种优化方法。
其中BP神经网络可以对复杂的非线性函数进行拟合和预测,而遗传算法则可以通过优秀的进化策略进行全局搜索。
这两种算法互补优势,可以有效地实现多目标优化。
实现船体结构多目标优化的第一步是确定目标函数,包括船体强度、稳定性、耐波性、速度等多个方面。
然后将这些目标函数作为BP神经网络的输入和输出。
通过训练使得BP神经网络能够预测不同设计参数下的目标函数值。
接下来,将遗传算法的进化策略应用到BP神经网络中,通过优秀的遗传算法调节各个设计参数,不断逼近最优解,从而实现优化目标的最大化。
基于BP-GA算法的船体结构多目标优化不仅可以提高船舶的性能和安全性,同时也可以降低船体结构的重量和成本,让船舶在满足多个目标的同时,达到更加理想的经济性能。
考虑到船舶的设计参数及船体结构的复杂性,这种基于算法的优化方法为船舶设计提供了一种高效可行的方式,能够加快进展并优化设计方案。
同时,它还为船体结构优化的研究提供了新的视角和思路,也将会在船舶制造业的发展中起到越来越重要的作用。
为了进行基于BP-GA算法的船体结构多目标优化,需要收集一定量的相关数据并进行分析。
以下是可能收集的数据和分析方法:1. 船体结构强度相关数据:包括钢板材质、厚度、尺寸、焊接缺陷等数据。
可以通过有限元分析等方法计算出结构强度的指标值。
2. 船体稳定性相关数据:包括船体形状、吃水等数据。
可以通过稳性计算软件进行计算,得出稳定性的各项参数。
3. 耐波性相关数据:包括波浪参数、船速等数据。
可以通过数值模拟软件进行计算,并得出船体受到波浪作用时的压力分布图和形变情况。
船舶结构优化设计方法及应用实践

船舶结构优化设计方法及应用实践摘要:近年来,经济快速发展,社会不断进步,任何船舶结构,都是非常具有复杂性的。
现阶段因为市场经济发展迅速,经济水平提升,促进科技迅速更新,国内的各个行业发展创新非常迅速,让船舶制造业也是要加强自身的转变,在船舶结构方面要运用合适的优化方法,让船舶结构可以符合客观的需求,达到良好的制造效果。
需要结合船舶的实际建造需求,对船舶结构展开适当优化设计。
该文是对船舶结构一些优化设计的方法展开分析,介绍船舶结构优化应用,希望对船舶制造业的实际发展有一定借鉴价值。
关键词:船舶结构;优化设计;方法;应用实践引言随着国民经济体制的不断改革,给各行各业带来了全新的机遇。
船舶制造领域,基于科技水平的提高实现了良好的发展。
目前,市场对船舶的质量和性能提出了全新的要求,为船舶制造企业带来了巨大的考验,因此,船舶制造企业必须秉承科技时代理念,积极开展船舶制造过程优化,并有效的提高船舶制造的速度和质量,才能确保船舶制造企业持续地发展。
在船舶制造领域中,在保障船舶质量问题的前提下,提高船舶制造效率是船舶企业最关注的问题,所以,实现船舶结构设计的全面优化具有重要意义。
1船舶结构设计概述船舶结构设计必须具备相应的使用性,同时在确保船舶行驶安全的基础上,针对船舶的外观进行设计、美化。
船舶航行安全是船舶结构设计的核心,结构设备必须要保证船舶的稳固性,满足力学建设的相关机理,同时应对船舶航行环境加以全面地分析,全面考虑航行时的水文、气候环境等,以使得船舶在航行过程中可以更好地应对突发性的极端天气。
船舶结构设计需结合各方面的因素,确保船舶建造的合理性。
例如在船舶建造过程中选择符合要求的高质量材料,船舶制造利用的板材必须具备合理的厚度、相应的弯曲度,不得为了过于追求成本的减少而选择质量较差的材料。
在船舶设计环节,需要高度关注设计时所选择的角度,同时将其全面列入到参考系统中,应当根据具体的船舶装载需求针对船舶的甲板、船体结构等加以科学、合理地设计,并且还需要给货物及船舶员工留有足够的空间;除此以外,在船舶结构设计的具体环节应高度重视船舶的舒适度、安全性等。
CFD在舰船阻力性能优化中的应用
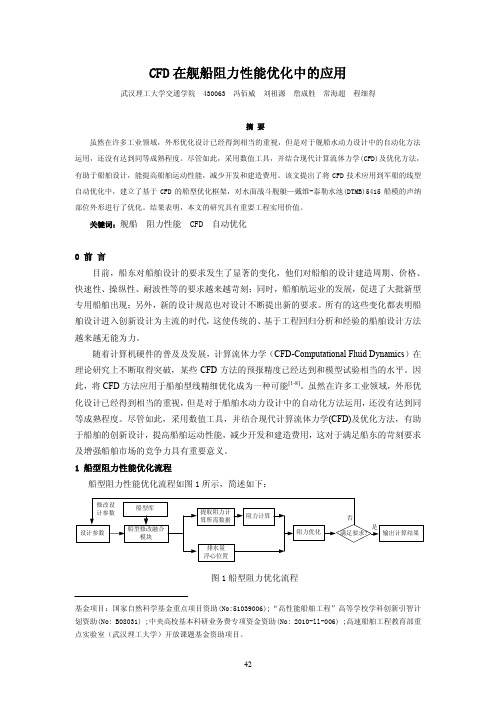
(2)优化前后波高等值线及舷侧纵切波形的比较(见图 7、8)
优化前
优化后
波高/船长
纵向位置/船长
图 7 波高等值线的比较
图 8 舷侧纵切波形比较(y/L=0.01)
46
母型A
改进船型
图 9 优化前后线型对比 从优化前后的结果对比可以看出,优化后船型的兴波阻力下降了 10.8%,而湿表面积、 浮心位置、排水量分别变化了 0.8%、0.4%、0.4%。从图 7 可以看到优化后船首部位的波形 数减少了, 而图 8 则进一步说明优化后在船首附近的波形切片幅值变小了。 图 9 为优化前后 的线型比较,从图 9 可以看到,优化后声纳罩的曲面显得更为丰满,同时声纳罩向前延伸了 一点。 3 结 语 本文在分析基于 CFD 的船型阻力性能优化流程的基础上, 以戴维-泰勒水池(DTMB)5415 船模的声纳罩为优化对象,利用课题组开发的船体型线多学科设计优化平台完成了优化工 作,结论如下: (1)本文所开发的船型参数化融合模块是可行的,随着母型数量的增多,经融合后将 会生成丰富多样的声纳罩外形,而且生成的曲面是光顺的,这保证了优化结果的可行性。 (2)母型库的建立区别于传统的优秀船型库,本文所阐述的母型库是指尽可能复杂而 多变的船体外形,在建库时不需要考虑船型性能好坏,也不需要考虑排水量等约束,如本文 中变型 C。这些特点大大方便了设计人员的建库工作。 (3)船型参数化融合模块是基于 NURBS 理论开发,这保证了和现有 CAD 系统的兼容 性。同时,由于该模块是以母型为基础通过融合的方式产生新船型,摆脱了船型参数化几何 表达的限制, 故该模块理论上可以应用于任何复杂船型, 这为船型优化系统走向实用化打下 了基础。 (4)在本文优化实例中,将排水量、浮心位置、湿表面积等作为约束条件,保证了优 化结果具有工程应用价值。 后期的研究还需要考虑将总布置等约束条件纳入到船型优化系统 当中,以进一步增强其工程实用性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=
=
( 阶矩 ) 一
。
11
式中, 是控制点,{ 是权重,{ p ) 是定义在非周期节点矢量 上的p次B样条基函数。除 ) )
,
非特 别 说 明 ,一 般假 定 =0、 b=1 、
可 改写 为
>0。如 果定 义
,
p =
,
,
) Z ,) 则 ( w p ,式1  ̄ / )
5卷 3
第3 ( 期 总第 22期 ) 0
中
国
造
船
Vo .3 No3 ( ei l . 0 1 5 . Sr a No 2 2)
S p. 0 2 e 2 1
21 02年 9 月
S IB I DNG O HIA H P U L I 2 30 6 .7 0 04 8 2 1 )0 .0 80
( a
b )
() 1
收稿 日期 :2 1-21 ;修 改稿 收稿 日期 :2 1.70 0 11.9 0 20 -8
5卷 3
第 3期 ( 总第 2 2期 ) 0
张
辉 , : 化算 法在 船体 型线 参数 化设 计 中的应 用 等 优
6 9
1
起 点 位 置 坐 标
X
r。 :
本文依据 由主尺度要素和承载船舶信息的基本曲线建立的数学模型,分别应用牛顿/ 拉夫森迭代法 J
和 微分 群体 智能 算法[来求解 该 问题 ,并编 制 了 c + 6 ] + 代码 ,以验证 不 同算 法 的有效性 。
1 船体 型线参数化设计 的数学模型
本数 学模 型优 先考虑 站线 的参 数化 设计 ,在获 得所 需 的站 线后 ,可 插值得 到其 它类 型 的型线 。 首先 根据 目标 船 舶主 尺度 要素 和基 本 曲线 ( 如横 剖面 面积 分布 曲线 、 首尾轮 廓 线等 ) ,获取某 站 线参 数化 设计 必须 的输入 信 息 ,并 将其 归纳 在表 1中。 最终 得 到的 、满足 上述 条件 的站线 可用 一条 具有 8个控 制 点的 N BS曲线表示 , 即 UR
0 引 言
船 体 型线参 数化 设计 方 法 ,就 是 设计 者根 据 已确 定 的船 舶主 尺度 要素 ,用 数学 方法 构建 满足 实用 要 求 的船 体型 线 。相对 于参 数化 设计 方法 ,传 统 的型 线设计 方 法通 常需 要一个 母 型船 ,再通 过船 型变 换得 到 目标 船 ,这在 大量 采用 C D技 术进行 船 型优化 的今 天 ,不 甚方 便 。 F 参数 化设 计方法 [虽然 提 出较早 ,但直 到 19 年 ,才 由 Ha is 用 NU BS曲线技术 生成 了较 为 】 98 re 应 r R 实用 的船 体型线 [。国 内学者 也提 出过基 于形状 参数 的船 体型 线设计 方法 L 2 ] 3 圳。 参数 化设 计 方法 的关 键是 建立 从主 尺度 要素 到船 体 型线 的非线 性数 学模 型 ,并求 解之 。 由于需 要 得 到 的是满 足主 尺度 要素 要 求且光 顺 的型 线 ,因此 ,该 数学模 型 相对 复杂 ,通 常可 归结 为多 参数 、多 目标 的优化 问题 ,其求解 过程 也相 对较 难 ,要求其 算法 的鲁 棒性 好 、求解速度 快 。
:
F+
h
( 4)
, 1 ]
至 此 ,建立 了非 线性优 化 问题 F ,未 知变 量是 5个 曲线控 制 点的坐标 和 5 拉格 朗 日乘子 。 个
2 数 学模 型求 解
21 传 统 数 学 方 法 求 解 优 化 l . 司题
2
Y Y : B 。
3
终点位置坐标
X E
xE
x
f :1
4
YE Y : 1
5
始 点切 角
对非周期 B样 条取 V V oa
=
6
终 点切 角
E
对非周期 B样条取 V 2V m m
一 —
l
7
始点 曲率
B
C
,
= 一
d
出
) 等
, , =U
() 2
为保证 所 得站 线 的光顺 性 ,令其 满足 二 阶应变 能最 小化 的光顺准 则 。二 阶应变 能 的表达 式为
F =E
=
( 3)
中
国
造
船
学术 论文
由此 ,站 线参 数化设 计 问题转化 为求解满 足表 1 式 ( )的 NU BS曲线 问题 。表 1中的某些 约 和 3 R
束在 数值 求解 的开 始 即可 自动满足 ,如 直接 指定 N B UR S曲线 的第 1 控制 点和 第 8控 制 点分别 为 曲线 的起 点和 终 点 。 有些约 束 需作 为约束 条件 在求解 过程 中得 到满足 。 为此 , 引入 拉格 朗 日乘 子 ( ) 可 ≠O , 对 于等式 约束 h 到 h , i来说 , 函数 可改 写为
优化算法在船体型线参数化设计 中的应用
张 辉 ,何 术龙,周 秀红
( 中国船舶科 学研 究中心 ,无锡 2 4 8 ) 10 2
摘
要
以目 标船舶主尺度要素和承载船舶信 息的基本 曲线为输入信 息,以曲线应变能为 目 函数 ,提 出参数化 标
生成以N R S U B 表示船体型线的数学模型, 采用两种优化计算方法( 牛顿/ 拉夫森迭代法和微分群体智能算法)
8
终 点 曲率
E
嚣-E X EX YE EY
Fx ) E ] d B f 一 E  ̄ + —B ( y i , Fx f  ̄ ( ] c = = +矿 ] 2
=
曲线 与 轴 之 间
9
i
L
的 面 积
所 围 面 积 的 浮 心
来数值求解该模型 , 比较 了 同算法所得 出的船体 曲线和计算过程。 并 不 结果表 明, 依据本文介绍的数值算 法, 经参数化生成的船体 型线能满足工程应用要求 ,并有望在船 型优 化设计 中应用 。
关 键 词 :参数化;型线设计;曲线应变能;光顺;智能群体 中图分 类号 :U 6. 62 2 文献 标识码 :A
