李春喜生物统计学第三版课后作业答案
生物统计学课后答案

生物统计学课后答案【篇一:生物统计学经典习题(期末复习)个人整理】class=txt>【例5.1】母猪的怀孕期为114天,今抽测10头母猪的怀孕期分别为116、115、113、112、114、117、115、116、114、113(天),试检验所得样本的平均数与总体平均数114天有无显著差异?根据题意,本例应进行双侧t检验。
1.提出无效假设与备择假设2、计算值经计算得:=114.5,s=1.581:=114,:≠114所以==10-1=9==1.0003、查临界值,作出统计推断由|t|,p0.05,故不能否定=9,查值表(附表3)得:=2.262,因为=114,表明样本平均数与总体平均数差异不显著,可以认为该样本取自母猪怀孕期为114天的总体。
【例5.2】按饲料配方规定,每1000kg某种饲料中维生素c不得少于246g,现从工厂的产品中随机抽测12个样品,测得维生素c含量如下:255、260、262、248、244、245、250、238、246、248、258、270g/1000kg,若样品的维生素c含量服从正态分布,问此产品是否符合规定要求?按题意,此例应采用单侧检验。
1、提出无效假设与备择假设经计算得:=252,s=9.115:=246,:246、计算值所以==12-1=11==2.2813、查临界值,作出统计推断因为单侧(11),p0.05,否定:=246,接受=双侧=1.796,|t|单侧t0.05:246,表明样本平均数与总体平均数差异显著,可以认为该批饲料维生素c含量符合规定要求。
第三节两个样本平均数的差异显著性检验【例5.3】某种猪场分别测定长白后备种猪和蓝塘后备种猪90kg时的背膘厚度,测定结果如表5-3所示。
设两品种后备种猪90kg时的背膘厚度值服从正态分布,且方差相等,问该两品种后备种猪90kg 时的背膘厚度有无显著差异?表5-3长白与蓝塘后备种猪背膘厚度:=,:≠=0.0998、=0.1096,1、提出无效假设与备择假设2、计算值此例=1.817、、=12、=11,经计算得=1.202、=0.1508=0.123、分别为两样本离均差平方和。
统计学第三版课后答案

统计学第三版课后答案第一章1.什么是统计学?统计学是一门研究如何收集、分析和解释数据的学科。
它涉及到收集数据的方法、数据的描述和分析、以及通过数据来进行推断和预测。
2.数据可以分为哪两种类型?数据可以分为定量数据和定性数据。
定量数据是可以用数字表示的,例如身高、体重等;定性数据是描述性的,例如颜色、性别等。
3.描述性统计与推论统计有什么区别?描述性统计是对收集到的数据进行总结、整理和展示的过程,主要通过统计指标如平均数、中位数等来描述数据的特征。
推论统计则是通过对样本数据进行推断,从而对整个总体进行推断和预测。
4.什么是样本?样本是从总体中选取出来的一部分个体。
通过对样本进行统计分析,我们可以对整个总体进行推断和预测。
5.什么是抽样误差?抽样误差是指由于样本选择的随机性所导致的样本统计量与总体参数之间的差异。
第二章1.总体和样本的区别是什么?总体是指研究对象的全体个体,而样本是从总体中选取出来的一部分个体。
2.简单随机抽样和分层抽样的区别是什么?简单随机抽样是指每个个体被抽中的概率相等且相互独立的抽样方法,适用于总体中各个个体之间没有明显分层的情况。
而分层抽样是将总体分为若干层次,然后从每个层次中分别抽取样本,适用于总体中各个层次之间存在明显差异的情况。
3.什么是系统抽样?系统抽样是指根据某种规则,从总体中以一定间隔选取样本的抽样方法。
例如,每隔k个个体选取一个个体作为样本。
4.方便抽样和判断抽样的特点是什么?方便抽样是指通过方便快捷的方法选取样本,例如通过问卷调查、网络调研等。
方便抽样的特点是样本选择的随机性不足,很容易导致样本与总体之间存在偏差。
判断抽样则是基于研究者的判断来选取样本,因此也可能存在主观性和偏见。
5.什么是多阶段抽样?多阶段抽样是指将总体分为若干个阶段,先从每个阶段中按一定方法抽取较小的样本,然后再从这些小样本中抽取最终的样本。
第三章1.什么是频率?频率是指某个数值或范围在样本或总体中出现的次数。
李春喜《生物统计学》第三版课后作业答案

《生物统计学》第三版课后作业答案(李春喜、姜丽娜、邵云、王文林编着)第一章概论(P7)习题1.1 什么是生物统计学?生物统计学的主要内容和作用是什么?答:(1)生物统计学(biostatistics)是用数理统计的原理和方法来分析和解释生物界各种现象和实验调查资料,是研究生命过程中以样本来推断总体的一门学科。
(2)生物统计学主要包括实验设计和统计推断两大部分的内容。
其基本作用表现在以下四个方面:①提供整理和描述数据资料的科学方法;②确定某些性状和特性的数量特征;③判断实验结果的可靠性;④提供由样本推断总体的方法;⑤提供实验设计的一些重要原则。
习题1.2 解释以下概念:总体、个体、样本、样本容量、变量、参数、统计数、效应、互作、随机误差、系统误差、准确性、精确性。
答:(1)总体(populatian)是具有相同性质的个体所组成的集合,是研究对象的全体。
(2)个体(individual)是组成总体的基本单元。
(3)样本(sample)是从总体中抽出的若干个个体所构成的集合。
(4)样本容量(sample size)是指样本个体的数目。
(5)变量(variable)是相同性质的事物间表现差异性的某种特征。
(6)参数(parameter)是描述总体特征的数量。
(7)统计数(statistic)是由样本计算所得的数值,是描述样本特征的数量。
(8)效应(effection)试验因素相对独立的作用称为该因素的主效应,简称效应。
(9)互作(interaction)是指两个或两个以上处理因素间的相互作用产生的效应。
(10)实验误差(experimental error)是指实验中不可控因素所引起的观测值偏离真值的差异,可以分为随机误差和系统误差。
(11)随机误差(random)也称抽样误差或偶然误差,它是有实验中许多无法控制的偶然因素所造成的实验结果与真实结果之间产生的差异,是不可避免的。
随机误差可以通过增加抽样或试验次数降低随机误差,但不能完全消。
生物统计学课后习题解答李春喜

生物统计学课后习题解答李春喜生物统计学是一门运用统计学原理和方法来处理和分析生物数据的学科,对于生物学、医学、农学等领域的研究和实践具有重要意义。
以下是针对李春喜编写的生物统计学教材课后习题的一些解答。
首先,让我们来看一道关于数据描述性统计的题目。
题目给出了一组生物样本的测量数据,要求计算均值、中位数、众数、方差和标准差。
均值是所有数据的算术平均值,通过将所有数据相加再除以数据的个数即可得到。
计算过程如下:假设这组数据为 X1, X2, X3,, Xn,均值=(X1 + X2 + X3 ++ Xn)/ n 。
中位数是将数据按照从小到大或从大到小的顺序排列后,位于中间位置的数值。
如果数据个数为奇数,中位数就是中间的那个数;如果数据个数为偶数,中位数则是中间两个数的平均值。
众数是数据中出现次数最多的数值。
方差反映了数据的离散程度,计算方法是先计算每个数据与均值的差的平方,再将这些平方差求和并除以数据个数。
标准差则是方差的平方根。
例如,给定一组数据:12, 15, 18, 15, 20, 12, 18。
首先将其从小到大排列:12, 12, 15, 15, 18, 18, 20。
数据个数 n = 7。
均值=(12 + 12 + 15 + 15 + 18 + 18 + 20)/ 7 = 1571 。
中位数是第 4 个数,即 15 。
众数是 12、15 和 18 ,因为它们都出现了两次。
接下来计算方差:先计算每个数据与均值的差:(12 1571) =-371 ,(12 1571) =-371 ,(15 1571) =-071 ,(15 1571) =-071 ,(18 1571) = 229 ,(18 1571) = 229 ,(20 1571) = 429 。
然后求差的平方:(-371)²= 137641 ,(-371)²= 137641 ,(-071)²= 05041 ,(-071)²= 05041 ,(229)²= 52441 ,(229)²= 52441 ,(429)²=184041 。
统计学第三版课后答案

统计学第三版答案第一章1.什么是统计学?怎样理解统计学与统计数据的关系?答:统计学是一门收集、整理、显示和分析统计数据的科学。
统计学与统计数据存在密切关系,统计学阐述的统计方法来源于对统计数据的研究,目的也在于对统计数据的研究,离开了统计数据,统计方法以致于统计学就失去了其存在意义。
2.简要说明统计数据的来源答:统计数据来源于两个方面:直接的数据:源于直接组织的调查、观察和科学实验,在社会经济管理领域,主要通过统计调查方式来获得,如普查和抽样调查。
间接的数据:从报纸、图书杂志、统计年鉴、网络等渠道获得。
3.简要说明抽样误差和非抽样误差答:统计调查误差可分为非抽样误差和抽样误差。
非抽样误差是由于调查过程中各环节工作失误造成的,从理论上看,这类误差是可以避免的。
抽样误差是利用样本推断总体时所产生的误差,它是不可避免的,但可以控制的。
4.答:(1)有两个总体:A品牌所有产品、B品牌所有产品(2)变量:口味(如可用10分制表示)(3)匹配样本:从两品牌产品中各抽取1000瓶,由1000名消费者分别打分,形成匹配样本。
(4)从匹配样本的观察值中推断两品牌口味的相对好坏。
第二章、统计数据的描述思考题1描述次数分配表的编制过程答:分二个步骤:(1)按照统计研究的目的,将数据按分组标志进行分组。
按品质标志进行分组时,可将其每个具体的表现作为一个组,或者几个表现合并成一个组,这取决于分组的粗细。
按数量标志进行分组,可分为单项式分组与组距式分组单项式分组将每个变量值作为一个组;组距式分组将变量的取值范围(区间)作为一个组。
统计分组应遵循“不重不漏”原则(2)将数据分配到各个组,统计各组的次数,编制次数分配表。
2.解释洛伦兹曲线及其用途答:洛伦兹曲线是20世纪初美国经济学家、统计学家洛伦兹根据意大利经济学家帕累托提出的收入分配公式绘制成的描述收入和财富分配性质的曲线。
洛伦兹曲线可以观察、分析国家和地区收入分配的平均程度。
最新生物统计学课后习题解答-李春喜

第一章概论解释以下概念:总体、个体、样本、样本容量、变量、参数、统计数、效应、互作、随机误差、系统误差、准确性、精确性。
第二章试验资料的整理与特征数的计算习题2.1 某地100 例30 ~40 岁健康男子血清总胆固醇(mol · L -1 ) 测定结果如下:4.77 3.37 6.14 3.95 3.56 4.23 4.31 4.715.69 4.124.56 4.375.396.30 5.217.22 5.54 3.93 5.21 6.515.18 5.77 4.79 5.12 5.20 5.10 4.70 4.74 3.50 4.694.38 4.89 6.255.32 4.50 4.63 3.61 4.44 4.43 4.254.035.85 4.09 3.35 4.08 4.79 5.30 4.97 3.18 3.975.16 5.10 5.85 4.79 5.34 4.24 4.32 4.776.36 6.384.885.55 3.04 4.55 3.35 4.87 4.17 5.85 5.16 5.094.52 4.38 4.31 4.585.726.55 4.76 4.61 4.17 4.034.47 3.40 3.91 2.70 4.60 4.095.96 5.48 4.40 4.555.38 3.89 4.60 4.47 3.64 4.34 5.186.14 3.24 4.90计算平均数、标准差和变异系数。
【答案】=4.7398, s=0.866, CV =18.27 %2.2 试计算下列两个玉米品种10 个果穗长度(cm) 的标准差和变异系数,并解释所得结果。
24 号:19 ,21 ,20 ,20 ,18 ,19 ,22 ,21 ,21 ,19 ;金皇后:16 ,21 ,24 ,15 ,26 ,18 ,20 ,19 ,22 ,19 。
【答案】 1 =20, s 1 =1.247, CV 1 =6.235% ; 2 =20, s 2 =3.400, CV 2 =17.0% 。
统计学(第三版课后习题答案
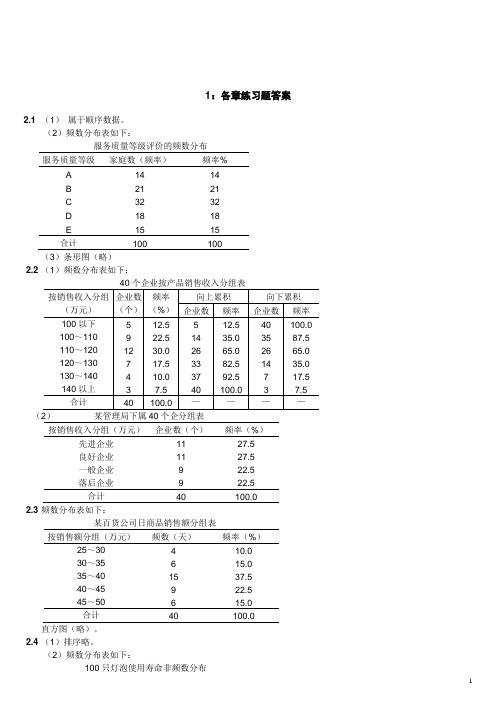
1:各章练习题答案2.1 (1)属于顺序数据。
(2)频数分布表如下:服务质量等级评价的频数分布服务质量等级家庭数(频率)频率%A1414B2121C3232D1818E1515合计100100(3)条形图(略)2.2 (1)频数分布表如下:40个企业按产品销售收入分组表按销售收入分组(万元)企业数(个)频率(%)向上累积向下累积企业数频率企业数频率100以下100~110 110~120 120~130 130~140 140以上591274312.522.530.017.510.07.55142633374012.535.065.082.592.5100.04035261473100.087.565.035.017.57.5合计40 100.0 ————(2)某管理局下属40个企分组表按销售收入分组(万元)企业数(个)频率(%)先进企业良好企业一般企业落后企业11119927.527.522.522.5合计40 100.0 2.3 频数分布表如下:某百货公司日商品销售额分组表按销售额分组(万元)频数(天)频率(%)25~30 30~35 35~40 40~45 45~5046159610.015.037.522.515.0合计40 100.0 直方图(略)。
2.4 (1)排序略。
(2)频数分布表如下:100只灯泡使用寿命非频数分布按使用寿命分组(小时)灯泡个数(只)频率(%)650~660 2 2660~670 5 5670~680 6 6680~690 14 14690~700 26 26700~710 18 18710~720 13 13720~730 10 10730~740 3 3740~750 3 3合计100 100 直方图(略)。
(3)茎叶图如下:65 1 866 1 4 5 6 867 1 3 4 6 7 968 1 1 2 3 3 3 4 5 5 5 8 8 9 969 0 0 1 1 1 1 2 2 2 3 3 4 4 5 5 6 6 6 7 7 8 8 8 8 9 970 0 0 1 1 2 2 3 4 5 6 6 6 7 7 8 8 8 971 0 0 2 2 3 3 5 6 7 7 8 8 972 0 1 2 2 5 6 7 8 9 973 3 5 674 1 4 72.5 (1)属于数值型数据。
生物统计学课后习题解答 李春喜

生物统计学课后习题解答李春喜生物统计学课后习题解答生物统计学是一门研究生物学数据分析和统计推断的学科,它在现代生物学研究中发挥着重要作用。
作为生物统计学的学习者,我们不仅需要掌握基本的统计概念和方法,还需要通过课后习题进行巩固和实践。
本文将对一些典型的生物统计学习题进行解答,帮助您更好地理解和应用生物统计学知识。
一、描述性统计解答1. 样本均值、中位数和众数有何区别?样本均值是指一组数据各个观测值之和除以观测值的个数,它代表了数据的集中趋势。
中位数是将数据按照大小排列后的中间值,它反映了数据的中间位置。
众数是指在一组数据中出现次数最多的数值,它表示数据的主要模式。
2. 什么是标准差?如何计算?标准差是衡量数据离散程度的一种统计量,它表示各个观测值与均值之间的差异程度。
标准差越大,表示数据的离散程度越大。
计算标准差的方法如下:a) 计算每个观测值与均值的差值;b) 将每个差值平方;c) 求平方和;d) 将平方和除以观测值的个数,再开平方。
二、参数估计解答1. 什么是参数估计?请举例说明。
参数估计是根据样本数据对总体参数进行估计的方法。
总体参数是指总体的均值、方差、比例等。
例如,我们想要估计某种药物的治疗成功率,可以通过从总体中取得一部分样本,计算样本中治愈的比例,然后以样本中的比例作为总体治愈成功率的估计值。
2. 什么是置信区间?如何计算?置信区间是用来估计总体参数真实值的范围。
置信区间由一个下限和一个上限组成,表示了总体参数估计值的可能范围。
计算置信区间的方法依赖于参数类型和样本大小,常用的方法有正态分布的置信区间和t分布的置信区间。
三、假设检验解答1. 什么是假设检验?请举例说明。
假设检验是一种统计方法,用于判断样本数据是否支持某个关于总体的假设。
假设检验首先假设一个原始假设(即零假设)和一个备择假设,然后通过计算样本数据得到的统计量和理论分布进行比较,判断是否拒绝原始假设。
例如,我们可以通过假设检验来判断某个新药物的疗效是否显著,原始假设可以是该药物无疗效,备择假设可以是该药物有疗效。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
李春喜生物统计学第三版课后作业答案Final approval draft on November 22, 2020《生物统计学》第三版课后作业答案(李春喜、姜丽娜、邵云、王文林编着)第一章概论(P7)习题什么是生物统计学生物统计学的主要内容和作用是什么答:(1)生物统计学(biostatistics)是用数理统计的原理和方法来分析和解释生物界各种现象和实验调查资料,是研究生命过程中以样本来推断总体的一门学科。
(2)生物统计学主要包括实验设计和统计推断两大部分的内容。
其基本作用表现在以下四个方面:①提供整理和描述数据资料的科学方法;②确定某些性状和特性的数量特征;③判断实验结果的可靠性;④提供由样本推断总体的方法;⑤提供实验设计的一些重要原则。
习题解释以下概念:总体、个体、样本、样本容量、变量、参数、统计数、效应、互作、随机误差、系统误差、准确性、精确性。
答:(1)总体(populatian)是具有相同性质的个体所组成的集合,是研究对象的全体。
(2)个体(individual)是组成总体的基本单元。
(3)样本(sample)是从总体中抽出的若干个个体所构成的集合。
(4)样本容量(sample size)是指样本个体的数目。
(5)变量(variable)是相同性质的事物间表现差异性的某种特征。
(6)参数(parameter)是描述总体特征的数量。
(7)统计数(statistic)是由样本计算所得的数值,是描述样本特征的数量。
(8)效应(effection)试验因素相对独立的作用称为该因素的主效应,简称效应。
(9)互作(interaction)是指两个或两个以上处理因素间的相互作用产生的效应。
(10)实验误差(experimental error)是指实验中不可控因素所引起的观测值偏离真值的差异,可以分为随机误差和系统误差。
(11)随机误差(random)也称抽样误差或偶然误差,它是有实验中许多无法控制的偶然因素所造成的实验结果与真实结果之间产生的差异,是不可避免的。
随机误差可以通过增加抽样或试验次数降低随机误差,但不能完全消。
(12) 系统误差(systematic)也称为片面误差,是由于实验处理以外的其他条件明显不一致所产生的倾向性的或定向性的偏差。
系统误差主要由一些相对固定的因素引起,在某种程度上是可控制的,只要试验工作做得精细,在试验过程中是可以避免的。
(13) 准确性(accuracy)也称为准确度,指在调查或实验中某一实验指标或性状的观测值与其真值接近的程度。
(14) 精确性(precision)也称精确度,指调查或实验中同一实验指标或性状的重复观测值彼此接近程度的大小。
(15)准确性是说明测定值堆真值符合程度的大小,用统计数接近参数真值的程度来衡量。
精确性是反映多次测定值的变异程度,用样本间的各个变量间变异程度的大小来衡量。
习题误差与错误有何区别答:误差是指实验中不可控制因素所引起的观测值偏离真值的差异,其中随机误差只可以设法降低,但不能避免,系统误差在某种程度上可控制、可克服的;而错误是指在实验过程中,人为的作用所引起的差错,是完全可以避免的。
第二章 实验资料的整理与特征数的计算(P22、P23)习题 什么是次数分布表什么是次数分布图制表和绘图的基本步骤有哪些制表和绘图时应注意些什么答:(1)对于一组大小不同的数据划出等距的分组区间(称为),然后将数据按其数值大小列入各个相应的组别内,便可以出现一个有规律的表式,这种称之为次数分布表。
(2)次数分布图是指把次数分布资料画成图状,包括条形图、饼图、直方图、多边形图和散点图。
(3)制表和绘图的基本步骤包括:①求全距;②确定组数和组距;③确定组限和组中值;④分组,编制次数分布表。
(4)制表和绘图时需要注意的是事先确定好全距、组数、组距、各组上下限,再按观测值的大小来归组。
习题 算数平均数与加权数形式上有何不同为什么说它们的实质是一致的答:(1)形式不同在于计算公式的不同:算数平均数的计算公式为M =nx x x n+++...21;加权平均数的计算公式为M =mmm f f f f x f x f x ++++++......212211。
(2)因为它们反映的都是同一组数据的平均水平。
习题平均数与标准差在统计分析中有什么作用它们各有哪些特性答:(1)平均数(mean)的用处:①平均数指出了一组数据资料内变量的中心位置,标志着资料所代表性状的数量水平和质量水平;②作为样本或资料的代表数据与其它资料进行比较。
(2)平均数的特性:①离均差之和等于零;②离均差平方和为最小。
(3)标准差(standard deviation)的用处:①标准差的大小,受实验或调查资料中多个观测值的影响,如果观测值与观测值之间差异较大,其离均差也大,因而标准差也大,反之则小;②在计算标准差时,如果对各观测值加上火减去一个常数a,标准差不变;如果给各观测值乘以或除以一个常数a,则所得的标准差扩大或缩小了a倍;③在正态分布中,一个样本变量的分布可以作如下估计:x±s内的观测值个数约占观测值总个数的%,x±2s内的观测值个数约占总个数的%,x±3s内的观测值个数约占观测值总个数的%。
(4)标准差的特性: ①表示变量的离散程度,标准差小,说明变量的分布比较密集在平均数附近,标准差大,则说明变量的分布比较离散,因此,可以用标准差的大小判断平均数代表性的强弱;②标准差的大小可以估计出变量的次数分布及各类观测值在总体中所占的比例;③估计平均数的标准误,在计算平均数的标准误时,可根据样本标准差代替总体标准差进行计算;④进行平均数区间估计和变异系数的计算。
习题总统和样本的平均数、标准差有什么共同点又有什么联系和区别答:(1)总体和样本的平均数都等于资料中各个观测值的总和除以观测值的个数所得的商。
二者区别在于,总体平均数用μ表示,μ=N x∑,公式中分母为总体观测值的个数N,样本平均数用x=n x∑,公式中的分分母为样本观测值的个数n。
样本平均数x是总体平均数μ的无偏估计值。
(2)总体和样本的标准差都等于离均差的平方和除以样本容量。
二者的区别在于,总体标准差用σ表示,σ=√∑(x−x̅)2N,分母上总体观测值的个数N;标准差用s表示,s=√∑(x−x̅)2n−1,分母上是样本自由度n-1。
样本标准差s是总体标准差σ的无偏估计值。
习题答:见下图——100例30-40岁健康男子血清总胆固醇(mol/L)的次数分布表习题答:见下图——这100例男子的血清总胆固醇基本呈正态分布,中间的最多,两边少,但 mol/L的没有。
习题答:见下图——由上表可知:平均数μ=,标准差s=,而CV=s /μ* 100% =18%习题答:由习题的表可知:中位数Median=,平均数μ=,两数相差,符合正态分布。
习题答:分析见下图:由上图可知:“24号”玉米的平均数Μ=20,标准差s=,而CV=s /Μ* 100% =%;“金皇后”玉米的平均数Μ=20,标准差s=,而CV=s /Μ* 100% =%,比较二者的变异系数CV,“24号”玉米的的变异系数CV 比“金皇后”玉米的小得多,说明“24号”玉米的整齐度大于“金皇后”玉米。
习题答:分析见下图:由上图可知,贻贝单养的平均数μ1=,极差R1=53-25=,标准差s1=,CV1=s1/μ1*100% =%;贻贝与海带混养的平均数μ2=,极差R1=69-39=,标准差s2=,CV2=s2/μ2* 100%=%,虽然单养的极差较小(28),但贻贝与海带混养的平均数更大(),且混养的变异系数更小,即其整齐度更有优势,由此得出,贻贝与海带混养的效果更好。
第三章概率与概率分布(P48)习题试解释必然事件、不可能事件和随机事件。
举出几个随机事件例子。
答:(1)必然事件(certain event)是指在一定条件下必然出现的事件;相反,在一定条件下必然不出现的事件叫不可能事件(impossible);而在某些确定条件下可能出现,也可能不出现的事件,叫随机事件(random event)。
(2)例如,发育正常的鸡蛋,在39℃下21天会孵出小鸡,这是必然事件;太阳从西边出来,这是不可能事件;给病人做血样化验,结果可能为阳性,也可能为阴性,这是随机事件。
习题什么是互斥事件什么是对立事件什么是独立事件试举例说明。
答:(1)事件A和事件B不能同时发生,即A·B=V,那么称事件A和事件B为互斥事件(mutually exclusion event),如人的ABO血型中,某个人血型可能是A型、B型、O型、AB型4中血型之一,但不可能既是A型又是B型。
(2)事件A和事件B必有一个发生,但二者不能同时发生即A+B=U,A×B=V,则称事件A与事件B为对立事件(contrary event),如抛硬币时向上的一面不是正面就是反面。
事件A与事件B的发生毫无关系。
(3)事件B的发生与事件A的发生毫无关系,则称事件A与事件B为独立事件(independent event),如第二胎生男生女与第一台生男生女毫无关系。
习题什么是频率什么是概率频率如何转化为概率答:(1)事件A在n次重复试验中发生了m次,则比值m/n称为事件A发生的频率(frequency),记为W(A)。
(2)事件A在n次重复试验中发生了m次,当试验次数n不断增加时,事件A发生的频率W(A)就越来越接近某一确定值p,则p即为事件A发生的概率(probability)。
(3)二者的关系是:当试验次数n充分大时,频率转化为概率。
习题什么是正态分布什么是标准正态分布正态分布曲线有何特点u和δ对正态分布曲线有何影响答:(1)正态分布是一种连续型随机变量的概率分布,它的分布特征是大多数变量围绕在平均数左右,由平均数到分布的两侧,变量数减小,即中间多,两头少,两侧对称。
(2)μ=0,σ2=1的正态分布为标准正态分布,记为N(0,1)。
(3)正态分布具有以下特点:①正态分布曲线是以平均数μ为峰值的曲线,当x=μ时,f(x)取最大值πσ21;②正态分布是以μ为中心向左右两侧对称的分布 ③σux -的绝对值越大,f(x)值就越小,但f(x)永远不会等于0,所以正态分布以x轴为渐近线,x 的取值区间为(-∞,+∞); ④正态分布曲线完全由参数μ和来决定 ⑤正态分布曲线在x=μ±处各有一个拐点;⑥正态分布曲线与x 轴所围成的面积必定等于1。
(4)正态分布具有两个参数μ和,μ决定正态分布曲线在x 轴上的中心位置,μ减小曲线左移,增大则曲线右移;决定正态分布曲线的展开程度,越小曲线展开程度越小,曲线越陡,越大曲线展开程度越大,曲线越矮宽。
习题答:查附表1可得:(1)P=<μ<=F(μ=-F(μ==(2)P=(-1<μ<1)=F(μ=1)-F(μ=-1)=(3)P=(-2<μ<2)=F(μ=2)-F(μ=-2)=(4)P=<μ<=F(μ=-F(μ==(5)P=<μ<=F(μ=-F(μ==习题解:因为x 服从μ=4,σ=4的正太分布N(4,16),故通过标准化转换公式u=σμ-x 可转化为:(1) P(-3<x ≤4)→→ P<μ≤0)P=<μ≤0)=F(μ=0)-F(μ== P(x<→→ P(μ<P=(μ<= F(μ= =(3) P(x>→→ P(μ>≈P(μ>P=(μ>=1-F(μ= ==(4) P(x ≥-1)→→ P(μ>P=(μ≥=1-F(μ= ==习题解:(1) 根据基因分离定律和基因自由组合定律可知:F 1代非糯稻Ww 与糯稻ww 回交,F 2代糯稻和非糯稻的概率均为1/2,其中糯稻有200*1/2=100株,非糯稻有200*1/2=100株。
