生物统计学课后答案
生物统计学课后重点题答案
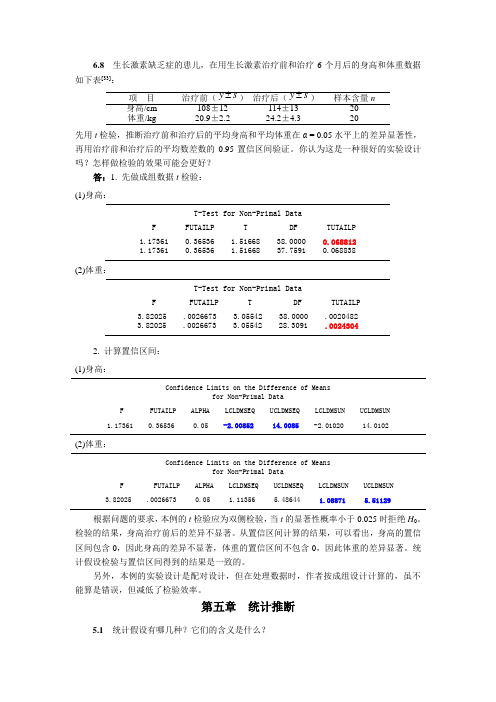
6.8生长激素缺乏症的患儿,在用生长激素治疗前和治疗6个月后的身高和体重数据如下表[33]:y±sy±s身高/cm 108±12 114±13 20体重/kg 20.9±2.2 24.2±4.3 20先用t检验,推断治疗前和治疗后的平均身高和平均体重在α = 0.05水平上的差异显著性,再用治疗前和治疗后的平均数差数的0.95置信区间验证。
你认为这是一种很好的实验设计吗?怎样做检验的效果可能会更好?答:1. 先做成组数据t检验:(1)身高:T-Test for Non-Primal DataF FUTAILP T DF TUTAILP1.17361 0.36536 1.51668 38.0000 0.0688121.17361 0.36536 1.51668 37.7591 0.068838(2)体重:T-Test for Non-Primal DataF FUTAILP T DF TUTAILP3.82025 .0026673 3.05542 38.0000 .00204823.82025 .0026673 3.05542 28.3091 .00243042. 计算置信区间:(1)身高:Confidence Limits on the Difference of Meansfor Non-Primal DataF FUTAILP ALPHA LCLDMSEQ UCLDMSEQ LCLDMSUN UCLDMSUN1.17361 0.36536 0.05 -2.0085214.0085 -2.01020 14.0102(2)体重:Confidence Limits on the Difference of Meansfor Non-Primal DataF FUTAILP ALPHA LCLDMSEQ UCLDMSEQ LCLDMSUN UCLDMSUN3.82025 .0026673 0.05 1.11356 5.48644 1.08871 5.51129根据问题的要求,本例的t检验应为双侧检验,当t的显著性概率小于0.025时拒绝H0。
生物统计学彭明春马纪著课后题答案

生物统计学彭明春马纪著课后题答案1、60°用弧度制表示为()[单选题] *π/3(正确答案)π/62π/32π/52、43.已知a+b=﹣3,a﹣b=1,则a2﹣b2的值是()[单选题] * A.8B.3C.﹣3(正确答案)D.103、已知二次函数f(x)=2x2-x+2,那么f(1)的值为()。
[单选题] * 12283(正确答案)4、若a=-3 ?2,b=-3?2,c=(-)?2,d=(-)?,则( ) [单选题] *A. a<d<c<bB. b<a<d<cC. a<d<c<bD. a<b<d<c(正确答案)5、1. 在实数0、-√3?、√2?、-2中,最小的是()[单选题] *A、-2(正确答案)B、-√3C、0D、√26、已知5m-2n-3=0,则2??÷22?的值为( ) [单选题] *A. 2B. 0C. 4D. 8(正确答案)7、11、在第二、四象限内两条坐标轴夹角平分线上的点,它们的横坐标与纵坐标是()[单选题] *A.相等B.互为相反数(正确答案)C.零D.以上结论都不对8、下列各式:①(x-2y)(2y+x);②(x-2y)(-x-2y);③(-x-2y)(x+2y);④(x-2y)(-x+2y).其中能用平方差公式计算的是()[单选题] *A. ①②(正确答案)B. ①③C. ②③D. ②④9、7.已知集合A={-13,12},B={x|ax+1=0},且B?A,则实数a的值不可能为( ) [单选题] * A.-3(正确答案)B.-1/12C.0D.1/1310、44.若a+b=6,ab=4,则a2+4ab+b2的值为()[单选题] *A.40B.44(正确答案)C.48D.5211、10.下列四个数中,属于负数的是().[单选题] * A-3(正确答案)B 3C πD 012、下列各角终边在第三象限的是()[单选题] *A. 60°B. 390°C. 210°(正确答案)D. -45°13、函数y=cosx与y=arcsinx都是()[单选题] *A、有界函数(正确答案)B、有界函数C、奇函数D、单调函数14、6. 某小组有男学生5人,女学生4人.从中选一人去参加座谈会,共有( )种不同的选法.[单选题] *A. 4种B. 5种C. 9种(正确答案)D. 20种15、300°是第()象限角?[单选题] *第一象限第二象限第三象限第四象限(正确答案)16、下面哪个式子的计算结果是9﹣x2() [单选题] *A. (3﹣x)(3+x)(正确答案)B. (x﹣3)(x+3)C. (3﹣x)2D. (3+x)217、42、如图,在AB、AC上各取一点E、D,使AE=AD,连接BD、CE相交于点O,再连接AO、BC,若∠1=∠2,则图中全等三角形共有()[单选题] *A.5对(正确答案)B.6对C.7对D.8对18、8.(2020·课标Ⅱ)已知集合U={-2,-1,0,1,2,3},A={-1,0,1},B={1,2},则?U(A∪B)=( ) [单选题] *A.{-2,3}(正确答案)B.{-2,2,3}C.{-2,-1,0,3}D.{-2,-1,0,2,3}19、9.如果向东走记为,则向西走可记为() [单选题] *A+3mB+2mC-3m(正确答案)D-2m20、15.已知命题p:“?x∈R,ex-x-1≤0”,则?p为()[单选题] *A.?x∈R,ex-x-1≥0B.?x∈R,ex-x-1>0C.?x∈R,ex-x-1>0(正确答案)D.?x∈R,ex-x-1≥021、9.如图,下列说法正确的是()[单选题] *A.直线AB与直线BC是同一条直线(正确答案)B.线段AB与线段BA是不同的两条线段C.射线AB与射线AC是两条不同的射线D.射线BC与射线BA是同一条射线22、2、在轴上的点的纵坐标是()[单选题] *A.正数B.负数C.零(正确答案)D.实数23、29.若(2,a)和(3,b)是直线y=x+k上的两点,那么这两点间的距离为()[单选题] *A.8B.10C.√2(正确答案)D.224、5.在下列四点中,与点所连的直线不与y轴相交的是().[单选题] * A.(-2,3)B.(2,-3)C(3,2)D(-3,2)(正确答案)25、如果平面a和平面β有公共点A,则这两个平面就相交()[单选题] *A、经过点A的一个平面B、经过点A的一个平面(正确答案)C、点AD、无法确定26、函数y=kx(k是不为0的常数)是()。
李春喜《生物统计学》第三版课后作业答案

《生物统计学》第三版课后作业答案(李春喜、姜丽娜、邵云、王文林编着)第一章概论(P7)习题1.1 什么是生物统计学?生物统计学的主要内容和作用是什么?答:(1)生物统计学(biostatistics)是用数理统计的原理和方法来分析和解释生物界各种现象和实验调查资料,是研究生命过程中以样本来推断总体的一门学科。
(2)生物统计学主要包括实验设计和统计推断两大部分的内容。
其基本作用表现在以下四个方面:①提供整理和描述数据资料的科学方法;②确定某些性状和特性的数量特征;③判断实验结果的可靠性;④提供由样本推断总体的方法;⑤提供实验设计的一些重要原则。
习题1.2 解释以下概念:总体、个体、样本、样本容量、变量、参数、统计数、效应、互作、随机误差、系统误差、准确性、精确性。
答:(1)总体(populatian)是具有相同性质的个体所组成的集合,是研究对象的全体。
(2)个体(individual)是组成总体的基本单元。
(3)样本(sample)是从总体中抽出的若干个个体所构成的集合。
(4)样本容量(sample size)是指样本个体的数目。
(5)变量(variable)是相同性质的事物间表现差异性的某种特征。
(6)参数(parameter)是描述总体特征的数量。
(7)统计数(statistic)是由样本计算所得的数值,是描述样本特征的数量。
(8)效应(effection)试验因素相对独立的作用称为该因素的主效应,简称效应。
(9)互作(interaction)是指两个或两个以上处理因素间的相互作用产生的效应。
(10)实验误差(experimental error)是指实验中不可控因素所引起的观测值偏离真值的差异,可以分为随机误差和系统误差。
(11)随机误差(random)也称抽样误差或偶然误差,它是有实验中许多无法控制的偶然因素所造成的实验结果与真实结果之间产生的差异,是不可避免的。
随机误差可以通过增加抽样或试验次数降低随机误差,但不能完全消。
生物统计学智慧树知到课后章节答案2023年下烟台大学

生物统计学智慧树知到课后章节答案2023年下烟台大学烟台大学绪论单元测试1.概率论是研究随机现象数量规律的数学分支。
A:对 B:错答案:对2.在18世纪概率论引进之后,统计才逐渐发展成为一门成熟的学科。
A:错 B:对答案:对3.同质基础上的变异是随机现象的基本属性。
A:对 B:错答案:对4.同质性是总体的基本特征。
A:对 B:错答案:对5.抽样研究的目的是用有限的样本信息推断总体特征。
A:错 B:对答案:对6.变异是导致抽样误差的根本原因。
A:错 B:对答案:对7.参数是描述样本特征的指标。
A:对 B:错答案:错8.数理统计以概率论为基础,通过对随机现象观察数据的收集整理和分析推断来研究其统计规律。
A:错 B:对答案:对9.统计方法体系的主体内容是A:推断 B:数据收集 C:描述 D:抽样答案:推断10.统计学的主要研究内容包括A:数据整理 B:数据收集 C:数据解释 D:数据分析答案:数据整理;数据收集;数据解释;数据分析第一章测试1.各样本观察值均加同一常数c后A:两者均不变 B:样本均值改变,样本标准差不变 C:样本均值不变,样本标准差改变 D:两者均改变答案:样本均值改变,样本标准差不变2.关于样本标准差,以下叙述错误的是A:反映了均值代表性的好坏 B:度量了数据偏离样本均值的大小 C:反映样本观察值的离散程度 D:不会小于样本均值答案:不会小于样本均值3.表示定性数据整理结果的统计图有条形图、圆形图。
A:对 B:错答案:对4.直方图、频数折线图、茎叶图、箱图是专用于表示定量数据的特征和规律的统计图。
A:对 B:错答案:对5.描述数据离散程度的常用统计量主要有极差、方差、标准差、变异系数等,其中最重要的是方差、标准差。
A:对 B:错答案:对6.统计数据可以分为定类数据、定序数据和数值数据等三类,其中定类数据、定序数据属于定性数据。
A:错 B:对答案:对7.描述数据集中趋势的常用统计量主要有均值、众数和中位数等,其中最重要的是均值。
生物统计第四版课后答案综合修改版

s 是总体标准差σ的无偏估计值。
2.1 某地 100 例 30 ~ 40 岁健康男子血清总胆固醇 (mol · L -1 ) 测定结 果如下: 4.77 3.37 6.14 3.95 3.56 4.23 4.31 4.71 5.69 4.12 4.56 4.37 5.39 6.30 5.21 7.22 5.54 3.93 5.21 6.51 5.18 5.77 4.79 5.12 5.20 5.10 4.70 4.74 3.50 4.69 4.38 4.89 6.25 5.32 4.50 4.63 3.61 4.44 4.43 4.25 4.03 5.85 4.09 3.35 4.08 4.79 5.30 4.97 3.18 3.97 5.16 5.10 5.85 4.79 5.34 4.24 4.32 4.77 6.36 6.38 4.88 5.55 3.04 4.55 3.35 4.87 4.17 5.85 5.16 5.09 4.52 4.38 4.31 4.58 5.72 6.55 4.76 4.61 4.17 4.03 4.47 3.40 3.91 2.70 4.60 4.09 5.96 5.48 4.40 4.55 5.38 3.89 4.60 4.47 3.64 4.34 5.18 6.14 3.24 4.90 计算平均数、标准差和变异系数。
【答案】1 =20, s 1 =1.247, CV 1 =6.235% ; 2 =20, s 2 =3.400, CV 2 =17.0% 。
2.3 某海水养殖场进行贻贝单养和贻贝与海带混养的对比试验,收获时各随机抽 取 50 绳测其毛重 (kg) ,结果分别如下:
单养 50 绳重量数据: 45 , 45 , 33 , 53 , 36 , 45 , 42 , 43 , 29 , 25 , 47 , 50 , 43 , 49 , 36 , 30 , 39 , 44 , 35 , 38 , 46 , 51 , 42 , 38 , 51 , 45 , 41 , 51 , 50 , 47 , 44 , 43 , 46 , 55 , 42 , 27 , 42 , 35 , 46 , 53 , 32 , 41 , 48 , 50 , 51 , 46 , 41 , 34 , 44 , 46 ;
生物统计学智慧树知到课后章节答案2023年下海南大学

生物统计学智慧树知到课后章节答案2023年下海南大学海南大学绪论单元测试1.生物统计学是数理统计的原理和方法在生物科学研究中的应用,属于理论数学。
()答案:错2.生物统计学的创始人是()。
答案:高尔登(F.Galton)3.生物学领域研究多属于实验科学,实验科学的研究方法主要有哪两类()。
答案:科学试验研究法;抽样调查法4.科学研究的基本过程包括三个环节:()答案:假说;试验或抽样调查;结论5.生物统计学十九世纪末发展起来的一门学科。
()答案:对6.试验设计概念正确的有()。
答案:按照预定目标制订适当的实验方案,以利于对实验结果进行有效的统计分析的数学原理和实施方法。
;指合理安排和实施试验取得正确、可靠、充分的数据资料的理论与方法。
7.试验设计有广义、狭义之分,生物统计学指的是广义的试验设计。
()答案:错8.试验设计的目的()。
答案:对总体作出可靠、正确的推断;避免系统误差;无偏估计处理效应;降低试验误差9.描述生物统计学的作用,正确的是()。
答案:提供试验设计的原则及方法;提供由样本推断总体的方法;;提供整理和描述数据资料的科学方法;;有助于阅读及撰写科技文献。
10.能否合理地进行试验设计,关系到科研工作的成败。
()答案:对第一章测试1.因素的水平是指()答案:因素质的不同状态;因素量的级别2.试验处理是指 ( )答案:因子间水平的组合;因子的水平;实施在试验单元上的具体措施3.一个试验中可以选用()作为试验指标。
答案:多个性状;经济性状;单个性状4.试验设计三原则包括:答案:重复原则;随机性原则;局部控制原则5.如果涉及试验因素多,难以确定因素或各因素的最佳起水平范围时,一般可采用先做单因素试验,后做精细选取因素和水平的试验。
答案:对6.在试验设计和统计分析方法中,控制误差指的是()。
答案:减小误差 ;无偏估计误差7.如果田间试验无法在一天内完成,以下那种做法是正确的()答案:同一区组必须在一天完成8.随机区组设计需要将全部处理抽签几次?()答案:有多少区组就抽签多少次9.局部控制原则指:同一重复区内的不同小区间环境条件最大程度地保持一致。
生物统计学(第3版)杜荣骞 课后习题答案 第三章 几种常见的概率分布律

第三章 几种常见的概率分布律3.1 有4对相互独立的等位基因自由组合,问有3个显性基因和5个隐性基因的组合有多少种?每种的概率是多少?这一类型总的概率是多少?答:代入二项分布概率函数,这里φ=1/2。
()75218.02565621562121!5!3!83835==⎪⎭⎫⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=p结论:共有56种,每种的概率为0.003 906 25(1/256 ),这一类型总的概率为0.218 75。
3.2 5对相互独立的等位基因间自由组合,表型共有多少种?它们的比如何? 答:(1)543223455414143541431041431041435434143⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎭⎫⎝⎛+ 表型共有1+5+10+10+5+1 = 32种。
(2)()()()()()()6976000.0024114165014.00241354143589087.002419104143107263.0024127104143105395.00241815414353237.0024124343554322345541322314==⎪⎭⎫⎝⎛==⨯=⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛==⨯=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==⨯=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛==⨯=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛===⎪⎭⎫⎝⎛=隐隐显隐显隐显隐显显P P P P P P它们的比为:243∶81(×5)∶27(×10)∶9(×10)∶3(×5)∶1 。
3.3 在辐射育种实验中,已知经过处理的单株至少发生一个有利突变的概率是φ,群体中至少出现一株有利突变单株的概率为P a ,问为了至少得到一株有利突变的单株,群体n 应多大?答: 已知φ为单株至少发生一个有利突变的概率,则1―φ为单株不发生一个有利突变的概率为:()()()()()φφφ--=-=--=-1lg 1lg 1lg 1lg 11a a an P n P n P3.4 根据以往的经验,用一般的方法治疗某疾病,其死亡率为40%,治愈率为60%。
生物统计学课后习题解答李春喜

第一章概论解释以下概念:总体、个体、样本、样本容量、变量、参数、统计数、效应、互作、随机误差、系统误差、准确性、精确性。
第二章试验资料的整理与特征数的计算习题某地 100 例 30 ~ 40 岁健康男子血清总胆固醇(mol · L -1 ) 测定结果如下:计算平均数、标准差和变异系数。
【答案】=, s=, CV = %试计算下列两个玉米品种 10 个果穗长度 (cm) 的标准差和变异系数,并解释所得结果。
24 号: 19 , 21 , 20 , 20 , 18 , 19 , 22 , 21 , 21 , 19 ;金皇后: 16 , 21 , 24 , 15 , 26 , 18 , 20 , 19 , 22 , 19 。
【答案】 1 =20, s 1 =, CV 1 =% ; 2 =20, s 2 =, CV 2 =% 。
某海水养殖场进行贻贝单养和贻贝与海带混养的对比试验,收获时各随机抽取 50 绳测其毛重 (kg) ,结果分别如下:单养 50 绳重量数据: 45 , 45 , 33 , 53 , 36 , 45 , 42 , 43 , 29 , 25 ,47 , 50 , 43 , 49 , 36 , 30 , 39 , 44 , 35 , 38 , 46 , 51 , 42 , 38 ,51 , 45 , 41 , 51 , 50 , 47 , 44 , 43 , 46 , 55 , 42 , 27 , 42 , 35 ,46 , 53 , 32 , 41 , 48 , 50 , 51 , 46 , 41 , 34 , 44 , 46 ;混养 50 绳重量数据: 51 , 48 , 58 , 42 , 55 , 48 , 48 , 54 , 39 , 58 ,50 , 54 , 53 , 44 , 45 , 50 , 51 , 57 , 43 , 67 , 48 , 44 , 58 , 57 ,46 , 57 , 50 , 48 , 41 , 62 , 51 , 58 , 48 , 53 , 47 , 57 , 51 , 53 ,48 , 64 , 52 , 59 , 55 , 57 , 48 , 69 , 52 , 54 , 53 , 50 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Chapter 4 4-1 For mean arterial pressure t = -1.969, and for total peripheral resistance t = -1.286. There are 23 degrees of freedom in each case. With 23 degrees of freedom 2.069 defines the most extreme 5% of the possible values of the t distribution when the treatment has no effect. Thus, these data do not provide sufficient evidence to reject the hypothesis that different anesthetic agents did not produce differences in mean arterial pressure or total peripheral resistance. 4-2 Yes. t = 3.14, = 20, P < .01. The blood pressure drops rather than increasing, however, so this change is not clinically desirable. 4-3 No. t = 1.33, = 20, P = .20. 4-4 Prob. 3-1: t= 3.967, = 40, P<.01; Prob. 3-5: t= -1.467, = 98, P<.01. In both these cases, we can reject the null hypothesis of no difference between the groups. t2=F. 4-5 The subgroups are nonsmokers, clean environment; nonsmokers, smoky environment and light smokers; moderate smokers and heavy smokers. Here are some of the resulting t values: nonsmokers, clean environment vs. nonsmokers, smoky environment, t = 6.249: light smokers vs. moderate smokers, t = 4.715; moderate smokers vs. heavy smokers, t = 2.358. Since there are a total of 10 pair-wise comparisons, to keep the overall error rate at 5%, these values of t must be compared with the critical value corresponding to P = .05/1 = .005 with 995 degrees of freedom, 2.807. These data support the hypothesis that chronic exposure to other peoples' smoke affects the lung function of nonsmokers. 4-6 All the groups have worse lung function than the nonsmokers breathing clean air (the control group). Nonsmokers in smoky office; q' = 6.249, p = 5; light smokers: q' = 7.499, p = 5; moderate smokers: q' = 12.220, p = 5; heavy smokers: q' = 14.558, p = 5. All exceed the critical values of q' for P < .01 with p = 5 and 995 degrees of freedom: 3.00. 4-7 Inactive vs. joggers, t = 5.616; inactive vs. runners, t = 8.214; joggers vs. runners, t = 2.598. To maintain the overall risk of erroneously rejecting the hypothesis of no difference at 5%, these values of t should be compared with the critical value for P = .05/3 = .017 with 207 degrees of freedom, 2.44. Therefore, the three samples are drawn from distinct populations. 4-8 Inactive vs. joggers, t = 5.616; inactive vs. runners, t = 8.214. To maintain the overall risk of erroneously rejecting the hypothesis of no difference at 5%, these values of t should be compared with the critical value for P = .05/2 = .025 with 207 degrees of freedom, 2.282. Therefore, the two
CHale Waihona Puke apter 22-1 Mean = 61,668, median = 13,956, standard deviation = 117,539, 25th percentile = 7861, 75th percentile = 70,133, mean – 0.67 standard deviations = 6623, mean + 0.67 standard deviations = 79,604. These data appear not to be drawn from a normally distributed population for several reasons. (1) The mean and median are very different. (2) All the observations are (and have to be, since you cannot have a negative viral load) greater than zero and the standard deviation is larger than the mean. If the population were normally distributed, it would have to include negative values of viral load, which is impossible. (3) The relationship between the percentiles and numbers of standards deviations about the mean are different from what you would expect if the data were drawn from a normally distributed population. 2-2 Mean = 4.30, median = 4.15, standard deviation = 0.67, 25th percentile = 3.89, 75th percentile = 4.84, mean – 0.67 standard deviations = 3.82, mean + 0.67 standard deviations = 4.90. These data appear to be drawn from a normally distributed population on the basis of the comparisons in the answer to Prob. 2-1. 2-3 Mean = 1709.3, median = 1750, standard deviation = 824.8, 25th percentile = 877.5, 75th percentile = 2350, mean – 0.67 standard deviations = 1156.7, mean + 0.67 standard deviations = 2261.9. These data appear to be drawn from a normally distributed population on the basis of the comparisons in the answer to Prob. 2-1. 2-4 There is 1 chance in 6 of getting each of the following values: 1, 2, 3, 4, 5, and 6. The mean of this population is 3.5. 2-5 The result is a sample drawn from the distribution of all means of samples of size 2 drawn from the population described in Prob. 2-4. Its mean is an estimate of the population mean, and its standard deviation is an estimate of the standard error of the mean of samples of size 2 drawn from the population in Prob. 2-4. 2-6 Given that the number of authors has to be an integer number and the size of the standard deviations compared with that of the means, the total number of authors is probably skewed toward larger numbers of authors, with a few papers containing many more authors than the rest of the population. Notice that the number of authors and spread of the population dramatically increased in 1976. The certainty with which you can estimate the mean number of authors is quantified with the standard error of the mean of each of the samples, the standard error of the mean decreasing as the precision with which you can estimate the true population means increases. The standard errors of the mean for the four different years are .11, .13, .10, .59.
