华科版工程传热学课后习题答案
《传热学》课后习题答案-第四章
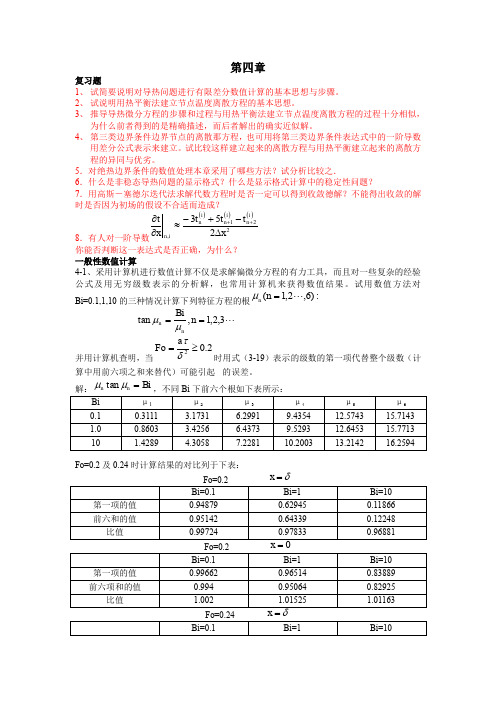
t k i,j 1 t k i,j t k i,j 1 t k i , j r r rj rj r 2 r 2 rj r
并简化,可以得出与上式完全一样相同的结果。
4-7、 一金属短圆柱在炉内受热厚被竖直地移植到空气中冷却, 底面可以认为是绝热的。为用数值法确定冷却过程中柱体温 度的变化, 取中心角为 1rad 的区域来研究 (如本题附图所示) 。 已知柱体表面发射率,自然对流表面传热系数,环境温度, 金属的热扩散率,试列出图中节点(1,1) , (M,1)(M,n)及 (M,N) 的离散方程式。 在 r 及 z 方向上网格是各自均分的。 解:应用热平衡法来建立四个节点点离散方程。 节点(1,1) :
, 离散方程的建立 4-5、试将直角坐标中的常物性无内热源的二维稳态导热微分方程化为显式差分格式,并指 出其稳定性条件( x y) 。 解:常物性无内热源二维非稳态方程微分方程为
4.3636t 2 2.53t1 1.8336t f
t2
2.53t f 1.8336t f
2t 2t t a x 2 y 2
Bi=0.1,1,10 的三种情况计算下列特征方程的根
n (n 1,2,6) :
n a Fo 2 0.2 并用计算机查明,当 时用式(3-19)表示的级数的第一项代替整个级数(计
算中用前六项之和来替代)可能引起 的误差。 解: n Bi 0.1 1.0 10
tan n
第四章
复习题 1、 试简要说明对导热问题进行有限差分数值计算的基本思想与步骤。 2、 试说明用热平衡法建立节点温度离散方程的基本思想。 3、 推导导热微分方程的步骤和过程与用热平衡法建立节点温度离散方程的过程十分相似, 为什么前者得到的是精确描述,而后者解出的确实近似解。 4、 第三类边界条件边界节点的离散那方程,也可用将第三类边界条件表达式中的一阶导数 用差分公式表示来建立。试比较这样建立起来的离散方程与用热平衡建立起来的离散方 程的异同与优劣。 5.对绝热边界条件的数值处理本章采用了哪些方法?试分析比较之. 6.什么是非稳态导热问题的显示格式?什么是显示格式计算中的稳定性问题? 7.用高斯-塞德尔迭代法求解代数方程时是否一定可以得到收敛德解?不能得出收敛的解 时是否因为初场的假设不合适而造成?
工程传热学智慧树知到课后章节答案2023年下华中科技大学

工程传热学智慧树知到课后章节答案2023年下华中科技大学华中科技大学第一章测试1.传热学是研究温差作用下热量传递规律的科学。
()答案:对2.传热系数与导热系数的单位不同。
()答案:对3.物体的导热系数越大,热扩散率就一定越大。
()答案:错4.导热系数的物理意义是什么?()答案:表明材料导热能力的强弱。
5.以下材料中,导热系数较大的是()答案:纯铜6.物体不论()高低,都在相互辐射能量,只是辐射能量的大小不同。
答案:温度7.工程中常遇到热量从固体壁面一侧的高温流体,通过固体壁面传递给另一侧低温流体的过程,称为()。
答案:传热过程8.热量传递的三种基本方式为()答案:热传导;热对流;热辐射9.下列哪几种传热方式不需要有物体的宏观运动?()答案:热传导;热辐射10.下列各参数中,属于物性参数的是?()答案:密度;热导率;热扩散率第二章测试1.下列哪些种传热过程是由于物体的宏观运动导致? ( )答案:对流;复合传热2.热流密度方向与等温线的法线方向总是处在同一条直线上。
( )答案:对3.通过长圆筒壁导热时,圆筒壁内的温度呈分布规律。
( )答案:对数曲线4.在稳态导热中,已知三层平壁的内外表面温度差为60℃,三层热阻之比Rλ1 :Rλ2 :Rλ3=1:3:8,则各层的温度降为。
( )5℃、15℃、40℃5.若已知某种气体的密度为0.617kg/m3,比热为1.122kJ/(kg K),导热系数为0.0484W/(m K) ,则其导温系数是89.9 错10-6m2/s。
( )答案:错6.稳态温度场中温度处处均匀。
( )答案:错7.第一类,第二类和第三类边界条件分别可以用下列哪些数学表达式表达。
①②③( )答案:①②③8.已知平壁的两个壁面的温差是30℃,材料的导热系数是50W/(m K),通过的热流密度是600W/m2,则该平壁的壁厚是多少? ( )2.5m9.通过圆筒壁的一维稳态导热时,单位面积上的热流密度是处处相等的。
工程传热学 答案 华中科大 许国良版

《工程传热学》习题解析 华中科大许国良版(1-4章)适用于以下版本教材(题号按中国电力出版社版,华中科大出版社版本题号需微调)1-4解:W K A R /103.14525.203.04-⨯=⨯⨯==λδKW tA15003.08010025.245=-⨯⨯⨯=∆=Φδλ 23/3025.210150m KW A q =⨯⨯=Φ= 1-7 解:22121/632015.0003.05.5152011m W h h t t q f f =++-=++-=λW q A Q 5.113=⨯= W K A R /103.35.05.12.1003.03-⨯=⨯⨯==λδ W K Ah /101.05.55.12.1111=⨯⨯=W K Ah /108.27205.12.11132-⨯=⨯⨯=1-17 解:若处于稳定工况,则)()(324241w w w w t t A t t A -=-=Φδλσε∴Kt t t t w w w w 5.2845.17)285300(1067.51.00.1285)(448424123=-⨯⨯⨯⨯-=--=-λεδσ 5.11= ℃1-19 解:221/1.2571016.14.0101001m W h t t q =+-=+-=λδ2-1 按题意q r r t≤+∆保墙则6786.03.102.01830301300=--=-∆≥墙保r q t r 则mm r 65.7407465.06786.011.0==⨯=⋅≥保保保λδ 2-4 根据稳态热平衡应有:222121111h t t h h t t f w B B A A f f -=+++-λδλδ 由此解得:m m A B 0793.0,0396.0==δδ 2-10m mr m m r m m r m mr 5.110405.90405.4540403214213121=+++==++==+==δδδδδδm W r r r r r rt t /77.31212.0)5.905.110ln(25.0)5.455.90ln(45)405.45ln()30250(14.32)ln()ln()ln()(233422311241=++-⨯⨯=++-=Φλλλπ2-17Ω⨯=⨯⨯==-=Φ=--∞227210908.9)0015.0(1107)(πρπA L R t t dL h R I w 故热平衡为)100)(103(300010908.9)180(322-⨯⨯⨯=⨯⨯--w t π由此解得5.213=w t ℃ 导线中心的温度为5.2131940015.0)0015.0(42222+⨯⨯⨯=+Φ=∙πλR I t r t w i94.226=℃3-1 解:(1)时间常数hAcVs ρτ=,已知094.2=AcVρ当)/(582K m W h ⋅=时,s s 1.3658/10094.231=⨯=τ 当)/(1162K m W h ⋅=时,s s 05.18116/10094.232=⨯=τ(2)过余温度s s e e ττττθθ//0300---=⋅=3-3解:根据能量守恒原理,有)(∞--=t t hA qA d dtcVτρ 对单位面积而言,其体积为301.0101m mm S A V =⨯=⋅= 代入其它参数,可得)20(7010001.01047.078003--=⨯⨯⨯t d dtτ)7/150(7036660--=⇒t d dtτ )7/150(36667--=⇒t d dt τ分离变量积分⎰⎰-=--ττ0300366677/150)7/150(d t t d tτ36667|)7/150ln(300-=-⇒t t 令975.218180=⇒=t τ 3-7解:首先判断能否用集总参数法求解m R l Rl R Rl l R A V 3221091.0)001.001.0(201.0002.0)5.0(22-⨯=+⨯⨯=+=+=πππ 05.0105.914.81091.085)/(33<⨯=⨯⨯==--λA V h Biv故可用集总参数法。
华中科技大学2004传热学答案

华中科技大学二零零四年招收硕士研究生入学考试试题答案一、简答题1、答:时间常数的定义为τ0=ρcv/aA采用热电偶测量温度时,根据非稳态积总参数法的无量纲温度表达式,时间常数越小,热电偶越能反映出流体温度的变动,动态温度测量精确度越高。
2、答:流体流动时,粘性的作用区域仅限于靠近壁面的薄层内,这一区域为速度边界层。
边界层外速度梯度很小,粘性作用可以忽略,流动可以认为是理想流体的无旋流动,求解容易得多,在外边界层内速度变化很快。
边界层厚度δ:通常规定达到主流速度外99%处的距离为流动边界的厚度。
在近壁面的一个薄层,流体温度沿法线方向剧烈变化,在薄层外,温度梯度几乎为零。
这个薄层为温度边界层。
一般温度达到来流99%的位置定义为热边界层。
Рr=v/a 是动量扩散能力之比。
当pr>1时,σ>σt当pr=1时,σt =σ当pr<1时,σ<σt3、答:△t/℃ 随着过热温度△t=t w -t s 的增加会有四个换热规律全然不同的区域:膜态沸腾 100 q1)自然对流区:壁面过热温度小时沸腾尚未开始,换热规律服从单相自然对流规律;2)核态沸腾区:从开始沸腾点开始,在加热面的某些特定点上产生气泡。
开始阶段,汽化核心产生气泡彼此互不干扰,称孤立气泡区。
随着△t的进一步增加,汽化核心增加,气泡互相影响,并会合成汽块及汽柱。
核太沸腾又称泡状沸腾。
特点是温差小,换热强,一般工业应用都设计在这个范围内。
这个区域的终点是临界热流密度点。
3)过渡沸腾:从峰值点进一步提高△t,热流密度不仅不升高,反而越来越降低。
这是因为气泡产生的速度大于它脱离加热面的速度,气泡汇聚覆盖在加热面上,传热过程只依靠蒸汽的导热和辐射,因而传热恶化。
这种情况持续到最低传热流密度为止。
过渡过程很不稳定。
4)稳定模态沸腾:从最低热流密度起换热规律再次发生转折。
这时随着t w的提高,辐射换热量占据的比例越来越大,所以q随△t的增加而增加。
工程传热学 习题解答 华中科技大学 许国良版 (5-7章)

G1 J2 Eb2 (1/ 2 1)q1,2 Eb2 2.32104W / m2
————————————————————————————————————
第二种:一板温度为 527℃,一板为 27℃
(1)板 1 的本身辐射 E1 Eb1 0.8 5.67 10 8 18579 W / m2
则 A1 X 1,2 A2 X 2,1 ,因 X 1,2 1, 所以 X 2,1 A1 / A2 ,于是有:
(a)
X 2,1
2(W
W / 2) / sin
s in
(b)
X 2,1
W 2H W
(c)
X 2,1
2H
W W
/ sin
7-3 解:第一种:两板温度都为 527℃。
(1)板 1 的本身辐射 E1 Eb1 0.8 5.67 10 8 (527 273)4 18579 W / m2
(2)
定性温度 t f
t
' f
t
'' f
2
45 ℃,物性参数与(1)相同,因为是被冷却,所以 n 取
0.3
Nu 0.023Re0.8 Pr0.3 hd
h 20 10 3 0.023 (3.95 10 4 )0.8 3.930.3 h 5294 .5W / m2 K 0.642
h 不同是因为:一个是被加热,一个是被冷却,速度分布受温度分布影响, Nu 不同。
5-9 解:
(1)
定性温度 t f
t
' f
t
'' f
2
45 ℃
查 45℃水的物性参数有:
990.2kg / m3 ,Cp 4.174kJ /(kg K), 0.642W /(m K),v 0.608106 m2 / s Pr 3.93, 601.4 106 kg / m s
传热学课后习题解答(20190506)

(1)当x= 3cm 时,
Re x
100 0.03 106 19.5
1.538105
0.87u Rex 0.2218
x 5.0 5 0.03 1.538105 1/2 0.383 Re x Pr1 3 t 0.429
w
(2)冬季时
tm
10
2
20
15
查空气的物性参数为
0.0255W /m k Pr 0.704
14.6110-6 m2 / s
1 1/ 288
15 273
Gr
gtH 3 2
2.49 1010
处于湍流区
hL
0.11
H
(Gr Pr)1/3
30 273
Gr
gtH 3 2
6.771 109
处于过渡区
hL
0.0292
H
(Gr Pr)0.39
2.646
Aht 43.26W
Q 43.62 243600 3769kJ
大空间自然对流 6-45
(1)夏季时
tm
35 2
25
30
查空气的物性参数为
Nux
hxl
9400.631
Stx
Nux Re x Pr
0.039
j Stx Pr 2/3 0.03
C f 2 j 0.06
第六章
• 相似理论 6-1
解:空气温度为20℃确定,υ1=15.06×10-6m2/s,Pr1=0.703,
华中科技大学工程传热学课后习题答案

45 2.5 2
100 80 150 KW 0.03
150 10 3 q 30 KW / m 2 A 2.5 2
1-6 一单层玻璃窗, 高 1.2m, 宽 1.5 m, 玻璃厚 0.3 mm, 玻璃导热系数为 = 1.05 W/(mK),室内外的空气温度分别为 20 ℃和 5 ℃,室内外空气与玻璃窗之间对 流换热的表面传热系数分别为 h1 = 5.5 W/(m2K) 和 h2 = 20 W/(m2K),试求玻 璃窗的散热损失及玻璃的导热热阻、两侧的对流换热热阻。
0 1 2 0.00378 0.00267 0.02646 0.03745 21.92% 0.02915 0.02915 0
2-4 一烘箱的炉门由两种保温材料 A 和 B 做成,且δA=2δB(见附图)。已知λ A=0.1 w/m•K,λB=0.06 w/m•K。烘箱内空气温度 tf1=400℃,内壁面的总表面 传热系数 h1=50 w/m2•K。为安全起见,希望烘箱炉门的外表面温度不得高于 50℃。设可把炉门导热作为一维导热问题处理,试决定所需保温材料的厚度。 环境温度 tf2=25℃,外表面总表面传热系数 h2=9.5 w/m2•K。
2-13 一直径为 30mm、 壁温为 100℃的管子向温度为 20℃的环境散热, 热损失率 为 100W/m。为把热损失减小到 50W/m,有两种材料可以同时被利用。材料 A 的导热系数为 0.5 w/m•K,可利用度为 3.14×10-3m3/m;材料 B 的导热系数为 0.1 w/m•K,可利用度为 4.0×10-3m3/m。试分析如何敷设这两种材料才能达到 上要求。假设敷设这两种材料后,外表面与环境间的表面传热系数与原来一样。
传热学课后习题答案

t t f (t0 t f ) 0.372
t t f (t0 t f ) 0.372
70 (200 70)0.372
118.36℃
求热损失:
16.38 Bi 1 0.061
hR
16.38
Fo 8.064
Bi2Fo 0.0612 8.064 0.03 查图: Q 0.64
1638hr00611638bi8064fo00618064003bifo270090000252007006406461995375396770439710311一温度为21横截面积为50mm100mm的矩形长杆放入温度为593的热处理炉中消除热应力宽100mm的一面置于炉子底面上长杆表面与高温流体的表面传热系数为114根据工艺要求要加热到580以上才能消除应力试说明1h后能否满足工艺要求
已知:d 400mm 42W /(mgK) a 1.18105 m2 / s h 116W /(m2 gK ) 2.5h
m 16W /(mgK ) am 0.53105 m2 / s
hm 150W /(m2 gK )
求: dm、 m
分析:属于第三类边界条件下的导热问题。
模化实验,要保证物理现象相似。
一温度为21℃,横截面积为50mm×100mm的矩 形长杆放入温度为593℃的热处理炉中消除热应力, 宽100mm的一面置于炉子底面上,长杆表面与高
温流体的表面传热系数为114 W /(m2,.K根) 据
工艺要求,要加热到580℃以上才能消除应力,试 说明1h后,能否满足工艺要求?
35W /(m .K ) a 0.037m2 / h
解:a 215 8.4105 m2 / s c 950 2700
Fo
a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
V
4
( d i 1 d i )
2
2
当 B 在内,A 在外时,B 与 A 材料的外径为 d2、d3 可分别由上式得出。
解:首先判断能否用集总参数法求解
0.002 0.01 R 2 l V Rl 0.91 10 3 m 2 2(l 0.5 R) 2 (0.01 0.001) A 2Rl R
ql 2 ( t 1 t 4 ) r r r ln( 2 ) ln( 3 ) ln( 4 ) r3 r1 r2
1
2
3
2 3.14 ( 250 30) 45.5 90.5 110.5 ln( ) ln( ) ln( ) 40 45.5 90.5 45 0.25 0.12 312.77W / m
第一章:
1-3 一大平板,高 2.5 m,宽 2 m,厚 0.03m,导热系数为 45 W/(mK),两侧表 面温度分别为 t1 = 100 ℃, t2 = 80 ℃,试求该板的热阻、热流量、热流密度。
解: R
0.03 1.3 104 K / W A 2.5 2 45
当 h 58W /( m K ) 时, s1 2.094 10 / 58 36.1s
2
3
当 h 116W /( m K ) 时, s 2 2.094 10 / 116 18.05s
2
3
(2)过余温度
0 e / s 300e / s
解:若处于稳定工况,则
A (Tw41 Tw42 )
A
(t w 2 t w 3 )
∴ tw3
(Tw41 Tw42 ) tw2
1.0 0.1 5.67 10 8 ( 3004 4004 ) 17.5 132.67 C 127
当 A 在内,B 在外时,A 与 B 材料的外径为 d2、d3 可分别由上式得出。
4
d2 V
0.785
3 d 12 3.14 10
0.785
0.03 2 0.07
d3 V
0.785
3 2 d2 4 10
0.785
0.07 2 0.1
此时每米长度上的散热量为:
由此解得 t w 213.5 ℃ 导线中心的温度为
I 2R 0.0015 2 2 2 r (0.0015) 213.5 ti tw 4 4 19
226.94 ℃
5
第三章:
3-1 一热电偶的ρcV/A 之值为 2.094 kJ/(m2K),初始温度为 20℃,后将其置于 320℃的气流中。试计算在气流与热电偶之间的表面传热系数为 58 W/(m2K)及 116 W/(m2K)的两种情形下, 热电偶的时间常数, 并画出两种情形下热电偶读数 的过余温度随时间的变化曲线。 cV cV 解: (1)时间常数 s ,已知 2.094 A hA
1-16 附图所示的空腔由两个平行黑体表面组成,孔腔内抽成真空,且空腔的厚 度远小于其高度与宽度。其余已知条件如图。表面 2 是厚δ=0.1 m 的平板的一 侧面, 其另一侧表面 3 被高温流体加热, 平板的平均导热系数λ = 17.5 W/(mK), 试问在稳态工况下表面 3 的 tw3 温度为多少?
dt 70(t 150 / 7) d
6
dt 7 (t 150 / 7) d 3666
t
d (t 150 / 7) 7 d 分离变量积分 t 150 / 7 3666 300 0
7 3666 令 180 t 218.975 ln(t 150 / 7) |t300
为 250 ℃ , 外 壁 覆 盖 有 两 层 保 温 层 , 内 保 温 层 厚 度 45mm , 导 热 系 数 为 0.25W/m•K,外保温层厚 20mm,导热系数为 0.12 W/m•K。若最外侧的壁面温
3
度为 30℃,求单位管长的散热损失。
解:
r1 40mm r2 40 1 45.5mm r3 40 1 2 90.5mm r4 40 1 2 3 110.5mm
解: q
t f1 t f 2 1 1 h1 h2
20 5 63W / m 2 1 0.003 1 5.5 0.5 20
Q A q 113.5W
R 0.003 3.3 10 3 K / W A 1.2 1.5 0.5
1 1 0.101K / W Ah1 1.2 1.5 5.5 1 1 27.8 10 3 K / W Ah2 1.2 1.5 20
0 1 2 0.00378 0.00267 0.02646 0.03745 21.92% 0.02915 0.02915 0
2-4 一烘箱的炉门由两种保温材料 A 和 B 做成,且δA=2δB(见附图)。已知λ A=0.1 w/m•K,λB=0.06 w/m•K。烘箱内空气温度 tf1=400℃,内壁面的总表面 传热系数 h1=50 w/m2•K。为安全起见,希望烘箱炉门的外表面温度不得高于 50℃。设可把炉门导热作为一维导热问题处理,试决定所需保温材料的厚度。 环境温度 tf2=25℃,外表面总表面传热系数 h2=9.5 w/m2•K。
Q l ln(70
100 20 74.2W / m 100 ) ln( ) 1 30 70 6.28 0.5 6.28 0.1 13.27 3.14 0.1
绝热性能好的材料 B 在内才能实现要求。
2-17 180A 的电流通过直径为 3mm 的不锈钢导线[λ=19W/(m·℃)]。导线浸在 ,导线的电阻率为 70 温度为 100℃的液体中,表面传热系数为 3000W/(m2·℃) μΩ·cm,长度为 1m,试求导线的表面温度及中心温度?
解: 根据能量守恒原理,有 cV
dt qA hA(t t ) d
3
对单位面积而言,其体积为 V A S 1 10mm 0.01m 代入其它参数,可得
7800 0.47 10 3 0.01 36660
dt 100 70(t 20) d
d2 V
0.785
3 d 12 4 10
0.785
0.03 2 0.0774
d3 V
0.785
3 2 d2 3.14 10
0.785
0.0774 2 0.1
此时每米长度上的散热量为:
Q l ln( 77.4
100 20 43.7 ) ln(100 ) 1 30 77.4 6.28 0.1 6.28 0.5 13.27 3.14 0.1
解:根据稳态热平衡应有:
1
1
0.0001
0.0001
t f1 t f 2 1 A B 1 h1 A B h2
tw t f 2 1 h2
由此解得: B 0.0396m, A 0.0793m 2-10 一内径为 80mm,厚度为 5.5mm,导热系数为 45 W/m•K 的蒸汽管道,内壁温度
2-2 在如图所示的平板导热系数测定装置中,试件厚度δ远小于直径 d。由于安 装制造不好,试件与冷、热表面之间存在着一厚度为Δ=0.1mm 的空气隙。设热 表面温度 t1=180℃,冷表面温度 t2=30℃,空气隙的导热系数可分别按 t1、t2 查取。试计算空气隙的存在给导热系数的测定带来的误差。通过空气隙的辐射 换热可以忽略不计。(Φ=58.2w d=120mm) 解:不考虑空气隙时侧得的导热系数记为λ0,则
3-7 一根体温计的水银泡长 10 mm,直径 4 mm,护士将它放入病人口中之前, 水银泡维持 18℃;放入病人口中时,水银泡表面的换热系数为 85 W/(m2K)。 如果要求测温误差不超过 0.2℃,试求体温计放入口中后,至少需要多长时间, 4℃的病人口中取出。 已别水银泡的物性参数为 = 13520 才能将它从体温为 39. kg/m3,c = 139.4 J/(kg·℃), = 8.14 W/(mK)。
A t
45 2.5 2
100 80 150 KW 0.03
150 10 3 q 30 KW / m 2 A 2.5 2
1-6 一单层玻璃窗, 高 1.2m, 宽 1.5 m, 玻璃厚 0.3 mm, 玻璃导热系数为 = 1.05 W/(mK),室内外的空气温度分别为 20 ℃和 5 ℃,室内外空气与玻璃窗之间对 流换热的表面传热系数分别为 h1 = 5.5 W/(m2K) 和 h2 = 20 W/(m2K),试求玻 璃窗的散热损失及玻璃的导热热阻、两侧的对流换热热阻。
s 2 18.05s
0
s1 36.1s
0 300
3-3 一厚 10 mm 的大平壁(满足集总参数分析法求解的条件),初温为 300℃,密 度为 7800 kg/m3,比热容为 0.47 kJ/(kg℃),导热系数为 45 W/(mK),一侧有恒 定热流 q = 100 W/m2 流入,另一侧与 20℃的空气对流换热,换热系数为 70 W/(m2K)。试求 3min 后平壁的温度。
解:
q
1 h
t1 t 2
100 10 257.1W / m 2 0.4 1 1.6 10
第二章:
2-1 按题意
