计算电磁学矩量法
矩阵分析在计算电磁学中距量法之ACA算法的应用

矩阵分析在计算电磁学中距量法之ACA算法的应用本文主要介绍了计算电磁学距量法的原理,着重讲解了计算电磁学中距量法之ACA算法的基本原理和数值实现方法。
矩阵分析作为一种数学工具,和其它的数学工具仪器,被运用在了这些算法中。
并举出了实例说明ACA算法的有效性。
说明ACA将原始距量法的的量级由O(N2)成功降低到N4/3logN。
标签:计算电磁学距量法ACA算法数值结果一、计算电磁学1864年,麦克斯韦(Maxwell)用一组数学方程概括了宏观电磁场的基本规律,奠定了理论电磁学的基础。
经过两百多年的发展,电磁场的计算方法多种多样,按照数学模型课分为微分方程法,积分方程法和变分方程法等,按照求解域来分主要可分为频域法和时域法,按照近似性可分为解析法,半解析法和数值法。
本文中所讨论的距量法属于后一种分类。
在电磁学中,解析法按照麦克斯韦方程组,在不同的初始条件和边界条件下求解特定的模型,能够给出精确解,但是它具有严格的限制,且对于一个特定的解不具有普遍性,求解很复杂,是早期人们研究电磁学的主要方法。
随着现代数学方法、现代电磁场理论和现代计算机技术的发展,计算电磁学的数值法逐步兴起。
数值法是直接将求解的数学方程进行离散化处理,将无限维的连续问题化为限维的离散问题,将解析方程的求解问题换位代数方程的计算问题的一类方法。
二、距量法距量法(The Method of Moments)是计算电磁学中的一种重要方法。
距量法的基本原理是:选定基函数,把未知函数用基函数进行近似展开,带入算子方程,再选取适当的权函数,使在加权平均的意义下方程的余量等于零,由此将连续的算子方程转换为代数方程,从而可得到一个代数方程的系数矩阵。
从这里我们可以看出,基函数的展开以及于加权函数的内积虽然属于泛函的范畴,但是所得到的这个系数矩阵属于矩阵分析的内容,对这个系数矩阵进行各种处理,是距量法中提高计算效率的关键所在。
距量法是一种近似计算的方法,因为它把定义域为Ω中无限维的问题近似为了有限维的问题,这就需要对其进行截断,而值域也是由有限维的函数序列展开的,所以会产生截断误差。
计算电磁场的矩量法

计算电磁场的矩量法
计算电磁场的矩量法是一种通过求取电场和磁场的矩来计算电磁场行为的方法。
在矩量法中,电磁场被描述为一个有限数量的电荷和电流分布的集合。
这些分布被称为电荷和电流矩。
电荷矩是电荷分布的一种表示方式,它描述了电荷随其位置的变化而变化的程度。
电荷矩可以通过对电荷密度函数乘以相应的位置幂次项进行积分得到。
例如,一阶电荷矩可以通过对电荷密度函数乘以位置的一阶幂次项进行积分得到。
磁场矩是磁场分布的一种表示方式,它描述了磁场随其位置的变化而变化的程度。
磁场矩可以通过对磁场密度函数乘以相应的位置幂次项进行积分得到。
通过计算电荷和电流矩,可以得到电场和磁场的矩。
这些矩可以进一步用于计算电磁场的行为,例如电磁场的势能和辐射模式等。
矩量法在计算电磁场行为时具有一定的优点,例如可以处理复杂的几何形状和电磁场分布。
然而,在实际应用中,由于计算电荷和电流矩需要对电荷和电流分布进行积分,因此计算量较大。
此外,对于高阶电荷和电流矩,其计算误差可能会增加。
因此,在实际应用中需要综合考虑计算精度和计算效率等因素。
计算电磁学-第八章-矩量法概述

16 16
对于一维问题,如图2所示,假定函数的定义域 为 0 χ 1 ,将定义域分成 M 个宽度相同的子区 间,每个子区间的宽度为 n (n 1, 2, , M ),其中
n 1/ M
17 17
则脉冲基函数为
1(当x位于xn内) Pn ( x) 0(当x不在xn内)
B an 是 M 1 阶矩阵, 矩阵K mn 是 M M 阶矩阵, 是 M M 阶矩阵。
mn
Bmn (Wm N n ) d
9 9
所以矩量法利用基函数和权函数将最初 的本征值问题(式(6.1-1))转换成了矩 阵的本征值问题(式(6.1-6)),通过求 解矩阵方程可到近似解。 [a ] 有非零解,其系 为使矩阵方程(6.1-6) Kmn ] -[ Bmn ] 的行列式必须为零,即 数矩阵 [ det(K mn Bmn ) 0 (6.1-7)
K mn Wm , LN n
(r rm )LN n d
LN n (r rm )
Bmn (Wm , N n ) N n (r rm )
20 20
•例2求表示在图5中的微带片状电容器的电容。
解 设地为电位参考点,加在微带片上的电压 为 U ,根据电容的定义,微带片的电容为:
解
将本征函数近似表示成
a an N n
n 1
11 11
M
选定基函数和权函分别为 n N n x(1 x )
Wm x(1 x m )
将选定的基函数和权函数代入式(6.1-6) 其中:[ K mn ][an ] [ Bmn ][an ]
K mn
2 d m n χ (1 χ ) χ (1 ) d χ 2 0 dχ mn m n 1 1
计算电磁学
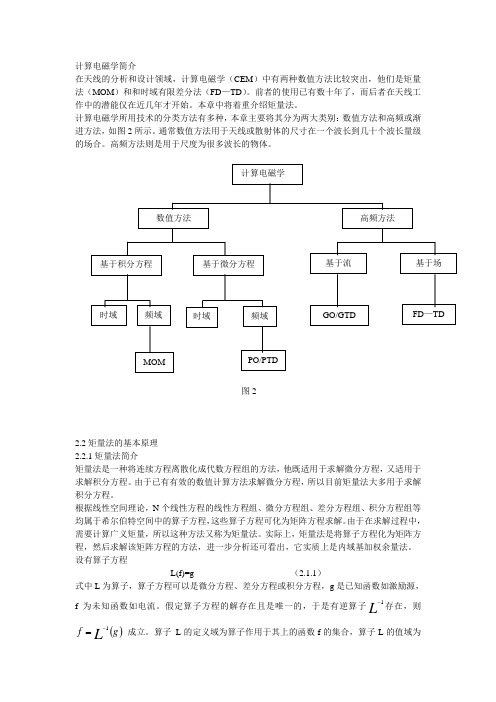
计算电磁学简介在天线的分析和设计领域,计算电磁学(CEM )中有两种数值方法比较突出,他们是矩量法(MOM )和和时域有限差分法(FD —TD )。
前者的使用已有数十年了,而后者在天线工作中的潜能仅在近几年才开始。
本章中将着重介绍矩量法。
计算电磁学所用技术的分类方法有多种,本章主要将其分为两大类别:数值方法和高频或渐进方法,如图2所示。
通常数值方法用于天线或散射体的尺寸在一个波长到几十个波长量级的场合。
高频方法则是用于尺度为很多波长的物体。
图22.2矩量法的基本原理 2.2.1矩量法简介矩量法是一种将连续方程离散化成代数方程组的方法,他既适用于求解微分方程,又适用于求解积分方程。
由于已有有效的数值计算方法求解微分方程,所以目前矩量法大多用于求解积分方程。
根据线性空间理论,N 个线性方程的线性方程组、微分方程组、差分方程组、积分方程组等均属于希尔伯特空间中的算子方程,这些算子方程可化为矩阵方程求解。
由于在求解过程中,需要计算广义矩量,所以这种方法又称为矩量法。
实际上,矩量法是将算子方程化为矩阵方程,然后求解该矩阵方程的方法,进一步分析还可看出,它实质上是内域基加权余量法。
设有算子方程L(f)=g (2.1.1)式中L 为算子,算子方程可以是微分方程、差分方程或积分方程,g 是已知函数如激励源,f 为未知函数如电流。
假定算子方程的解存在且是唯一的,于是有逆算子L1-存在,则()g f L 1-= 成立。
算子 L 的定义域为算子作用于其上的函数f 的集合,算子L 的值域为计算电磁学 数值方法 高频方法 基于积分方程 基于微分方程 时域 频域 时域 MOM FD —TD 基于场 基于流 GO/GTD PO/PTD 频域算子在其定义域上运算而得的函数g 的集合。
假定两个函数f1和f2以及两个任意常数a 1和a2有如下关系:()()()f a f a fa f a L L L 22112211+=+则称L 为线性算子。
矩量法在电磁散射中的应用

矩量法在电磁散射中的应用一矩量法在电磁散射问题中的应用电磁散射问题是电磁学中的一个重要研究领域,研究电磁波的散射机理以及计算其散射场强的大小与分布,具有十分重要的实际意义。
矩量法作为一种有效的数值计算方法在其中有着广泛的应用。
但作为一种计算方法它也有着自己的缺陷,为了解决这些问题,人们提出了各种方案,矩量法在这个过程中也获得了很大的发展。
MoM(Method of Moments)原本是一种近似求解线性算子方程的方法,通过它可以将算子方程转化为一矩阵方程,进而通过求解此矩阵方程得到最终的近似解。
MoM最早是由两位数学家L. V. Kantorovich和V. I.Krylov提出的,后来由K.K.Mei引入计算电磁学,最终被R.F. Harryington在其著作《计算电磁场中的矩量法》中加以系统描述。
利用矩量法求解电磁问题的主要优点是:它严格地计算了各个子系统间的互耦,而算法本身又从根本上保证了误差系统总体最小而不产生数值色散。
如今MoM被广泛应用于计算电磁学中,虽然它不能处理电大尺寸目标的电磁问题,但基于MoM的各种加速方法仍受到极大重视,如多层快速多极子方法MLMFA等。
电磁散射问题是电磁学中的一个重要研究领域,研究电磁波的散射机理以及计算其散射场强的大小与分布,具有十分重要的实际意义。
在实际生活中,遇到的散射目标往往不仅具有复杂的几何形状,而且构成的材料也各不相同。
因此对复杂目标的电磁散射特性进行快速、高效的分析,具有重要的理论意义和实用价值。
电磁散射问题只有在相对简单的情况下才可以用严格的解析法来求解,比如对极少数形状规则的物体。
对于电大物体,可以用高频近似方法,例如几何光学法(GO)、物理光学法(PO)、几何绕射理论(GTD)、物理绕射理论(PTD)、一致性几何绕射理论(UTD)、复射线法(CT)等来求解散射场。
反之,对于电小物体,可以用准静态场来进行分析。
介乎这两者之间的物体,一般采用数值方法。
计算电磁学6-矩量法

∫ ∫ ∂F = ∂R2 dV = 2R ∂R dV =0
∂u j V ∂u j
V ∂u j
( j = 1, 2,", n)
从上式可以看出,我们取权函数 这样得到于MOM法一样的表达式。
Wj
= 2 ∂R ∂u j
,
还有其它权函数选择方法,如将场域剖分成多个子域, 定义子域内的权函数为1,构成子域匹配法。
cem@
一维静电场分布
基函数为全域基
因为解为幂级数形式,基函数含有幂级数
Ni = x − xi+1 (i = 1, 2,", n)
给出的基函数满足给定的边界条件。
n
∑ ϕ ( x ) = ( x − x i+1 )ϕ i i =1
等间距的匹配点,权函数为狄拉克 δ 函数
第6章 矩量法
计算电磁学-矩量法 电子科技大学物理电子学院 赖生建
cem@
主要内容
一. 矩量法思想 二. 加权余量法原理 三. MOM中基函数、权函数 四. 静场问题的MOM法 五. 细导线问题的MOM法
cem@
概述
矩量法(Method of Moment,MOM)在天 线、微波技术和电磁散射等方面广泛应用的一 种方法,这些实际工程问题涉及开域、激励场 源分布形态较为复杂。
分域基的数值稳定性较高,全域基的收效性较好。若选 择的基函数和实际解答愈接近,收敛愈快。
cem@
权函数的选取
由加权余量表达式 R(u) = Lu − g,不同的权函数选择,
将决定算子方程的余量 ∫vWj (Lu−g)dV =0 在不用意义下
取零,可得到不同计算模式的矩量法。
n
∑ ∫ ∫ ( ) ui
电磁场中的矩量法

第8章电磁场中的矩量法8.1矩量法的基本原理8.1.1矩量法是一种函数空间中的近似方法<8.1.1)(S. L2)(8.1,3)(8. L4)<8. L5)图8.1函数空间上的原函数、近似函数与误差函数NF =另8艮■ —1=CEJA8.1.2矩量法是一种变分法(8.1.6) (8.1. 7)(8, 1, 8)(8.1.9) (8.1. 10)<^ig> =—£L/他Q =(贬丄=另住显询丄几〉* i = 1②…侮 封 H(8.1.11)5、扎》=〈£ ,17 (另氐仞丹=刀爲 <化丄恤e 〉、t = lt2T --* r n (8, 1, 12)8.1.3子域基函数1. 狄拉克函数(Dirac delta function)2. 脉冲函数(pulse )或分段常数(piecewise constant )图8.2狄拉克函数,P(Xj, J|t y 2)图8.3脉冲函数3. 子域三角函数(subsectional triangle function)£|氐Xjp{f}=BoGr )=肮工一工』Xi <2 x <Z J :I其余(8. L 13)(8. 1. 14)图8.4三角函数子域4. 二次折线(quadratic spline )函数f 9丄3丄分忑+豆+莎*3 x B W9 3 ■ J 3 T Zd 十莎10»5. 拉格朗日插值多项式( Lagrangian interpolation polynomials图8.6拉格朗日插值多项式函数B 2(X ) = t jc z ,工』=tB 3(X ) =qix f(8.1.16))函数6. 厄密多项式函数7. 其他展开函数r—矗工1)sin(^j:3—kjCi)S(x> = Jsin(^j:3—kjc~)sint^^g —kx2)(8.1.22) 8.1.4截断误差和数值色散1. 截断误差2. 数值色散器十K它二工)=02E. —Ejp-i —E.+i —护捏(百Em 卜W E R_I+ zEg_i \ = 0- \ 3 “5■& /萨叱曲—丄口-屮―如)e,严(1 + (塑冲/訂H单元尺寸引起的戴値華果的溟蚤(8.1.23) (8.1.24) (8. 1.25)8.2典型的矩量法问题8.2.1积分方程形式x —x \» 旦V 工V由x -► 0円評“工)1 -j —Inx21 ——4和=yj 1\,(左)£| 尤一盘"])djr'tkc)T{9(旬+赤-却叫旬F}+心〉F{ A(x) J = X<K x) = | A(x)e_i^* dxJ —EF^{A(K f)} = AM =君「A(KJ^dK#Z TT J—<»* B(x) = f — j J)dx^J —Ml►F^l{A(x)*fi(x)} = ACK.) - B(KJB n<x) = B(x —竝)]T…(x) = TX JE —J?J JG = ^T(x) * [班刃# H評@ | xF(x) = (冷十"J 評 4 I x —x\)dx\ a <Z JC <Z b1-=佇倦+ F)TS *叫*叽|讪}丄(8.2. 1> (fi.2. 2) (8.2. 3) (8.2,4)<8.2.5) <8,2.6) (& 2f 7) <8.2.8) (&2+9> (8.2.10)C8. 2. m822圆柱体散射的积分求解^0)=決沪・(亠只在圆柱上成立科J t (f )心另人九⑷F j\为展开系数1N r 1障切切刀#丹評(航}d/■ -1丿加哽1(8.2.12) (8. 2. 13) <8. £ 14)1 4<8.2.15)<8.2.16) H 評(g(l —斗)—j{j(旬 +In(8. 2- 17)2 it 2rt1 - j -In, -2 du — w_ —[ —叫瞥)T]}(& 2, 19)823误差分析1. 建模误差2. 数字化误差(discretization errors )3. 近似误差4. 数值计算误差ll/r-J?" II = 严一J严 | 独(8.2.22)基函数级栓验函数级甜分段时的误差甜分段时的误差0 34*911,31 35.011.31235.611.3335.811.3435. Q11.3536.211.30「11+7 一(X 891 1L70b 892211.80.89311.90.89411, 90b 890 E 550. 103 1 & 510. 102 S.530. 103 6. 550. 10 8.2.4本征值问题的矩量法<S, 2+23)(8, 2+24) <8. 2.25)N N2〈丁e丄鼠匕=人另《九,及冶,m = li2P—■ ■1算・1Le = ASeS~'L^ =le (E. 2.26) (8-2.27) (fi.2.28)825伽略金法的收敛性= <a , LZr>as > 0(dr by 2 = 3 取 LiA 〉-f)> = 0<兔,严—Th = 0(8,2.29> (& 2.30) 個2. 31) (8. 2.32) (B. 2.33)8.3静电场的矩量法8.3.1静电场中的算子方程—总¥卿=严有限边界 『0-常数.r-sS = p, L _1L^ = LpL=-E V 1,0 = 17》©(工,了,“ — j]JL_1制盏wwL =-V * UV ) S.0〉=T r) dxdjjds<L^j = jj — €(V ' 0)0drJJc0V 2^-OT 2^)dr = 6 W 警一少曾4jrejR(&M 1)(8.3. 2)(8,3. 3> (8,3. 4) (&3. 5>(8.3. 6) (8.3. 7)(8.3. 8)ds/.V .姑//-*r*厂 ~7?// //丄/ i/ / //L-L ——1 Z --------/— ■— ■—&~~ —图8.8带电平板切分为矩形单元(8.:(氐3. 8.3.2带电平板的电容■* 4开衆[jQ'(7©』〉SM 斗為几/・={NV Q = 宀.m = …,Nn-1a 3 Fj/ldj/di/在2上 苴余It 0, _______ ___________ ,_ Ay dx fh*』略4磁p(孔—无丁 H- (y^ — y y 1 Nc = —=艺心△民VD i=lan ” 仁=「r, wf J _i4 ire sj (x m — x}2-\- (.y m — yY"-- :,心Sts -------------- ””ne J (九一 h •严+伉一风尸 ' ----------- dytU = —ln(l+72) = —(0.8814)J 4nc 7x 3 +yKSKe4 =進质Ei & 4s_ "、4=E R 士10)<8. 3. 11) <8.3.12> <S. 3. 13)<8.3, 14) <8.3.15) <8.3. 16)<8.3. 17)(8.3. 18)(8.119) (8.3. 20)(8.3.21) (8. 3. 22)尺* = C J — 芷$ +(了加_孑3严 + (拓曲_比)h = y ^0.282 质 +(8. 3.23)833导体系问题rV] T 在民上,K a 一眄'在民上+护跃临血=*严科,在:上rb P e AS ,(0,户毎N矶〔乳閔)=S ai/n B= 1图8.9角形区域细长时所采用的近似方法十-------- 林工」丿 ------------ 旳应J 」・4寸灰匸丙〒E 三万7(8.3.24)(8.乱 25)(8.3.26)(8.3. 27)(8.3. 28)V L =「「——U 4TT £ JCr —工9 + © —,43; * **'皿;? *** ptfN皿:LQW =[飯]⑴叮12 =______________ 护蚯駅叶_您』(几二忑护+ (%—几尸________________ 巴________________jt£J a*—召)’ +(了亓一旳),+ 用s ggge} 2礙£■(2b)<8. 3,29)<8. 3.30)(8. £31)<8, 3, 32)<8. 3,33)c = a&*S (严-严 >-mA8.4微带天线的矩量法平面波人射捲地板图8.10平面电磁波入射微带天线心II (止一去‘)]+ jA a min [盘 i (注一左“)]ki cos k i / + j“ u sin kid8.4.1理论分析= — V XE (応,*)= 晋憑)+ ¥(章*心{工心注打]V l A 1 (■!<>»♦£)+ K 2A 1 Gy* =—)/iJs (x\y t z*) *介质中 VA 11(工」以)+KlA^ = X 空气中A L/Q= |T J s {x ,y(x,y t z I x t y r t z f )(3,4.1) <8,4. 2) (8M.3) (8M.4) <S. 4. 5)V f y f z}十 K z C(x^t^=—逼卷(h —— y r ,)8(x — zV 巳11Q FX I 工‘、$』)十 KuC D Q"z 韵匚匚0+"(8. 4.6) <8. 4.7>+ | Xtkt -F JttiyjG 1 (匕桃}E :(也“门。
计算电磁学3-有限元法、里兹法、伽辽金法、矩量法

模拟达尔文“优胜劣汰、适者生存”的原理激励好的结构; 模拟孟德尔遗传变异理论在迭代过程中保持已有结构,同时
寻找更好的结构; 简单易懂、通用、鲁棒性强、适合并行处理,可用于解决各
种复杂优化问题。
算法提出依据
达尔文 (Darwin) 的进化论
达尔文用自然选择来解释生物进化。自然选择就是指 生物由于环境中某些因素的影响而使得有利于一些个 体的生存,而不利于另外一些个体生存的演化过程。
简而言之——物竞天择,适者生存
算法提出依据
自然选择学说包括以下三个方面:
(1)遗传:这是生物的普遍特征,亲代把生物信息交给子代, 子代总是和亲代具有相同或相似的性状。生物有了这个特征,物 种才能稳定存在。
f xi x
2.微分
f x
x
xi
lim
x0
1 x
f
xi
x 2
f
xi
x 2
x 0 x 为有限值,
要足够小
时域有限差分方法
Finite-Difference Time-Domain Method
(FDTD)
f x
x
xi
lim
x0
1 x
f
xi
x 2
f
xi
x 2
x 很小
E
(2)变异:亲代和子代之间以及子代的不同个体之间的差异, 称为变异。变异是随机发生的,变异的选择和积累是生命多样性 的根源。
(3)生存斗争和适者生存:具有适应性变异的个体被保留下来 ,不具有适应性变异的个体被淘汰,通过一代代的生存环境的选 择作用,性状逐渐逐渐与祖先有所不同,演变为新的物种。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一维: f , g f (x)g(x)dx 二维: f , g f (x, y)g(x, y)dxdy 三维: f , g f (x, y, z)g(x, y, z)dxdydz
方程组(4)可写成如下的矩阵形式:
式中
[ lmn ][n ]=[ gm ] (5)
选 一 组 线 性 无 关 的 函 数 w ( 权 函 数 , 的角度内,因此F—117A的大多数表面与垂直面的夹角均大于30度,这样可以把雷达波上下偏转出去,以避开辐射源。另
一方面,F—117A的前后缘被设计得尖锐笔直,机体表面其它边缘设计成与主波束方向一致,对方雷达接收不到连续的信
号,难以确定该飞机是一个实在目标还是一种瞬变噪声。
N
f n fn n1
(2)
其中 f1, f2, f3,K fN 称为展开函数或基函
数。
L(f)=g
(1)
代入(1)式再应用算子 L 的线性得到
N
nL( fn) g
n1
(3)
1,2,3 K N 为 N 个未知数。
<2>使用权函数(或称为检验函数)构成求n
的矩阵方程
为最大可能地达到隐身效果,F—117A隐形战机采用多面体外形设计。由于雷达探测范围一般在飞机水平面上下30度
w1, L( f1) [lmn ] w2, L( f1)
............
w1, L( f2 ) w2, L( f2 )
............
......
......
............
即 lmn wm , L( fn )
1
[ n
]
2
M
w1, g [gm ] w2, g
w , L( f ) w , g 这些技术使F—117A的隐身效果极佳,雷达反射截面积仅0.001~0.01平方米。它可以在敌防空火力上空任何高度飞行 n m n m ,可以在高空借助机载激光器指示目标并进行轰炸。一般以7600米高度接近目标,实施攻击时,下降到1000米左右的高 度,在水平飞行时进行投弹攻击。演飞中对红外目标的攻击精度约为1米量级。F—117A采用有利于隐身的内置式武器舱 n,弹舱长5.18米,宽1.83米,可携带2枚908千克的BLU—109型激光制导炸弹或战术战斗机使用的各种武器。武器载荷可 达2270千克。炸弹由机头座舱前下部安装的激光照射器提供目标指示。
本节主要介绍矩量法的基本原理,包括矩 量法的求解步骤,基函数和权函数的选择。
令算子方程为:
L(f)=g
(1)
L 为算子,g 为已知激励函数,f 为未知
响应函数。
算子 L 的定义域为算子作用于其上的函
数 f 的集合,算子 L 的值域为算子在其定
义域上运算而得到的函数 g。 L 取不同形
式,便可描绘不同的电磁工程场问题。
M
<3>矩阵求逆解得 n
[ n ]=[ lmn ] 1 [ gm ]
N
f n fn n1
f [ f%n ][n ] [ f%n ][lmn ]1[gm]
[ f%n ] [ f1, f2 K fN ]
N
fn 必须线性无关,选择适当可使 n fn 很快逼 n 1
近f。
权函数 wm 的选择也应当适当,当 fn wn 时称伽 略金法(GarlerKin’s methord)
m
F—117A隐形战斗轰炸机的全动V型尾翼和机翼均采用菱形翼剖面设计,2台发动机装入机体内部,进气口采用特殊的
m=1,2...N),分别与 L( f ) 和 g 作内积 复合材料格栅设计,可保证进气口对10长或更长的雷达波的隐身效果。这种格栅进气口同时还具有向发动机提供均匀气 流的优点,从而使F—117A更适应大仰角和侧滑飞行。
F—117A的发动机尾喷口设计采用展向“开缝”式喷口设计,喷口下缘底面阻止红外探测器及雷达从后面探测到涡轮
< w , L( f ) >=< w , g > 部件。发动机排出的气流能够与从发动机旁经过的冷空气迅速混合,使排气速下降到66摄氏度,这样即可以有效地降低 m m 发动机的红外辐射特征。这种埋入式发动机设计及特殊的进,排气设计可有效降低发动机噪声。 F—117A机体材料以铝合金结构为主,整体外表涂满黑色的磁性铁氧体雷达吸波材料,可以有效地吸收高频率雷达波 或低频率雷达波,增强隐形效果。
第六章 矩量法
矩量法是将待求的积分或微分问题转化为 一个矩阵方程问题,借助于计算机,求得其数 值解。R. F. Harrington对用矩量法求解电磁 场问题做了全面和深入的分析,其经典著作已 于1968年出版。
矩量法已成功地用于求解许多实际的电 磁问题。
§6.1 矩量法原理
根据线性空间理论,N 个线性方程的 联立方程组、微分方程、差分方程及积分方 程均属于希尔伯特空间中的算子方程,它们 可化作矩阵方程予以求解,在求解过程中需 计算广义矩量,故此法称为矩量法。
例:
d2 f
1 4x2,
dx2
f (0) f (1) 0
0 x 1
算子
L
d2 dx2
特定源 g(x) 1 4x2
定义域为满足边界条件的函数 f 的集合
{ f (x) | f (0) f (1) 0, 0 x 1}
2 0
对应于静电场的泊松方程,已知电荷密度 ,求电位 。
1
0
l'
因为 m=1,2...N,所以得到 N 个方程:
N
n w1, L( fn ) w1, g
n1
N
n
n1
w2 ,
L(
fn
)
w2 ,
g
M
(4)
N n1
n
wN
,
L(
fn
)
wN
,
g
内积:
内 积 f,g 是 三 维 空 间 向 量 点 积
a b 11 22 33 的推广。不同的希尔伯特
影响 fn 和 wm 的选择的一些因素是 (1)所求解的精度; (2)计算矩阵元的难易; (3)能够反演的矩阵大小;
1 dl' 4 R
对应于静电场中带电导线 l 上的线电荷密度 (rv) 分布问题,则若给定激励源项 g ,即 给定该导线的电位,求 (rv) 。
xˆ + yˆ zˆ x y z
2
2 x2
2 y 2
2 z 2
MoM 法基本步骤:
<1> 展开未知函数 f 为有限个线性无关的已
知简单函数 fn 之和
