第四讲-二次函数的图像与性质
二次函数的图像和性质(共82张PPT)

y=ax2
向上
y轴 (0,0)
向下
y轴 (0,0)
4、二次函数y=2x2+1的图象与二次函数y=
2x2的图象开口方向、对称轴和顶点坐标是否相
同?它们有什么关系?我们应该采取什么方法
来研究这个问题?
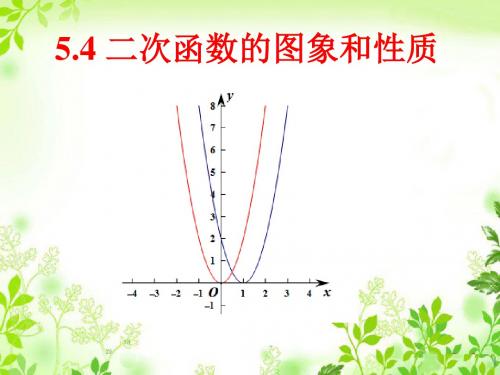
画出函数y=2x2和函数y= 2x2+1的图象, 并加以比较
x … –1.5 –1 –0.5 0 0.5 1 1.5 …
y 1 x2 ··· 2
8
4.5
2 0.5 0 0.5 2 4.5
8
···
x
·· -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 ···
y 2x2 · 8 4.5 2 0.5 0 0.5 2 4.5 8
·· ·
y y x2 8
y 2x2
···
6
y 1 x2
4
2
2
-4
-2 O
24
在对称轴左侧,y都随x的增大而增大,
在对称轴右侧,y都随 x的增大而减小 .
联系: y=a(x-h)²+k(a≠0) 的图象可以看成y=ax²的图象先沿x轴整体左(右)平移| |个单位(当 >0时,向右平移;当 <0时,向左平移),
再沿对称轴整体上(下)平移|
|个单位 (当
>0时向上平移;当 <0时,向下平移)得到的.
y 1 x2
y1
1 3
x2
2
3
y2
1 3
x2
2
的图像
在同一直角坐标系中
画出函数 y 1 x2 5 y
y1
1 3
x2
2
3
y2
的图像
第04讲 二次函数图像的图像与性质

一、二次函数的图像性质011. 二次函数基本形式:2y ax =的性质:a 的绝对值越大,抛物线的开口越小。
2. 2y ax k =+的性质:上加下减。
a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()0k ,y 轴0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值k .0a <向下()0k ,y 轴0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值k .题型一 考察函数的开口方向、对称轴及顶点坐标例1二次函数211y x =-的开口______,对称轴是_______,顶点坐标是______;抛物线2132y x =-+的开口______,对称轴是_______,顶点坐标是______;二次函数23(2)y x =+的开口______,对称轴是______,顶点坐标是_____.a 的符号开口方向 顶点坐标 对称轴 性质0a >向上()00, y 轴0x >时,y 随x 的增大而增大;0x <时,y 随x 的增大而减小;0x =时,y 有最小值0. 0a <向下()00,y 轴0x >时,y 随x 的增大而减小;0x <时,y 随x 的增大而增大;0x =时,y 有最大值0.经典例题剖析知识重难点梳理第04讲 二次函数的图像与性质例2 关于抛物线22y x =与抛物线223y x =--,下列说法正确的是( ) . ① 它们的对称轴都是y 轴 ② 它们的顶点坐标相同③ 它们的形状相同,开口方向不同 ④ 它们可通过平移得到函数解析式 A.①② B .②③ C .①③ D .③④题型二 考察函数的简单平移例3 要将二次函数21(2)3y x =-的图像平移成213y x =的图像,只需将图像( ) .A . 向上平移2个单位B . 向下平移2个单位C . 向右平移2个单位D . 向左平移2个单位题型三 考察函数的图像例4 函数y ax =和2(0)y ax b ab =+>在同一坐标系中的大致图像是( )A .B .C .D .例5 如图所示,若0a <,则函数21(1)y a x =+与221y ax =-+在同一坐标平面中的大致图像是( )A B C D例6 已知二次函数268y x =-.求(1)这个二次函数的图像与x 轴的两个交点A 、B 之间的距离;(2)若图像上另有一点(,)3M m -,求△ABM 的面积.(★★)1.二次函数252y x =-+的开口_____,对称轴是______,顶点坐标是_______;当120x x <<时,则1y ____ 2y (填“>”、“=”或“<”). .2.已知二次函数2y ax c =-,下列结论中正确的个数有( ) . ① 图象的顶点在原点 ② 图象的对称轴是y 轴 ③ 图象与x 轴必有交点 ④ y =-c 一定是它的最小值 A. 1个 B .2个 C .3个 D .4个3.把函数22(1)y x =--的图像旋转180°后,再向_____平移_____个单位就能得到顶点为原点的抛物线__________. . 4.反比例函数ky x=和二次函数2()y k x k =+在同一坐标系中的大致图像是( )5.抛物线21(1)2y x =-+经过点A (-3,a ).(1)求A 点关于抛物线对称轴的对称点B 的坐标; (2)若此抛物线的顶点为C .,求ΔABC 的面积.课堂练习二、二次函数y=a (x-h )2的图象和性质1.考查抛物线y=a (x-h )²开口方向、对称轴和顶点坐标【例1】抛物线y=﹣3(x ﹣1)2的开口向 ,对称轴是 ,顶点坐标是 .总结:1. 函数y=ax 2与y=a (x-h )²的图象开口方向相同,对称轴和顶点坐标不同.2. 函数y=a (x-h )²的对称轴是直线x =h ,顶点坐标是(h ,0).2.考查二次函数y=a (x-h )²的增减性【例2】已知二次函数y=(x ﹣2)2,当x 时,y 随x 增大而减小.精讲精练知识梳理总结:1.当a>0时,在对称轴(x=h)的左侧,y 随着x 的增大而减小;在对称轴(x=h)右侧,y 随着x 的增大而增大;当x=h 时函数y 的值最小(是0).2.当a<0时,在对称轴(x=h)的左侧,y 随着x 的增大而增大;在对称轴(x=h)的右侧,y 随着x 增大而减小;当x=h 时,函数y 的值最大(是0).3.考查抛物线y=a (x-h )²和y=ax ²之间的平移规律【例3】将抛物线y=x 2向右平移2个单位,得到新抛物线的表达式是 . 总结:1.抛物线的平移不改变二次项的系数,主要是移动顶点位置.2.抛物线y=ax ²向右平移h (h>0)个单位得到抛物线y=a (x-h )², y=ax ²向左平移h (h>0)个单位得到抛物线y=a (x+h )² ,简称“左加右减”.1.二次函数252y x =-+的开口_____,对称轴是______,顶点坐标是_______;当120x x <<时,则1y ____ 2y (填“>”、“=”或“<”). .2.已知二次函数2y ax c =-,下列结论中正确的个数有( ) . ① 图象的顶点在原点 ② 图象的对称轴是y 轴 ③ 图象与x 轴必有交点 ④ y =-c 一定是它的最小值 A. 1个 B .2个 C .3个 D .4个3.把函数22(1)y x =--的图像旋转180°后,再向_____平移_____个单位就能得到顶点为原点的抛物线__________. .4.抛物线21(1)2y x =-+经过点A (-3,a ).(1)求A 点关于抛物线对称轴的对称点B 的坐标; (2)若此抛物线的顶点为C .,求ΔABC 的面积.对应练习三、二次函数的图像性质031. 函数y=a(x -h)2+k 的图象与性质:(1)函数y=a(x -h)2+k 的图象是一条抛物线,它的顶点坐标是(h,k ),对称轴是直线x=h. (2)2. 抛物线y=a(x -h)2+k 与y=ax 2的关系,抛物线y=a(x -h)2+k 可由抛物线y=ax 2平行移动得到,它们形状相同,只有位置不同.把y=ax 2的图象先沿x 轴向左或向右平移|h|个单位后,得到y=a(x -h)2的图象,再沿y 轴向上或向下平移|k|个单位,便可得到y=a(x -h)2+k 的图象.题型一 考察函数的开口方向、对称轴及顶点坐标例1 分别指出下列抛物线的开口方向、对称轴及顶点坐标..(1)1)2(312++-=x y (2)3)21(2-+-=x y例2 若二次函数2()(0)y a x m k a =++≠中,0,0m k <<.则它的图像顶点落在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限例3 若抛物线1)(2+++=m m x y 的对称轴是直线1x =,则它的顶点坐标是______ .(★)题型二 考察函数图像的平移例4 (1)将抛物线23y x =向左平移2个单位,再向下平移3个单位,得到的抛物线的解析式是_________;经典例题剖析知识重难点梳理(2)将抛物线22y x =-向右平移3个单位,再向上平移2个单位,得到的抛物线的解析式是_______________;(3)抛物线3)4(312-+=x y 可看作由抛物线231x y =向____平移____个单位,再向___平移___个单位得到;(4)抛物线3)4(212+--=x y 可看作由抛物线221x y -=向___平移__个单位,再向___平移___个单位得到。
二次函数图像与性质ppt课件

D.f(1)>25
答案:A
三基能力强化
2.若函数f(x)=ax2+bx+c满足 f(4)=f(1),那么( )
A.f(2)>f(3) B.f(3)>f(2) C.f(3)=f(2) D.f(3)与f(2)的大小关系不确定 答案:C
三基能力强化
3.已知函数y=x2-2x+3在闭区
间[0,m]上有最大值3,最小值2,则
课堂互动讲练
【思路点拨】 (1)待定系数法.(2) 二次函数的单调性.
【解】 (1)依题意,方程f(x)=ax2 +bx=x有等根,
则有Δ=(b-1)2=0,∴b=1. 2分 又f(-x+5)=f(x-3), 故f(x)的图象关于直线x=1对称, ∴-2ba=1,解得 a=-12,
∴f(x)=-21x2+x. 5 分
基础知识梳理
2.二次函数的图象及其性质
基础知识梳理
基础知识梳理
基础知识梳理
二次函数可以为奇函数吗? 【思考·提示】 不会为奇 函数.
三基能力强化
1.已知函数f(x)=4x2-mx+5在
区间[-2,+∞)上是增函数,则f(1)的
范围是( )
A.f(1)≥25
B.f(1)=25
C.f(1)≤2+2=(x+a)2+2 -a2的对称轴为x=-a,
∵f(x)在[-5,5]上是单调函数, ∴-a≤-5,或-a≥5, 解得a≤-5,或a≥5. 10分
规律方法总结
1.二次函数f(x)=ax2+bx+c(a >0)在区间[m,n]上的最值.
当-2ba<m 时,函数在区间[m, n]上单调递增,最小值为 f(m),最大 值为 f(n);
基础知识梳理
1.二次函数的解析式有三种常用表 达形式
《二次函数的图象和性质》
函数y=ax2+c(a<0)的性质 平移: 由y=ax2向上或向下 平移︱c︱个单位得到 开口方向: 向下 对称轴: y轴 顶点坐标:(0,c)
增减性: x<0时,y随x的增大而增大 x>0时,y随x的增大而减小
最值: 当x=0时,y取得最大值 y最大值=c
y=2x2-1的图象:
y=2x2
由y=2x2的图象向下平移 1个单位得到
y=2x2-1
开口方向:向上
对称轴:y轴
顶点坐标:(0,-1)
函数y=ax2+c(a>0)的图象性质 平移: 由y=ax2向上或向下 平移︱c︱个单位得到 开口方向: 向上 对称轴: y轴 顶点坐标:(0,c)
增减性: x<0时,y随x的增大而减小 x>0时,y随x的增大而增大
=2(x- 5 )2- 9
4
8
对称轴:
直线x= 5 4
顶点坐标:
( 5 ,- 9) 48
y=2x2
y=2(x+1)2的图象:由y=2x2的图象向左 平移1个单位得到.
随堂练习:
对于二次函数y=-3(x+2)2:
(1)它的图象与二次函数y=-3x2的 图象有什么关系?它是轴对称图形吗? 它的开口方向、对称轴、顶点坐标分 别是什么?
(2)当x取哪些值时,y的随x值的增 大而增大?当x取哪些值时,y的值随 x值的增大而减小?
增减性: x<0时,y随x的增大而减小 x>0时,y随x的增大而增大
最值: 当x=0时,y取得最小值 y最小值=0
函数y=ax2(a<0)的图象性质 图象:
开口方向:_向__下___, 对称轴:_y_轴___ 顶点坐标:_(__0,_0_)___.
二次函数的图像与性质-完整版课件

二次函数与一元二次方程关系
一元二次方程 $ax^2 + bx + c = 0$($a neq 0$)的解即为二次函数 $y = ax^2 + bx + c$ 与 $x$ 轴交点的横坐标。
当 $Delta = b^2 - 4ac > 0$ 时,二次函数与 $x$ 轴有两个交点;当 $Delta = 0$ 时,有 一个交点;当 $Delta < 0$ 时,没有交点。
• 分析:根据题意设交点坐标为$(-1, y_1)$和$(3, y_2)$,代入直线方程可得两个方程。又因为这两个点也在抛 物线上,所以代入抛物线方程也可得两个方程。联立这四个方程即可求出二次函数的解析式。
• 示例2:已知二次函数$y = ax^2 + bx + c (a • eq 0)$的图像与直线$y = x + m (m • eq 0)$相交于两点,且这两点关于原点对称,求二次函数的解析式。 • 分析:根据题意设交点坐标为$(x_1, y_1)$和$(x_2, y_2)$,由于两点关于原点对称,所以有$x_1 = -x_2$和
BIG DATA EMPOWERS TO CREATE A NEW ERA
二次函数的图像与性质-完
整版课件
汇报人:XXX
2024-01-29
• 二次函数基本概念 • 二次函数图像特征 • 二次函数性质探讨 • 典型例题分析与解答 • 实际应用场景举例说明 • 总结回顾与拓展延伸
目录
CONTENTS
零点存在性及个数判断方法
零点定义
二次函数零点存在 性判断方法
对于函数f(x),若存在x0∈D, 使得f(x0)=0,则称x0为函数 f(x)的零点。
通过判别式Δ=b^2-4ac来判断 。当Δ>0时,二次函数有两个 不相等的零点;当Δ=0时,二 次函数有两个相等的零点(即 一个重根);当Δ<0时,二次 函数无零点。
二次函数 的图象和性质 (课件)

2.若点A(2,m)在抛物线y=x2上, 则点A关于y轴对称点的坐标是?
解: 因为A(2,m)在抛物线y=x2上 所以m=4,即A(2,4)
则点A(2,4)关于y轴对称点的坐标 是(-2,4)
3.已知y=mxm2+1 的图像是不在第一、
二象限的抛物线,则m=_______.
解:由题意的: m2+1=2 且 m<0 解得m=-1
4.二次函数y=mxm2-1 的图像有最低点
则m是多少?
小结:二次函数y=± x2的性质
在对称轴左侧,y随x的增大而减小,
在对称轴右侧,y随x的增大而增大.
在y=-x2的图象中正好相反.
3.y=x2有最低点,y=-x2有最高点
即 y=x2有最小值而y=-x2有最大值
y=x2
x
y=-x2
二次函数y=x2 与 y=-x2 的异同点:
相同点:
1. 形状:图像都是抛物线 2.图象都与y轴交于点( 0,0 ) 3.图象都关于y轴对称.
当x=1时,y=1 当x=2时,y=4
向上,并且向上无限
伸展;当x=0时,函数y
的值最小,最小值是ww0w.
探究二次函数y=-x2的图象
二次函数y=-x2的图象是什么形状?先想一想,然后作出
它的图象,它与二次函数y=x2的图象有什么关系?与同伴进行
交流。
y
y=x2
y 它与抛物线y=x2
(1)满足条件的m 的值;
(2)m为何值时,抛物线有最低点?求 出这个最低点,
二次函数的图像和性质PPT课件(共21张PPT)

相同点
相同点:开口都向下,顶点是
原点而且是抛物线的最高点,
对称轴是 y 轴.
不同点
不同点:|a|越大,抛物线的
开口越小.
x
O
y
-4 -2
2
4
-2
-4
-6
y 1 x2 2
-8
y x2
y 2x2
尝试应用
1、函数y=2x2的图象的开向口上 ,对称轴y轴 ,顶点是(0,0;)
2、函数y=-3x2的图象的开口向下 ,对称轴y轴 ,顶点是(0,0;) 3、已知抛物线y=ax2经过点A(-2,-8).
不在此抛物线上。
小结
1. 二次函数的图像都是什么图形?
2. 抛物线y=ax2的图像性质: (1) 抛物线y=ax2的对称轴是y轴,顶点是原点.
(2)当a>0时,抛物线的开口向上,顶点是抛物 线的最低点;
当a<0时,抛物线的开口向下,顶点是抛物 线的最高点;
(3)抛物线的增减性
(4)|a|越大,抛物线的开口越小;
得到y=-x2的图像.
y 1
-5 -4 -3 -2 -1-1 o 1 2 3 4 5 x
-2
-3 -4
-5
-6
y=-x2
-7
-8 -9
-10
二次函数的图像
从图像可以看出,二次函数y=x2和y=-x2的图像都是一条
曲线,它的形状类似于投篮球或投掷ห้องสมุดไป่ตู้球时球在空中所经过
的路线.
这样的曲线叫做抛物线.
y=x2的图像叫做抛物线y=x2.
解:分别填表,再画出它们的图象,如图 当a<0时,抛物线的开口向下,顶点是抛物线的最高点;
在同一直角坐标系中画出函数y=-x2、y=-2x2、y=- x2的图象,有什么共同点和不同点? -8=a(-2)2,解出a= -2,所求函数解析式为y= -2x2.
《二次函数的图像与性质》数学教学PPT课件(4篇)

的联系;
3.掌握二次函数 y = ax2 + c 及 y a(x h)2 的性
质,并会应用.
用描点法画出y=-2x2的图象,并指出它的开 口方向、对称轴以及顶点坐标.
参照下表画出函数y=x2+1与y=x2-1的图象.
【规律总结】
二次函数y=ax2的“两关系四对等” 1.a>0⇔开口向上⇔有最小值⇔
x>0时,y随x的增大而增大, x<0时,y随x的增大而减小. 2.a<0⇔开口向下⇔有最大值⇔
x>0时,y随x的增大而减小, x<0时,y随x的增大而增大.
1.物体从某一高度落下,已知下落的高度h(m)和下落的时间 t(s)的关系式是:h=4.9t2,h是t的二次 函数,它的图象的 顶点坐标是(0,0). 2.已知抛物线y=ax2经过点A(-2,-8). (1)求此抛物线的函数解析式. y = -2x2 (2)判断点B(-1,-4)是否在此抛物线上. 不在抛物线上 (3)求出此抛物线上纵坐标为-6的点的坐标.
m 1 x, 5
E F
4.已知a≠0,b<0,一次函数是y=ax+b,二次函数是y
= ax2,则下面图中,可以成立的是( C )
5.填空:已知二次函数
(1)其中开口向上的有_②__③__⑥__(填题号); (2)其中开口向下且开口最大的是__⑤__(填题号); (3)当自变量由小到大变化时,函数值先逐渐变大,然后
(0,0) (0,0)
最小 值0最值是大是
(0,c)
0最小 值是
(0,c)
最c 大 值是
y随x的
增大而减 小
y随x的
增大而增
大 y随x的
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第四讲二次函数的图像与性质(一)学习目标:1会用描点法画出二次函数y=ax2+k与y=a(x-h) 2的图象.2•使学生了解并会求抛物线y=ax2+k与y=a(x-h)2的对称轴与顶点。
学习难点:二次函数y=ax2+k,y=a(x-h) 2与y=ax2的联系及如何平移以及对于抛物线y=ax2+k, y=a(x-h) 2的对称轴方程的理解.一、学前准备:1 一次函数y 2x与y 2x 1的图象关系是 ___________________________________________________2、二次函数卩匕的开口方向_____________ ,对称轴_____________ ,顶点坐标 _________ 。
y=-2x 的开口方向___________ ,对称轴________________ ,顶点坐标______________ 。
3、抛物线y=-2x 上有两点(x i,y 1) ,(x 2,y 2),且x i<X2<0,那么y i ( )y 2二、探究归纳21、抛物线y=2(x+5)的顶点坐标是 ____________ ,对称轴是__________2、抛物线y=-4x 2-4的开口方向向____________ ,当x=时,y有最__________ 值,此时y= _____3、抛物线y=-3(4x 2-2)的开口方向向___________ ,顶点坐标是 ________ ,对称轴是__________ ,当x ______ 时,y随x的增大而增大。
4、写出符合条件的二次函数表达式:1(1) y=a(x-2) 2的图象与y= x2-2的开口方向相反,形状相同。
21 2 2(2) y=a(x-2) 的图象与y= x-2的图象交点是(1, m ).2(二)学习目标:1、使学生会用描点法画出二次函数y=a(x-h) 2+k 的图象.2、使学生了解并会求抛物线y=a(x-h) 2+k 的对称轴与顶点.学习重点:用描点法画出二次函数y=a(x-h) 2+k 型的图象学习难点:二次函数y=a(x-h) 2+k 与y=a(x-h) 2的联系及如何平移.. 一、学前准备:1、 二次函数y=ax 2+k 的图象和性质,二次函数 y=a(x-h) 2的图象和性质。
2、 二次函数y=ax 2+k , y=a(x-h) 2与y=ax 2的联系及如何平移.3、 猜想抛物线y=a(x-h) 2+k 与y=ax 2的形状 ____________ ,只是 _____ 不同,当a>0时,开口当a<0时,开口 ____ ,对称轴是直线 ________ ,顶点坐标 _________ 。
二、探究活动 探索二次函数y=a(x-h) 2+k 的图象和性质1 2 5例、求二次函数y 2x x2的顶点坐标和对称轴,并作出函数图象 (三) 探究应用1、指出下列二次函数图象的开口方向、对称轴和顶点坐标2 2 2(1) y=2(x-3) -5 (2)y=-0.5(x+1) (3)y=2(x-2) +53 2 12⑷ y-x 2 1(5)y2(x 1) 52、下列函数,x 取何值时y 随x 的增大而增大? x 取何值时y 随x 的增大而减小?(注意21数形结合)(1) y=-2(x-8) 2+5 (2) y 4 x -3四.自我测试1.将抛物线y 2(x 4)2 1如何平移可得到抛物线y 2x 2 ( )A.向左平移4个单位,再向上平移1个单位B .向左平移4个单位,再向下平移1个单位 C.向右平移4个单位,再向上平移1个单位D .向右平移4个单位,再向下平移1个单位3 22.把抛物线y -x 向左平移3个单位,再向下平移4个单位,所得的抛物线的函数关系式为 _________________________ .3、 二次函数y=-(x-1) 2+3图象的顶点坐标是 __________________ 。
1 2 1 24、 抛物线y 1 2xx 2可由抛物线y x 2向 ______________ 平移 _____ 个单位,再向 _______ 平 2 232(6) y ~(x 3)移_____ 个单位而得到.3、学习目标: 1、 体会建立二次函数对称轴和顶点坐标公式的必要性.2、 能够利用二次函数的对称轴和顶点坐标公式解决问题.学习重点: 运用二次函数的对称轴和顶点坐标公式解决实际问题. 学习难点: 把数学问题与实际问题相联系的过程. 、学前准备1 2 一1、 抛物线 戸丄(x +3)的顶点坐标是 __________ .22、 将抛物线y =3x 2向上平移3个单位后,所得抛物线的顶点坐标是 _______________ .1 2 1 2 1 23、 抛物线y =— — x +1, y =— — (x +1)与抛物线y =— — (x +1)的 _____ 相冋, 不冋.4 4 4 — —二、探究活动__ 2(一)探索二次函数y=ax +bx+c 的对称轴和顶点坐标 例:求二次函数 y = ax +bx+c 的对称轴和顶点坐标.2 2(点拨:用 配方法将ax +bx+c 转化成a(x-h) +k 的形式即可。
) 解:把y = ax 2+bx+c 的右边配方,得y = ax 2+bx+c z 2b c=a(x + x )a a2 b b 2 c=a[x +2 •x+( ) +2a 2a a四. 1、 2、=a(x+ A )2+2a 4a.对称轴为x=-—,顶点燃坐标为2a/ b 4ac b 2、(- ,■2a 4a自我测试 确定下列二次函数图象的开口方向、对称轴和顶点坐标。
2 (1) y=2x -4x-1 (2)y=-3(x+3)(x+9) 对于二次函数y=ax 2+bx+a,如果2a+b=0,那么此函数的顶点坐标是当一枚火箭被竖直向上发射时,它的高度h(m)与时间2_____对称轴方程是—t(s)之间可以用公式h=-5t +150t+10表示。
经过多长时间,火箭到达最高点?最高点的高度是多少?(四)22系数的符号 图像特征a 的符号 a>0. 抛物线开口向 a<0 抛物线开口向b 的符号b>0. 抛物线对称轴在y 轴的 侧 b=0 抛物线对称轴是轴b<0抛物线对称轴在y 轴的—侧 c 的符号c>0. 抛物线与y 轴交于 C=0 抛物线与y 轴交于 c<0抛物线与y 轴交于 2b 2 4ac 的符号b 24ac >0. 抛物线与x 轴有 个交点 b 4ac =0 抛物线与x 轴有个交点b 24ac <0抛物线与x 轴有 个交点数二次噸散,十虹+厂为常散・吃工£|)1图' J_X ____ __ 工/ r 1练习O 骂e AO 旳,拋韧続幵口口〉当PVQ 时播物裁开口-*£3对称铀是 、加点足 倨)刘称轴是 .侦点悬*n 在对称轴左侧.即为心)在对称嚇左侧・即为昜时 皿 殖工 的增大而一昙时+潭幽立 的1営大而»山对称抽£側•呵当 ,任蹲称做曲侧当时F 随工的増人而— g 时…随比肿墉大而■*麵物馋布最低点,半 拋物钱有最斉应*鬥 Jt = 时・有駁小ffl * J := 酎祁走值" y h ■一. **龙逐一 -1. 二次函数y =ax 2+bx +c ( 0)的图象如图,a , b , c 的取值范围( A. a <0, b <0, c <0 B. a <0, b >0, c <0 C. a >0, b >0, c <0D. a >0, b <0, c <02. 与抛物线y x 2 2x 4关于y 轴对称的图象表示的函数关系式是2 2A. y x 2x 4B. y x 2x 4A.m 1 或m 2 B .1 m 2C. 1 m 0D. m 14. 二次函数y x 2 4x 3的图象交x 轴于A 、B 两点,交y 轴于点。
,则厶ABC 勺面积为()A. 6B . 4 C. 3 D. 15. 抛物线y x 2 4与x 轴交于B C 两点,顶点为人则厶ABC 勺面积为()A 16B 8C 4D 2226.若抛物线ya 1x , y a ?x 的形状相同,那么()B. a-i a 2为( )C. y x 2 2x 4D. y x 2 2x 43.若抛物线y x 2 2mx m 2m 1的顶点在第二象限,则常数m 的取值范围是(C. |a 1|=| a 2|D. a 1与a 2的关系无法确定7.与抛物线4x 2关于x 轴对称的图象表示为(A - yx 24x 2B . y x 2 4x 2 C. yx 2 4x 2D. yax 2 4x 28.二次函数ax 2 bx c的图象如图,则点M( c , &)在()A.第一象限B.第二象限C.第三象限D.第四象限9.若二次函数ax2C ,当X 取X 1, X 2(X 严X 2)时,函数值相等,则当X 取X 1+X 2时,函数值 A. a cB . a cC. cD. c)10.二次函数y a(x m)2 2m(a 0)的顶点在( )A. y 2xB. y 2xC. x 轴上D. y 轴上11. 函数y ax b与y ax2 bx c如图所示,则下列选项中正确的是( )A. ab>0, c>0B. ab<0, c>0C. ab>0, c<0D. ab<0, c<0 ■■:12. 抛物线y ax2 bx c(a 0),关于x轴对称的图象的关系式是_________________________________ .13. 抛物线y x k的顶点为P,与x轴交于A、B两点,如果△ ABP是正三角形,那么,k= ________ .214. 判断函数y x 4x 2的图象是否经过第三象限?说明理由.第33题.是否存在以y轴为对称轴的抛物线,经过(3,-4 )和(-3 , 4)两点,若存在,请写出抛物线的解析式;若不存在请说明理由.15. 设二次函数y ax2 bx c的图象开口向下,顶点在第二象限内.①确定a, b, b2 4ac的符号;②若此二次函数的图象经过原点,且顶点的横坐标与纵坐标互为相反数,顶点与原点的距离为3、2,求此二次函数的关系式16. 抛物线y 2x2 6x m与x轴交于A、B两点,如果要求点A在(0 , 0)与(1 , 0)之间,点B在(2 , 0)与(3 , 0)之间,请确定m的取值范围17. 已知抛物线y = ,2和直线y = ax+ 1(1)求证:不论a取何值,抛物线与直线必有两个不同的交点。
