数据库系统基础教程第二章答案
大数据库系统基础教程(第二版)课后习题问题详解

Database Systems: The CompleteBookSolutions for Chapter 2Solutions for Section 2.1Exercise 2.1.1The E/R Diagram.Exercise 2.1.8(a)The E/R DiagramKobvxybzSolutions for Section 2.2Exercise 2.2.1The Addresses entity set is nothing but a single address, so we would prefer to make address an attribute of Customers. Were the bank to record several addresses for a customer, then it might make sense to have an Addresses entity set and make Lives-at a many-many relationship.The Acct-Sets entity set is useless. Each customer has a unique account set containing his or her accounts. However, relating customers directly to their accounts in a many-many relationship conveys the same information and eliminates the account-set concept altogether.Solutions for Section 2.3Exercise 2.3.1(a)Keys ssNo and number are appropriate for Customers and Accounts, respectively.Also,we think it does not make sense for an account to be related to zero customers, so we should round the edge connecting Owns to Customers. It does not seem inappropriate to have a customer with 0 accounts; they might be a borrower, for example, so we put no constraint on the connection from Owns to Accounts. Here is the The E/R Diagram,showing underlined keys and the numerocity constraint.Exercise 2.3.2(b)If R is many-one from E1 to E2, then two tuples (e1,e2) and (f1,f2) of the relationship set for R must be the same if they agree on the key attributes for E1. To see why, surely e1 and f1 are the same. Because R is many-one from E1 to E2, e2 and f2 must also be the same. Thus, the pairs are the same.Solutions for Section 2.4Exercise 2.4.1Here is the The E/R Diagram.We have omitted attributes other than our choice for the key attributes of Students and Courses. Also omitted are names for the relationships. Attribute grade is not part of the key for Enrollments. The key for Enrollements is studID from Students and dept and number from Courses.Exercise 2.4.4bHere is the The E/R Diagram Again, we have omitted relationship names and attributes other than our choice for the key attributes. The key for Leagues is its own name; this entity set is not weak. The key for Teams is its own name plus the name of theleague of which the team is a part, e.g., (Rangers, MLB) or (Rangers, NHL). The key for Players consists of the player's number and the key for the team on which he or she plays. Since the latter key is itself a pair consisting of team and league names, the key for players is the triple (number, teamName, leagueName). e.g., Jeff Garcia is (5, 49ers, NFL).Database Systems: The CompleteBookSolutions for Chapter 3Solutions for Section 3.1Exercise 3.1.2(a)We can order the three tuples in any of 3! = 6 ways. Also, the columns can be ordered in any of 3! = 6 ways. Thus, the number of presentations is 6*6 = 36.Solutions for Section 3.2Exercise 3.2.1Customers(ssNo, name, address, phone)Flights(number, day, aircraft)Bookings(ssNo, number, day, row, seat)Being a weak entity set, Bookings' relation has the keys for Customers and Flights and Bookings' own attributes.Notice that the relations obtained from the toCust and toFlt relationships are unnecessary. They are:toCust(ssNo, ssNo1, number, day)toFlt(ssNo, number, day, number1, day1)That is, for toCust, the key of Customers is paired with the key for Bookings. Since both include ssNo, this attribute is repeated with two different names, ssNo and ssNo1. A similar situation exists for toFlt.Exercise 3.2.3Ships(name, yearLaunched)SisterOf(name, sisterName)Solutions for Section 3.3Exercise 3.3.1Since Courses is weak, its key is number and the name of its department. We do not have a relation for GivenBy. In part (a), there is a relation for Courses and a relation for LabCourses that has only the key and the computer-allocation attribute. It looks like:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, allocation)For part (b), LabCourses gets all the attributes of Courses, as:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, room, allocation)And for (c), Courses and LabCourses are combined, as:Depts(name, chair)Courses(number, deptName, room, allocation)Exercise 3.3.4(a)There is one relation for each entity set, so the number of relations is e. The relation for the root entity set has a attributes, while the other relations, which must include the key attributes, have a+k attributes.Solutions for Section 3.4Exercise 3.4.2Surely ID is a key by itself. However, we think that the attributes x, y, and z together form another key. The reason is that at no time can two molecules occupy the same point.Exercise 3.4.4The key attributes are indicated by capitalization in the schema below:Customers(SSNO, name, address, phone)Flights(NUMBER, DAY, aircraft)Bookings(SSNO, NUMBER, DAY, row, seat)Exercise 3.4.6(a)The superkeys are any subset that contains A1. Thus, there are 2^{n-1} such subsets, since each of the n-1 attributes A2 through An may independently be chosen in or out.Solutions for Section 3.5Exercise 3.5.1(a)We could try inference rules to deduce new dependencies until we are satisfied we have them all. A more systematic way is to consider the closures of all 15 nonempty sets of attributes.For the single attributes we have A+ = A, B+ = B, C+ = ACD, and D+ = AD. Thus, the only new dependency we get with a single attribute on the left is C->A.Now consider pairs of attributes:AB+ = ABCD, so we get new dependency AB->D. AC+ = ACD, and AC->D is nontrivial. AD+ = AD, so nothing new. BC+ = ABCD, so we get BC->A, and BC->D. BD+ = ABCD, giving us BD->A and BD->C. CD+ = ACD, giving CD->A.For the triples of attributes, ACD+ = ACD, but the closures of the other sets are each ABCD. Thus, we get new dependencies ABC->D, ABD->C, and BCD->A.Since ABCD+ = ABCD, we get no new dependencies.The collection of 11 new dependencies mentioned above is: C->A, AB->D, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.Exercise 3.5.1(b)From the analysis of closures above, we find that AB, BC, and BD are keys. All other sets either do not have ABCD as the closure or contain one of these three sets.Exercise 3.5.1(c)The superkeys are all those that contain one of those three keys. That is, a superkey that is not a key must contain B and more than one of A, C, and D. Thus, the (proper) superkeys are ABC, ABD, BCD, and ABCD.Exercise 3.5.3(a)We must compute the closure of A1A2...AnC. Since A1A2...An->B is a dependency, surely B is in this set, proving A1A2...AnC->B.Exercise 3.5.4(a)Consider the relationThis relation satisfies A->B but does not satisfy B->A.Exercise 3.5.8(a)If all sets of attributes are closed, then there cannot be any nontrivial functional dependencies. For suppose A1A2...An->B is a nontrivial dependency. Then A1A2...An+ contains B and thus A1A2...An is not closed.Exercise 3.5.10(a)We need to compute the closures of all subsets of {ABC}, although there is no need to think about the empty set or the set of all three attributes. Here are the calculations for the remaining six sets:A+ = AB+ = BC+ = ACEAB+ = ABCDEAC+ = ACEBC+ = ABCDEWe ignore D and E, so a basis for the resulting functional dependencies for ABC are: C->A and AB->C. Note that BC->A is true, but follows logically from C->A, and therefore may be omitted from our list.Solutions for Section 3.6Exercise 3.6.1(a)In the solution to Exercise 3.5.1 we found that there are 14 nontrivial dependencies, including the three given ones and 11 derived dependencies. These are: C->A, C->D, D->A, AB->D, AB-> C, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.We also learned that the three keys were AB, BC, and BD. Thus, any dependency above that does not have one of these pairs on the left is a BCNF violation. These are: C->A, C->D, D->A, AC->D, and CD->A.One choice is to decompose using C->D. That gives us ABC and CD as decomposed relations. CD is surely in BCNF, since any two-attribute relation is. ABC is not in BCNF, since AB and BC are its only keys, but C->A is a dependency that holds in ABCD and therefore holds in ABC. We must further decompose ABC into AC and BC. Thus, the three relations of the decomposition are AC, BC, and CD.Since all attributes are in at least one key of ABCD, that relation is already in 3NF, and no decomposition is necessary.Exercise 3.6.1(b)(Revised 1/19/02) The only key is AB. Thus, B->C and B->D are both BCNF violations. The derived FD's BD->C and BC->D are also BCNF violations. However, any other nontrivial, derived FD will have A and B on the left, and therefore will contain a key.One possible BCNF decomposition is AB and BCD. It is obtained starting with any of the four violations mentioned above. AB is the only key for AB, and B is the only key for BCD.Since there is only one key for ABCD, the 3NF violations are the same, and so is the decomposition.Solutions for Section 3.7Exercise 3.7.1Since A->->B, and all the tuples have the same value for attribute A, we can pair the B-value from any tuple with the value of the remaining attribute C from any othertuple. Thus, we know that R must have at least the nine tuples of the form (a,b,c), where b is any of b1, b2, or b3, and c is any of c1, c2, or c3. That is, we can derive, using the definition of a multivalued dependency, that each of the tuples (a,b1,c2), (a,b1,c3), (a,b2,c1), (a,b2,c3), (a,b3,c1), and (a,b3,c2) are also in R.Exercise 3.7.2(a)First, people have unique Social Security numbers and unique birthdates. Thus, we expect the functional dependencies ssNo->name and ssNo->birthdate hold. The same applies to children, so we expect childSSNo->childname and childSSNo->childBirthdate. Finally, an automobile has a unique brand, so we expect autoSerialNo->autoMake.There are two multivalued dependencies that do not follow from these functional dependencies. First, the information about one child of a person is independent of other information about that person. That is, if a person with social security number s has a tuple with cn,cs,cb, then if there is any other tuple t for the same person, there will also be another tuple that agrees with t except that it has cn,cs,cb in its components for the child name, Social Security number, and birthdate. That is the multivalued dependencyssNo->->childSSNo childName childBirthdateSimilarly, an automobile serial number and make are independent of any of the other attributes, so we expect the multivalued dependencyssNo->->autoSerialNo autoMakeThe dependencies are summarized below:ssNo -> name birthdatechildSSNo -> childName childBirthdateautoSerialNo -> autoMakessNo ->-> childSSNo childName childBirthdatessNo ->-> autoSerialNo autoMakeExercise 3.7.2(b)We suggest the relation schemas{ssNo, name, birthdate}{ssNo, childSSNo}{childSSNo, childName childBirthdate}{ssNo, autoSerialNo}{autoSerialNo, autoMake}An initial decomposition based on the two multivalued dependencies would give us {ssNo, name, birthDate}{ssNo, childSSNo, childName, childBirthdate}{ssNo, autoSerialNo, autoMake}Functional dependencies force us to decompose the second and third of these.Exercise 3.7.3(a)Since there are no functional dependencies, the only key is all four attributes,ABCD. Thus, each of the nontrvial multivalued dependencies A->->B and A->->C violate 4NF. We must separate out the attributes of these dependencies, first decomposing into AB and ACD, and then decomposing the latter into AC and AD because A->->C is still a 4NF violation for ACD. The final set of relations are AB, AC, and AD.Exercise 3.7.7(a)Let W be the set of attributes not in X, Y, or Z. Consider two tuples xyzw and xy'z'w' in the relation R in question. Because X ->-> Y, we can swap the y's, so xy'zw and xyz'w' are in R. Because X ->-> Z, we can take the pair of tuples xyzw and xyz'w' and swap Z's to get xyz'w and xyzw'. Similarly, we can take the pair xy'z'w' and xy'zw and swap Z's to get xy'zw' and xy'z'w.In conclusion, we started with tuples xyzw and xy'z'w' and showed that xyzw' and xy'z'w must also be in the relation. That is exactly the statement of the MVD X ->-> Y-union-Z. Note that the above statements all make sense even if there are attributes in common among X, Y, and Z.Exercise 3.7.8(a)Consider a relation R with schema ABCD and the instance with four tuples abcd, abcd', ab'c'd, and ab'c'd'. This instance satisfies the MVD A ->-> BC. However, it does not satisfy A ->-> B. For example, if it did satisfy A ->-> B, then because the instance contains the tuples abcd and ab'c'd, we would expect it to contain abc'd and ab'cd, neither of which is in the instance.Database Systems: The Complete Array BookSolutions for Chapter 4Solutions for Section 4.2Exercise 4.2.1class Customer {attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account {attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Exercise 4.2.4class Person {attribute string name;relationship Person motherOfinverse Person::childrenOfFemalerelationship Person fatherOfinverse Person::childrenOfMalerelationship Set<Person> childreninverse Person::parentsOfrelationship Set<Person> childrenOfFemaleinverse Person::motherOfrelationship Set<Person> childrenOfMaleinverse Person::fatherOfrelationship Set<Person> parentsOfinverse Person::children}Notice that there are six different relationships here. For example, the inverse of the relationship that connects a person to their (unique) mother is a relationship that connects a mother (i.e., a female person) to the set of her children. That relationship, which we call childrenOfFemale, is different from the children relationship, which connects anyone -- male or female -- to their children.Exercise 4.2.7A relationship R is its own inverse if and only if for every pair (a,b) in R, the pair (b,a) is also in R. In the terminology of set theory, the relation R is ``symmetric.''Solutions for Section 4.3Exercise 4.3.1We think that Social Security number should me the key for Customer, and account number should be the key for Account. Here is the ODL solution with key and extent declarations.class Customer(extent Customers key ssNo){attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account(extent Accounts key number){attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Solutions for Section 4.4Exercise 4.4.1(a)Since the relationship between customers and accounts is many-many, we should create a separate relation from that relationship-pair.Customers(ssNo, name, address, phone)Accounts(number, type, balance)CustAcct(ssNo, number)Exercise 4.4.1(d)Ther is only one attribute, but three pairs of relationships from Person to itself. Since motherOf and fatherOf are many-one, we can store their inverses in the relation for Person. That is, for each person, childrenOfMale and childrenOfFemale will indicate that persons's father and mother. The children relationship is many-many, and requires its own relation. This relation actually turns out to be redundant, in the sense that its tuples can be deduced from the relationships stored with Person. The schema:Persons(name, childrenOfFemale, childrenOfMale)Parent-Child(parent, child)Exercise 4.4.4You get a schema like:Studios(name, address, ownedMovie)Since name -> address is the only FD, the key is {name, ownedMovie}, and the FD has a left side that is not a superkey.Exercise 4.4.5(a,b,c)(a) Struct Card { string rank, string suit };(b) class Hand {attribute Set theHand;};For part (c) we have:Hands(handId, rank, suit)Notice that the class Hand has no key, so we need to create one: handID. Each hand has, in the relation Hands, one tuple for each card in the hand.Exercise 4.4.5(e)Struct PlayerHand { string Player, Hand theHand };class Deal {attribute Set theDeal;}Alternatively, PlayerHand can be defined directly within the declaration of attribute theDeal.Exercise 4.4.5(h)Since keys for Hand and Deal are lacking, a mechanical way to design the database schema is to have one relation connecting deals and player-hand pairs, and another to specify the contents of hands. That is:Deals(dealID, player, handID)Hands(handID, rank, suit)However, if we think about it, we can get rid of handID and connect the deal and the player directly to the player's cards, as:Deals(dealID, player, rank, suit)Exercise 4.4.5(i)First, card is really a pair consisting of a suit and a rank, so we need two attributes in a relation schema to represent cards. However, much more important is the fact that the proposed schema does not distinguish which card is in which hand. Thus, we need another attribute that indicates which hand within the deal a card belongs to, something like:Deals(dealID, handID, rank, suit)Exercise 4.4.6(c)Attribute b is really a bag of (f,g) pairs. Thus, associated with each a-value will be zero or more (f,g) pairs, each of which can occur several times. We shall use an attribute count to indicate the number of occurrences, although if relations allow duplicate tuples we could simply allow duplicate (a,f,g) triples in the relation. The proposed schema is:C(a, f, g, count)Solutions for Section 4.5Exercise 4.5.1(b)Studios(name, address, movies{(title, year, inColor, length,stars{(name, address, birthdate)})})Since the information about a star is repeated once for each of their movies, there is redundancy. To eliminate it, we have to use a separate relation for stars anduse pointers from studios. That is:Stars(name, address, birthdate)Studios(name, address, movies{(title, year, inColor, length,stars{*Stars})})Since each movie is owned by one studio, the information about a movie appears in only one tuple of Studios, and there is no redundancy.Exercise 4.5.2Customers(name, address, phone, ssNo, accts{*Accounts})Accounts(number, type, balance, owners{*Customers})Solutions for Section 4.6Exercise 4.6.1(a)We need to add new nodes labeled George Lucas and Gary Kurtz. Then, from the node sw (which represents the movie Star Wars), we add arcs to these two new nodes, labeled directedBy and producedBy, respectively.Exercise 4.6.2Create nodes for each account and each customer. From each customer node is an arc to a node representing the attributes of the customer, e.g., an arc labeled name to the customer's name. Likewise, there is an arc from each account node to each attribute of that account, e.g., an arc labeled balance to the value of the balance. To represent ownership of accounts by customers, we place an arc labeled owns from each customer node to the node of each account that customer holds (possibly jointly). Also, we place an arc labeled ownedBy from each account node to the customer node for each owner of that account.Exercise 4.6.5In the semistructured model, nodes represent data elements, i.e., entities rather than entity sets. In the E/R model, nodes of all types represent schema elements, and the data is not represented at all.Solutions for Section 4.7Exercise 4.7.1(a)<STARS-MOVIES><STAR starId = "cf" starredIn = "sw, esb, rj"><NAME>Carrie Fisher</NAME><ADDRESS><STREET>123 Maple St.</STREET><CITY>Hollywood</CITY></ADDRESS><ADDRESS><STREET>5 Locust Ln.</STREET><CITY>Malibu</CITY></ADDRESS></STAR><STAR starId = "mh" starredIn = "sw, esb, rj"><NAME>Mark Hamill</NAME><ADDRESS><STREET>456 Oak Rd.<STREET><CITY>Brentwood</CITY></ADDRESS></STAR><STAR starId = "hf" starredIn = "sw, esb, rj, wit"> <NAME>Harrison Ford</NAME><ADDRESS><STREET>whatever</STREET><CITY>whatever</CITY></ADDRESS></STAR><MOVIE movieId = "sw" starsOf = "cf, mh"><TITLE>Star Wars</TITLE><YEAR>1977</YEAR></MOVIE><MOVIE movieId = "esb" starsOf = "cf, mh"><TITLE>Empire Strikes Back</TITLE><YEAR>1980</YEAR></MOVIE><MOVIE movieId = "rj" starsOf = "cf, mh"><TITLE>Return of the Jedi</TITLE><YEAR>1983</YEAR></MOVIE><MOVIE movieID = "wit" starsOf = "hf"><TITLE>Witness</TITLE><YEAR>1985</YEAR></MOVIE></STARS-MOVIES>Exercise 4.7.2<!DOCTYPE Bank [<!ELEMENT BANK (CUSTOMER* ACCOUNT*)><!ELEMENT CUSTOMER (NAME, ADDRESS, PHONE, SSNO)> <!ATTLIST CUSTOMERcustId IDowns IDREFS><!ELEMENT NAME (#PCDATA)><!ELEMENT ADDRESS (#PCDATA)><!ELEMENT PHONE (#PCDATA)><!ELEMENT SSNO (#PCDATA)><!ELEMENT ACCOUNT (NUMBER, TYPE, BALANCE)><!ATTLIST ACCOUNTacctId IDownedBy IDREFS><!ELEMENT NUMBER (#PCDATA)><!ELEMENT TYPE (#PCDATA)><!ELEMENT BALANCE (#PCDATA)>]>Database Systems: The Complete Array BookSolutions for Chapter 5Solutions for Section 5.2Exercise 5.2.1(a)PI_model( SIGMA_{speed >= 1000} ) (PC)Exercise 5.2.1(f)The trick is to theta-join PC with itself on the condition that the hard disk sizes are equal. That gives us tuples that have two PC model numbers with the same value of hd. However, these two PC's could in fact be the same, so we must also require in the theta-join that the model numbers be unequal. Finally, we want the hard disk sizes, so we project onto hd. The expression is easiest to see if we write it using some temporary values. We start by renaming PC twice so we can talk about two occurrences of the same attributes.R1 = RHO_{PC1} (PC)R2 = RHO_{PC2} (PC)R3 = R1 JOIN_{PC1.hd = PC2.hd AND PC1.model <> PC2.model} R2R4 = PI_{PC1.hd} (R3)Exercise 5.2.1(h)First, we find R1, the model-speed pairs from both PC and Laptop. Then, we find from R1 those computers that are ``fast,'' at least 133Mh. At the same time, we join R1 with Product to connect model numbers to their manufacturers and we project out the speed to get R2. Then we join R2 with itself (after renaming) to find pairs of different models by the same maker. Finally, we get our answer, R5, by projecting onto one of the maker attributes. A sequence of steps giving the desired expression is:R1 = PI_{model,speed} (PC) UNION PI_{model,speed} (Laptop)R2 = PI_{maker,model} (SIGMA_{speed>=700} (R1) JOIN Product)R3 = RHO_{T(maker2, model2)} (R2)R4 = R2 JOIN_{maker = maker2 AND model <> model2} (R3)R5 = PI_{maker} (R4)Exercise 5.2.2Here are figures for the expression trees of Exercise 5.2.1 Part (a)Part (f)Part (h). Note that the third figure is not really a tree, since it uses a common subexpression. We could duplicate the nodes to make it a tree, but using common subexpressions is a valuable form of query optimization. One of the benefits one gets from constructing ``trees'' for queries is the ability to combine nodes that represent common subexpressions.Exercise 5.2.7The relation that results from the natural join has only one attribute from each pair of equated attributes. The theta-join has attributes for both, and their columns are identical.Exercise 5.2.9(a)If all the tuples of R and S are different, then the union has n+m tuples, and this number is the maximum possible.The minimum number of tuples that can appear in the result occurs if every tuple of one relation also appears in the other. Surely the union has at least as many tuples as the larger of R and that is, max(n,m) tuples. However, it is possible for every tuple of the smaller to appear in the other, so it is possible that there are as few as max(n,m) tuples in the union.Exercise 5.2.10In the following we use the name of a relation both as its instance (set of tuples) and as its schema (set of attributes). The context determines uniquely which is meant.PI_R(R JOIN S) Note, however, that this expression works only for sets; it does not preserve the multipicity of tuples in R. The next two expressions work for bags.R JOIN DELTA(PI_{R INTERSECT S}(S)) In this expression, each projection of a tuple from S onto the attributes that are also in R appears exactly once in the second argument of the join, so it preserves multiplicity of tuples in R, except for those that do not join with S, which disappear. The DELTA operator removes duplicates, as described in Section 5.4. R - [R - PI_R(R JOIN S)] Here, the strategy is to find the dangling tuples of R and remove them.Solutions for Section 5.3Exercise 5.3.1As a bag, the value is {700, 1500, 866, 866, 1000, 1300, 1400, 700, 1200, 750, 1100, 350, 733}. The order is unimportant, of course. The average is 959.As a set, the value is {700, 1500, 866, 1000, 1300, 1400, 1200, 750, 1100, 350, 733}, and the average is 967. H3>Exercise 5.3.4(a)As sets, an element x is in the left-side expression(R UNION S) UNION Tif and only if it is in at least one of R, S, and T. Likewise, it is in the right-side expressionR UNION (S UNION T)under exactly the same conditions. Thus, the two expressions have exactly the same members, and the sets are equal.As bags, an element x is in the left-side expression as many times as the sum of the number of times it is in R, S, and T. The same holds for the right side. Thus, as bags the expressions also have the same value.Exercise 5.3.4(h)As sets, element x is in the left sideR UNION (S INTERSECT T)if and only if x is either in R or in both S and T. Element x is in the right side(R UNION S) INTERSECT (R UNION T)if and only if it is in both R UNION S and R UNION T. If x is in R, then it is in both unions. If x is in both S and T, then it is in both union. However, if x is neither in R nor in both of S and T, then it cannot be in both unions. For example, suppose x is not in R and not in S. Then x is not in R UNION S. Thus, the statement of when x is in the right side is exactly the same as when it is in the left side: x is either in R or in both of S and T.Now, consider the expression for bags. Element x is in the left side the sum of the number of times it is in R plus the smaller of the number of times x is in S and the number of times x is in T. Likewise, the number of times x is in the right side is the smaller ofThe sum of the number of times x is in R and in S.The sum of the number of times x is in R and in T.A moment's reflection tells us that this minimum is the sum of the number of times x is in R plus the smaller of the number of times x is in S and in T, exactly as for the left side.Exercise 5.3.5(a)For sets, we observe that element x is in the left side(R INTERSECT S) - Tif and only if it is in both R and S and not in T. The same holds for the right sideR INTERSECT (S-T)so as sets, the equivalence holds.Now suppose we have bags. Let R = {x}, S = {x,x}, and T = {x}. Then R INTERSECT S = {x}, and the left side is {x}-{x}, or EMPTYSET. However, on the right, S-T = {x}, so the right side is {x} INTERSECT {x}, which is {x}.Solutions for Section 5.4Exercise 5.4.1(a){(1,0,1), (5,4,9), (1,0,1), (6,4,16), (7,9,16)}.Exercise 5.4.1(c)。
数据库系统基础学习知识原理与设计(第2版)课后习题集详细规范标准答案

数据库系统原理与设计习题集第一章绪论一、选择题1. DBS是采用了数据库技术的计算机系统,DBS是一个集合体,包含数据库、计算机硬件、软件和()。
A. 系统分析员B. 程序员C. 数据库管理员D. 操作员2. 数据库(DB),数据库系统(DBS)和数据库管理系统(DBMS)之间的关系是()。
A. DBS包括DB和DBMSB. DBMS包括DB和DBSC. DB包括DBS和DBMSD. DBS就是DB,也就是DBMS3. 下面列出的数据库管理技术发展的三个阶段中,没有专门的软件对数据进行管理的是()。
I.人工管理阶段II.文件系统阶段III.数据库阶段A. I 和IIB. 只有IIC. II 和IIID. 只有I4. 下列四项中,不属于数据库系统特点的是()。
A. 数据共享B. 数据完整性C. 数据冗余度高D. 数据独立性高5. 数据库系统的数据独立性体现在()。
A.不会因为数据的变化而影响到应用程序B.不会因为系统数据存储结构与数据逻辑结构的变化而影响应用程序C.不会因为存储策略的变化而影响存储结构D.不会因为某些存储结构的变化而影响其他的存储结构6. 描述数据库全体数据的全局逻辑结构和特性的是()。
A. 模式B. 内模式C. 外模式D. 用户模式7. 要保证数据库的数据独立性,需要修改的是()。
A. 模式与外模式B. 模式与内模式C. 三层之间的两种映射D. 三层模式8. 要保证数据库的逻辑数据独立性,需要修改的是()。
A. 模式与外模式的映射B. 模式与内模式之间的映射C. 模式D. 三层模式9. 用户或应用程序看到的那部分局部逻辑结构和特征的描述是(),它是模式的逻辑子集。
A.模式B. 物理模式C. 子模式D. 内模式10.下述()不是DBA数据库管理员的职责。
A.完整性约束说明B. 定义数据库模式C.数据库安全D. 数据库管理系统设计选择题答案:(1) C (2) A (3) D (4) C (5) B(6) A (7) C (8) A (9) C (10) D二、简答题1.试述数据、数据库、数据库系统、数据库管理系统的概念。
数据库系统基础教程(第二版)课后习题答案

Database Systems: The Complete BookSolutions for Chapter 2Solutions for Section 2.1Exercise 2.1.1The E/R Diagram.Exercise 2.1.8(a)The E/R DiagramKobvxybzSolutions for Section 2.2Exercise 2.2.1The Addresses entity set is nothing but a single address, so we would prefer to make address an attribute of Customers. Were the bank to record several addresses for a customer, then it might make sense to have an Addresses entity set and make Lives-at a many-many relationship.The Acct-Sets entity set is useless. Each customer has a unique account set containing his or her accounts. However, relating customers directly to their accounts in a many-many relationship conveys the same information and eliminates the account-set concept altogether.Solutions for Section 2.3Exercise 2.3.1(a)Keys ssNo and number are appropriate for Customers and Accounts, respectively. Also, we think it does not make sense for an account to be related to zero customers, so we should round the edgeconnecting Owns to Customers. It does not seem inappropriate to have a customer with 0 accounts;they might be a borrower, for example, so we put no constraint on the connection from Owns to Accounts. Here is the The E/R Diagram,showing underlined keys and the numerocity constraint.Exercise 2.3.2(b)If R is many-one from E1 to E2, then two tuples (e1,e2) and (f1,f2) of the relationship set for R must be the same if they agree on the key attributes for E1. To see why, surely e1 and f1 are the same. Because R is many-one from E1 to E2, e2 and f2 must also be the same. Thus, the pairs are the same.Solutions for Section 2.4Exercise 2.4.1Here is the The E/R Diagram.We have omitted attributes other than our choice for the key attributes of Students and Courses. Also omitted are names for the relationships. Attribute grade is not part of the key for Enrollments. The key for Enrollements is studID from Students and dept and number from Courses.Exercise 2.4.4bHere is the The E/R Diagram Again, we have omitted relationship names and attributes other than our choice for the key attributes. The key for Leagues is its own name; this entity set is not weak. The key for Teams is its own name plus the name of the league of which the team is a part, e.g., (Rangers, MLB) or (Rangers, NHL). The key for Players consists of the player's number and the key for the team on which he or she plays. Since the latter key is itself a pair consisting of team and league names, the key for players is the triple (number, teamName, leagueName). e.g., JeffGarcia is (5, 49ers, NFL).Database Systems: The Complete BookSolutions for Chapter 3Solutions for Section 3.1Exercise 3.1.2(a)We can order the three tuples in any of 3! = 6 ways. Also, the columns can be ordered in any of 3! = 6 ways. Thus, the number of presentations is 6*6 = 36.Solutions for Section 3.2Exercise 3.2.1Customers(ssNo, name, address, phone)Flights(number, day, aircraft)Bookings(ssNo, number, day, row, seat)Being a weak entity set, Bookings' relation has the keys for Customers and Flights and Bookings' own attributes.Notice that the relations obtained from the toCust and toFlt relationships are unnecessary. They are:toCust(ssNo, ssNo1, number, day)toFlt(ssNo, number, day, number1, day1)That is, for toCust, the key of Customers is paired with the key for Bookings. Since both include ssNo, this attribute is repeated with two different names, ssNo and ssNo1. A similar situation exists for toFlt.Exercise 3.2.3Ships(name, yearLaunched)SisterOf(name, sisterName)Solutions for Section 3.3Exercise 3.3.1Since Courses is weak, its key is number and the name of its department. We do not havearelation for GivenBy. In part (a), there is a relation for Courses and a relation for LabCourses that has only the key and the computer-allocation attribute. It looks like:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, allocation)For part (b), LabCourses gets all the attributes of Courses, as:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, room, allocation)And for (c), Courses and LabCourses are combined, as:Depts(name, chair)Courses(number, deptName, room, allocation)Exercise 3.3.4(a)There is one relation for each entity set, so the number of relations is e. The relation for the root entity set has a attributes, while the other relations, which must include the key attributes, have a+k attributes.Solutions for Section 3.4Exercise 3.4.2Surely ID is a key by itself. However, we think that the attributes x, y, and z together form another key. The reason is that at no time can two molecules occupy the same point.Exercise 3.4.4The key attributes are indicated by capitalization in the schema below:Customers(SSNO, name, address, phone)Flights(NUMBER, DAY, aircraft)Bookings(SSNO, NUMBER, DAY, row, seat)Exercise 3.4.6(a)The superkeys are any subset that contains A1. Thus, there are 2^{n-1} such subsets, since each of the n-1 attributes A2 through An may independently be chosen in or out.Solutions for Section 3.5Exercise 3.5.1(a)We could try inference rules to deduce new dependencies until we are satisfied we have them all.A more systematic way is to consider the closures of all 15 nonempty sets of attributes.For the single attributes we have A+ = A, B+ = B, C+ = ACD, and D+ = AD. Thus, the only new dependency we get with a single attribute on the left is C->A.Now consider pairs of attributes:AB+ = ABCD, so we get new dependency AB->D. AC+ = ACD, and AC->D is nontrivial. AD+ = AD, so nothing new. BC+ = ABCD, so we get BC->A, and BC->D. BD+ = ABCD, giving usBD->A and BD->C. CD+ = ACD, giving CD->A.For the triples of attributes, ACD+ = ACD, but the closures of the other sets are each ABCD. Thus, we get new dependencies ABC->D, ABD->C, and BCD->A.Since ABCD+ = ABCD, we get no new dependencies.The collection of 11 new dependencies mentioned above is: C->A, AB->D, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.Exercise 3.5.1(b)From the analysis of closures above, we find that AB, BC, and BD are keys. All other sets either do not have ABCD as the closure or contain one of these three sets.Exercise 3.5.1(c)The superkeys are all those that contain one of those three keys. That is, a superkey that is not a key must contain B and more than one of A, C, and D. Thus, the (proper) superkeys are ABC, ABD, BCD, and ABCD.Exercise 3.5.3(a)We must compute the closure of A1A2...AnC. Since A1A2...An->B is a dependency, surely B is in this set, proving A1A2...AnC->B.Exercise 3.5.4(a)Consider the relationThis relation satisfies A->B but does not satisfy B->A.Exercise 3.5.8(a)If all sets of attributes are closed, then there cannot be any nontrivial functional dependencies. For suppose A1A2...An->B is a nontrivial dependency. Then A1A2...An+ contains B and thus A1A2...An is not closed.Exercise 3.5.10(a)We need to compute the closures of all subsets of {ABC}, although there is no need to think about the empty set or the set of all three attributes. Here are the calculations for the remaining six sets: A+ = AB+ = BC+ = ACEAB+ = ABCDEAC+ = ACEBC+ = ABCDEWe ignore D and E, so a basis for the resulting functional dependencies for ABC are: C->A and AB->C. Note that BC->A is true, but follows logically from C->A, and therefore may be omitted from our list.Solutions for Section 3.6Exercise 3.6.1(a)In the solution to Exercise 3.5.1 we found that there are 14 nontrivial dependencies, including the three given ones and 11 derived dependencies. These are: C->A, C->D, D->A, AB->D, AB-> C, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.We also learned that the three keys were AB, BC, and BD. Thus, any dependency above that does not have one of these pairs on the left is a BCNF violation. These are: C->A, C->D, D->A, AC->D, and CD->A.One choice is to decompose using C->D. That gives us ABC and CD as decomposed relations. CD is surely in BCNF, since any two-attribute relation is. ABC is not in BCNF, since AB and BC are its only keys, but C->A is a dependency that holds in ABCD and therefore holds in ABC. We must further decompose ABC into AC and BC. Thus, the three relations of the decomposition are AC, BC, and CD.Since all attributes are in at least one key of ABCD, that relation is already in 3NF, and no decomposition is necessary.Exercise 3.6.1(b)(Revised 1/19/02) The only key is AB. Thus, B->C and B->D are both BCNF violations. The derived FD's BD->C and BC->D are also BCNF violations. However, any other nontrivial, derived FD will have A and B on the left, and therefore will contain a key.One possible BCNF decomposition is AB and BCD. It is obtained starting with any of the four violations mentioned above. AB is the only key for AB, and B is the only key for BCD.Since there is only one key for ABCD, the 3NF violations are the same, and so is the decomposition.Solutions for Section 3.7Exercise 3.7.1Since A->->B, and all the tuples have the same value for attribute A, we can pair the B-value from any tuple with the value of the remaining attribute C from any other tuple. Thus, we know that R must have at least the nine tuples of the form (a,b,c), where b is any of b1, b2, or b3, and c is any of c1, c2, or c3. That is, we can derive, using the definition of a multivalued dependency, that each of the tuples (a,b1,c2), (a,b1,c3), (a,b2,c1), (a,b2,c3), (a,b3,c1), and (a,b3,c2) are also in R.Exercise 3.7.2(a)First, people have unique Social Security numbers and unique birthdates. Thus, we expect the functional dependencies ssNo->name and ssNo->birthdate hold. The same applies to children, so we expect childSSNo->childname and childSSNo->childBirthdate. Finally, an automobile has a unique brand, so we expect autoSerialNo->autoMake.There are two multivalued dependencies that do not follow from these functional dependencies. First, the information about one child of a person is independent of other information about that person. That is, if a person with social security number s has a tuple with cn,cs,cb, then if there isany other tuple t for the same person, there will also be another tuple that agrees with t except that it has cn,cs,cb in its components for the child name, Social Security number, and birthdate. That is the multivalued dependencyssNo->->childSSNo childName childBirthdateSimilarly, an automobile serial number and make are independent of any of the other attributes, so we expect the multivalued dependencyssNo->->autoSerialNo autoMakeThe dependencies are summarized below:ssNo -> name birthdatechildSSNo -> childName childBirthdateautoSerialNo -> autoMakessNo ->-> childSSNo childName childBirthdatessNo ->-> autoSerialNo autoMakeExercise 3.7.2(b)We suggest the relation schemas{ssNo, name, birthdate}{ssNo, childSSNo}{childSSNo, childName childBirthdate}{ssNo, autoSerialNo}{autoSerialNo, autoMake}An initial decomposition based on the two multivalued dependencies would give us {ssNo, name, birthDate}{ssNo, childSSNo, childName, childBirthdate}{ssNo, autoSerialNo, autoMake}Functional dependencies force us to decompose the second and third of these.Exercise 3.7.3(a)Since there are no functional dependencies, the only key is all four attributes, ABCD. Thus, each of the nontrvial multivalued dependencies A->->B and A->->C violate 4NF. We must separate out the attributes of these dependencies, first decomposing into AB and ACD, and then decomposing the latter into AC and AD because A->->C is still a 4NF violation for ACD. The final set of relations are AB, AC, and AD.Exercise 3.7.7(a)Let W be the set of attributes not in X, Y, or Z. Consider two tuples xyzw and xy'z'w' in the relation R in question. Because X ->-> Y, we can swap the y's, so xy'zw and xyz'w' are in R. Because X ->-> Z, we can take the pair of tuples xyzw and xyz'w' and swap Z's to get xyz'w and xyzw'. Similarly, we can take the pair xy'z'w' and xy'zw and swap Z's to get xy'zw' and xy'z'w.In conclusion, we started with tuples xyzw and xy'z'w' and showed that xyzw' and xy'z'w must also be in the relation. That is exactly the statement of the MVD X ->-> Y-union-Z. Note that the above statements all make sense even if there are attributes in common among X, Y, and Z.Exercise 3.7.8(a)Consider a relation R with schema ABCD and the instance with four tuples abcd, abcd', ab'c'd, and ab'c'd'. This instance satisfies the MVD A ->-> BC. However, it does not satisfy A ->-> B. For example, if it did satisfy A ->-> B, then because the instance contains the tuples abcd and ab'c'd, we would expect it to contain abc'd and ab'cd, neither of which is in the instance.Solutions for Chapter 4Solutions for Section 4.2Exercise 4.2.1class Customer {attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account {attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Exercise 4.2.4class Person {attribute string name;relationship Person motherOfinverse Person::childrenOfFemalerelationship Person fatherOfinverse Person::childrenOfMalerelationship Set<Person> childreninverse Person::parentsOfrelationship Set<Person> childrenOfFemaleinverse Person::motherOfrelationship Set<Person> childrenOfMaleinverse Person::fatherOfrelationship Set<Person> parentsOfinverse Person::children}Notice that there are six different relationships here. For example, the inverse of the relationship that connects a person to their (unique) mother is a relationship that connects a mother (i.e., a female person) to the set of her children. That relationship, which we call childrenOfFemale, is different from the children relationship, which connects anyone -- male or female -- to their children.Exercise 4.2.7A relationship R is its own inverse if and only if for every pair (a,b) in R, the pair (b,a) is also in R. In the terminology of set theory, the relation R is ``symmetric.''Solutions for Section 4.3Exercise 4.3.1We think that Social Security number should me the key for Customer, and account number should be the key for Account. Here is the ODL solution with key and extent declarations.class Customer(extent Customers key ssNo){attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account(extent Accounts key number){attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Solutions for Section 4.4Exercise 4.4.1(a)Since the relationship between customers and accounts is many-many, we should create a separate relation from that relationship-pair.Customers(ssNo, name, address, phone)Accounts(number, type, balance)CustAcct(ssNo, number)Exercise 4.4.1(d)Ther is only one attribute, but three pairs of relationships from Person to itself. Since motherOf and fatherOf are many-one, we can store their inverses in the relation for Person. That is, for each person, childrenOfMale and childrenOfFemale will indicate that persons's father and mother. The children relationship is many-many, and requires its own relation. This relation actually turns out to be redundant, in the sense that its tuples can be deduced from the relationships stored with Person. The schema:Persons(name, childrenOfFemale, childrenOfMale)Parent-Child(parent, child)Exercise 4.4.4You get a schema like:Studios(name, address, ownedMovie)Since name -> address is the only FD, the key is {name, ownedMovie}, and the FD has a left side that is not a superkey.Exercise 4.4.5(a,b,c)(a) Struct Card { string rank, string suit };(b) class Hand {attribute Set theHand;};For part (c) we have:Hands(handId, rank, suit)Notice that the class Hand has no key, so we need to create one: handID. Each hand has, in the relation Hands, one tuple for each card in the hand.Exercise 4.4.5(e)Struct PlayerHand { string Player, Hand theHand };class Deal {attribute Set theDeal;}Alternatively, PlayerHand can be defined directly within the declaration of attribute theDeal. Exercise 4.4.5(h)Since keys for Hand and Deal are lacking, a mechanical way to design the database schema is to have one relation connecting deals and player-hand pairs, and another to specify the contents of hands. That is:Deals(dealID, player, handID)Hands(handID, rank, suit)However, if we think about it, we can get rid of handID and connect the deal and the player directly to the player's cards, as:Deals(dealID, player, rank, suit)Exercise 4.4.5(i)First, card is really a pair consisting of a suit and a rank, so we need two attributes in a relation schema to represent cards. However, much more important is the fact that the proposed schema does not distinguish which card is in which hand. Thus, we need another attribute that indicates which hand within the deal a card belongs to, something like:Deals(dealID, handID, rank, suit)Exercise 4.4.6(c)Attribute b is really a bag of (f,g) pairs. Thus, associated with each a-value will be zero or more (f,g) pairs, each of which can occur several times. We shall use an attribute count to indicate the number of occurrences, although if relations allow duplicate tuples we could simply allow duplicate (a,f,g) triples in the relation. The proposed schema is:C(a, f, g, count)Solutions for Section 4.5Exercise 4.5.1(b)Studios(name, address, movies{(title, year, inColor, length,stars{(name, address, birthdate)})})Since the information about a star is repeated once for each of their movies, there is redundancy. To eliminate it, we have to use a separate relation for stars and use pointers from studios. That is: Stars(name, address, birthdate)Studios(name, address, movies{(title, year, inColor, length,stars{*Stars})})Since each movie is owned by one studio, the information about a movie appears in only one tuple of Studios, and there is no redundancy.Exercise 4.5.2Customers(name, address, phone, ssNo, accts{*Accounts})Accounts(number, type, balance, owners{*Customers})Solutions for Section 4.6Exercise 4.6.1(a)We need to add new nodes labeled George Lucas and Gary Kurtz. Then, from the node sw (which represents the movie Star Wars), we add arcs to these two new nodes, labeled directedBy and producedBy, respectively.Exercise 4.6.2Create nodes for each account and each customer. From each customer node is an arc to a node representing the attributes of the customer, e.g., an arc labeled name to the customer's name. Likewise, there is an arc from each account node to each attribute of that account, e.g., an arc labeled balance to the value of the balance.To represent ownership of accounts by customers, we place an arc labeled owns from each customer node to the node of each account that customer holds (possibly jointly). Also, we placean arc labeled ownedBy from each account node to the customer node for each owner of that account.Exercise 4.6.5In the semistructured model, nodes represent data elements, i.e., entities rather than entity sets. In the E/R model, nodes of all types represent schema elements, and the data is not represented at all. Solutions for Section 4.7Exercise 4.7.1(a)<STARS-MOVIES><STAR starId = "cf" starredIn = "sw, esb, rj"><NAME>Carrie Fisher</NAME><ADDRESS><STREET>123 Maple St.</STREET><CITY>Hollywood</CITY></ADDRESS><ADDRESS><STREET>5 Locust Ln.</STREET><CITY>Malibu</CITY></ADDRESS></STAR><STAR starId = "mh" starredIn = "sw, esb, rj"><NAME>Mark Hamill</NAME><ADDRESS><STREET>456 Oak Rd.<STREET><CITY>Brentwood</CITY></ADDRESS></STAR><STAR starId = "hf" starredIn = "sw, esb, rj, wit"><NAME>Harrison Ford</NAME><ADDRESS><STREET>whatever</STREET><CITY>whatever</CITY></ADDRESS></STAR><MOVIE movieId = "sw" starsOf = "cf, mh"><TITLE>Star Wars</TITLE><YEAR>1977</YEAR></MOVIE><MOVIE movieId = "esb" starsOf = "cf, mh"><TITLE>Empire Strikes Back</TITLE><YEAR>1980</YEAR></MOVIE><MOVIE movieId = "rj" starsOf = "cf, mh"><TITLE>Return of the Jedi</TITLE><YEAR>1983</YEAR></MOVIE><MOVIE movieID = "wit" starsOf = "hf"><TITLE>Witness</TITLE><YEAR>1985</YEAR></MOVIE></STARS-MOVIES>Exercise 4.7.2<!DOCTYPE Bank [<!ELEMENT BANK (CUSTOMER* ACCOUNT*)><!ELEMENT CUSTOMER (NAME, ADDRESS, PHONE, SSNO)><!A TTLIST CUSTOMERcustId IDowns IDREFS><!ELEMENT NAME (#PCDATA)><!ELEMENT ADDRESS (#PCDA TA)><!ELEMENT PHONE (#PCDATA)><!ELEMENT SSNO (#PCDA TA)><!ELEMENT ACCOUNT (NUMBER, TYPE, BALANCE)><!A TTLIST ACCOUNTacctId IDownedBy IDREFS><!ELEMENT NUMBER (#PCDA TA)><!ELEMENT TYPE (#PCDA TA)><!ELEMENT BALANCE (#PCDATA)>]>BookSolutions for Chapter 5Solutions for Section 5.2Exercise 5.2.1(a)PI_model( SIGMA_{speed >= 1000} ) (PC)Exercise 5.2.1(f)The trick is to theta-join PC with itself on the condition that the hard disk sizes are equal. That gives us tuples that have two PC model numbers with the same value of hd. However, these two PC's could in fact be the same, so we must also require in the theta-join that the model numbers be unequal. Finally, we want the hard disk sizes, so we project onto hd.The expression is easiest to see if we write it using some temporary values. We start by renaming PC twice so we can talk about two occurrences of the same attributes.R1 = RHO_{PC1} (PC)R2 = RHO_{PC2} (PC)R3 = R1 JOIN_{PC1.hd = PC2.hd AND PC1.model <> PC2.model} R2R4 = PI_{PC1.hd} (R3)Exercise 5.2.1(h)First, we find R1, the model-speed pairs from both PC and Laptop. Then, we find from R1 those computers that are ``fast,'' at least 133Mh. At the same time, we join R1 with Product to connect model numbers to their manufacturers and we project out the speed to get R2. Then we join R2 with itself (after renaming) to find pairs of different models by the same maker. Finally, we get our answer, R5, by projecting onto one of the maker attributes. A sequence of steps giving the desired expression is: R1 = PI_{model,speed} (PC) UNION PI_{model,speed} (Laptop)R2 = PI_{maker,model} (SIGMA_{speed>=700} (R1) JOIN Product)R3 = RHO_{T(maker2, model2)} (R2)R4 = R2 JOIN_{maker = maker2 AND model <> model2} (R3)R5 = PI_{maker} (R4)Exercise 5.2.2Here are figures for the expression trees of Exercise 5.2.1 Part (a)Part (f)Part (h). Note that the third figure is not really a tree, since it uses a common subexpression. We could duplicate the nodes to make it a tree, but using common subexpressions is a valuable form of query optimization. One of the benefits one gets from constructing ``trees'' for queries is the ability to combine nodes that represent common subexpressions.Exercise 5.2.7The relation that results from the natural join has only one attribute from each pair of equated attributes. The theta-join has attributes for both, and their columns are identical.Exercise 5.2.9(a)If all the tuples of R and S are different, then the union has n+m tuples, and this number is the maximum possible.The minimum number of tuples that can appear in the result occurs if every tuple of one relation also appears in the other. Surely the union has at least as many tuples as the larger of R and that is, max(n,m) tuples. However, it is possible for every tuple of the smaller to appear in the other, so it is possible that there are as few as max(n,m) tuples in the union.Exercise 5.2.10In the following we use the name of a relation both as its instance (set of tuples) and as its schema (set of attributes). The context determines uniquely which is meant.PI_R(R JOIN S) Note, however, that this expression works only for sets; it does not preserve the multipicity of tuples in R. The next two expressions work for bags.R JOIN DELTA(PI_{R INTERSECT S}(S)) In this expression, each projection of a tuple from S onto the attributes that are also in R appears exactly once in the second argument of the join, so it preserves multiplicity of tuples in R, except for those thatdo not join with S, which disappear. The DELTA operator removes duplicates, as described in Section 5.4.R - [R - PI_R(R JOIN S)] Here, the strategy is to find the dangling tuples of R and remove them.Solutions for Section 5.3Exercise 5.3.1As a bag, the value is {700, 1500, 866, 866, 1000, 1300, 1400, 700, 1200, 750, 1100, 350, 733}. The order is unimportant, of course. The average is 959.As a set, the value is {700, 1500, 866, 1000, 1300, 1400, 1200, 750, 1100, 350, 733}, and the average is 967. H3>Exercise 5.3.4(a)As sets, an element x is in the left-side expression(R UNION S) UNION Tif and only if it is in at least one of R, S, and T. Likewise, it is in the right-side expressionR UNION (S UNION T)under exactly the same conditions. Thus, the two expressions have exactly the same members, and the sets are equal.As bags, an element x is in the left-side expression as many times as the sum of the number of times it is in R, S, and T. The same holds for the right side. Thus, as bags the expressions also have the same value.Exercise 5.3.4(h)As sets, element x is in the left sideR UNION (S INTERSECT T)if and only if x is either in R or in both S and T. Element x is in the right side(R UNION S) INTERSECT (R UNION T)if and only if it is in both R UNION S and R UNION T. If x is in R, then it is in both unions. If x is in both S and T, then it is in both union. However, if x is neither in R nor in both of S and T, then it cannot be in both unions. For example, suppose x is not in R and not in S. Then x is not in R UNION S. Thus, the statement of when x is in the right side is exactly the same as when it is in the left side: x is either in R or in both of S and T.Now, consider the expression for bags. Element x is in the left side the sum of the number of times it is in R plus the smaller of the number of times x is in S and the number of times x is in T. Likewise, the number of times x is in the right side is the smaller ofThe sum of the number of times x is in R and in S.The sum of the number of times x is in R and in T.A moment's reflection tells us that this minimum is the sum of the number of times x is in R plus the smaller of the number of times x is in S and in T, exactly as for the left side.Exercise 5.3.5(a)For sets, we observe that element x is in the left side(R INTERSECT S) - T。
数据库第二章课后习题解答
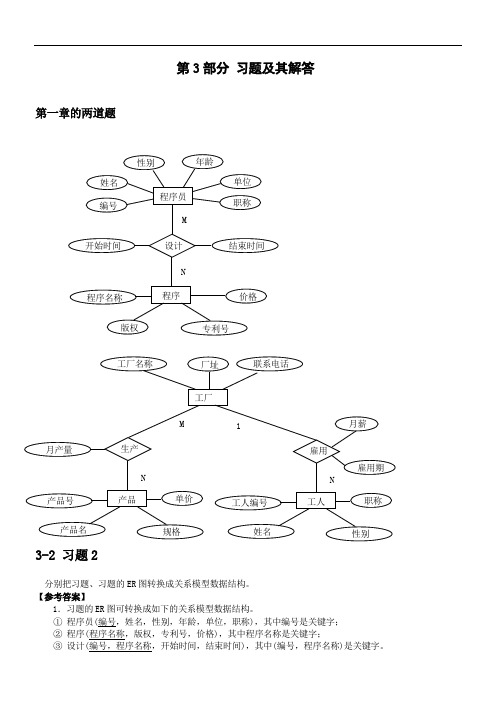
第3部分习题及其解答第一章的两道题3-2 习题2分别把习题、习题的ER图转换成关系模型数据结构。
【参考答案】1.习题的ER图可转换成如下的关系模型数据结构。
①程序员(编号,姓名,性别,年龄,单位,职称),其中编号是关键字;②程序(程序名称,版权,专利号,价格),其中程序名称是关键字;③设计(编号,程序名称,开始时间,结束时间),其中(编号,程序名称)是关键字。
2.习题的ER 图可转换成如下的关系模型数据结构。
① 工厂(工厂名称,厂址,联系电话),其中工厂名称是关键字; ② 产品(产品号,产品名,规格,单价),其中产品号是关键字;③ 工人(工人编号,姓名,性别,职称,工厂名称,雇用期,月薪),其中工人编号是关键字,工厂名称是外关键字,雇用期和月薪是联系属性;④ 生产(工厂名称,产品号,月产量),其中(工厂名称,产品号)是关键字,生产关系是表示联系的。
判断下列情况,分别指出它们具体遵循那一类完整性约束规则1.用户写一条语句明确指定月份数据在1~12之间有效。
2.关系数据库中不允许主键值为空的元组存在。
3.从A 关系的外键出发去找B 关系中的记录,必须能找到。
【解答】1.用户用语句指定月份数据在1~12之间有效,遵循用户定义的完整性约束规则。
2.关系数据库中不允许主键值为空的元组存在,遵循实体完整性约束规则;3.从A 关系的外键出发去找B 关系的记录,必须能找到,遵循引用完整性约束规则。
判断下列情况,分别指出他们是用DML 还是用DDL 来完成下列操作1.创建“学生”表结构。
2.对“学生”表中的学号属性,其数据类型由“整型”修改为“字符型”。
3.把“学生”表中学号“021”修改为“025”。
【解答】1.创建“学生”表结构,即定义一个关系模式,用DDL 完成。
2.修改“学生”表中学号属性的数据类型,即修改关系模式的定义,用DDL 完成。
3.修改“学生”表中学号属性的数据值,即对表中的数据进行操作,用DML 完成。
数据库系统基础教程(第二版)课后习题答案2

Database Systems: The Complete BookSolutions for Chapter 2Solutions for Section 2.1Exercise 2.1.1The E/R Diagram.Exercise 2.1.8(a)The E/R DiagramKobvxybzSolutions for Section 2.2Exercise 2.2.1The Addresses entity set is nothing but a single address, so we would prefer to make address an attribute of Customers. Were the bank to record several addresses for a customer, then it might make sense to have an Addresses entity set and make Lives-at a many-many relationship.The Acct-Sets entity set is useless. Each customer has a unique account set containing his or her accounts. However, relating customers directly to their accounts in a many-many relationship conveys the same information and eliminates the account-set concept altogether.Solutions for Section 2.3Exercise 2.3.1(a)Keys ssNo and number are appropriate for Customers and Accounts, respectively. Also, we think it does not make sense for an account to be related to zero customers, so we should round the edge connecting Owns to Customers. It does not seem inappropriate to have a customer with 0 accounts;they might be a borrower, for example, so we put no constraint on the connection from Owns to Accounts. Here is the The E/R Diagram,showing underlined keys andthe numerocity constraint.Exercise 2.3.2(b)If R is many-one from E1 to E2, then two tuples (e1,e2) and (f1,f2) of the relationship set for R must be the same if they agree on the key attributes for E1. To see why, surely e1 and f1 are the same. Because R is many-one from E1 to E2, e2 and f2 must also be the same. Thus, the pairs are the same.Solutions for Section 2.4Exercise 2.4.1Here is the The E/R Diagram.We have omitted attributes other than our choice for the key attributes of Students and Courses. Also omitted are names for the relationships. Attribute grade is not part of the key for Enrollments. The key for Enrollements is studID from Students and dept and number from Courses.Exercise 2.4.4bHere is the The E/R Diagram Again, we have omitted relationship names and attributes other than our choice for the key attributes. The key for Leagues is its own name; this entity set is not weak. The key for Teams is its own name plus the name of the league of which the team is a part, e.g., (Rangers, MLB) or (Rangers, NHL). The key for Players consists of the player's number and the key for the team on which he or she plays. Since the latter key is itself a pair consisting of team and league names, the key for players is the triple (number, teamName, leagueName). e.g., JeffGarcia is (5, 49ers, NFL).Database Systems: The Complete BookSolutions for Chapter 3Solutions for Section 3.1Exercise 3.1.2(a)We can order the three tuples in any of 3! = 6 ways. Also, the columns can be ordered in any of 3! = 6 ways. Thus, the number of presentations is 6*6 = 36.Solutions for Section 3.2Exercise 3.2.1Customers(ssNo, name, address, phone)Flights(number, day, aircraft)Bookings(ssNo, number, day, row, seat)Being a weak entity set, Bookings' relation has the keys for Customers and Flights and Bookings' own attributes.Notice that the relations obtained from the toCust and toFlt relationships are unnecessary. They are:toCust(ssNo, ssNo1, number, day)toFlt(ssNo, number, day, number1, day1)That is, for toCust, the key of Customers is paired with the key for Bookings. Since both include ssNo, this attribute is repeated with two different names, ssNo and ssNo1. A similar situation exists for toFlt.Exercise 3.2.3Ships(name, yearLaunched)SisterOf(name, sisterName)Solutions for Section 3.3Exercise 3.3.1Since Courses is weak, its key is number and the name of its department. We do not have arelation for GivenBy. In part (a), there is a relation for Courses and a relation for LabCourses that has only the key and the computer-allocation attribute. It looks like:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, allocation)For part (b), LabCourses gets all the attributes of Courses, as:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, room, allocation)And for (c), Courses and LabCourses are combined, as:Depts(name, chair)Courses(number, deptName, room, allocation)Exercise 3.3.4(a)There is one relation for each entity set, so the number of relations is e. The relation for the root entity set has a attributes, while the other relations, which must include the key attributes, have a+k attributes.Solutions for Section 3.4Exercise 3.4.2Surely ID is a key by itself. However, we think that the attributes x, y, and z together form another key. The reason is that at no time can two molecules occupy the same point.Exercise 3.4.4The key attributes are indicated by capitalization in the schema below:Customers(SSNO, name, address, phone)Flights(NUMBER, DAY, aircraft)Bookings(SSNO, NUMBER, DAY, row, seat)Exercise 3.4.6(a)The superkeys are any subset that contains A1. Thus, there are 2^{n-1} such subsets, since each of the n-1 attributes A2 through An may independently be chosen in or out.Solutions for Section 3.5Exercise 3.5.1(a)We could try inference rules to deduce new dependencies until we are satisfied we have them all.A more systematic way is to consider the closures of all 15 nonempty sets of attributes.For the single attributes we have A+ = A, B+ = B, C+ = ACD, and D+ = AD. Thus, the only new dependency we get with a single attribute on the left is C->A.Now consider pairs of attributes:AB+ = ABCD, so we get new dependency AB->D. AC+ = ACD, and AC->D is nontrivial. AD+ = AD, so nothing new. BC+ = ABCD, so we get BC->A, and BC->D. BD+ = ABCD, giving usBD->A and BD->C. CD+ = ACD, giving CD->A.For the triples of attributes, ACD+ = ACD, but the closures of the other sets are each ABCD. Thus, we get new dependencies ABC->D, ABD->C, and BCD->A.Since ABCD+ = ABCD, we get no new dependencies.The collection of 11 new dependencies mentioned above is: C->A, AB->D, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.Exercise 3.5.1(b)From the analysis of closures above, we find that AB, BC, and BD are keys. All other sets either do not have ABCD as the closure or contain one of these three sets.Exercise 3.5.1(c)The superkeys are all those that contain one of those three keys. That is, a superkey that is not a key must contain B and more than one of A, C, and D. Thus, the (proper) superkeys are ABC, ABD, BCD, and ABCD.Exercise 3.5.3(a)We must compute the closure of A1A2...AnC. Since A1A2...An->B is a dependency, surely B is in this set, proving A1A2...AnC->B.Exercise 3.5.4(a)Consider the relationThis relation satisfies A->B but does not satisfy B->A.Exercise 3.5.8(a)If all sets of attributes are closed, then there cannot be any nontrivial functional dependenc ies. For suppose A1A2...An->B is a nontrivial dependency. Then A1A2...An+ contains B and thus A1A2...An is not closed.Exercise 3.5.10(a)We need to compute the closures of all subsets of {ABC}, although there is no need to think about the empty set or the set of all three attributes. Here are the calculations for the remaining six sets: A+ = AB+ = BC+ = ACEAB+ = ABCDEAC+ = ACEBC+ = ABCDEWe ignore D and E, so a basis for the resulting functional dependencies for ABC are: C->A and AB->C. Note that BC->A is true, but follows logically from C->A, and therefore may be omitted from our list.Solutions for Section 3.6Exercise 3.6.1(a)In the solution to Exercise 3.5.1 we found that there are 14 nontrivial dependencies, including the three given ones and 11 derived dependencies. These are: C->A, C->D, D->A, AB->D, AB-> C, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.We also learned that the three keys were AB, BC, and BD. Thus, any dependency above that does not have one of these pairs on the left is a BCNF violation. These are: C->A, C->D, D->A, AC->D, and CD->A.One choice is to decompose using C->D. That gives us ABC and CD as decomposed relations. CD is surely in BCNF, since any two-attribute relation is. ABC is not in BCNF, since AB and BC are its only keys, but C->A is a dependency that holds in ABCD and therefore holds in ABC. We must further decompose ABC into AC and BC. Thus, the three relations of the decomposition are AC, BC, and CD.Since all attributes are in at least one key of ABCD, that relation is already in 3NF, and no decomposition is necessary.Exercise 3.6.1(b)(Revised 1/19/02) The only key is AB. Thus, B->C and B->D are both BCNF violations. The derived FD's BD->C and BC->D are also BCNF violations. However, any other nontrivial, derived FD will have A and B on the left, and therefore will contain a key.One possible BCNF decomposition is AB and BCD. It is obtained starting with any of the four violations mentioned above. AB is the only key for AB, and B is the only key for BCD.Since there is only one key for ABCD, the 3NF violations are the same, and so is the decomposition.Solutions for Section 3.7Exercise 3.7.1Since A->->B, and all the tuples have the same value for attribute A, we can pair the B-value from any tuple with the value of the remaining attribute C from any other tuple. Thus, we know that R must have at least the nine tuples of the form (a,b,c), where b is any of b1, b2, or b3, and c is any of c1, c2, or c3. That is, we can derive, using the definition of a multivalued dependency, that each of the tuples (a,b1,c2), (a,b1,c3), (a,b2,c1), (a,b2,c3), (a,b3,c1), and (a,b3,c2) are also in R.Exercise 3.7.2(a)First, people have unique Social Security numbers and unique birthdates. Thus, we expect the functional dependencies ssNo->name and ssNo->birthdate hold. The same applies to children, so we expect childSSNo->childname and childSSNo->childBirthdate. Finally, an automobile has a unique brand, so we expect autoSerialNo->autoMake.There are two multivalued dependencies that do not follow from these functional dependencies. First, the information about one child of a person is independent of other information about that person. That is, if a person with social security number s has a tuple with cn,cs,cb, then if there isany other tuple t for the same person, there will also be another tuple that agrees with t except that it has cn,cs,cb in its components for the child name, Social Security number, and birthdate. That is the multivalued dependencyssNo->->childSSNo childName childBirthdateSimilarly, an automobile serial number and make are independent of any of the other attributes, so we expect the multivalued dependencyssNo->->autoSerialNo autoMakeThe dependencies are summarized below:ssNo -> name birthdatechildSSNo -> childName childBirthdateautoSerialNo -> autoMakessNo ->-> childSSNo childName childBirthdatessNo ->-> autoSerialNo autoMakeExercise 3.7.2(b)We suggest the relation schemas{ssNo, name, birthdate}{ssNo, childSSNo}{childSSNo, childName childBirthdate}{ssNo, autoSerialNo}{autoSerialNo, autoMake}An initial decomposition based on the two multivalued dependencies would give us {ssNo, name, birthDate}{ssNo, childSSNo, childName, childBirthdate}{ssNo, autoSerialNo, autoMake}Functional dependencies force us to decompose the second and third of these.Exercise 3.7.3(a)Since there are no functional dependencies, the only key is all four attributes, ABCD. Thus, each of the nontrvial multivalued dependencies A->->B and A->->C violate 4NF. We must separate out the attributes of these dependencies, first decomposing into AB and ACD, and then decomposing the latter into AC and AD because A->->C is still a 4NF violation for ACD. The final set of relations are AB, AC, and AD.Exercise 3.7.7(a)Let W be the set of attributes not in X, Y, or Z. Consider two tuples xyzw and xy'z'w' in the relation R in question. Because X ->-> Y, we can swap the y's, so xy'zw and xyz'w' are in R. Because X ->-> Z, we can take the pair of tuples xyzw and xyz'w' and swap Z's to get xyz'w and xyzw'. Similarly, we can take the pair xy'z'w' and xy'zw and swap Z's to get xy'zw' and xy'z'w.In conclusion, we started with tuples xyzw and xy'z'w' and showed that xyzw' and xy'z'w must also be in the relation. That is exactly the statement of the MVD X ->-> Y-union-Z. Note that the above statements all make sense even if there are attributes in common among X, Y, and Z.Exercise 3.7.8(a)Consider a relation R with schema ABCD and the instance with four tuples abcd, abcd', ab'c'd, and ab'c'd'. This instance satisfies the MVD A->-> BC. However, it does not satisfy A->-> B. For example, if it did satisfy A->-> B, then because the instance contains the tuples abcd and ab'c'd, we would expect it to contain abc'd and ab'cd, neither of which is in the instance.Database Systems: The Complete BookSolutions for Chapter 4Solutions for Section 4.2Exercise 4.2.1class Customer {attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account {attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Exercise 4.2.4class Person {attribute string name;relationship Person motherOfinverse Person::childrenOfFemalerelationship Person fatherOfinverse Person::childrenOfMalerelationship Set<Person> childreninverse Person::parentsOfrelationship Set<Person> childrenOfFemaleinverse Person::motherOfrelationship Set<Person> childrenOfMaleinverse Person::fatherOfrelationship Set<Person> parentsOfinverse Person::children}Notice that there are six different relationships here. For example, the inverse of the relationship that connects a person to their (unique) mother is a relationship that connects a mother (i.e., a female person) to the set of her children. That relationship, which we call childrenOfFemale, is different from the children relationship, which connects anyone -- male or female -- to their children.Exercise 4.2.7A relationship R is its own inverse if and only if for every pair (a,b) in R, the pair (b,a) is also in R. In the terminology of set theory, the relation R is ``symmetric.''Solutions for Section 4.3Exercise 4.3.1We think that Social Security number should me the key for Customer, and account number should be the key for Account. Here is the ODL solution with key and extent declarations.class Customer(extent Customers key ssNo){attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account(extent Accounts key number){attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Solutions for Section 4.4Exercise 4.4.1(a)Since the relationship between customers and accounts is many-many, we should create a separate relation from that relationship-pair.Customers(ssNo, name, address, phone)Accounts(number, type, balance)CustAcct(ssNo, number)Exercise 4.4.1(d)Ther is only one attribute, but three pairs of relationships from Person to itself. Since motherOf and fatherOf are many-one, we can store their inverses in the relation for Person. That is, for each person, childrenOfMale and childrenOfFemale will indicate that persons's father and mother. The children relationship is many-many, and requires its own relation. This relation actually turns out to be redundant, in the sense that its tuples can be deduced from the relationships stored with Person. The schema:Persons(name, childrenOfFemale, childrenOfMale)Parent-Child(parent, child)Exercise 4.4.4Y ou get a schema like:Studios(name, address, ownedMovie)Since name -> address is the only FD, the key is {name, ownedMovie}, and the FD has a left side that is not a superkey.Exercise 4.4.5(a,b,c)(a) Struct Card { string rank, string suit };(b) class Hand {attribute Set theHand;};For part (c) we have:Hands(handId, rank, suit)Notice that the class Hand has no key, so we need to create one: handID. Each hand has, in the relation Hands, one tuple for each card in the hand.Exercise 4.4.5(e)Struct PlayerHand { string Player, Hand theHand };class Deal {attribute Set theDeal;}Alternatively, PlayerHand can be defined directly within the declaration of attribute theDeal. Exercise 4.4.5(h)Since keys for Hand and Deal are lacking, a mechanical way to design the database schema is to have one relation connecting deals and player-hand pairs, and another to specify the contents of hands. That is:Deals(dealID, player, handID)Hands(handID, rank, suit)However, if we think about it, we can get rid of handID and connect the deal and the player directly to the player's cards, as:Deals(dealID, player, rank, suit)Exercise 4.4.5(i)First, card is really a pair consisting of a suit and a rank, so we need two attributes in a relation schema to represent cards. However, much more important is the fact that the proposed schema does not distinguish which card is in which hand. Thus, we need another attribute that indicates which hand within the deal a card belongs to, something like:Deals(dealID, handID, rank, suit)Exercise 4.4.6(c)Attribute b is really a bag of (f,g) pairs. Thus, associated with each a-value will be zero or more (f,g) pairs, each of which can occur several times. We shall use an attribute count to indicate the number of occurrences, although if relations allow duplicate tuples we could simply allow duplicate (a,f,g) triples in the relation. The proposed schema is:C(a, f, g, count)Solutions for Section 4.5Exercise 4.5.1(b)Studios(name, address, movies{(title, year, inColor, length,stars{(name, address, birthdate)})})Since the information about a star is repeated once for each of their movies, there is redundancy. To eliminate it, we have to use a separate relation for stars and use pointers from studios. That is: Stars(name, address, birthdate)Studios(name, address, movies{(title, year, inColor, length,stars{*Stars})})Since each movie is owned by one studio, the information about a movie appears in only one tuple of Studios, and there is no redundancy.Exercise 4.5.2Customers(name, address, phone, ssNo, accts{*Accounts})Accounts(number, type, balance, owners{*Customers})Solutions for Section 4.6Exercise 4.6.1(a)We need to add new nodes labeled George Lucas and Gary Kurtz. Then, from the node sw (which represents the movie Star Wars), we add arcs to these two new nodes, labeled direc tedBy and producedBy, respectively.Exercise 4.6.2Create nodes for each account and each customer. From each customer node is an arc to a node representing the attributes of the customer, e.g., an arc labeled name to the customer's name. Likewise, there is an arc from each account node to each attribute of that account, e.g., an arc labeled balance to the value of the balance.To represent ownership of accounts by customers, we place an arc labeled owns from each customer node to the node of each account that customer holds (possibly jointly). Also, we placean arc labeled ownedBy from each account node to the customer node for each owner of that account.Exercise 4.6.5In the semistructured model, nodes represent data elements, i.e., entities rather than entity sets. In the E/R model, nodes of all types represent schema elements, and the data is not represented at all. Solutions for Section 4.7Exercise 4.7.1(a)<STARS-MOVIES><STAR starId = "cf" starredIn = "sw, esb, rj"><NAME>Carrie Fisher</NAME><ADDRESS><STREET>123 Maple St.</STREET><CITY>Hollywood</CITY></ADDRESS><ADDRESS><STREET>5 Locust Ln.</STREET><CITY>Malibu</CITY></ADDRESS></STAR><STAR starId = "mh" starredIn = "sw, esb, rj"><NAME>Mark Hamill</NAME><ADDRESS><STREET>456 Oak Rd.<STREET><CITY>Brentwood</CITY></ADDRESS></STAR><STAR starId = "hf" starredIn = "sw, esb, rj, wit"><NAME>Harrison Ford</NAME><ADDRESS><STREET>whatever</STREET><CITY>whatever</CITY></ADDRESS></STAR><MOVIE movieId = "sw" starsOf = "cf, mh"><TITLE>Star Wars</TITLE><YEAR>1977</YEAR></MOVIE><MOVIE movieId = "esb" starsOf = "cf, mh"><TITLE>Empire Strikes Back</TITLE><YEAR>1980</YEAR></MOVIE><MOVIE movieId = "rj" starsOf = "cf, mh"><TITLE>Return of the Jedi</TITLE><YEAR>1983</YEAR></MOVIE><MOVIE movieID = "wit" starsOf = "hf"><TITLE>Witness</TITLE><YEAR>1985</YEAR></MOVIE></STARS-MOVIES>Exercise 4.7.2<!DOCTYPE Bank [<!ELEMENT BANK (CUSTOMER* ACCOUNT*)><!ELEMENT CUSTOMER (NAME, ADDRESS, PHONE, SSNO)> <!A TTLIST CUSTOMERcustId IDowns IDREFS><!ELEMENT NAME (#PCDA TA)><!ELEMENT ADDRESS (#PCDA TA)><!ELEMENT PHONE (#PCDA TA)><!ELEMENT SSNO (#PCDA TA)><!ELEMENT ACCOUNT (NUMBER, TYPE, BALANCE)><!A TTLIST ACCOUNTacctId IDownedBy IDREFS><!ELEMENT NUMBER (#PCDA TA)><!ELEMENT TYPE (#PCDA TA)><!ELEMENT BALANCE (#PCDA TA)>]>Database Systems: The CompleteBookSolutions for Chapter 5Solutions for Section 5.2Exercise 5.2.1(a)PI_model( SIGMA_{speed >= 1000} ) (PC)Exercise 5.2.1(f)The trick is to theta-join PC with itself on the condition that the hard disk sizes are equal. That gives us tuples that have two PC model numbers with the same value of hd. However, these two PC's could in fact be the same, so we must also require in the theta-join that the model numbers be unequal. Finally, we want the hard disk sizes, so we project onto hd.The expression is easiest to see if we write it using some temporary values. We start by renaming PC twice so we can talk about two occurrences of the same attributes.R1 = RHO_{PC1} (PC)R2 = RHO_{PC2} (PC)R3 = R1 JOIN_{PC1.hd = PC2.hd AND PC1.model <> PC2.model} R2R4 = PI_{PC1.hd} (R3)Exercise 5.2.1(h)First, we find R1, the model-speed pairs from both PC and Laptop. Then, we find from R1 those computers that are ``fast,'' at least 133Mh. At the same time, we join R1 with Product to connect model numbers to their manufacturers and we project out the speed to get R2. Then we join R2 with itself (after renaming) to find pairs of different models by the same maker. Finally, we get our answer, R5, by projecting onto one of the maker attributes. A sequence of steps giving the desired expression is: R1 = PI_{model,speed} (PC) UNION PI_{model,speed} (Laptop)R2 = PI_{maker,model} (SIGMA_{speed>=700} (R1) JOIN Product)R3 = RHO_{T(maker2, model2)} (R2)R4 = R2 JOIN_{maker = maker2 AND model <> model2} (R3)R5 = PI_{maker} (R4)Exercise 5.2.2Here are figures for the expression trees of Exercise 5.2.1 Part (a)Part (f)Part (h). Note that the third figure is not really a tree, since it uses a common subexpression. We could duplicate the nodes to make it a tree, but using common subexpressions is a valuable form of query optimization. One of the benefits one gets from constructing ``trees'' for queries is the ability to combine nodes that represent common subexpressions.Exercise 5.2.7The relation that results from the natural join has only one attribute from each pair of equated attributes. The theta-join has attributes for both, and their columns are identical.Exercise 5.2.9(a)If all the tuples of R and S are different, then the union has n+m tuples, and this number is the maximum possible.The minimum number of tuples that can appear in the result occurs if every tuple of one relation also appears in the other. Surely the union has at least as many tuples as the larger of R and that is, max(n,m) tuples. However, it is possible for every tuple of the smaller to appear in the other, so it is possible that there are as few as max(n,m) tuples in the union.Exercise 5.2.10In the following we use the name of a relation both as its instance (set of tuples) and as its schema (set of attributes). The context determines uniquely which is meant.PI_R(R JOIN S) Note, however, that this expression works only for sets; it does not preserve the multipicity of tuples in R. The next two expressions work for bags.R JOIN DELTA(PI_{R INTERSECT S}(S)) In this expression, each projection of a tuple from S onto the attributes that are also in R appears exactly once in the second argument of the join, so it preserves multiplicity of tuples in R, except for those thatdo not join with S, which disappear. The DELTA operator removes duplicates, as described in Section 5.4.R - [R - PI_R(R JOIN S)] Here, the strategy is to find the dangling tuples of R and remove them.Solutions for Section 5.3Exercise 5.3.1As a bag, the value is {700, 1500, 866, 866, 1000, 1300, 1400, 700, 1200, 750, 1100, 350, 733}. The order is unimportant, of course. The average is 959.As a set, the value is {700, 1500, 866, 1000, 1300, 1400, 1200, 750, 1100, 350, 733}, and the average is 967. H3>Exercise 5.3.4(a)As sets, an element x is in the left-side expression(R UNION S) UNION Tif and only if it is in at least one of R, S, and T. Likewise, it is in the right-side expressionR UNION (S UNION T)under exactly the same conditions. Thus, the two expressions have exactly the same members, and the sets are equal.As bags, an element x is in the left-side expression as many times as the sum of the number of times it is in R, S, and T. The same holds for the right side. Thus, as bags the expressions also have the same value.Exercise 5.3.4(h)As sets, element x is in the left sideR UNION (S INTERSECT T)if and only if x is either in R or in both S and T. Element x is in the right side(R UNION S) INTERSECT (R UNION T)if and only if it is in both R UNION S and R UNION T. If x is in R, then it is in both unions. If x is in both S and T, then it is in both union. However, if x is neither in R nor in both of S and T, then it cannot be in both unions. For example, suppose x is not in R and not in S. Then x is not in R UNION S. Thus, the statement of when x is in the right side is exactly the same as when it is in the left side: x is either in R or in both of S and T.Now, consider the expression for bags. Element x is in the left side the sum of the number of times it is in R plus the smaller of the number of times x is in S and the number of times x is in T. Likewise, the number of times x is in the right side is the smaller ofThe sum of the number of times x is in R and in S.The sum of the number of times x is in R and in T.A moment's reflection tells us that this minimum is the sum of the number of times x is in R plus the smaller of the number of times x is in S and in T, exactly as for the left side.Exercise 5.3.5(a)For sets, we observe that element x is in the left side(R INTERSECT S) - T。
(完整版)数据库系统基础教程第二章答案解析

For relation Accounts, the attributes are:acctNo, type, balanceFor relation Customers, the attributes are:firstName, lastName, idNo, accountExercise 2.2.1bFor relation Accounts, the tuples are:(12345, savings, 12000),(23456, checking, 1000),(34567, savings, 25)For relation Customers, the tuples are:(Robbie, Banks, 901-222, 12345),(Lena, Hand, 805-333, 12345),(Lena, Hand, 805-333, 23456)Exercise 2.2.1cFor relation Accounts and the first tuple, the components are:123456 → acctNosavings → type12000 → balanceFor relation Customers and the first tuple, the components are:Robbie → firstNameBanks → lastName901-222 → idNo12345 → accountExercise 2.2.1dFor relation Accounts, a relation schema is:Accounts(acctNo, type, balance)For relation Customers, a relation schema is:Customers(firstName, lastName, idNo, account) Exercise 2.2.1eAn example database schema is:Accounts (acctNo,type,balance)Customers (firstName,lastName,idNo,account)A suitable domain for each attribute:acctNo → Integertype → Stringbalance → IntegerfirstName → StringlastName → StringidNo → String (because there is a hyphen we cannot use Integer)account → IntegerExercise 2.2.1gAnother equivalent way to present the Account relation:Another equivalent way to present the Customers relation:Exercise 2.2.2Examples of attributes that are created for primarily serving as keys in a relation:Universal Product Code (UPC) used widely in United States and Canada to track products in stores.Serial Numbers on a wide variety of products to allow the manufacturer to individually track each product.Vehicle Identification Numbers (VIN), a unique serial number used by the automotive industry to identify vehicles.Exercise 2.2.3aWe can order the three tuples in any of 3! = 6 ways. Also, the columns can be ordered in any of 3! = 6 ways. Thus, the number of presentations is 6*6 = 36.Exercise 2.2.3bWe can order the three tuples in any of 5! = 120 ways. Also, the columns can be ordered in any of 4! = 24 ways. Thus, the number of presentations is 120*24 = 2880Exercise 2.2.3cWe can order the three tuples in any of m! ways. Also, the columns can be ordered in any of n! ways. Thus, the number of presentations is n!m!Exercise 2.3.1aCREATE TABLE Product (maker CHAR(30),model CHAR(10) PRIMARY KEY,type CHAR(15));CREATE TABLE PC (model CHAR(30),speed DECIMAL(4,2),ram INTEGER,hd INTEGER,price DECIMAL(7,2));Exercise 2.3.1cCREATE TABLE Laptop (model CHAR(30),speed DECIMAL(4,2),ram INTEGER,hd INTEGER,screen DECIMAL(3,1),price DECIMAL(7,2));Exercise 2.3.1dCREATE TABLE Printer (model CHAR(30),color BOOLEAN,type CHAR (10),price DECIMAL(7,2));Exercise 2.3.1eALTER TABLE Printer DROP color;Exercise 2.3.1fALTER TABLE Laptop ADD od CHAR (10) DEFAULT ‘none’; Exercise 2.3.2aCREATE TABLE Classes (class CHAR(20),type CHAR(5),country CHAR(20),numGuns INTEGER,bore DECIMAL(3,1),displacement INTEGER);Exercise 2.3.2bCREATE TABLE Ships (name CHAR(30),class CHAR(20),launched INTEGER);Exercise 2.3.2cCREATE TABLE Battles (name CHAR(30),date DATE);Exercise 2.3.2dCREATE TABLE Outcomes (ship CHAR(30),battle CHAR(30),result CHAR(10));Exercise 2.3.2eALTER TABLE Classes DROP bore;Exercise 2.3.2fALTER TABLE Ships ADD yard CHAR(30); Exercise 2.4.1aR1 := σspeed ≥ 3.00 (PC)R2 := πmodel(R1)model100510061013Exercise 2.4.1bR1 := σhd ≥ 100 (Laptop)R2 := Product (R1)R3 := πmaker (R2)makerEABFGExercise 2.4.1cR1 := σmaker=B (Product PC)R2 := σmaker=B (Product Laptop)R3 := σmaker=B (Product Printer)R4 := πmodel,price (R1)R5 := πmodel,price (R2)R6: = πmodel,price (R3)R7 := R4 R5 R6model price1004 6491005 6301006 10492007 1429Exercise 2.4.1dR1 := σcolor = true AND type = laser (Printer)R2 := πmodel (R1)model30033007Exercise 2.4.1eR1 := σtype=laptop (Product)R2 := σtype=PC(Product)R3 := πmaker(R1)R4 := πmaker(R2)R5 := R3 – R4Exercise 2.4.1fR1 := ρPC1(PC)R2 := ρPC2(PC)R3 := R1 (PC1.hd = PC2.hd AND PC1.model <> PC2.model) R2R4 := πhd(R3)Exercise 2.4.1gR1 := ρPC1(PC)R2 := ρPC2(PC)R3 := R1 (PC1.speed = PC2.speed AND PC1.ram = PC2.ram AND PC1.model < PC2.model) R2R4 := πPC1.model,PC2.model(R3)Exercise 2.4.1hR1 := πmodel(σspeed ≥ 2.80(PC)) πmodel(σspeed ≥ 2.80(Laptop))R2 := πmaker,model(R1 Product)R3 := ρR3(maker2,model2)(R2)R4 := R2 (maker = maker2 AND model <> model2) R3R5 := πmaker(R4)Exercise 2.4.1iR1 := πmodel,speed(PC)R2 := πmodel,speed(Laptop)R3 := R1 R2R4 := ρR4(model2,speed2)(R3)R5 := πmodel,speed (R3 (speed < speed2 ) R4)R6 := R3 – R5makerBExercise 2.4.1jR1 := πmaker,speed(Product PC)R2 := ρR2(maker2,speed2)(R1)R3 := ρR3(maker3,speed3)(R1)R4 := R1 (maker = maker2 AND speed <> speed2) R2R5 := R4 (maker3 = maker AND speed3 <> speed2 AND speed3 <> speed) R3R6 := πmaker(R5)makerFGhd25080160PC1.model PC2.model1004 1012makerBEmakerADEExercise 2.4.1kR1 := πmaker,model(Product PC)R2 := ρR2(maker2,model2)(R1)R3 := ρR3(maker3,model3)(R1)R4 := ρR4(maker4,model4)(R1)R5 := R1 (maker = maker2 AND model <> model2) R2R6 := R3 (maker3 = maker AND model3 <> model2 AND model3 <> model) R5R7 := R4 (maker4 = maker AND (model4=model OR model4=model2 OR model4=model3)) R6R8 := πmaker(R7)makerABDEExercise 2.4.2aπmodelσspeed≥3.00PCExercise 2.4.2bπmakerσhd ≥ 100 ProductLaptopExercise 2.4.2cσmaker=B πmodel,priceσmaker=B πmodel,price σmaker=Bπmodel,priceProduct PC Laptop Printer ProductProductExercise 2.4.2dPrinter σcolor = true AND type = laserπmodelExercise 2.4.2e σtype=laptop σtype=PC πmakerπmaker –Product ProductExercise 2.4.2fρPC1ρPC2 (PC1.hd = PC2.hd AND PC1.model <> PC2.model)πhdPC PCExercise 2.4.2gρPC1ρPC2PC PC(PC1.speed = PC2.speed AND PC1.ram = PC2.ram AND PC1.model < PC2.model)πPC1.model,PC2.modelExercise 2.4.2hPC Laptop σspeed ≥ 2.80σspeed ≥ 2.80πmodelπmodel πmaker,modelρR3(maker2,model2)(maker = maker2 AND model <> model2)makerExercise 2.4.2iPCLaptopProductπmodel,speed πmodel,speed ρR4(model2,speed2)πmodel,speed(speed < speed2 )–makerExercise 2.4.2jProduct PC πmaker,speed ρR3(maker3,speed3)ρR2(maker2,speed2)(maker = maker2 AND speed <> speed2)(maker3 = maker AND speed3 <> speed2 AND speed3 <> speed)πmakerExercise 2.4.2kπmaker(maker4 = maker AND (model4=model OR model4=model2 OR model4=model3)) (maker3 = maker AND model3 <> model2 AND model3 <> model)(maker = maker2 AND model <> model2)ρR2(maker2,model2)ρR3(maker3,model3)ρR4(maker4,model4)πmaker,modelProduct PCExercise 2.4.3aR1 := σbore ≥ 16 (Classes)R2 := πclass,country (R1)Exercise 2.4.3bR1 := σlaunched < 1921 (Ships)R2 := πname (R1)KirishimaKongoRamilliesRenownRepulseResolutionRevengeRoyal OakRoyal SovereignTennesseeExercise 2.4.3cR1 := σbattle=Denmark Strait AND result=sunk(Outcomes)R2 := πship (R1)shipBismarckHoodExercise 2.4.3dR1 := Classes ShipsR2 := σlaunched > 1921 AND displacement > 35000 (R1)R3 := πname (R2)nameIowaMissouriMusashiNew JerseyNorth CarolinaWashingtonWisconsinYamatoExercise 2.4.3eR1 := σbattle=Guadalcanal(Outcomes)R2 := Ships (ship=name) R1R3 := Classes R2R4 := πname,displacement,numGuns(R3)name displacement numGuns Kirishima 32000 8Washington 37000 9Exercise 2.4.3fR1 := πname(Ships)R2 := πship(Outcomes)R3 := ρR3(name)(R2)R4 := R1 R3nameCaliforniaHarunaHieiIowaKirishimaKongoMissouriMusashiNew JerseyExercise 2.4.3gFrom 2.3.2, assuming that every class has one ship named after the class.R1 := πclass (Classes) R2 := πclass (σname <> class (Ships)) R3 := R1 – R2Exercise 2.4.3hR1 := πcountry (σtype=bb (Classes)) R2 := πcountry (σtype=bc (Classes)) R3 := R1 ∩ R2Exercise 2.4.3iR1 := πship,result,date (Battles (battle=name) Outcomes)R2 := ρR2(ship2,result2,date2)(R1)R3 := R1 (ship=ship2 AND result=damaged AND date < date2) R2R4 := πship (R3)No results from sample data.Exercise 2.4.4aσbore ≥ 16πclass,countryClassesExercise 2.4.4bNorth Carolina Ramillies Renown Repulse Resolution Revenge Royal Oak Royal Sovereign Tennessee Washington Wisconsin Yamato Arizona Bismarck Duke of York Fuso Hood King George V Prince of Wales Rodney Scharnhorst South Dakota West Virginia Yamashiro class Bismarck country Japan Gt. Britainπnameσlaunched < 1921ShipsExercise 2.4.4cπshipσbattle=Denmark Strait AND result=sunkOutcomesExercise 2.4.4dπnameσlaunched > 1921 AND displacement > 35000Classes Ships Exercise 2.4.4eσbattle=Guadalcanal Outcomes Ships(ship=name)πname,displacement,numGunsExercise 2.4.4f Ships Outcomesπnameπship ρR3(name)Exercise 2.4.4g Classes Shipsπclass σname <> class πclass–Exercise 2.4.4hClasses Classesσtype=bb σtype=bcπcountry πcountry∩Exercise 2.4.4iBattles Outcomes (battle=name)πship,result,dateρR2(ship2,result2,date2)(ship=ship2 AND result=damaged AND date < date2)πshipExercise 2.4.5The result of the natural join has only one attribute from each pair of equated attributes. On the other hand, the result of the theta-join has both columns of the attributes and their values are identical.Exercise 2.4.6UnionIf we add a tuple to the arguments of the union operator, we will get all of the tuples of the original result and maybe the added tuple. If the added tuple is a duplicate tuple, then the set behavior will eliminate that tuple.Thus the union operator is monotone.IntersectionIf we add a tuple to the arguments of the intersection operator, we will get all of the tuples of the originalresult and maybe the added tuple. If the added tuple does not exist in the relation that it is added but does exist in the other relation, then the result set will include the added tuple. Thus the intersection operator is monotone.DifferenceIf we add a tuple to the arguments of the difference operator, we may not get all of the tuples of the originalresult. Suppose we have relations R and S and we are computing R – S. Suppose also that tuple t is in R but not in S. The result of R – S would include tuple t. However, if we add tuple t to S, then the new result will not have tuple t. Thus the difference operator is not monotone.ProjectionIf we add a tuple to the arguments of the projection operator, we will get all of the tuples of the original result and the projection of the added tuple. The projection operator only selects columns from the relation and does not affect the rows that are selected. Thus the projection operator is monotone.SelectionIf we add a tuple to the arguments of the selection operator, we will get all of the tuples of the original result and maybe the added tuple. If the added tuple satisfies the select condition, then it will be added to the newresult. The original tuples are included in the new result because they still satisfy the select condition. Thusthe selection operator is monotone.Cartesian ProductIf we add a tuple to the arguments of the Cartesian product operator, we will get all of the tuples of the original result and possibly additional tuples. The Cartesian product pairs the tuples of one relation with the tuples ofanother relation. Suppose that we are calculating R x S where R has m tuples and S has n tuples. If we add a tuple to R that is not already in R, then we expect the result of R x S to have (m + 1) * n tuples. Thus the Cartesianproduct operator is monotone.Natural JoinsIf we add a tuple to the arguments of a natural join operator, we will get all of the tuples of the original result and possibly additional tuples. The new tuple can only create additional successful joins, not less. If, however, the added tuple cannot successfully join with any of the existing tuples, then we will have zero additionalsuccessful joins. Thus the natural join operator is monotone.Theta JoinsIf we add a tuple to the arguments of a theta join operator, we will get all of the tuples of the original result and possibly additional tuples. The theta join can be modeled by a Cartesian product followed by a selection onsome condition. The new tuple can only create additional tuples in the result, not less. If, however, the addedtuple does not satisfy the select condition, then no additional tuples will be added to the result. Thus the theta join operator is monotone.RenamingIf we add a tuple to the arguments of a renaming operator, we will get all of the tuples of the original result and the added tuple. The renaming operator does not have any effect on whether a tuple is selected or not. In fact, the renaming operator will always return as many tuples as its argument. Thus the renaming operator is monotone.Exercise 2.4.7aIf all the tuples of R and S are different, then the union has n + m tuples, and this number is the maximum possible.The minimum number of tuples that can appear in the result occurs if every tuple of one relation also appears in the other. Then the union has max(m , n) tuples.Exercise 2.4.7bIf all the tuples in one relation can pair successfully with all the tuples in the other relation, then the natural join has n * m tuples. This number would be the maximum possible.The minimum number of tuples that can appear in the result occurs if none of the tuples of one relation can pairsuccessfully with all the tuples in the other relation. Then the natural join has zero tuples.Exercise 2.4.7cIf the condition C brings back all the tuples of R, then the cross product will contain n * m tuples. This number would be the maximum possible.The minimum number of tuples that can appear in the result occurs if the condition C brings back none of the tuples of R. Then the cross product has zero tuples.Exercise 2.4.7dAssuming that the list of attributes L makes the resulting relation πL(R) and relation S schema compatible, then the maximum possible tuples is n. This happens when all of the tuples of πL(R) are not in S.The minimum number of tuples that can appear in the result occurs when all of the tuples in πL(R) appear in S. Then the difference has max(n–m , 0) tuples.Exercise 2.4.8Defining r as the schema of R and s as the schema of S:1.πr(R S)2.R δ(πr∩s(S)) where δ is the duplicate-elimination operator in Section 5.2 pg. 2133.R – (R –πr(R S))Exercise 2.4.9Defining r as the schema of R1.R - πr(R S)Exercise 2.4.10πA1,A2…An(R S)Exercise 2.5.1aσspeed < 2.00 AND price > 500(PC) = øModel 1011 violates this constraint.Exercise 2.5.1bσscreen < 15.4 AND hd < 100 AND price ≥ 1000(Laptop) = øModel 2004 violates the constraint.Exercise 2.5.1cπmaker(σtype = laptop(Product)) ∩ πmaker(σtype = pc(Product)) = øManufacturers A,B,E violate the constraint.Exercise 2.5.1dThis complex expression is best seen as a sequence of steps in which we define temporary relations R1 through R4 that stand for nodes of expression trees. Here is the sequence:R1(maker, model, speed) := πmaker,model,speed(Product PC)R2(maker, speed) := πmaker,speed(Product Laptop)R3(model) := πmodel(R1 R1.maker = R2.maker AND R1.speed ≤ R2.speed R2)R4(model) := πmodel(PC)The constraint is R4 ⊆ R3Manufacturers B,C,D violate the constraint.Exercise 2.5.1eπmodel(σLaptop.ram > PC.ram AND Laptop.price ≤ PC.price(PC × Laptop)) = øModels 2002,2006,2008 violate the constraint.Exercise 2.5.2aπclass(σbore > 16(Classes)) = øThe Yamato class violates the constraint.Exercise 2.5.2bπclass(σnumGuns > 9 AND bore > 14(Classes)) = øNo violations to the constraint.Exercise 2.5.2cThis complex expression is best seen as a sequence of steps in which we define temporary relations R1 through R5 that stand for nodes of expression trees. Here is the sequence:R1(class,name) := πclass,name(Classes Ships)R2(class2,name2) := ρR2(class2,name2)(R1)R3(class3,name3) := ρR3(class3,name3)(R1)R4(class,name,class2,name2) := R1 (class = class2 AND name <> name2) R2R5(class,name,class2,name2,class3,name3) := R4 (class=class3 AND name <> name3 AND name2 <> name3) R3The constraint is R5 = øThe Kongo, Iowa and Revenge classes violate the constraint.Exercise 2.5.2dπcountry(σtype = bb(Classes)) ∩ πcountry(σtype = bc(Classes)) = øJapan and Gt. Britain violate the constraint.Exercise 2.5.2eThis complex expression is best seen as a sequence of steps in which we define temporary relations R1 through R5 that stand for nodes of expression trees. Here is the sequence:R1(ship,bat tle,result,class) := πship,battle,result,class(Outcomes (ship = name) Ships)R2(ship,battle,result,numGuns) := πship,battle,result,numGuns(R1 Classes)R3(ship,battle) := πship,battle(σnumGuns < 9 AND result = sunk (R2))R4(ship2,battle2) := ρR4(ship2,battle2)(πship,battle(σnumGuns > 9(R2)))R5(ship2) := πship2(R3 (battle = battle2) R4)The constraint is R5 = øNo violations to the constraint. Since there are some ships in the Outcomes table that are not in the Ships table, we are unable to determine the number of guns on that ship.Exercise 2.5.3Defining r as the schema A1,A2,…,A n and s as the schema B1,B2,…,B n:πr(R) πs(S) = øwhere is the antisemijoinExercise 2.5.4The form of a constraint as E1 = E2 can be expressed as the other two constraints.Using the “equating an expression to the empty set” method, we can simply say:E1– E2 = øAs a containment, we can simply say:E1⊆ E2 AND E2⊆ E1Thus, the form E1 = E2 of a constraint cannot express more than the two other forms discussed in this section.。
数据库系统原理教程习题答案第2章习题

第2章关系数据库1 .试述关系模型的三个组成部分。
答:关系模型由关系数据结构、关系操作集合和关系完整性约束三部分组成。
2 .试述关系数据语言的特点和分类。
答:关系数据语言可以分为三类:关系代数语言。
关系演算语言:元组关系演算语言和域关系演算语言。
SQL:具有关系代数和关系演算双重特点的语言。
这些关系数据语言的共同特点是,语言具有完备的表达能力,是非过程化的集合操作语言,功能强,能够嵌入高级语言中使用。
4 .试述关系模型的完整性规则。
在参照完整性中,为什么外部码属性的值也可以为空?什么情况下才可以为空?答:实体完整性规则是指若属性A是基本关系R的主属性,则属性A不能取空值。
若属性(或属性组)F是基本关系R的外码,它与基本关系S的主码Ks相对应(基本关系R和S不一定是不同的关系),则对于R中每个元组在F上的值必须为:或者取空值(F的每个属性值均为空值);或者等于S中某个元组的主码值。
即属性F本身不是主属性,则可以取空值,否则不能取空值。
5.设有一个SPJ数据库,包括S,P,J,SPJ四个关系模式:1)求供应工程J1零件的供应商号码SNO:πSno(σSno=‘J1’(SPJ))2)求供应工程J1零件P1的供应商号码SNO:πSno(σSno=‘J1’∧Pno=‘P1‘(SPJ))3)求供应工程J1零件为红色的供应商号码SNO:πSno(σPno=‘P1‘(σCOLOR=’红‘(P)∞SPJ))4)求没有使用天津供应商生产的红色零件的工程号JNO:πJno(SPJ)- πJNO(σcity=‘天津’∧Color=‘红‘(S∞SPJ∞P)5)求至少用了供应商S1所供应的全部零件的工程号JNO:πJno,Pno(SPJ)÷πPno(σSno=‘S1‘(SPJ))6.试述等值连接与自然连接的区别和联系。
答:连接运算符是“=”的连接运算称为等值连接。
它是从关系R与S的广义笛卡尔积中选取A,B属性值相等的那些元组自然连接是一种特殊的等值连接,它要求两个关系中进行比较的分量必须是相同的属性组,并且在结果中把重复的属性列去掉。
数据库系统教程课后答案(施伯乐)(第二版)

目录第1部分课程的教与学第2部分各章习题解答及自测题第1章数据库概论1.1 基本内容分析1.2 教材中习题1的解答1.3 自测题1.4 自测题答案第2章关系模型和关系运算理论2.1基本内容分析2.2 教材中习题2的解答2.3 自测题2.4 自测题答案第3章关系数据库语言SQL3.1基本内容分析3.2 教材中习题3的解答3.3 自测题3.4 自测题答案第4章关系数据库的规范化设计4.1基本内容分析4.2 教材中习题4的解答4.3 自测题4.4 自测题答案第5章数据库设计与ER模型5.1基本内容分析5.2 教材中习题5的解答5.3 自测题5.4 自测题答案第6章数据库的存储结构6.1基本内容分析6.2 教材中习题6的解答第7章系统实现技术7.1基本内容分析7.2 教材中习题7的解答7.3 自测题7.4 自测题答案第8章对象数据库系统8.1基本内容分析8.2 教材中习题8的解答8.3 自测题8.4 自测题答案第9章分布式数据库系统9.1基本内容分析9.2 教材中习题9的解答9.3 自测题9.4 自测题答案第10章中间件技术10.1基本内容分析10.2 教材中习题10的解答10.3 自测题及答案第11章数据库与WWW11.1基本内容分析11.2 教材中习题11的解答第12章 XML技术12.1基本内容分析12.2 教材中习题12的解答学习推荐书目1.国内出版的数据库教材(1)施伯乐,丁宝康,汪卫. 数据库系统教程(第2版). 北京:高等教育出版社,2003(2)丁宝康,董健全. 数据库实用教程(第2版). 北京:清华大学出版社,2003(3)施伯乐,丁宝康. 数据库技术. 北京:科学出版社,2002(4)王能斌. 数据库系统教程(上、下册). 北京:电子工业出版社,2002(5)闪四清. 数据库系统原理与应用教程. 北京:清华大学出版社,2001(6)萨师煊,王珊. 数据库系统概论(第3版). 北京:高等教育出版社,2000(7)庄成三,洪玫,杨秋辉. 数据库系统原理及其应用. 北京:电子工业出版社,20002.出版的国外数据库教材(中文版或影印版)(1)Silberschatz A,Korth H F,Sudarshan S. 数据库系统概念(第4版). 杨冬青,唐世渭等译. 北京:机械工业出版社,2003(2)Elmasri R A,Navathe S B. 数据库系统基础(第3版). 邵佩英,张坤龙等译. 北京:人民邮电出版社,2002(3)Lewis P M,Bernstein A,Kifer M. Databases and Transaction Processing:An Application-Oriented Approach, Addison-Wesley, 2002(影印版, 北京:高等教育出版社;中文版,施伯乐等译,即将由电子工业出版社出版)(4)Hoffer J A,Prescott M B,McFadden F R. Modern Database Management. 6th ed. Prentice Hall, 2002(中文版,施伯乐等译,即将由电子工业出版社出版)3.上机实习教材(1)廖疆星,张艳钗,肖金星. PowerBuilder 8.0 & SQL Server 2000数据库管理系统管理与实现. 北京:冶金工业出版社,2002(2)伍俊良. PowerBuilder课程设计与系统开发案例. 北京:清华大学出版社,20034.学习指导书(1)丁宝康,董健全,汪卫,曾宇昆. 数据库系统教程习题解答及上机指导. 北京:高等教育出版社,2003(2)丁宝康,张守志,严勇. 数据库技术学习指导书. 北京:科学出版社,2003(3)丁宝康,董健全,曾宇昆. 数据库实用教程习题解答. 北京:清华大学出版社,2003 (4)丁宝康. 数据库原理题典. 长春:吉林大学出版社,2002(5)丁宝康,陈坚,许建军,楼晓鸿. 数据库原理辅导与练习. 北京:经济科学出版社,2001第1部分课程的教与学1.课程性质与设置目的现在,数据库已是信息化社会中信息资源与开发利用的基础,因而数据库是计算机教育的一门重要课程,是高等院校计算机和信息类专业的一门专业基础课。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Exercise 2.2.1aFor relation Accounts, the attributes are:acctNo, type, balanceFor relation Customers, the attributes are:firstName, lastName, idNo, accountExercise 2.2.1bFor relation Accounts, the tuples are:(12345, savings, 12000),(23456, checking, 1000),(34567, savings, 25)For relation Customers, the tuples are:(Robbie, Banks, 901-222, 12345),(Lena, Hand, 805-333, 12345),(Lena, Hand, 805-333, 23456)Exercise 2.2.1cFor relation Accounts and the first tuple, the components are: 123456 → acctNosavings → type12000 → balanceFor relation Customers and the first tuple, the components are: Robbie → firstNameBanks → lastName901-222 → idNo12345 → accountExercise 2.2.1dFor relation Accounts, a relation schema is:Accounts(acctNo, type, balance)For relation Customers, a relation schema is:Customers(firstName, lastName, idNo, account) Exercise 2.2.1eAn example database schema is:Accounts (acctNo,type,balance)Customers (firstName,lastName,idNo,account)Exercise 2.2.1fA suitable domain for each attribute:acctNo → Integertype → Stringbalance → IntegerfirstName → StringlastName → StringidNo → String (because there is a hyphen we cannot use Integer)account → IntegerExercise 2.2.1gAnother equivalent way to present the Account relation:Another equivalent way to present the Customers relation:Exercise 2.2.2Examples of attributes that are created for primarily serving as keys in a relation:Universal Product Code (UPC) used widely in United States and Canada to track products in stores.Serial Numbers on a wide variety of products to allow the manufacturer to individually track each product.Vehicle Identification Numbers (VIN), a unique serial number used by the automotive industry to identify vehicles.Exercise 2.2.3aWe can order the three tuples in any of 3! = 6 ways. Also, the columns can be ordered in any of 3! = 6 ways. Thus, the number of presentations is 6*6 = 36. Exercise 2.2.3bWe can order the three tuples in any of 5! = 120 ways. Also, the columns can be ordered in any of 4! = 24 ways. Thus, the number of presentations is120*24 = 2880Exercise 2.2.3cWe can order the three tuples in any of m! ways. Also, the columns can be ordered in any of n! ways. Thus, the number of presentations is n!m!Exercise 2.3.1aCREATE TABLE Product (maker CHAR(30),model CHAR(10) PRIMARY KEY,type CHAR(15));Exercise 2.3.1bCREATE TABLE PC (model CHAR(30),speed DECIMAL(4,2),ram INTEGER,hd INTEGER,price DECIMAL(7,2));Exercise 2.3.1cCREATE TABLE Laptop (model CHAR(30),speed DECIMAL(4,2),ram INTEGER,hd INTEGER,screen DECIMAL(3,1),price DECIMAL(7,2));Exercise 2.3.1dCREATE TABLE Printer (model CHAR(30),color BOOLEAN,type CHAR (10),price DECIMAL(7,2));Exercise 2.3.1eALTER TABLE Printer DROP color;Exercise 2.3.1fALTER TABLE Laptop ADD od CHAR (10) DEFAULT ‘none’; Exercise 2.3.2aCREATE TABLE Classes (class CHAR(20),type CHAR(5),country CHAR(20),numGuns INTEGER,bore DECIMAL(3,1),displacement INTEGER);Exercise 2.3.2bCREATE TABLE Ships (name CHAR(30),class CHAR(20),launched INTEGER);Exercise 2.3.2cCREATE TABLE Battles (name CHAR(30),date DATE);Exercise 2.3.2dCREATE TABLE Outcomes (ship CHAR(30),battle CHAR(30),result CHAR(10));Exercise 2.3.2eALTER TABLE Classes DROP bore;Exercise 2.3.2fALTER TABLE Ships ADD yard CHAR(30);Exercise 2.4.1aR1 := σspeed ≥ 3.00 (PC)R2 := πmodel(R1)model100510061013Exercise 2.4.1bR1 := σhd ≥ 100 (Laptop)R2 := Product (R1)R3 := πmaker (R2)makerEABFGExercise 2.4.1cR1 := σmaker=B (Product PC)R2 := σmaker=B (Product Laptop)R3 := σmaker=B (Product Printer)R4 := πmodel,price (R1)R5 := πmodel,price (R2)R6: = πmodel,price (R3)R7 := R4 R5 R6model price1004 6491005 6301006 10492007 1429Exercise 2.4.1dR1 := σcolor = true AND type = laser (Printer)R2 := πmodel (R1)model30033007Exercise 2.4.1eR1 := σtype=laptop (Product)R2 := σtype=PC(Product)R3 := πmaker(R1)R4 := πmaker(R2)R5 := R3 – R4makerFGExercise 2.4.1fR1 := ρPC1(PC)R2 := ρPC2(PC)R3 := R1 (PC1.hd = PC2.hd AND PC1.model <> PC2.model) R2R4 := πhd(R3)hd25080160Exercise 2.4.1gR1 := ρPC1(PC)R2 := ρPC2(PC)R3 := R1 (PC1.speed = PC2.speed AND PC1.ram = PC2.ram AND PC1.model < PC2.model) R2R4 := πPC1.model,PC2.model(R3)PC1.model PC2.model1004 1012Exercise 2.4.1hR1 := πmodel(σspeed ≥ 2.80(PC)) πmodel(σspeed ≥ 2.80(Laptop))R2 := πmaker,model(R1 Product)R3 := ρR3(maker2,model2)(R2)R4 := R2 (maker = maker2 AND model <> model2) R3R5 := πmaker(R4)makerBEExercise 2.4.1iR1 := πmodel,speed(PC)R2 := πmodel,speed(Laptop)R3 := R1 R2R4 := ρR4(model2,speed2)(R3)R5 := πmodel,speed (R3 (speed < speed2 ) R4)R6 := R3 – R5R7 := πmaker(R6 Product)makerBExercise 2.4.1jR1 := πmaker,speed(Product PC)R2 := ρR2(maker2,speed2)(R1)R3 := ρR3(maker3,speed3)(R1)R4 := R1 (maker = maker2 AND speed <> speed2) R2R5 := R4 (maker3 = maker AND speed3 <> speed2 AND speed3 <> speed) R3R6 := πmaker(R5)makerADEExercise 2.4.1kR1 := πmaker,model(Product PC)R2 := ρR2(maker2,model2)(R1)R3 := ρR3(maker3,model3)(R1)R4 := ρR4(maker4,model4)(R1)R5 := R1 (maker = maker2 AND model <> model2) R2R6 := R3 (maker3 = maker AND model3 <> model2 AND model3 <> model) R5R7 := R4 (maker4 = maker AND (model4=model OR model4=model2 OR model4=model3)) R6R8 := πmaker(R7)makerABDEExercise 2.4.2aπmodelσspeed≥3.00PCExercise 2.4.2bLaptopσhd ≥ 100 ProductmakerExercise 2.4.2cσmaker=B πmodel,price σmaker=B πmodel,price σmaker=B πmodel,priceProduct PC Laptop Printer ProductProductExercise 2.4.2d Printerσcolor = true AND type = laserπmodelExercise 2.4.2eσtype=laptopσtype=PC πmakerπmaker ProductProductExercise 2.4.2fρPC1ρPC2 (PC1.hd = PC2.hd AND PC1.model <> PC2.model)πhdPC PCExercise 2.4.2gρPC1ρPC2PC PC(PC1.speed = PC2.speed AND PC1.ram = PC2.ram AND PC1.model < PC2.model)πPC1.model,PC2.modelExercise 2.4.2hPC Laptop σspeed ≥ 2.80σspeed ≥ 2.80πmodelπmodel Productπmaker,modelρR3(maker2,model2)(maker = maker2 AND model <> model2)makerExercise 2.4.2iPCLaptopProductπmodel,speed πmodel,speed ρR4(model2,speed2)πmodel,speed(speed < speed2 )–makerExercise 2.4.2jProduct PC πmaker,speed ρR3(maker3,speed3)ρR2(maker2,speed2)(maker = maker2 AND speed <> speed2)(maker3 = maker AND speed3 <> speed2 AND speed3 <> speed)makerExercise 2.4.2kπmaker(maker4 = maker AND (model4=model OR model4=model2 OR model4=model3)) (maker3 = maker AND model3 <> model2 AND model3 <> model)(maker = maker2 AND model <> model2)ρR2(maker2,model2)ρR3(maker3,model3)ρR4(maker4,model4)πmaker,modelProduct PCExercise 2.4.3aR1 := σbore ≥ 16 (Classes)R2 := πclass,country (R1)Exercise 2.4.3bR1 := σlaunched < 1921 (Ships)R2 := πname (R1)RamilliesRenownRepulseResolutionRevengeRoyal OakRoyal SovereignTennesseeExercise 2.4.3cR1 := σbattle=Denmark Strait AND result=sunk(Outcomes)R2 := πship (R1)shipBismarckHoodExercise 2.4.3dR1 := Classes ShipsR2 := σlaunched > 1921 AND displacement > 35000 (R1)R3 := πname (R2)nameIowaMissouriMusashiNew JerseyNorth CarolinaWashingtonWisconsinYamatoExercise 2.4.3eR1 := σbattle=Guadalcanal(Outcomes)R2 := Ships (ship=name) R1R3 := Classes R2R4 := πname,displacement,numGuns(R3)name displacement numGuns Kirishima 32000 8Washington 37000 9Exercise 2.4.3fR1 := πname(Ships)R2 := πship(Outcomes)R3 := ρR3(name)(R2)R4 := R1 R3nameCaliforniaHarunaHieiIowaKirishimaKongoMissouriMusashiNew JerseyNorth CarolinaRamilliesRenownRepulseResolutionRevengeRoyal OakRoyal SovereignTennesseeWashingtonExercise 2.4.3gFrom 2.3.2, assuming that every class has one ship named after the class.R1 := πclass (Classes) R2 := πclass (σname <> class (Ships)) R3 := R1 – R2Exercise 2.4.3hR1 := πcountry (σtype=bb (Classes))R2 := πcountry (σtype=bc (Classes))R3 := R1 ∩ R2Exercise 2.4.3iR1 := πship,result,date (Battles (battle=name) Outcomes)R2 := ρR2(ship2,result2,date2)(R1)R3 := R1 (ship=ship2 AND result=damaged AND date < date2) R2R4 := πship (R3)No results from sample data.Exercise 2.4.4aσbore ≥ 16πclass,country ClassesExercise 2.4.4bσlaunched < 1921πname ShipsExercise 2.4.4cWisconsin Yamato Arizona Bismarck Duke of York Fuso Hood King George V Prince of Wales Rodney Scharnhorst South Dakota West Virginia Yamashiro class Bismarck countryJapan Gt. BritainOutcomesπshipσbattle=Denmark Strait AND result=sunkExercise 2.4.4dClasses Ships σlaunched > 1921 AND displacement > 35000πnameExercise 2.4.4e σbattle=Guadalcanal Outcomes ShipsClasses(ship=name)πname,displacement,numGunsExercise 2.4.4fShipsOutcomesπnameπship ρR3(name)Exercise 2.4.4g ClassesShips πclass σname <> class πclass –Exercise 2.4.4hClasses Classesσtype=bb σtype=bcπcountry πcountry∩Exercise 2.4.4iπship(ship=ship2 AND result=damaged AND date < date2)ρR2(ship2,result2,date2)πship,result,date(battle=name)Battles OutcomesExercise 2.4.5The result of the natural join has only one attribute from each pair of equated attributes. On the other hand, the result of the theta-join has both columns of the attributes and their values are identical.Exercise 2.4.6UnionIf we add a tuple to the arguments of the union operator, we will get all of the tuples of the original result and maybe the added tuple. If theadded tuple is a duplicate tuple, then the set behavior will eliminate that tuple. Thus the union operator is monotone.IntersectionIf we add a tuple to the arguments of the intersection operator, we will get all of the tuples of the original result and maybe the added tuple. If the added tuple does not exist in the relation that it is added but does exist in the other relation, then the result set will include the added tuple.Thus the intersection operator is monotone.DifferenceIf we add a tuple to the arguments of the difference operator, we may not get all of the tuples of the original result. Suppose we have relations R and S and we are computing R – S. Suppose also that tuple t is in R but not in S. The result of R – S would include tuple t. However, if we add tuple t to S, then the new result will not have tuple t. Thus the difference operator is not monotone.ProjectionIf we add a tuple to the arguments of the projection operator, we will get all of the tuples of the original result and the projection of the added tuple. The projection operator only selects columns from the relation and does not affect the rows that are selected. Thus the projection operator is monotone.SelectionIf we add a tuple to the arguments of the selection operator, we will get all of the tuples of the original result and maybe the added tuple. If the added tuple satisfies the select condition, then it will be added to the new result. The original tuples are included in the new result because they still satisfy the select condition. Thus the selection operator is monotone.Cartesian ProductIf we add a tuple to the arguments of the Cartesian product operator, we will get all of the tuples of the original result and possibly additional tuples. The Cartesian product pairs the tuples of one relation with the tuples of another relation. Suppose that we are calculating R x S where R has m tuples and S has n tuples. If we add a tuple to R that is not already in R, then we expect the result of R x S to have (m + 1) * n tuples.Thus the Cartesian product operator is monotone.Natural JoinsIf we add a tuple to the arguments of a natural join operator, we will get all of the tuples of the original result and possibly additional tuples.The new tuple can only create additional successful joins, not less. If, however, the added tuple cannot successfully join with any of theexisting tuples, then we will have zero additional successful joins. Thus the natural join operator is monotone.Theta JoinsIf we add a tuple to the arguments of a theta join operator, we will get all of the tuples of the original result and possibly additional tuples. The theta join can be modeled by a Cartesian product followed by a selection on some condition. The new tuple can only create additional tuples in the result, not less. If, however, the added tuple does not satisfy the select condition, then no additional tuples will be added to the result. Thus the theta join operator is monotone.RenamingIf we add a tuple to the arguments of a renaming operator, we will get all of the tuples of the original result and the added tuple. The renaming operator does not have any effect on whether a tuple is selected or not. In fact, the renaming operator will always return as many tuples as its argument. Thus the renaming operator is monotone.Exercise 2.4.7aIf all the tuples of R and S are different, then the union has n + m tuples, and this number is the maximum possible.The minimum number of tuples that can appear in the result occurs if every tuple of one relation also appears in the other. Then the union has max(m , n) tuples.Exercise 2.4.7bIf all the tuples in one relation can pair successfully with all the tuples in the other relation, then the natural join has n * m tuples. This number would be the maximum possible.The minimum number of tuples that can appear in the result occurs if none of the tuples of one relation can pair successfully with all the tuples in the other relation. Then the natural join has zero tuples.Exercise 2.4.7cIf the condition C brings back all the tuples of R, then the cross product will contain n * m tuples. This number would be the maximum possible.The minimum number of tuples that can appear in the result occurs if the condition C brings back none of the tuples of R. Then the cross product has zero tuples.Exercise 2.4.7dAssuming that the list of attributes L makes the resulting relation πL(R) and relation S schema compatible, then the maximum possible tuples is n. This happens when all of the tuples of πL(R) are not in S.The minimum number of tuples that can appear in the result occurs when all of the tuples in πL(R) appear in S. Then the difference has max(n–m , 0) tuples.Exercise 2.4.8Defining r as the schema of R and s as the schema of S:1.πr(R S)2.R δ(πr∩s(S)) where δ is the duplicate-elimination operator in Section 5.2 pg. 2133.R – (R –πr(R S))Exercise 2.4.9Defining r as the schema of R1.R - πr(R S)Exercise 2.4.10πA1,A2…An(R S)Exercise 2.5.1aσspeed < 2.00 AND price > 500(PC) = øModel 1011 violates this constraint.Exercise 2.5.1bσscreen < 15.4 AND hd < 100 AND price ≥ 1000(Laptop) = øModel 2004 violates the constraint.Exercise 2.5.1cπmaker(σtype = laptop(Product)) ∩ πmaker(σtype = pc(Product)) = øManufacturers A,B,E violate the constraint.Exercise 2.5.1dThis complex expression is best seen as a sequence of steps in which we define temporary relations R1 through R4 that stand for nodes of expression trees. Here is the sequence:R1(maker, model, speed) := πmaker,model,speed(Product PC)R2(maker, speed) := πmaker,speed(Product Laptop)R3(model) := πmodel(R1 R1.maker = R2.maker AND R1.speed ≤ R2.speed R2)R4(model) := πmodel(PC)The constraint is R4 ⊆ R3Manufacturers B,C,D violate the constraint.Exercise 2.5.1eπmodel(σLaptop.ram > PC.ram AND Laptop.price ≤ PC.price(PC × Laptop)) = øModels 2002,2006,2008 violate the constraint.Exercise 2.5.2aπclass(σbore > 16(Classes)) = øThe Yamato class violates the constraint.Exercise 2.5.2bπclass(σnumGuns > 9 AND bore > 14(Classes)) = øNo violations to the constraint.Exercise 2.5.2cThis complex expression is best seen as a sequence of steps in which we define temporary relations R1 through R5 that stand for nodes of expression trees. Here is the sequence:R1(class,name) := πclass,name(Classes Ships)R2(class2,name2) := ρR2(class2,name2)(R1)R3(class3,name3) := ρR3(class3,name3)(R1)R4(class,name,class2,name2) := R1 (class = class2 AND name <> name2) R2R5(class,name,class2,name2,class3,name3) := R4 (class=class3 AND name <> name3 AND name2 <> name3) R3The constraint is R5 = øThe Kongo, Iowa and Revenge classes violate the constraint.Exercise 2.5.2dπcountry(σtype = bb(Classes)) ∩ πcountry(σtype = bc(Classes)) = øJapan and Gt. Britain violate the constraint.Exercise 2.5.2eThis complex expression is best seen as a sequence of steps in which we define temporary relations R1 through R5 that stand for nodes of expression trees. Here is the sequence:R1(ship,battle,result,class) := πship,battle,result,class(Outcomes (ship = name) Ships)R2(ship,battle,result,numGuns) := πship,battle,result,numGuns(R1 Classes)R3(ship,battle) := πship,battle(σnumGuns < 9 AND result = sunk (R2))R4(ship2,battle2) := ρR4(ship2,battle2)(πship,battle(σnumGuns > 9(R2)))R5(ship2) := πship2(R3 (battle = battle2) R4)The constraint is R5 = øNo violations to the constraint. Since there are some ships in the Outcomes table that are not in the Ships table, we are unable to determine the number of guns on that ship.Exercise 2.5.3Defining r as the schema A1,A2,…,A n and s as the schema B1,B2,…,B n:πr(R) πs(S) = øwhere is the antisemijoinExercise 2.5.4The form of a constraint as E1 = E2 can be expressed as the other two constraints.Using the “equating an expression to the empty set” method, we can simply say:E1– E2 = øAs a containment, we can simply say:E1⊆ E2 AND E2⊆ E1Thus, the form E1 = E2 of a constraint cannot express more than the two other forms discussed in this section.。
